Generalization of the mixed-space cluster expansion method for arbitrary lattices

Abstract

Mixed-space cluster expansion (MSCE), a first-principles method to simultaneously model the configuration-dependent short-ranged chemical and long-ranged strain interactions in alloy thermodynamics, has been successfully applied to binary FCC and BCC alloys. However, the previously reported MSCE method is limited to binary alloys with cubic crystal symmetry on a single sublattice. In the current work, MSCE is generalized to systems with multiple sublattices by formulating compatible reciprocal space interactions and combined with a crystal-symmetry-agnostic algorithm for the calculation of constituent strain energy. This generalized approach is then demonstrated in a hypothetical HCP system and Mg-Zn alloys. The current MSCE can significantly improve the accuracy of the energy parameterization and account for all the fully relaxed structures regardless of lattice distortion. The generalized MSCE method makes it possible to simultaneously analyze the short- and long-ranged configuration-dependent interactions in crystalline materials with arbitrary lattices with the accuracy of typical first-principles methods.

Introduction

The site occupation of atoms on parent lattice determines the thermodynamic interaction, and thus the variation of the site occupation gives rise to the configurational degrees of freedom for alloy thermodynamics^1,2,3,4,5,6. The equilibration from disordered state to thermodynamically favored alloy configurations give rise to short-, long-ranged ordering or clustering, all of which are closely related to the phase stability and physical, chemical and mechanical properties of materials.

It has been proven that, for an $m$ component system on a lattice of $N$ sites, the total energy of ${m}^{N}$ possible configurations can be exactly mapped onto a generalized Ising model based on the energetic contributions of atomic clusters on parent lattice⁷. With the popularization of first-principles total energy calculations based on density functional theory (DFT)^8,9, the energetic contributions of atomic clusters, or effective cluster interactions (ECIs), can be obtained given the total energies of a few coherent structures¹⁰. This method is commonly known as cluster expansion (CE)^4,5,11. In theory, infinite number of clusters and ECIs are needed to exactly map the energy of ordering structures for any nonlinear dependence¹². In practice, applications of CE to wide varieties of materials show that the energy of ordering structures can be parameterized with adequate accuracy using relatively simple clusters (e.g., pairs, triplets, and quadruplets) with small diameters (i.e., largest two-site distance in a cluster). In addition, only a small number of energies for coherent structures with small unit cell (~10 atoms) are required in the training set of CE¹¹.

In materials, long-ranged interactions, other than short-ranged chemical interactions, may play important roles in phase stability and morphology. In some size-mismatched systems, the displacement field due to relaxation decay slowly along particular directions, leading to long-ranged strain interactions^13,14. Such long-ranged strain interactions can affect the phase stability and shape of phase diagram, hence are non-negligible for size-mismatched alloys¹⁵. Modeling such long-ranged strain interaction using DFT is proven to be challenging, as only structures with relatively small cells (up to hundreds of atoms if high accuracy is desired) can be efficiently handled. To incorporate the medium-ranged strain interactions in CE of Al-Cu system, the structures with large supercells (256 atoms) optimized by DFT are included in the training set of CE¹⁶. The practical challenges of CE with supercells in the training set arise due to the computational cost of DFT for larger structures and longer cut-off distances for clusters in CE. Energetics of large structures (e.g., hundreds of atoms) are needed to properly parameterize the magnitude and orientation dependence of the long-ranged interactions. Apart from the larger structures, longer cut-off distances for the clusters means significantly large number of clusters and the corresponding ECIs need to be included in the CE training. For any lattices, the number of symmetrically distinct clusters increases dramatically with cut-off distances; see Supplementary Fig. 1. As the cut-off distance is increased, the number of fitting parameters increases quickly and can easily exceeds the number of training structures, making the fitting process meaningless due to the infinite number of solutions for such situations. Even with large structures in the training set, cut-off distances for clusters are still needed in CE, making it incapable of modeling the long-ranged interactions¹⁴.

In order to incorporate long-ranged strain interactions in CE, Laks et al. performed the Fourier transform to the pair interaction terms in CE and obtained the interaction energy in reciprocal space (k-space) based on the static concentration wave method¹⁴. The interaction parameters in k-space are obtained based on the strain energy required for alloy constituents to maintain coherency in the epitaxial configuration, which is termed constituent strain energy (CSE). Such formulation corresponds to the ${{\rm{A}}}_{q}{{\rm{B}}}_{q}$ type ordering in the long-periodicity limit ($q\to \infty$). Further incorporating the attenuation for medium-ranged interactions¹⁷, the CSE captures the strain interactions beyond the cut-off distance in real space (r-space) CE (e.g., ~15 Å). This method is called mixed-space cluster expansion (MSCE)^18,19,20, since the short- and long-ranged interactions are modeled in r- and k-space, respectively. The name mixed-basis cluster expansion is also adopted in some papers^21,22,23. The MSCE has been applied to many systems, i.e., Ga_1-xIn_xP^14,24,25, Cu-Pd^24,26, Cu-Au^20,27,28, Cu-Ag^20,27,28, Ni-Au^20,27,28, Ag-Pd²⁹, Al-Cu^19,30, Al-Zn^19,31, Al-Mg¹⁸, Ga_1-xIn_xN^21,32 alloys on FCC lattice and Mo-Ta²², V-Nb³³, V-Ta³³, and Nb-Ta³³ alloys on BCC lattice. Note that the calculations for Ga_1-xIn_xP or Ga_1-xIn_xN are essentially binary, since only the sites for Ga or In in Ga_1-xIn_xP or Ga_1-xIn_xN are subjected to change of occupations.

The application of MSCE is scarce in recent years. In the original publication¹⁴, the k-space energy was formulated for the case of single sublattice and the method for the orientation dependence of CSE was designed for cubic systems with harmonic elastic response. The algorithm for CSE was later generalized to the case of anharmonic elastic response due to large lattice mismatches^27,28,34 and hexagonal systems^35,36. In the current work, the theory of MSCE is extended to systems with multiple sublattices and combined with a crystal-symmetry-agnostic algorithm for CSE. The generalized CSE is applied to Mg-Zn alloy and accurate parameterization of the formation energies is achieved.

Methods

Formulation of k-space pair interactions for multiple sublattices

The convergence of r-space CE becomes very challenging when the long-ranged interaction is strong in the system^13,14. Although some medium-ranged components of interactions can be incorporated in r-space CE to some extent using larger structures in training sets¹⁶, the long-ranged interactions beyond the cut-off distance and its long periodicity limit cannot be correctly incorporated. To resolve this issue, the MSCE approach was proposed to simultaneously consider the configuration-dependent short- and long-ranged interactions, including the long periodicity limit¹⁴. In MSCE, the long-ranged interaction is reformulated in k-space and can be solved over a few k-points in the first Brillouin zone (BZ) of the parent lattice, as long as the alloy configuration follows periodic boundary conditions.

Previous formulation by Laks et al. was derived for phases with a single sublattices¹⁴, i.e., only one atom corresponds to each Bravais lattice site. In general, there can be multiple atoms in the basis of each lattice site and, in this case, the crystallography is usually described by multiple interpenetrating simple Bravais lattices, i.e., multiple sublattices. For a crystalline structure with multiple sublattices, the Fourier transform of the spin variable (i.e., the structural factor) follows^37,38,

$${S}_{{\bf{k}},m}\left(\sigma \right)=\frac{1}{N}\mathop{\sum }\limits_{l=1}^{N}{S}_{l,m}\left(\sigma \right)\cdot {e}^{-i{\bf{k}}{\cdot }{{\bf{R}}}_{l}}$$

(1)

where $N$ is the number of primitive cells of the parent lattice in the crystal (or the number of basis), $v$ is the number of sublattices (the number of atoms in the primitive cell or in the basis of the parent lattice), ${{\bf{R}}}_{l}$ denotes the coordinate of the origin of the l-th primitive cell in the structure and $m$ is the index for the m-th atom in the basis of the primitive cell. Following Eq. (1), the inverse Fourier transform is,

$${S}_{l,m}\left(\sigma \right)=\sum _{{\bf{k}}}{S}_{{\bf{k}},m}\left(\sigma \right)\cdot {e}^{+i{\bf{k}}\cdot {{\bf{R}}}_{l}}$$

(2)

Although long-ranged multi-body interactions can be important in principle, the long-ranged interaction in MSCE is formulated using only pair interactions, due to the mathematical complexity and additional physical parameters associated with multi-body interactions in k-space^1,14,38. For the case with multiple sublattices, the interaction from a pair of atoms at ${{\bf{R}}}_{i}+{{\bf{h}}}_{m}$ and ${{\bf{R}}}_{j}+{{\bf{h}}}_{n}$ follow,

$$\begin{array}{c}{E}_{2}(\sigma )=\frac{1}{2}\mathop{\sum}\limits_{i,j}\mathop{\sum}\limits_{m,n}{J}_{m,n}({{\bf{R}}}_{i},{{\bf{R}}}_{j})\cdot {S}_{i,m}(\sigma )\cdot {S}_{j,n}(\sigma )\\ =\frac{1}{2}\mathop{\sum}\limits_{i,j}{\tilde{S}}_{i}^{T}(\sigma )\cdot \tilde{J}({{\bf{R}}}_{j}-{{\bf{R}}}_{i})\cdot {\tilde{S}}_{j}(\sigma )\end{array}$$

(3)

where $i$ and $j$ run over the basis and $m$ and $n$ run over the sublattices. ${J}_{m,n}\left({{\bf{R}}}_{i},{{\bf{R}}}_{j}\right)={J}_{m,n}\left({{{\bf{R}}}_{j}{\boldsymbol{-}}{\bf{R}}}_{i}\right)$ is the pair interaction between atoms on $m$- and $n$-th sublattice. The last line in Eq. (3) gives the pair interaction in matrix form, where ${\widetilde{S}}_{i}\left(\sigma \right)$ is the column vector of the spin variables of atoms in the basis located at ${{\bf{R}}}_{i}$ and the superscript $T$ denotes transposition. $\widetilde{J}\left({{\bf{R}}}_{j}-{{\bf{R}}}_{i}\right)$ is the $v\times v$ matrix of pair ECIs. Since the spin variable must be real numbers in r-space, ${S}_{{\bf{k}},p}={S}_{-{\bf{k}},p}^{* }$ where the superscript * indicates the complex conjugate. Substitute Eq. (2) into Eq. (3) leads to the pair interaction in k-space,

$$\begin{array}{c}{E}_{2}(\sigma )=N \mathop{\sum}\limits_{{\bf{k}}} \mathop{\sum}\limits_{m,n}{S}_{{\bf{k}},m}(\sigma )\cdot {V}_{m,n}({\bf{k}})\cdot {S}_{{\bf{k}},n}^{\ast }(\sigma )\\ =N \mathop{\sum}\limits_{{\bf{k}}}{\tilde{S}}_{{\bf{k}}}^{\dagger }\cdot \tilde{V}({\bf{k}})\cdot {\tilde{S}}_{{\bf{k}}}^{\ast }\end{array}$$

(4)

where superscript $\dagger$ indicates the conjugate transpose of complex matrix, ${{\bf{R}}}_{l}={{\bf{R}}}_{j}-{{\bf{R}}}_{i}$ and ${V}_{m,n}\left({\bf{k}}\right)$ is the Fourier transform of r-space pair interaction energy,

$${V}_{m,n}\left({\bf{k}}\right)=\frac{1}{2}\sum _{l}{J}_{m,n}\left({{\bf{R}}}_{l}\right)\cdot {e}^{-i{\bf{k}}\cdot {{\bf{R}}}_{l}}$$

(5)

And ${\widetilde{S}}_{{\bf{k}}}=\frac{1}{N}\sum _{l}{\widetilde{S}}_{l}\cdot {e}^{-i{\bf{k}}\cdot {{\bf{R}}}_{l}}$ is the Fourier transform of ${\widetilde{S}}_{l}$, i.e., the column vector of the r-space spin variable corresponding to site ${{\bf{R}}}_{l}$. $\widetilde{V}\left({\bf{k}}\right)$ is the $v\times v$ matrix of the ${V}_{m,n}\left({\bf{k}}\right)$. In the derivation of Eqs. (4) and (5), the translational invariance of ${J}_{m,n}\left({{\bf{R}}}_{l}\right)$ and $\mathop{\sum}\nolimits_{j}{e}^{-i\left({\bf{k}}{{-}}{{\bf{k}}}^{{{{\prime} }}}\right)\cdot {{\bf{R}}}_{j}}=N{\delta }_{{\bf{k}}{,{\bf{k}}}^{{\prime} }}$ are used. For the case of single sublattice (i.e., $v=1$), Eqs. (1–5) reduce to the formulation by Laks et al.¹⁴. So far, Eqs. (4, 5) are equivalent to the pair interactions in r-space CE, since the Fourier transform simply gives k-space description of pair interactions. Consequently, both formulations share the convergence issue for systems with long-ranged interactions.

Long-ranged strain interactions in k-space

Besides the computational challenges due to large structures and longer cut-offs for clusters (see INTRODUCTION), the failure of the r-space CE for long-ranged interactions can also be interpreted in k-space in the long periodicity limit for compound ${A}_{q}{B}_{q}$ ($q\to \infty$)¹⁴. Non-vanishing interactions in the long periodicity limit means that the interaction is non-analytic at the origin of k-space (i.e., Γ). Since long-ranged interactions are generally orientation-dependent, they approach Γ with different values along different orientations and lead to varying magnitudes of interactions in the neighborhood of Γ. Using spherical coordinates, the value of CSE only depends on the azimuthal or polar angle of k-point, but stays constant along the radial direction^14,39,40; see RESULTS for the case in Mg-Zn alloy.

The CSE arising from the size-mismatch of alloy constituents is long-ranged in nature, and cannot be accounted for by any r-space method, where a cut-off for the interaction distance is always required. To overcome the incapability of r-space CE for long-ranged interactions, Laks et al.¹⁴ proposed MSCE to attribute the long-ranged CSE to pair clusters, separate it from the total energy and model all the pair interactions in k-space, while the non-pair cluster interactions are modeled in r-space. In this way, the calculation of pair interactions in k-space requires Fourier transform of the r-space ECIs. In the current modeling, the CSE from the long-ranged pair interactions (modeled in k-space) is explicitly separated from the relatively short-ranged pair interactions (modeled in r-space, i.e., Eq. (9)). After separating the short- and long-ranged interactions, the pair interaction follows

$$\begin{array}{c}{E}_{2}(\sigma )={E}_{2}^{{\rm{SR}}}(\sigma )+{E}_{2}^{{\rm{LR}}}(\sigma )\\ =N \mathop{\sum}\limits _{{\bf{k}}} \mathop{\sum}\limits _{m,n}{S}_{{\bf{k}},m}(\sigma )\cdot [{V}_{m,n}^{{\rm{SR}}}({\bf{k}})+{V}_{m,n}^{{\rm{LR}}}({\bf{k}})]\cdot {S}_{{\bf{k}},n}^{\ast }(\sigma )\end{array}$$

(6)

where ${V}_{m,n}^{{\rm{SR}}}\left({\bf{k}}\right)$ and ${V}_{m,n}^{{\rm{LR}}}\left({\bf{k}}\right)$ are the short- and long-ranged parts of the pair interactions in k-space. The goal of such separation is to let ${V}_{m,n}^{{\rm{LR}}}\left({\bf{k}}\right)$ contain the singularity of ${V}_{m,n}\left({\bf{k}}\right)$ at $\Gamma$, so that, after separation, ${V}_{m,n}^{{\rm{SR}}}\left({\bf{k}}\right)$ is zero at $\Gamma$ and can be handled by r-space methods with a cut-off distance. In practice, ${V}_{m,n}^{{\rm{SR}}}\left({\bf{k}}\right)$ is interpreted as the chemical interactions of pair clusters and can be obtained by the Fourier transform of the r-space pair ECIs using Eq. (5). Meanwhile ${V}_{m,n}^{{\rm{LR}}}\left({\bf{k}}\right)$ is considered as the long-ranged interactions due to the size-mismatch between alloy constituents along ${\bf{k}}$, and must be obtained independent of r-space CE. Therefore, the configuration dependent CSE follows,

$$\Delta {E}_{{\rm{CS}}}\left(\sigma \right)=N\sum _{{\bf{k}}}\sum _{m,n}{S}_{{\bf{k}},m}\left(\sigma \right)\cdot {V}_{m,n}^{{\rm{CS}}}\left({\bf{k}}\right)\cdot {S}_{{\bf{k}},n}^{* }\left(\sigma \right)$$

(7)

Once the long-ranged strain interaction parameters in k-space ${V}_{m,n}^{{\rm{CS}}}\left({\bf{k}}\right)$ are known, Eq. (7) along with the definitions of structural factors (Eqs. (1–2)) is sufficient to calculate the CSE for a given structure.

To model the strain interaction arising from size-mismatch between alloy constituent, the long-ranged interaction parameter ${V}_{m,n}^{{\rm{CS}}}\left({\bf{k}}\right)$ in Eq. (7) needs to be calculated for each pair of endmembers for the underlying lattice. For example, for a complex lattice of (A,B)₂(C,D,E)₃, there are 6 endmembers and ${V}_{m,n}^{{\rm{CS}}}\left({\bf{k}}\right)$ for 15 binary combinations of the endmembers needs to be calculated. If all the sites within the primitive cell (or the sublattices) are equivalent, ${V}_{m,n}^{{\rm{CS}}}\left({\bf{k}}\right)$ becomes independent of the sublattice on which atoms reside, i.e., ${V}_{m,n}^{{\rm{CS}}}\left({\bf{k}}\right)={V}^{{\rm{CS}}}\left({\bf{k}}\right)$, in the long-range limit. In this case, the long-ranged interaction is modeled using pairs of primitive cells, rather than pairs of atoms. This means that the long-ranged interaction energy is zero between two atoms within the same primitive cell, since long-ranged interaction is expected to have much larger length scales than the primitive cell. Therefore, the removal of the dependence on sublattice for ${V}_{m,n}^{{\rm{CS}}}\left({\bf{k}}\right)$ in the long-ranged limit is only applicable to the case where all sublattices are equivalent, which does not lead to the loss of resolution on the description of configuration dependent strain energy. Moreover, the vector connecting the origins of primitive cells, rather than the vector using the spatial positions of atomic pairs, is used for the orientation of the interaction, since the difference in between is vanishingly small for long-ranged pair interaction. Later, a method to calculate ${V}^{{\rm{CS}}}\left({\bf{k}}\right)$ for long-ranged CSE from DFT will be presented.

Anisotropic attenuation of the long-ranged interactions

Combining the r-space CE and the formulation of long-ranged interactions, the expansion formula of MSCE can be written as,

$$\begin{array}{c}{E}^{{\rm{MSCE}}}(\sigma )=N {\mathop{\sum}\limits_{{\rm{F}}}}^\prime{D}_{{\rm{F}}}{J}_{{\rm{F}}}{\mathop{{\Pi }}\limits^{-}}_{{\rm{F}}}(\sigma )+N \mathop{\sum}\limits_{{\bf{k}}}\mathop{\sum}\limits _{m,n}{S}_{{\bf{k}},m}(\sigma )\cdot {V}_{m,n}^{{\rm{SR}}}({\bf{k}})\cdot {S}_{{\bf{k}},n}^{\ast }(\sigma )\,\\ +\,N \mathop{\sum}\limits _{{\bf{k}}}\cdot {V}^{{\rm{CS}}}({\bf{k}}) \mathop{\sum}\limits_{m,n}{S}_{{\bf{k}},m}(\sigma )\cdot {S}_{{\bf{k}},n}^{\ast }(\sigma )\end{array}$$

(8)

On the right-hand-side (RHS) of Eq. (8), the first term is the r-space CE and the summation (with prime sign) runs over all the non-pair clusters. And the symmetrically equivalent clusters are grouped into a class of clusters (or figures ${\rm{F}}$), ${D}_{{\rm{F}}}$ is the number of equivalent clusters (or multiplicity) in ${\rm{F}}$, ${J}_{{\rm{F}}}$ is the corresponding ECI for the equivalent clusters in ${\rm{F}}$, ${\bar{\varPi }}_{{\rm{F}}}$ is correlation function by averaging the product of spin variables. The second term on the RHS of Eq. (8) is the chemical interaction from pairs and the third term is the CSE, both modeled in k-space.

To perform calculations using Eq. (8), Fourier transform of the r-space pair interactions is needed to obtain ${V}_{m,n}^{{\rm{SR}}}\left({\bf{k}}\right)$, as in Laks et al.¹⁴. Note that the second term on RHS of Eq. (8) is equivalent to the pair interaction in r-space CE if the derivation in Eqs. (4) and (5) is inversed. In this way, the expansion of configuration-dependent energy using MSCE follows,

$${E}^{{\rm{MSCE}}}\left(\sigma \right)=N\mathop{\sum}\limits_{{\rm{F}}}{D}_{{\rm{F}}}{J}_{{\rm{F}}}{\bar{\varPi }}_{{\rm{F}}}\left(\sigma \right)+N\sum _{{\bf{k}}}{V}^{{\rm{CS}}}\left({\bf{k}}\right)\cdot {\rm{exp }}\left[-\frac{{\left|{\bf{k}}\right|}^{2}}{{A\left({\bf{k}}\right)}^{2}}\right]\sum _{m,n}{S}_{{\bf{k}},m}\left(\sigma \right)\cdot {S}_{{\bf{k}},n}^{* }\left(\sigma \right)$$

(9)

From Eqs. (6–9), a question arises concerning the modeling of the medium-ranged interactions that are not explicitly included in r-space CE or ${V}^{{\rm{CS}}}\left({\bf{k}}\right)$, since r-space CE is short-ranged and ${V}^{{\rm{CS}}}\left({\bf{k}}\right)$ is formulated in the long periodicity limit. Analysis by Ferreira et al. showed that the CSE decays exponentially with magnitude of the major wave vector with largest $\left|{S}_{{\bf{k}}}\left(\sigma \right)\right|$, when applied to medium-ranged structures¹⁷. In the formula by Ferreira et al.¹⁷ and others that followed^18,30, it is assumed that the attenuation coefficient is orientation independent. However, it is reasonable to expect that attenuation of ${V}^{{\rm{CS}}}\left({\bf{k}}\right)$ as a function of $\left|{\bf{k}}\right|$ may vary along different orientations due to anisotropic response to long-ranged interactions. In Eq. (9), an exponential factor ${{\exp}}\left[-\frac{{\left|{\bf{k}}\right|}^{2}}{{A\left({\bf{k}}\right)}^{2}}\right]$ for the decay of ${V}^{{\rm{CS}}}\left({\bf{k}}\right)$ is added so that medium-ranged strain interactions can be modeled as well. In the current application to HCP system, the orientation-dependent decay coefficient is parameterized using $A\left({\bf{k}}\right)=\sum _{i}{c}_{i}{H}_{i}\left({\bf{k}}\right)$, where ${H}_{i}\left({\bf{k}}\right)$ is the hexagonal harmonic function and ${c}_{i}$ is the coefficient. The coefficients ${c}_{i}$ are optimized together with r-space ECI during the fitting of MSCE.

Calculation of the CSE for arbitrary mismatch and crystal symmetries

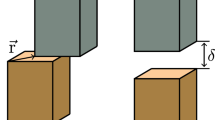
With Eqs. (7) and (9), the MSCE method is incomplete without the knowledge of the long-ranged interaction ${V}^{{\rm{CS}}}\left({\bf{k}}\right)$. In size-mismatched alloys, ${V}^{{\rm{CS}}}\left({\bf{k}}\right)$ represent the long-ranged limit of the CSE for a compound ${A}_{q}{B}_{q}$ as $q\to \infty$, in which case ${A}_{q}{B}_{q}$ becomes an epitaxial configuration as visualized in Fig. 1. Previously, the CSE from DFT were incorporated in MSCE for binary cubic systems and the anharmonic lattice response due to large lattice mismatch were analyzed comprehensively^{18,19,27,28,34}. The corresponding method is already implemented in Alloy Theoretic Automation Toolkit (ATAT)^41,42. The CSEs for HCP Mg-Ca and Mg-Y systems were calculated previously, but the details of the calculation process were not reported³⁵. Herein, a crystal-symmetry-agnostic algorithm for the calculation of CSE is detailed.

Fig. 1: Schematic illustration of the epitaxial configuration.

This schematic diagram is used to illustrate the algorithm to calculate the orientation dependence of the CSE along ${\bf{G}}$. Generally, there are two independent lattice parameters on the epitaxial plane with normal ${\bf{G}}$, i.e., ${a}_{\perp ,1}$ and ${a}_{\perp ,2}$. The lattice parameters on the epitaxial plane (${a}_{\perp ,1}$ and ${a}_{\perp ,2}$) are fixed to maintain coherency, while the lattice parameter along ${\bf{G}}$ (${a}_{\parallel }^{{\rm{A}}}$ or ${a}_{\parallel }^{{\rm{B}}}$) is free to relax.

For a given crystallographic orientation ${\bf{G}}$ (i.e., normal of the epitaxial plane), we can find two orientations perpendicular to ${\bf{G}}$, namely ${{\bf{V}}}_{1}$ and ${{\bf{V}}}_{2}$. Here ${{\bf{V}}}_{1}$ can be any vector perpendicular to ${\bf{G}}$ and ${{\bf{V}}}_{2}={\bf{G}}{{\times}}{{\bf{V}}}_{1}$. Similar to the previous calculations, the shear strain is not considered here in epitaxial deformations. Along ${{\bf{V}}}_{1}$ and ${{\bf{V}}}_{2}$, the lattice parameters on the epitaxial plane are ${a}_{\perp ,1}$ and ${a}_{\perp ,2}$, which are stretched from the end member with smaller lattice parameter to the one with larger lattice parameter. For example, if ${a}_{\perp ,1}^{{\rm{A}}}\, < \,{a}_{\perp ,1}^{{\rm{B}}}$, then ${a}_{\perp ,1}^{{\rm{A}}}\le {a}_{\perp ,1}\le {a}_{\perp ,1}^{{\rm{B}}}$. In practice, several values of ${a}_{\perp ,1}$ serve as the grid points between ${a}_{\perp ,1}^{A}$ and ${a}_{\perp ,1}^{B}$. Once the values of ${a}_{\perp ,1}$ and ${a}_{\perp ,2}$ are picked, they are kept constant while the lattice parameter along ${\bf{G}}$ for both end members, i.e., ${a}_{\parallel }^{{\rm{A}}}$ or ${a}_{\parallel }^{{\rm{B}}}$, are relaxed to minimize the energy of the distorted cell. For an end member with lattice parameters of ${a}_{\perp ,1}$, ${a}_{\perp ,2}$ and ${a}_{\parallel }$ along ${{\bf{V}}}_{1}$, ${{\bf{V}}}_{2}$ and ${\bf{G}}$, the 3 × 3 matrix for the distorted lattice vector ${{\bf{L}}}^{{\boldsymbol{{\prime} }}}$ follows,

$${{\bf{L}}}^{{\prime} }={{\bf{L}}}^{{\bf{0}}}\cdot \left[{\bf{Q}}\cdot {\bf{S}}\cdot {{\bf{Q}}}^{T}\right]$$

(10)

where ${{\bf{L}}}^{0}$ is the 3 × 3 matrix for the lattice vectors of the end members at equilibrium (defined in the same coordinate system as ${\bf{G}}$, ${{\bf{V}}}_{1}$ and ${{\bf{V}}}_{2}$), ${\bf{S}}$ is the 3 × 3 matrix with dimensionless stretch of the lattice along ${\bf{G}}$, ${{\bf{V}}}_{1}$ and ${{\bf{V}}}_{2}$, and ${\bf{Q}}$ is the 3 × 3 matrix for the orientation of the epitaxial configuration using normalized vectors.

$${\bf{S}}=\left[\begin{array}{ccc}{a}_{\parallel }/{a}_{\parallel }^{0} & 0 & 0\\ 0 & {a}_{\perp ,1}/{a}_{\perp ,1}^{0} & 0\\ 0 & 0 & {a}_{\perp ,2}/{a}_{\perp ,2}^{0}\end{array}\right],\,{\bf{Q}}=\left[\frac{{\bf{G}}}{\left|{\bf{G}}\right|}{\boldsymbol{,}}\frac{{{\bf{V}}}_{1}}{\left|{{\bf{V}}}_{1}\right|}{\boldsymbol{,}}\frac{{{\bf{V}}}_{2}}{\left|{{\bf{V}}}_{2}\right|}\right]$$

(11)

Here ${\bf{G}}$, ${{\bf{V}}}_{1}$ and ${{\bf{V}}}_{2}$ are given by 3 × 1 column vectors. With the lattice vectors of the distorted cell, DFT calculation can be performed to obtain the distortion energy as a function of the ${a}_{\perp ,1}$ and ${a}_{\perp ,2}$ for both A and B, i.e., $\Delta {E}_{{\rm{epi}}}^{{\rm{A}}}\left({a}_{\perp ,1},\,{a}_{\perp ,2}\right)$ and $\Delta {E}_{{\rm{epi}}}^{{\rm{B}}}$ $\left({a}_{\perp ,1},\,{a}_{\perp ,2}\right)$. The orientation and composition dependence of CSE follows,

$$\Delta {E}_{{\rm{CS}}}\left({\bf{G}},x\right)=\mathop{{\rm{min }}}\limits_{{a}_{\perp ,1},\,{a}_{\perp ,2}}\left\{\left(1-x\right)\Delta {E}_{{\rm{epi}}}^{{\rm{A}}}\left({a}_{\perp ,1},\,{a}_{\perp ,2}\right)+x\Delta {E}_{{\rm{epi}}}^{{\rm{B}}}\left({a}_{\perp ,1},\,{a}_{\perp ,2}\right)\right\}$$

(12)

where $x$ is the molar fraction of B in A-B system. In the calculations, $\Delta {E}_{{\rm{epi}}}^{{\rm{A}}}$ and $\Delta {E}_{{\rm{epi}}}^{{\rm{B}}}$ are calculated using the primitive cell for A and B on a pre-defined lattice.

The composition and orientation dependence of the CSE in Eq. (12) (i.e., $\Delta {E}_{{\rm{CS}}}\left({\bf{G}},x\right)$) needs to be converted to obtain ${V}^{{\rm{CS}}}\left({\bf{k}},x\right)$. Since the long-ranged interaction is non-analytical at $\Gamma$, we define the long-ranged interaction at $\Gamma$ to be zero following Laks et al.¹⁴. This definition does not affect the fitting results by MSCE, since ${\mathbf{k}}={\bf{{0}}}$ does not represent the orientation dependence. Following the argument in Laks et al.¹⁴, ${V}^{{\rm{CS}}}({\hat{{\bf{k}}}},x)$ can be obtained as,

$${V}^{{\rm{CS}}}({\hat{{\bf{k}}}},x)=\Delta {E}_{{\rm{CS}}}({\hat{{\bf{k}}}},x)/4x(1-x)v$$

(13)

Once the parent lattice and spin variables are defined for a system, the structural factor can be readily calculated, and Eq. (13) can relate $\Delta {E}_{{\rm{CS}}}\left({\bf{G}},x\right)$ to ${V}^{{\rm{CS}}}({\hat{{\bf{k}}}},x)$ for a structure with composition $x$. Since the $\Delta {E}_{{\rm{CS}}}\left({\bf{k}},x\right)$ and ${V}^{{\rm{CS}}}\left({\bf{k}},x\right)$ are only dependent on the orientation of ${\bf{k}}$, but not the magnitude, the orientation is presented using only the normalized vector $\hat{{\bf{k}}}={\bf{k}}/\left|{\bf{k}}\right|$.

In MSCE, the CSE surface that changes continuously with the orientation in k-space is needed. This can be accomplished using the spherical harmonics adapted to the symmetry of the lattice^14,43,44. In principle, any data on spherical coordinates can be fitted if infinite number of spherical harmonic functions are used. With prior knowledge of the symmetry of the lattice, spherical harmonics adapted to certain symmetry can be used to eliminate the redundant terms. For a structure with a given composition, the orientation dependence of ${V}^{{\rm{CS}}}({\hat{{\bf{k}}}},x)$ are parameterized by the symmetry-adapted spherical harmonics and the long-ranged CSE (without attenuation) for the structure can be calculated by Eq. (7). For HCP Mg alloys, the hexagonal harmonic functions (HHFs) will be used⁴⁵; see Supplementary Fig. 3.

Generally, there are two independent lattice parameters on the epitaxial plane (e.g., for hexagonal crystals). The number of independent lattice parameters can be reduced to one as long as the symmetry of lattice points on crystallographic plane ${\bf{G}}$ is retained. For a lattice with cubic symmetry, there is only one independent lattice parameter on high-symmetry planes (e.g., $\{001\}$ and $\{111\}$) and two for the low-symmetry planes (e.g., $\{110\}$). For the former, the above process can be simplified and reduces to the existing algorithm in ATAT^41,42. In the current approach, the deformation energies, i.e., $\Delta {E}_{{\rm{epi}}}^{{\rm{A}}}\left({a}_{\perp ,1},\,{a}_{\perp ,2}\right)$ and $\Delta {E}_{{\rm{epi}}}^{{\rm{B}}}\left({a}_{\perp ,1},\,{a}_{\perp ,2}\right)$ are calculated based on DFT and is not limited to small size-mismatch between constituents, crystal symmetry or the number of sublattices.

In the calculation of CSE, the deformation energy of the endmember stretched or compressed on the epitaxial plane and along the plane normal is needed from DFT. However, the ground state DFT calculations become problematic if the endmembers are mechanically unstable, i.e., the relaxed structure does not resemble the corresponding structure on the parent lattice. In this case the output energy from DFT does not reflect the stability of the endmember on parent lattice. For the energy of unstable endmembers, van de Walle et al.⁴⁶ proposed to use the energy of the inflection point along the transition path from the initial mechanically unstable structure to the relaxed stable structure that does not resemble the initial structure. In principle, this method can solve this problem though the computational cost would increase.

Regularization of the ECIs

To ensure the smoothness of interaction parameters in k-space, Laks et al., proposed a smoothening term and added it as a penalty to the loss function in the optimization process¹⁴. In the current method, the smoothening of ${V}_{m,n}\left({\bf{k}}\right)$ after separating the CSE at any k-point is equivalent to minimizing the magnitude of the secondary derivative (or the curvature) with respect to the k-point,

$${\nabla }_{{\bf{k}}}^{2}{V}_{m,n}\left({\bf{k}}\right)=-\frac{1}{2}\sum _{l}{J}_{m,n}\left({{\bf{R}}}_{l}\right)\cdot {R}_{l}^{2}\cdot {e}^{-i{\bf{k}}\cdot {{\bf{R}}}_{l}}$$

(14)

From Eq. (14), smoothening of $\left|{\nabla }_{{\bf{k}}}{V}_{m,n}\left({\bf{k}}\right)\right|$ is equivalent to prioritizing the small clusters over larger ones, which is in accordance with the physical intuition that smaller clusters tend to have larger contribution to short-ranged chemical interaction. The loss function ($\rho$) in the training of MSCE follows,

$$\rho =\mathop{\sum}\limits _{\sigma \in s}{w}_{\sigma }{\left|{E}^{{\rm{DFT}}}\left(\sigma \right)-{E}^{{\rm{MSCE}}}\left(\sigma \right)\right|}^{2}+\frac{t}{\alpha }\mathop{\sum }\limits_{l}{{R}_{l}}^{4}\,\mathop{\sum}\limits_{k}{J}_{k}^{2}\left(\left|{{\bf{R}}}_{l}\right|\right)$$

(15)

where ${w}_{\sigma }$ is the weight of a configuration $\sigma$, $\alpha \equiv {\sum }_{l}{R}_{l}^{4}\,$ is a normalizing factor and $t$ is a scaling factor for the smoothness term. Note that, to regularize multi-body ECIs, the inner summation in the second term is over all clusters with size (or largest two-site distance) of $\left|{{\bf{R}}}_{l}\right|$. Compared with pair clusters, the number of multi-body clusters increases more rapidly as a function of cut-off distances. The number of symmetrically distinct clusters as a function of cut-off distances for the lattice of HCP Mg is shown in Supplementary Fig. 1. Consequently, the multi-body clusters adopted in CE are generally much smaller than the largest pair and regularization of multi-body ECIs will only slightly shrink their magnitudes. Note that the smoothness condition is similar to the ridge technique (or ${L}^{2}$ norm) used in machine learning to avoid overfitting⁴⁷. In machine learning community, ${L}^{1}$ norm is also frequently used in regularization of parameters. MSCE with ${L}^{1}$ norm for regularization leads to the loss function of

$$\rho =\mathop{\sum}\limits_{\sigma \in s}{w}_{\sigma }{\left|{E}^{{\rm{DFT}}}\left(\sigma \right)-{E}^{{\rm{MSCE}}}\left(\sigma \right)\right|}^{2}+\frac{t}{\alpha }\mathop{\sum }\limits_{l}{{R}_{l}}^{4}\,\mathop{\sum}\limits_{k}\left|{J}_{k}\left(\left|{{\bf{R}}}_{l}\right|\right)\right|$$

(16)

Compared with techniques in machine learning literatures, the current penalty terms are weight averaged by the 4th power of the diameter of clusters. This term can enforce the physical intuition that, in general, clusters with small $\left|{{\bf{R}}}_{l}\right|$ tends to have larger ECIs and is different from the compressive sensing approach. Therefore, the smoothness term acts as a shrinkage technique for the chemical ECIs in r-space, i.e., the ECIs with smaller magnitudes will be favored over the larger ones if the loss functions are the same. The regularization of ECIs helps to reduce the prediction error for the testing dataset. With the regularization, the number of fitting parameters (i.e., ECIs) can be larger than the number of energies in the training set, thus significantly improves the fitting capability.

Results

The steps of implementing the current MSCE is similar to that of ATAT^42,48 and is detailed in Supplementary Methods 2. The MSCE is combined with MC to sample the configurational space considering both chemical and strain interactions. The role of CSE on morphology of solute clusters is demonstrated using a hypothetical HCP Mg-X system. Lastly, the MSCE approach is applied to the size-mismatched Mg-Zn alloys.

Effects of CSE on solute clusters in HCP Mg-X system

To test the generalized MSCE theory and algorithm, the current MSCE and MC are applied to a hypothetical Mg-X system with manually tuned MSCE parameters to reveal the effect of long-ranged CSE on the morphology and orientation of the coherent solute clusters in HCP Mg alloys. The variation of the chemical ECIs for the 1st and 2nd nearest neighbors (NN) can induce morphological changes of the solute clusters, as shown in Supplementary Figs. 8 and 9. In principle, chemical interactions alone can lead to solute clusters with large aspect ratios (e.g., plate- or rod) if, in the hypothetical system, the 1st and 2nd NN interactions have relatively large magnitudes, but opposite signs (e.g., repulsive vs. attractive). The goal here is to show the trend of chemical interactions on the morphologies of solute clusters and it may be difficult for real alloys to meet such extreme conditions.

Using the chemical interaction that favors the solute cluster of ellipsoids with the long axis along $[0001]$, the roles of CSE on basal and prismatic planes are analyzed. In addition to the chemical ECIs, CSE is manually tuned to examine its effects. The details are shown in Supplementary Discussion 5. The effect of the CSE on the solute clusters are shown in Fig. 2. In all the three orientations, the CSE gradually pushes the solute cluster from ellipsoid towards plates on elastically soft orientations. As the CSE is reduced on specific planes, the plates of solute cluster on the corresponding plane becomes thinner. The effect of CSE has been demonstrated theoretically and verified experimentally in Al-Cu alloys³⁰, where preferential arrangement of single layer of Cu atoms on $\left\{001\right\}$ plane is dominant in the early stages of aging. Therefore, it is expected that CSE also affects the morphology and orientation of solute clusters or coherent precipitates in size-mismatched HCP Mg alloys, especially when CSE is strongly anisotropic.

Fig. 2: Effects of the constituent strain energy (CSE) in HCP Mg-X alloys.

Effects of the magnitude of CSE on the orientation and morphology of solute clusters: a basal plane; b $\{10\bar{1}0\}$ plane; c $\{2\bar{1}\bar{1}0\}$ plane. The chemical interaction is fixed with ${J}_{{pair}}^{1{st}}=-0.02$ eV per atom. The CSE on specified plane is scaled by parameter $s$. When $s=1$, CSE is isotropic and does not affect the morphology of solute clusters. When $s \,<\, 1$, the chosen plane is the elastically softest plane and solute cluster is gradually compressed to a plate on this plane as $s$ becomes smaller.

Application to Mg-Zn system

In this section, MSCE and MC are applied to Mg-Zn alloys, which is chosen due to the large lattice mismatch between Mg and Zn. Defining the lattice mismatch as ${\delta }_{a}=\left({a}_{{Zn}}-{a}_{{Mg}}\right)/{a}_{{Mg}}$, the lattice mismatch between Mg and Zn is −16% along a-axis and −4% along c-axis. Therefore, it is expected that the magnitude of CSE is large in this system. Additionally, ${\delta }_{a}=-16 \%$ is beyond the limit of harmonic elastic response³⁴.

First-principles calculations based on DFT were employed to calculate the ground state structures and energies of ordering phases on HCP Mg-Zn alloys. The ion-electron interaction was described by the projector augmented plane-wave method⁴⁹ and the exchange-correlation functional was described by an improved general gradient approximation of Perdew-Burke-Ernzerhof⁵⁰, as implemented in the Vienna Ab-initio Simulation Package (VASP, version 5.4)^51,52. The cell shape, volume, and internal atomic positions of structures are relaxed. The maximal residual forces on atoms are smaller than 0.002 eV/Å. The computational details of DFT can be found in ref. ⁵³.

Choosing seven crystallographically independent orientations³⁵, the orientation and composition dependence of CSE in Mg-Zn system is calculated based on DFT, as shown in Fig. 3a. The maximum of CSEs along different orientations are within $0.5\, <\, x \,< \,0.75$ and the maximum values are between 44 to 50 meV per atom. The magnitude of CSE is dependent on both the lattice mismatch along a certain orientation and the stiffness of the end members. Despite the large magnitude of the CSE, the anisotropy is not very strong, as the CSEs along different orientations are very close to each other, especially at the Mg-rich side. Given the large lattice mismatch on the basal plane, the weak anisotropy of CSE is counterintuitive. However, for the case of severe lattice distortion, the response to lattice deformation is highly nonlinear. Due to the strongly anharmonic distortion, the epitaxial strain energy on basal plane is much smaller than that estimated from linear elasticity⁵³. Consequently, it is much close to the CSE of other planes (i.e., weak anisotropy). Note that plate-like Guinier-Preston (GP) zones on $\{0001\}$, $\{10\bar{1}0\}$ and $\{11\bar{2}0\}$ planes have been experimentally reported in Mg-Zn alloys⁵³. This indicates that, unlike the Al-Cu system³⁰, there is no single crystallographic plane in Mg-Zn alloy that is significantly elastically softer than others, which indirectly validates the weak anisotropy of CSE.

Fig. 3: The constituent strain energy (CSE) of Mg-Zn system.

a Orientation and composition dependence of CSE for seven crystallographic orientations; b The surface of CSE parameterized by hexagonal harmonic functions (HHFs) for ${x}_{{Zn}}=0.75$.

To obtain the continuous change of CSE as a function of orientations, HHFs were adopted to fit the CSE data in Fig. 3a. The coefficients of the HHFs can be used to calculate the CSE along any orientation at the corresponding Zn concentration. As an example, the CSE surface $\Delta {E}_{{\rm{CS}}}\left({\bf{G}},x\right)$ corresponding to $x=0.75$ is shown in Fig. 3b. Although the anisotropy of CSE is not strong in Mg-Zn system, the CSE surface clearly shows a hexagonal symmetry.

For a structure with a given Zn concentration, the coefficients for HHFs can be obtained by fitting the $\Delta {E}_{{\rm{CS}}}({\bf{G}},x)$ for seven orientations and then further used to calculate ${V}^{{\rm{CS}}}({\hat{{\bf{k}}}})$. In the Mg-Zn system, the $\Delta {E}_{{CS}}({\bf{k}},x)$ for $x=0.75$ is plotted on three planes in the first BZ of k-space and shown in Fig. 4. Since $\Delta {E}_{{\rm{CS}}}({\hat{{\bf{k}}}},x)$ has different values along different orientations, but stays constant on the same orientation irrespective of the magnitude of the k-point, $\Delta {E}_{{\rm{CS}}}({{\bf{k}}}_{1},x)-\Delta {E}_{{\rm{CS}}}({{\bf{k}}}_{2},x)$ stays constant as ${{\bf{k}}}_{1}{{\to}}{\bf{0}}$ and ${{\bf{k}}}_{2}{{\to}}{\bf{0}}$. Therefore, the curvature of $\Delta {E}_{{\rm{CS}}}({\bf{k}},x)$ gets infinitely large as ${\bf{k}}{{\to}}{\bf{0}}$, leading to the so-called singularity and the convergence issue in r-space CE.

Fig. 4: The constituent strain energy (CSE) visualized in k-space.

The CSE of Mg-Zn system at ${x}_{{Zn}}=0.75$ is shown: a basal plane; b $\left\{10\bar{1}0\right\}$ prismatic plane; c $\{11\bar{2}0\}$ prismatic plane. The blue line marks the boundary of the first Brillouin Zone.

With the composition and orientation dependence of CSE parameterized by the HHFs, the magnitude of long-ranged component of k-space interactions ${V}^{{\rm{CS}}}({\hat{{\bf{k}}}},x)$ needs to be calculated from $\Delta {E}_{{\rm{CS}}}({\hat{{\bf{k}}}},x)$ using Eq. (13). In Fig. 5, the k-space interaction parameter as a function of Zn concentration for seven orientations are shown. Clearly, ${V}^{{\rm{CS}}}({\hat{{\bf{k}}}},x)$ is composition dependent, which is the general case and implicitly incorporates all the terms when expanding $\Delta {E}_{{\rm{CS}}}(\sigma )$ as a function of composition¹⁴.

Fig. 5: The k-space parameters for constituent strain energy (CSE).

Variation of the k-space interaction parameters ${V}^{\rm{CS}}\left({\bf{{k}}},x\right)$ are shown as functions of Zn concentration.

The current MSCE is tested with various numerical settings and compared with r-space CE. The tested effects include: (1) the exclusion of structures far away from HCP lattice using the criterion in ATAT^42,48; (2) the regularization using ${L}^{1}$ vs. ${L}^{2}$ norm in the penalty term of the loss function (i.e., Eqs. (15) and (16)); (3) short-ranged structures (SR-str) and layered structures ${A}_{q}{B}_{q}$ stacked along $[0001]$, $[10\bar{1}0]$ and $[11\bar{2}0]$ directions in the training and testing set; (4) changing the weights of structures in the fitting to lower the training error for ground state structures. The results are shown in Table 1 and the details are described in Supplementary Discussion 3. It can be concluded that: (i) MSCE has higher accuracy than CE irrespective of the regularization technique (tests 1–5 vs. 6–9); (ii) the incorporating of CSE can improve the accuracy of predicted energy (test 3 vs.6 and 4 vs. 8), especially for layered structures ${A}_{q}{B}_{q}$ as q increases (test 5 vs. 7); (iii) regularization with ${L}^{2}$ norm generally leads to higher accuracy than ${L}^{1}$ norm, although the latter gives more regularized ECIs; (iv) Increasing the weights can help reducing the error of some structures but increases the overall fitting error, suggesting only slight adjustment for a few important structures is acceptable.

Table 1 Comparison of the accuracies of cluster expansions (CE) and mixed-space cluster expansion (MSCE) with various algorithms.

The formation energies of the training set from DFT calculation and MSCE fitting with adjusted weights (test 9 in Table 1) are shown in Fig. 6, with the convex hull of on-lattice structures with dimensionless lattice distortion $d\, < \,0.1$^42,48, convex hull of all the structures in DFT calculations, and the global convex hull for all structures in Mg-Zn system. If the structures with d > 0.1 are excluded from the training set, the convex hull (blue dashed line) is well above the convex hull with experimentally observed structures (black solid line). Meanwhile, the current MSCE yields a more realistic convex hull (red solid line) and accurate description of the formation energies (red + sign). In the current MSCE calculations, the numbers of pair to 6-body clusters are 387, 135, 109, 31 and 3, respectively. The number of clusters are gradually increased to make sure that adding more clusters would not further improve accuracy of MSCE. The ECIs of pair to 6-body clusters are shown in Fig. 7. Although the magnitudes of pair ECIs regularized by L² norm slightly decrease with diameters, the trend is not obvious compared with regularization using L¹ norm (see Supplementary Fig. 6). This indicates that long-ranged pairs are effective in reducing the fitting error in Mg-Zn system. Generally, L² norm leads to smaller error while L¹ norm leads to more regularized ECIs. In Mg-Zn system, there are several metastable GP zones that have similar energies (a few meV per atom)⁵³, it is necessary to reduce the prediction error of MSCE to ~1 meV per atom and regularization by L² norm is chosen. If, in another system, the energies of competing phases are not close and the requirement on accuracy of energies can be relaxed, MSCE with L¹ norm and more regularized ECIs may be preferred.

Fig. 6: The formation energy vs. composition of ordering structures in Mg-Zn alloys.

The dimensionless lattice distortion (d) of 0.1 is adopted to evaluate the relxation of HCP ordering from ideal parent lattice⁴⁸. The formation energies of stable structures on the global convex hull are also added for comparison⁵³.

Fig. 7: The effective cluster interactions (ECI) due to chemial interactions.

The ECIs in Mg-Zn alloys are obtained using ${L}^{2}$ norm regularization based on the 4th power of the diameter of clusters (Eq. (15)).

Using all the structures originated from the HCP ordering, the ground state structures after relaxation include C37 Mg₂Zn and C14 MgZn₂, which have dimensionless lattice distortion of 0.19 and 0.11. These structures would not be included in the training set if the exclusion criterion is adopted. The structures of the coherent HCP orderings that lead to C37 Mg₂Zn and C14 MgZn₂ after structural relaxation are shown in Fig. 8a, b, respectively. Using ${V}^{{\rm{CS}}}\left({\bf{k}}\right)$, the coefficients of HHFs for attenuation $A\left({\bf{k}}\right)$, and the r-space ECIs in Fig. 7, the equilibrium configuration of solutes can be obtained by MC. In the current MC, the canonical and semi-grand canonical (SGC) ensembles were adopted to simulate the case under constant overall composition and chemical potential, respectively. The initial configuration is set to be a random configuration for the canonical mode and the ground state C14 MgZn₂ for the SGC mode, respectively. In all structures equilibrated in MC, two types of solute configurations are observed at low (less than 3%) and high Zn concentrations (over 35%), shown in Fig. 8c, d. When the Zn concentration is low, the local Zn atoms rearrange in a pattern similar to the Zn orderings that relaxes to C37 Mg₂Zn, as shown by the blue lines in Fig. 8c. The perspective view show that the Zn rods prefer to be aligned along $[0001]$ direction. When Zn concentration is high, the equilibrium arrangement of Zn follows the pattern of the HCP ordering that leads to C14 MgZn₂ after relaxation. In this case, the local arrangement shows switching pattern of Zn-rich and Zn-poor layers on the basal plane, which is a key feature in C14 MgZn₂, where, in the Zn-poor layer, Zn atoms are surrounded by six Mg atoms (see the right figure in Fig. 8b). Local orderings along $[0001]$ that exactly matches that of C14 MgZn₂ is shown in Fig. 8d. These local arrangements of Zn atoms from MC simulation agree with the ground state structures by DFT.

Fig. 8: Structures of dominant HCP orderings in Mg-Zn alloys.

a HCP ordering Mg₂Zn that leads to C37 structure after relaxation; b HCP ordering MgZn₂ that leads to C14 structure after relaxation with the right figure showning the basal layer with both Mg and Zn atoms; c Dominant local ordering of Zn in Monte Carlo with low overall Zn concentration; d Dominant local ordering of Zn in Monte Carlo with high overall Zn concentration. The green and orange spheres represent Mg and Zn atoms, respectively. The red dashed lines show the primitive cell of the ordering. The blue lines shows prefered local arrangement of Zn atoms in Mg₂Zn.

Despite multiple reports of GP zones in Mg-Zn alloys without other element additions, direct imaging of GP zones in Mg-Zn system with atomic scale resolution is challenging. This indicates the GP zones in this system are not very stable, as compared with the GP zone in Al-Cu system⁴⁸. Consequently, the GP zones in Mg-Zn alloy can easily be obscured by the other more stable precipitates (e.g., C14 MgZn₂). Due to the incorporation of the C37 Mg₂Zn, C15 MgZn₂ and C14 MgZn₂ in the training set, the convex hull (red line in Fig. 6) is much lower than the energies of potential GP zone structures with very small amount of relaxation from ideal HCP lattice ($d\, < \,0.1$, blue dashed line in Fig. 6), which explains the absence of GP zones in the current MC with MSCE that includes all structure irrespective of the degree of relaxation. If the training set is limited to structures with small degree of relaxation from HCP lattice ($d \,< \,0.1$), then various GP zones can be identified⁵³.

Discussion

The MSCE method owes the high accuracy, compared with r-space CE, to three aspects. (1) The long-ranged limit of the CSE due to size-mismatch are explicitly incorporated using the k-space formalism. (2) The attenuation of the long-ranged interactions accommodates for medium-ranged structures, which is the case for the majority of the structures in the training set. (3) The regularization of r-space ECIs allow us to include much larger number of clusters, which enhances the fitting capability.

In recently years, machine learning potentials (MLPs) have been actively developed for various materials^54,55,56,57. In terms of purposes, MSCE focus on the energy of the structures using the lattice model and the atomic displacements are not considered, while MLP is designed to describe the energy as a function of the atomic positions without an underlying lattice. Consequently, MSCE focuses on configurational thermodynamics, e.g., order/disordering transition, ordering and clustering of solutes, coherent/semi-coherent precipitations. Meanwhile, MLP is intended for dynamical trajectories by molecular dynamics. In terms of accuracy, the MLP typically reaches RMSE of a few meV per atom^54,55,56,57, while the current MSCE can yield RMSE and CV of ~1 meV per atom (Table 1). In terms of range of interactions, the MLP often solely relies on the training set from DFT where long-ranged interactions using large supercells can pose computational challenges, while long-ranged interactions are modeled explicitly in k-space in MSCE and parameterized using DFT with primitive cells of end members (e.g., 2 atoms for HCP structures).

In Mg-Zn system, the preferred orderings of Zn atoms are identified with Zn-rods and local C14 MgZn₂ arranged along $[0001]$. Noteworthy, C14 MgZn₂ rods here agree with the peak-age precipitates ${\beta }_{1}{\prime}$ rods along ${\left[0001\right]}_{{\rm{\alpha }}}$ with the orientation relationship of ${\left(0001\right)}_{{\rm{C}}14}\parallel {\left(0001\right)}_{\alpha }$ and ${\left[10\bar{1}0\right]}_{{\rm{C}}14}\parallel {\left[12\bar{1}0\right]}_{\alpha }$ in Mg-Zn system⁵⁸. In the current MSCE and MC, all the fully relaxed HCP orderings in DFT are included in the training set, which enables the energy predicted by MSCE to be fully incorporate the relaxations from HCP lattice sites. In the calculations with only moderately relaxed structures (with d < 0.1), many overly relaxed structures are excluded in r-space CE (Fig. 6). Such calculation reflects the energies of orderings very close to HCP lattice sites and coherent orderings resembling GP zones were revealed⁵³. However, such potential GP zones were not found in the current MSCE and MC simulations. In Mg-Zn system, experimental evidences of GP zones were reported⁵⁹, which, however, is deemed insufficient⁶⁰. Comparison of the calculations using r-space CE and MSCE offers a possible explanation. When Zn atoms start to aggregate in local regions of Mg matrix, lattice distortion will be involved due to the lattice mismatch between Mg and Zn atoms. When such distortions are small and the atoms sit close to the ideal HCP lattice sites, local arrangements of Zn atoms resembling GP zones can be found. When the local Zn concentration gets high and local lattice distortion becomes severe, the local Zn-rich regions prefer to transform to more stable structures, such as C14 or C15 MgZn₂. Considering the lattice becomes less rigid when the temperature is elevated, the GP zones are more likely to be found at low aging temperatures in the samples with low overall Zn concentrations. This may explain why concrete evidence of GP zones in Mg-Zn is elusive even with modern microscopy. A more detailed discussion can be found in⁵³.