Graph neural network modeling of grain-scale anisotropic elastic behavior using simulated and measured microscale data

Abstract

Here we assess the applicability of graph neural networks (GNNs) for predicting the grain-scale elastic response of polycrystalline metallic alloys. Using GNN surrogate models, grain-averaged stresses during uniaxial elastic tension in low solvus high-refractory (LSHR) Ni Superalloy and Ti 7 wt%Al (Ti-7Al) are predicted as example face-centered cubic and hexagonal closed packed alloys, respectively. A transfer learning approach is taken in which GNN surrogate models are trained using crystal elasticity finite element method (CEFEM) simulations and then the trained surrogate models are used to predict the mechanical response of microstructures measured using high-energy X-ray diffraction microscopy (HEDM). The performance of using various microstructural and micromechanical descriptors for input nodal features to the GNNs is explored through comparisons to traditional mean-field theory predictions, reserved full-field CEFEM data, and measured far-field HEDM data. The effects of elastic anisotropy on GNN model performance and outlooks for the extension of the framework are discussed.

Introduction

The local micromechanical response of grains embedded within a polycrystal is dictated not only by an isolated grain’s features (e.g., defect state or crystallographic lattice orientation), but also by the features and mechanical response of adjoining grains (i.e., the local grain “neighborhood”). Various linking hypotheses or methods in which grains are embedded within homogeneous matrices—most notably the Eshelby method¹—attempt to capture the average features of grain-scale response, but, by construction, do not consider the variation of behavior created by the interactions of specific grains within their local neighborhoods. The relatively recent ability to explicitly model grains and grain neighborhoods in three-dimensional (3D) polycrystals using both finite element² and spectral³ methods has allowed these neighborhood effects to be more thoroughly explored. However, the use of these methods comes at a sometimes-significant computational cost. Increasing computational complexity, particularly with increases in microstructural fidelity or the inclusion of various plastic deformation mechanisms in modeling efforts, limits the number of microstructural configurations that can be tested, which consequently limits the ability of these models to be embedded within larger-scale simulations (considering current computational capabilities). To address these challenges, low-computational-cost surrogate models which can rapidly evaluate the micromechanical response and evaluate large regions of microstructure-parameter space are necessary. In this work, we propose and demonstrate that the fundamental network (or graph) structure of polycrystals make them candidates for surrogate mechanical modeling through graph neural networks (GNNs)^4,5,6. We demonstrate the utility of this surrogate modeling with GNNs trained to predict grain-scale elastic response in two example alloy systems. The GNNs are trained with microscale crystal elasticity finite element method (CEFEM) simulations, and then tested against grain-scale elastic response measured using high-energy X-ray diffraction microscopy (HEDM).

Supervised machine learning has become a primary choice for generating surrogate models for predicting the mechanical properties and performance of engineering alloys⁷. At the microscale, multiple efforts have utilized convolutional neural networks (CNNs) to predict deformation fields at sub-grain length scales in virtual polycrystals^8,9,10. In these efforts, polycrystals are represented by a grid of voxels containing microstructural descriptors such as lattice orientation, and the CNN learns spatial correlations between the voxels to generate full-field predictions. In particular, CNNs take advantage of the grid structure of the data to learn filter structures consisting of a series of weights. These weights group (pool) together neighboring grid values (in this case microstructural features) to capture and predict the effects of the neighborhood. The results of this approach are very promising, but an issue is that (most) materials are not naturally structured in a grid-like fashion (although due to data collection strategies, materials are often represented as such). In the cases of polycrystalline materials at the microscale, the grains themselves are more naturally represented in an unstructured, connected format often referred to as a graph.

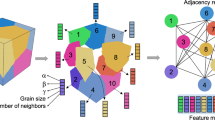
Broadly, a graph is a structure in which “vertices” or “nodes” are connected through “edges”. Both nodes and edges can further be described via associated attributes or features. In the case of a polycrystal represented via a graph, grains are considered as nodes, while grain boundaries are considered edges. Features of nodes (grains) could include local micromechanical properties such as stiffness or strength, as well as microstructural features such as lattice orientation or dislocation density. Features of edges (grain connections or boundaries) may be the distance between grains or grain boundary characteristics. GNNs, which are the focus of this work, adapt the data pooling technique of CNNs on structured data to the pooling of neighboring data on unstructured graph data. Instead of pooling features from neighboring grid points, features are pooled from connected nodes¹¹. A recent study has demonstrated that these GNN models can be developed and trained for predicting grain-scale response, particularly magnetostriction¹².

In this study, we apply GNNs to predict the elastic response in two alloy systems: Low solvus high-refractory (LSHR) Ni superalloy and Ti 7 wt%Al (Ti-7Al), representing cubic and hexagonal elastic responses, respectively. Two GNN surrogate models for predicting LSHR and Ti-7Al grain-averaged elastic response (grain stress tensor components along the loading direction) that utilize Gaussian Mixture (GM) convolutions are implemented, trained, and preliminarily tested using CEFEM deformation simulations that explicitly consider grain microstructure. During training, the accuracy of the predictions are compared against predictions from traditional mean-field theories and reserved CEFEM simulations. The GNN models trained with CEFEM simulations are then transferred to a separate data domain to predict the grain-averaged elastic response in polycrystals with microstructures measured with near-field HEDM. GNN model predictions are then compared to stresses measured using far-field HEDM. As part of the GNN model training effort, learning rates of the models and the accuracy of using various nodal features for stress predictions are explored.

In this paper, vectors are generally lower-case bold characters (a), second-order tensors are upper-case bold characters (A), and fourth-order tensors are underlined, bold characters ($\underline{{{{\boldsymbol{A}}}}}$). Unless otherwise noted, quantities are expressed in the sample frame. Prime characters are generally used to indicate quantities in subsequent layers within GNNs, i.e., ${a}^{{\prime} }$ for Hidden Layer n+1, while an overbar $\bar{a}$ indicates an average.

Results

The results are divided into three subsections. The first subsection covers the learning behavior of GNN surrogate models using CEFEM data. The second subsection details how the trained GNN surrogate models perform predicting micromechanical response in comparison to reserved CEFEM data. The final subsection analyzes the performance of the trained surrogate GNN models in predicting the mechanical response of microstructures characterized experimentally.

Model training

After generating the various graph data from both CEFEM simulations and HEDM results (see: Sections “Polycrystal anisotropic elasticity data” and “High-energy X-ray diffraction microscopy data”) for GNN surrogate model training, a study was completed to examine the performance of the GNNs predicting the stress response along the loading direction (σ_zz) in individual grains. For GNN model training, graphs generated from various numbers of CEFEM simulations (1, 5, 10, and 20, corresponding to 1500, 7500, 15,000, and 30,000 grains in total, respectively) were used to train the LSHR and Ti-7Al GNN surrogates. Respectively for each training scenario, a total of 1, 2, 3, and 4 CEFEM simulations (1500, 3000, 4500, and 6000 grains in total) were reserved for evaluating the accuracy of the surrogate model predictions. The accuracy of surrogacy models in predicting simulated stresses were quantified using the mean of a 1-norm error:

$$\bar{e}({\sigma }_{zz})=\frac{1}{{N}_{G}}\sum \frac{| {\sigma }_{zz,i}^{{{{\rm{SIM}}}}}-{\sigma }_{zz,i}^{{{{\rm{GNN}}}}}| }{{\sigma }_{zz,i}^{{{{\rm{SIM}}}}}}\quad .$$

(1)

During training, this error metric provides a direct comparison of the accuracy of GNN predictions versus the full-field CEFEM simulations.

Figure 1 shows the learning rates (epoch vs error) for LSHR elastic response using the various numbers of training data sets described above. Figure 1a shows the learning rate using the directional modulus E(r) as a nodal feature, while Fig. 1b shows the learning rates using components of the Rodrigues vector r describing a grain’s lattice orientation as nodal features. It is important to note that while these quantities are related (the directional modulus is a function of the grain lattice orientation), the directional modulus is a micromechanical property that should have a linear relationship to the stress state, while the components of the lattice orientation are a microstructural feature that should have a nonlinear relationship to the stress state. Solid lines show the mean error of grain stress predictions of the surrogate model on the training data while the dashed lines show the mean error in comparison to the reserved testing data sets. As a benchmark, mean errors as predicted by various mean-field theories (models), isostress (all grains have the same stress state as the macroscopic stress, ${\sigma }_{zz}={\tilde{\sigma }}_{zz}$) and isostrain (all grains have the same strain state as macroscopic strain, ${\sigma }_{zz}=E({{{\boldsymbol{r}}}}){\tilde{\varepsilon }}_{zz}$), are provided. In most cases, there is no evidence of over-fitting which would be seen as divergence between mean errors on predictions of training and reserved testing data, except for the case when only one training data set is used with lattice orientation used as the nodal feature input. The ‘spikes’ during the learning process are related to the use of Adam stochastic gradient descent algorithm for fitting, which will perturb the solution intermittently to try to ensure that a global minimum is reached.

Fig. 1: Learning rates of LSHR grain-scale elastic response using various numbers of CEFEM simulations for training and testing.

Insets show a magnified view of the learning rate at larger epochs. a Learning rates using the directional modulus E(r) as a nodal feature. b Learning rates using the lattice orientation (components of the Rodrigues vector r) as nodal features.

In Fig. 1, we can see that using the GNN surrogate model with either the directional modulus or lattice orientation as nodal features outperforms the predictions of the mean-field theories (red dashed and dotted lines) reaching average errors of ~0.05 (5%) for LSHR, with the lattice orientation performing slightly better after 10,000 epochs of training. The fact that surrogate models using directional modulus and lattice orientation have approximately the same performance indicate that nominally the same information is encoded into the two grain descriptors. This can be rationalized in that the directional modulus is calculated using the lattice orientation and the single crystal elastic moduli as previously mentioned. However, this relationship between lattice orientation and directional stiffness is nonlinear and naturally, the rate at which the relationship is learned is slower, but the GNN surrogate model does in fact learn the relationship. We note that when using only a single hidden layer, the surrogate model is incapable of learning this relationship (not shown).

Similar to Figs. 1, 2 shows learning rates of the grain-scale elastic response using different numbers of CEFEM simulations for training, using directional modulus (Fig. 2a) and lattice orientation (Fig. 2b) as input nodal features for Ti-7Al. In Fig. 2b, it can be seen that using 1 and 5 CEFEM simulations for training along with lattice orientation as nodal features show signs of over-fitting for Ti-7Al as opposed to only 1 FEM simulation for the LSHR data. Like the LSHR, using directional modulus or lattice orientation as input nodal features gives approximately the same performance (0.035 mean error) at large epochs. The magnitude of the final mean error is lower than that of the LSHR (0.035 for Ti-7Al versus 0.05 for LSHR) which is discussed further in “Discussion”. In addition, the GNN surrogate model only performs slightly better than using an isostress assumption to determine grain average stresses in the Ti-7Al, which will be discussed.

Fig. 2: Learning rates of Ti-7Al grain-scale elastic response using various numbers of CEFEM simulations for training and testing.

Insets show a magnified view of the learning rate at larger epochs. a Learning rates using the directional modulus E(r) as a nodal feature. b Learning rates using the lattice orientation (components of the Rodrigues vector r) as nodal features.

GNN surrogate model performance: source domain (CEFEM Data)

Besides directional modulus and lattice orientation, the performance of GNN surrogate models in predicting stresses in the Source Domain (i.e., the domain where the surrogate models are trained using CEFEM data) using other sets of nodal features were also tested. These include incorporating transverse contraction ratios, ν_x(r) and ν_y(r), and the volume, V, of grains into the fitting, for a total of four different nodal feature sets. A summary of the training results for the different nodal feature sets using 20 CEFEM simulations (30,000 grains) for training and 4 CEFEM simulations for testing (6000 grains) are shown in Fig. 3. This figure compares the results of the GNN-based stress predictions against those from the full-field CEFEM simulations reserved solely for testing and not included in the model training, providing a benchmark against existing modeling capabilities. Beyond what can be seen in Figs. 1a, 2a, the inclusion of transverse contraction ratios generally does not improve accuracy. This is consistent with the observation that the directional modulus and lattice orientation nominally have nominally the same accuracy: if transverse contraction ratios improved accuracy, it would be expected that lattice orientation would also perform better (contraction ratios are calculated from orientation). Somewhat surprisingly, inclusion of grain volume V into the nodal features does not improve the surrogate model prediction accuracy. For this work, however, the spread of grain size is minimal, and we note that this observation may not be general. Volume may be a necessary descriptor for accuracy in other microstructures with larger or bimodal distributions of grain size.

Fig. 3: Summary of learning rates for various nodal features included in the GNN surrogate models.

Comparison of learning rates using various mechanical and microstructural descriptors for nodal features within the GNN surrogate models for a LSHR and b Ti-7Al.

To examine if there were systematic errors in the GNN surrogate model predictions, the stress predictions from the surrogate models using lattice orientation (Rodrigues vectors) as nodal features were compared to stresses from the CEFEM reserved testing data sets. Comparison of surrogate model predictions using 20 CEFEM simulations for training and compared to stresses from four testing CEFEM simulations are shown in 2D histograms in Fig. 4a, c for LSHR and Ti-7Al respectively. The solid red diagonal lines correspond to perfect correspondence (100% accuracy) while the dashed and dotted lines correspond to 5 and 10% error bounds respectively. For the LSHR, 64% of the GNN stress predictions fall within the 5% bound, and 93% of stress predictions fall within the 10% bound. Similarly, Fig. 4b and d show the same comparison for both materials in the form of a scatter plot to better display outlier data points, along with a linear regression fit to the comparison. We observe here that the spread of stresses across the LSHR grains is significantly larger than that seen in the Ti-7Al grains due to the much larger elastic anisotropy. The LSHR fit shows no evidence of systematic bias and is able to predict stresses within the full ranges of stresses generated by the significant elastic anisotropy in LSHR. For the Ti-7Al material, the GNN surrogate model captures most of the grain stress spread, but appears to be truncating the bounds of the most extreme values of the prediction. In Fig. 4b, 78 and 98% of the GNN stress predictions fall within the 5% bound and 10% bound respectively. These observations will be discussed further in “Discussion”.

Fig. 4: Comparison of stress predictions along the loading direction (σ_zz) from GNN surrogate models using lattice orientation as nodal features with CEFEM simulations.

Histogram comparisons for a LSHR and c Ti-7Al. Also shown are scatter plots of the same comparisons for b LSHR and d Ti-7Al.

GNN surrogate model performance: target domain (HEDM Data)

After evaluating the performance of the surrogate models in the Source Domain, the surrogate models were then transferred to the Target Domain where stresses during elastic loading was predicted from a graph generated from a 3D microstructure measured using near-field high-energy X-ray diffraction microscopy (nf-HEDM). As the performance of various nodal features used for prediction were fairly similar (Fig. 3), only GNN surrogate models using lattice orientation as nodal features were tested as lattice orientation is directly measured using HEDM. The stresses predicted by the GNN surrogate models were then compared to the stresses measured from the same microstructure during elastic loading using far-field high-energy X-ray diffraction microscopy (ff-HEDM). Here we note that uncertainty exists in (i) the application of perfect uniaxial load; (ii) the potential presence of minor microplasticity and (iii) measurement of applied strain, grain lattice orientations, grain elastic strain states, and single crystal moduli used to calculate grain stresses from elastic strains. This uncertainty clearly influences the accuracy of stresses measured with ff-HEDM, but also will influence the GNN predictions of stress (as orientations measured with HEDM are used for prediction). For these reasons, a decrease in correlation is expected between GNN predictions and stresses measured with ff-HEDM, but this does not necessarily indicate a decrease in the accuracy of the GNN predictive capability. In general, the increased average error is expected, and is a product of the fact that these comparisons now include GNN model prediction error as well as experimental uncertainty. Comparison of the GNN predicted versus ff-HEDM measured stresses for the LSHR and Ti-7Al specimens are shown in Figs. 5, 6, respectively. The stresses measured during two different applied strain states (Load 1 and Load 2) for 2873 LSHR grains and 559 Ti-7Al grains were used to explore the contribution of experimental uncertainty when compared to GNN predictions. For prediction of stresses using the GNN surrogates, the output stresses are scaled by the ratio of macroscopic applied strain in the experiments to the macroscopic applied strain for the CEFEM simulations in the Source Domain (0.001). The applied experimental strains during the ff-HEDM measurements were 0.0015 and 0.0033 for the LSHR and 0.0009 and 0.0018 for the Ti-7Al.

Fig. 5: Comparisons of stress predictions along the loading direction (σ_zz) from GNN surrogate models using lattice orientation as nodal features with those measured using ff-HEDM during in situ elastic loading for LSHR.

Histograms of comparisons at a Load 1 (applied strain of 0.0015) and b Load 2 (applied strain of 0.0033). c Scatter plot comparing GNN predictions and ff-HEDM results from the two load steps along with regression lines fit the comparisons.

Fig. 6: Comparisons of stress predictions along the loading direction (σ_zz) from GNN surrogate models using lattice orientation as nodal features with those measured using ff-HEDM during in situ elastic loading for Ti-7Al.

Histograms of comparisons at a Load 1 (applied strain of 0.0009) and b Load 2 (applied strain of 0.0018). c Scatter plot comparing GNN predictions and ff-HEDM results from the two load steps along with regression lines fit to the comparisons.

Figure 5 a, b show histograms comparing stresses along the loading direction measured by HEDM for Loads 1 and 2, respectively, while 5c shows the same comparison on a scatter plot with both applied strain states combined. For the GNN LSHR predictions, there does not appear to be any major systematic error in the prediction of stresses. However as expected, the mean of the errors are higher ($\bar{e}=12.1 \%$ for Load 1 and $\bar{e}=9.2 \%$ for Load 2) than those for the GNN model compared to CEFEM predictions. The reduction in error between Load 1 and Load 2 is due to the fact that the relative measurement uncertainty in the ff-HEDM measurements decreases with applied load. Figure 6 shows the comparison between GNN predictions and stress measurements from ff-HEDM for Ti-7Al across two loading states in the fashion as Fig. 5. We can see the GNN stress predictions are fairly tightly clustered around the average stresses in the specimen in the two load steps. There appears to be a systematic error in which the GNN predictions for Ti-7Al do not capture the full spread of grain stresses in the simulation, similar to observations in the Source Domain, but likely increased due to the various factors contributing to experimental uncertainty. In addition, the slope of the regression line fit to the stresses in 6c is particularly flat. Although the systematic error is present, the Ti-7Al stress predictions still have a lower mean error ($\bar{e}=8.7 \%$ for Load 1 and $\bar{e}=5.4 \%$ for Load 2) in comparison to the LSHR due to the lower elastic anisotropy of the Ti-7Al which is discussed further in “Discussion”.

Discussion

Here the efficacy of using GNN surrogate models to predict grain-scale elastic response on both simulated and experimentally measured microstructures (represented as graphs) was explored. The GNN models use a graph convolution (Gaussian Mixture) to capture the inherent non-locality in both mechanical equilibrium and deformation compatibility which govern mechanical response. Elasticity was chosen as an initial test case for exploring the prediction of micromechanical response due to our generally strong theoretical understanding of the constitutive relationship (Hooke’s Law) and primary material characteristics (the single crystal elastic moduli and lattice orientation of a grain) governing elasticity at the grain-scale. It was found that, once trained, the accuracy of the GNN surrogate models exceeded that of both isostrain (Taylor) and isostress (Sachs) mean-field theory assumptions in both a highly anisotropic FCC alloy (LSHR) and a moderately isotropic HCP alloy (Ti-7Al). Various sets of microstructural and micromechanical descriptors were tested and found to have generally similar accuracy after full training (Fig. 3), although it is noted that the choice of descriptors was informed by our generally strong theoretical understanding of the elastic response. Importantly though, the two hidden layer architecture employed was demonstrated to be capable of learning the complex nonlinear relationship between lattice orientation and directional stiffness as evidenced by the similar final performances.

In our approach, transfer learning was successful in enabling the prediction of the mechanical response of microstructures (as represented by graphs) that were experimentally measured using HEDM, as opposed to only predicting the response of synthetic microstructures. The ability to move between various data domains opens up the possibility of training schemes that could further improve the accuracy of the model. In particular, using both simulated and experimental data to train GNN surrogate models is a promising avenue for future efforts as both data types have strengths and weaknesses for use in learning material response. Large amounts of simulated data is generally more readily acquired than experimental data, however, simulations are generally not capable of capturing phenomena not explicitly included into the model. Experimental data will naturally represent the physics of the phenomenon at hand, but is susceptible to measurement error and bias. Creating training data sets in the future containing both simulation and experimental data can help to further improve the accuracy of GNN surrogate model predictions.

At this point, it is worth discussing differences between the elastic responses of LSHR and Ti-7Al and the utility of GNN surrogate models for predicting elastic responses. While the LSHR is crystallographically more symmetric, it is actually significantly more elastically anisotropic. The directional moduli in the LSHR vary by a factor of approximately 2.5 (ratio of maximum to minimum), while the directional moduli of the Ti-7Al only vary by a factor of approximately 1.5. The value of the use of the GNN surrogate model in comparison to mean-field theory will increase as material becomes increasingly elastically (or plastically) anisotropic and the converse. At the extreme, if a material is nearly elastically isotropic, assuming the macroscopic stress state is equal to the grain stress state is highly accurate. It was observed for the Ti-7Al, that there was a systematic error in the GNN predictions in both the Source and Target domains. The predictions for the Ti-7Al model are tightly bound around the average stress indicating the model is only learning minor adjustments from an isostress mean-field theory, as opposed to learning full neighborhood effects. However, this is simply a consequence of the fact that any GNN model will converge to an isostress prediction as the material approaches isotropy.

It is well established that neighborhood plays a role in the deformation of polycrystals in both the elastic and plastic deformation regime^13,14,15 which informed the choice of GNN for polycrystalline modeling and the GM convolution operator selected. Following this, questions arise regarding the influence of these neighborhood effects in the GNN predictions in this work. As a relatively straightforward means to test the neighborhood effects of the GNN, explicit edge features were removed from the LSHR GNN model formulation and the model was then retrained using the same procedure described above. LSHR was chosen here for its increased anisotropic elasticity. Removing edge features can be physically interpreted as the model knowing the nodal features (orientations) of each neighboring grain, but not necessarily the explicit position of the neighbors with respect to loading. This model formulation lies between that which was shown in the section “Results” and a more standard mean-field theory which contains no information about the neighborhood in its prediction. The results from training and testing against reserved simulations using no edge features and orientation as nodal features (Rodrigues parameterization) are given in Fig. 7. Along with isostrain and isostress mean theory predictions included as before, the final accuracy from the full LSHR GNN model described in the results are included. As would be expected from the physical interpretation of this model without edge features, the accuracy of model prediction lies between that of the full GNN model considering both nodes and edges described above and the isostress prediction. Beyond using five CEFEM simulations for training, the model accuracy stabilizes at ~6% in comparison to ~4.5% for the full GNN model and ~10% for the isostress prediction.

Fig. 7: Effects of removal of edge features in GNN model prediction accuracy.

Learning rates of LSHR grain-scale elastic response using various numbers of CEFEM simulations for training and testing without the inclusion of edge features and using the lattice orientation (components of the Rodrigues vector r) as nodal features.

Another question is: how important are the exact grain morphology configurations of a neighborhood for GNN model training? To explore this effect, a single microstructural instantiation of LSHR was generated and the orientations were then shuffled through the fixed grain tessellation. This produces 25 unique microstructures, but with a less diverse number of grain morphologies for training than considered previously. These data were then used to train and test the same GNN model shown in the section “Results” with lattice orientation as the nodal features (model labeled GNN-S). Learning rates from model training and reserved data testing are given in Fig. 8a. The final accuracies at 10,000 epochs for these training data sets are comparable to the more diverse learning set described in the results, ~4.5%. These training and testing results indicate that for the relatively equiaxed microstructures tested in this work, a less diverse pool of grain-shape configurations is necessary. However, to fully evaluate this mode of training with reduced numbers of grain morphology configurations, the GNN-S model was tested on a new tessellation that had also been deformed using CEFEM. Figure 8b shows a histogram and Fig. 8c a scatter plot comparing the two sets of predictions. The accuracy of the grain-by-grain predictions are comparable to the GNN model trained using a wider array of grain morphology instantiations (see Fig. 4a). Considering these observations, we take care to note that while a limited number of tessellations are necessary for training for this case, we do not expect the results here to necessarily be valid when applied to more complex microstructures (e.g., columnar shaped or bimodal grain size distributions) or during plasticity.

Fig. 8: Results of a GNN model for LSHR grain-scale elastic response generated with a single tessellation and “shuffled” orientation sets using the lattice orientation (components of the Rodrigues vector r) as nodal features.

a Learning rates using various numbers of CEFEM simulations for training and testing. b Histogram and c scatter plot of the grain-scale stress predictions on a new microstructure comparing those from a GNN trained with data from the shuffled orientation sets in a single tessellation (GNN-S) and full-field CEFEM.

With the ability of the GNNs to predict elastic response shown here, the extension of the approach to predicting plasticity should be considered. In this work, the prediction of the mechanical response of each node is static and does not evolve with time or deformation. To address material evolution that occurs during plastic deformation, recurrent neural networks (RNNs) can be layered on top of the GNN surrogate. In the RNN framework, the neural network has a ‘memory’ that transmits output nodal features through time, enabling dynamic processes to be modeled. This approach has been successful in time-evolving graph problems such as traffic forecasting¹⁶, but has mostly been developed for cases where the temporal data is largely stationary (e.g., regular traffic data) and the nodal features are static (e.g., location information of roads is static). However, existing approaches for modeling plasticity present a path forward as there are significant commonalities between nodal features in a graph and internal state variables characterizing the local microstructure of material points¹⁷. One can imagine not being limited to the prediction of the mechanical response at nodes after a loading increment (i.e., this work), but also to predict nodal features that are either implicit descriptors of microstructure (e.g., slip system strengths) or explicit descriptors (e.g., dislocation density).

Once trained, the GNN surrogate models are highly efficient in predicting mechanical response as they do not require the inversion of large systems of equations or any nonlinear optimization. This provides an opportunity for embedding into larger-scale models. Efforts to include grain-scale evolution in the larger-scale deformation or forming operations generally require homogenization¹⁸ or a linking hypothesis^19,20, usually a Taylor assumption, which will remove local neighborhood effects from consideration, although inclusion of non-explicit neighborhood effects have been attempted²¹. While successful for predicting a bulk property such as anisotropic strength²² or a microstructural feature such as phase fraction²³, this approach will be unable to predict mechanical responses, such as fracture and fatigue, which are dictated by rare, extreme events. Embedding GNN surrogate models, which naturally incorporate neighborhood effects without a large computational overhead, within a larger-scale simulation is a possible avenue for predicting extreme events in full-size components, opening a path for truly microstructurally-sensitive predictions of material failure in component-scale simulations.

In total, a transfer learning approach was taken for training and evaluating the performance of GNN surrogate models. These surrogate models provide an opportunity for implementation in multiscale mechanical modeling where a micromechanical response can be rapidly evaluated using a GNN surrogate. Models were used to predict the elastic response of grains in samples deformed under uniaxial tension. From this work we find that:

• GNNs can exceed the accuracy of traditional mean-field theories (models) for predicting anisotropic elastic micromechanical response through incorporation of information regarding the local neighborhood.

• Micromechanical descriptors such as directional modulus and near equivalent microstructural descriptors such as lattice orientation provide similar accuracy for GNN surrogate model predictions of elasticity.

• As mechanical response becomes increasingly isotropic, GNN surrogate model predictions converge toward traditional mean-field predictions.

• Using a transfer learning approach, prediction of micromechanical response using GNNs is possible even in scenarios when little training data is available (i.e., experimentally measured microstructures).

GNN surrogate modeling, beyond predicting grain-scale elastic response, provides a framework for rapidly predicting more complex processes such as plasticity which can in turn be embedded into larger-scale simulation for the prediction of complex material behaviors such as fracture and fatigue.

Methods

In this section, we give a broad overview of the various methods employed in this work for GNN training and accuracy evaluation including virtual sample generation, CEFEM modeling, HEDM, and GNN surrogate modeling. In addition, details regarding the various training and testing data used are provided. A schematic of the various components of the effort, displaying LSHR data, are given in Fig. 9. Briefly, a transfer learning approach²⁴ is taken in which the GNN models for LSHR and Ti-7Al are trained using simulated data from microscale CEFEM modeling (the Source Domain) and then transferred to predict the mechanical response in a microstructure measured experimentally via HEDM (the Target Domain).

Fig. 9: Overview of transfer learning approach for GNN surrogate model evaluation.

Connectivity of the various efforts used to evaluate the accuracy of GNN surrogate models for predicting the stress response in individual grains during elastic loading.

Virtual sample generation

Virtual polycrystals upon which mechanical deformations are imposed and used to create microstructure graphs are generated using the Neper polycrystal generation and meshing software (https://neper.info)^25,26. Generally, Neper utilizes Laguerre tessellations to generate polycrystalline samples. Laguerre tessellations produce convex, space-filling grains in a user-specified sample domain. Specifically, Neper allows for user-specified target distributions of grain size and grain shape. This affords the ability to create a wide range of microstructures with various geometric features. An attendant finite element mesh is then generated via Neper using Gmsh²⁷, in which the geometric features of the microstructure (tessellation) are preserved.

Here, Neper is used to generate 50 virtual polycrystals (25 LSHR and 25 Ti-7Al) for elastic finite element simulations. The simulated domains are 1 mm × 1 mm × 3 mm, each containing 1500 grains. Each polycrystal had ~16,500 shared grain boundaries which serve as edges. Grain size and shape distributions are set to create nominally equiaxed grains with diameters of approximately 150 μm and minimal spread. Each polycrystal is meshed with ten node tetrahedral elements and ~120,000 elements per sample. Orientations are assigned randomly to grains from the cubic and hexagonal fundamental regions for the LSHR and Ti-7Al virtual specimens, respectively.

Polycrystal anisotropic elasticity data

For generating training data for the GNN surrogate elasticity model deformation response, we utilize the finite element solver within FEPX (https://fepx.info)²⁸ which interfaces directly with tessellations and meshes generated via Neper²⁹. Generally, FEPX considers the elasto-viscoplastic deformation response of single crystals (grains) belonging to explicit representations of polycrystalline aggregates. However, here, viscoplasticity is inhibited by ensuring grain level stresses are significantly lower than those required to cause appreciable slip. In the model, grain-to-grain interactions are assumed to be rigid (no grain boundary sliding or separation). As the implementation and use of these models are well established^2,30,31,32, and as this study considers elastic deformation, only a truncated description of the model as implemented in FEPX is included below. Please refer to ref. ²⁸ for a complete description of kinematics, models, and finite element implementation. For the uniaxial deformation studied in this work, loading is along the z direction in the sample frame.

At each point in a finite element mesh, FEPX considers the elastic response to be governed by the anisotropic form of Hooke’s law:

$${{{\boldsymbol{\sigma }}}}=\underline{{{{\boldsymbol{C}}}}}({{{\boldsymbol{r}}}}):{{{\boldsymbol{\varepsilon }}}},$$

(2)

where σ is the stress, $\underline{{{{\boldsymbol{C}}}}}$ is the lattice-orientation-dependent elastic stiffness tensor, r is the lattice orientation (a coordinate transformation from crystal frame to sample frame) of a given crystal, and ε is the strain, assumed to be fully elastic. Due to symmetry, crystals with cubic symmetry have three independent constants (${C}_{11}^{C}$, ${C}_{12}^{C}$, and ${C}_{44}^{C}$ in Voigt notation in the crystal frame), while crystals with hexagonal symmetry have five independent constants (${C}_{11}^{C}$, ${C}_{12}^{C}$, ${C}_{13}^{C}$, ${C}_{33}^{C}$, and ${C}_{44}^{C}$ in Voigt notation in the crystal frame). We note that due to the deformation decomposition formulation in FEPX, in hexagonal crystals further dependence is required in the form of ${C}_{33}^{C}={C}_{11}^{C}+{C}_{12}^{C}-{C}_{13}^{C}$. The elastic moduli employed for LSHR³³ in this work are: ${C}_{11}^{C}=247$, ${C}_{12}^{C}=147$, ${C}_{44}^{C}=$ 125 GPa, while the Ti-7Al³⁴ moduli are: ${C}_{11}^{C}=162$, ${C}_{12}^{C}=92$, ${C}_{13}^{C}=69$, ${C}_{33}^{C}=185$, and ${C}_{44}^{C}=$ 45 GPa.

In uniaxial deformation, the effective stiffness along the loading direction can be approximated using a directional modulus E(r). Generally, in grains embedded in polycrystals, the stress along the loading direction is correlated to the directional modulus³⁵. Under uniaxial stress along the z direction in the sample frame, the directional modulus is defined as:

$$E({{{\boldsymbol{r}}}})=\frac{{\sigma }_{zz}}{{\varepsilon }_{zz}({{{\boldsymbol{r}}}})}.$$

(3)

To further describe the anisotropy of the grains embedded within a polycrystal during uniaxial deformation, we define effective transverse contraction ratios ν_x(r) and ν_y(r):

$${\nu }_{x}({{{\boldsymbol{r}}}})=\frac{{\varepsilon }_{xx}({{{\boldsymbol{r}}}})}{{\varepsilon }_{zz}({{{\boldsymbol{r}}}})},$$

(4)

and

$${\nu }_{y}({{{\boldsymbol{r}}}})=\frac{{\varepsilon }_{yy}({{{\boldsymbol{r}}}})}{{\varepsilon }_{zz}({{{\boldsymbol{r}}}})}.$$

(5)

Each of the 50 virtual polycrystals generated (see: section “Virtual sample generation”) are deformed elastically in FEPX. As all uniaxial loading linear elasticity solutions can simply be scaled to account for increasing or decreasing deformation, each polycrystal is only deformed with a single deformation increment to an applied strain of 0.1% (chosen arbitrarily). Minimal displacement boundary conditions are employed on the top and bottom surfaces of the specimen to prevent rigid translation and rotation of the virtual specimens without impeding the contraction of the specimen perpendicular to the loading direction.

High-energy X-ray diffraction microscopy data

For the final GNN evaluation, graph data derived from experimentally measured microstructures and micromechanical response measured using HEDM are utilized. HEDM is comprised of two variants, near-field and far-field, capable of non-destructively characterizing the microstructure and micromechanical response of polycrystalline materials^36,37,38. The commonality between the two techniques is the utilization of forward projection simulations of X-ray diffraction peaks of individual grains to reconstruct information about the local lattice state of crystalline materials in 3D. LSHR and Ti-7Al samples were probed using the near-field variant to measure the grain structure, orientation, and connectivity of the grains, and the far-field variant was used to determine the stress in the same grains during elastic loading. Detailed descriptions of the data collection for the LSHR sample can be found in ref. ³⁹ and for the Ti-7Al sample in ref. ⁴⁰, but summaries of the methodology and specimens are given below.

The nf-HEDM technique is capable of reconstructing a 3D voxelized distribution of lattice orientation with resolution on the order of μm from a series of diffraction images collected as a specimen is rotated. In the near-field variant, the detector is placed ~5 to 10 mm away from the specimen, making the measurements sensitive to the spatial locations of diffracting volumes⁴¹. For this work, the LSHR and Ti-7Al microstructures were reconstructed with 5 μm voxel spacing. The reconstructed volume for the LHSR specimen was 1.0 mm × 1.0 mm × 0.5 mm with the short dimension aligned with the loading direction. Similarly, the reconstructed volume for the Ti-7Al specimen was 1.0 mm × 1.0 mm × 0.75 mm, again with the short dimension along the loading direction.

The ff-HEDM technique can reconstruct the average grain orientation, position, and elastic strain state of grains embedded in a polycrystal during in situ loading⁴². In this HEDM variant, a large area detector is placed approximately 1 m away from the specimen. This positioning provides more sensitivity to peak shifts due to changes in orientation and strain state, as opposed to locations of diffraction events as utilized for nf-HEDM reconstructions. Here ff-HEDM measurements collected prior to and during in situ elastic loading at two applied strain levels are used for GNN prediction evaluation. The full elastic strain tensors from individual grains are then used to calculate the stresses in each of the grains, including the component of stress along the loading direction which is of interest here. The uncertainty per elastic strain component for HEDM measurements are generally reported to be 1 to 3 × 10^−4 43 which corresponds to ~10 to 50 MPa per stress component depending on the material stiffness.

Graph neural network modeling

As previously described, the surrogate models employed in this work are graph neural networks (GNNs). The GNNs are comprised of layered graphs in which the features of each node in subsequent graph layers are weighted combinations (convolutions) of N_F nodal features from neighbors in the previous graph layer. The weights may be independent or functions of nodal or edge features and are learned throughout the training process. Similar to other neural network formulations, nonlinear activation functions (functions which control the flow of information between layers, i.e., nominally turning on and off) control the passing of nodal feature information between layered graphs. The input data is the graph itself—a set of nodes and a set of edges—along with features associated with the nodes and edges expected to be useful for predicting stress. Here graphs are generated from CEFEM or HEDM data using a series of custom Python scripts.

Nodal features represent different microstructural descriptors or local mechanical properties. Various nodal features, and combinations of nodal features, were explored, including the directional modulus (E(r)), contraction ratios (ν_x(r), ν_y(r)), volume (V), and lattice orientation (r, Rodrigues parameterization) of each grain. We note that no appreciable accuracy difference was observed utilizing different orientation parameterizations (e.g., Euler angles or other angle-axis parameterizations). These nodal features alone could be useful for predicting stress. However, rather than just treating all nodes independently, the GNN combines these features with the same features of connected nodes in the graph, along with additional edge features associated with the connections. The edge features used here for a connected pair of grains i and l are the coordinates of the vector between the grain centroids ${{{{\boldsymbol{p}}}}}_{i}$ and ${{{{\boldsymbol{p}}}}}_{l}$:

$${{{{\boldsymbol{e}}}}}_{il}={{{{\boldsymbol{p}}}}}_{i}-{{{{\boldsymbol{p}}}}}_{l}.$$

(6)

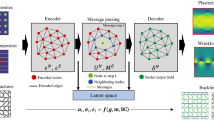
Rather than just looking at immediate connections, the GNN also works recursively, learning a vector representation of node features at subsequent layers. For this work, a common GNN architecture was utilized with two hidden graph layers. A schematic of the architecture is given in Fig. 10. Each node within the two hidden graph layers contains 16 features obtained from a convolution of the previous layer’s features over neighboring nodes. For the first hidden graph layer, the convolution is over the input nodal features. Two hidden graph layers provide substantial flexibility for learning the nonlinear relationship between grain lattice orientation and elastic response. After the two hidden graph layers, the second 16-dimensional vector representation of the nodal features is passed through a final dense layer that maps to a single nodal feature, which is the predicted stress tensor component σ_zz. In total, there are four layers: one input graph with the input nodal features, two hidden convolutional graphs with learned features, and the final mapping layer. While the number of nodal features in the two hidden graph layers could be slightly oversized for the problem at hand, over-fitting was only observed when very small amounts of training data were employed, as will be seen.

Fig. 10: Schematic of the GNN surrogate architecture used for this work.

An input graph with various sets of nodal features maps to a final output layer for predicting stress along the loading direction σ_zz.

The graph convolution operator used in the anisotropic elasticity surrogate models is a Gaussian Mixture Model⁴⁴, implemented in PyTorch Geometric⁴⁵, with the form (no sum over indices i and j):

$${x}_{ij}^{{\prime} }=\frac{1}{|{N}(i)|}\mathop{\sum }\limits_{k=1}^{{N}_{F}}{\theta }_{jk}\mathop{\sum}\limits_{l\in N(i)}{w}_{k}({{{{\boldsymbol{e}}}}}_{il}){x}_{lk},$$

(7)

where x is a nodal feature (either the initial inputs, or the learned vector representation in the hidden layers), i indicates node (grain) number ranging from 1 to N_G, k indicates a nodal feature in a current layer ranging from 1 to N_F, j indicates a nodal feature in a subsequent layer ranging from 1 to ${N}_{F}^{{\prime} }$, w is a Gaussian weighting function, l indexes a neighbor to grain i, N(i) is the set of indices of nodes connected to i, e_il is the vector of edge features between nodes i and l from Eq. (6), and θ is a (learned) weight for a given nodal feature in the current layer. The weighting functions are comprised of N_K Gaussian kernels:

$${w}_{k}({{{{\boldsymbol{e}}}}}_{il})=\mathop{\sum }\limits_{m=1}^{{N}_{K}}\exp \left(-\frac{1}{2}{({{{{\boldsymbol{e}}}}}_{il}-{{{{\boldsymbol{\mu }}}}}_{m})}^{T}{{{\boldsymbol{{{{\Sigma }}}}}_{m}}}({{{{\boldsymbol{e}}}}}_{il}-{{{{\boldsymbol{\mu }}}}}_{m})\right),$$

(8)

with μ_m and Σ_m being Gaussian kernel and diagonal covariance matrices. In total, θ, μ, and Σ are coefficients learned during the training process. Using the 3D vector between grain centroids as edge features (Eq. (6)), each layer in the neural network requires ${N}_{F}^{{\prime} }\times ({N}_{F}^{{\prime} }\times (1+{N}_{K}\times (3+3)))$ coefficients to be learned. The choice of a Gaussian Mixture convolution was informed by our physical understanding of deformation compatibility and mechanical equilibrium. In this model, GNN has sufficient degrees of freedom to weight various positions around a grain differently (e.g., parallel and transverse to applied uniaxial load). In addition, during the process of developing the GNNs presented in this work, several spectral- and spatial-based convolution operators were initially tested. In general, spatial-based convolutions performed better than spectral-based, consistent with our understanding of the spatial nature of stress equilibrium. The GM convolution operator presented here was the best performing, while many other common convolutional operators (such as that found here in ref. ⁴⁶) did not outperform the accuracy of more traditional mean-field theories, and as such, are not presented.

For the final fitting, seven Gaussian kernels (N_K = 7) were used for the Gaussian convolution operator in Eq. (8) with the goal of providing the surrogate model the freedom to weight neighborhood grains arranged in various positions differently (i.e., parallel and transverse to loading). Leaky ReLU was chosen for the activation function, with a scaling value of −0.1 for input values less than 0 as it provided better accuracy than a standard ReLU activation function. Training of the surrogate models was performed by minimizing the mean square error between grain average stress components in the training data and those predicted by the GNN surrogate model using Adam stochastic gradient descent with a learning rate parameter of 0.01. Training of a surrogate model for 10,000 epochs nominally takes 2–15 min depending on the amount of training data (1500 grains to 3000 grains) using an NVIDIA Quaddro GPU with 5 GB of memory.