Abstract
The ever-increasing capability of computational methods has resulted in their general acceptance as a key part of the materials design process. Traditionally this has been achieved using a so-called computational funnel, where increasingly accurate - and expensive – methodologies are used to winnow down a large initial library to a size which can be tackled by experiment. In this paper we present an alternative approach, using a multi-output Gaussian process to fuse the information gained from both experimental and computational methods into a single, dynamically evolving design. Common challenges with computational funnels, such as mis-ordering methods, and the inclusion of non-informative steps are avoided by learning the relationships between methods on the fly. We show this approach reduces overall optimisation cost on average by around a factor of three compared to other commonly used approaches, through evaluation on three challenging materials design problems.
Similar content being viewed by others
Introduction
Engineers and material scientists frequently seek to discover new materials that exhibit specific sets of properties. Most properties of active interest whether they be opto-electronic, structural, catalytic or physio-chemical have a complex relationship with the variables that are under experimental control. This fact, in combination with the vast number of synthesisable materials and the relatively high cost of experimental synthesis and characterisation is the central challenge of materials discovery1,2,3.
One tool in the material designers toolbox is the use of simulation as a proxy for experiment4. Due to the reduced cost of simulation over synthesis and characterisation of a material this offers the potential for orders of magnitude increases in the number of materials that can be evaluated during the materials discovery process. The mitigating factor for most cases of molecular and materials design is that given practical limits on computational resources, simulation is not sufficiently accurate to match experiment5. This means that materials discovery cannot proceed using simulation alone and consequently some means of combining simulation and experimental synthesis and characterisation must be used6. This remains the case despite the significant improvements in underlying electronic structure methods and the increases in computational resources that have occurred over the past decades.
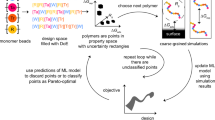
Inspired by drug discovery, the traditional way workflows make use of cheaper approximate measures is through the use of a screening approach known as a computational funnel7 –Fig. 1. Here, starting with cheap less accurate methods (e.g. QSAR models), increasingly more expensive and accurate methods including more complex simulation methodologies (e.g. molecular dynamics and/or ab-initio quantum calculations) and readily accessible experimental measures (e.g. single property measurements or spectroscopic characterisation in the materials discovery setting or in-vitro experiments in the drug discovery setting) are applied to screen out a smaller and smaller fraction of a potential material candidate pool eventually yielding a small set of highly promising candidates which can be evaluated using the most accurate experimental measurements (e.g. full experimental characterisation in the materials discovery setting or animal and human trials in the drug discovery setting).
An entire pool of molecules is evaluated with the cheapest and assumed least accurate method, a fixed fraction of the highest performing species are then evaluated with the next cheapest and assumed second least accurate method passing on a fixed fraction of the highest performing species to the next method. In this way the pool of candidate molecules progressively reduced until a final set of candidates remain.
Recently, emerging technologies such as machine-learning have driven ever-more efficient materials screening campaigns8,9. One particularly impactful approach has been to replace the expensive to evaluate simulations with data driven models, either through replacement of the potential energy calls10,11,12 or through direct modelling of the property of interest13,14,15.
Whilst computational funnels have proven successful, several disadvantages can be identified:
-
To construct the hierarchy of methods detailed upfront knowledge about the relative accuracies of each method along with its cost is required.
-
The total quantity of resources to be used in the entire design process need to be known and specified a priori.
-
The relative spread of resources amongst the different levels must also be known and specified a priori.
The first of these challenges is particularly relevant when integrating machine-learning models as layers within the funnel since it is often impossible to know the true accuracy of a data-driven model ahead of time, for an arbitrary data-point, since generalised performance is often intrinsically linked to the data and methods used to train the model, rather than the model itself.
In this paper, we present an alternative to the computational funnel for materials discovery which instead relies on an extension of Bayesian optimization that can make use of cheaper approximate measurements- Fig. 2. In our approach, a Bayesian model is constructed which dynamically learns to relate the different approximate methods and the ground truth experimental value (referred to here as the different methodological fidelities) to each other. This model is used to dynamically traverse the full set of candidate materials in a budget aware, accuracy aware manner. It is progressive rather than hierarchical, allows termination to be decided by the user rather than fixed ahead of time, is implicitly dynamic in its allocation of resources to the different methods and does not require knowledge of the accuracies of the different fidelities ahead of time.
For iteration i, the model is trained on data for all molecules and measured fidelities, then based on this new model (and a suitable acquisition function) a new target molecule and fidelity is chosen trading off exploration of new molecular species, exploitation of the areas of molecular space predicted to be good, the relative costs of evaluating the different fidelities and how informative those evaluations are likely to be.
Results and discussion
We demonstrate the effectiveness of our proposed approach through application to three hybrid simulation-experiment discovery challenges, comparing its performance to the commonly used computational funnel, and Bayesian optimization – an emerging approach to sample-efficient experimental design applied only to the target fidelity. We also investigate how fidelity cost and cross-correlation influence the behaviour of our approach relative to these reference methods through the use of a set of artificial functions where these factors can be directly controlled.
Multi-Fidelity machine learning
Whilst machine learning has shown strong potential as an emerging paradigm for rapidly generating predictions of materials’ properties of interest, as a data-driven technology its utility can be limited by the availability of high-quality data. An emerging approach to deal with this challenge is to build machine learning models built from multiple different fidelities of data, which can then act as predictors for cases where sufficient amounts of data are not available to build traditional QSAR or machine-learning models16,17. These approaches typically rely on building a model which is able to relate the different fidelities of information to each other, typically by building a single model with multiple output values – one per fidelity. It should be noted that this is distinct from the D-machine learning approach18, in which a single-output model learns a correction to apply to a low fidelity to better approximate a high-fidelity output. Applying multi-fidelity machine learning approaches to the materials domain has seen some notable early successes. For example, Chen et al. apply a multi-fidelity setting of a graph network to the prediction of band-gaps19. They found that the inclusion of information from a lower fidelity calculation, in their case using the Perdew-Burke-Ernzehof methodology20, led to an improvement in the mean absolute error they were able to achieve of between 22 and 45%. Similar information fusion approaches have been used in the polymer space, for example Patra et al. use a co-kriging scheme to fuse information from a variety of sources to build a predictive model for polymer bandgaps21. In their study, they observed both an increased performance over a single-fidelity Gaussian process approach, but also greater generalisation for their model.
Bayesian optimization
Bayesian optimisation is a family of sample efficient optimisers which balance the twin pressures of exploration (knowledge generation) and exploitation (knowledge utilisation) through the iterative construction of a scoring function based on Bayesian machine-learning models22. It has shown promise in diverse fields from hyper-parameter optimization23 to drug discovery24 to engineering25 to materials discovery26,27.
This scoring function - sometimes known as the acquisition function - relates the parameters being optimised to their expected utility given the current state of the model. Perhaps the most commonly used acquisition function is Expected Improvement (EI)28, which balances exploration and exploitation through considering both the likelihood of an improvement and its potential magnitude. Iterative training of the model, calculating posterior predictions followed by maximisation of the acquisition function then drives the candidate selection within the Bayesian optimization paradigm. Gaussian processes are the most commonly utilised Bayesian machine learning model for this task, though others such as Bayesian neural networks (BNNs) have also been effectively deployed29,30,31. We note that the proliferation of new Bayesian models such as BNNs which can scale to large data sizes together with advances that mitigate the cubic scaling32 previously associated with GPs mean that practical limitations that prevented Bayesian optimisation being applied large scale design problems are no longer the barrier they once were.
Multi-fidelity bayesian optimization
Inspired by the successes of the inclusion of lower fidelity information through multi-fidelity model building, and the emerging area of Bayesian optimization for materials screening, this paper extends standard approaches to Bayesian optimization of materials from a sample-efficient method for optimising a target property, to a multi-fidelity technique, capable of taking advantage of all available fidelities. Since this approach is agnostic to the source of the data, this naturally allows for combination of experimental and theoretical data in a way not achieved by current machine-learning driven screening approaches. To achieve this goal, it is necessary to build a model which is able to link data from each fidelity and draw inferences from the composite information. For this purpose, we utilise a multi-output Gaussian process33.
Multi-fidelity Bayesian optimization makes use of the same approach of iteratively training a probabilistic model and using it to rank possible materials for measurement. It extends the search space from a set of materials or molecules to a combination of these candidates and a choice of a particular measurement modality or fidelity. Therefore, given an effective acquisition function, it is possible to efficiently trade off information collection at cheap but noisy fidelities with targeted acquisition of data at the highest fidelity when required. Typically, the reason for employing such an approach is to reduce the total budget spent on the optimization, since the highest fidelity may be very technically or financially challenging to acquire. Throughout this paper we use the terms low fidelity and high fidelity to mean low expense and high expense for continuity of language with previous works in the field. We note, however, that our approach does not require that the accuracy and the cost of the fidelities be both monotonic and ranked, rather the only requirement is that a target fidelity be specified at the start of the optimization.
Different approaches to multi-fidelity optimization can be decomposed into choices modelling the relationships between the different fidelities and choices regarding how to construct the acquisition function. For example, Song et al. utilise a phased approach, with initial exploration performed using a low fidelity until some stopping criterion is hit, at which point high-fidelity data acquisition is considered34. Palizhati et al. consider both epsilon-greedy and lower-confidence-bound (LCB) settings to build multi-fidelity screening approaches. They found that the best results were when the entire low-fidelity data set was given as a priori knowledge to a multi-fidelity model, which resulted in acceleration of at least 20% on materials discovery tasks35. Our approach, which we name Targeted Variance Reduction (TVR), naturally extends arbitrary single fidelity Bayesian optimization acquisition functions to a multi-fidelity domain. The TVR algorithm is described in detail in the Methods section with pseudo-code presented in the ESI, but is summarised as follows: after computing a standard acquisition function on the target fidelity samples, (in this paper, we use the aforementioned EI acquisition function) the combination of the choice of input sample and fidelity is made by picking the pair that will minimise the variance of the model prediction at the point with the greatest acquisition function score per unit cost. This process is repeated iteratively until the budget is exhausted.
Synthetic data set
Approaches to screening challenges, such as those encountered in materials discovery, are affected by two main effects – the relative cost of making evaluations at the different fidelities, and the correlation between each of the fidelities. In an ideal system, cheaper fidelities are highly correlated both to each other, and to the target fidelity, enabling an efficient winnowing of the candidate pool without significant computational expense. In a worst-case scenario, fidelities are completely uncorrelated, essentially reducing each stage of a computational funnel to a lottery.
To demonstrate and systematically probe the effects of cost and accuracy of the lower fidelity proxies on optimisation based on computational funnels and the TVR-EI algorithm, we make use of a synthetic function as the target of our optimisation, and generate lower fidelity proxies in a manner that allows us to control the degree to which the lower fidelity is correlated to the ground truth target. We utilise Liu’s 1D function -Eq. (1) - as our target function, as it is complex enough to differentiate different optimization strategies, but not so complex as to obfuscate the effects of algorithmic component choices.
We generate a set of functions with differing degrees of correlation to our target function using our previously described method36 to act as the lower fidelity proxy to (1). Plotted examples of generated functions can be found in the ESI. To examine the effect of the relative cost we consider range of discount factors that express the degree to which the lower fidelity proxy is cheaper to evaluate than the target function.
The results of the experiments making use of the synthetic functions are seen in Fig. 3 which shows a heatmap indicating relative performance of TVR-EI, and a computational funnel. Performance is scored by the difference between the total computational cost the optimal computational funnel required to discover a solution scored at the 99th percentile best values and the total computational cost required by TVR-EI to discovery a 99th percentile value, averaged over computational replicates where a unit of cost is defined by the price of a single evaluation of the ground truth target. The two axes show the effect of the discount (in cost) of taking measurements using the lower fidelity proxy relative to the ground truth function and the Pearson correlation of the lower fidelity proxy to the ground truth function. The lower left corner of the grid is associated with expensive accurate proxies whilst the upper right corner is associated with cheap inaccurate proxies.
The x-axis shows the effect of varying the magnitude of the discount of the low fidelity measurement relative to a measurement of the actual target function, while the y-axis shows the effect of varying the correlation of the lower fidelity to the target function. Each cell in the heatmap is shaded to reflect the difference between the number of epochs taken by the computational funnel and TVR-EI. Positive (blue shading) indicates that the TVR-EI algorithm was more efficient, whilst negative (red shading) indicates that the computational funnel was more efficient.
The figure shows that for the synthetic case the TVR-EI algorithm outperforms when either the expense of the proxy is relatively high, or when the accuracy of the proxy is relatively high, whilst the computational funnel shows higher performance when the proxy is both lower cost and lower accuracy. The greater performance for both the expensive, yet inaccurate proxy functions and the cheap accurate proxies can be rationalised by TVR-EI’s capacity to dynamically adjust how it allocates budget based upon information gained during the optimization. Unlike a computational funnel, where budget is fixed and pre-allocated, TVR-EI can dynamically allocate more budget to proxies if it is determined that the proxy is informative, or less if the correlation is deemed to be low. We postulate that the utility of the funnel for cheaper lower accuracy proxies may be because TVR-EI is more sensitive to mismatches between the proxy and the target and thus can exhibit an overly conservative behaviour, avoiding proxies that can still be somewhat useful.
It can also be observed that the magnitude of the difference between the two methods is marked, with no score lower than −20 (i.e. the computational funnel effectively required 20 fewer target samples), but with the highest score over 100 (i.e. TVR-EI effectively required 100 fewer target samples).
Materials discovery challenges
Building from our understanding of the algorithm taken from its use on synthetic functions, we now test our approach on three materials discovery examples. A detailed description of these data sets can be found in the Data Sets section, but in summary each contain a mixture of computationally calculated and experimentally measured fidelities for impactful materials properties - polarizability (Alexandria), power conversion efficiency (HOPV-15) and band-gap (Chen).
As we have previously stated, computational funnels require the user to provision the computational budget in advance. It is worth noting that throughout this study we effectively assume that the funnel is capable of being provisioned perfectly, which is not a situation which reflects reality. Our primary point of comparison for each task is to a composite of funnels, where for each budget we run separate funnel which are provisioned with the specified budget and report the final performance of said funnel. This is contrasted with the other methods which are being run once and their performance tracked as they expend increasingly greater resources. We note that this represents an upper limit on the performance of a computational funnel – perfectly budgeted, ideally provisioned. A comparison of performance between TVR-EI, single fidelity EI, an ideally provisioned composite funnel and random (Monte Carlo) are shown in Fig. 4. In this study, we use ‘regret’ as a measure of performance, where a score of zero regret indicates that the best possible solution has been discovered. Here, regret was calculated with respect to an exhaustive search at the highest fidelity.
Normalised Regret vs. cost expenditure for the single fidelity EI, multi-fidelityTVR-EI, a composite of computational funnels and random search algorithms applied to the materials discovery challenges (a) Alexandria, b HOPV-15 and (c) Chen. The composite funnel displays results associated with separately provisioned funnels one for each potential budget value and the associated final regret of these funnels, it thus represents the best case scenario for the method. Median regret values are plotted from 15 optimisations with different random seeds. Shading shows the interquartile range of the runs.
We can observe that for each of these challenges, the multi-fidelity Bayesian optimisation approach using TVR-EI equals or betters the performance of both the computational funnel and the single fidelity EI method. However, as we would expect given the insight given by the varying of correlation and cost with the synthetic function, the behaviour of the different optimisation algorithms varies considerably among the different datasets.
Table 1 shows a numerical summary of performance of TVR-EI in comparison to an ideally provisioned composite funnel and expected improvement Bayesian optimization run on the target fidelity. We can measure performance in two ways:
-
Relative efficiency of the methodologies compared to TVR-EI (Expense multiplier in the table): Here a score of 1 means that the same budget is consumed, and greater than one means that TVR-EI was more efficient
-
Relative regret compared to TVR-EI: here we calculate how much worse a solution has been discovered by the comparison methods when TVR-EI has found the optimal solution. A score of zero means that the method has also discovered the optimal solution.
We observe that on average TVR-EI has an average efficiency gain of 2.8x compared to competitive methods analysed in this study, and an average normalised relative regret gain of 20%, indicating the potential for this approach to deliver significant improvements in materials screening challenges.
The Chen dataset results highlight the advantages of using well-correlated lower fidelity proxies with both the computational funnel and TVR-EI able to reach 99th percentile insulators with an order of magnitude reduction in cost relative to the random search baseline and a factor of 5 decrease in cost relative to the single fidelity EI optimisation. The good performance of the funnel can be attributed to the large difference in cost between the experimental target and computational surrogates. The relatively poor performance of a single fidelity Bayesian optimization approach suggests that the relationship between the molecular representations and the bandgap poses challenges to building a powerful internal model in the low data regime demanded by the high data acquisition cost. We posit that this could be due to a rough functional relationship, where small changes in structure can lead to large differences in bandgap, requiring a greater volume of data to resolve satisfactorily. Thus, this optimization challenge is characterised by informative proxies in combination with a relatively challenging optimisation target function. We see that TVR-EI offers comparable performance to the funnel. A breakdown of how the algorithm allocates its budget (Table 2) indicate that it achieves this by making significant use of the lower fidelities to focus on sampling only the most valuable of the more expensive experimental samples.
In contrast to the Chen dataset, for the HOPV dataset both the single the EI and the TVR algorithms were able to rapidly identify optimal candidates, significantly outperforming the random search baseline which itself significantly outperforms the computational funnel. We note that this problem represents the worst-case scenario for the computational funnel approach, and is characterised by reasonably constructed, yet poorly correlated fidelities, as demonstrated in Fig. 5. We also note that the success of the single fidelity Bayesian optimisation algorithm (EI) indicates that the functional relationship between the reduced dimensional representation and the experimental power conversion efficiency does not suffer pathologies.
Since this dataset is characterised by relatively expensive, yet mostly low-quality surrogate fidelities in combination with a relatively easy optimisation target function, it is easy to perceive why TVR-EI will outperform a computational funnel approach. This is born out through inspection of the budget allocation, which can be seen in Table 3, with a significant number of the samples being drawn from the target fidelity, despite the large cost of doing so. This indicates that the method has learned that for this target, the surrogate fidelities do not carry much information and once this is determined, allocates almost no budget to these fidelities. Further inspection of the breakdown of budget allocation can yield additional insights. For example, in this task, the MO6-2x fidelity is both relatively expensive and yet also uncorrelated to the target (see Fig. 5), and indeed TVR-EI consistently allocates almost no budget to investigating this fidelity. Additionally, Fig. 5 also shows that the PBE0 and B3LYP fidelities are strongly correlated, leading to the TVR-EI algorithm to consistently invest more budget into the cheaper PBE0 fidelity, given that the information content is similar. Correlation plots of the other two data sets can be found in the supplementary information.
In contrast to Chen and HOPV-15, which have been chosen to demonstrate situations that favour either a computational funnel or Bayesian optimization approach, the Alexandria dataset shows an intermediate case. Both the computational funnel and the single-fidelity EI method have comparable performance - despite achieving this performance through fundamentally different mechanisms - with both outperforming random searches. This indicates that the target function is effectively optimisable and that the balance of cost vs. correlation for the computational proxies means they are highly informative. For this challenge, we observe that our approach significantly outperforms both computational funnels and single-fidelity Bayesian optimization approaches, enhancing the signal exploited by the single fidelity Bayesian optimization approach with additional information taken from the lower fidelity approaches.
It is also informative to consider the effects of non-ideal provisioning, which is more akin to a real-world situation. The results of such a comparison are shown in Fig. 6. When comparing to a non-ideal (either over, or under, provisioned) funnel, we observe that the effects we describe throughout are enhanced. For the purposes of this study, we define an ideally provisioned funnel as the minimum budget required to reach zero regret in the median case, an over-provisioned funnel as having twice this budget, and an under provisioned funnel as having half this budget. An equivalent to Fig. 4 where the worst case is tracked in place of the median – thus providing a lower bound to the composite funnel performance – can be found in the ESI.
Normalised Regret vs. cost expenditure for ideally provisioned, under provisioned and over provisioned computational funnels alongside TVR-EI applied to the materials discovery challenges (a) Alexandria, (b) HOPV-15 and (c) Chen. The ideally provisioned funnel is defined as the funnel with the lowest possible budget that is able to achieve 0 median regret while the under-provisioned funnel is assigned half this budget and the over provisioned funnel is assigned twice this budget. In contrast to Fig. 4 these funnel results show the change in regret as the funnel uses its budget. Median regret values are plotted from 15 optimisations with different random seeds. Shading shows the interquartile range of the runs.
These three challenges span a range of thermochemical and optoelectronic properties including both experimental and computational value, and represent a wide spectrum of characteristics, designed to test our approach against a variety of situations in which it may reasonably be applied. In the datasets we have examined, we observe clear benefits can be seen to application of TVR-EI which matches or betters best case performance of the commonly used computational funnel and emerging Bayesian optimization methodology, while not requiring front loading of resources nor definitive knowledge of the relative accuracy of possible proxies. Our method is demonstrated to be robust to uninformative proxies and able to leverage internal correlations to remove the requirement to expend budget on proxies which share high correlation to lower cost alternatives. We believe that this demonstrates that our TVR-EI algorithm has promise as a tool for molecular and materials design where cheaper proxy measures are available as an alternative to the well-established computational funnel or single-fidelity Bayesian optimization methods, and establishes its utility for mixed simulation-experiment experimental designs.
Methods
Targeted variance reduction
Multi-Fidelity Targeted Variance Reduction (MF-TVR) is a conceptually simple algorithm. After computing a standard acquisition function on the target fidelity, in this case EI, the combination of the choice of input sample and fidelity is made by picking the pair that minimise the variance of the model prediction at the point with the greatest Expected Improvement, scaled by the cost of making the evaluation. We do not separate out the low fidelity search, and high fidelity exploit, into distinct stages, but instead use the lower fidelities to improve the quality of the acquisition function itself, thus directly impacting the sampling efficiency. These steps are illustrated graphically in Fig. 7 and pseudo-code for the TVR-EI algorithm can be found in the ESI.
a–f Show the 6 stages of the algorithm. Within each panel the top (blue) plots refer to the ground truth fidelity whilst the middle (green) and lower (orange) plots refer to the two approximate fidelities. a, b Show a set of initial data points (a) used to train a Bayesian model and the posterior predictions of that Bayesian model (b) juxtaposed against the reference fidelity functions (dashed lines). c Shows the Expected Improvement acquisition function applied to the high fidelity posterior used to discover the optimal high fidelity point which is highlighted with a dashed blue line. d Shows the posterior squared correlation between the identified optimal high fidelity point (location shown again with the dashed blue line) and points within the domain for the three different fidelities. e Shows the final scoring function which is a scaled version of d that takes into account the cost of evaluating the different fidelities and shows the highest scoring point chosen (shown with a dashed green line) which in this case is within the second fidelity. f Shows the new set of data points after evaluating the highest scoring point (indicated with the green circle).
Multi-output Gaussian process
In the case of a single fidelity GP, training data takes the form of a matrix of material representations X and corresponding property values \(\vec y\), and we have another matrix of representations X* for which we would like to make predictions. We suppose we have a kernel function defined by a set of hyperparameters, which is typically a universal smoothing kernel such as the radial basis function (RBF) or a Matern kernel. This kernel function can be used to compute prior covariances between vector representations of materials, and by extension can be used to compute a prior covariance matrix among a set of materials. The posterior predicted means for the materials to be evaluated are then given by:
where \(\overrightarrow {\mu _ \ast }\) is the vector of predicted mean values, K* is the prior covariance matrix between X and X* as determined by the kernel function, and K−1 is the inverse prior covariance matrix between X and X again as determined using the kernel function. Similarly, the posterior covariances for the materials to be evaluated are given by:
where σ* is the posterior covariance matrix between X* and X* and K** is the equivalent prior covariance matrix between X* and X*.
Hyper parameters of the kernel function can either be sampled or learned by maximising the log marginal likelihood of the training data37.
This setup can be extended to the multifidelity case by creating a representation for the fidelities and concatenating it with the representation of the materials. This allows us to make use of the same kernel functions to generate a prior sample-fidelity covariance matrix.
We choose to represent the fidelities via a one-hot encoding, where we drop the ground truth high fidelity dimension – this results in representing a fidelity by a vector with the number of dimensions equal to the number of approximate fidelities, with the high fidelity reference mapping to the zero vector, and the other fidelities mapping to the unit vectors in each axis. This choice to drop the dimension that would normally represent the high fidelity biases the model to care more about the relationship between the various fidelities and the high fidelity than between the lower fidelities themselves. This is of direct benefit to our use cases, since here we care explicitly about the former rather than the latter.
Thus the only addition to the single fidelity case defined above is that training/evaluation data for materials and property values have been replaced by training/evaluation data for material/fidelity combinations and property values. i.e. previously where the ith row of the matrix of material representations X corresponded simply to the vector \(\overrightarrow {x_i}\) representing material i, we now have rows defined by
where \(\overrightarrow {x_i^k}\) is the representation of the ith material at the kth fidelity, and \(\overrightarrow {f_k}\) is the one-hot representation of the kth fidelity.
The prior covariance matrix for multifidelity training data can be thought of as a block matrix by partitioning it according to the fidelities. The on-diagonal blocks of this matrix characterise correlation between materials measured within the same fidelity (and are therefore equivalent to the covariance matrices for corresponding single fidelity GPs), while the off-diagonal blocks characterise correlation between materials measured at different fidelities. By optimising or sampling kernel hyperparameters the degree to which lower fidelities are correlated with the ground truth measurements is learned; if within the training data a given approximate fidelity is not correlated with the ground truth high fidelity measurements then the length-scale associated with that fidelity’s one-hot encoded dimension will shrink and correspondingly the prior covariance between the measurements at that fidelity and ground truth measurements will tend towards zero, while the opposite will occur for fidelities that are highly correlated with the ground truth high fidelity function.
For our model, the full prior covariance matrix is constructed using a Matern 5/2 kernel in combination with automatic relevance determination. Hyperparameters are optimised via the log marginal likelihood.
Data sets
As previously stated, the three datasets used in this study were chosen to span a range of thermochemical and optoelectronic properties including both experimental and computational values. The three datasets selected were the Harvard organic photovoltaic dataset (HOPV)38, the Alexandria quantum chemical library (Alexandria)39 and the Chen Alchemical library40.
Harvard Organic Photovoltaic Dataset (HOPV)
350 molecular structures were extracted alongside their experimental power conversion efficiencies and computational analogs computed using the Scharber model41 built from energy levels calculated using four different density functionals - BP8642,43, PBE020,44, B3LYP42,45 and M062X46,47 in combination with the double-ζ def2-SVP basis set48. For this dataset the optimization target was to discover the material with the highest power conversion efficiency, with the computational analogs available as lower fidelity proxies. Costs for each fidelity were assigned as 1.0, 1.25, 1.75, 2.0 and 20.0 to evaluating at the BP86, PBE0, B3LYP, M062X level of theory and experiment respectively. Molecular structures were described using the SOAP descriptors49 which were reduced to a 20D representation using principle component analysis.
Alexandria dataset
946 structures were extracted from the Alexandria dataset, containing structure which had both experimental polarizabilities and computational analogs calculated at both the Hartree-Fock level of theory in combination with the 6-31 G** basis set50,51,52 and using the B3LYP functional42,45 in combination with the aug-cc-pVTZ basis set53,54. For this dataset the optimization target was to locate the material with the highest experimental polarisability with the HF and B3LYP calculations available as lower fidelity proxies for the experimental target. Costs for each fidelity were assigned at of 1.0, 2.0 and 6.0 to evaluating at the HF and B3LYP levels of theory and via experiment respectively. Molecular structures were described using MAACS keys55, which were reduced to 20D using a principle component analysis.
Chen dataset
1766 structures were extracted containing examples containing measurements of experimental bandgaps and a computational analog using the PBE functional using the projector augmented wave method and a 520 eV cut off. For this dataset the optimization target was to discover the most insulating i.e. highest bandgap material as determined by the experimental measurement with the PBE calculations available as lower fidelity proxies for the experimental target. Costs were assigned as 0.5 for evaluating the PBE calculated bandgap and 10 for evaluating the experimental values. Molecular structures were described using the SOAP descriptors49 which were reduced to a 20D representation using principle component analysis.
Code availability
Experiments were performed using IBM’s Bayesian Optimization Accelerator, a commercial program. In order to aid reproducibility, the authors have included implementation details, including pseudocode, for functions key to this paper as a dedicated section in the supplementary information.
References
Rajan, K. Combinatorial materials sciences: Experimental strategies for accelerated knowledge discovery. Ann. Rev. Mater. Res 38, 299–322 (2008).
Potyrailo, R. et al. Combinatorial and high-throughput screening of materials libraries: Review of state of the art. ACS combinatorial Sci. 13, 579–633 (2011).
Mennen, S. M. et al. The evolution of high-throughput experimentation in pharmaceutical development and perspectives on the future. Org. Process Res Dev. 23, 1213–1242 (2019).
Pyzer-Knapp, E. O., Suh, C., Gómez-Bombarelli, R., Aguilera-Iparraguirre, J. & Aspuru-Guzik, A. What is high-throughput virtual screening? A perspective from organic materials discovery. Ann. Rev. Mater. Res 45, 195–216 (2015).
Pyzer-Knapp, E. O., Simm, G. N. & Guzik, A. A. A Bayesian approach to calibrating high-throughput virtual screening results and application to organic photovoltaic materials. Mater. Horiz. 3, 226–233 (2016).
Bajorath, J. Integration of virtual and high-throughput screening. Nat. Rev. Drug Disco. 1, 882–894 (2002).
Hautier, G. Finding the needle in the haystack: Materials discovery and design through computational ab initio high-throughput screening. Comput. Mater. Sci. 163, 108–116 (2019).
Suh, C., Fare, C., Warren, J. A. & Pyzer-Knapp, E. O. Evolving the materials genome: How machine learning is fueling the next generation of materials discovery. Ann. Rev. Mater. Res 50, 1–25 (2020).
Pyzer-Knapp, E. O. et al. Accelerating materials discovery using artificial intelligence, high performance computing and robotics. NPJ Comput. Mater. 8, 1–9 (2022).
Smith, J. S., Isayev, O. & Roitberg, A. E. ANI-1: An extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci. 8, 3192–3203 (2017).
Behler, J. Representing potential energy surfaces by high-dimensional neural network potentials. J. Phys.: Condens. Matter 26, 183001 (2014).
Behler, J., Martoňák, R., Donadio, D. & Parrinello, M. Metadynamics simulations of the high-pressure phases of silicon employing a high-dimensional neural network potential. Phys. Rev. Lett. 100, 185501 (2008).
Pyzer-Knapp, E. O., Li, K. & Aspuru-Guzik, A. Learning from the harvard clean energy project: The use of neural networks to accelerate materials discovery. Adv. Funct. Mater. 25, 6495–6502 (2015).
Balachandran, P. V. Machine learning guided design of functional materials with targeted properties. Comput. Mater. Sci. 164, 82–90 (2019).
Chibani, S. & Coudert, F.-X. Machine learning approaches for the prediction of materials properties. APL Mater. 8, 080701 (2020).
Meng, X. & Karniadakis, G. E. A composite neural network that learns from multi-fidelity data: Application to function approximation and inverse PDE problems. J. Comput. Phys. 401, 109020 (2020).
Yang, C.-H. et al. Multi-fidelity machine learning models for structure–property mapping of organic electronics. Comput. Mater. Sci. 213, 111599 (2022).
Ramakrishnan, R., Dral, P. O., Rupp, M. & von Lilienfeld, O. A. Big data meets quantum chemistry approximations: The Δ-machine learning approach. J. Chem. Theory Comput. 11, 2087–2096 (2015).
Chen, C., Zuo, Y., Ye, W., Li, X. & Ong, S. P. Learning properties of ordered and disordered materials from multi-fidelity data. Nat. Comput Sci. 1, 46–53 (2021).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Patra, A. et al. A multi-fidelity information-fusion approach to machine learn and predict polymer bandgap. Comput. Mater. Sci. 172, 109286 (2020).
Brochu, E., Cora, V. M. & de Freitas, N. A. Tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and Hierarchical reinforcement learning. Preprint at https://arxiv.org/abs/1012.2599
Kandasamy, K. et al. Tuning hyperparameters without grad students: Scalable and Robust Bayesian optimisation with dragonfly. J. Mach. Learn. Res. 21, 1–27 (2020).
Pyzer-Knapp, E. Bayesian optimization for accelerated drug discovery. IBM J. Res Dev. 62, 2–1 (2018).
Lam, R., Poloczek, M., Frazier, P. & Willcox, K. E. Advances in Bayesian optimization with applications in aerospace engineering. In 2018 AIAA Non-Deterministic Approaches Conference 1656 (2018).
Pyzer-Knapp, E. O., Chen, L., Day, G. M. & Cooper, A. I. Accelerating computational discovery of porous solids through improved navigation of energy-structure-function maps. Sci. Adv. 7, eabi4763 (2021).
Zhang, Y., Apley, D. W. & Chen, W. Bayesian optimization for materials design with mixed quantitative and qualitative variables. Sci. Rep. 10, 1–13 (2020).
Mockus, J. The Bayesian approach to global optimization. in System Modeling and Optimization 473–481 (Springer, Berlin, Heidelberg, 1982).
Springenberg, J. T., Klein, A., Falkner, S. & Hutter, F. Bayesian optimization with robust Bayesian neural networks. Adv. Neural Inform. Process. Sys. 29, 2171–2180 (2016).
Snoek, J. et al. Scalable Bayesian Optimization Using Deep Neural Networks. arXiv Preprint at https://arxiv.org/abs/1502.05700 (2015).
Hernández-Lobato, J. M., Requeima, J., Pyzer-Knapp, E. O. & Aspuru-Guzik, A. Parallel and distributed Thompson sampling for large-scale accelerated exploration of chemical space. in International Conference On Machine Learning 1470–1479 (PMLR, 2017).
Wang, K. A. et al. Exact Gaussian Processes on a Million Data Points. Preprint at https://arxiv.org/abs/1903.08114 (2019).
Liu, H., Cai, J. & Ong, Y.-S. Remarks on multi-output Gaussian process regression. Knowl. Based Syst. 144, 102–121 (2018).
Song, J., Yuxin, C. & Yue, Y. A General Framework for Multi-fidelity Bayesian Optimization with Gaussian Processes. The 22nd International Conference on Artificial Intelligence and Statistics. PMLR, 2019.
Palizhati, A., Aykol, M., Suram, S., Hummelshøj, J. S. & Montoya, J. H. Multi-fidelity Sequential Learning for Accelerated Materials Discovery. Preprint at https://doi.org/10.26434/chemrxiv.14312612.v1 (2021)
Fare, C., Fenner, P. & Pyzer-Knapp, E. O. A Principled Method for the Creation of Synthetic Multi-fidelity Data Sets. Preprint at https://arxiv.org/abs/2208.05667 (2022).
Rasmussen, C. & Williams, C. Gaussian Processes for Machine Learning. (MIT Press, 2006).
Lopez, S. A. et al. The Harvard organic photovoltaic dataset. Sci. Data 3, 1–7 (2016).
Ghahremanpour, M. M., Van Maaren, P. J. & Van Der Spoel, D. The Alexandria library, a quantum-chemical database of molecular properties for force field development. Sci. Data 5, 1–10 (2018).
Chen, G. et al. Alchemy: A quantum chemistry dataset for benchmarking ai models. Preprint at https://arxiv.org/abs/1906.09427 (2019).
Scharber, M. C. et al. Design rules for donors in bulk-heterojunction solar cellstextemdashtowards 10% energy-conversion efficiency. Adv. Mater. 18, 789–794 (2006).
Becke, A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38, 3098–3100 (1988).
Perdew, J. P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 33, 8822–8824 (1986).
Perdew, J. P., Ernzerhof, M. & Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 105, 9982–9985 (1996).
Becke, A. D. Densityfunctional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Zhao, Y. & Truhlar, D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 120, 215–241 (2008).
Zhao, Y. & Truhlar, D. G. Density functionals with broad applicability in chemistry. Acc. Chem. Res. 41, 157–167 (2008).
Weigend, F. & Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 7, 3297–3305 (2005).
Bartók, A. P., Kondor, R. & Csányi, G. On representing chemical environments. Phys. Rev. B 87, 184115 (2013).
Hehre, W. J., Stewart, R. F. & Pople, J. A. SelfConsistent molecularorbital methods. I. Use of gaussian expansions of slatertype atomic orbitals. J. Chem. Phys. 51, 2657–2664 (1969).
Hehre, W. J., Ditchfield, R., Stewart, R. F. & Pople, J. A. SelfConsistent molecular orbital methods. IV. Use of gaussian expansions of slatertype orbitals. extension to secondrow molecules. J. Chem. Phys. 52, 2769–2773 (1970).
Hehre, W. J., Ditchfield, R. & Pople, J. A. Self—consistent molecular orbital methods. XII. Further extensions of Gaussian—type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys. 56, 2257–2261 (1972).
Kendall, R. A., Dunning, T. H. Jr. & Harrison, R. J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 96, 6796–6806 (1992).
Woon, D. E. & Dunning, T. H. Jr. Benchmark calculations with correlated molecular wave functions. I. Multireference configuration interaction calculations for the second row diatomic hydrides. J. Chem. Phys. 99, 1914–1929 (1993).
Durant, J. L., Leland, B. A., Henry, D. R. & Nourse, J. G. Reoptimization of MDL keys for use in drug discovery. J. Chem. Inf. Comput. Sci. 42, 1273–1280 (2002).
Acknowledgements
This work was supported by the Hartree National Centre for Digital Innovation, a collaboration between Science and Technology Facilities Council and IBM.
Author information
Authors and Affiliations
Contributions
E.P.K. and C.F. conceived the project, E.P.K. supervised the project, C.F., P.F., and A.V. performed the computational experiments and all authors analysed the output of the experiments and contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fare, C., Fenner, P., Benatan, M. et al. A multi-fidelity machine learning approach to high throughput materials screening. npj Comput Mater 8, 257 (2022). https://doi.org/10.1038/s41524-022-00947-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-022-00947-9