Physics-embedded graph network for accelerating phase-field simulation of microstructure evolution in additive manufacturing

Abstract

The phase-field (PF) method is a physics-based computational approach for simulating interfacial morphology. It has been used to model powder melting, rapid solidification, and grain structure evolution in metal additive manufacturing (AM). However, traditional direct numerical simulation (DNS) of the PF method is computationally expensive due to sufficiently small mesh size. Here, a physics-embedded graph network (PEGN) is proposed to leverage an elegant graph representation of the grain structure and embed the classic PF theory into the graph network. By reformulating the classic PF problem as an unsupervised machine learning task on a graph network, PEGN efficiently solves temperature field, liquid/solid phase fraction, and grain orientation variables to minimize a physics-based loss/energy function. The approach is at least 50 times faster than DNS in both CPU and GPU implementation while still capturing key physical features. Hence, PEGN allows to simulate large-scale multi-layer and multi-track AM build effectively.

Introduction

Metal additive manufacturing (AM) processes fabricate geometrically complex parts by melting metal powders layer-by-layer with a focused laser or electron beam^1,2. Breaking the design constraints of traditional manufacturing routes, metal AM has gained increased popularity in the past years³. Metal AM usually results in irregular and complex polycrystalline microstructures due to various processing conditions such as the heat source power, scanning speed and strategy, etc^4,5,6. These microstructures are often featured with long, curved columnar grains⁷ and having various orientations^4,8. The microstructure significantly affects the functions and properties of the AM as-built parts in a variety of ways, such as mechanical properties (e.g., tensile strength⁹, fatigue properties³, fracture modes¹⁰), thermal conductivity¹¹, electrochemical/corrosion properties^12,13, electrical conductivity¹⁴, etc. Therefore, it is of critical importance to understand and predict microstructure evolution during metal AM processes.

Being cost-effective compared with experimentation, numerical simulation techniques have made remarkable progress as a powerful tool to help understand metal AM processes, in particular microstructure evolution. There are three commonly adopted approaches for simulating microstructure evolution in AM processes: the cellular automata (CA) method^15,16, Kinetic Monte Carlo (KMC)^17,18, and the phase-field (PF) method^19,20,21. Among them, the PF method is regarded as a relatively accurate method due to its detailed modeling of relevant physics and thermodynamically-consistent foundations^21,22. The PF method is used to solve interfacial problems and has wide applications in crystalline structure modelling²³, cell biology^24,25, fracture mechanics^26,27, etc. However, the high-fidelity PF method is plagued by being extremely expensive in computation because it usually requires to solve a system of coupled partial differential equations for a set of continuous field variables and the spatial discretization must be fine enough to resolve microstructure features like grain boundaries. The majority of existing PF simulations for microstructure evolution during metal AM processes are in two dimensions^19,28,29. Chadwick and Voorhees²⁰ proposed a 3D PF modeling framework that tracks solidification 316L stainless steel in AM processes, but the simulation only considers a single-layer and single-track process in a 192 μm × 76.8 μm × 38.4 μm domain. Yang et al.²¹ developed a 3D PF model that simulates a three-layer three-track powder bed fusion process, where notably the simulation had 17.88 million finite difference cells and took about 13 days to finish. In this work, we propose a graph-network-based modeling approach that significantly accelerates the phase-field simulation (about 50 × faster in our numerical experiments) while achieving an accuracy level that is comparable to the direct numerical simulation (DNS) approach. Our main contribution is to break the curse of scalability of the PF method. We are able to simulate a typical millimeter-scale AM build with 10+ layers and multiple scan tracks within only several hours.

Our method reformulates the classic PF problem using a framework we refer to as physics-embedded graph network (PEGN). By leveraging machine learning (ML) algorithms such as message-passing on graph³⁰, we are able to solve the problem in a computationally efficient way. Broadly speaking, graph networks are a class of machine learning methods that operate on graph-like data structures. As noted in³¹, graph networks carry strong relational inductive biases that facilitate the description of graph nodal entities and their relations. Graph networks have been widely applied in many scientific and engineering problems, such as visual scene understanding³², predicting lattice structure dynamics³³, predicting chemical properties of molecules³⁴, etc. Of particular relevance to this work, graph networks have recently been used to describe material microstructures and have been demonstrated as distinguished representations of polycrystal structures. Xie et al.³⁵ proposed a crystal graph convolutional neural network framework to learn material properties from the connection of atoms in the crystal. Graph data structures were employed to study anisotropic constitutive relations of hyperelastic polycrystals in³⁶. Dai et al.³⁷ developed a graph neural network model to accurately predict the magnetostriction of polycrystalline alloys.

Although the term ‘graph neural networks’ may be better known than ‘graph networks’, the functions that graph networks employ do not need to be neural networks³¹. In fact, our PEGN approach does not contain any neural networks. The core of the proposed PEGN is to formulate the discretization of PF equations as a machine learning problem on a graph, inspired by recent findings³⁸ where it was shown that deep graph neural networks can be viewed as the discretization of an underlying diffusive partial differential equation. PEGN offers a perspective of efficiently solving the PF problem in metal AM. We use powder bed fusion (PBF) of 316L stainless steel as a testing bed for demonstrating the effectiveness of the proposed PEGN. Furthermore, we compare the PEGN with the classic DNS approach with the finite difference method in several key aspects such as temperature field, melt pool development and grain evolution, which demonstrates the proposed approach can speed up the PF method by orders of magnitude while preserving significantly high accuracy.

Results

The section is structured as follows. We first introduce the key ingredients of the PEGN in Section hysics-embedded graph network. Then in Section Single-layer single-track simulation we present a detailed comparison between DNS and PEGN using a single-layer single-track example as a benchmark. In the comparison, we focus on both qualitative and quantitative evaluations of temperature field, melt pool development and grain evolution. Finally in Section Multi-layer multi-track simulation, we present several multi-layer multi-track AM simulation examples to demonstrate the scalability of the PEGN.

Physics-embedded graph network

An overview of the proposed method is presented in Fig. 1. We view the microstructure evolution problem as a machine learning task defined on a graph network. The process of dynamic microstructure evolution is treated analogous to the message-passing³⁰ procedure of a graph network. In a typical machine learning task, loss function is defined and learnable parameters are trained to minimize the loss value. In our problem, a physics-based free energy F(θ) is defined and those dynamic features θ are solved to minimize the free energy. As shown in Fig. 1, by taking the gradient of the free energy we obtain the set of governing differential equations $\frac{{{{\rm{d}}}}{{{\boldsymbol{\theta}}}}}{{{{\rm{d}}}}t}=-{{{\bf{L}}}}\frac{\partial F}{\partial {{{\boldsymbol{\theta }}}}}$, where L are the pre-coefficients and will be discussed in Section PEGN approach. Note that this can be viewed as a gradient flow problem³⁹. A time integration scheme like explicit Euler gives ${{{{\boldsymbol{\theta}}}}}^{n+1}={{{{\boldsymbol{\theta}}}}}^{n}-\Delta t{{{\bf{L}}}}\frac{\partial F}{\partial {{{\boldsymbol{\theta}}}}}{\left|\right.}_{{{{{\boldsymbol{\theta}}}}}^{n}}$, which recovers the predominant gradient descent algorithm in machine learning. While F(θ) may depend on θ in a complicated way (see details in Equations 11 to 14), we use backpropagation, i.e., reverse-mode automatic differentiation⁴⁰ for an automated computation of the derivative $\frac{\partial F}{\partial {{{\boldsymbol{\theta}}}}}$. In the context of training a neural network, backpropagation refers to find out the derivative of the loss function with respect to weights. In our work, it means to find out the derivative of the energy function F(θ) with respect to θ. Compared to grid-based spatial discretization method used in DNS, PEGN essentially perform spatial discretization with a graph that respects the initial grain structure. The phase-field physics is mapped into the framework of the graph network by considering each individual grain and adjacent grain interactions. We leave the detailed description of the PEGN method to Section PEGN approach.

Fig. 1: An overview of the PEGN approach using single-layer single-track PBF as an example.

In (a), the polycrystalline structure is interpreted as an undirected graph, with associated node features and edge features. In (b), PEGN updates dynamic node features θ such as temperature and grain orientation variables in iterations. The computational iterations can be viewed as solving a machine learning problem on graph using gradient descent method.

Single-layer single-track simulation

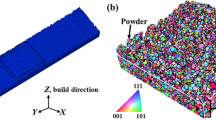
As a first example, we consider a single-layer single-track PBF process. As shown in the upper left part of Fig. 1a, the simulation domain (1000 × 400 × 100 μm³) consists of equiaxed grains with different orientations colored by the IPF (inverse pole figure) color with respect to the build direction (z-axis). For memory efficiency, 20 randomly generated orientations are used and each grain is randomly assigned with one of these orientations at the initial step. Those random orientations are shown in Supplementary Fig. 2. A total number of 40,000 grains are generated using the open source software package Neper⁴¹ for polycrystal generation. The laser beam scanning starts at position (200, 200, 100) μm and ends at position (800, 200, 100) μm using 1200 μs with a uniform scan speed of 0.5 m ⋅ s⁻¹. After scanning, we simulate an additional 1800 μs time period for cooling down the sample. Material parameters are shared between DNS and PEGN, and can be found in Supplementary Table 1.

Besides the proposed PEGN-based simulation, we have also implemented a classic finite difference method as a direct numerical simulation (DNS) approach serving as the ground truth, and its implementation generally follows the previous work²¹. In the following sections, we will compare the simulation results of DNS and PEGN in three aspects: temperature field, melt pool morphology, and grain evolution. In all these comparisons, PEGN shows consistent outcomes with DNS.

Temperature field

The full-field tempo-spatial temperature evolution is solved on the fly with other variables like grain orientations. We treat the laser heat source used in the PBF process as a time-dependent heat flux boundary condition on the top surface of the domain, while convection and radiation boundary conditions are considered with an ambient temperature. Figure 2a, b show the temperature profile at t = 1200 μs, at which time the laser finishes scanning. Note that PEGN inherently uses a graph network representation of the temperature field, and Fig. 2b shows a reconstructed profile using a polyhedron mesh for clearer visualization.

Fig. 2: Comparison of temperature profiles between DNS and PEGN.

In (a) and (b), the color map ranges from ambient temperature 300 K to melt point 1700 K. In (c), the temperature history of the center point on the top surface is shown. In (d), the temperature profile along the center line on the top surface is shown.

Quantitatively, we select the center point (position = (500, 200, 100) μm) on the top surface and show its temperature history in Fig. 2(c). As seen, the temperature history by DNS and PEGN match almost exactly for the center point. The temperature field is in an one-way coupling with the liquid/solid fraction variable and grain orientation field, and we have made a truncation to 2000 K for the coupling to avoid spuriously high temperature values. As another example, we fix the time frame (t = 1200 μs) and check the temperature profile along the center line of the top surface, and show the result in Fig. 2(d). It is observed that DNS and PEGN produce similar temperature profiles.

Melt pool morphology

Melt pool dynamics is an important subject to study since it reflects the interactions between PBF process parameters and materials solidification. The solid/liquid fraction field ζ is part of the DNS or PEGN solutions and is used to represent melt pool development. The variable ζ continuously varies from 0 to 1, indicating a transition from liquid state to solid state. The melt pool is identified for regions with ζ < 0.5. We select five consecutive time frames and show the melt pool morphology in Fig. 3. The melt pool marches towards the positive x-axis direction, transforms into a long and shallow shape, and shrinks after the laser is turned off at t = 1200 μs. As shown, PEGN is capable of producing a qualitatively similar morphology as compared with DNS.

Fig. 3: Comparison between DNS and PEGN.

A sequence of melt pool development is illustrated for different time steps.

For quantitative comparison, we evaluate the length, width, height, and volume of the melt pool. These quantities evolve with time and are shown in Fig. 4. In general, we observe good agreements between DNS and PEGN results. For the melt pool height, there is a discrepancy of around 0.01 mm, which is roughly at the scale of one grain.

Fig. 4: Quantitative comparison of melt pool shape evolution between DNS and PEGN.

In (a), (b), and (c), melt pool length, width, and height are shown with respect to time. In (d), melt pool volume is shown.

Grain evolution

A central task in this work is to predict microstructure evolution in PBF process. The variables to solve are grain orientations η using one-hot encoding⁴² to indicate which orientation a certain grain takes. The DNS approach is implemented under the framework of the classic phase-field method^43,44. In contrast, the proposed PEGN method solves the phase-field problem defined on a graph³⁹. Here, we select five consecutive time frames and show grain evolution in Fig. 5, where the IPF color with respect to the z-axis indicates grain orientations. In Fig. 5, the melt pool regions have been removed, and only the solid parts are shown. The phenomenon of epitaxial grain growth is reproduced such that grains continuously grow from previously solidified regions into the newly solidifying area. Near the melt pool boundary, it is also observed that grain coarsening in heat-affected zones occurs so that smaller grains merge into larger grains.

Fig. 5: Comparison of grain evolution between DNS and PEGN at various time steps.

The size is (1000 × 200 × 100 μm³), which is half of the entire simulation domain.

We perform quantitative comparisons of grain size and grain morphology between DNS and PEGN. First, we inspect the total number of grains in all solidified areas of the scanning track, and show the result in Fig. 6a. It is observed that both curves of DNS and PEGN first peak around 1400 μs, then decrease due to grain coarsening, and finally approach a stable value during the cool down process. In Fig. 6b, the trend of average grain volume is shown to be increasing with time for both DNS and PEGN. To study grain morphology, we compute the aspect ratio Φ = 2a/(b + c) defined to be the ratio between the longer axis and shorter axes of the ellipsoid equivalent to the grain shape. The definition of aspect ratio is made clear in the diagram of Fig. 6c, where the histogram plot of aspect ratio at the final time step for both DNS and PEGN are shown. It is observed that the the aspect ratios of DNS and PEGN follow a similar distribution. The distribution exhibits a long-tailed feature, demonstrating the existence of long columnar grain structures. The median of aspect ratio for DNS is 1.71 and that of PEGN is 1.62, showing that columnar grains are predominant over equiaxed grains. The observation can also be made from Fig. 5, where the slanted inward columnar grains eventually lead to anisotropic mechanical properties of the as-built components⁷. Nevertheless, the results above show that PEGN is capable of generating grains with size and morphology comparable with that from DNS.

Fig. 6: Quantitative comparison of grain size and morphology between DNS and PEGN.

In (a), the total number of grains along the scanning track is shown with respect to time. In (b), the average grain volume with respect to time is shown. In (c), the empirical distribution of aspect ratio at the final time step is plotted. The number of grains is 40,000 and the number of unique grain orientations is 20.

To study how the quantitative comparison results in Fig. 6 are affected by several key factors including the number of initial grains and grain orientations, the initial size distribution of the grains, as well as the laser parameter, we perform additional numerical experiments and report the results and discussion in Supplementary Note 5. In most cases, PEGN agrees well with DNS.

Since PEGN models grain growth by combining adjacent grains with the same orientation, it is worthwhile tracking the growth kinetics of a given individual grain so that the discrepancy between PEGN and DNS is understood better. In Fig. 7, we first filter out a group of grains with the same orientation, and then focus on the growth of a single grain for both DNS and PEGN. We show the morphology of these two selected grains and their growing history from t = 1500 μs to t = 3000 μs. The two selected grains from DNS and PEGN both grow into irregular shapes. The morphology difference between DNS and PEGN is caused partly by their different underlying spatial discretization schemes (structured grid for DNS and graph for PEGN). Quantitatively, we compute the evolving history of volume and surface area of these two grains, and show the comparison in the bottom part of Fig. 7, whose trends are similar.

Fig. 7: Comparison of individual grain growth kinetics between DNS and PEGN.

We select a set grains with the same orientation and show the grain volume and surface area of a typical grain for both DNS and PEGN.

Computational efficiency

In previous sections, we have made detailed comparisons between DNS and PEGN in terms of temperature field, melt pool development and grain evolution. It has been shown that the proposed PEGN is able to produce consistent outcomes with DNS results. The key advantage of PEGN, however, lies in that it is computationally more efficient than the DNS.

In this single-layer single-track example, the DNS domain is discretized into 3,969,984 finite difference cells and the cells are connected with 11,793,748 edges. Each cell stores a total number of 22 degrees of freedom (1 for temperature, 1 for solid/liquid fraction, 20 for grain orientation). The number of explicit time integration steps is 15,000. In constrast, the PEGN uses a graph network for discretization, and the total number of nodes is only 40,000 (each node represents a single grain) and the number of edges is 289,986. Each node stores a total number of 22 degrees of freedom, and the number of time integration steps is 15,000.

The wall time measurement of DNS is 1298 seconds, while it is 25 seconds for PEGN, both performed on an NVIDIA Quadro RTX 8000 GPU with 48 GB Graphics memory. The proposed PEGN is therefore 52× faster than the classic PF DNS method. When performing wall time measurement, we have disabled all I/O processing and only focused on the simulation itself. In fact, DNS requires much more time for I/O processing, which gives PEGN extra advantage in computational savings. Note that the number of total degrees of freedom for DNS is around 100× of PEGN, while the acceleration is only around 50×. The acceleration ratio is due to another limiting factor that the number of edges in DNS is only 40× of PEGN. To further study the effect of the initial number of grains and grain orientations on the computational performance, we perform additional numerical experiments and analyze the results in Supplementary Note 4.

In terms of space, PEGN consumes less memory than DNS, and is promising for larger scale simulations that requires a large amount of memory. For completeness, the same program also runs on a CPU (2.4 GHz 8-Core Intel Core i9) with 32 GB memory. The wall time for DNS is about 29 hours, while it is 2018 seconds for PEGN. The simulation on CPU for PEGN is also around 52 times faster than DNS, a result consistent with our findings on GPU.

Multi-layer multi-track simulation

Adaptive computational scheme

The scalability of PEGN in both computational time and space allows for simulation of larger size problems that are practically difficult for DNS method. Here, we employ PEGN to perform a multi-layer multi-track simulation of the PBF process. Figure 8(a) shows the layered computational domain with size (2 × 2 × 1 mm³). For each layer, the graph contains 200,000 nodes so that the entire domain has 4,000,000 nodes, with 22 degrees of freedom attached to each node. Since most critical physical processes like grain evolution only happen in the top few layers (the other layers is fully cooled solid structure), our strategy is to limit the simulation domain to only the current top two layers so that computational resources can be saved. The description of this strategy is illustrated in Fig. 8(a), where in each iteration, we take the current top layer from last iteration as the initial condition (the green layer), combine it with the newly added layer (blue layer), and perform the simulation using the domain that consists of these two layers. The procedure is then repeated for all of the 20 layers, and the entire simulation takes around 6.5 hours on GPU.

Fig. 8: A multi-layer multi-track example that builds within a 2 × 2 × 1 mm³ domain.

In (a), a local computational strategy that focuses on only two layers in each iteration is presented. In (b), the laser scanning path for each layer is shown. In (c), the full domain is shown. In (d) and (e), the 3D as-built sample and a representative cross-sectional view of the microstructure are visualized. The IPF color is along the z-axis. Scale bar in (e) is 0.2 mm.

The scanning path is shown in Fig. 8b that resembles the acronym ‘NU’, and is kept the same for a total number of 20 layers, each having a thickness of 0.05 mm. In Fig. 8c, we show the grain structure of the entire simulated domain. The grain structure of the as-built sample is shown in Fig. 8d, with one representative y-z plane cross sectional view shown in Fig. 8e. The simulation is able to take account of re-melting and re-solidifying of grains and that columnar grains across several layers are formed (see Fig. 8e). Due to the repeated directional scanning of multiple layers, a number of grains show an angle of inclination of around 60^∘, which is aligned with the inclination angle of the melt pool during the scanning process. This pattern is also found in previous works both with simulation¹⁶ and experiment⁵. In Fig. 8d, we observe a clearly layered surface of the as-built sample, which can be explained due to melt pool shape along the scanning path. Note that in this case we are not just building the ‘NU’ pattern in 3D while the other part of a layer is vacant. The additive manufacturing process is assumed to be a laser-based powder bed fusion, so the black region in Fig. 8b also contains randomly generated grains representing unmelted powder. In the case where the black region is vacant, the grain structure near the boundaries will not be affected by surrounding grains, and we anticipate the grain structures will respect their initial orientations better.

Effect of scan strategies

Laser scan strategies have critical effects on the development of microstructure and texture during PBF process^45,46. With PEGN, we can now study the effect of scan strategies by considering a 10-layer building process with a computational domain of size (2 × 2 × 0.5 mm³), as shown in Fig. 9. We consider two different scan strategies and compare the generated grain structures. As in Fig. 9a, the first scan strategy is unidirectional for all scanning tracks within each layer, and the same pattern repeats for all layers. In Fig. 9b, the second scan strategy has a bidirectional pattern within each layer, and the pattern successively rotates for 90^∘ across layers. Figure 9c, d show the entire computational domains at the final step. Due to the different scan strategies, the top surfaces of these two parts show distinct grain structure patterns that seem to be orthogonal to each other. The x-z plane cross sectional views are plotted in Fig. 9e, f. For the first scan strategy, we observe the characteristic V-shaped grains. These V-shaped grains are stacked vertically, and the vertical boundaries of these repeated stacks are aligned with laser scanning paths. For the second scan strategy, the generated grains are arranged more arbitrarily and do not show such an organized pattern like the first scan strategy. These observations indicate that unidirectional scan strategies can lead to grain structures with high anisotropy, whereas alternating scan patterns between layers introduce certain randomness in grain structures and may alleviate the strong anisotropy. Furthermore, we hide the regions that are never melt during the entire PBF process and show the results in Fig. 9g, h. In addition to distinct boundary/surface features for the two scanning strategies, we also observe certain regions due to lack of fusion. We show grain volume distributions in Fig. 9i. The mean grain size are 49162 μm³ and 56332 μm³ for the two scan strategies, and the total number generated grains are 22,438 and 19,593, respectively Therefore, the second scan strategy generates 12.6% fewer grains, and with an increase of 14.6% in averaged grain size.

Fig. 9: A multi-layer multi-track example that compares two laser scan strategies.

In (a) and (b), the two scanning patterns are described. In (c) and (d), the entire simulation domains are shown, where the size of the domain is 2 × 2 × 0.5 mm³. In (e) and (f), we show the x-z plane cross sectional views that correspond to the windows indicated by the black solid lines in (d) and (d). In (g) and (h), we only show those regions that are at least melt once. In (i), we plot the grain size distribution for the two scan strategies. Scale bar in (f) is 0.2 mm.

Discussion

Graph networks as a general machine learning framework have gained rapidly increasing attention in the past few years^31,47. We strongly believe that the interdisciplinary studies of graph networks in applied sciences and engineering will create many opportunities, and we are just at the beginning of this exciting field. We have shown in this work that by leveraging techniques from graph networks, PEGN greatly reduces the computational burden of the classic PF method. In the single-layer single-track example, we have compared PEGN with DNS in temperature field, melt pool development and grain evolution, and the results of PEGN agree well with DNS.

The scalability of PEGN is demonstrated with multi-layer and multi-track examples, and this is the first work that uses a PF-based approach to conduct a millimeter-scale AM simulation. As shown, our PEGN method provides an effective means to study the impact of scan strategies on grain structure generation. The analysis indicates that in order to avoid strong anisotropic grain structures, more complex and alternating scan patterns should be adopted. Furthermore, this scan strategy generates fewer regions that are in lack of fusion and is considered more advantageous than the simple unidirectional scan strategy. In fact, the alternating scan strategy and its variants have been practiced in industry based on practical knowledge. The PEGN method also uncovers grain morphologies observed in experiments, such as grains with an inclined angle and re-melted long grains across layers. Since PEGN is implemented with automatic differentiation technique, it is promising to use gradient-based optimization for optimal grain structure control.

In this work, we have introduced an efficient reduced-order computational tool. As graph networks are a flexible framework, more features can be integrated to incorporate complex physics-based mechanisms, such as dendritic growth^48,49, or randomness in grain nucleation^50,51. To introduce new grains, PEGN can adopt an adaptive graph strategy similar to mesh adaptivity⁵² in classic numerical algorithms so that more nodes (new grains) are introduced. The adaptive graph strategy can be flexible such that one grain is partitioned with several nodes and that the solution has higher resolution in certain regions of interest. By expanding the set of pre-defined grain orientations, PEGN can consider more grain orientations like DNS. The abilities to introduce new grains and grain orientations are beneficial for microstructure evolution problems such as columnar-to-equiaxed transition and recrystallization. Other possible future work includes more realistic modelling that considers gas phase/voids, which can be modelled by expanding the node features to include the void phase and modifying the physics-based loss function accordingly. In addition, the classic PF DNS can adopt the ‘active parameter tracking’ method⁵³ to improve efficiency, and this method also applies to PEGN by limiting the number of active order parameters defined on the nodes to a limited active set.

Methods

Figure 1 shows an overview of the method. We formulate the problem of microstructure evolution using a physics-embedded graph network. The graph network represents the microstructure such that each node in the graph represents a grain, and if two grains share a common face, they are considered as connected in the graph, i.e., there exists an edge between the two corresponding nodes (see Fig. 1a). As shown in Fig. 1b, each node has an associated feature vector as a descriptor of the current grain status. The feature vector is composed of both static and dynamic entries. For example, the volume or the centroid position of a grain is considered as a static feature that does not change with respect to time. In contrast, dynamic features (denoted as θ) consist of temperature T, solid/liquid fraction ζ, and grain orientation η, all of which evolve with time and are variables remaining to be solved. Similarly, we define edge features, such as contact face areas or thermal conductivity coefficients, to reflect communication between grains. Edges are assumed to be non-directional (or bidirectional), which is consistent with physical principles. For example, heat can flow from one grain to another, and vice versa. Edge features in this work are all assumed to be static. The information that is passed through edges for η and ζ is implicitly embedded with the Ginzburg–Landau free energy, while the information passed for T is the heat flux between grains. Nodes are affected directly by their neighbors. They are indirectly affected by their ‘farther neighbors’, e.g., neighbors of neighbors due to message-passing on the graph. For the three dynamic features, η and ζ depend on T in a one-way coupled manner. In our explicit iteration framework, we update the three features monolithically as a whole, rather than separately analyze them with a staggered scheme.

All static node and edge features are considered as part of the inputs to the PEGN algorithm. We also need to specify the initial values for the dynamic node features, such as initial temperature and initial grain orientations. The outputs of the PEGN algorithm are the solved dynamic node features with respect to time. During the simulation, adjacent grains may have the same orientation, and this is regarded as they merge into a larger grain so that grain growth can be modeled. In other words, it is important to correctly identify each individual grain, especially in the post-processing procedures (e.g., computing grain sizes or aspect ratios). Since the computational domain is treated as a graph, we solve the problem with the classic breadth-first search algorithm⁵⁴ so that the entire graph is partitioned into (self-connected) subgraphs where each subgraph represents exactly one grain (see Supplementary Fig. 1). For example, the grains calculation for PEGN in Fig. 6 involves a total number of 355 grains, i.e., 355 subgraphs. On average, each subgraph has 11.7 nodes and 40.7 edges.

DNS formulation

We first briefly introduce the DNS approach. The coupled governing equations for the full-field tempo-spatial temperature evolution and the phase-field model are given by

$$\begin{array}{l}\frac{\partial (\rho {c}_{p}T)}{\partial t}={\scriptstyle\nabla \cdot ({\kappa }_{T}\nabla T}),\\\quad\;\;\, \frac{\partial \zeta }{\partial t}=-{\scriptstyle{L}_{p}(T)\frac{\delta F}{\delta \zeta }},\\\quad\;\; \frac{\partial {\eta }_{i}}{\partial t}=-{\scriptstyle{L}_{g}(T)\frac{\delta F}{\delta {\eta }_{i}}}.\end{array}$$

(1)

In Equation 1, T(x, t) is the temperature field, ρ is the density, c_p is the specific heat, and κ_T is the thermal conductivity. Latent heat effect is neglected in the current formulation. The initial condition is set to be ambient temperature T_a. For boundary conditions, we consider heat flux at the part surface that includes both convection and radiation heat transfer so that

$${\kappa }_{T}\nabla T\cdot {{{\bf{n}}}}=h({T}_{a}-T)+{\varepsilon }_{R}{\sigma }_{R}({T}_{a}^{4}-{T}^{4}),$$

(2)

where n is the boundary normal vector, h is the heat convection coefficient, ε_R is the emissivity, and σ_R is the Stefan-Boltzmann constant. The laser heat source q is treated as a time-dependent heat flux boundary condition on the top surface, defined by:

$$q=\frac{2Q\eta }{\pi {r}_{b}^{2}}\exp \left(\frac{-2\left({\left(x-{v}_{s}t\right)}^{2}+{y}^{2}\right)}{{r}_{b}^{2}}\right),$$

(3)

where Q is the laser power, η is the absorbed fraction of the laser energy, r_b is the radius of the laser spot, and v_s is the laser scan speed. The definition in Equation 3 is for single-track scanning only, but it generalizes to multi-track scanning easily.

In Equation 1, ζ(x, t) is an indicator variable that continuously varies from liquid phase (ζ = 0) to solid phase (ζ = 1). In Equation (1), η_i(x, t) (i = 1, 2, …, N_o, where N_o is the number of orientations) are non-conservative phase-field parameters. If a certain grain takes the ith orientation, then η_i = 1 and η_j = 0 (j ≠ i). The second and third equations in Equation (1) are known as the Ginzburg–Landau equations⁵⁵, and the specific formulation in this work generally follows²¹. Here, L_p and L_g are the kinetic coefficients related to interfacial mobility of the liquid/solid interface and grain boundary, and we assume

$${L}_{g}(T)={L}_{0}\exp \left(-\frac{{Q}_{g}}{RT}\right),\quad {L}_{p}(T)={L}_{0}\exp \left(-\frac{{Q}_{g}}{R{T}_{m}}\right)$$

(4)

where L₀ is the pre-exponential coefficient, Q_g is the activation energy, R is the gas constant, and T_m is the melting temperature. The total free energy F is given by

$$F={\int}_{V}({f}_{{{{\rm{phase}}}}}+{f}_{{{{\rm{grain}}}}}+{f}_{{{{\rm{grad}}}}}){{{\rm{d}}}}V,$$

(5)

where f_phase and f_grain are the free energy densities from liquid/solid phases and grains, respectively, and f_grain is the gradient energy density. Specifically, we have

$${f}_{{{{\rm{phase}}}}}={m}_{p}\left({\left(1-\zeta \right)}^{2}\varphi (\tau )+{\zeta }^{2}(1-\varphi (\tau ))\right),$$

(6)

where m_p is the phase energy pre-coefficient and $\varphi (\tau )=\frac{1}{2}(1-\tanh (\tau -1))$, τ = T/T_m. Here, φ(τ) approaches 1 for τ > 1, and approaches 0 for τ < 1. Therefore, the role of temperature field on liquid/solid transformation is reflected. Note that f_phase achieves a local minimum at ζ = 0 and ζ = 1. As for the grain energy density, we have

$$\begin{array}{l}{f}_{{{{\rm{grain}}}}}={m}_{g}\left(\mathop{\sum }\limits_{i=1}^{{N}_{o}}\left(\frac{{\left({\eta }_{i}\right)}^{4}}{4}-\frac{{\left({\eta }_{i}\right)}^{2}}{2}\right)+\gamma \mathop{\sum }\limits_{i=1}^{{N}_{o}}\mathop{\sum}\limits_{j\ne i}{\left({\eta }_{i}\right)}^{2}{\left({\eta }_{j}\right)}^{2}\right.\\\qquad\quad\;\; \left.+\,\frac{1}{4}+{\left(1-\zeta \right)}^{2}\mathop{\sum }\limits_{i=1}^{{N}_{o}}{\left({\eta }_{i}\right)}^{2}\right),\end{array}$$

(7)

where m_g is the grain energy pre-coefficient, and γ is a model parameter. Here, f_grain takes the local minimum at $[{\eta }_{1},{\eta }_{2},\ldots ,{\eta }_{{N}_{o}}]=[1,0,\ldots ,0],[0,1,\ldots ,0],\ldots ,[0,0,\ldots ,1]$. The gradient energy density is given by

$${f}_{{{{\rm{grad}}}}}=\frac{{\kappa }_{p}}{2}{\left(\nabla \zeta \right)}^{2}+\mathop{\sum }\limits_{i=1}^{{N}_{o}}\frac{{\kappa }_{g}}{2}{\left(\nabla {\eta }_{i}\right)}^{2},$$

(8)

where κ_p and κ_g are the gradient term coefficients for liquid/solid interface and grain boundary, respectively. Grain boundary anisotropy is also included in the current DNS model. We encourage the interested readers to check²¹ for details.

The set of governing Equation 1 are discretized spatially with the centered finite difference method, and temporally discretized with the explicit Euler method.

PEGN approach

We describe the detailed formulation of the PEGN approach. Consider an undirected graph ${{{\mathcal{G}}}}=({{{\mathcal{V}}}},{{{\mathcal{E}}}})$, where ${{{\mathcal{V}}}}=\{1,2,\ldots ,{N}_{n}\}$ are a set of nodes and ${{{\mathcal{E}}}}\subset {{{\mathcal{V}}}}\times {{{\mathcal{V}}}}$ are a set of edges. As a reminder (see Fig. 1), each node in PEGN represents an individual grain, while each edge represents the connection between two grains if they share a common face. Nodes have associated features, e.g., grain volume or temperature. There are two kinds such node features: static features that do not change with time, and dynamic features that evolve with time. A static node feature can be formally described with a static node function ${f}_{{{{\rm{static}}}}}:{{{\mathcal{V}}}}\to {\mathbb{R}}$, while a dynamic node feature can be defined with a dynamic node function ${f}_{{{{\rm{dynamic}}}}}:{{{\mathcal{V}}}}\times [{t}_{i},{t}_{f}]\to {\mathbb{R}}$, where t_i and t_f defines the time window. Static features such as grain volume or grain centroid location are fixed once and for all. Dynamic features are denoted by ${{{\boldsymbol{\theta }}}}={\{{(T,\zeta ,{\eta }_{0},{\eta }_{1},\ldots ,{\eta }_{{N}_{0}})}^{(k)}\}}_{k = 1}^{{N}_{n}}\in {{\mathbb{R}}}^{(2+{N}_{o})\times {N}_{n}}$, that represent the collection of temperature, liquid/solid fraction, and grain orientation at all grains. Dynamic features θ are unknown variables that must be solved by the algorithms of PEGN. Similarly, PEGN also contains edge features. Only static edge features are used, and they can be formally described by a static edge function ${g}_{{{{\rm{static}}}}}:{{{\mathcal{E}}}}\to {\mathbb{R}}$. Typical static edge features include thermal conductivity coefficients, contact face areas, etc.

As an analogy, a graph version of Ginzburg–Landau energy functional³⁹ F(θ) can therefore be constructed. The corresponding graph Allen-Cahn equation therefore reads as

$$\frac{{{{\rm{d}}}}{{{\boldsymbol{\theta }}}}}{{{{\rm{d}}}}t}=-{{{\bf{L}}}}\frac{\partial F}{\partial {{{\boldsymbol{\theta }}}}},$$

(9)

where ${{{\bf{L}}}}\in {{\mathbb{R}}}^{(2+{N}_{o})\times {N}_{n}}$ are the pre-coefficients that make Equation 9 physically consistent. The pre-coefficients L are set such that

$${L}_{T}^{(k)}=1/(\rho {c}_{p}{V}^{(k)}),\quad {L}_{\zeta }^{(k)}={L}_{p}({T}^{(k)})/{V}^{(k)},\quad {L}_{{\eta }_{i}}^{(k)}={L}_{g}({T}^{(k)})/{V}^{(k)},$$

(10)

where ${L}_{T}^{(k)}$, ${L}_{\zeta }^{(k)}$, and ${L}_{{\eta }_{i}}^{(k)}$ are the coefficients for T, ζ, and η_i at node k, respectively, and V^(k) is the grain volume at node k.

Equation 9 are a system ODEs that can be solved with discretization method like the explicit Euler method. It is important to note that this time integration procedure resembles message-passing³⁰ process on graph, and F(θ) is simply the loss function in the language of machine learning with θ being the learnable parameters. Our implementation is built upon JAX⁵⁶, a Python library designed for high-performance numerical computing and machine learning research. Specially, JAX has shown potential for scientific computing such as molecular dynamics simulation⁵⁷ or computational fluid dynamics⁵⁸. The graph networks are constructed using Jraph⁵⁹, a lightweight library for working with graph networks in JAX. While F depends on θ in a complex way, we use jax.grad, the automatic differentiation feature provided by JAX, to compute the gradient $\frac{\partial F}{\partial {{{\boldsymbol{\theta }}}}}$ efficiently. Since the loss/energy function F(θ) is defined with physical intuition, the ‘learning’ process of PEGN is essentially performed in an unsupervised fashion, a similar concept also found in recent works of the so-called physics-informed neural networks method⁶⁰.

The energy function F(θ) is decomposed into several parts:

$$F({{{\boldsymbol{\theta }}}})={F}_{{{{\rm{phase}}}}}+{F}_{{{{\rm{grain}}}}}+{F}_{{{{\rm{grad}}}}},$$

(11)

where F_phase and F_grain are free energy associated with liquid/solid transformation and grain evolution, and ${F}_{{{{\rm{grad}}}}}$ represents the diffusive part of the energy. The phase energy F_phase is constructed by an aggregation over all nodes in the graph:

$${F}_{{{{\rm{phase}}}}}=\mathop{\sum}\limits_{k\in {{{\mathcal{V}}}}}{m}_{p}({(1-{\zeta }^{(k)})}^{2}\varphi ({\tau }^{(k)})+{({\zeta }^{(k)})}^{2}(1-\varphi ({\tau }^{(k)}))),$$

(12)

where τ^(k) = T^(k)/T_m. Here, ζ^(k) represents the liquid/solid fraction variable at the k^th node. Similarly, the grain energy F_grain consists of the sum over all the nodes and the interaction between phases and grain orientations is reflected with the last term in the expression:

$$\begin{array}{l}\begin{array}{ll}{F}_{{{{\rm{grain}}}}}=\mathop{\sum}\limits_{k\in {{{\mathcal{V}}}}}{m}_{g}\left(\mathop{\sum }\limits_{i=1}^{{N}_{o}}\left(\frac{{({\eta }_{i}^{(k)})}^{4}}{4}-\frac{{({\eta }_{i}^{(k)})}^{2}}{2}\right)+\mathop{\sum }\limits_{i=1}^{{N}_{o}}\mathop{\sum}\limits_{j\ne i}{({\eta }_{i}^{(k)})}^{2}{({\eta }_{j}^{(k)})}^{2}\right.\\ \qquad\quad\left.+\,\frac{1}{4}+{(1-{\zeta }^{(k)})}^{2}\mathop{\sum }\limits_{i=1}^{{N}_{o}}{({\eta }_{i}^{(k)})}^{2}\right),\end{array}\end{array}$$

(13)

where ${\eta }_{i}^{(k)}$ represents the ith grain orientation variable at the kth node. Finally, the diffusive energy ${F}_{{{{\rm{grad}}}}}$ represents the communication between nodes, so that it consists of a summation over all the edges:

$$\begin{array}{l}{F}_{{{{\rm{grad}}}}}=\mathop{\sum}\limits_{(k,m)\in {{{\mathcal{E}}}}}\left(\frac{{\kappa }_{T}{l}_{c}}{2}{({T}^{(k)}-{T}^{(m)})}^{2}+\mathop{\sum }\limits_{i=1}^{{N}_{o}}\frac{{\kappa }_{g}{l}_{c}}{2}{({\eta }_{i}^{(k)}-{\eta }_{i}^{(m)})}^{2}\right.\\ \qquad\quad\left.+\,\frac{{\kappa }_{p}{l}_{c}}{2}{({\zeta }^{(k)}-{\zeta }^{(m)})}^{2}\right),\end{array}$$

(14)

where for instance T^(k) and T^(m) are temperature variables at two connected nodes k and m. In Equation 14, l_c is the characteristic length that quantifies the effective distance between two connected grains. The parameter l_c is edge dependent, and the value is defined to be the division of contact face area divided by grain center-to-center distance. This particular definition of l_c is consistent in the sense that if the graph represents a regular lattice-like structure, then PEGN exactly degenerates to the centered finite difference algorithm. An interesting fact is that when implementing the DNS approach, we did not follow the traditional way of discretizing the Laplace operator directly. Rather, we employed a graph network that is similar to PEGN. As for the energy input from laser scanning process, it is straightforward to modify Equation 9 so that a source term can be added. We omit the details here, but the heat transfer process in PEGN is treated in consistency with DNS, e.g., see Equation 2 and Equation 3. Also, grain boundary anisotropy is included for PEGN in a consistent way with DNS. Interested readers may consult our code for further details.

Summary of DNS and PEGN

To illustrate the differences between DNS and PEGN more clearly, we use Table 1 to conclude several key aspects of the two methods.

Table 1 Summary of DNS and PEGN.