Introduction

Active Peltier cooling materials can accelerate heat transfer by consuming electric energy, which have applications in integrated circuit chip cooling, lithium-ion batteries, microthermostat, medical temperature controlling, etc1,2,3,4. With the development of batteries and computer chips toward more compact and higher power density, these applications require more sophisticated thermal management techniques, and thermal flow management becomes increasingly important5,6,7. From the application of the active cooling material mentioned above, its operating temperature is general around the room temperature. Figure 1 is a schematic diagram of active cooling. TH is the temperature of the heat source, QP and QF are the heat pumped by the work done through the Peltier effect and Fourier effect, respectively. The current Is passes through the p-n leg to pump heat from the hot end to the ambient temperature. The main parameter for assessing the performance of active cooling materials is the effective thermal conductivity κeff8

$$\kappa _{eff} = \kappa _{pas} + \kappa _{ac} = \kappa _{pas} + \frac{{PF \cdot T_H^2}}{{2{{\Delta }}T}},$$
(1)

where κpas is the passive thermal conductivity (including the electronic thermal conductivity κe and lattice thermal conductivity κL) affected by the Fourier effect, and κac is the active thermal conductivity affected by the Peltier effect. ∆T is the temperature difference of the hot source and room temperature. Power factor (PF = S2σ) is composed of the Seebeck coefficient S and the electrical conductivity σ. Materials with high power factor and high passive thermal conductivity are required to quickly and effectively remove heat from the hot region of the device8,9,10.

Fig. 1: Schematic diagram of active cooling.
figure 1

The current Is pumps heat from the hot end to the ambient temperature through the p-n leg. QP and QF are the heat extracted by the Peltier effect and Fourier effect, respectively.

Full size image

Generally speaking, metals with large κe dominate the passive cooling applications11,12. As for active cooling, however, metals generally have small Seebeck coefficients and therefore small PFs, so currently only some metals with strong localized f electrons have been considered in active cooling applications8. Most of the thermoelectric semiconductors with large PFs, on the other hand, have the best working temperature range far above 300 K13,14,15,16,17, which is not applicable to the desired working temperature of active cooling. As for some room temperature thermoelectric materials such as Bi2Te318,19, due to their low κLs, the κeffs are far below the passive thermal conductivity of Cu at the room temperature. Therefore, conventional metals and thermoelectric semiconductors are not suitable for active cooling.

Semimetals naturally have large electrical conductivity σs as well as thermal conductivity κs20, and they are potentially good active cooling materials. Semimetals have zero band gap with EF usually passing through conduction band minimum (CBM) or valence band maximum (VBM) or both, and their Seebeck coefficients are generally small. However, Markov et al. proposed that if semimetal materials have great asymmetry between conduction band and valence band, it is possible for them to have large Seebeck coefficients21. Therefore, semimetals with energy band asymmetry may be an option for room-temperature active cooling application.

Heusler alloys (including half-Heusler and full-Heusler) are a class of materials worthy of systematic study due to their wide variety of compositions and functional properties. Although there are many studies on Heusler alloys22,23,24,25,26,27,28,29,30,31, room temperature active cooling application in these compounds has never been discussed. In this work, based on the MatHub-3d database32,33, the Heusler alloys are systematically screened for room temperature active cooling in a high-throughput (HTP) manner. Within all the 2958 Heusler entries in the database (274 half-Heusler and 2684 full-Heusler), most of them have the band gaps lower than 0.1 eV, which are able to be treated as semimetal (or very narrow band-gap) systems mentioned above. After the evaluations of electronic structures, electrical and thermal transport properties, five Heusler materials with large effective thermal conductivity (κeff at room temperature is greater than that of Cu at ΔT = 1 K) were found, which are GaSbLi2, HgPbCa2, SnTiRu2, GeYbLi2, and GeTiFe2. The asymmetry of electronic density of states (DOS) and/or electronic group velocities are responsible for the large κeff in these Heusler compounds. This work provides strategies and material systems for the active Peltier cooling application.

Results

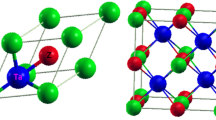
Figure 2a shows the crystal structures of half-Heusler compound ABX and full-Heusler compound AB2X. Elements A and X form a rock-salt structure. For half-Heusler, element B locates at one of the two body diagonal position (1/4, 1/4, 1/4) in the cell. When the other body diagonal position (3/4, 3/4, 3/4) is also occupied, it becomes the structure of full-Heusler. In the repository MatHub-3d, there are 274 half-Heusler entries (under the search criteria of space group No. 216, atomic ratio as 1:1:1), and 2684 full-Heusler entries (under the search criteria of space group No. 225, atomic ratio as 1:2:1). For the HTP study in this work, in order to obtain a relatively better description of the band structures for Heusler alloys, the SCAN semilocal functional was adopted, as mentioned in the Methods section.

Fig. 2: High-throughput workflow of screening Heusler systems in active cooling application.
figure 2

a The crystal structures of half-Heusler and full-Heusler alloys. b The workflow of the present work.

Full size image

To effectively screen the active Peltier cooling materials in Heusler alloys, we designed the workflow as shown in Fig. 2b. As discussed before, we eliminated those entries with Eg ≥ 0.1 eV under the SCAN level, and obtained 122 half-Heusler and 2641 full-Heusler alloys as potential semimetal or very narrow band-gap entries. The electrical transport properties of these systems are then calculated under the CEPCA with the DOS-influenced relaxation time considered (Eq. 6). And Seebeck coefficients are independent with the electron-phonon coupling parameters under this method34. Both the p-type and n-type Pisarenko curves for all the 2763 entries at 300 K are calculated, which can be found at the database of Mathub-3d (http://www.mathub3d.net/static/database/Seebeckdata.zip). Taking the Ioffe’s criterion for potentially good candidates with high PFs, i.e., |S|≥180 μV K−1 35,36,37 for either p-type and n-type transport properties, 12 half-Heusler, and 7 full-Heusler entries are screened.

Due to the fact that some of these 19 systems have heavy elements with strong spin-orbital coupling (SOC), the SCAN+SOC electronic structures are further carried out. The deformation potentials and Young’s moduli, which are needed for the relaxation times under the deformation potential method (Eq. 6), are also calculated, and the absolute values of power factors can be obtained. Combining the room temperature maximum PFs (PFmaxs) at the band edge33 and κLs (Eq. 7), the κeffs vs ΔT (from 1 K to 10 K) for the 19 systems at TH = 300 K are plotted in Supplementary Fig. 1. Five full-Heusler alloys with κeff under either carrier type larger than κCu (400 W mK−1 at 300 K)38 are finally obtained under ΔT = 1 K. Supplementary Table 1 in the supplemental material shows the values of c11, c12 and c44 for GaSbLi2, HgPbCa2, SnTiRu2, GeYbLi2, and GeTiFe2. According to the Born-Huang stability criterion (c44 > 0, c11-c12 > 0, and c11+2c12 > 0), the five screened potential Heusler alloys are all thermally stable39.

Table 1 lists the key parameters for the five compounds, including the Edefs, Gs, Smaxs, PFmaxs, κLs, the electron group velocity ves, carrier concentration ns, and electrical conductivity σs. The carrier concentration, Smax and ve are corresponding to the PFmax. All the transport properties in Table 1 are the values at 300 K. Except for GaSbLi2, all the other four compounds have better n-type electrical transport performance than p-type.

Table 1 Parameters of five screened Heusler systems for active cooling application.
Full size table

Figure 3 shows the active cooling performance of the five screened compounds in their favorable carrier types at the room temperature, with ΔT in the range of 1 K-10 K. The experimental κeffs of the metals Co and CePd3 are also labeled in Fig. 3. According to Eq. 1, the κeff decreases with increasing temperature difference. When ΔT = 1 K, the κeffs of all the five compounds are greater than that of Cu at 300 K, and the κeffs of GaSbLi2, SnTiRu2, and GeTiFe2 are even greater than that of Co and CePd38. However, when ΔT ≥ 5 K, the κeffs of all the compounds are lower than the passive thermal conductivity of Cu, indicating that the applications of the active cooling only dominate at small temperature difference, such as in the precise temperature control. Figure 3 also shows that the contribution of PF-induced κac plays a leading role comparing with the passive thermal conductivity when ΔT is small. For the future material selection for active cooling, the fact that PF dominates κeff indicates that it is not necessary to search compounds within metals or semimetals; any material with large power factor, e.g., 89 × 10−4 W mK−2, will have a better κeff than that of Cu at room temperature with ΔT = 1 K, without even considering the contribution of κpas.

Fig. 3: Effective thermal conductivities with ΔT = 1 K–10 K.
figure 3

a GaSbLi2 b HgPbCa2 c SnTiRu2 d GeYbLi2 e GeTiFe2. In each plot, the black line represents κeff, the red line κac, the blue line κpas, and the green line represents the thermal conductivity of Cu at room temperature. The orange and purple asterisks represent the effective thermal conductivity of Co and CePd3 at ΔT = 1 K8, respectively.

Full size image

Discussion

The very high PFs of the five compounds are the underlying reason for their large κac, which can be rationalized by the band asymmetry. Figure 4 shows the band structures and DOS of (a) SnTiRu2 (b) GeYbLi2 (c) GeTiFe2 (d) HgPbCa2 (e) GaSbLi2. For SnTiRu2, GeYbLi2, GeTiFe2, HgPbCa2 full-Heusler, there is a large band asymmetry with larger DOS at CBM. We define N(εF+ε)/N(εF-ε) or N(εF-ε)/N(εF+ε) as the DOS asymmetry ratio at the same energy points above / below (below / above) the Fermi levels40, and εF refers to the default Fermi energy level. As can be found in Fig. 4(f)–(i), the maximum N(εF+ε)/N(εF-ε) are from 4 to above 30. For SnTiRu2, GeTiFe2, and GeYbLi2, the large DOS of CBM come from the flat band along Г-X with a large effective mass. Further wave function analyses in Supplementary Fig. 2 indicate that the flat band is caused by the localized d orbitals from transition metal elements Ru, Fe, and Yb. For HgPbCa2, the difference in DOS mainly comes from the additional pocket at L around CBM. When considering the contribution from group velocity, the asymmetry ratio for transport distribution function (TD)37 for the above four compounds is greatly reduced (Fig. 4(f)–(i)) due to the relatively small group velocity for heavy bands, though the TD for the conduction band is still larger than that for the valence band. The asymmetry of the band-related quantities causes better n-type PFmax than the p-type in these four compounds, as shown in Table 1.

Fig. 4: Electronic structures of five screened systems.
figure 4

The band structures and density of states for a SnTiRu2 b GeYbLi2 c GeTiFe2 d HgPbCa2 e GaSbLi2 and the asymmetry ratio of TD and density of states DOS for f SnTiRu2 g GeYbLi2 h GeTiFe2 i HgPbCa2 j GaSbLi2, with εF+ε and εF-ε representing the physical quantities above and below the Fermi energy level, respectively. The dashed lines in each band structure represent the positions of the Fermi energy levels for both p-type and n-type PFmaxs.

Full size image

Besides the band asymmetry, other physical quantities are also necessary for high PFmax. As shown in Eq. 6, small deformation potentials and large Young’s moduli are responsible for high electronic relaxation times and power factors. As shown in Table 1, SnTiRu2 and GeTiFe2 possess small deformation potentials, at least for the favorable carrier type (lower than 2 eV). And their Young’s moduli are ultra-high, around 300 GPa, indicating the stiffness of the two compounds. The two factors ensure the PFmax of the two larger than 200 × 10−4 W mK−2. For GaSbLi2, due to the fact that bands at both sides of the Fermi level are very dispersive (Fig. 4e), the p-type and n-type group velocities are both high (Table 1). Given the pseudogap at the Fermi level, the large group velocities result in large PFmaxs for both p-type and n-type in this compound, though the band asymmetry is not large (Fig. 4j).

In conclusion, based on the MatHub-3d, a high-throughput workflow was carried out to find active Peltier cooling Heusler systems with large κeff. By calculating the electronic structure, electrical transport, and lattice thermal conductivity, five alloys of full-Heusler systems that meet the requirements were finally screened out, namely GaSbLi2, HgPbCa2, SnTiRu2, GeYbLi2, GeTiFe2. These five systems have both high electrical conductivity and/or Seebeck coefficient for high active Peltier cooling. The electrical conductivities are high due to the narrow band-gap or gapless electronic structures, as well as very high group velocity as shown in GaSbLi2. For materials with high Seebeck coefficient, such as HgPbCa2, SnTiRu2, GeYbLi2, GeTiFe2, their heavier conduction bands ensure the band asymmetry. This work demonstrates that the active thermal conductivity κac induced by PF is the most important component of active Peltier cooling at small temperature differences relative to the passive thermal conductivity κpas.

Methods

All first-principles calculations in the work were based on Vienna ab initio Simulation Package with the projector augmented wave method implemented41,42. For the calculations of the electronic structures, the Strongly Constrained and Appropriately Normed (SCAN)43 semilocal density functional was used throughout the work. Plane-wave energy cutoff energy of 520 eV and energy convergence criterion of 10−4 eV for self-consistent were adopted for all the calculations, the k-grid used in the calculation of the self-consistent calculation is 60/L+1, where L is the lattice constant of the systems. For the systems with magnetic properties, we considered the ferromagnetic ordering and did not further consider possible antiferromagnetic ordering. Moreover, the five systems we screened were all non-magnetic. Supplementary Table 2 lists the VASP pseudopotential names adopted for the lanthanide elements in this work. TransOpt44 was used for the electrical transport properties, the k-grid used in the calculation of the transport properties is 240/L+1. The electrical conductivity σ, Seebeck coefficient S, and electronic thermal conductivity κe were written using the Levi-Civita symbol,

$$\sigma _{\alpha \beta }\left( {\mu ,T} \right) = \frac{1}{V}\mathop {\sum}\limits_{n{{{\bf{k}}}}} {{{{\boldsymbol{v}}}}_{n{{{\bf{k}}}}\alpha }{{{\boldsymbol{v}}}}_{n{{{\bf{k}}}}\beta }\tau _{n{{{\bf{k}}}}}} \left[ { - \frac{{\partial f_\mu \left( {\varepsilon _{n{{{\bf{k}}}}},T} \right)}}{{\partial \varepsilon _{n{{{\bf{k}}}}}}}} \right],$$
(2)
$$S_{\alpha \beta }\left( {\mu ,T} \right) = \frac{1}{{eTV}}\sigma _{\alpha \beta }(\mu ,T)^{ - 1}\mathop {\sum}\limits_{n{{{\bf{k}}}}} {{{{\boldsymbol{v}}}}_{n{{{\bf{k}}}}\alpha }{{{\boldsymbol{v}}}}_{n{{{\bf{k}}}}\beta }\tau _{n{{{\bf{k}}}}}} (\mu - \varepsilon _{n{{{\boldsymbol{k}}}}})\left[ { - \frac{{\partial f_\mu \left( {\varepsilon _{n{{{\bf{k}}}}},T} \right)}}{{\partial \varepsilon _{n{{{\bf{k}}}}}}}} \right],$$
(3)
$$\begin{array}{l}\kappa _{e\alpha \beta }\left( {\mu ,T} \right) = \frac{1}{{e^2TV}}\mathop {\sum }\limits_{n{{{\bf{k}}}}} {{{\boldsymbol{v}}}}_{n{{{\bf{k}}}}\alpha }{{{\boldsymbol{v}}}}_{n{{{\bf{k}}}}\beta }\tau _{n{{{\bf{k}}}}}(\mu - \varepsilon _{n{{{\bf{k}}}}})^2\left[ { - \frac{{\partial f_\mu \left( {\varepsilon _{n{{{\bf{k}}}}},T} \right)}}{{\partial \varepsilon _{n{{{\bf{k}}}}}}}} \right]\\ \quad \quad \quad \quad \quad - \frac{1}{{eV}}\mathop {\sum }\limits_{n{{{\bf{k}}}}} {{{\boldsymbol{v}}}}_{n{{{\bf{k}}}}\alpha }{{{\boldsymbol{v}}}}_{n{{{\bf{k}}}}\gamma }\tau _{n{{{\bf{k}}}}}(\mu - \varepsilon _{n{{{\bf{k}}}}})\left[ { - \frac{{\partial f_\mu \left( {\varepsilon _{n{{{\bf{k}}}}},T} \right)}}{{\partial \varepsilon _{n{{{\bf{k}}}}}}}} \right]S_{{{{\boldsymbol{\gamma }}}}\beta }\left( {\mu ,T} \right),\end{array}$$
(4)

here vnk is electron group velocity corresponding to band index n and reciprocal coordinate k, and τnk is electronic relaxation time. T, μ, V, fμ, e, and εnk are respectively absolute temperature, Fermi level, volume of unit cell, the Fermi-Dirac distribution, electron charge, and band energy. The electron group velocity corresponding to energy μ is calculated as shown in Eq. 5,

$$v_e(\mu ,T) = \frac{{\sqrt {\mathop {\sum}\nolimits_{n{{{\mathbf{k}}}}} {\left( {{{{\boldsymbol{v}}}}_{n{{{\mathbf{k}}}}x}^2 + {{{\boldsymbol{v}}}}_{n{{{\mathbf{k}}}}y}^2 + {{{\boldsymbol{v}}}}_{n{{{\mathbf{k}}}}z}^2} \right)} \left[ { - \frac{{\partial f_\mu \left( {\varepsilon _{n{{{\mathbf{k}}}}},T} \right)}}{{\partial \varepsilon _{n{{{\mathbf{k}}}}}}}} \right]} }}{{\mathop {\sum}\nolimits_{n{{{\mathbf{k}}}}} {\left[ { - \frac{{\partial f_\mu \left( {\varepsilon _{n{{{\mathbf{k}}}}},T} \right)}}{{\partial \varepsilon _{n{{{\mathbf{k}}}}}}}} \right]} }}.$$
(5)

It is notable that ve is the average of each anisotropic electron group velocity vkx, vky, and vkz. In order to balance the efficiency and accuracy in the HTP study, the method of constant electron−phonon coupling approximation (CEPCA) combined with deformation potential method were adopted,

$$\frac{1}{{\tau _{n{{{\mathbf{k}}}}}}} = \frac{{2\pi k_BTE_{def}^2}}{{V\hbar G}}\mathop {\sum}\limits_{m{{{\mathbf{k}}}}^\prime } {\delta (\varepsilon _{n{{{\mathbf{k}}}}} - \varepsilon _{m{{{\mathbf{k}}}}^\prime })} ,$$
(6)

where n and k are the band index and wave vector, Edef is the deformation potential of the band edge, G is the Young’s modulus, and \(\delta (\varepsilon _{n{{{\mathbf{k}}}}} - \varepsilon _{m{{{\mathbf{k}}}}^\prime })\) takes the form of Gaussian function. For the calculation of the deformation potential, the average value of the first energy band was used as the reference level. In this work, the deformation potentials for the VBM and CBM were considered separately.

The Slack model was adopted to obtain the lattice thermal conductivity45,46,47,

$$\kappa _L = A\frac{{\bar mV_m^{\frac{1}{3}}v_q^3}}{{n^{\frac{2}{3}}\gamma ^2T}},$$
(7)

where \(\bar m\) is the average atomic mass, vq is sound velocity, Vm is the atomic volume, n is the number of atoms in the original cell, γ is the Gruneisen constant, and A is the quantity related to γ, respectively. Here, the Gruneisen constant and the mean sound velocity are related to the elastic matrices cij, which are calculated by the home-made elastic property automated calculation code (EPAC)39,48. The detailed formulas can be found in the supplemental material.