Phase-field framework with constraints and its applications to ductile fracture in polycrystals and fatigue

Abstract

Modeling of ductile fracture in polycrystalline structures is challenging, since it requires integrated modeling of cracks, crystal plasticity, and grains. Here we extend the typical phase-field framework to the situations with constraints on the order parameters, and formulate two types of phase-field models on ductile fracture. The Type-I model incorporates three sets of order parameters, which describe the distributions of cracks, plastic strain, and grains, respectively. Crystal plasticity is employed within grain interiors accommodated by J₂ plasticity at grain boundaries. The applications of the Type-I model to single crystals and bicrystals demonstrate the influences of grain orientations and grain boundaries on crack growth. In the Type-II model, J₂ plasticity is assumed for the whole system and grain structures are neglected. Taking advantage of the efficiency of the fast Fourier transform, our Type-II model is employed to study low cycle fatigue. Crack closure and striation-like patterning of plastic strain are observed in the simulations. Crack growth rate is analyzed as a function of the J-integral, and the simulated fatigue life as a function of plastic strain agrees with the Coffin–Manson relation without a priori assumption.

Introduction

Modeling of crack initiation and propagation is critical to understand different failure modes of structural materials such as cleavage fracture and fatigue¹. Traditionally, fracture is modeled by treating crack surfaces as sharp interfaces, which often requires remeshing after crack propagation. Recently, the phase-field method has emerged as a powerful tool to model crack initiation and propagation^2,3,4,5,6. In contrast to the sharp interface models, the phase-field model utilizes a diffused interface to describe the transition from intact to fully damaged regions that can conveniently handle the evolution of complex crack patterns with no need for remeshing nor ad hoc criteria for crack propagation^7,8. The phase-field modeling has first been applied to brittle fractures^2,3,9,10. Later, phase-field ductile fracture models were also constructed by considering the interaction between plasticity and fracture^{4,11,12,13,14}, starting from the small strain framework, which successfully capture a variety of anticipated ductile fracture responses at the macroscale. Subsequently, the ductile fracture model has been successfully extended to finite strain regime¹⁵.

At the mesoscale, the growth of short cracks depends on the heterogeneous plastic/elastic deformation in a polycrystalline structure, characterized by grain orientations and grain boundaries¹. A phase-field model incorporating brittle fracture with grain structures is developed to describe the intergranular cracking due to the reduced fracture toughness at grain boundaries, whereas no plasticity is considered¹⁶. On the other hand, a coupled crystal plasticity-phase field fracture model is developed in which a finite element model of crystal plasticity is applied to grain structures reconstructed from experimental images^17,18. However, in this finite element model, the grain boundaries are modeled as sharp interfaces, and the distinct physical properties of grain boundaries are ignored. A phase-field model with diffuse interfaces between grains is thus desired for polycrystalline ductile fracture in which the evolutions of plasticity, cracks, and grains are consistently governed by the minimization of a unified free energy functional.

When considering J₂ plasticity or crystal plasticity, the plastic strain is constrained by the volume conservation or orientation of the dislocation slip directions, which requires the modification of the evolution equations^19,20. In fact, certain constraints also exist on other order parameters such as chemical compositions in electrochemical reactions²¹ and the quaternion representation of crystallographic orientations²². In addition to the constraints that need to be satisfied everywhere, there exist constraints on system boundaries, i.e., boundary conditions of partial differential equations (PDE)²³. Conventionally, the Lagrange multiplier method is employed to obtain the minimum of a function/functional under constraints, which represents the equilibrium state of the system. However, the phase-field models also describe the kinetic process from non-equilibrium states to the equilibrium state, which is important in materials science due to the various time scales of different kinetics. In this case, the constraints need to be maintained throughout the kinetic process, and a general method for solving the Lagrange multipliers in the non-equilibrium states is required for the derivation of kinetic equations.

To solve PDE in the mechanical problems, different numerical methods can be employed, including the finite element method (FEM)^2,4,9, the finite difference method (FDM)¹⁶, the fast Fourier transform (FFT)^19,20,24, and the recently developed nonlocal operator method (NOM)^25,26,27. The FDM and FFT work on the differential form of PDE. Since the spatial differentiation can be transformed into multiplication in the Fourier space, the FFT method possesses distinct advantages in efficiency if periodic boundary conditions can be employed. On the other hand, the FEM and NOM work on the integral form of PDE, which can effectively relieve the possible numerical singularities near the crack surfaces. Note that due to the diffuse-interface nature of the phase-field method, such singularities are mostly avoided. It is demonstrated that the FFT method is more than 10 times faster than the classical FEM for the same regular grids^28,29, and thus the FFT method is employed in this work.

Thanks to the efficient FFT algorithm, we are able to investigate crack growth in ductile materials under cyclic loading. The fatigue process is traditionally described by two types of empirical models: the stress/strain life (S-N or ε-N) approach such as the Wöhler curve and the Coffin–Manson relation^30,31, and the damage tolerance approach based on fracture mechanics such as the Paris law³². The phase-field fracture models, as an emerged type of models which easily track the fatigue paths, has also been used to investigate fatigue^7,33,34. The basic idea of the fatigue models is that the repetitive loading reduces the fracture toughness based on the magnitude of locally accumulative elastic energy density and plastic strain. Applying the phase-field model of brittle fracture to fatigue allows the successful reproduction of the Paris law^7,33. The calculated Wöhler curves are also consistent with experimental observations^33,34. The phase-field fracture models coupled with cyclic plasticity are formulated and successfully validated using several numerical examples^35,36. To reduce the immense computational cost in the elastoplastic solver based on the finite element method (FEM) under high numbers of cycles, an effective method is developed by combining the phase-field method for brittle fracture with a classic durability concept³⁷.

In this paper, we first develop a framework in which the kinetic equations in a phase-field model are subject to a general type of constraints on the order parameters. It is demonstrated that the introduced Lagrange multipliers can be solved from the time invariance of the constraints, resulting in modified time-dependent Ginsburg-Landau (TDGL) equations. The applications of the framework to J₂ plasticity and crystal plasticity recover the flow equations from classical plasticity theories.

Based on the framework, we formulate two types of phase-field models on ductile fracture. The Type-I model is constructed with the capability of describing crystal plasticity and crack growth in a polycrystalline structure, as sketched in Fig. 1. Specifically, the grain structure is described by phase-field order parameters, and the grain boundaries could possess distinct physical properties including fracture toughness and yield strength. The Type-I model is applied to single crystals and bicrystals with face centered cubic (FCC) lattices, and the simulation results demonstrate that the crack paths are determined by crystal orientations and grain boundary locations. In the Type-II model, J₂ plasticity is assumed for the whole system and the grain structure is neglected for simplicity. The Type-II model is applied to study low cycle fatigue (LCF), by direct simulation of coupled plastic flow and fatigue crack propagation. Our simulation results reproduce the phenomena of crack closure and striation-like deformation patterning^38,39. The calculated fatigue life versus plastic strain predictions agree with the Coffin–Manson relation, and the underlying mechanism is discussed.

Fig. 1: Schematics for the order parameters considered in this work.

a–c Schematic distributions of plastic strain, cracks, and grains, respectively.

Results and discussion

General phase-field framework without and with constraints

Materials performance and properties depend on the spatial distribution of certain physical quantities inside the materials themselves. The distribution of the physical quantities can be described by a set of order parameters ${\eta }_{i}({\bf{x}}),1\le i\le m$, where x is the spatial coordinates and m is the number of order parameters. As a function of ${\eta }_{i}$ and their gradients, the total free energy of the system is given by

$$F=\int f({\eta }_{i},\nabla {\eta }_{i})d{\bf{x}},$$

(1)

where $f({\eta }_{i},\nabla {\eta }_{i})$ is the free energy density.

Based on the variational principle, the equilibrium state of the system corresponds to the situation when the total free energy is at the minimum with respect to local variations in ${\eta }_{i}({\bf{x}})$, i.e., the variational derivatives equal to zero everywhere^40,41

$$\frac{\delta F}{\delta {\eta }_{i}}=\frac{\partial f}{\partial {\eta }_{i}}-\frac{\partial }{\partial {x}_{k}}\frac{\partial f}{\partial (\partial {\eta }_{i}/\partial {x}_{k})}=0.$$

(2)

The Einstein summation convention is employed in this work unless otherwise noted. Equation (2) is referred to as the Euler-Lagrange equation⁴¹.

Next we consider the evolution of the system from a non-equilibrium state to the equilibrium state, which is described by the phase-field kinetic equations. S. M. Allen and J. W. Cahn proposed that if ${\eta }_{i}({\bf{x}})$ is a non-conserved order parameter, its local change is given by⁴²

$$\frac{\partial {\eta }_{i}}{\partial t}=-{L}_{ij}\frac{\delta F}{\delta {\eta }_{j}},$$

(3)

where ${L}_{ij}$ is the kinetic coefficient. Equation (3) is thus named as the Allen-Cahn equation⁴³. Since its format is the same as the TDGL equation, Eq. (3) is also referred to as the TDGL equation^42,43.

In a system described above, the order parameters are free to evolve, with the path exclusively described by Eq. (3). However, in certain situations, the order parameters must satisfy certain constraints. In this work, the phase-field framework will be extended to the situation with constraints by introducing Lagrange multipliers. We restrict our discussions on the constraints that are only functions of the order parameters ${\eta }_{i}$ themselves while independent of the gradient of the order parameter $\nabla {\eta }_{i}$. This type of constraints is common in various physical processes, e.g., electrochemical reaction²¹, grain growth²², and plasticity^19,20, which is analogous to the holonomic constraints in classical mechanics⁴⁰. Two typical sub-types of constraints are considered, i.e., integral constraints and non-integral constraints^40,41. The situation of integral constraints is discussed in Supplementary Note 1, while the case of non-integral constraints, typically given by

$${g}_{j}({\eta }_{i})=0,1\le j\le n,$$

(4)

is discussed here.

The energy minimization problem with local constraints can be solved by introducing Lagrange multipliers λ_j, where λ_j are fields. The Lagrangian is given by ${F}^{\ast }=\int (f+{\lambda }_{j}{g}_{j})d{\bf{x}}$, and the equilibrium condition is that the variational derivatives of ${F}^{\ast }$ equal to zero⁴¹, i.e.,

$$\frac{\delta {F}^{\ast }}{\delta {\eta }_{i}}=\frac{\partial (f+{\lambda }_{j}{g}_{j})}{\partial {\eta }_{i}}-\frac{\partial }{\partial {x}_{k}}\frac{\partial f}{\partial (\partial {\eta }_{i}/\partial {x}_{k})}=0,1\le i\le m,$$

(5)

Analogous to the TDGL Eq. (3), the kinetic equations with non-integral constraints are assumed to be given by

$$\frac{\partial {\eta }_{i}}{\partial t}=-{L}_{ij}^{\eta }\frac{\delta {F}^{\ast }}{\delta {\eta }_{j}}=-{L}_{ij}^{\eta }\left[\frac{\partial (f+{\lambda }_{k}{g}_{k})}{\partial {\eta }_{j}}-\frac{\partial }{\partial {x}_{l}}\frac{\partial f}{\partial (\partial {\eta }_{i}/\partial {x}_{l})}\right],1\le i\le m,1\le j\le m,$$

(6)

Next our goal is to solve the n Lagrange multipliers ${\lambda }_{k}$ in a general state from the n constraints ${g}_{k}=0,1\le k\le n$. To guarantee that the constraints in Eq. (4) are always satisfied during the evolution of ${\eta }_{i}$, the total derivative of ${g}_{k}$ with respect to time should equal zero, i.e., $\frac{d{g}_{k}}{dt}=0$. From the chain rule, we have

$$\frac{d{g}_{k}}{dt}=\frac{\partial {g}_{k}}{\partial {\eta }_{i}}\frac{\partial {\eta }_{i}}{\partial t}=0,$$

(7)

Substituting Eq. (6) into Eq. (7) will result in a system of linear equations with n equations and n variables ${\lambda }_{k}$, which generally guarantees the existence of solutions. Thus ${\lambda }_{k}$ can be solved as functions of ${L}_{ij}^{\eta }$, $\frac{\partial {g}_{k}}{\partial {\eta }_{i}}$, and $\frac{\delta F}{\delta {\eta }_{j}}$. Substituting the solutions of ${\lambda }_{k}$ back into Eq. (6) will give rise to the modified TDGL equations, which describe the evolution path toward equilibrium and guarantee that the evolution path is on the surface defined by the constraints.

As a special example, if ${g}_{k}$is a linear function of ${\eta }_{i}$, given by the expression ${g}_{k}={a}_{ik}{\eta }_{i}+b=0$, Eq. (6) becomes

$$\frac{\partial {\eta }_{i}}{\partial t}=-{L}_{ij}^{\eta }\left[\left(\frac{\partial f}{\partial {\eta }_{j}}-\frac{\partial }{\partial {x}_{w}}\frac{\partial f}{\partial (\partial {\eta }_{j}/\partial {x}_{w})}+{\lambda }_{k}{a}_{jk}\right)\right],1\le i\le m,1\le j\le m,1\le k\le n,$$

(8)

Then Eq. (7) is expressed by

$$-{a}_{ik}{L}_{ij}^{\eta }\left[\left(\frac{\partial f}{\partial {\eta }_{j}}-\frac{\partial }{\partial {x}_{w}}\frac{\partial f}{\partial (\partial {\eta }_{j}/\partial {x}_{w})}+{\lambda }_{l}{a}_{jl}\right)\right]=0,1\le k\le n,1\le l\le n,$$

(9)

The closed-form expressions of ${\lambda }_{l}$ can be derived as functions of ${a}_{ik}$, ${L}_{ij}^{\eta }$, and $\frac{\partial f}{\partial {\eta }_{j}}-\frac{\partial }{\partial {x}_{w}}\frac{\partial f}{\partial (\partial {\eta }_{j}/\partial {x}_{w})}$. Substituting the close-form expressions into Eq. (8) results in the kinetic equations with ${\lambda }_{l}$ eliminated.

In the above phase-field framework, the evolution of the systems with and without constraints is fully described by the respective kinetic Eqs. (3) and (6), which are derived based on the variational derivatives of the total free energy or Lagrangian. For the case with constraints, the Lagrange multipliers ${\lambda }_{k}$ in a non-equilibrium state can be solved by combining the time invariance of constraints and TDGL equations. Note that, strictly speaking, we should not solve ${\lambda }_{j}$ from the equilibrium conditions Eq. (5) as in Refs. ^19,20,21, since the constraints need to be satisfied throughout the kinetic process, not just the final equilibrium state. Furthermore, Eq. (5) represents a system of linear equations with m equations and n variables. Since we usually have m > n (otherwise, the order parameters ${\eta }_{i}$ can be fully determined by the constraints), i.e., the rank of the coefficient matrix is larger than the number of variables, there is no way to solve Eq. (5) directly. Ref. ¹⁹ shows such an example in which there are three equations but only one Lagrange multiplier (m = 3, n = 1). In this situation the Lagrange multiplier can only be obtained by summing up all the equations into one. Such an operation, however, does not have a reasonable basis.

Formulation for J₂/crystal plasticity and ductile fracture

In this section, we apply the above phase-field framework to J₂ plasticity and crystal plasticity by introducing non-integral constraints onto the order parameters of local plastic strains. The models are formulated within the small strain assumption. Then the grain order parameters are introduced, resulting in a polycrystalline crystal plasticity model with grain boundaries described by J₂ plasticity. Finally, the fracture order parameter is incorporated into the model, leading to two types of ductile fracture models with J₂ plasticity and/or crystal plasticity.

In ductile materials, when the stress magnitude is larger than their yield strength, plastic strain ${{\mathbf{\upepsilon }}}^{{\rm{p}}}$ begins to develop. The elastic strain ${{\mathbf{\upepsilon }}}^{{\rm{ela}}}$ is defined as the difference between the total strain and inelastic strain. If plastic strain is the only inelastic strain, then ${{\mathbf{\upepsilon }}}^{{\rm{ela}}}={\mathbf{\upepsilon }}-{{\mathbf{\upepsilon }}}^{{\rm{p}}}$, and the elastic energy density is given by

$${f}_{{\rm{elas}}}=\frac{1}{2}{c}_{ijkl}({\bf{x}}){\varepsilon }_{ij}^{{\rm{elas}}}{\varepsilon }_{kl}^{{\rm{elas}}}=\frac{1}{2}{c}_{ijkl}({\bf{x}})({\varepsilon }_{ij}-{\varepsilon }_{ij}^{{\rm{p}}})({\varepsilon }_{kl}-{\varepsilon }_{kl}^{{\rm{p}}}),$$

(10)

where ${c}_{ijkl}({\bf{x}})$ is the position-dependent elastic stiffness tensor.

First we consider the J₂ plastic strain ${{\boldsymbol{\varepsilon }}}^{{\rm{p}}({\rm{J}})}$, which is driven by the second invariant of the stress tensor. Due to the volume conservation during the plastic deformation⁴⁴, the constraint on ${{\boldsymbol{\varepsilon }}}^{{\rm{p}}({\rm{J}})}$ is given by

$${\varepsilon }_{11}^{{\rm{p}}({\rm{J}})}+{\varepsilon }_{22}^{{\rm{p}}({\rm{J}})}+{\varepsilon }_{33}^{{\rm{p}}({\rm{J}})}=0,$$

(11)

Based on Eq. (8), the evolution of ${\varepsilon }_{ij}^{{\rm{p}}({\rm{J}})}$ is governed by¹⁹

$$\frac{\partial {\varepsilon }_{ij}^{{\rm{p}}({\rm{J}})}}{\partial t}=-{L}_{ijkl}^{({\rm{J}})}\frac{\partial ({f}_{{\rm{elas}}}+\lambda {\varepsilon }_{mm}^{{\rm{p}}({\rm{J}})})}{\partial {\varepsilon }_{kl}^{{\rm{p}}({\rm{J}})}}={L}_{ijkl}^{({\rm{J}})}({\sigma }_{kl}-\lambda {\delta }_{kl}),$$

(12)

where ${\delta }_{kl}$ is the Kronecker delta. Based on Eq. (9), we have

$$\begin{array}{ll}\frac{\partial ({\varepsilon }_{11}^{{\rm{p}}({\rm{J}})}+{\varepsilon }_{22}^{{\rm{p}}({\rm{J}})}+{\varepsilon }_{33}^{{\rm{p}}({\rm{J}})})}{\partial t}={L}_{1111}^{({\rm{J}})}({\sigma }_{11}-\lambda )+{L}_{2222}^{({\rm{J}})}({\sigma }_{22}-\lambda )\\ \qquad\qquad\qquad\qquad+\,{L}_{3333}^{({\rm{J}})}({\sigma }_{33}-\lambda )=0,\end{array}$$

(13)

from which $\lambda$ is solved to be $\lambda =\frac{{L}_{1111}^{({\rm{J}})}{\sigma }_{11}+{L}_{2222}^{({\rm{J}})}{\sigma }_{22}+{L}_{3333}^{({\rm{J}})}{\sigma }_{33}}{{L}_{1111}^{({\rm{J}})}+{L}_{2222}^{({\rm{J}})}+{L}_{3333}^{({\rm{J}})}}$. If the system possesses cubic or higher symmetry, the properties of a forth rank tensor gives ${L}_{1111}^{({\rm{J}})}={L}_{2222}^{({\rm{J}})}={L}_{3333}^{({\rm{J}})}$⁴⁵, and then we obtain $\lambda =\frac{1}{3}({\sigma }_{11}+{\sigma }_{22}+{\sigma }_{33})$. In this case, Eq. (12) becomes

$$\frac{\partial {\varepsilon }_{ij}^{{\rm{p}}}}{\partial t}={L}_{ijkl}^{({\rm{J}})}{\sigma {\prime} }_{kl},$$

(14)

where ${\sigma ^{\prime} }_{kl}$ is the deviatoric stress expressed by ${\sigma ^{\prime} }_{kl}={\sigma }_{kl}-{\sigma }_{mm}{\delta }_{kl}/3$. ${K}_{ijkl}^{({\rm{J}})}$ is position dependent given by¹⁹

$${L}_{ijkl}^{({\rm{J}})}=\Bigg\{\begin{array}{c}0,{J}_{2}\le {\sigma}_{{\rm{Y}}}^{0}+R\\ {L}_{{\rm{p}}}{\delta}_{ij}{\delta}_{kl},{J}_{2}\, > \,{\sigma}_{{\rm{Y}}}^{0}+R\end{array},$$

(15)

where ${J}_{2}={\left[\frac{3}{2}{\sigma ^{\prime} }_{ij}{\sigma ^{\prime} }_{ij}\right]}^{1/2}$ is the second invariant of stress tensor, ${\sigma }_{{\rm{Y}}}^{0}$ denotes the initial yield strength, R represents the isotropic hardening, and ${L}_{{\rm{p}}}$ is a positive quantity characterizing the kinetics of plastic flow. Therefore, the plasticity evolution equation derived from the variational principle with a cubic crystal symmetry agrees with the classical J₂ plasticity theory by choosing a proper ${L}_{ijkl}^{({\rm{J}})}$¹⁹. Equation (15) is related to the Kuhn–Tucker conditions, which are used in the phase-field ductile fracture models in earlier reports^4,11. In the derivation of the J₂ plastic flow equation, we employ the constraints of volume conservation. For the non-associated plasticity model, usually the volume is not conserved under plastic deformation, which is thus out of the scope of this work.

Note that the J₂ plasticity can be assumed for the whole system and directly coupled with the fracture model^4,11, which is the case of our Type-II model as will be discussed later. Alternatively, the J₂ plasticity can be assumed only at grain boundaries, accommodating crystal plasticity within each grain²⁰, which will be the case of our Type-I model.

Next we discuss the plastic flow in a single crystal. Based on the crystal plasticity theory, the plastic flow within a single crystal is anisotropic, and contributed from dislocation slips in a total of S (active) slip systems⁴⁶. The total plastic strain within a grain g is given by ${\varepsilon }_{ij}^{{\rm{p}}}=\mathop{\sum }\nolimits_{\alpha =1}^{S}{\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)}$. ${\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)}$ in each slip system should satisfy the constraint²⁰

$${h}_{ij}^{(\alpha ;g)}={\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)}-{\varepsilon }_{kl}^{{\rm{p}}(\alpha ;g)}{m}_{kl}^{(\alpha ;g)}{m}_{ij}^{(\alpha ;g)}=0,\alpha =1,\mathrm{..}.,S,$$

(16)

where ${{\bf{m}}}^{(\alpha ;g)}=({{\bf{s}}}^{(\alpha ;g)}\otimes {{\bf{n}}}^{(\alpha ;g)}+{{\bf{n}}}^{(\alpha ;g)}\otimes {{\bf{s}}}^{(\alpha ;g)})/\sqrt{2}$ is the symmetric Schmid tensor (${{\bf{n}}}^{(\alpha ;g)}$ is the normal to the slip plane and ${{\bf{s}}}^{(\alpha ;g)}$ the slip direction). Note that ${{\bf{m}}}^{(\alpha ;g)}$ differs by a factor of $\sqrt{2}$ from the one frequently used in crystal plasticity models such that it satisfies the normalization condition ${m}_{ij}^{(\alpha ;g)}{m}_{ij}^{(\alpha ;g)}=1$. In a grain with arbitrary orientation, the Schmid tensor is calculated by ${m}_{ij}^{(g)}={R}_{im}^{(g)}{R}_{jn}^{(g)}{m}_{mn}$, where ${m}_{mn}$ is the Schmid tensor in the reference coordinate system and ${{\bf{R}}}^{(g)}$ is the rotation matrix charactering the crystallographic orientation of the grain relative to the reference coordinate system⁴⁵.

Equation (16) indicates that the magnitude of a plastic strain component is proportional to that of the corresponding Schmid tensor component, i.e., ${\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)} \sim {m}_{ij}^{(\alpha ;g)}$. Denoting the number of nonzero independent components of ${m}_{ij}^{(\alpha ;g)}$ as nnic ($2\le {\rm{nnic}}\le 6$) and the last nonzero component as ${m}_{bd}^{(\alpha ;g)}\ne 0$, the number of independent constraints in Eq. (16) is nnic-1, since the summation $\sum _{ij\ne bd}{m}_{ij}^{(\alpha ;g)}{h}_{ij}^{(\alpha ;g)}$ gives rise to the last constraint ${h}_{bd}^{(\alpha ;g)}=0$ utilizing the relation ${m}_{ij}^{(\alpha ;g)}{m}_{ij}^{(\alpha ;g)}=1$. Therefore, we introduce nnic-1 Lagrange multipliers ${\lambda }_{ij}^{(\alpha ;g)},ij\,\ne \,bd$, and the Lagrangian is given by

$${F}^{\ast }=\int \left[\frac{1}{2}{c}_{ijkl}^{(g)}({\varepsilon }_{ij}-\mathop{\sum }\limits_{\alpha =1}^{S}{\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)})({\varepsilon }_{kl}-\mathop{\sum }\limits_{\alpha =1}^{S}{\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)})+\sum _{ij\ne bd}{\lambda }_{ij}^{(\alpha ;g)}{h}_{ij}^{(\alpha ;g)}\right]dV.$$

(17)

Here ${c}_{ijkl}^{(g)}={R}_{im}^{(g)}{R}_{jn}^{(g)}{R}_{kw}^{(g)}{R}_{lq}^{(g)}{C}_{mnwq}$, where ${C}_{mnwq}$ is the elastic tensor in the reference coordinate system. Based on Eq. (8) and since that ${L}_{ijkl}^{{\rm{p}}(\alpha ;g)}$possesses a property that ${L}_{ijkl}^{{\rm{p}}(\alpha ;g)}\,\ne \,0$ only if $i=k$ and $j=l$ (this property is due to the assumption of the TDGL equation), the kinetic equation for ${\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)}$ is given by

$$\begin{array}{ll}\frac{\partial {\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)}}{\partial t}=-{L}_{ijkl}^{{\rm{p}}(\alpha ;g)}\left[\left(-{\sigma }_{kl}+{\lambda }_{kl}^{(\alpha ;g)}-\mathop{\sum}\limits_{qw\ne bd}{\lambda }_{qw}^{(\alpha ;g)}{m}_{qw}^{(\alpha ;g)}{m}_{kl}^{(\alpha ;g)}\right)\right],ij\,\ne \,bd,kl\,\ne \,bd\\ \frac{\partial {\varepsilon }_{bd}^{{\rm{p}}(\alpha ;g)}}{\partial t}=-{L}_{bdbd}^{{\rm{p}}(\alpha ;g)}\left[\left(-{\sigma }_{bd}-\mathop{\sum}\limits_{qw\ne bd}{\lambda }_{qw}^{(\alpha ;g)}{m}_{qw}^{(\alpha ;g)}{m}_{bd}^{(\alpha ;g)}\right)\right],\end{array}$$

(18)

where the relation $\frac{\partial {f}_{{\rm{elas}}}}{\partial {\varepsilon }_{kl}^{{\rm{p}}(\alpha ;g)}}=-{\sigma }_{kl}$ is used²⁴. Instead of taking the total derivative of Eq. (16) directly, we transform Eq. (16) into

$${\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)}{m}_{bd}^{(\alpha ;g)}-{\varepsilon }_{bd}^{{\rm{p}}(\alpha ;g)}{m}_{ij}^{(\alpha ;g)}=0,$$

(19)

Taking the total derivative of Eq. (19), substituting Eq. (18), and assuming that ${L}_{ijkl}^{{\rm{p}}(\alpha ;g)}$ can be written as ${L}_{ijkl}^{{\rm{p}}(\alpha ;g)}=\chi {\delta }_{ik}{\delta }_{jl}$ with $\chi$ a constant scalar, we obtain

$${m}_{bd}^{(\alpha ;g)}{\lambda }_{ij}={m}_{bd}^{(\alpha ;g)}{\sigma }_{ij}-{m}_{ij}^{(\alpha ;g)}{\sigma }_{bd},$$

(20)

The solution to Eq. (20) is

$${\lambda }_{ij}={\sigma }_{ij}-\frac{{m}_{ij}^{(\alpha ;g)}}{{m}_{bd}^{(\alpha ;g)}}{\sigma }_{bd},$$

(21)

Substituting Eq. (21) into Eq. (18) and utilizing the relation ${m}_{ij}^{(\alpha ;g)}{m}_{ij}^{(\alpha ;g)}=1$, we obtain the kinetic equation

$$\frac{\partial {\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)}}{\partial t}={L}_{ijkl}^{{\rm{p}}(\alpha ;g)}{\sigma }_{qw}{m}_{qw}^{(\alpha ;g)}{m}_{kl}^{(\alpha ;g)},$$

(22)

which is basically the same as Eq. 10 in ref. ²⁰. Here we strictly derive the Lagrange multipliers in the kinetic equations by using the time invariance of the constraints, without using the equilibrium conditions. ${L}_{ijkl}^{{\rm{p}}(\alpha ;g)}$ is chosen as^20,47

$${L}_{ijkl}^{{\rm{p}}(\alpha ;g)}=\Bigg\{\begin{array}{c}0,|{\tau }^{(\alpha ;g)}|\le {R}^{(\alpha ;g)}\\ \frac{{L}_{{\rm{p}}}}{{\tau}^{(\alpha ;g)}}{\left(\frac{|{\tau}^{(\alpha ;g)}|-{R}^{(\alpha ;g)}}{{D}_{{\rm{slip}}}}\right)}^{\varpi}sign({\tau}^{(\alpha ;g)}){\delta}_{ik}{\delta}_{jl},|{\tau }^{(\alpha ;g)}|\, > \,{R}^{(\alpha ;g)}\end{array},$$

(23)

where ${\tau }^{(\alpha ;g)}={\sigma }_{qw}{m}_{qw}^{(\alpha ;g)}$ is the resolved shear stress on each slip plane, and ${D}_{{\rm{slip}}}$, ${R}^{(\alpha ;g)}$, and $\varpi$ are the temperature dependent drag, slip resistance, and rate sensitivity of slip, respectively. Substituting Eq. (23) into Eq. (22), the common crystal plasticity flow rule (phenomenological constitutive model) is recovered^20,47. Therefore, both the J₂ and crystal plasticity flow rules can be derived from the phase-field framework with appropriate constraints, which makes it convenient to couple plasticity with other order parameters under a common and unified free energy functional.

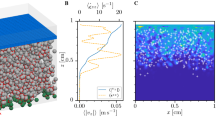
The grain structure in a polycrystal is described by a set of order parameters ${\eta }_{g}(1\le g\le N)$, which represents the distribution of the grain g, respectively (Fig. 1c). The plasticity within each grain interior is described by crystal plasticity, accommodated by J₂ plasticity near grain boundaries²⁰. The total plastic strain is given by the summation of two types of plastic strains, i.e.,

$${\varepsilon }_{ij}^{{\rm{p}}}={\varepsilon }_{ij}^{{\rm{p}}({\rm{J}})}+\mathop{\sum }\limits_{g=1}^{N}\mathop{\sum }\limits_{\alpha =1}^{{S}_{g}}{\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)},$$

(24)

The order parameters ${\varepsilon }_{ij}^{{\rm{p}}({\rm{J}})}$ and ${\varepsilon }_{ij}^{{\rm{p}}(\alpha ;g)}$ should satisfy the constraints Eqs. (11) and (16), respectively. Following similar approaches as described above, we can derive the kinetic equation for the total plastic strain,

$$\frac{\partial {\varepsilon }_{ij}^{{\rm{p}}}}{\partial t}={L}_{ijkl}^{({\rm{J}})}{\sigma ^{\prime} }_{kl}+\mathop{\sum }\limits_{g=1}^{N}\mathop{\sum }\limits_{\alpha =1}^{{S}_{g}}{L}_{ijkl}^{{\rm{p}}(\alpha )}{\sigma }_{qw}{m}_{qw}^{(\alpha )}{m}_{kl}^{(\alpha )},$$

(25)

The kinetic coefficients are given as functions of the grain order parameters,

$${L}_{ijkl}^{({\rm{J}})}=\Bigg\{\begin{array}{c}0,{J}_{2}\le {\sigma}_{{\rm{Y}}}^{{\rm{GB}}}\\ {L}_{{\rm{p}}}{\delta}_{ij}{\delta}_{kl}[1-\mathop{\sum}\limits_{g=1}^{N}y({\eta}_{g})],{J}_{2}\, > \,{\sigma }_{{\rm{Y}}}^{{\rm{GB}}}\end{array},$$

(26)

$${L}_{ijkl}^{{\rm{p}}(\alpha ;g)}=\Bigg\{\begin{array}{c}0,|{\tau}^{(\alpha ;g)}|\le {R}^{(\alpha ;g)}\\ \frac{{L}_{{\rm{p}}}}{{\tau}^{(\alpha ;g)}}{(\frac{|{\tau}^{(\alpha ;g)}|-{R}^{(\alpha ;g)}}{K})}^{n}sign({\tau}^{(\alpha ;g)})y({\eta}_{g}){\delta}_{ik}{\delta}_{jl},|{\tau}^{(\alpha ;g)}|\, > \,{R}^{(\alpha ;g)}\end{array},$$

(27)

where $y({\eta }_{g})$ is the interpolation function defined by²⁰ $y({\eta }_{g})={\eta }_{g}^{12}(3-2{\eta }_{g}^{6})$. The elastic tensor in a polycrystalline structure is given by ${c}_{ijkl}({\eta }_{g})=\sum _{g}y({\eta }_{g}){c}_{ijkl}^{(g)}+[1-\sum _{g}y({\eta }_{g})]{c}_{ijkl}^{({\rm{GB}})}$, where ${c}_{ijkl}^{({\rm{GB}})}$ is the elastic tensor at the grain boundary.

The spatial distribution of cracks is described by a scalar parameter ϕ, where ϕ = 0 indicates the undamaged region, and ϕ = 1 refers to the fully cracked region, as illustrated in Fig. 1b. The order parameter ϕ continuously changes from 0 to 1, and the width of the transition region is determined by a length scale parameter ${l}_{0}$. Rigorous analysis shows that the phase-field brittle fracture model converges to Griffith’s theory of brittle fracture in the sense of Γ-convergence when ${l}_{0}\to 0$^2,3,48.

In the presence of cracks, the total free energy is given by^2,9

$$F={\int }_{\varOmega }[{f}_{{\rm{elas}}}+{f}_{{\rm{frac}}}+{f}_{{\rm{g}}}]d\Omega ={\int }_{\Omega }[{(1-\phi )}^{2}{f}_{{\rm{elas}}}^{+}+{f}_{{\rm{elas}}}^{-}+{f}_{{\rm{frac}}}+{f}_{{\rm{g}}}]d\Omega ,$$

(28)

In Eq. (28), ${f}_{{\rm{elas}}}^{+}$ and ${f}_{{\rm{elas}}}^{-}$ are the tensile and compressive parts of the elastic energy density, respectively, ${f}_{{\rm{frac}}}$ is the fracture energy density, and ${f}_{{\rm{g}}}$ is the grain energy density. In the absence of cracks, ${f}_{{\rm{elas}}}={f}_{{\rm{elas}}}^{+}+{f}_{{\rm{elas}}}^{-}$. The elastic energy is split into the tensile and compressive parts since only the tensile elastic energy can be released by crack growth. Volumetric/deviatoric split⁵ and spectral split¹⁰ are two popular methods to split the elastic energy. In most cases, numerical results based on these two methods are similar². However, when the three principal strains are all negative, only the spectral split method produces reasonable results⁶, which is therefore adopted in this work. Note that the spectral split method does not consider the influence of the crack orientation, which requires more complex decomposition methods of the stress tensor^49,50.

In the spectral split method, the elastic strain tensor is decomposed as ${{\boldsymbol{\varepsilon }}}_{\pm }^{{\rm{elas}}}=\mathop{\sum }\nolimits_{I=1}^{3} < {\varepsilon }_{I}^{{\rm{elas}}}{ > }_{\pm }{{\bf{n}}}_{I}\otimes {{\bf{n}}}_{I}$, where $< \cdot { > }_{\pm }:=(\cdot \pm |\cdot |)/2$, and ${\varepsilon }_{I}^{{\rm{elas}}}$ and ${{\bf{n}}}_{I}$ are the eigenvalues and eigenvectors of the elastic strain tensor. The split of the elastic energy density associated with a general elastic stiffness tensor can be found in the Supplementary Note 2. For the isotropic elasticity, the expression for the tensile and compressive elastic energy density is simply⁹

$${f}_{{\rm{elas}}}^{\pm }=\frac{\lambda }{2}{\langle tr({{\boldsymbol{\varepsilon }}}^{{\rm{elas}}})\rangle }_{\pm }^{2}+\mu\, tr({({{\boldsymbol{\varepsilon }}}^{{\rm{elas}}})}_{\pm }^{2}),$$

(29)

where λ and μ are the Lamé constants.

To describe the influence of cracks on the stress distribution, an effective stiffness tensor ${c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi )$ is introduced, which can be obtained by taking the partial derivatives⁴⁵,

$${c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi )=\frac{{\partial }^{2}[{(1-\phi )}^{2}{f}_{{\rm{elas}}}^{+}+{f}_{{\rm{elas}}}^{-}]}{\partial {\varepsilon }_{ij}^{{\rm{elas}}}\partial {\varepsilon }_{kl}^{{\rm{elas}}}}.$$

(30)

The expression for each component of ${c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi )$ for the isotropic elasticity is provided in ref. ⁹. Utilizing ${c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi )$, the elastic energy density is rewritten as

$${f}_{{\rm{elas}}}=\frac{1}{2}{c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi ){\varepsilon }_{ij}^{{\rm{elas}}}{\varepsilon }_{kl}^{{\rm{elas}}}=\frac{1}{2}{c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi )({\varepsilon }_{ij}-{\varepsilon }_{ij}^{{\rm{p}}})({\varepsilon }_{kl}-{\varepsilon }_{kl}^{{\rm{p}}}),$$

(31)

which is in the same format with Eq. (10) except that the effective elastic tensor changes from ${c}_{ijkl}({\eta }_{g})$ to ${c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi )$. Therefore, the plastic flow equations derived above are still valid in the presence of cracks, and the only change is that currently the elastic tensor is a function of $\phi$.

The fracture energy density is expressed by⁹

$${f}_{{\rm{frac}}}={G}_{{\rm{c}}}({\bf{x}})\left(\frac{{\phi }^{2}}{2{l}_{0}}+\frac{{l}_{0}}{2}\frac{\partial \phi }{\partial {x}_{i}}\frac{\partial \phi }{\partial {x}_{i}}\right),$$

(32)

where ${G}_{{\rm{c}}}({\bf{x}})$ is the fracture toughness. Since ${G}_{{\rm{c}}}({\bf{x}})$ and ${l}_{0}$ are both positive, the fracture energy in Eq. (32) is zero in the regions with ϕ = 0, and becomes positive in the vicinity of cracked regions with 0 < ϕ ≤ 1. Thus cracks are energetically unfavored when only considering the fracture energy expressed by Eq. (32). When the load is larger than the critical value, cracks grow since the increase of the fracture energy can be compensated by the decrease of the tensile elastic energy through the coupling term ${(1-\phi )}^{2}{f}_{{\rm{elas}}}^{+}$ in Eq. (28). When ϕ increases to the value of 1, the driving force from the coupling term ${(1-\phi )}^{2}{f}_{{\rm{elas}}}^{+}$ vanishes, and the further increase of ϕ beyond 1 is unfavored by the fracture energy. Thus the value of ϕ is confined within the range 0 < ϕ ≤ 1. When the load is removed, cracks (the regions with ϕ ≥ 0.5) are maintained by the irreversible conditions as discussed below.

In our model, the fracture toughness ${G}_{{\rm{c}}}({\bf{x}})$ is a function of grain structures¹⁶ and plastic strain¹¹. First we only consider the influence of grain structures, which is expressed by

$${G}_{{\rm{c}}}({\eta }_{g})=\sum _{g}y({\eta }_{g}){G}_{{\rm{c}}}^{{\rm{in}}(g)}+\left[1-\sum _{g}y({\eta }_{g})\right]{G}_{{\rm{c}}}^{{\rm{GB}}},$$

(33)

where ${G}_{{\rm{c}}}^{{\rm{in}}(g)}$ and ${G}_{{\rm{c}}}^{{\rm{GB}}}$ are the fracture toughness in the grain interior and at grain boundaries, respectively. In the previous brittle fracture model for polygrains¹⁶, the fracture toughness only depends on ${G}_{{\rm{c}}}^{{\rm{in}}(g)}$, and the decrease of fracture toughness at grain boundaries is modeled by introducing an interface weakening coefficient. Here, the fracture toughness is a function of both ${G}_{{\rm{c}}}^{{\rm{in}}(g)}$ and ${G}_{{\rm{c}}}^{{\rm{GB}}}$, which are summed through the interpolation function, in the same format as yield strength and elastic tensor. Equation (33) clearly defines the dependence of the overall fracture toughness on ${G}_{{\rm{c}}}^{{\rm{GB}}}$, compared to the previous method by introducing the interface weakening coefficient¹⁶.

Next the influence of plastic strain on fracture toughness is incorporated. It is assumed that ${G}_{{\rm{c}}}$ is decreased as a function of the von Mises equivalent plastic strain ${\varepsilon }_{{\rm{eq}}}$, which is defined by ${\varepsilon }_{{\rm{eq}}}=\sqrt{\frac{2}{3}}{\int }_{0}^{t}\sqrt{{\dot{{\mathbf{\upepsilon }}}}^{{\rm{p}}}:{\dot{{\mathbf{\upepsilon }}}}^{{\rm{p}}}}d\tau$¹¹. Here a smoothed degradation function is proposed as

$${G}_{{\rm{c}}}({\eta }_{g},{\varepsilon }_{{\rm{eq}}})={G}_{{\rm{c}}}({\eta }_{g})\left\{\left(0.5-\frac{{g}_{{\rm{res}}}}{2}\right)\tanh \,\left[2\left(1-\frac{{\varepsilon }_{{\rm{eq}}}}{{\varepsilon }_{{\rm{half}}}}\right)\right]+\left(0.5+\frac{{g}_{{\rm{res}}}}{2}\right)\right\},$$

(34)

where ${g}_{{\rm{res}}}$ is the residual fracture toughness with a large plastic strain, and ${\varepsilon }_{{\rm{half}}}$ denotes the strain value when the fracture toughness decreases to about half of the initial value. The value of ${\varepsilon }_{{\rm{half}}}$ controls the decreasing rate of ${G}_{{\rm{c}}}({\bf{x}})$ as ${\varepsilon }_{{\rm{eq}}}$ increases, and thus ${\varepsilon }_{{\rm{half}}}$ describes the coupling strength between plastic strain and fracture toughness. Based on the comparison between phase-field simulations and experiments¹¹, the value of ${\varepsilon }_{{\rm{half}}}$ is between 0.05 and 0.15, and the crack morphologies at different values of ${\varepsilon }_{{\rm{half}}}$ is discussed in Supplementary Note 4. In ref. ¹¹, the toughness degradation function is written as a piecewise function of ${\varepsilon }_{{\rm{eq}}}$, and the profile based on the proposed tanh function in Eq. (34) is similar to that described by a piecewise function, as shown in Supplementary Fig. 1. Note that the fracture toughness is independent of elastic strain in this work, and thus the simulations under cyclic loads correspond to the LCF with plasticity dominant in the fatigue process.

For simplicity, here ${\varepsilon }_{{\rm{eq}}}$ is treated as a history variable, which depends on the value of ${\varepsilon }_{ij}^{{\rm{p}}}$ in all the previous time steps and independent of the current value of ${\varepsilon }_{ij}^{{\rm{p}}}$. To derive the same plastic flow equations as in the presence of cracks, the relation $\frac{\partial {\varepsilon }_{{\rm{eq}}}}{\partial {\varepsilon }_{ij}^{{\rm{p}}}}=0$ is employed. A similar assumption is used in ref. ¹¹.

The free energy density for the grain structure part is given by⁵¹

$${f}_{{\rm{g}}}=B\left[1-4\mathop{\sum }\limits_{g=1}^{N}{\eta }_{g}^{3}+3{\left(\mathop{\sum }\limits_{g=1}^{N}{\eta }_{g}^{2}\right)}^{2}\right]+\frac{1}{2}{\beta }_{\eta }\mathop{\sum }\limits_{g=1}^{N}{|\nabla {\eta }_{g}|}^{2},$$

(35)

where $B$ and ${\beta }_{\eta }$ are the coefficients for the bulk term and gradient term, respectively.

The grain structure is relaxed at high temperatures in the absence of plastic strain and cracks, i.e., ${\varepsilon }_{ij}^{{\rm{p}}}$ and $\phi$ are maintained zero. Therefore, the evolution of the grain order parameter ${\eta }_{g}$ is described by a typical TDGL equation

$$\frac{\partial {\eta }_{g}}{\partial t}=-{L}_{g}\frac{\delta F}{\delta {\eta }_{g}}=-{L}_{g}\left\{12B\left[-{\eta }_{g}^{2}+{\eta }_{g}\sum _{g}{\eta }_{g}^{2}\right]-{\beta }_{\eta }{\nabla }^{2}{\eta }_{g}\right\},$$

(36)

On the other hand, the evolution of $\phi$ and ${\varepsilon }_{ij}^{{\rm{p}}}$ is assumed to occur at room temperature, with the grain structure frozen. The evolution of $\phi$ is described by solving a TDGL equation

$$\frac{\partial \phi }{\partial t}=-{L}_{\varphi }\frac{\delta F}{\delta \phi },$$

(37)

where ${L}_{\phi }$ is the kinetic coefficient.

The quasi-static state is assumed so that the system is in the mechanical equilibrium at every time step, i.e.

$$\frac{\partial {\sigma }_{ij}}{\partial {x}_{j}}=0,$$

(38)

Based on the above derivations, we construct two types of phase-field models on ductile fracture. In the Type-I model, the grain structure and crystal plasticity are considered, and the plastic strain is evolved by solving Eq. (25). Compared to previous ductile fracture models with crystal plasticity^17,18, our Type-I model describes the grain structure by phase-field order parameters. The introduction of the grain order parameters has two advantages. First, the grain boundaries become diffuse interfaces, and by utilizing the interpolation function, our model can naturally describe the distinct properties of grain boundaries such as elastic stiffness, yield strength, and fracture toughness. Second, the evolution of grain structures can be described by solving the grain order parameters from the kinetic equations, and thus our model can be readily extended to simulate the kinematic hardening. It is noted that, although kinematic hardening is not explicitly included in our formulation, since it is caused by heterogeneous plastic deformation and microstructure change^52,53, macroscopically the simulated structure can automatically exhibit kinematic hardening behaviors. The fidelity depends on how many factors that contribute to the heterogeneity are incorporated into the model. In classical plasticity theories, kinematic hardening is introduced by directly defining a phenomenological non-convex dissipation potential, which however does not have a clear physical meaning consistent with the defined phase-field free energy.

The simulations based on the Type-I model are time consuming when the model is applied to a polycrystalline structure with many grains. At a length scale much larger than the grain size, the influence of grain structures could be mostly averaged out, and then J₂ plasticity becomes a reasonable approximation for the whole system.

Based on pure J₂ plasticity, we construct the Type-II model, where the grain structure is neglected, and the plastic strain is evolved by solving Eq. (14). In our Type-II model, the plastic strain and crack order parameter are treated equally, all governed by TDGL-type equations, which are obtained from the variational derivatives of the same free energy functional, i.e. Equation (28). On the other hand, in previous ductile fracture models with only J₂ plasticity, the plastic strain is evolved by an elastic predictor and plastic corrector (return-mapping) algorithm utilizing the Kuhn–Tucker relations^4,11. From numerical perspective, our Type-II model and the J₂ ductile fracture model produce similar final results. However, the TDGL equation for plasticity in our model fits better to a typical phase-field framework as discussed above.

In previous ductile fracture models^4,11, the elastic energy is split based on volumetric/deviatoric split, which is easier to implement compared to the spectral split². However, the volumetric/deviatoric split cannot correctly deal with the case when all the three principal strain components are negative⁶. Here we employ the spectral split method for the elastic energy split when modeling ductile fracture, which could produce reasonable results even when the principal strain components are all negative. To implement the spectral split, the effective stiffness tensor ${c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi )$ is used in the elasticity and plasticity solvers, as will be shown below.

Numerical scheme and simulation setup

The numerical scheme is developed within the quasi-static regime, i.e., the loading rate is assumed to be small enough that all the mechanical processes reach their equilibria. The goal of the numerical scheme is to obtain the distribution of plastic strain ${{\boldsymbol{\varepsilon }}}^{{\rm{p}}}$, total strain ${\boldsymbol{\varepsilon }}$, and crack order parameter ϕ. A staggered method is adopted, which leads to significantly improved robustness compared to the monolithic scheme^2,9,10.

Mode-I fracture is studied in this work, and the system setting is sketched in Fig. 2a, where we change the displacement on the top surface with the bottom surface fixed. The flow chart of the staggered method is illustrated in Fig. 2b. First, the surface displacement is updated in each loop. Second, the elasticity solver provides the updated distribution of total strain and stress based on the distributions of plastic strain and crack from the previous time step. Third, the updated stress is used to obtain the distribution of plastic strain with the fixed crack distribution. Finally, the crack order parameter is updated using the new total strain and new plastic strain. The details of each solver are provided below, and all the three solvers are iterative in nature. Note that there are two types of time steps in the staggered scheme, i.e. the real physical time step where the surface displacement is updated and the iteration time steps in the three solvers that do not have physical meaning given the quasi-static assumption. In the three iterative solvers, the time step is set as $\Delta t=1$.

Fig. 2: Illustrations for numerical implementation.

a Schematic for the mechanical boundary conditions. b Flowchart for the staggered scheme with the updated variables marked in red.

In the numerical solver, the elastic energy is rewritten as

$${f}_{{\rm{elas}}}^{{\rm{eff}}}=[(1-k){(1-\phi )}^{2}+k]{f}_{{\rm{elas}}}^{+}+{f}_{{\rm{elas}}}^{-},$$

(39)

where k is a small quantity to avoid numerical singularity⁹.

In this work, we assume that the elastic tensors of both grain interior and grain boundaries are isotropic, and the close-form expression of ${c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi )$ as a function of $\phi$ given by ref. ⁹ is employed. The distribution of ${c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi )$ is calculated based on the distribution of $\phi$ from the previous time step. Then the obtained ${c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi )$ serves as input to the elasticity solver, which is based on a TDGL equation in terms of a virtual strain⁵⁴. The kinetic coefficient in the virtual strain TDGL equation is chosen as 0.5. Note that the elasticity solver is based on the efficient FFT method, which enables us the simultaneous simulations of plastic flow and crack evolution under cyclic loads. The final solution from the heterogeneous elastic solver guarantees the equilibrium condition given by Eq. (38), and the proof is provided in ref. ⁵⁴.

Strain controlled boundary conditions are employed. The surface displacement is controlled by the average strain $\overline{{\varepsilon }_{33}}$, and the other average strain components are maintained zero. During the loading process, the incremental strain $\Delta {\overline{{\epsilon }}_{33}}=2.4\times {10}^{-6}$, and during unloading process, the incremental strain $\Delta \overline{{\epsilon }_{33}}=-4.8\times {10}^{-6}$. Within the infinitesimal strain theory, the surface displacement is ${u}_{t}=\overline{{\varepsilon }_{33}}{L}_{3}$ with ${L}_{3}$ the system dimension along the x₃ direction. The outputs of the elasticity solver are the total strain field ${\mathbf{\upepsilon }}$, elastic strain field ${{\mathbf{\upepsilon }}}^{{\rm{ela}}}$, and stress field ${\mathbf{\upsigma }}$. The outputs of the elasticity solver are used to update the plastic strain and cracks as shown below.

An explicit Euler method is employed to solve Eq. (25) for the Type-I model and Eq. (14) for the Type-II model, respectively. The kinetic coefficient is chosen as ${L}_{{\rm{p}}}=1.0\times {10}^{-4}$. We run two test simulations based on the Type-II model by enlarging and decreasing the values of ${L}_{{\rm{p}}}$ by four times, and negligible differences are present in the resulting displacement-load curves, as shown in Supplementary Fig. 9. In each iteration step, after ${{\mathbf{\upepsilon }}}^{{\rm{p}}}$ is updated, the elastic strain ${{\mathbf{\upepsilon }}}^{{\rm{elas}}}$and stress ${\mathbf{\upsigma }}$ are updated based on the following expressions

$${{\mathbf{\upepsilon }}}^{{\rm{elas}}}={\mathbf{\upepsilon }}-{{\mathbf{\upepsilon }}}^{{\rm{p}}},{\sigma }_{ij}={c}_{ijkl}^{{\rm{eff}}}({\eta }_{g},\phi ){\epsilon }_{kl}^{{\rm{elas}}},$$

(40)

The convergence is considered achieved if at the nth iteration ${\rm{Max}}\,[{{\boldsymbol{\epsilon }}}_{n}^{{\rm{p}}}({\bf{x}})-{{\boldsymbol{\epsilon }}}_{n-1}^{{\rm{p}}}({\bf{x}})]\le {10}^{-7}$is satisfied, where n denotes the iteration step.

An explicit Euler scheme is adopted for the temporal evolution of Eq. (37). The kinetic coefficient is chosen as${L}_{\phi }=1.0\times {10}^{-2}$. The crack order parameter is considered to reach equilibrium when the criterion ${\rm{Max}}\,[{\phi }_{n}({\bf{x}})-{\phi }_{n-1}({\bf{x}})]\le {10}^{-4}$ is satisfied. The explicit scheme is adopted in the plasticity and crack solvers for simplicity, as discussed in ref. ⁵⁵. Note that the most computationally intensive part of the simulation is the elasticity solver, and the smaller time step required in the explicit algorithm does not significantly increase the computation time. For the spatial discretization of the crack solver, we employ the FDM since ${G}_{{\rm{c}}}({\bf{x}})$ is position-dependent.

In our model, the region with ${\phi }_{n}({\bf{x}})\, > \,0.5$ is regarded as cracked, and the irreversible condition ${\phi }_{n+1}({\bf{x}})\ge {\phi }_{n}({\bf{x}})$ is guaranteed at cracked regions. In previous fracture models^9,16, the irreversible condition ${\phi }_{n+1}({\bf{x}})\ge {\phi }_{n}({\bf{x}})$is maintained regardless of the value of ${\phi }_{n}({\bf{x}})$, which considers the increase of the crack order parameter to any magnitude as dissipation. In our model, we assume that ${\phi }_{n}({\bf{x}})\le 0.5$ corresponds to the region with elastic deformation and the positive value of $\phi ({\bf{x}})$ under a small tensile load is allowed to decrease after the load is removed. We run simulations with both settings of irreversible condition, and the resulting differences are negligible in the quasi-static regime.

The simulations employ regular grids ${n}_{x}\Delta x\times {n}_{y}\Delta x\times {n}_{z}\Delta x$ where $\Delta x$ is the grid spacing with the unit of length. In the above solvers, several dimensionless parameters are used, i.e., ${l}_{0}^{\ast }=\frac{{l}_{0}}{\Delta x}$, ${x}_{i}^{\ast }=\frac{{x}_{i}}{\Delta x}$, ${G}_{{\rm{c}}}^{\ast }=\frac{{G}_{{\rm{c}}}}{{c}_{0}\Delta x}$, and ${c}_{ijkl}^{\ast }=\frac{{c}_{ijkl}^{{\rm{eff}}}}{{c}_{0}}$, where ${c}_{0}$ is a normalization constant with the value of 1 GPa. In terms of the dimensionless parameters, Eq. (32) becomes

$${f}_{{\rm{frac}}}={G}_{{\rm{c}}}^{\ast }({\bf{x}})\left(\frac{{\phi }^{2}}{2{l}_{0}^{\ast }}+\frac{{l}_{0}^{\ast }}{2}\frac{\partial \phi }{\partial {x}_{i}^{\ast }}\frac{\partial \phi }{\partial {x}_{i}^{\ast }}\right),$$

(41)

From Eq. (41), the grid number of the cracked region is mainly determined by the dimensionless factor ${G}_{{\rm{c}}}^{\ast }{l}_{0}^{\ast }$. When ${G}_{{\rm{c}}}^{\ast }{l}_{0}^{\ast }$ is set between 0.89 and 3.5, the grid number of the cracked region is between 5 and 23, as demonstrated in Supplementary Fig. 2. The Gibbs phenomenon and grid pinning effect will be reduced with more grids near the transition region. Therefore, in our simulations, the factor ${G}_{{\rm{c}}}^{\ast }{l}_{0}^{\ast }$ is set to be 3.5. Since ${l}_{0}^{\ast }=\frac{{l}_{0}}{\Delta x}$ and ${G}_{{\rm{c}}}^{\ast }=\frac{{G}_{{\rm{c}}}}{{c}_{0}\Delta x}$, the real values of ${l}_{0}$ and ${G}_{{\rm{c}}}$ are proportional to the grid spacing $\Delta x$. Since ${G}_{{\rm{c}}}$ is a material property independent of sample dimensions, the dependence of ${G}_{{\rm{c}}}^{\ast }$ on $\Delta x$ indicates that the cracking problem is size-dependent and samples with the larger dimensions can be cracked with smaller elastic energy density (the pure elastic problem is scale independent).

In the following sections, we apply the two types of ductile fracture models to several numerical examples. All the simulations are run in one computer node with 32 cores using the Message Passing Interface (MPI). Under the monotonic loads, the simulations can be finished within ~26 hours. Under cyclic loads, the simulations can be finished within ~7 days.

Simulation results based on the Type-I model

In this section, the Type-I model is employed. Crack growth with crystal plasticity is studied with FCC crystal structures as an example, which possess 12 slip systems⁵⁶. In a FCC crystal, the slip plane ${\bf{n}}$ is along $\{111\}$, and the slip direction ${\bf{s}}$ is along $< 1\overline{1}0 >$. Based on the parameter setting of previous reports^4,11, the material parameters are set as ${E}^{({\rm{g}})}={E}^{{\rm{GB}}}=72\,GPa$, ${\upsilon }^{({\rm{g}})}={\upsilon }^{{\rm{GB}}}=0.33$, ${l}_{0}=3\,\upmu {\rm{m}}$, ${g}_{{\rm{res}}}=0.1$, ${\varepsilon }_{{\rm{half}}}=0.15$, and $k=1.0\times {10}^{-9}$ unless otherwise noted. The yield strength at grain boundaries is ${\sigma }_{{\rm{Y}}}^{{\rm{GB}}}=750\,{\rm{MPa}}$. The initial slip resistance is ${R}^{0}=200\,{\rm{MPa}}$. For simplicity, it is assumed that the self and latent hardening parameters are equal, i.e., ${H}^{\alpha \alpha }={H}^{\alpha \beta }=H$, and the hardening law is given by⁴⁷ ${R}^{(\alpha ;g)}={R}^{0}+H(1+{b}^{\alpha })\frac{{\varepsilon }_{{\rm{eq}}}}{1+{b}^{\alpha }{\varepsilon }_{{\rm{eq}}}}$ with $H=10\,{\rm{MPa}}$ and ${b}^{\alpha }=8$. The other slip parameters are ${D}_{{\rm{slip}}}=1GPa$ and $\varpi =1$. The system dimension is 256Δx × 1Δx × 128Δx with Δx = 0.78 μm. We assume that the fracture toughness within grain interior and at grain boundaries are equal, i.e., ${G}_{{\rm{c}}}^{{\rm{in}}({\rm{g}})}={G}_{{\rm{c}}}^{{\rm{GB}}}=7.02\times {10}^{2}{{\rm{Jm}}}^{-2}$. The purpose of the assumption is to remove the influence of grain boundary weakening, and exclusively reveal the dependence of crack paths on the plastic strain in polycrystals. Note that a pre-damaged region is added in the middle to simulate the system subjected to tension with single edge notched (see Supplementary Note 3 for detailed reasons), and the pre-damaged region serves as the initial crack.

We run simulations with the load applied to different lattice orientations of a single crystal, choosing the [100] and [111] lattice orientations as two examples. As seen in Fig. 3a, when the load is applied along the [111] direction, the maximal load is larger and the displacement before fully broken is smaller compared to those along the [100] direction. The crystal is more brittle when the load is applied along the [111] direction than the [100] direction in the sense of crack growth.

Fig. 3: Crack growth in (100)- and (111)-oriented single crystals.

a Load-displacement curves with the load applied to (100)- and (111)-oriented single crystals. b, c Distribution of equivalent plastic strain in (100)- and (111)-oriented single crystals, respectively. The red lines indicate the newly grown cracks and the green lines represent the initial crack.

Our simulation results demonstrate that the anisotropy of plastic flow leads to anisotropy of crack growth in a single crystal. As shown in Fig. 3b, when the load is applied along the [100] direction of the crystal, the distribution of plastic strain is symmetric with respect to the initial crack, and the crack growth direction is perpendicular to the load direction. The total plastic strain is decomposed to contributions from each slip system. As demonstrated in Supplementary Fig. 4, the plastic strain is mainly contributed from four slip systems with the slip directions contained within the 2D plane, consistent with the previous report⁵⁷. On the other hand, when the load is applied along the [111] direction, the distribution of plastic strain is asymmetric with respect to the initial crack, with the plastic strain concentrated on the upper-right and lower-left regions of the system as shown in Fig. 3c. The contributions from each slip system for the (111)-oriented crystal are shown in Supplementary Fig. 5, which demonstrates that the slip directions of two dominant slip systems form an angle of 30° with the 2D plane, and the two slip systems dominate over the two with the slip directions contained within the 2D plane. This is because the resolved shear stress on the dominant slip systems is larger, as illustrated by the sizes of plastic zones in Supplementary Fig. 6, which are plotted following an analytical method⁵⁷. The asymmetric distribution of the plastic strain results in the deviation of the crack paths from the horizontal direction, as demonstrated in Fig. 3c. Therefore, the anisotropy of crystal plasticity could lead to a change from pure Mode-I cracking to mixed-mode cracking, which is consistent with experimental observations⁵⁸.

FCC bicrystals with the alternation of (100)- and (111)-oriented grains are studied as an example. As shown in Fig. 4b, the distribution of plastic strain is highly dependent on the grain structures. Specifically, the plastic strain is concentrated at some grain boundaries. The heterogeneous plastic deformation in Fig. 4b is a sign of kinematic hardening, which indicates that kinematic hardening is automatically captured by our phase-field model with a strong structural inhomogeneity, although it is not explicitly introduced into the free energy functional.

Fig. 4: Crack growth in FCC bicrystals.

a, b Distribution of grains, cracks, and equivalent plastic strain considering crystal plasticity within each grain. c, d Distribution of grains, cracks, and equivalent plastic strain assuming J₂ plasticity within each grain. The green lines indicate the position of the initial crack.

Since the accumulation of plastic strain reduces the fracture toughness as indicated by Eq. (34), the crack deflects into the grain boundaries, resulting in intergranular crack growth, as demonstrated in Fig. 4a. Note that the crack deflection is purely caused by the inhomogeneous distribution of plastic strain, rather than by the lower fracture toughness at grain boundaries as discussed in previous work¹⁶, since here it is set that ${G}_{{\rm{c}}}^{{\rm{in}}({\rm{g}})}={G}_{{\rm{c}}}^{{\rm{GB}}}$. Therefore, our simulation results demonstrate that the crack paths can be deflected by the underlying grain structures when crystal plasticity is considered within each grain and J₂ plasticity is assumed near grain boundaries.

As a comparison, crack growth is simulated under the same system settings except that J₂ plasticity is employed within each grain, as did in ref. ²⁰. As shown in Fig. 4c, d, the crack grows straightly along the horizontal direction, and the distribution of plastic strain is symmetric with respect to the crack plane. Both the crack path and plastic strain distribution with J₂ plasticity are consistent with earlier reports^4,11.

Simulation results based on the Type-II model

In this section, we study the crack growth based on the Type-II model. Ductile fracture growth under monotonic loads is studied first, followed by the simulations of fatigue crack growth under cyclic loads.

The elastic constants are $E=72\,GPa$ and $\upsilon =0.33$. The initial yield strength is given by ${\sigma }_{{\rm{Y}}}^{0}=345\,{\rm{MPa}}$, and power-law strain hardening is assumed, with the expression $R=\frac{E}{250}{({\varepsilon }_{{\rm{eq}}})}^{1/2}$ following ref. ⁵⁹. The length scale parameters are changed to ${l}_{0}=0.3\,{\rm{mm}}$ and Δx = 78 μm, and the system dimensions are sketched in Fig. 5a. The fracture toughness is ${G}_{{\rm{c}}}=7.02\times {10}^{4}{{\rm{Jm}}}^{-2}$.

Fig. 5: Crack growth under monotonic displacement-controlled tests.

a Schematic for system setup. b Load-displacement curves with and without plasticity. c, d Stress component along the loading direction with and without plasticity corresponding to Points C and D in (b), respectively. e Distribution of equivalent plastic strain corresponding to (d).

To demonstrate the influence of J₂ plastic strain, we run simulations with and without plasticity, where the latter is achieved by maintaining ${{\mathbf{\upepsilon }}}^{{\rm{p}}}$ as 0. As shown in Fig. 5b, the system can endure a larger displacement before fully broken with J₂ plasticity compared to the case without plasticity. The influence of plastic strain on crack growth is manifested in two aspects. First, the development of plastic strain reduces the stress magnitude ahead of the crack tip. As demonstrated in Fig. 5c, d, under the same displacement, the stress component ahead of the crack tip with plasticity is roughly half of that without plasticity. From this aspect, the development of plasticity slows down crack growth, since both can release the elastic energy under tension. Second, the accumulation of the equivalent plastic strain reduces the fracture toughness based on Eq. (34). As shown in Fig. 5e, the equivalent plastic strain is concentrated near the crack tip, resulting in local degradation of the fracture toughness. From the second aspect, the development of plasticity facilitates the crack growth. In our simulation results, the first factor dominates over the second under monotonic loads. Crack growth behaviors are further simulated at different values of ε_half, and crack bifurcation is observed with a small ε_half due to significant plastic degradation, as demonstrated in Supplementary Fig. 7.

Next, the mechanical boundary condition is changed to cyclic loads. The surface displacement is varied periodically between 0 and a fixed value, as sketched in Fig. 6(a). Note that the maximal displacement is large enough to cause significant plasticity, and thus the fatigue belongs to the LCF.

Fig. 6: Displacement and load evolution under cyclic loads.

a Schematic for the evolution of the surface displacement. b Load-displacement curve with the displacement varying between 0.0 mm and 0.3 mm. The number and the color of the curve indicate the number of cycles.

Figure 6b shows a typical cyclic load-displacement curve with the maximal displacement of 0.3 mm, which corresponds to an average strain of 3.0%. The load of the first loading cycle increases from zero to the maximum value, distinct from those of the following cycles, which alternate between negative and positive values. The maximal load decreases cycle by cycle, and after 9 cycles, the maximal load decreases to zero, indicating that the sample is fully broken. Note that the maximal displacement of 0.3 mm is about half of the maximal displacement before fully broken under monotonic displacement-controlled condition as shown in Fig. 5b. Compared to the case of monotonic loads, the influence of cyclic loads comes from two contributions. First, the stress ahead of the crack tip increases over cycles due to plastic hardening. Second, the fracture toughness ahead of the crack tip is decreased due to the accumulation of the equivalent plastic strain.

The evolution of the average equivalent plastic strain during an exemplary 6th cycle is analyzed in detail. As shown in Fig. 7a, the plastic flow is not activated in the initial stages of loading and unloading, i.e., from Point B to C and from D to E. Instead, the plastic deformation occurs mainly in the late stages of loading and unloading, i.e., from Point C to D and from E to F. On the other hand, the crack grows only in the late stage of loading. The distributions of a plastic strain component at Points B-F are shown in Fig. 7b–f. Figure 7b demonstrates the periodic distribution of plastic strain on the flanks of a fatigue crack, and each maximum corresponds to a cycle. When the displacement increases from Point B to C, there are almost no changes as shown in Fig. 7b, c. When the displacement is further increased to its maximum at Point D, a new peak of plastic strain appears ahead of the crack tip, as shown in Fig. 7d. Note that the magnitude of the plastic strain at the new peak is larger than that caused by previous cycles in Fig. 7(d). When the displacement decreases from Point D to E, there is no plastic flow from the comparison between Fig. 7d, e. When the displacement further decreases to its minimum at Point F, the plastic strain at the new peak decreases, and reaches a value similar to that from previous cycles, as demonstrated in Fig. 7(f). Note that the equivalent plastic strain as shown in Fig. 7(a) always increases over cycles regardless of the increasing or decreasing of the plastic strain component. Figure 7(b)–(f) demonstrate that the striped pattern of plastic strain is caused by the stress variation near the crack tip under cyclic loads. The temporal evolution of plastic strain as demonstrated in Fig. 7 is qualitatively consistent with Laird’s plastic blunting concept model^1,39.

Fig. 7: Evolution of plastic strain during a loading cycle.

a Evolution of the average equivalent plastic strain and crack length. b–f Distribution of the plastic strain component along the loading direction, corresponding to Points B-F in (a), respectively. The red curve in each figure represents the contour of the crack. The color legend is shown on the top right. The numbers on (b–f) indicate the numbers of cycles.

The plastic strain on the crack flanks results in contacted crack surfaces, i.e., crack closure. During the unloading process of the 8th cycle, under a positive load, as labeled by a red dot in Fig. 6b, the distribution of plastic strain is shown in Fig. 8a, which demonstrates that the plastic strain alternates between negative to positive. Positive plastic strain leads to local crack closure and compressive stress, as demonstrated in Fig. 8b.

Fig. 8: Crack closure and fatigue striations after eight load cycles.

a Distribution of a plastic strain component. b Distribution of a normal stress component. The red curves in (a and b) represent the contour of the crack. c Distribution of the displacement field. d Profile of the displacement along the purple line in (c).

The simulation results indicate that the cyclic plastic flow is the origin of the fatigue striations, which are commonly observed as saw-like marks on the crack faces. We calculate the displacement field caused by the plastic strain by ${u}_{i}=\int \frac{{d}^{3}q}{{(2\pi )}^{3}}{\Omega }_{ij}{c}_{ijkmn}{n}_{k}{\tilde{\varepsilon }}_{mn}^{{\rm{p}}}{e}^{i{\bf{q}}\cdot {\bf{r}}}$where ${\Omega }_{ij}={({c}_{ijkl}{n}_{k}{n}_{l})}^{-1}$and ${\tilde{\varepsilon }}_{mn}^{{\rm{p}}}=\int {\varepsilon }_{mn}^{{\rm{p}}}{e}^{-i{\bf{q}}\cdot {\bf{r}}}{d}^{3}x$^60,61. The result is plotted in Fig. 8c, which demonstrates a periodic variation along the crack growth direction. Note that the displacement field is symmetric with respect to the crack, i.e., the crack surfaces show the patterns of peak-to-peak and valley-to-valley. The displacement profile along the purple line in Fig. 8c is shown in Fig. 8d. As can be seen from Fig. 8d, one load cycle produces one minimum on the displacement profile, and the striation spacing is equal to the crack growth per cycle, consistent with the claim of Laird’s Plastic blunting model³⁹.

Crack growth rate is analyzed based on the simulation results. For the LCF, plasticity dominates and the condition near the crack tip is described by the J-integral $\Delta J$, which is defined by^1,62

$$\Delta J={\int }_{\varGamma }(W{n}_{1}-{n}_{j}\Delta {\sigma }_{jk}\frac{\partial \Delta {u}_{k}}{\partial x})ds,$$

(42)

where ${n}_{1}$ is the x₁ component of the normal to the path, and $\Delta {\sigma }_{jk}$ and $\Delta {u}_{k}$ are the changes in the stress tensor and displacement between the minimal loads and maximal loads. The quantity W has the physical meaning of stored elastic energy density, and is calculated by the expression $W={\int }_{0}^{{\varepsilon }^{\max }}({\sigma }_{ij}-{\sigma }_{ij}^{0})d{\varepsilon }_{ij}$ with ${\sigma }_{ij}^{0}$ the stress under the minimal loads. It is proven that $\Delta J$ is path independence¹. Analogous to the Paris law, it is proposed that under large scale yielding, the crack growth rate is given by¹⁰

$$\frac{da}{dN}=k{(\Delta J)}^{n},$$

(43)

By changing the magnitude of the surface displacement, we study the crack growth behavior as a function of $\Delta J$. As shown by the red line in Fig. 9a, the crack growth rate is fitted by $\frac{da}{dN} \sim {(\Delta J)}^{n}$ with $n \sim 1.6$. Since $\Delta J \sim {(\Delta K)}^{2}$ under small scale yielding¹, the calculated growth law corresponds to a Paris exponent of ~3.2, which agrees with experimental observations (Fig. 10A. 3 of the book¹).

Fig. 9: Crack growth rate versus the path integral ΔJ.

a Results with different initial yield strength. b Results with different values of ε_half. The dots with different colors represent the results from phase-field simulations, and the dotted lines are fitted based on the simulation results. The slopes of the fitted lines are labeled.

Fig. 10: Magnitude of plastic strain $\Delta {\varepsilon }^{{\rm{p}}}$ versus cycle number to failure N_f.

a Results with different initial yield strength ${\sigma }_{{\rm{Y}}}^{0}$. b Results with different values of ε_half. The dots denote the results from phase-field simulations, and the dotted lines are fitted based on the simulation results. The slopes of the fitted lines are labeled.

The simulation results reveal the influence of different yield strength on the fatigue crack growth. When the initial yield strength ${\sigma }_{{\rm{Y}}}^{0}$ becomes larger, the material is stiffer, closer to a brittle material. As shown in Fig. 9a, the exponent of the growth law becomes larger with increasing ${\sigma }_{{\rm{Y}}}^{0}$. This agrees with the experimental observations that brittle materials typically have larger Paris-law exponents than ductile materials⁷. Note that there exists a crossover between the blue line with larger ${\sigma }_{{\rm{Y}}}^{0}$ and the red line with smaller ${\sigma }_{{\rm{Y}}}^{0}$ in Fig. 9a. This is because larger yield strength leads to larger stress and smaller plastic strain near the crack tip, and the two factors have opposite effects on crack growth. When ΔJ is large, the crack propagates faster with larger ${\sigma }_{{\rm{Y}}}^{0}$ due to the larger stress ahead of the crack tip. From the simulation results, the crack growth is dominated by stress magnitude in this case. On the other hand, when ΔJ is small, larger ${\sigma }_{{\rm{Y}}}^{0}$ gives rise to smaller plastic strain near the crack tip. As a result, the decrease of the fracture toughness is smaller, leading to slower crack growth. In this situation, the crack growth is dominated by the degradation rate of fracture toughness. At an intermediate ΔJ, a crossover occurs when the two factors are balanced. The crack growth rate is also studied as a function of ε_half. As shown in Fig. 9b, smaller ε_half, i.e., stronger coupling between plastic strain and fracture toughness, generally gives rise to faster crack growth and larger exponent of the growth law.

The fatigue behaviors are also analyzed based on the strain/life method by calculating the relation between plastic strain and cycle numbers to failure. The LCF is typically described by the Coffin–Manson relation³¹, which assumes the following relation

$$\Delta {\varepsilon }^{{\rm{p}}}={\alpha }_{{\rm{f}}}{N}_{{\rm{f}}}^{\beta },$$

(44)

where $\Delta {\varepsilon }^{{\rm{p}}}$ is the magnitude of plastic strain, ${\alpha }_{{\rm{f}}}$ an empirical constant, N_f number of cycles to failure, and $\beta$ is known as the fatigue ductility exponent. The value of $\Delta {\varepsilon }^{{\rm{p}}}$ is calculated from the first loading cycle of the load-displacement curves. As shown in Fig. 10, the calculated exponent $\beta$ is between −0.3 to −0.53, close to the typical experimental value, which is ~$-0.5$³¹.

The simulation results reveal the influences of initial yield strength and ε_half on the fatigue life. As shown in Fig. 10a, with a larger value of ${\sigma }_{{\rm{Y}}}^{0}$, the exponent $\beta$ becomes smaller in its magnitude, and the fatigue life becomes shorter under the same plastic strain. The decrease of the fatigue life is mainly caused by the increase of the stress ahead of the crack tip. Note that when the magnitude of $\Delta {\varepsilon }^{{\rm{p}}}$ is smaller, the difference of fatigue life caused by different ${\sigma }_{{\rm{Y}}}^{0}$ becomes smaller. In this case the crack growth is dominated by the degradation of fracture toughness, which is determined by the magnitude of $\Delta {\varepsilon }^{{\rm{p}}}$. The effect of ε_half on the value of $\beta$ is demonstrated in Fig. 10b, which shows that the value of $\beta$ changes from −0.53 to −0.48 when ε_half decreases from 0.15 to 0.075. The cycle number N decreases with a decreasing ε_half, which suggests that the fatigue life becomes shorter when the coupling between plastic strain and fracture toughness is stronger.

To reveal the underlying mechanism of the Coffin–Manson relation, crack growth rate is plotted as a function of $\Delta {\varepsilon }^{{\rm{p}}}$. As shown in Supplementary Fig. 8, the exponent of the power law in the logarithmic scale is close to 2, i.e.,

$$\frac{da}{dN}={C}_{{\rm{\varepsilon }}}{(\Delta {\varepsilon }^{{\rm{p}}})}^{2},$$

(45)

Integrating Eq. (45) with respect to both a and N gives,

$${a}_{{\rm{c}}}-{a}_{0}={C}_{{\rm{\varepsilon }}}{(\Delta {\varepsilon }^{{\rm{p}}})}^{2}{N}_{{\rm{f}}},$$

(46)

where ${a}_{{\rm{c}}}$ is the critical crack size before the catastrophic failure and ${a}_{0}$ is the initial crack size. Equation (46) is equivalent to the Coffin–Manson relation with $\beta \sim 0.5$. Therefore, the Coffin–Manson relation results from the fact that the crack growth rate is a power law function of $\Delta {\varepsilon }^{{\rm{p}}}$ in LCF. The value of $\beta$ is close to the reciprocal of the exponent in the crack growth law.

Summary of the work

A general phase-field framework with constraints on order parameters is developed from the variational principle using the Lagrange multiplier method. It is shown that the Lagrange multipliers in a non-equilibrium state can be solved from the time invariance of the constraints, and the modified TDGL equations can be derived. Based on this framework, we formulate two types of phase-field models on ductile fracture. The Type-I model incorporates three sets of order parameters, which describe the distributions of cracks, plastic strain, and grains, respectively. In the Type-I model, crystal plasticity is employed in the grain interior, accommodated by J₂ plasticity at grain boundaries. The Type-I model is applied to FCC single crystals and bicrystals, and the simulation results demonstrate that grain orientation and grain boundary location strongly affect the plastic flow and consequently crack paths.

In the Type-II model, J₂ plasticity is assumed for the whole system and the grain structure is neglected, which approximates the situation at the continuum length scale. The Type-II model is applied to investigate LCF, and our simulation results reproduce several features of fatigue cracks in ductile materials. It is demonstrated that crack closure and striations are caused by the periodic distribution of plastic strain on the crack flanks, and that the striation spacing is equal to the crack growth per cycle. Crack growth rate is analyzed based on the J-integral, and the calculated growth law is consistent with experiments. The dependence of crack growth rate on yield strength and on the coupling strength between plasticity and fracture toughness is investigated, and a crossover is observed between the calculated curves with different yield strength. Fatigue life is studied as a function of plastic strain, and without a priori assumption, the Coffin–Manson relation is reproduced. The proposed phase-field models have demonstrated their capabilities to study crack growth in ductile materials and reveal the dependence on the grain structures and loading conditions.