Introduction

New materials with attractive properties are springing up, sparking the exploration of their potential for electronics. During exploration, it is necessary to determine the band structures and transport properties of these systems. Fortunately, both of these factors can be derived from the Hamiltonian of the system1,2,3.

For a realistic large-scale system, especially with limited periodicity, the calculation of the corresponding Hamiltonian is often intractable in a conventional ab-initio study. Additionally, the resultant Hamiltonian usually has a large number of basis functions, thus increasing the temporal complexity of transport property calculations in which many matrix diagonalization operations are involved. In this regard, the tight-binding (TB) method becomes a practicable approach, describing a system as real-space TB Hamiltonian matrices expressed on a manageable number of parameters4,5 to reduce the subsequent computing time. The choice of the TB parameters thus determines the reliability of the TB calculations. Traditionally, considering the amount of time required to obtain the reasonable TB parameters on one’s own, the TB parameters are often obtained from the published TB parameter sets to construct the empirical TB models for the desired systems. However, these published empirical parameters are usually obtained by fitting to the ab-initio results of certain materials with fixed geometries and boundary conditions. As a result, the TB models constructed from these parameters can hardly reproduce the ab-initio band structures of the materials with different geometries and boundary conditions quantitatively, which becomes a source of the unreliability of this typical empirical TB method in quantitative research. In recent years, the reliability of the TB method has been greatly improved by the introduction of several ab-initio TB methods, which are based on the projection of the extended Bloch states obtained from the ab-initio calculations onto a much smaller set of localized orbitals6,7,8,9,10. Such methods drive the TB parameters directly from the ab-initio results of the desired material systems without the fitting process. The resulting ab-initio TB models are compatible with the typical TB form and reproduce the selected ab-initio energy bands with high accuracy. However, though successfully adopted in numerical studies of a variety of materials and devices11,12,13,14,15, these projection-based methods have their own challenges.

First, these methods require full knowledge of the eigenenergies and eigenfunctions calculated from the ab-initio methods. The corresponding time-consuming ab-initio calculations must be performed before the TB Hamiltonian construction, which hinders massive high-throughput investigations. Additionally, the abundant experience is needed when selecting TB basis functions in these methods. An accurate representation of the ab-initio bands in the much smaller TB basis requires the good projectability16 of the corresponding ab-initio Bloch states onto the finite Hilbert space spanned by these TB basis functions. For methods based on non-iterative projection schemes, such as the direct projection10 and Quasi-atomic orbitals9, the TB basis is predetermined as a specific set of atomic or atomic-like orbitals, so the choice of the ab-initio bands to be reproduced is limited to those with satisfactory projectability on the specific Hilbert space considered. Though improved by a series of studies16,17,18, such methods are still not good at dealing with the projection of unoccupied states far above the Fermi level unless increasing the richness of the basis. For iterative methods such as the maximally localized Wannier functions (MLWFs)19,20 approach and muffin-tin orbitals of arbitrary order (NMTO)6 approach, any bundle of the ab-initio bands can be selected for projection, whereas the TB basis functions should be iteratively optimized to span a suitable Hilbert space, which requires detailed knowledge of the underlying system and sufficient time for trial-and-error procedures21. Finally, even well-projected orbitals may produce Hamiltonian matrix elements associated with long-range neighbor interactions22. Suppose the desired TB representation (like the nearest-neighbor TB model) does not consider such long-range interactions. In that case, these elements need to be truncated, and the resulting TB representation will suffer a loss of accuracy7.

This work explores another way for TB Hamiltonian parameterization, with machine learning (ML) techniques. This method uses a fast scheme to fit the ab-initio energy bands by focusing directly on adjusting the TB matrix elements. Specifically, a neural network (NN) model is introduced to fill the preselected real-space TB Hamiltonian matrices with the neurons by treating them as the matrix elements. The values of these neurons, which determine the TB matrices, will be flexibly updated to achieve a satisfactory match between the produced TB bands and the ab-initio bands during the training phase by a back-propagation algorithm23,24. This method assigns an individual NN model to every desired system for TB parametrization, which is affordable because of the fast fitting scheme. The resulting one-to-one empirical TB model can achieve better reliability on the chosen system, than the typical empirical model constructed from TB parameter sets, because of the concentration on the reproduction of the given bands without considering the transferability to other systems. Additionally, the matrix element adjustment scheme is free from the issues mentioned above that bother the projection-based methods. Within this method, the ab-initio band structure data of the desired material are used as the only training data, and no other input, such as atomic coordinate information or eigenfunction data, is needed. Therefore, the vast existing resources of band structures in public databases can be used, bypassing the ab-initio calculations. This approach implicitly defines the TB basis functions by directly parameterizing the TB Hamiltonian matrices, so no prior knowledge of the functions is involved. Furthermore, this method can in advance exclude the matrix elements that need to be truncated according to the desired TB model so that the truncation error can be avoided. Most importantly, this method is applicable to any material system with accessible and reliable band structure data. In the following article, this method is described in detail, and its merits are verified.

Results

Parameterized TB Hamiltonian matrix

The empirical TB method works by writing the eigenstates of the Hamiltonian \(\hat H\) in a basis set of atomic or atomic-like orbitals, \(\left| {\phi _i} \right\rangle\), and replacing the exact many-body Hamiltonian operator with a parametrized Hamiltonian matrix H, which can then be used to compute the desired electronic and transport properties of the given system. Typically, the basis set is not explicitly constructed but defined by the empirical parameters used to form H. Generally, the parametrized TB Hamiltonian matrix H can be written as follows:

$$\begin{array}{*{20}{c}} {H = \mathop {\sum }\limits_i {\it{\epsilon }}_in_i + \mathop {\sum }\limits_{i \ne j} t_{ij}c_i^\dagger c_j,} \end{array}$$
(1)

where i and j run over the considered basis orbitals, \({\it{\epsilon }}_i\) denotes the energy of the electron at site i, tij is the hopping energy between the sites i and j, and \(c_i^\dagger\) (cj) are the creation (annihilation) operator of electrons at site i(j). Since these on-site and hopping terms are usually obtained from the existing TB parameter sets, specific optimizations have to be performed according to the studied system at hand, or the numerical accuracy should be significantly lower than the ab-initio calculations. We address these problems with our tight-binding Hamiltonian construction neural network (TBHCNN), which uses the neurons to represent the TB matrix elements. The number and values of the neurons are adjusted continuously during the training phase with the ab-initio bands as references. After training, the neurons can be used to form the parameterized TB Hamiltonian, which conforms to the matrix form as Eq. (1) and at the same time reproduces the reference bands.

Workflow of the TBHCNN

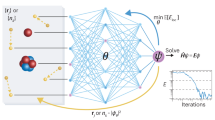
Figure 1 schematically illustrates the workflow of using the TBHCNN model for TB Hamiltonian parametrization, taking the examples of a one-dimensional (1D) periodic system and a uniform 1D non-periodic system.

Fig. 1: Workflow of the TBHCNN.
figure 1

a The workflows of obtaining the TB model for a 1D periodic system and constructing the TB Hamiltonian matrix for a uniform 1D non-periodic system. There are two additional steps for the latter, which are marked with the red arrows. b Structure diagram of the TBHCNN model. The matrix elements layer in the TBHCNN will be initialized according to the number of the reference ab-initio bands and the real-space TB Hamiltonian matrices considered in the desired TB model. The reference bands data are used as the training set, of which the eigenenergies \(\varepsilon _{i,{\mathbf{k}}}^{{\mathrm{Ab}}}\) are encoded within the ab-initio bands layer for computing the loss function by comparing with the TB results encoded in the tight-binding bands layer. The loss function value will be backpropagated to train the value of the neurons in the matrix element layer, which will be used as the matrix elements to construct the considered real-space Hamiltonians. When the loss function cannot touch down the predefined threshold, the TBHCNN model will add new neurons to the matrix element layer and reinitialize the whole layer to start a new round of training.

Full size image

For the periodic system, we first obtain its band structure data by searching in the online database if possible or by performing the ab-initio calculations on it, and then we select the energy bands of interest as the training set. When preparing the ab-initio calculations, although the unit cells of arbitrary sizes can be chosen, we advocate keeping the unit cell as small as possible. As the unit cell becomes larger, the corresponding first Brillouin zone shrinks and the calculated band structure becomes gradually dense energy levels25. It is hard to extract useful information from such a heavily folded band structure26, and thus hard to determine the selection of the energy bands as references. Also, more computing time is required with a larger unit cell for the ab-initio calculations. After selecting the unit cell and the ab-initio energy bands as references, we then determine the interaction range (i.e., the distances range in which two orbitals are considered to have hopping terms) considered in the desired TB model. Since our method does not assume the knowledge of the atomic coordinate information, we determine the interaction range by deciding on the real-space Hamiltonian matrices used in the chosen unit cell representation. For example, we may just use H0–1, H00, and H01, which denote the real-space Hamiltonian matrices between the unit cell of the lattice vector R = 0 and the cells of the lattice vector R = −1, 0, and 1, to construct the TB model where the interactions beyond the nearest unit cells are made negligible. Of course, other choices can be made on-demand. Then, we initialize the TBHCNN model according to the selected energy bands and real-space Hamiltonian matrices. Specifically, the Hamiltonian matrix size will default to the number of reference bands to ensure that the eventual TB model contains enough bands, and the proper number of neurons will be added to the TBHCNN model to fill in these matrices as their elements. These neurons have the initial values sampled from a standard normal distribution and will remain real numbers during training. Note to ensure that H00 should maintain a symmetric form, and the real-space Hamiltonian matrices with opposite lattice vectors should transpose each other. Now, we get a randomly initialized TB model. To obtain the TB band structure, ensure the orthogonality of the TB basis and diagonalize the reciprocal-space Hamiltonian,

$$\begin{array}{*{20}{c}} {H^{{\mathrm{TB}}}\left( {\mathbf{k}} \right) = \mathop {\sum }\limits_{\mathbf{R}} e^{{\mathrm{i}}{\mathbf{k}} \cdot {\mathbf{R}}}H^{0{\mathbf{R}}},} \end{array}$$
(2)

where R runs over the lattice vectors of the selected real-space Hamiltonian matrices, for desired k vectors in the Brillouin zone to obtain the band energies \(\varepsilon _{n,{\mathbf{k}}}^{{\mathrm{TB}}}\) and the eigenvectors \(\psi _{n,{\mathbf{k}}}^{\mathrm{TB}}\),

$$\begin{array}{*{20}{c}} {H^{{\mathrm{TB}}}\left( {\mathbf{k}} \right)\psi _{n,{\mathbf{k}}}^{{\mathrm{TB}}} = \varepsilon _{n,{\mathbf{k}}}^{{\mathrm{TB}}}\psi _{n,{\mathbf{k}}}^{{\mathrm{TB}}},} \end{array}$$
(3)

where n is the band index. The TB band structure can be obtained by assembling all the band energies \(\varepsilon _{n,{\mathbf{k}}}^{TB}\) for all the k vectors considered. The quality of the TB model can be evaluated by comparing the TB bands with the chosen ab-initio bands. As a measure of their mismatch, the mean squared error (MSE) between the energy eigenvalues is adopted (in units of (eV)2):

$$\begin{array}{*{20}{c}} {{\Delta}_E = \frac{1}{N}\frac{1}{{N_{\mathrm{k}}}}\mathop {\sum }\limits_{i = 1}^N \mathop {\sum }\limits_{\mathbf{k}} (\varepsilon _{i,{\mathbf{k}}}^{{\mathrm{TB}}} - \varepsilon _{i,{\mathbf{k}}}^{{\mathrm{Ab}}})^2,} \end{array}$$
(4)

where Nk is the number of k-points sampled in the reference bands. The procedure mentioned above is the forward pass, and ΔE serves as the loss function Loss. In the backward pass, the derivative of the loss function with respect to the elements of the real-space TB Hamiltonian H0R, denoted by \(\overline {H^{0{\mathbf{R}}}}\) using standard algorithmic differentiation terminology27, will be computed as

$$\begin{array}{*{20}{c}} {\overline {H^{0{\mathbf{R}}}} = \mathop {\sum }\limits_{\mathbf{k}} e^{{\mathrm{i}}{\mathbf{k}} \cdot {\mathbf{R}}}{\Psi}_{\mathbf{k}}\bar E_{\mathbf{k}}{\Psi}_{\mathbf{k}}^T,} \end{array}$$
(5)

with

$$\begin{array}{*{20}{c}} {\bar E_{\mathbf{k}} = {\mathrm{diag}}\left( {\frac{{\partial {\mathrm{Loss}}}}{{\partial \varepsilon _{1,{\mathbf{k}}}^{{\mathrm{TB}}}}},\frac{{\partial {\mathrm{Loss}}}}{{\partial \varepsilon _{2,{\mathbf{k}}}^{{\mathrm{TB}}}}} \ldots ,\frac{{\partial {\mathrm{Loss}}}}{{\partial \varepsilon _{N,{\mathbf{k}}}^{{\mathrm{TB}}}}}} \right),} \end{array}$$
(6)

and

$$\begin{array}{*{20}{c}} {{\Psi}_{\mathbf{k}} = \left( {\psi _{1,{\mathbf{k}}}^{{\mathrm{TB}}},\psi _{2,{\mathbf{k}}}^{{\mathrm{TB}}} \ldots ,\psi _{n,{\mathbf{k}}}^{{\mathrm{TB}}}} \right).} \end{array}$$
(7)

Then, the matrix elements in the Hamiltonian can be updated by using the gradient descent algorithm

$$\begin{array}{*{20}{c}} {H_{n + 1}^{0{\mathbf{R}}} = H_n^{0{\mathbf{R}}} - \alpha \overline {H_n^{0{\mathbf{R}}}} ,} \end{array}$$
(8)

where α is the learning rate, and the subscripts of the matrices represent the number of training steps in the TBHCNN.

Through the back-propagation process, the values of the neurons are continuously adjusted to minimize the loss function, leading to an improved match between the resultant TB bands and the ab-initio references. The numerical threshold for the loss function and the maximum number of training steps should be predefined as the criteria for ending the training. Once the loss function value touches down the preset threshold, the TBHCNN will end the training, and its neurons will be used for TB Hamiltonian parameterization, resulting in the TB model reproducing the reference bands with the MSE being the value of the preset threshold. However, If the loss function value remains higher than the preset threshold after the maximum number of training steps, the TBHCNN will add extra neurons and increase the basis size of the real-space Hamiltonian by a predefined number to enlarge the basis set; then, the whole network will be reinitialized, and a new round of training will begin. It can be seen that the TBHCNN model is in fact a dynamic network with a variable number of neurons. The additional bands induced by the increase of basis will be put above or below the set of reference bands and will not be used for loss function computation. These procedures will be repeated until a satisfactory agreement between the produced TB bands and references is achieved. No manual intervention is needed. We hasten to add that the selection of the hyperparameters mentioned above should not be strictly fixed but rather a choice on demand. The loss function threshold should be determined according to the accuracy desired; the setting of the maximum number of training steps depends on the convergence of the loss function on the selected reference bands; the neurons added, i.e., the basis functions increased, should be chosen considering the tradeoff between the training time and the basis size of the resulting Hamiltonian. A large number may result in the TB model consisting of more basis functions than is actually needed to reproduce the reference bands, whereas a small number might lead to more training time.

For the uniform 1D system with limited periodicity, which cannot be represented by a set of real-space Hamiltonian matrices H0R labeled with lattice vector R but rather a whole real-space Hamiltonian matrix containing all the considered on-site and hopping terms, we present a simple TB Hamiltonian construction scheme with the principal-layer (PL) approximation28. Compared with the 1D periodic system, two additional steps are required within the construction scheme. One is to select a fragment7 of this system. The fragment should be a repeating structural unit of the system. We then use the fragment as a unit cell of the corresponding periodic system to obtain its band structure. For the same reasons we stated above, the size of the fragment should be as small as possible. Then we can obtain the TB model of the corresponding periodic system using the same procedures as we demonstrated above. There comes the other additional step where the Hamiltonian matrix of the 1D non-periodic system is constructed by the produced TB model. Using the PL approach, we let the PL consist of one unit cell and make the TB model consider the real-space Hamiltonian H0–1, H00, and H01 only. In this case, the Hamiltonian of the desired 1D non-periodic system can be constructed by these matrices as

$$\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {H^{\mathbf{00}}} & {H^{\mathbf{01}}} & 0 & 0 & 0 \\ {H^{\mathbf{0} - {\mathbf{1}}}} & {H^{\mathbf{00}}} & {H^{\mathbf{01}}} & 0 & 0 \\ 0 & {H^{\mathbf{0} - {\mathbf{1}}}} & {H^{\mathbf{00}}} & {H^{\mathbf{01}}} & 0 \\ 0 & 0 & {H^{\mathbf{0} - {\mathbf{1}}}} & {H^{\mathbf{00}}} & \ddots \\ 0 & 0 & 0 & \ddots & \ddots \end{array}} \right)_{\left( {N_{\mathrm{f}} \times N_{\mathrm{r}}} \right) \times \left( {N_{\mathrm{f}} \times N_{\mathrm{r}}} \right)},} \end{array}$$
(9)

where Nf is the final size of the trained real-space Hamiltonian matrices and Nr is the number of fragments required to rebuild the 1D non-periodic system.

Theoretically, the TBHCNN applies to systems of any dimension. The 1D models above are used as examples for the sake of simplicity and brevity. To extend the above procedures to arbitrary periodic systems, take into account the real-space Hamiltonian matrices which describe the interactions along every periodic direction. And these matrices can be used to construct TB Hamiltonians of the corresponding uniform non-periodic systems in the same way as stated above.

We must emphasize that, within the method presented above, only the ab-initio energies are used for training the TBHCNN without the involvement of any information of the basis functions and atomic coordinate of the given system. Therefore, the method in its current form cannot ensure the match of the symmetry characters between the predicted TB bands and reference bands, nor the resulting Hamiltonian elements could reflect the geometrical symmetries. These should be considered as the limitations of the proposed method. However, we will show the validity of the resulting TB Hamiltonian parameterization for transport property calculations in the following text. We will also present a variation of this method to deal with the limitations by introducing and exploiting the additional information of geometry and the symmetry of reference bands in later sections.

Additionally, the construction scheme that is shown in Eq. (9) with the PL approximation is suitable for the presented uniform system but would not apply to a general inhomogeneous system. In this case, the common practices are to divide the inhomogeneous system into several homogeneous subsystems, and then to perform the TB Hamiltonian parameterizations for these subsystems, respectively. And the proper stitching of these TB models should be performed to construct the Hamiltonian of the whole inhomogeneous system, which is also an important research aspect where serval research findings have been published14,29 but would be out of the scope of this paper. Therefore, we do not expand on the stitching schemes in detail but recommend the cited references to the interested readers.

Application and validation of the proposed method

For novel material systems, the experience with and knowledge of the basis functions are not sufficient, so relevant TB models are rare, which severely hampers transport analyses with and applications of these systems. For example, 2D-InSe nanosheet is a prospective system since this typical III–VI semiconductor has many attractive properties, such as high electron mobility30,31,32 and good ohmic contact33. Few-layer and monolayer InSe nanosheets have been successfully synthesized34, but there have been few direct theoretical studies on quantum transport in 2D-Inse-based devices for the above reason. Here, the simulation of an InSe nanoribbon metal-oxide-semiconductor field-effect transistor (MOSFET) is performed with the TB Hamiltonian generated by the proposed ML method to illustrate the capacity of this method to accurately and efficiently solve cutting-edge problems.

The device geometry is shown in Fig. 2. A 13-atom-wide InSe nanoribbon with a hydrogen-passivated boundary is sandwiched between 2-nm-thick oxide layers with a relative dielectric constant of 3.9. The length of the source and drain is 5 nm, and the channel length is 10 nm. Both the source and the drain regions are doped with a molar fraction of fully ionized donors of 5 × 10−3. The channel region is undoped, and the double gates cover the whole channel. The gates and oxide layers are not modeled atomically but are introduced to change the potential of the channel region and to act as the dielectric layers with a desired dielectric permittivity, respectively. To eliminate the impact of the work function values of different gate metals, we located the Fermi level of the channel in the middle of the bandgap in the following calculations.

Fig. 2: Sketch of the simulated InSe nanoribbon-based transistor.
figure 2

Only the InSe nanoribbon is modeled atomically, whereas the gate metals and oxide layers are not introduced as entities but used to change the gate voltage and provide the dielectric layers.

Full size image

To verify the merits of the proposed method, two TB models for the periodic InSe nanoribbon using the TBHCNN model and the MLWFs method, the most popular projection-based method, were obtained. Their corresponding device Hamiltonians were constructed according to Eq. (9), considering the interactions between adjacent unit cells only. During training, the TBHCNN model added the proper number of neurons to increase the TB basis size by 2 every 10000 training steps until that Loss ≤ 1.0 × 10−5 was achieved, resulting in the TB model with a basis size of 18. And the MLWFs method obtained the TB model containing 208 basis functions, taking into account the outermost s and p orbitals of each In and Se atom in the unit cell, which is a common choice in existing research on layered InSe materials35. In the following sections, the two TB models are called the machine learning tight-binding (MLTB) model and the Wannier tight-binding (WTB) model, and the corresponding device Hamiltonians are called the MLTB Hamiltonian and the WTB Hamiltonian, respectively. The band structures of the two TB models were calculated and compared with the ab-initio band structure, as shown in Fig. 3. Only the 7 conduction bands and 7 valence bands around the Fermi level with a 1 × 1 × 26 uniform k-points sampling along the k-path from high symmetry points Γ (0, 0, 0) to X (0, 0, 1/2), which reflect the key physical properties and notably influence the determination of transport properties, were selected as references. That is to say, there were 14 × 26 = 364 ab-initio energies as the training data. There was little difference between these two TB models in the reproduction of the ab-initio band structure; both of them fit the selected ab-initio bands with high accuracy. However, considering their respective TB basis sizes, the complexities of our method and the MLWFs method were completely different. The automated creation of the MLTB model was finished in 110 s within our method. Figure 4 shows the convergence of the loss function over the training time; the loss function value quickly decreases before the predefined threshold is reached. The MLWFs method required over 30 h to obtain the 208-orbital WTB model in the same computing environment, even without considering the time required to find the optimal parameter values, which in fact took up much time. Furthermore, even with a smaller basis and lower computational cost, the band structure generated by the proposed MLTB model is more accurate (ΔE = 1.0 × 10−5) than that derived from the WTB model (ΔE = 1.7 × 10−5).

Fig. 3: Geometrical and electronic structure of the InSe nanoribbon.
figure 3

a Optimized structure of the 13-atom-wide InSe nanoribbon. The orange, brown, and white balls represent Se, In, and H atoms, respectively. The unit cell used is marked with a dotted rectangle. b Comparison between the ab-initio band structure (black) and the band structures calculated from the WTB model (orange) and the MLTB model (lilac) for the InSe nanoribbon. Only the 14 bands selected for reference are plotted for clarity.

Full size image
Fig. 4: Loss function for the TBHCNN.
figure 4

The red line represents the value of the loss function. The TBHCNN added neurons to increase the TB basis functions by 2 to restart training every 10,000 training steps until the ending criterion Loss ≤ 1 × 10−5 was achieved. The blue, yellow, and red blocks denote the time regions when the TB basis contains 14, 16, and 18 basis functions, respectively.

Full size image

In addition to the ab-initio band structure reproduction, the transport properties of the InSe nanoribbon-based MOSFET were also investigated. With the MLTB Hamiltonian and the WTB Hamiltonian, the corresponding quantum transport properties were obtained by self-consistently coupling the Schrodinger and Poisson equations using the NanoTCAD ViDES software package36. Figure 5 plots the IGS − VGS and IGS − VDS curves. Each pair of curves under different voltage biases is almost the same in trends while slightly different in values. Considering the widespread acceptance of the reliability of the MLWFs method, the consistency here reflects the excellent applicability of our method to the device-performance level. Similar to the energy band computation, the device simulation with the MLTB Hamiltonian was more efficient than that with the WTB Hamiltonian. Specifically, the above device simulation was finished within 1 h using the MLTB Hamiltonian but more than 2 days with the WTB Hamiltonian.

Fig. 5: Transfer characteristics of the InSe MOSFET.
figure 5

a Transfer characteristics of the device with the drain-source voltage VDS being 0.5, 0.3, and 0.1 V. b Transfer characteristics of the device with the gate voltage VGS being −0.3, 0.0, and 0.3 V.

Full size image

As can be seen from the applications above, unlike previous ML methods introduced to handle the TB models37,38,39,40,41,42,43,44,45,46, our algorithm does not require a large training set to make predictions. These predictive methods are introduced in an attempt to build a general mapping from the input data to the output data, using the input–output pairs within the training set. The predictive power of those methods will decrease when data considerably different from the training data are considered; as a result, these methods are not suitable for applications with limited datasets. Our method, instead, provides a generic way to construct the one-to-one TBHCNN model, which will be trained on the selected energy bands of the desired system and apply exclusively to the system. Hence, the required training set consists of the corresponding ab-initio energy bands only. The TBHCNN model here is introduced to represent the TB Hamiltonian elements directly rather than to act as the inferred function for mapping an external input to the Hamiltonian elements. Once a set of energy bands need to be reproduced, we can use them as the training data to initialize and train a TBHCNN model to obtain the TB model specifically suitable for the system with such energy bands. We hope that our method provides insight into applying ML tools to physical problems, especially when data-driven methods are inaccessible.

To verify the generalization ability of the proposed method on different systems, extra simulations on 13-atom-wide graphene nanoribbon (13-AGNR), 2D MoS2, and the devices based on these two materials were performed. The simulation results showed that our method could apply to different material systems and achieve better ab-initio band structure reproduction than the MLWFs method (Supplementary Note 1). Furthermore, to showcase the capability of the TBHCNN model of being trained on previously published data, we performed the TB Hamiltonian parameterizations for Si of the diamond structure and GaN of the wurtzite structure using the band structure data from the online data set Materials Project47 (Supplementary Note 2). Additionally, we studied the impacts of the initialization of the TBHCNN model and the k-point sampling used in the loss function on the quality of the resulting TB Hamiltonian for bands reproduction and transport property calculations. We found that, as long as the training hyperparameters were fixed, different initializations of the TBHCNN model would result in the TB models with different TB parameters that could reproduce the reference bands with the same accuracy. And the utilization of the device Hamiltonians from these different TB models on device simulation obtained very close results (Supplementary Note 3).

Two variations of the proposed method

Since the TBHCNN employed within our method can be conveniently customized, our method has the potential to be modified to meet the requirements of personalized analysis. Here, we develop two variations of the proposed method, which extend the applications of the TBHCNN to the fields outside the energy-space transport property calculations.

Variation I is to optimize a given TB model by fine-tuning the Hamiltonian elements. The basic version of our method focuses on constructing an accurate TB Hamiltonian with a minimal basis for the desired system to perform band structure and I–V curve calculations. However, it can also be modified to optimize a given TB model without breaking down the real-space Hamiltonian matrix structures.

Real-space information and time-consuming searches for optimal parameter values are not needed in Variation I by initializing the values of the neurons in the TBHCNN based on the matrix elements of the unoptimized TB model. Such a TB model can be obtained from projection-based approaches or the existing empirical TB parameter sets; both methods should retain the symmetry characters of the atomic basis to some extent. Then, a regularization term ΔR, which penalizes the deviation of the Hamiltonian matrix elements from the original values, is added to the loss function.

$$\begin{array}{*{20}{c}} {{\Delta}_R = \lambda \mathop {\sum }\limits_i (V_i - U_i)^2,} \end{array}$$
(10)

where λ sets the magnitude of the penalty, for which the sum is over all matrix elements of the real-space Hamiltonians involved; Vi is the current value of the ith matrix element, and Ui is the value of the corresponding element in the unoptimized TB model. During training, the TBHCNN will hold the number of neurons but adjust their values to obtain an improved description of the selected ab-initio energy bands. By doing so, we can maintain the initial form of the given TB model to a large extent while greatly increase its accuracy for band reproduction. Variation I would also be very suitable for truncating a given TB model to have a smaller number of real-space Hamiltonian matrices while maintaining the band reproduction accuracy. The loss of accuracy caused by the truncated TB matrices, which describe the interactions in a longer range than is needed, can be mitigated by adjusting the elements of the TB matrices considered to implicitly include the impact of the truncated interactions.

To test the validity of Variation I, a 2D phosphorene system was tested. The sp TB model obtained by the MLWFs method was employed as the initial template, which could ensure the completeness of the TB basis48. However, as illustrated in the left panel of Fig. 6a, the band structure obtained by this TB model deviates substantially from the corresponding ab-initio band structure. This sp TB model, deemed the WTB model here still, consisted of the real-space Hamiltonian matrices describing the interactions within a unit cell and between this unit cell with its 8 neighbor cells, as shown in Fig. 6b. This deviation indicated that the hopping terms describing the interactions in a longer range should be considered. Using the proposed variation, we constructed the optimized TB model on top of the WTB model, which is deemed the MLTB model here. It can be seen that the MLTB model succeeds in including the impact of longer-range interactions by modifying the elements in considered Hamiltonian matrices, as it reduced the MSE in-band energies from ΔE = 0.14 to ΔE = 8.8 × 10−7 when reproducing the 8 bands around the Fermi level. And the average absolute deviation per element of the 9 considered matrices was less than 0.04 eV. The difference matrices between these matrices before and after the optimization are plotted in Fig. 6c. It can be shown that Variation I has the potential to optimize the given TB model in the desired basis of atomic orbitals and maintain the symmetry characters of the basis to a large extent.

Fig. 6: The optimization for the sp TB model for the 2D phosphorene system using Variation I.
figure 6

a Comparison of the ab-initio band structure (black lines) and those calculated from the unoptimized WTB model (orange lines) and MLTB model (lilac lines) for the phosphorene. b The geometrical structure of the phosphorene. The unoptimized WTB model comprises the real-space Hamiltonian matrices describing the interactions within a unit cell (marked with the solid rectangle) and between this unit cell with its 8 neighbor cells (marked with the dotted rectangles). c The difference matrices between the considered real-space TB Hamiltonians before and after the optimization. The difference matrix of H00 is placed in the center while others are labeled with the lattice vectors alongside.

Full size image

Variation II can construct the Slater–Koster TB Hamiltonian for the desired system from scratch by changing the mapping from the neurons to Hamiltonian elements.

To achieve this goal, the values of neurons are no longer assigned to the Hamiltonian elements directly. Instead, neurons are now used as adjustable parameters to calculate the Slater–Koster parameters, such as Vssσ, Vspσ, and Vppπ, to obtain the matrix elements, using the two-center or three-center approximations proposed by Slater and Koster5. Variation II requires that the reference bands be analyzed in advance for choosing the types of atomic orbitals used for fitting the bands and thus for determining the fitting formulae. And the atomic coordinate information of the studied system needs to be obtained for providing the distance information used in the fitting formulae. This form is like the traditional methods for the determination of the Slater–Koster parameters. However, the gradient descent algorithm makes this method faster than the least-squares process used in traditional methods. During training, the types and number of the basis orbitals will be fixed, i.e., the fitting formulae and Hamiltonian matrix size will be held. And the Slater–Koster parameters will be optimized by adjusting the neuron values to better describe the ab-initio bands.

Taking the 13-atom-wide armchair graphene nanoribbon (13-AGNR) presented in Supplementary Note 1 as an example, we considered the pz orbital of each C atom in the unit cell, and the real-space Hamiltonian matrices \(H^{\mathbf{00}}\), \(H^{{\mathbf{0}} - {\mathbf{1}}}\), and \(H^{\mathbf{01}}\), which describe the interactions within a unit cell and between the unit cell with its 2 neighbor cells. With two-center approximations, the hopping parameters are expressed as49:

$$\begin{array}{*{20}{c}} {V_{{\mathrm{pp}}\pi }\left( {r_{ij}} \right) = \alpha _1r_{ij}^{ - \alpha _2}\exp \left( { - \alpha _3r_{ij}^{\alpha _4}} \right),} \end{array}$$
(11)

where rij is the distance between atom i and j, which can be read directly from the real-space structure of the 13-AGNR, and α1, α2, α3, and α4 are variable parameters, which will be represented by four different neurons, respectively. Still, the loss function was the mean squared error between the ab-initio energy eigenvalues and the TB ones. After training, the optimal values of these parameters were obtained, and the TB Hamiltonian matrices calculated by these parameters were in the desired Slater–Koster form on the basis of pz orbitals. Since much fewer neurons were used in Variation II than in the basic TBHCNN method, the produced TB Hamiltonian reproduced the ab-initio bands qualitatively. However, we advocate using Variation II for TB Hamiltonian parameterization when the information of the geometry is accessible, and the symmetry characters of reference bands are known, for analyzing the properties on which the symmetry characters have a significant impact. Variation II can be considered as a complement to our basic method to deal with its limitations on the match of the symmetry characters of the reference bands and on the reflection of geometric symmetry of the given system.

Figure 7 plots the comparison between the TB models obtained by using Variation II and the well-known empirical TB parameterization for graphene systems, which employs a value of −2.7 eV as the hopping parameter between the nearest-neighbor C atoms and 0 eV for otherwise. The Hamiltonian matrices of these two TB models have the same structures and slightly different matrix elements, and their TB band structures have similar accuracy.

Fig. 7: The TB Hamiltonians for 13-AGNR in Slater–Koster form constructed from Variation II.
figure 7

a Comparison of the Hamiltonian elements of the produced TB model in Slater–Koster form and the empirical TB model. b Comparison of the ab-initio band structure (blue lines) and those calculated from the produced TB model (red dashed lines) and empirical TB model (green dashed lines) for 13-AGNR.

Full size image

Figure 8 shows the charge distribution of the 13-AGNR-MOSFET, which is presented in Supplementary Note 1. The device simulations were performed with the device Hamiltonians constructed by the produced TB model and a Wannier TB model from the MLWFs method. The comparison between the simulation results showed that the produced TB model could be used for qualitatively accurate real-space transport analysis.

Fig. 8: Comparison of the charge distributions of the 13-AGNR-MOSFET using the WTB device Hamiltonian (above) and the produced TB device Hamiltonian (below).
figure 8

The gate voltage VGS is set to be 0 V, and the drain-source voltage VDS is set to be 0.2 V. The gray balls represent C atoms, whereas H atoms on the edges are not plotted.

Full size image

Discussion

In summary, we developed a generic method for TB Hamiltonian parameterization from the ab-initio band structure with ML algorithms. Our method’s validity was tested through the calculations of the electronic structure of layered InSe and the transport characteristics of the InSe-based MOSFET. In the proposed case, our method surpassed the MLWFs method in both efficiency and accuracy. As an approach for TB model construction, the proposed method is free from prior knowledge requirements and truncation error. Additionally, the introduction of the one-to-one dynamic NN model can provide insights into applying ML methods to practical problems when it is difficult or even impossible to gather sufficient training data to build a general ML model. Also, two variations of our method were presented, which can to some extent deal with the mentioned limitations of our basic method, showing the flexibility of the proposed TBHCNN model. We believe our method cannot only promote the development of materials and device research but also help to improve the combination of ML techniques in the physics, chemistry, and materials science research communities.

Methods

Neural network training

The proposed ML algorithm and neural network architecture can be conveniently achieved using mainstream ML platforms. In this work, we choose the widely used TensorFlow50 framework, and employ its built-in Adam optimizer51 to perform relevant automatic differentiation tasks with an initial learning rate of α = 0.001.

Ab-initio band structure calculation details

The ab-initio band structure calculations on the InSe nanoribbon, the 2D phosphorene, and the 13-AGNR, were carried out using the open-source ab-initio package QUANTUM ESPRESSO52. The exchange and correlation interactions between valence electrons are described by the Perdew−Burke−Ernzerhof (PBE) functional within the generalized gradient approximation (GGA)53. The ultrasoft pseudopotential is used. The kinetic energy cutoff of the wave functions is 40 Ry, and the estimated energy error is less than 1 × 10−6 Ry.

For the InSe nanoribbon, in the chosen unit cell, the vacuum space is 20 Å, to ensure the interaction between periodic images can be safely avoided. The Brillouin zone is sampled with 1 × 1 × 10 and 1 × 1 × 200 Monkhorst–Pack54 k-points for the structure relaxation as well as self-consistent calculations and for the band structure calculations, respectively. The geometry is fully relaxed using the BFGS quasi-newton algorithm, with the criteria being that all components of all forces are smaller than 1 × 10−3 Ry/au, and the total energy changes are <1 × 10−4 Ry.

For the 2D phosphorene, in the chosen unit cell, the vacuum space is 15 Å, to ensure the interaction between periodic images can be safely avoided. The Brillouin zone is sampled with 1 × 10 × 10 Monkhorst–Pack k-points for structure relaxation and self-consistent calculations. And 100 k-points per k-path are sampled uniformly for the band structure calculations on the three k-paths: from Γ (0, 0, 0) to X (0, 1/2, 0), from X (0, 1/2, 0) to Y (0, 0, 1/2), and from Y (0, 0, 1/2) to Γ (0, 0, 0).

For the 13-AGNR, in the chosen unit cell, the vacuum space is 15 Å, to ensure the interaction between periodic images can be safely avoided. The Brillouin zone is sampled with 1 × 1 × 10 and 1 × 1 × 50 Monkhorst–Pack k-points for the self-consistent calculations and the band structure calculations, respectively.

Here, we declare that the utilization of the calculation methods within the density functional theory (DFT) framework is not a strict request. When the effective single-particle band structures derived from DFT are qualitatively wrong, other more accurate methods for electronic structure calculations (e.g., DFT’s many-body extensions like GW approximation) may be considered in place of the DFT method for obtaining the band structures. And It will not affect the existing framework of the proposed method since the TBHCNN model does not require a specific source of the energy band data.

MLWFs transformation details

The MLWFs method was implemented using Wannier90 software package55.

For the InSe nanoribbon, the number of MLWFs is set to 208, which are initialized to the outermost s and p orbitals of In and Se atoms within the unit cell. The outer energy window is set to [−8 eV, 6 eV] and the inner energy window is set to [−2.6 eV, 0.4 eV]. The transformation is performed on top of the corresponding ab-initio calculation results with a 1 × 1 × 50 Monkhorst–Pack k-points sampling.

For the 2D phosphorene, the number of MLWFs is set to 16, which are initialized to the outermost s and p orbitals of P atoms within the unit cell. The outer energy window is set to [−11.5 eV, 6 eV] and the inner energy window is set to [−2.0 eV, 0.0 eV]. The transformation is performed on top of the corresponding ab-initio calculation results with a 1 × 10 × 10 Monkhorst–Pack k-points sampling.

For the 13-AGNR, the number of MLWFs is set to 26, which are initialized to the pz orbitals of C atoms within the unit cell. The outer energy window is set to [−15.0 eV, 9.0 eV] and the inner energy window is set to [−4.0 eV, −2.0 eV]. The transformation is performed on top of the corresponding ab-initio calculation results with a 1 × 1 × 50 Monkhorst–Pack k-points sampling.