Abstract
The gas and ice giants in our solar system can be seen as a natural laboratory for the physics of highly compressed matter at temperatures up to thousands of kelvins. In turn, our understanding of their structure and evolution depends critically on our ability to model such matter. One key aspect is the miscibility of the elements in their interiors. Here, we demonstrate the feasibility of X-ray Thomson scattering to quantify the degree of species separation in a 1:1 carbon–hydrogen mixture at a pressure of ~150 GPa and a temperature of ~5000 K. Our measurements provide absolute values of the structure factor that encodes the microscopic arrangement of the particles. From these data, we find a lower limit of \(2{4}_{-7}^{+6}\)% of the carbon atoms forming isolated carbon clusters. In principle, this procedure can be employed for investigating the miscibility behaviour of any binary mixture at the high-pressure environment of planetary interiors, in particular, for non-crystalline samples where it is difficult to obtain conclusive results from X-ray diffraction. Moreover, this method will enable unprecedented measurements of mixing/demixing kinetics in dense plasma environments, e.g., induced by chemistry or hydrodynamic instabilities.
Similar content being viewed by others
Introduction
The current state of the large bodies in our solar system is an essential benchmark for our understanding how planetary systems form and evolve. Modern planetary probes such as the Juno mission1 provide a growing wealth of data, such as magnetic field configurations2, gravitational moments3 and zonal winds4, even for distant planets like Jupiter. However, such data can only be obtained for the space outside the planets or their upper layers. To construct the internal structure and composition from these data, knowledge about the properties of the compressed matter deep inside a planet is required. In particular, a better understanding of high-pressure, high-temperature mixtures is of paramount importance for describing the internal structure of gas and ice giants, where gravity compresses matter into the 100 GPa to 10 TPa range. The high internal temperatures of these planets create an environment with thermal energies similar to those of chemical bonds and above. In the deeper layers, thermal excitations can thus trigger a complex series of material modifications and phase transitions, possibly including species separation and demixing5.
Miscibility-driven phase transitions in compressed matter are very important for planetary modeling for two reasons: (i) they may be significant enough to define layer boundaries prohibiting full convective mixing within the planet and, thus, strongly influence the mass distribution inside planets6 and (ii) heavier components created by demixing will liberate gravitational energy by precipitation and, thus, may strongly modify the energy balance of the planets. For gas planets like Jupiter and Saturn, a separation into helium-rich and helium-poor phases has been predicted for some region inside the planet and the potential presence of a corresponding boundary layer has a significant impact on the interpretation of observational data and our understanding of planetary formation and evolution4,7,8,9,10. On icy giants like Uranus and Neptune, water, methane and other hydrocarbons are highly abundant. Experimental evidence shows the dissociation and polymerization of methane under pressure, leading to a heavy hydrocarbon fluid11,12. Under certain conditions, diamond can form13,14,15 and will precipitate towards lower layers due to its high density.
The highly compressed matter inside large planets is in a complex state called warm dense matter covering densities comparable to solids and temperatures from several thousand to several hundred thousand kelvins. Although its study has gained significant momentum in recent years, it still holds many challenges for a theoretical description due to strongly interacting particles and the quantum nature of its electrons16,17. In particular, the complex interplay between the different components is extremely hard to model and basic mixing schemes generally fail to adequately represent the physics, although they are widely applied due to their simplicity18. To move beyond such simple models, dedicated laboratory experiments are needed to determine the properties of mixtures in this parameter regime.
Mixing and demixing processes in dense plasma environments also significantly impact state-of-the-art ICF capsule implosions19,20. In particular, hydrodynamic instabilities can result in ablator-fuel mix which prevents efficient compression and ignition of the fuel21. Furthermore, phase separation of carbon and hydrogen may be relevant when using CH plastic ablator materials. This phenomenon could lead to local density fluctuations and seed hydrodynamic instabilities21,22. Such instabilities, in particular ablation-front Rayleigh–Taylor growth, were identified as one of the primary issues that led to reduced implosion performance during the National Ignition Campaign, where the first shock of the implosion drive creates pressures of 100–200 GPa and temperatures of 6000–10,000 K in the ablator material19, i.e., conditions similar to the environment inside gas and ice giants.
In this article, we investigate the phase separation of hydrocarbons under warm dense matter conditions as they occur inside icy planets and during the first compression stages in ICF implosions using plastic ablators. Whereas previous analysis has established diamond formation in these samples with X-ray diffraction (XRD) from diamond crystallites15,23, here, we present a quantitative analysis of species separation applying X-Ray Thomson scattering (XRTS) that does not rely on the presence of crystalline structures. The theory of XRTS predicts strong sensitivity of the elastic scattering to different degrees of mixing24, while the inelastic scattering from free electrons can be used as a reliable diagnostics for the basic plasma parameters like density, temperature and ion charge state25,26,27. We now extend the applicability of XRTS and demonstrate the feasibility of a quantitative measurement of the degree of species separation in carbon-hydrogen mixtures.
Results
Experimental method
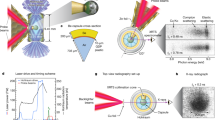
A schematic of the experimental setup is shown in Fig. 1. Polystyrene (C8H8)n samples were irradiated by two co-propagating high-energy laser beams forming a stepped pulse profile, resulting in two shock compression waves coalescing at the sample rear side. The compressed samples were probed in situ by X-rays with a photon energy of 8180 eV and a pulse duration of 50 fs. The scattered X-rays were detected by two spectrometers, one in backward scattering geometry (BXRTS, θb = 123°, k = 7.30 Å−1) and one in forward scattering geometry (FXRTS, θf = 17°, k = 1.23 Å−1). Examples of the recorded spectra are shown in Fig. 2. More details on the experimental setup can be found in the “Methods” section.
The scattered X-ray signals are recorded with the (a) backward and (b) forward spectrometers, at scattering angles of 123° and 17° to the incident X-rays, respectively. The integrated areas for Eqs. (2) and (3) are shaded in red and green, respectively. Both spectra have been corrected for energy-dependent influences and are normalized to the integrated inelastic scattering measured on the backward spectrometer.
One-dimensional radiation hydrodynamic simulations were applied to estimate the thermodynamic conditions inside the compressed sample. We obtain a pressure of (60 ± 7) GPa and a temperature of (4000 ± 500) K in the first shock, whereas the second shock reaches (150 ± 15) GPa and (5000 ± 500) K. The quoted uncertainties are based on the observed gradients in time and space in the simulations28. More details can be found in the “Methods” section. These conditions are similar to those predicted at a depth of ~10,000 km inside Uranus and Neptune29,30. Additionally, these results are in good agreement with XRD measurements during the same experiment15.
To measure the amount of species separation, we use X-ray Thomson scattering (XRTS). Here, the recorded scattering intensity is proportional to the total electron structure factor. In our experiment, we investigate temperatures well below 1 eV and thus, the contribution of free electrons can be neglected. Accordingly, the total electron structure factor for a multi-component system can be expressed as ref. 24
where xi = ni/∑αnα is the concentration of the ion species i. For an isotropic system, all terms solely depend on the magnitude of the scattering vector ∣k∣ = k. The first term in Eq. (1) is referred to as weight of Rayleigh or elastic scattering WR. Here, it accounts for scattering from electrons that are bound to ions and thus dynamically follow their motion. The form of the bound state is given by the atomic form factor fα(k) for species α. The ionic microstructure is accounted for by the partial structure factors that can be treated statically Sαβ(k, ω) = Sαβ(k)δ(ω), since the ion motion cannot be resolved in the discussed experiment. The second term represents scattering inducing bound-free transitions. \({Z}_{\alpha }^{{\rm{c}}}\) bound core electrons of each species are described by the inelastic structure factor for bound electrons \({\tilde{S}}_{\alpha }^{{\rm{ce}}}(k,\omega )\) modulated by the self-motion of the ions \({S}_{\alpha }^{{\rm{s}}}(k,\omega )\).
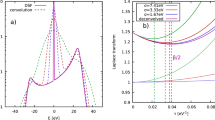
In order to extract the degree of species separation, a minimum of two spectra are required; here, we have forward (FXRTS) and backward (BXRTS) scattering. The much better understood backward scattering provides the absolute calibration of the forward scattering signal, from which the degree of species separation can be inferred. Moreover, this scheme requires the inelastic contribution of the FXRTS to be known with high accuracy including any potential influence of condensed matter physics effects, e.g. originating from compressed diamond31,32. For these tasks, we apply quantum ab initio simulations using density functional theory and molecular dynamics (DFT-MD) for the Rayleigh scattering and time-dependent DFT together with a linear response formalism for the determination of the inelastic structure33,34,35,36,37,38,39 (for more details, see the “Methods” section). From DFT-MD, it is also possible to estimate the expected Rayleigh scattering40 WR(k) for pure carbon (in the liquid form or diamond), pure hydrogen as well as mixed and fully demixed CH. As shown in Fig. 3, the Rayleigh scattering is highly sensitive to demixing of the material compound at low values of k, which are probed by FXRTS.
Structure calculations for p = 156 GPa and T = 5000 K show a significant drop in the Rayleigh scattering WR for CH in a demixed state for k ≲ 2.5 × 1010 m−1 when assuming either liquid carbon or diamond in the pure carbon phase. The dashed vertical lines mark the wavenumbers probed by the spectrometers.
For absolute calibration of the elastic scattering strength, we employ our backward scattering spectrum BXRTS. This quantity can be expressed by the intensities of elastic and inelastic scattering41,42,43:
Here, \({Z}_{\alpha }^{{\rm{wb}}}\) includes all weakly bound electrons of ion species α and fn,α(k) denote their atomic form factors of each electron44. Iel and Iinel are the spectrally integrated scattering intensities of the elastic and inelastic scattering. Eq. (2) is only dependent on the ratio of these two intensities and does not rely on the absolute inelastic scattering signal intensity. Therefore, it can be used to calculate WR(k) in backward direction. Here, the Compton shift EC = 198 eV is large enough to clearly separate the elastic and inelastic scattering signals. At this energy, the electrons of the carbon K-shell with a binding energy significantly larger than EC are neglected in the bound-free scattering for the analysis. Summing over all other more weakly bound electrons in Eq. (2) results in \({W}_{\mathrm{R}}^{\mathrm{b}}=2.50\frac{{I}_{{\rm{el}}}^{{\rm{b}}}}{{I}_{{\rm{inel}}}^{{\rm{b}}}}\) for a 1:1 mixture of hydrogen and carbon.
Inferred C–H species separation
We are now able to process our data by normalizing the FXRTS data, that carries information about miscibility, to the BXRTS signal via
The indices b and f denote the backward and forward spectrometer, respectively. The polarization factors26 for the two spectrometer geometries due to the horizontal polarization of the XFEL beam are given by ϵb = 0.320 and ϵf = 0.915. \({\chi }_{{\rm{c}}}=1.9{8}_{-0.11}^{+0.12}\) accounts for the relative difference in spectrometer and detector sensitivity which was obtained by recording Ni-Kβ emission simultaneously with both spectrometers. \({I}_{{\rm{el}}}^{{\rm{b}}}\) and \({I}_{{\rm{el}}}^{{\rm{f}}}\) are the spectrally integrated elastic signals marked in Fig. 2. Due to the overlap of elastic and inelastic scattering on the forward spectrometer, the inelastic part has been modeled using TD-DFT simulations for the experimental conditions reached.
Using Eq. (3), the Rayleigh scattering in forward direction \({W}_{{\rm{R}}}^{{\rm{f}}}\) can now be calculated. Comparing this value to the DFT-MD simulations shown in Fig. 3, the Rayleigh scattering can be converted into an amount of species separation, which we define as the fraction of carbon atoms clustered in single-component regions. Here, we perform a linear interpolation between an expected value of WR = 2.70 for completely mixed CH (no species separation) and WR = 0.38 for fully demixed CH (100% species separation and the isolated carbon being in a diamond state) to obtain the corresponding values for the degree of species separation inside the sample. This procedure omits the first shock, however, DFT-MD simulations predict the Rayleigh scattering to be of very similar magnitude or slightly larger as for the double-shock conditions for mixed CH45. Moreover, the linear interpolation assumes demixing into pure constituents and no splitting into carbon-rich and hydrogen-rich phases in the regions where phase separation occurs. This assumption is consistent with previously published XRD data showing diamond formation and the remaining liquid structure well matched with a 1:1 CH mixture28. In case of demixing into significantly non-pure constituents, e.g. C2H + CH2, the inferred demixing would be larger due to a non-linear scaling of WR for this case45.
The results obtained by the procedure above are shown in Fig. 4. Once the second shock wave enters the target material, carbon and hydrogen start to separate from each other. With the progression of the second shock wave, the degree of species separation is increasing up to a maximum value of \(\left(2{4}_{-7}^{+6}\right)\)%. The later timings shown in Fig. 4 start to overlap with the shock release, where the rapid decompression leads to a significant signal increase at low k, which therefore obscures the inferred demixing. In particular, the liquid peak of the compressed mixture at ~3 Å−1 broadens and shifts once the release starts15. Thus, the depicted data and error bars generally relate to the Rayleigh weight WR and can only directly be connected to species separation as along as the shock waves are traveling inside the sample.
The measured Rayleigh scattering in forward direction \({W}_{{\rm{R}}}^{{\rm{f}}}\) is converted into a degree of species separation using DFT-MD simulations from Fig. 3. The probe time of each data point is normalized to the individually determined shock breakout time. The dashed vertical lines mark the start of the second shock wave and the onset of the shock release, respectively. The gray areas illustrate the corresponding temporal uncertainties. As the second shock propagates, the observed degree of species separation is in good agreement with diffraction data taken in the same experiment. The light blue area ilustrates the uncertainty of the diffraction measurements and the orange error bars depict the combined errors of timing and Rayleigh scattering intensity.
Discussion
The observed results are in good agreement with XRD data recorded in the same experiment which show the formation of nanodiamonds induced by the second shock wave15,23. In contrast to the diffraction method, the absolute values for the C–H separation obtained by XRTS do not rely on the formation of crystalline structures in the experiment. However, the close match with XRD indeed suggests that the pure carbon clusters nearly exclusively consist of diamond, which is not embedded in a significant amount of liquid carbon. Assuming the carbon clusters consisting of only liquid carbon would lead to slightly larger values (~28%) for the degree of species separation inferred from XRTS due to the difference of WR at the wavenumber of the FXRTS diagnostics (cf. Fig. 3).
Our measurements and its analysis also indicate that for a generalized use of this method, the boundary conditions of mixed and demixed state need to be known to some extent to obtain quantitative results. This is particularly true for experiments where no additional XRD measurements are available. However, there exist many important cases where the boundary conditions seem very clear, e.g. hydrogen-helium demixing inside giant planets. Moreover, this method can be used for determining mixing on microscopic level of previously fully separated atomic species where the boundary conditions are again very well defined.
In conclusion, we have determined the degree of species separation as a function of time in a CH sample dynamically compressed to warm dense matter conditions from spectrally resolved X-ray scattering data obtained in forward and backward scattering geometry. These results are in good agreement with XRD data from the same sample. In this way, we demonstrate the capability of X-ray Thomson scattering to characterize dynamic miscibility properties of fluid mixtures. In subsequent experiments, these data can be used to provide access to diffusivity, the kinetics of chemical reactions or (de)mixing due to hydrodynamic instabilities in warm dense matter. In principle, the demonstrated method is therefore capable to shed light on the complex transitions of liquids deep inside giant planets, such as hydrogen-helium demixing as predicted to happen inside Saturn or, potentially, Jupiter. Moreover, our results also suggest that ablator-fuel mixing as observed in contemporary inertial confinement fusion schemes can quantitatively be investigated by X-ray scattering. Indeed, this is very practical since, for an appropriate choice of the investigated wavenumbers k, it is often much easier to field accurate XRTS measurements at two distinct values of k than XRD which needs to cover a broad k-range, in particular when investigating low-Z samples at optical laser-only facilities. Corresponding drive schemes at X-ray free electron lasers as well as the implementation of precise X-ray Thomson scattering at ICF facilities46 will soon allow for such measurements to be performed.
Methods
Experiment
The experiment was performed at the instrument for Matter in Extreme Conditions (MEC), an endstation of the Linac Coherent Light Source (LCLS) at the SLAC National Accelerator Laboratory47,48. The polystyrene samples had a thickness of 83.4 μm and were coated with 100 nm aluminum on the front and rear sides. The laser drive beams were each delivering up to 15 J in 10 ns at 527 nm with a focal spot of 200 μm in diameter using phase plates. The beams were combined and delayed relative to each other by 4.5 ns to achieve a step pulse laser profile on the target. The laser intensities of the two steps were (2.7 ± 0.25) TW/cm2 and (7.3 ± 0.5) TW/cm2, respectively. Shock dynamics and timing to realize coalescing shock waves at the sample’s rear side were adjusted and recorded by a Velocity Interferometer System for Any Reflector (VISAR)49, in some cases using LiF windows attached to the rear side of the polystyrene samples15. Each spectrometer uses a cylindrically bent Highly Annealed Pyrolytic Graphite (HAPG) crystal50 with a radius of curvature of 51.7 mm in von Hámos geometry coupled to a Cornell-SLAC Pixel Array Detector (CSPAD)51 to detect spectrally resolved X-rays. The relative sensitivity of both spectrometers was cross-calibrated by Ni-Kβ emission at (8 264.78 ± 0.01) eV, which was detected simultaneously by both spectrometers. The signals of both spectrometers have been flat field corrected, eliminating any systematic energy-dependent influences on the signal. Additionally, contributions of unshocked material due to an early probe time have been removed by scaling remaining diffraction features of cold material to the previously collected scattering and diffraction from the ambient samples.
Hydrodynamic simulations
The hydrodynamic simulation results using the code package HELIOS52 are based on the SESAME equation of state (EOS)53 table 7590 for polystyrene, which is strongly constrained on the Hugoniot curve by precision gas gun and laser shock experiments54. The drive intensities set in the simulations (2.25 and 6.7 TW/cm2 for the first and second step, respectively) have been adjusted to match the VISAR measurements and are in reasonable agreement with the experimental values. We find that the second shock wave enters the pre-compressed sample material at ~6 ns and coalesces with the first compression wave at the target rear side at around 7.6 ns.
DFT-MD simulations
All DFT-MD simulations were performed using the VASP package, version 5.233,34,35,36. The electronic density in the simulation box with periodic boundary conditions was represented by a plane wave expansion with a cut-off energy of Ecut = 1000 eV. We used the Mermin formulation of DFT to optimize the Helmholtz free energy at a given temperature55. The electron–ion interaction was modeled using the projector augmented wave (PAW) approach, specifically the hard PAW pseudopotentials for carbon (four valence electrons, Ch and Hh from Feb 2004) and hydrogen as provided with VASP37,56. The exchange-correlation potential was taken in generalized gradient approximation in Perdew–Burke–Ernzerhof parametrisation (GGA-PBE)38. We generally sampled the Brillouin zone of the supercell at the Γ-point only. The electronic bands where populated using a Fermi distribution at the chosen temperature. We had to increase the number of computed electronic bands to at maximum 2000 in order to sample the tail of the Fermi distribution for all cases. The supercell contained approximately 500 atoms of carbon and hydrogen with the relevant stoichiometry, the movements of which were calculated using the Hellman–Feynman forces derived from the electron densities of DFT under the Born-Oppenheimer approximation. The time step was t = 0.2 fs and the DFT-MD run covered a time span of 4–20 ps. The ion temperature was controlled by a Nosé–Hoover thermostat57. From the recorded coordinates, the ion and electron structure, and therefore the intensity of the elastic X-ray scattering in this multi-component system, can be obtained40. In order to predict the effect of demixing on the ionic structure, and therefore on the X-ray scattering, we combined the outputs of simulations with different atomic ratios, weighted to give the correct overall atomic ratio. The inelastic scattering signal is dominated by the carbon component and we thus approximate it by the inelastic scattering signal of diamond. We use time-dependent density functional theory (TDDFT) computations for the inelastic scattering signal using a full-potential linearized augmented-plane wave code implemented in elk58. The bootstrap kernel was used in a TDDFT calculation using the Kohn–Sham orbitals applying PBE-GGA for the exchange-correlation potential. Bootstrap is a parameter free long-range exchange-correlation kernel implemented in elk, which has been shown to reproduce excitonic effects at a reasonable computational cost59,60. The TDDFT calculations were performed on a 20 × 20 × 20 k-point mesh and 16 bands in the unit cell at the experimentally obtained density of ρ = 4.1 g/cm3. TDDFT is capable of computing the response functions at finite momentum transfer. In order to choose the complementary k and q-points we use the relation \({n}_{{k}_{i}}\times {q}_{i}=N\) where \({n}_{{k}_{i}}\) is the number of k-points along x, qi is the number of q-points along x, N is an integer which is also a factor of \({n}_{{k}_{i}}\) in accordance with the Monkhorst-Pack k-point-sampling61. For \({\bf{k}}=({N}_{{k}_{1}},{N}_{{k}_{2}},{N}_{{k}_{3}})\), we choose \({\bf{q}}=(\frac{i}{{N}_{{k}_{1}}},\frac{j}{{N}_{{k}_{2}}},\frac{k}{{N}_{{k}_{3}}})\) where i, j, k are integers62. This results in qi = qj = qk and a smearing width of 0.01 a.u. is used to approximate the Dirac delta function. The Bootstrap kernel59, although expensive, is chosen due to the self-consistency procedure compared to the parameter dependent LRC kernel of Botti et al.60,63. Furthermore, the effect of the system size and the influence of the exchange-correlation kernel in TDDFT for diamond under high pressure and warm dense matter conditions is shown in the work of Ramakrishna et al.64. For the experimental conditions (ρ = 4.1 g/cm3), the imaginary part of the inverse dielectric function is more sensitive to the pressure/density than the temperature of the system64. An increase in pressure causes the band gap to increase and therefore the inelastic peak to red shift. On the other hand, the increasing temperature tends to close the band gap. In our case, the temperature effect is significantly smaller compared to the change induced by the elevated pressure. This is seen in the close resemblance of the plasmon peak locations obtained using TDDFT in the optical limit under ambient (~1.35–1.4 Ha at ρ = 4.1 g/cm3) and warm dense conditions (1.3 Ha at 150 GPa, 6000 K)64.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. The raw data of the experiment are stored on tape (long term storage) at SLAC National Accelerator Laboratory. Processing and reduction of the raw data requires the computational services at SLAC.
References
Bolton, S. J. Juno celebrates a year at Jupiter. Nat. Astron. 1, 0178 (2017).
Connerney, J. E. P. et al. Jupiter’s magnetosphere and aurorae observed by the Juno spacecraft during its first polar orbits. Science 356, 826–832 (2017).
Iess, L. et al. Measurement of Jupiter’s asymmetric gravity field. Nature 555, 220–222 (2018).
Guillot, T. et al. A suppression of differential rotation in Jupiter’s deep interior. Nature 555, 227–230 (2018).
Guillot, T. Interiors of giant planets inside and outside the solar system. Science 286, 72–77 (1999).
Stevenson, D. J. & Salpeter, E. E. The dynamics and helium distribution in hydrogen-helium fluid planets. Astrophysical J. Suppl. Ser. 35, 239–261 (1977).
Nettelmann, N. et al. Ab initio equation of state data for hydrogen, helium, and water and the internal structure of Jupiter. Astrophysical J. 683, 1217 (2008).
Militzer, B., Hubbard, W. B., Vorberger, J., Tamblyn, I. & Bonev, S. A. A massive core in Jupiter predicted from first-principles simulations. Astrophysical J. Lett. 688, L45–L48 (2008).
Lorenzen, W., Holst, B. & Redmer, R. Demixing of hydrogen and helium at megabar pressures. Phys. Rev. Lett. 102, 115701 (2009).
Wilson, H. F. & Militzer, B. Sequestration of noble gases in giant planet interiors. Phys. Rev. Lett. 104, 121101 (2010).
Chau, R., Hamel, S. & Nellis, W. J. Chemical processes in the deep interior of Uranus. Nat. Commun. 2, 203 (2011).
Lobanov, S. S. et al. Carbon precipitation from heavy hydrocarbon fluid in deep planetary interiors. Nat. Commun. 4, 2446 (2013).
Ross, M. The ice layer in Uranus and Neptune-diamonds in the sky? Nature 292, 435–436 (1981).
Benedetti, L. R., Nguyen, J. H., Caldwell, W. A., Liu, H. K. & Jeanloz, R. Dissociation of CH4 at high pressures and temperatures: diamond formation in giant planet interiors? Science 286, 100–103 (1999).
Kraus, D. et al. Formation of diamonds in laser-compressed hydrocarbons at planetary interior conditions. Nat. Astron. 1, 606–611 (2017).
Graziani, F., Desjarlais, M. P., Redmer, R. & Trickey, S. B. (eds). Frontiers and Challenges in Warm Dense Matter (Springer, Berlin, 2014).
Riley, D. Generation and characterisation of warm dense matter with intense lasers. Plasma Phys. Control. Fusion 60, 014033 (2018).
Bethkenhagen, M. et al. Planetary ices and the linear mixing approximation. Astrophysical J. 848, 67 (2017).
Lindl, J., Landen, O., Edwards, J. & Moses, E., NIC team. Review of the national ignition campaign 2009-2012. Phys. Plasmas 20, 070501 (2014).
Hurricane, O. A. et al. Fuel gain exceeding unity in an inertially confined fusion implosion. Nature 506, 343 (2014).
Ma, T. et al. X-ray scattering measurements of strong ion-ion correlations in shock-compressed aluminum. Phys. Rev. Lett. 111, 085004 (2013).
Orth, C. D. Spallation as a dominant source of pusher-fuel and hot-spot mix in inertial confinement fusion capsules. Phys. Plasmas 23, 022706 (2016).
Schuster, A. K. et al. Measurement of diamond nucleation rates from hydrocarbons at conditions comparable to the interiors of icy giant planets. Phys. Rev. B 101, 054301 (2020).
Wünsch, K., Vorberger, J., Gregori, G. & Gericke, D. O. X-ray scattering as a probe for warm dense mixtures and high-pressure miscibility. EPL 94, 25001 (2011).
Gregori, G., Glenzer, S. H., Rozmus, W., Lee, R. W. & Landen, O. L. Theoretical model of x-ray scattering as a dense matter probe. Phys. Rev. E 67, 026412 (2003).
Glenzer, S. H. & Redmer, R. X-ray Thomson scattering in high energy density plasmas. Rev. Mod. Phys. 81, 1625–1663 (2009).
McBride, E. E. et al. Setup for meV-resolution inelastic X-ray scattering measurements and X-ray diffraction at the Matter in Extreme Conditions endstation at the Linac Coherent Light Source. Rev. Sci. Instrum. 89, 10F104 (2018).
Kraus, D. et al. High-pressure chemistry of hydrocarbons relevant to planetary interiors and inertial confinement fusion. Phys. Plasmas 25, 056313 (2018).
Helled, R., Anderson, J. D., Podolak, M. & Schubert, G. Interior models of Uranus and Neptune. Astrophys. J. 7, 15 (2011).
Guillot, T. & Gautier, D. Giant planets. Treatise Geophysics 10, 439–464 (2007).
Gamboa, E. J. et al. Single-shot measurements of plasmons in compressed diamond with an x-ray laser. Phys. Plasmas 22, 056319 (2015).
Kraus, D. et al. Nanosecond formation of diamond and lonsdaleite by shock compression of graphite. Nat. Commun. 7, 10970 (2016).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Kresse, G. & Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 49, 14251 (1994).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Erratum: Generalized gradient approximation made simple. Phys. Rev. Lett. 78, 1396 (1997).
Vorberger, J. & Gericke, D. O. Ab initio approach to model x-ray diffraction in warm dense matter. Phys. Rev. E 91, 033112 (2015).
James, R. W. The Optical Principles of the Diffraction of X-Rays. (G. Bell and Sons LTD, London, 1962).
Kraus, D. et al. Probing the complex ion structure in liquid carbon at 100 GPa. Phys. Rev. Lett. 111, 255501 (2013).
Kraus, D. et al. The complex ion structure of warm dense carbon measured by spectrally resolved x-ray scattering. Phys. Plasmas 22, 056307 (2015).
Pauling, L. & Sherman, J. Screening constants for many-electron atoms. the calculation and interpretation of X-ray term values, and the calculation of atomic scattering factors. Z. für Kristallographie - Crystalline Mater. 81, 1–29 (1932).
Hartley, N. J. et al. Liquid structure of shock-compressed hydrocarbons at megabar pressures. Phys. Rev. Lett. 121, 245501 (2018).
Kraus, D. et al. Platform for spectrally resolved x-ray scattering from imploding capsules at the National Ignition Facility. J. Phys.: Conf. Ser. 717, 012067 (2016).
Gauthier, M. et al. New experimental platform to study high density laser-compressed matter. Rev. Sci. Instrum. 85, 1E616 (2014).
Glenzer, S. H. et al. Matter under extreme conditions experiments at the Linac Coherent Light Source. J. Phys. B: Mol. Opt. Phys. 49, 092001 (2016).
Barker, L. M. & Hollenbach, R. E. Laser interferometer for measuring high velocities of any reflecting surface. J. Appl. Phys. 43, 4669–4675 (1972).
Zastrau, U., Woldegeorgis, A., Förster, E., Loetzsch, R. & Marschner, H. et al. Characterization of strongly-bent HAPG crystals for von-Hamos x-ray spectrographs. JINST 8, P10006 (2013).
Blaj, G. et al. X-ray detectors at the Linac Coherent Light Source. J. Synchrotron Radiat. 22, 577 (2015).
MacFarlane, J. J., Golovkin, I. E. & Woodruff, P. R. HELIOS-CR - A 1-D radiation-magnetohydrodynamics code with inline atomic kinetics modeling. J. Quant. Spectrosc. Rad. Transf. 99, 381–397 (2006).
Lyon, S. P. & Johnson, J. D. SESAME: The Los Alamos National Laboratory Equation of State Database LANL Report No. LA-UR-92-3407 (National Laboratory, Los Alamos, 1992).
Barrios, M. A. et al. High-precision measurements of the equation of state of hydrocarbons at 1-10 Mbar using laser-driven shock waves. Phys. Plasmas 17, 056307 (2010).
Mermin, N. D. Thermal properties of the inhomogeneous electron gas. Phys. Rev. 137, A1441 (1965).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Nosé, S. Constant temperature molecular dynamics methods. Prog. Theor. Phys. Suppl. 103, 1–46 (1991).
Dewhurst, J. K. et al. ELK, all-electron full-potential linearised augmented-plane wave (FP-LAPW) code, http://elk.sourceforge.net/ (2019).
Sharma, S., Dewhurst, J. K., Sanna, A. & Gross, E. K. U. Bootstrap Approximation for the exchange-correlation kernel of time-dependent density-functional theory. Phys. Rev. Lett. 107, 186401 (2011).
Botti, S. et al. Long-range contribution to the exchange-correlation kernel of time-dependent density functional theory. Phys. Rev. B 69, 155112 (2004).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
Onida, G., Reining, L. & Rubio, A. Electronic excitations: density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 74, 601 (2002).
Botti, S. et al. Energy dependence of the exchange-correlation kernel of time-dependent density functional theory: a simple model for solids. Phys. Rev. B 72, 125203 (2005).
Ramakrishna, K. & Vorberger, J. Ab initio dielectric response function of diamond and other relevant high pressure phases of carbon. J. Phys. Condens. Matter 32, 095401 (2020).
Acknowledgements
Use of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The Matter in Extreme Conditions (MEC) instrument of LCLS has additional support from the DOE, Office of Science, Office of Fusion Energy Sciences under contract No. SF00515. SLAC HED research acknowledges funding through FES FWP-100182. S.F. and M.R. acknowledge supprt by the Bildungsministerium für Bildung und Forschung under the support No. 05P15RDFA1. The work of S.F., A.P. and T.D. was performed under the auspices of the DOE by Lawrence Livermore National Laboratory under Contract No. DE-AC52-07NA27344. T.D. was supported by Laboratory Directed Research and Development (LDRD) Grant No. 18-ERD-033. N.J.H., A.K.S., K.V. and D.K. acknowledge support by the Helmholtz Association under VH-NG-1141. A.M.S., R.W.F. and D.K. were supported by the DOE Office of Science, Office of Fusion Energy Sciences and by the National Nuclear Security Administration under awards DE-FG52-10NA29649 and DE-NA0001859.
Author information
Authors and Affiliations
Contributions
D.K., T.D., A.P, R.W.F., J.V., S.H.G., D.O.G., M.R., E.Ga., E.Gr., P.N. and A.J.M. were involved in the project planning. S. F., D.K., E.Ga., N.J.H., A.P., T.D., P.N., E.E.M., A.M.S., L.B.F., P.S., M.J.M., E.J.G., E.Gr., I.N. and T.v.D. carried out the experiment. Experimental data was analyzed and discussed by S.F., D.K., J.V., N.J.H., A.K.S., K.V., S.H.G., D.O.G. and T.D. The DFT calculations were performed by J.V. and K.R. The manuscript was written by S.F. and D.K. with input from J.V., N.J.H., D.O.G., K.R. and T.D.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Andrew Baczewski and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frydrych, S., Vorberger, J., Hartley, N.J. et al. Demonstration of X-ray Thomson scattering as diagnostics for miscibility in warm dense matter. Nat Commun 11, 2620 (2020). https://doi.org/10.1038/s41467-020-16426-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-16426-y
This article is cited by
-
Nonequilibrium band occupation and optical response of gold after ultrafast XUV excitation
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.