Abstract
Vanadium dioxide (VO2) is a material that undergoes an insulator–metal transition upon heating above 340 K. It remains debated as to whether this electronic transition is driven by a corresponding structural transition or by strong electron–electron correlations. Here, we use apertureless scattering near-field optical microscopy to compare nanoscale images of the transition in VO2 thin films acquired at both mid-infrared and terahertz frequencies, using a home-built terahertz near-field microscope. We observe a much more gradual transition when THz frequencies are utilized as a probe, in contrast to the assumptions of a classical first-order phase transition. We discuss these results in light of dynamical mean-field theory calculations of the dimer Hubbard model recently applied to VO2, which account for a continuous temperature dependence of the optical response of the VO2 in the insulating state.
Similar content being viewed by others
Introduction
Vanadium dioxide (VO2) is a canonical example of an insulator–metal transition (IMT) material1,2 with many exciting potential technological applications3,4,5. Although this material has been studied for decades, the precise physics behind its phase transition is still not fully understood. There is an ongoing debate as to whether the transition is a structurally-driven Peierls-like one, or whether it is Mott-like and due to electronic correlations6,7,8,9,10,11,12,13. This complex interplay between Coulomb interaction and structural effects is characteristic of many correlated oxide materials14,15.
One major difficulty in disentangling the complexity of VO2 physics is that conventional experimental methods for examining the phase transition, such as transport or optical spectroscopy, are necessarily insensitive to the state of the material at short length scales16,17. Apertureless scattering near-field optical microscopy (SNOM)18,19,20,21,22,23 has been used to image the electronic phase transition of VO2 at mid-infrared frequencies. This technique is able to discriminate between metallic and insulating domains that form near Tc in VO2 thin films24,25,26. These experiments show that VO2 phase-separates into coexisting metallic and insulating domains near the transition temperature Tc, consistent with the first-order nature of the phase transition24,25,26,27.
Here, we use SNOM to investigate the nanoscale optical response through the temperature-driven IMT of VO2 films grown on sapphire. Our key innovation is to perform this experiment at both mid-infrared (MIR) and terahertz (THz) frequencies, using a home-built THz-SNOM with a broadband spectrum from 0.1 to 2 THz (see Methods). THz light interrogates the electronic response at energies on the order of meV, which involve excitations very close to the Fermi level and provides a much closer connection to DC transport. The ability to investigate the THz response of VO2 with sub-micron spatial resolution allows us to probe the local low-frequency conductivity of individual domains through the transition. We find that the phase transition in the THz appears to be smooth and continuous, in contrast to the abrupt transition at MIR frequencies. We attribute this smoothness in the THz to the gradual filling of the band gap in the insulating state as the system approaches the transition. We find that a dynamical mean-field theory (DMFT) calculation of the dimer Hubbard model (DHM) for VO228 qualitatively reproduces our experimental observations.
Results
Imaging the IMT in VO2 at THz and MIR frequencies
The principle behind our home-built THz-SNOM is similar in operation to others reported in the literature29,30,31. However, unlike any other THz-SNOM, the sample stage in our system is coupled to a variable temperature liquid helium flow cryostat and situated in ultra-high vacuum (Fig. 1a). This allows for measurements from 30 to 400 K with uncompromised environmental stability which was essential for the measurements we describe below. The spatial resolution of this THz measurement is approximately 130 nm, limited only by the radius of the custom atomic force microscope (AFM) tips used in our apparatus (see Methods).
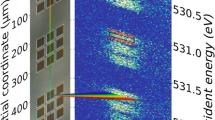
Schematic and typical performance of the THz-SNOM. a Schematic of the THz-SNOM. The THz pulse (red arrow) is sent through a UHV vacuum chamber housing the custom SNOM. The sample is coupled to a heater and liquid-He flow cryostat (CRYO), allowing for operation at temperatures from 40 to 400 K. b Detail view of the SNOM inside the chamber. The same focusing parabola (FP) is used to both focus the THz pulse onto the tip (not shown to scale) and collect the tip-scattered light. c Broadband THz pulse (blue, S0) and the near-field THz pulse measured in the system on gold in a dry-air-purged environment. S1, S2, and S3 are the detected THz signal demodulated at the first, second, and third harmonic of the tip tapping frequency. d Measured THz spectrum of the far-field pulse (blue) and the near-field spectrum for different harmonics, collected on gold
In Fig. 2, we show the key experimental data of this work, temperature-dependent images at THz and MIR frequencies of the near-field response of a 100 nm thick VO2 film grown on sapphire (see Methods). The top row of images are taken at THz frequencies with our novel instrument as described above, and the images in the bottom row are taken in the MIR with a commercial SNOM (Neaspec GmbH) using a 10 μm CO2 laser source. The detected signal Sn is the light scattered by the tip demodulated at the nth harmonic of the tip tapping frequency20. Contrast in near-field signal Sn has been shown to reliably discriminate between metallic and insulating regions of VO2 at MIR frequencies24,25,26, and of other spatially inhomogeneous samples at THz frequencies29,30. We detect the amplitude of the peak of the THz pulse scattered by the tip, demodulated at the second harmonic (S2) due to limited signal to noise. At THz wavelengths, background contamination of the near-field signal is much less severe, making the second harmonic a good measure of spatially local electromagnetic response32. In the MIR images we report S3, the tip-scattered light demodulated at the third harmonic of the tapping frequency. Here we choose a linear color scale with red corresponding to high Sn metallic regions, and blue to low Sn insulating regions of the sample. In both the THz and MIR images, the signal Sn is shown normalized to that collected over a region of gold in the same field of view.
SNOM images of the VO2 IMT. The images shown are taken at THz (top row) and MIR (bottom row) frequencies during a heating cycle. The temperature of each image is noted in the bottom left corner. In all images, the signal at every temperature is normalized to the average signal obtained on gold (bright red region in the upper right or right of the image, for THz and MIR respectively). The dashed yellow line denotes the boundary between VO2 and gold regions. The THz and MIR data are S2 and S3, which is the detected signal demodulated at the second and third harmonic of the tip tapping frequency, respectively. Low near-field signal (blue) is measured in insulating regions, while high near-field signal (red) corresponds to a metallic state. The scales are different for the THz and MIR images to highlight the transition from insulator to metal in both cases. Scale bar, 2 μm
The MIR images reveal that upon heating, the VO2 sample phase-separates into metallic domains within the insulating background. The metallic regions extend through the sample as temperature is increased. This is similar to previous MIR near-field measurements of VO224. In stark contrast, the THz images appear to evolve much more homogeneously and continuously from insulating to metallic signal levels through the same temperature region. A histogram representation of the pixel intensity in each image, as shown in Fig. 3, elucidates this distinction. These histograms exclude the pixels in the gold region of each image. We show histograms of the THz images in Fig. 3a, and histograms of the MIR images in Fig. 3b. At temperatures in the middle of the area-averaged transition, the MIR histograms are bimodal. There is an abrupt change in MIR near-field signal between metallic and insulating domains, represented by the separation between the two peaks in the histograms. The pixels in the THz images, on the other hand, are distributed according to a single Gaussian at all temperatures; there is no clear separation in THz near-field signal between insulating and metallic domains. We can track the average THz near-field signal as a function of temperature by fitting the histograms in Fig. 3a to a single Gaussian distribution and extracting its mean (see Supplementary Note 1 and Supplementary Fig. 1 for details). We plot the mean of each THz histogram as a function of temperature in Fig. 3c as circles, connected by a dashed line as a guide to the eye. The error in the parameter estimation of the fitted histogram is dominated by random noise in the THz-SNOM measurement, which is approximately 5% of the metallic near-field signal level. The THz near-field signal appears to evolve continuously with temperature.
Histogram analysis of the VO2 SNOM images at THz and MIR frequencies. a Pixel intensity histograms of selected THz images shown in Fig. 2. The signal level S is shown normalized to that obtained on gold (SM). b Same, for MIR images. c Peak signal level as a function of temperature in the THz (circles) and MIR (diamonds) extracted from single or bi-modal Gaussian fits to the histograms. The error bars (s.d.) in the THz are derived from parameter estimation in a non-linear least-squares fit, and are limited by the random noise in the THz near-field signal measurement. The MIR error bars are smaller than the symbols and so are omitted. In the MIR case, there are two peaks at intermediate temperatures due to the bimodal nature of the pixel intensity distribution. The maximum peak at intermediate temperatures is an open diamond, while the smaller peak is a filled diamond (Supplementary Note 1). The dashed (THz) and dotted (MIR) lines are guides to the eye
Transport measurements taken with the THz-SNOM apparatus show strong correlation between the transition temperature as revealed by DC transport and Tc in the THz near-field signal (see Supplementary Note 2 and Supplementary Fig. 2 for details). In addition, the THz near-field signal displays hysteretic behavior, in agreement with a first-order IMT. This evidence indicates that the change in the THz near-field signal between 340 and 350 K is due to a phase transition from an insulating to a fully metallic state. Furthermore, we note that the observed increase in THz near-field signal through the transition is not to be confused with the gradual increase in carrier density before the transition1.
There are two important differences between the THz and MIR SNOM measurements. The first is the spatial resolution; the THz-SNOM employs custom AFM probes which have a larger radius than the MIR probes (see Methods). Although the spatial resolution in our THz-SNOM is coarser than that of the MIR-SNOM, autocorrelation analysis of the THz and MIR images shows that the THz-SNOM resolution is sufficient to resolve the inhomogeneity apparent in the MIR images (Supplementary Note 3 and Supplementary Fig. 3). The second and most relevant difference is the variation in near-field signal level between insulating and metallic end states, which is a function of the probing frequency. As we describe below, the THz images are best explained by assuming that the THz near-field signal close to Tc is very similar in the insulating and metallic state. If the relative signal level between these two phases falls below the THz-SNOM noise floor, then the THz images will not be able to resolve the phase boundary. However, an insulating state whose THz near-field signal is close to that of the metallic state at Tc implies that the insulating state conductivity is increasing continuously as the temperature approaches Tc.
A closer examination of the MIR near-field images reveals a similar continuous change in signal level. We fit the MIR histograms at temperatures in the middle of the transition to the sum of two skewed Gaussians, whose means are the insulating and metallic signal levels at each temperature (Supplementary Note 1 and Supplementary Fig. 1). For temperatures far from Tc, where the entire image is predominately high or low MIR near-field signal, the MIR histograms could only be fit to a single Gaussian. We plot these extracted mean signals in Fig. 3c as diamonds, of which there are two for temperatures in the middle of the transition. The larger diamond at those temperatures is the center signal of the taller Gaussian, corresponding to the signal level of the majority of pixels (insulating or metallic) in the image. We plot the difference in near-field signal level between the two Gaussian means at intermediate temperatures in Supplementary Fig. 4, which is a good measure of the width of the transition.
We connect the majority signal levels with a dotted line in Fig. 3c, which has an abrupt jump in magnitude at Tc. Although this abrupt jump in the MIR near-field signal between insulating and metallic domains is indicative of a first-order transition, we also observe that the MIR near-field signal within the insulating or metallic phase is changing continuously with temperature below and above Tc. The gradual continuous change in MIR near-field signal of the insulating or metallic state is similar to what we observe in the entire film in the THz, and is contrary to the assumptions of a conventional first-order phase transition. We also note that the signal-to-noise ratio in the MIR-SNOM is significantly higher than that in the THz, such that the error in the parameter estimation is less than the size of the symbols shown in Fig. 3c.
Nanoscale contrast in the vicinity of the IMT
A first-order phase transition implies an order parameter that changes discontinuously with temperature. In the case of an IMT, that order parameter describes the metallicity of the material, and is closely related to the density of states (DOS) at the Fermi level33. In the insulating state the DOS is vanishingly small, and in the metallic state the DOS is finite. As the temperature crosses Tc, the DOS “jumps” from insulating to metallic. Although the MIR near-field images reveal a jump in near-field signal from insulating to metallic, we also observe that the MIR near-field signals in the insulating and metallic state are both temperature dependent. In addition, and rather surprisingly, we observe a homogeneous and continuous evolution of the near-field signal at THz frequencies, which probe the electronic response at energies very close to the Fermi level (Fig. 3a–c). A traditional first-order IMT does not account for these behaviors. Instead, the continuous change in near-field signal evokes a gradual filling of the DOS in the band gap with increasing temperature. This curious discrepancy calls for resolution.
VO2 exhibits hysteretic resistance and a divergent molar heat capacity at constant pressure1,34, both indicative of a first-order transition. Thus it seems unlikely that the IMT is truly continuous as suggested by the THz near-field images. Another possibility is that a long-range interaction, such as strain, disorder, or even electronic correlations, leads to a micro-emulsion phase whose characteristic domain size is smaller than the spatial resolution of our near-field measurements35,36. This latter line of reasoning disagrees with our own observation of clear domain formation of 100–200 nm in the MIR images (Supplementary Note 3 and Supplementary Fig. 3).
Of course, the ability to resolve separate domains depends not only on spatial resolution, but also on the relative signal levels associated with the two states compared to instrumental signal-to-noise. As mentioned above, we interpret the apparent homogeneity of the THz images as most likely due to a reduced THz contrast between the insulating and metallic state at temperatures very close to the transition. The SNOM scattering amplitude is essentially a measure of local reflectivity. Several factors could lead to a high reflectivity in the insulating state, such as a finite or large real part of the dielectric permittivity \(\epsilon _1\) of the sample/substrate system. Another possibility for the THz reflectivity in the insulating state being comparable to that of the metallic state is a finite DC conductivity in the insulating state. A small but finite conductivity corresponds to a reflectivity which geometrically increases as the frequency decreases (Supplementary Note 5 and Supplementary Fig. 5). Thus, at THz frequencies films with even a very small optical conductivity in an insulating state would translate into a near-field signal of similar magnitude to that of a metallic state. A finite DC conductivity in the insulating state implies that there is a finite DOS at the Fermi level at temperatures below Tc. Moreover, this qualitative scenario of a gradual filling of the gap can still be consistent with a first-order transition, according to model calculations of a strongly correlated system relevant for VO2 that we describe below.
This picture of finite insulating state conductivity near the transition is not necessarily inconsistent with far-field THz studies of VO2 films16,37,38,39, which observe a gradual increase in THz conductivity just below Tc. The results of area-averaging far-field experiments and our nano-THz imaging measurements below Tc where VO2 is phase-separated can only be directly compared to each other provided some form of effective medium theory (EMT) is utilized. Any version of the EMT requires multiple inputs including the optical constants of metallic and insulating domains, the filling fractions of the two phases, and also the depolarization factors determined by the shape of the domains24. All published attempts of the EMT analysis across the insulator-to-metal transition required assumptions of not only the conductivities but also of the real space characteristics. We note that the nano-scale morphology of VO2 in the phase-separated state can widely vary from film to film depending on the substrate material, strain and details of thin film synthesis40. Thus, the EMT analysis inevitably hinges on various assumptions that complicate head-to-head comparison of nano-THz data in Fig. 2 and previously reported far-field THz transmission data16,37,38,39. A challenge for future experiments is to perform both far-field THz spectroscopy and nano-THz imaging for the same samples. This is now technically feasible, in principle, and the implementation of this task presents a difficult but attainable goal for future research.
DMFT solutions of the dimer Hubbard model
An explanation for the formation of in-gap states prior to the metallic transition has an explicit realization in DMFT solutions of the dimer Hubbard model (DHM) (see Methods). The DHM incorporates structural effects into the Mott–Hubbard Hamiltonian by introducing an additional hopping amplitude t⊥, which accounts for the favorability of intra-dimer interaction relevant to the monoclinic structure of VO22. The DHM has been recently recognized to capture non-trivial aspects of the IMT in VO2, including a first-order insulator to metal transition with increasing temperature28. Moreover, we show below that for certain values of the ratio t⊥/U within the coexistence regime of the model, the DHM predicts both an abrupt, first-order jump in the DOS at Tc and a gradual, almost continuous filling of the gap at temperatures above and below Tc. These features lead to a qualitative account of our experimental observations.
In Fig. 4, we show the frequency- and temperature-dependent DOS, optical conductivity, and simulated SNOM signal for two different values of the ratio t⊥/U. Both t⊥ and U are given in units of the half-bandwidth D = 2t, where t is the interdimer lattice hopping amplitude. For VO2, D ≈ 1 eV. The DOS is calculated from DMFT solutions of the DHM, which in turn is used to calculate the optical conductivity. Finally, we use the resulting optical constants to simulate the near-field signal using a lightning-rod (LR) model of the tip–sample interaction (see Methods and ref. 41 for details). Panels (a)–(c) correspond to a case with small t⊥/U, and panels (d)–(f) are for large t⊥/U. The values of t⊥ and U we show are carefully chosen to represent the most physically relevant cases of the model. Both cases are for values of t⊥/U within the coexistence regime of the DHM phase diagram (see Supplementary Fig. 6), meaning that both parameter sets support a first-order temperature-driven IMT with Tc ≈ 0.04D consistent with experiment28. The low t⊥/U case represents a model where intra-dimer hopping is relatively weak, similar to a conventional Mott–Hubbard model. The high t⊥/U case corresponds to relatively strong intra-dimer hopping, still within the coexistence region of the phase diagram but closer to the crossover to a Peierls-like transition (see Supplementary Fig. 6). Even though both cases discussed here correspond to a first-order IMT material, the temperature dependence of all three plotted quantities is strongly affected by the value of t⊥/U.
Spectra at different temperatures around Tc, calculated from DMFT for the dimer Hubbard model. Spectra calculated with parameters t⊥ = 0.2, U = 3.1 (a–c) and t⊥ = 0.5, U = 2.405 (d–f) as a function of energy normalized to the half-bandwidth D. The temperatures (normalized to Tc) of each curve for small t⊥/U (a–c) are shown to the left of panel (a). The temperatures used for large t⊥/U (d–f) are shown to the left of panel (d). The local density of states (LDOS) at different temperatures as a function of energy is shown for small t⊥/U (a) and large t⊥/U (d). The black line is the LDOS at T = 0. The sharp peak in the T = 0 LDOS in (d) is due to the formation of an intra-dimer singlet at very low temperatures (see text for details). The real part of the optical conductivity at different temperatures is shown for small t⊥/U (b) and large t⊥/U (e). All conductivities are normalized to the DC conductivity at the highest temperature shown (i.e., the DC conductivity of the metallic state). The calculated near-field signal at different temperatures as a function of frequency is shown for small t⊥/U (c) and large t⊥/U (f). The vertical gray lines in all figures indicate the THz (dashed) and MIR (dotted) frequencies used for calculating histograms in Fig. 5
First we consider the small t⊥/U case, which corresponds to a material with strong electronic correlations compared to the intra-dimer hopping amplitude. In Fig. 4a, the DOS exhibits an abrupt shift from insulating to metallic at a specific temperature Tc, but does not display strong temperature dependence at temperatures below or above Tc. This behavior is echoed in the optical conductivity (Fig. 4b); the insulating state has a spectrally flat, insulating conductivity for all temperatures below Tc, which abruptly jumps to a large Drude-like metallic conductivity at all temperatures above Tc. In Fig. 4c, we show the simulated near-field signal on VO2 as a function of frequency for different temperatures, which repeats the same general trends as the DOS and the optical conductivity. It is low for T < Tc and high for T > Tc, with an abrupt jump in signal level between the two states at all frequencies. There is very little temperature dependence otherwise. We note that the spectra calculated from the DHM are not meant to be quantitative predictions of experiment, but are rather a quasi-qualitative picture of how the near-field spectrum would appear in VO2 as described by this simplified model.
The temperature dependence is markedly different for the case of large t⊥/U, which corresponds to a material with strong dimerization compared to the electronic correlations. In Fig. 4d, there is still an abrupt jump in the DOS at Tc, but the DOS below and above Tc is more temperature dependent. We see that the gap is continuously filling at temperatures below Tc. This is due to the melting of the intra-dimer singlet at low temperature, whose spectral weight is then spread incoherently over the gap as the temperature increases42. The transfer of spectral weight over energy scales that are much higher than Tc is a hallmark of strong correlations15. In the present context, it is related to the competition between the intra-dimer screening of the magnetic moments in the insulator and the lattice Kondo-like screening of each lattice site in the metallic state. Namely, the two magnetic sites that screened each other and formed the singlet suddenly experience a qualitative change upon heating and become screened by their respective baths (i.e., Kondo screening). In other words, this feature can be interpreted as a local RKKY-versus-Kondo screening at the level of a single dimer42,43,44. Similarly, in Fig. 4e the optical conductivity at T < Tc is still flat and insulating, but is continuously increasing as temperature increases. There is an abrupt jump in conductivity at Tc from flat and insulating to Drude-like and metallic, but as temperature continues to rise for T > Tc the conductivity continuously increases. The metallic state of the model at higher T corresponds to a (bad) metal controlled by Kondo-like physics, with two parallel quasiparticle bands that are split by an effective t⊥28,42. For the choice of t⊥/U shown in the bottom row of Fig. 4, the low-frequency conductivity changes by an order of magnitude across the transition. This is smaller than the 3–5 orders of magnitude change in DC resistance observed in transport experiments, and is likely due to the fact that our model does not include a structural transition, but nevertheless is consistent with a first-order IMT.
Notably, the insulating state optical conductivity in the high t⊥/U case has a very different behavior at all frequencies with respect to the low-t⊥/U case. The small but finite low-frequency optical conductivity in the insulating state translates to a 1/ω behavior in reflectivity, as is expected for a Drude metal whose scattering rate is comparable to the plasma frequency (Supplementary Note 3 and Supplementary Fig. 3). Concurrently, the calculated near-field signal shown in Fig. 4f has a 1/ω-like behavior at low temperatures, with a frequency width that is a function of the DC conductivity σ0 and increases with temperature. Thus, the low-frequency near-field signal has a more continuous and smaller relative change with increasing temperature as the conductivity evolves from insulating to metallic. This is reflected in the modeled near-field signal in Fig. 4f, which shows very little temperature variation at low frequencies, but an abrupt jump with temperature at higher frequencies. As remarked on above, the difference between our THz near-field images on granular thin films and microwave nanoscale images on strained single crystals40 might be accounted for by our model as a difference in the value of t⊥/U for disparate sample morphologies.
We wish to emphasize that the DHM model is not a complete description of the phase transition in VO2, in that the DHM does not consider the structural transition from monoclinic to rutile. In fact, the metallic state predicted by the DHM is more closely related to that of the so-called “monoclinic metal” reported in previous works24,26,45,46,47,48,49,50. The experimental and theoretical results presented here allow us to form a qualitative description of how the near-field spectrum would appear in a material undergoing an insulator–metal transition with either strong or weak inter-dimer coupling. As such, the DHM is, to first order, a viable model of the VO2 system.
Modeling the VO2 near-field imaging experiment
To compare the results of the DHM to our experimental data, we use the calculated frequency-dependent near-field signals in Fig. 4c, f to simulate the histogram one would obtain in a near-field imaging experiment (Supplementary Note 6). The simulated histograms for the small t⊥/U case are shown in Fig. 5a. In this case, the temperature dependence of both the THz and MIR near-field signals is similar. The histograms at both frequencies are clearly bimodal. There is a distinct near-field signal level for the insulating and metallic states, with an abrupt jump in signal between the two states. As temperature increases, the near-field signal level in an individual domain does not change, but rather the relative distribution of pixels shifts from majority insulating to majority metallic. The evolution of S(T) for both THz and MIR frequencies is plotted in Fig. 5b for the small t⊥/U case. At both frequencies, there is an abrupt jump in near-field signal at Tc, but no temperature dependence above or below Tc. Thus, the small t⊥/U case is quite different from what we observe experimentally.
Histograms of a phase-separated image using near-field signals at different temperatures calculated from the DHM. a The simulated histograms for a THz and MIR image in the case of small t⊥/U. The signals are calculated at the frequencies represented by the dashed (THz) and dotted (MIR) vertical lines in Fig. 4c. The temperatures shown are normalized to Tc. b Plot of the calculated near-field signal as a function of temperature for small t⊥/U at THz (dashed) and MIR (dotted) frequencies. c Same as (a), but for large t⊥/U. The signals are calculated at the frequencies represented by the dashed (THz) and dotted (MIR) vertical lines in Fig. 4f. d Same as (b), but for large t⊥/U
The histograms calculated for large t⊥/U, which are shown in Fig. 5c, qualitatively agree with our experimental data. The THz histograms are single Gaussians with a mean near-field signal level that increases continuously with temperature. The MIR histograms are bimodal with an abrupt jump between the two Gaussian centers, yet still display an insulating and metallic near-field signal level that changes continuously with temperature. This is reflected in the temperature-dependent near-field signal at both frequencies, plotted in Fig. 5d. The THz signal at low temperatures is already very close to the signal at high temperatures, and evolves almost continuously from low to high signal as temperature is increased. The MIR near-field signal, in contrast, has an abrupt jump at Tc, and is also clearly changing with temperature above and below Tc. This is similar to what we observe in the experimentally extracted S(T) curves shown in Fig. 3c.
Discussion
Using a novel THz-SNOM with 130 nm spatial resolution, we find that the nature of the domain formation through the phase transition in VO2 thin films appears homogeneous and continuous at THz frequencies. Moreover, MIR near-field images reveal that the local reflectivity of the insulating or metallic state is changing with temperature below and above Tc. A relevant additional experiment would be to enhance these data with THz and MIR nano-spectroscopy of the VO2 films through the transition. Currently, our apparatus is unable to perform a complete series of nano-spectroscopy measurements across the transition (analogous to the data shown in Fig. 1d) due to tip degradation coupled with the necessary long averaging times. Future developments in instrumentation will hopefully soon overcome these experimental difficulties.
The DHM appears to provide a framework for understanding how a continuously varying electronic response as revealed by the THz and MIR near-field images can be consistent with a first-order transition. Increased intra-dimer hopping with respect to the Coulomb interaction (large t⊥/U) leads to the formation of intra-dimer singlets below a characteristic temperature T*42. The dissolution of these singlets as T approaches Tc results in an incoherent spread of spectral weight across the gap at finite T < Tc. Gap filling in the insulating state at finite temperature is consistent with previous measurements of both bulk and thin film VO251,52. This more continuous filling of the DOS for T < Tc leads to a small but finite THz conductivity in the insulating state. A small optical conductivity in turn generates a reflectivity which is low but abruptly increases as the frequency approaches 0. Thus, the increased t⊥/U generates a small, finite THz optical conductivity for T ≤ Tc, which translates into an insulating state whose THz reflectivity is larger than the MIR reflectivity. At temperatures very close to the transition, the insulating THz near-field signal is already within the experimental detection limit of the metallic signal. Even though there is an abrupt first-order jump in the optical conductivity at Tc, the relative change in THz near-field signal across the IMT remains below the experimental detection limit. Therefore, the transition appears homogeneous in the THz images. The transition at Tc from insulating to metallic remains abrupt in the MIR near-field signal, but the continuous filling of the gap translates into a continuous shift of the MIR near-field signal in the insulating and metallic state.
The DHM shows that the first order transition involves a qualitative change of the state, from an insulator with dynamical local singlets to a (bad) metal with the dimer moments independently (Kondo) screened by the rest of the lattice. In this sense, the IMT in VO2 is due to Mott physics. However, with regard to previous works utilizing the DHM42, the present work seems to indicate that the behavior of VO2 may be better characterized by a larger value of t⊥. In previous works42, t⊥ was 0.3 W/D, and here we find that the value 0.5 W/D represents the experiments best. Both values, nevertheless, result in a first-order thermally driven IMT and yield the same underlying physics. The key aspect of the DHM is to explicitly incorporate dimerization into the Hamiltonian, thus merging structural effects of the monoclinic state with a correlation-driven IMT. The success of the DHM in explaining our experiments support the conclusion made by others10,52,53 that VO2 is neither purely a Mott nor a Peierls insulator, but a hybrid of the two. This interpretation could have profound effects on the understanding of the IMT in related materials such as V2O3, which also display gradual change of the insulating or metallic state response through the transition54.
Methods
THz near-field imaging
We use commercially available LT-GaAs photoconductive antennas (PCAs, Neaspec GmbH)55,56 as the THz emitter and detector to form a time-domain spectrometer (TDS)57,58,59 based off of a commercially available system (TeraView Ltd.). The PCA emits a broadband pulse with frequencies from 0.1 to 3 THz. We couple that pulse onto a metallic AFM tip (Rocky Mountain Nanotechnology, LLC) whose length is engineered so as to form an antenna resonance with the peak wavelength of the incoming THz pulse. The resonant tip enhances the field at the apex of the tip and increases tip–sample interaction60. Our AFM is home-built and incorporates a commercial piezoelectric scanning stage (Attocube Systems). THz light is scattered by the tip into the far field, where it is collected and focused onto the detector PCA. Only frequencies up to 2 THz are efficiently scattered by the tip, limiting the bandwidth of the near-field signal to slightly less than that of the PCA. Detection is identical to conventional THz-TDS, except that the detected THz signal is demodulated at higher order harmonics of the tapping frequency of the tip in order to isolate the near-field component of the scattered light61. We measure the scattered amplitude of the peak of the THz pulse, corresponding to a frequency-integrated response over the full bandwidth. We show a typical tip-scattered THz pulse in Fig. 1c and the corresponding spectra in Fig. 1d collected over gold and demodulated at the first, second, and third harmonic of the tip tapping frequency. For comparison we also show the far-field (S0) THz pulse and spectrum.
VO2 film growth
The VO2 thin films were fabricated on r-cut Al2O3 substrates by a pulsed laser-deposition method with a 248 nm KrF excimer laser. Prior to the deposition, the chamber was evacuated to a background pressure of ~10−6 Torr and the substrate was heated up to 600 °C. To grow the VO2 film, a metallic vanadium target was ablated in an oxygen atmosphere at a partial pressure of 30 mTorr. A 30 min deposition process, at the laser pulse energy of 300 mJ and a repetition rate of 10 Hz, yields ~100 nm thick VO2 films. Au pads were fabricated on the top of the films, using standard photolithography processes and e-beam evaporation.
DMFT calculations of the dimer Hubbard model
The theoretical calculations were done on a DHM solved within cluster-dynamical mean-field theory (C-DMFT). This model consists of dimers on each unit cell with intra-dimer hopping, in addition to the standard inter-dimer hopping and a Hubbard-type local Coulomb repulsion. The model Hamiltonian is given by
where \(\left\langle {i,j} \right\rangle\) denotes nearest-neighbor sites, α = {1, 2} denote the dimer orbitals, σ is the spin, t is the inter-dimer (lattice) hopping amplitude, t⊥ is the intra-dimer hopping amplitude, and U is the Coulomb repulsion. The DHM was recently shown to capture a thermally driven insulator-to-metal transition for parameters relevant to VO228. It also provides a consistent description of the near-field optical conductivity data across the IMT in that compound.
The model is defined on a semi-circular non-interacting DOS, which is realized on a Bethe lattice62. The bandwidth of the model is W = 2D = 4t. The qualitative behavior of the model is not strongly affected by the specific type of lattice adopted. The C-DMFT equations are solved within the iterated perturbation theory (IPT) approximation. At half filling, this approximation is excellent28,42. It was found to be asymptotically exact in many cases, including the weak interacting limit (U → 0) and in the atomic limit (t → 0) for all values of the inter-dimer hopping t⊥.
We have extensively benchmarked the approximation against exact but more numerically costly quantum Monte Carlo (QMC) calculations. The IPT approximation is found to capture all qualitative features seen in QMC such as a first-order transition and coexistence of solutions for smaller t⊥ and a continuous transition at higher t⊥. They also show a similar crossover at higher T, and comparison of Green’s functions on the Matsubara axis show very similar behavior. The differences between IPT and QMC solutions of the DHM are similar to the differences of the two methods in the well-studied one band model. Namely, the IPT and QMC solutions differ by about a factor of 2 in the value of the upper finite temperature tip of the coexistence region28, and the coexistence region appears somewhat wider within the IPT approximation. Nevertheless, these differences are merely quantitative. Therefore IPT is a very useful approximation for the present study, which remains qualitative or semi-quantitative at most.
Key for our present study, we have implemented a novel finite temperature and real frequency impurity solver, which avoids the technical difficulties of analytic continuation. This allows us to obtain the detailed evolution of the entire DOS with temperature with unprecedented precision.
Lightning-rod model calculations of near-field signals
For modeling of our near-field data we employed the LR model of probe-sample near-field interaction41. The Fresnel reflection coefficient rp of the sample for light polarized parallel to the tip axis determines the near-field signal and is evaluated for a VO2 single crystal. By formulating the quasi-electrostatic near-field interaction as a scattering problem in momentum space, the LR model generally provides excellent quantitative agreement with near-field spectroscopy measurements at very low computational cost41. Experimental details, such as scattering of light from the probe to the detector and demodulation of the detected signal, are included explicitly in the model. Input parameters include the tip radius a and tapping amplitude A, as well as the overall probe geometry, modeled here as a metallic cone 19 μm in height with half-angle ≈30°, in qualitative accordance with the geometry of commercial probes used for this study. Best results were obtained with a = 100 nm and A = 200 nm, which agree well with nominal experimental values of a ≈ 140 nm and A ≈ 250 nm.
Code availability
The packages used for calculating DMFT solutions are available from M.R. upon reasonable request. The packages used for calculating the lightning-rod model of the near-field signal are available from the corresponding author upon reasonable request.
Data availability
The data supporting the findings of this work are available from the corresponding author upon reasonable request.
References
Morin, F. Oxides which show a metal-to-insulator transition at the Néel temperature. Phys. Rev. Lett. 3, 34–36 (1959).
Goodenough, J. B. The two components of the crystallographic transition in VO2. J. Solid State Chem. 3, 490–500 (1971).
Eden, D. Some applications involving the semiconductor-to-metal phase transition in VO2. Proc. Soc. Photo-Opt. Instrum. Eng. 185, 97–102 (1979).
Chain, E. E. Optical properties of vanadium dioxide and vanadium pentoxide thin films. Appl. Opt. 30, 2782–2787 (1991).
Yang, Z., Ko, C. & Ramanathan, S. Oxide electronics utilizing ultrafast metal–insulator transitions. Annu. Rev. Mater. Res. 41, 337–367 (2011).
Imada, M., Fujimori, A. & Tokura, Y. Metal–insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998).
Wentzcovitch, R. M., Schulz, W. W. & Allen, P. B. VO2: Peierls or Mott–Hubbard? A view from band theory. Phys. Rev. Lett. 72, 3389–3392 (1994).
Rice, T., Launois, H. & Pouget, J. Comment on “VO2 Peierls or Mott–Hubbard? A view from band theory”. Phys. Rev. Lett. 73, 3042 (1994).
Cavalleri, A., Dekorsy, T., Chong, H. H., Kieffer, J.-C. & Schoenlein, R. W. Evidence for a structurally-driven insulator-to-metal transition in VO2: a view from the ultrafast timescale. Phys. Rev. B 70, 161102 (2004).
Biermann, S., Poteryaev, A., Lichtenstein, A. & Georges, A. Dynamical singlets and correlation-assisted Peierls transition in VO2. Phys. Rev. Lett. 94, 026404 (2005).
Koethe, T. et al. Transfer of spectral weight and symmetry across the metal–insulator transition in VO2. Phys. Rev. Lett. 97, 116402 (2006).
Kim, H.-T. et al. Monoclinic and correlated metal phase in VO2 as evidence of the Mott transition: coherent phonon analysis. Phys. Rev. Lett. 97, 266401 (2006).
Arcangeletti, E. et al. Evidence of a pressure-induced metallization process in monoclinic VO2. Phys. Rev. Lett. 98, 196406 (2007).
Dagotto, E. Complexity in strongly correlated electronic systems. Science 309, 257–262 (2005).
Basov, D. N., Averitt, R. D., Van Der Marel, D., Dressel, M. & Haule, K. Electrodynamics of correlated electron materials. Rev. Mod. Phys. 83, 471–541 (2011).
Jepsen, P. U. et al. Metal–insulator phase transition in a VO2 thin film observed with terahertz spectroscopy. Phys. Rev. B 74, 205103 (2006).
Qazilbash, M. et al. Correlated metallic state of vanadium dioxide. Phys. Rev. B 74, 205118 (2006).
Pohl, D. W., Denk, W. & Lanz, M. Optical stethoscopy: Image recording with resolution λ/20. Appl. Phys. Lett. 44, 651–653 (1984).
Denk, W. & Pohl, D. W. Near-field optics: microscopy with nanometer-size fields. J. Vac. Sci. Technol. B: Microelectron. Nanometer Struct. Process. Meas. Phenom. 9, 510–513 (1991).
Cvitkovic, A., Ocelic, N. & Hillenbrand, R. Material-specific infrared recognition of single sub-10 nm particles by substrate-enhanced scattering-type near-field microscopy. Nano Lett. 7, 3177–3181 (2007).
Amarie, S., Ganz, T. & Keilmann, F. Mid-infrared near-field spectroscopy. Opt. Express 17, 21794–21801 (2009).
Novotny, L. & Hecht, B. Principles of Nano-optics. (Cambridge University Press, NY, 2006; 188–194.
Atkin, J. M., Berweger, S., Jones, A. C. & Raschke, M. B. Nano-optical imaging and spectroscopy of order, phases, and domains in complex solids. Adv. Phys. 61, 745–842 (2012).
Qazilbash, M. M. et al. Mott transition in VO2 revealed by infrared spectroscopy and nano-imaging. Science 318, 1750–1753 (2007).
Jones, A. C., Berweger, S., Wei, J., Cobden, D. & Raschke, M. B. Nano-optical investigations of the metal–insulator phase behavior of individual VO2 microcrystals. Nano Lett. 10, 1574–1581 (2010).
Liu, M. et al. Anisotropic electronic state via spontaneous phase separation in strained vanadium dioxide films. Phys. Rev. Lett. 111, 096602 (2013).
Abreu, E. et al. Ultrafast electron-lattice coupling dynamics in VO2 and V2O3 thin films. Phys. Rev. B 96, 094309 (2017).
Nájera, O., Civelli, M., Dobrosavljević, V. & Rozenberg, M. Resolving the VO2 controversy: Mott mechanism dominates the insulator-to-metal transition. Phys. Rev. B 95, 035113 (2017).
Von Ribbeck, H.-G. et al. Spectroscopic THz near-field microscope. Opt. Express 16, 3430–3438 (2008).
Moon, K. et al. Quantitative coherent scattering spectra in apertureless terahertz pulse near-field microscopes. Appl. Phys. Lett. 101, 011109 (2012).
Böhmler, M., Huber, A. & Eisele, M. THz nano-spectroscopy with 25 nm spatial and 10 fs time resolution. In Proc. 41st International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz) 1–2 (IEEE, 2016).
Sternbach, A. et al. Artifact free time resolved near-field spectroscopy. Opt. Express 25, 28589–28611 (2017).
Kotliar, G., Lange, E. & Rozenberg, M. Landau theory of the finite temperature Mott transition. Phys. Rev. Lett. 84, 5180–5183 (2000).
Berglund, C. & Guggenheim, H. Electronic properties of VO2 near the semiconductor–metal transition. Phys. Rev. 185, 1022–1033 (1969).
Jamei, R., Kivelson, S. & Spivak, B. Universal aspects of Coulomb-frustrated phase separation. Phys. Rev. Lett. 94, 056805 (2005).
Spivak, B. & Kivelson, S. A. Transport in two dimensional electronic micro-emulsions. Ann. Phys. 321, 2071–2115 (2006).
Qazilbash, M. et al. Infrared spectroscopy and nano-imaging of the insulator-to-metal transition in vanadium dioxide. Phys. Rev. B 79, 075107 (2009).
Cocker, T. et al. Terahertz conductivity of the metal–insulator transition in a nanogranular VO2 film. Appl. Phys. Lett. 97, 221905 (2010).
Hilton, D. et al. Enhanced photosusceptibility near T c for the light-induced insulator-to-metal phase transition in vanadium dioxide. Phys. Rev. Lett. 99, 226401 (2007).
Tselev, A. et al. Interplay between ferroelastic and metal–insulator phase transitions in strained quasi-two-dimensional VO2 nanoplatelets. Nano Lett. 10, 2003–2011 (2010).
McLeod, A. S. et al. Model for quantitative tip-enhanced spectroscopy and the extraction of nanoscale-resolved optical constants. Phys. Rev. B 90, 085136 (2014).
Najera, O. & Rozenberg, M. Multiple crossovers and coherent states in a Mott–Peierls insulator. Phys. Rev. B 97, 045108 (2018).
Degiorgi, L. The electrodynamic response of heavy-electron compounds. Rev. Mod. Phys. 71, 687–734 (1999).
Rozenberg, M., Kotliar, G. & Kajueter, H. Transfer of spectral weight in spectroscopies of correlated electron systems. Phys. Rev. B 54, 8452–8468 (1996).
Kim, H. T. et al. Micrometer diffraction study of VO2 films: separation between metal–insulator transition and structural transition. Phys. Rev. B 77, 235401 (2008).
Yao, T. et al. Understanding the nature of the kinetic process in a VO2 metal–insulator transition. Phys. Rev. Lett. 105, 226405 (2010).
Tao, Z. et al. Decoupling of structural and electronic phase transition in VO2. Phys. Rev. Lett. 109, 166406 (2012).
Kumar, S. et al. Sequential electronic and structural transitions in VO2 observed using X-ray absorption spectromicroscopy. Adv. Mater. 26, 7505–7509 (2014).
Laverock, J. et al. Direct observation of decoupled structural and electronic transition and an ambient pressure monocliniclike metallic phase of VO2. Phys. Rev. Lett. 113, 216402 (2014).
Morrison, V. et al. A photoinduced metal-like phase of monoclinic VO2 revealed by ultrafast electron diffraction. Science 346, 445–448 (2014).
Ladd, L. A. & Paul, W. Optical and transport properties of high quality crystals of V2O4 near the metallic transition temperature. Solid State Commun. 7, 425–428 (1969).
Liu, W.-T. et al. Intrinsic optical properties of vanadium dioxide near the insulator–metal transition. Nano Lett. 11, 466–470 (2010).
Tomczak, J. M., Aryasetiawan, F. & Biermann, S. Effective band structure in the insulating phase versus strong dynamical correlations in metallic VO2. Phys. Rev. B 78, 115103 (2008).
Mcleod, A. et al. Nanotextured phase coexistence in the correlated insulator V2O3. Nat. Phys. 13, 80–86 (2017).
Auston, D., Cheung, K. & Smith, P. Picosecond photoconducting hertzian dipoles. Appl. Phys. Lett. 45, 284–286 (1984).
Fattinger, C. & Grischkowsky, D. Point source terahertz optics. Appl. Phys. Lett. 53, 1480–1482 (1988).
Grischkowsky, D., Keiding, S., Van Exter, M. & Fattinger, C. Far-infrared time-domain spectroscopy with terahertz beams of dielectrics and semiconductors. J. Opt. Soc. Am. B 7, 2006–2015 (1990).
Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 1, 97–105 (2007).
Jepsen, P. U., Cooke, D. G. & Koch, M. Terahertz spectroscopy and imaging-modern techniques and applications. Laser Photonics Rev. 5, 124–166 (2011).
Huth, F. et al. Resonant antenna probes for tip-enhanced infrared near-field microscopy. Nano Lett. 13, 1065–1072 (2013).
Hillenbrand, R., Knoll, B. & Keilmann, F. Pure optical contrast in scattering-type scanning near-field microscopy. J. Microsc. 202, 77–83 (2001).
Moeller, G., Dobrosavljević, V. & Ruckenstein, A. E. RKKY interactions and the Mott transition. Phys. Rev. B 59, 6846–6854 (1999).
Acknowledgements
We acknowledge the valuable discussions about optical design and principles of operation for customized terahertz instruments with Dr. Ian Gregory of TeraView Limited, Cambridge. Research at ETRI is supported by a principal project (18ZB1320). Work at UC-San Diego and Columbia University is supported by ARO-W911nf-17-1-0543. D.N.B. is the Gordon and Betty Moore Foundation’s EPiQS Initiative investigator, Grant GBMF4533. The development of THz nano-imaging is supported by ONR-DURIP: N00014-18-1-2737. The development of the cryogenic scanner and rapid sample exchange is supported by DE-SC-0012375 and DE-SC0018218. M.R. acknowledges the support by public grants from the French National Research Agency (ANR), project LACUNES No. ANR-13-BS04-0006-01, and the French–US Associated International Laboratory on Nanoelectronics funded by CNRS.
Author information
Authors and Affiliations
Contributions
D.N.B., H.T.S., A.S., T.V.S. and H.T.K. conceived the experiment. H.T.S. performed the THz near-field imaging experiments. H.T.S. and A.S. performed the MIR near-field imaging experiments. H.T.S., R.J., A.S.M., A.M. and L.A. contributed to the design and construction of the THz near-field microscope. T.V.S. and H.T.K. grew the VO2 samples. O.N. and M.R. conducted the DMFT studies on the dimer Hubbard model. All authors prepared the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stinson, H.T., Sternbach, A., Najera, O. et al. Imaging the nanoscale phase separation in vanadium dioxide thin films at terahertz frequencies. Nat Commun 9, 3604 (2018). https://doi.org/10.1038/s41467-018-05998-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05998-5
This article is cited by
-
Two-dimensional heavy fermions in the van der Waals metal CeSiI
Nature (2024)
-
Visualizing heterogeneous dipole fields by terahertz light coupling in individual nano-junctions
Communications Physics (2023)
-
Nanoscale-Resolved Spatial Mapping of Tip-Mediated Terahertz Emission from Semiconductors
Journal of Infrared, Millimeter, and Terahertz Waves (2023)
-
Infrared nano-imaging of Dirac magnetoexcitons in graphene
Nature Nanotechnology (2023)
-
Terahertz Measurements on Subwavelength-Size Samples Down to the Tunneling Limit
Journal of Infrared, Millimeter, and Terahertz Waves (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.