Abstract
Monolayer transition metal dichalcogenides have strong Coulomb-mediated many-body interactions. Theoretical studies have predicted the existence of numerous multi-particle excitonic states. Two-particle excitons and three-particle trions have been identified by their optical signatures. However, more complex states such as biexcitons have been elusive due to limited spectral quality of the optical emission. Here, we report direct evidence of two biexciton complexes in monolayer tungsten diselenide: the four-particle neutral biexciton and the five-particle negatively charged biexciton. We distinguish these states by power-dependent photoluminescence and demonstrate full electrical switching between them. We determine the band states of the elementary particles comprising the biexcitons through magneto-optical spectroscopy. We also resolve a splitting of 2.5 meV for the neutral biexciton, which we attribute to the fine structure, providing reference for subsequent studies. Our results unveil the nature of multi-exciton complexes in transitionmetal dichalcogenides and offer direct routes towards deterministic control in many-body quantum phenomena.
Similar content being viewed by others
Introduction
In monolayer (1L) transitionmetal dichalcogenides (TMDs), the three-atom thickness of the material reduces the dielectric screening with respect to their bulk counterparts1,2. As a result of this and of their large effective mass, excitons (quasi-particle states formed of electrons and holes via Coulomb interaction) have binding energies of hundreds of meV1,2 and are stable at room temperature. The physics of light–matter interaction is also enriched by two inequivalent valleys having opposite spin-locked valley indices3 at the K points of the Brillouin zone, in which radiative recombination generates photons carrying opposite angular momenta4,5. These properties motivated the exploration of exciton and polariton6 condensation7,8 and superfluidity9, and the exploitation of the spin and valley degrees of freedom as means to carry and manipulate information in quantum optoelectronic devices3,10. In the limit of quantum-confined excitons, the presence of localised single-photon emitters that can be induced deterministically11,12 and generated by electroluminescence13, makes TMDs a promising platform for the field of quantum photonics. Contrary to the exciton14,15 and trion16,17 states, optical studies of biexciton complexes18,19 in 1L-TMDs have been challenging20,21,22,23,24,25,26: inhomogeneous broadening27 and defect bands28 have limited their unambiguous identification and control. As a consequence, previous experimental findings20,21,22,23,25,26 assigned neutral biexcitons a larger binding energy than trions, in contrast to theoretical predictions29,30,31,32,33, whereas ref. 24 observed a peak in 1L-molybdenum diselenide (MoSe2) in the expected energy range, which they labelled as the neutral biexciton.
Here, we use continuous wave photoluminescence (PL) measurements at cryogenic temperature combined with electrical gating and magnetic field to identify the four-particle neutral biexciton (XX0) and the five-particle negatively charged biexciton, the quinton29 (XX−) in 1L-tungsten diselenide (WSe2). We also observe a splitting in XX0, which we attribute to its fine structure. Our results demonstrate tuneable access to multi-exciton complexes in TMDs and provide new ways to study and control multi-exciton phenomena.
Results
Design and optical characterisation of heterostructures
We use recent advances in material and device processing27,34 to suppress the effects that degrade the optical quality of 1L-WSe2. To reduce the PL spectral linewidths27 we place a layered material heterostructure (LMH) formed of 1L-WSe2 encapsulated between two flakes of multilayer hexagonal boron nitride (ML-hBN) on a Si/SiO2 substrate. To suppress the effect of SiO2 charge traps we place a few-layer graphene (FLG) crystal below the bottom ML-hBN. The inset of Fig. 1a shows a schematic of the LMH (see Methods, and Supplementary Notes 1 and 2 for sample preparation and characterisation).
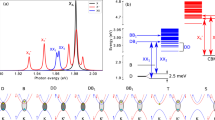
PL spectrum and power dependence of encapsulated 1L-WSe2 at 4 K. a PL spectrum (black curve, linear scale) of encapsulated 1L-WSe2. Excitation wavelength: 658 nm. The top part of the figure lists the calculated spectral locations of X0 (grey), XX0 (red) and XX− (blue) in the presence of a screening environment. b Double logarithmic plot of PL intensity as a function of excitation power for X0 (black filled circles), XX0 (red filled circles) and XX−(blue filled circles). The solid curves represent I ∝ Pα for a quadratic (α = 2, red) and linear (α = 1, black) behaviour. The dashed blue curve is a fit to PL intensity, yielding an α of 1.55. For clarity of display, we multiply XX0 by 4 and X0 by 0.4
We illuminate the LMH with continuous laser excitation at 658 nm and collect its optical emission at 4 K (see Methods for further details on the optical measurements): Fig. 1a is a representative PL spectrum. Consistent with previous reports, we identify the bright neutral exciton10, X0, at ~1.728 eV (width ~5 meV), the negatively charged intervalley trion35, X−inter, at ~1.699 eV, the negatively charged intravalley trion35, X−intra, at ~1.692 eV, and the dark neutral exciton36,37, X0dark, at ~1.685 eV. Here, bright refers to excitons with in-plane dipole and spin-allowed radiative recombination2,36,37, whereas dark refers to excitons with out-of-plane dipole and spin-forbidden radiative recombination2,36,37, for which emission only occurs in plane but is captured partially by our high numerical aperture objective. The peak at ~1.711 eV, ~4 meV wide, is a good candidate for XX0, as it appears in the theoretically predicted energy range29,30,31,32. The peak at ~1.679 eV, ~6 meV wide, was previously labelled as neutral biexciton emission20, although it appears in the energy range predicted29,31 for XX−. In the top part of Fig. 1a, we include the emission energies of single- and multi-exciton species in ML-WSe2 calculated via diffusion Quantum Monte Carlo29 combined with environment screening (See Methods for details).
Unveiling the presence and nature of biexcitons
Figure 1b displays the PL intensity I, defined as peak area, as a function of excitation power P (with I ∝ Pα) for X0 (filled black circles), XX0 (filled red circles) and XX− (filled blue circles). For reference, we plot solid curves corresponding to a linear (α = 1, black) and quadratic (α = 2, red) behaviour. We expect superlinear behaviour for biexcitons reaching α = 2 in thermodynamic equilibrium18,19. The power dependence of XX0 follows the quadratic curve, while that of XX−is superlinear with fitted α ~ 1.55 ± 0.03 (dashed blue curve). Both trends of XX0 and XX−are therefore consistent with a biexcitonic origin and contrast the linear behaviour of X0. The deviation of XX− from α = 2 possibly stems from the competition of electron capture from other optically induced excitons. Remaining peaks of Fig. 1a follow an approximately linear power dependence.
To differentiate the charged and neutral biexciton XX0 and XX−, we fabricate a charge-tuneable device starting from a new LMH analogous to the first one but with the addition of one electrode to the FLG and of a second electrode to an uncovered 1L-WSe2 portion (see Methods). Figure 2a, b shows the schematic and the optical image of the device, respectively. Figure 2c displays how the PL spectrum is modified as a function of voltage V. The charging regime modifies the optical signatures of 1L-WSe2 strongly. The presence of X0 and X0dark at V ~ 0 V shows that the material has a negligible intrinsic charge doping. At the same bias, Fig. 2c also shows emission from XX0. In the electron-charged regime (V > 0) fluorescence from X0, XX0 and X0dark vanishes, while emission from X−inter, X−intra and XX−arises. Around 2 V the X− emission switches to a new peak at ~1.681 eV, likely the next charging state of the trion, X−−. This peak was previously assigned to the fine structure of X− in experiments on bare material10. Negative bias is the hole-charged regime, where only X0 and the positively charged trion X+ are visible (refs. 10,35). The voltage-dependence of our PL measurements thus clarifies the difference between the two biexciton species: the presence of XX0 only at charge neutrality confirms this is the charge-neutral biexciton, and the appearance of XX− only in the electron-charged regime proves it to be the negatively charged biexciton.
Charge dependence of PL. a Schematic and b optical image of the charge-tuneable device. The red dashed frame highlights the 1L-WSe2 flake. The scale bar is 5 μm. c Circular co-polarised PL intensity (Iσ+/σ+ + Iσ-/σ-) as a function of applied bias. The dashed lines are a guide to the eye to highlight each peak. d DoP of PL as a function of bias and energy in the same range as (c). The colour code is such that blue regions indicate co-polarisation, whereas the red regions indicate counter-polarisation with respect to excitation polarisation
We then analyse the correlation between excitation and emission polarisations in the different charging regimes (Fig. 2d). We plot the degree of circular polarisation [DoP = (Ico.- Icross.) / (Ico. + Icross.)4] where Ico. (Icross.) is the intensity of the circularly polarised light with the same (opposite) helicity in the excitation and detection paths. We refer to the two orthogonal helicities as σ− and σ+. At 0 V, XX0 has DoP > 80%, while X0dark shows no circular polarisation36,37, as expected. At 0.8 V, X−inter has DoP > 90%, X−intra has DoP < 10% and XX− has DoP ~ 55%. The circular polarisation of photons from both XX0 and XX− thus implies that dissociation occurs with the recombination of a bright exciton, as a dark exciton would emit linearly polarised light36,37. The DoP of XX− is close to the average of the DoP of X−inter and X−intra, suggesting that the recombination mechanisms of both X−inter and X−intra contribute38 to that of XX−.
Behaviour of exciton complexes in magnetic field
The electrons and holes comprising the biexcitons can occupy multiple combinations of band states. To identify them, we resort to the variation of PL as a function of an out-of-plane magnetic field. Figure 3a shows the σ− polarised PL of X0 and XX0 under co-polarised (σ−) excitation. We resolve a finite splitting in the XX0 emission, with a separation of 2.5 meV between the two peaks labelled XX01 and XX02 (line-cut spectra at different magnetic fields are shown in Supplementary Fig. 3). Figure 3b shows the σ+ polarised PL of X0 and XX0 under cross-polarised (σ−) excitation. Here, only XX02 remains visible, revealing a different DoP for XX01 and XX02, in analogy to the different DoP between X−inter and X−intra.
Magnetic field dependence of PL. a Magnetic field dependent PL of X0 and XX0 in circular co-polarised and b cross-polarised configurations, for σ− excitation. The fine-structure lines are indicated as XX01 and XX02. The emission of XX0 brightens with increasing emission energy. X0 is displayed for reference. c Magnetic field dependent PL of XX− in a circular co-polarised configuration, for σ− excitation. In a, b and c the colour scale is linear. d Zeeman shift in the PL spectrum of X0 (filled black circles), XX0 (filled red and pink circles for the two components of the fine-structure) and XX− (filled blue circles). The double arrow is a scale bar of 2.5 meV. e PL intensity ratio of circular co-polarisation with opposite helicity I(σ-/σ-)/I(σ+/σ+) for X0, XX01 + XX02 and XX− as a function of magnetic field
The energy of the splitting excludes one of the peaks to be a phonon replica, and the two peaks reveal different DoP, thus we assign this doublet to fine structure introduced by exchange interaction, in analogy to the case of the splitting between X−inter and X−intra39. This experimental observation of the XX0 fine structure will set a reference for further computational studies, which otherwise suffer from limitations due to the complex treatment of the exchange interaction. Additionally, the PL intensity of XX0 emission increases when it shifts to higher energies, in contrast to that of X0. We observe the same behaviour for XX− in Fig. 3c, where the co-polarised PL from the recombination of the quasi-particle also shows valley-dependent Zeeman shift.
In Fig. 3d we plot the energies of X0, XX01, XX02 and XX− as a function of magnetic field. For each multi-exciton species, we calculate the Landé factor g, defined as ΔE = gμBB, where ΔE = Eσ+−Eσ− is the difference in the emission energy of excitons in opposite valleys, μB = eħ/2me = 58 μeV T−1 is the Bohr magneton and B is the magnetic field. We derive g ~ -4.44 ± 0.12 for X0 consistent with previous observations40, ~ -4.10 ± 0.15 for XX0 and ~ -3.86 ± 0.17 for XX−. We note that these values do not represent the total g factor of the multi-particle states, but rather belong to their optically active components.
The emission intensities of XX0 and XX− change dramatically with magnetic field, being stronger when shifted to higher energy. Figure 3e displays the Iσ-/σ-/Iσ+/σ+ ratio as a function of magnetic field for XX01 + XX02 and XX−. For comparison, we also include Iσ-/σ-/Iσ+/σ+ for X0. At zero magnetic field Iσ-/σ-/Iσ+/σ+ is ~1 for all peaks, i.e., the two valleys have the same exciton population. When magnetic field is applied, Iσ-/σ-/Iσ+/σ+ remains unaffected for X0. This can be explained by X0 in each valley recombining before reaching thermal equilibrium. In stark contrast, XX0 and XX− display strongly anti-symmetric magnetic-field dependence: for increasing magnetic field, the lower-energy transition is weaker.
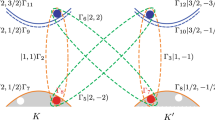
We can understand the complex behaviour of the magnetic-field dependent PL through the single-particle picture of the energy bands. Figure 4a, b, c illustrates the effect of B > 0 on the band structure of 1L-WSe2 around the K and K′ points, considering the contribution of the spin, valley and atomic orbital magnetic moments. The 1L-WSe2 bandgap decreases (increases) in the K (K′) valley as the energies of both hole and electron experience the same spin upshift (downshift), while the hole experiences a larger orbital upshift (downshift)40,41 with respect to the electron. Further, the contribution from the valley magnetic moment results in an additional upshift (downshift) of all bands in the K (K′) valley40. The applied magnetic field induces unequal bright exciton populations in the two valleys (Fig. 3e). This excludes the possibility that XX0 (Fig. 4a, b) may be formed by two bright or two dark excitons, as both cases would result in equally intense radiative recombination from both K and K′ at all magnetic fields. XX0 is therefore a combination of a bright and a dark exciton. Under positive magnetic field, the bright exciton component of XX0 occupies the higher-radiative energy transition in the K′ valley (Fig. 3a, b, e) due to thermalisation of the photogenerated electrons. We expect this to be allowed by a longer lifetime of XX0 compared to X0, in analogy to XX−, where the lifetime was measured to be ~2–100 times longer than single excitons20,25, and also exhibiting similar polarisation properties. In parallel, the electron of the dark component of XX0 can be either in the opposite (Fig. 4a) or in the same (Fig. 4b) valley as the bright exciton component, yielding an energy shift between these two configurations, which is the origin of the fine-structure of XX0 observed in Fig. 3d.
Composition of biexciton species with applied magnetic field. a, b, c Single-particle picture of the internal structure of (a, b) XX0 and (c) XX− for B > 0. The eigenstates shift inequivalently in K and K′ (dashed curves indicate no magnetic field, solid curves indicate applied magnetic field, red and blue colours indicate opposite spin). XX0 comprises a bright exciton with highest radiative energy and a dark exciton with the electron (a) inter- or (b) intra-valley with the bright exciton. d Many-body picture of the magnetic field effect on XX0, comprising a bright and a dark exciton. Applying a magnetic field shifts the energy of the dark exciton more than that of XX0 due to the higher g of the former. This results in the dissociation of the biexciton in the form XX0 → X0dark + γ(σ−), where γ(σ−) is a photon with σ− helicity
Figure 4c illustrates the single-particle configuration of XX−. As for XX0, the combination of two bright excitons is excluded due to different recombination intensities in K and K′. From the similar g of XX0 and XX−, we can understand this five-particle complex as a bound state of a bright exciton with a dark trion, or a bright trion with a dark exciton. Both configurations would show inequivalent valley population as for XX0 in Fig. 3e.
Figure 4d is a qualitative many-body picture for XX0 formed by a bright and a dark exciton component in opposite valleys under magnetic field. As its total Zeeman splitting depends on both the bright and the dark component, XX0 splits with a reversed energy order compared to its bright exciton component and dissociates into a dark exciton and a photon due to the dark exciton having larger g than X0 with opposite sign42. The distribution of biexciton states follows the case near thermal equilibrium, which is the reason behind the inequivalent circularly co-polarised emission intensity under σ+ or σ−, as shown in Fig. 3.
Discussion
We have discovered the quinton, the five-particle negatively charged biexciton in 1L-WSe2, unambiguously, as well as the neutral biexciton and its fine structure. Immediate next steps include the unequivocal verification of the X−− state and the identification of bound states within the lower-energy peaks. A complete understanding of multi-exciton complexes is key to study coherent many-body phenomena, such as condensation7,8 and superfluidity9. Further, the ability to access and manipulate biexciton complexes in TMD-based heterostructures offers new routes towards probing other fundamental excitations in this system and the interplay between free and localised excitons. Extending our findings to the quantum confined regime will open new capabilities for cascaded emission of entangled photons and spin-multiphoton interfaces.
Methods
Sample fabrication and room-temperature characterisation
Bulk WSe2 crystals are prepared by the flux zone growth method (see Supplementary Note 1). Bulk hBN crystals are grown by the temperature-gradient method under high pressure and high temperature. Graphite is sourced from NGS Naturgrafit. All bulk crystals are exfoliated by micromechanical cleavage43 on Si/SiO2 (oxide thickness 285 nm). 1L- and FL-samples are identified by optical contrast44. Selected crystals are assembled within ~5 h into LMHs via dry-transfer13,34. The LMH sample used for power-dependent and magnetic field-dependent PL measurements is formed, from top to bottom, of ML-hBN flakes (~5 nm thick as determined by optical contrast), 1L-WSe2, and a second ML-hBN flake (~10 nm thick as determined by optical contrast) and FLG (~5 layers thick as determined by optical contrast). That used for voltage-dependent measurements is prepared in a similar way, but the top ML-hBN does not fully cover the 1L-WSe2 to allow for Cr/Au (5/50 nm) electrodes to directly contact it. The second electrode contacts FLG. The electrodes are patterned by e-beam lithography followed by lift-off. The ML-hBN thickness is chosen to isolate the 1L-WSe2 from the environment, smoothen the roughness of SiO2, shield the charge-traps of the substrate and avoid tunnelling between FLG and 1L-WSe2, while not compromising the optical contrast under the optical microscope. Raman spectroscopy (Supplementary Fig. 1) and PL (Supplementary Fig. 2) are performed on the bulk crystals and after the assembly of LMH to characterise the starting material and confirm the 1L-WSe2 thickness45,46,47. Raman and PL spectra are acquired at room temperature using a Horiba LabRam Evolution (spectral resolution ~0.3 cm−1) at 514.5 nm. See Supplementary Note 2 for details on the room-temperature optical characterisation.
Optical measurements at 4 K
Power dependent and gate-controlled measurements are performed in a variable-temperature Helium flow cryostat (Oxford Instruments Microstat HiRes2) with a home-built confocal microscope at a nominal temperature of 4.2 K. The magneto-optical measurements are performed in a close-cycle bath cryostat (Attocube Attodry 1000) equipped with a superconducting magnet (maximum out-of-plane magnetic field 8 T) at a nominal sample temperature of 3.8 K. In the main text we refer to measurements at 4 K as an average of these two nominal temperatures.
Theoretical calculations
We use Mott–Wannier model and quantum Monte Carlo (QMC) as implemented in CASINO48 to calculate the energies of X0, XX0 and XX−in ML-WSe229. The full photoemission spectra of ML-WSe2 in vacuum are reported in ref. 29. To consider the effect of the dielectric screening provided by hBN, we use the experimental value of the binding energy of XX0 and use Eq. (48) of ref. 29 to derive the screening parameter r* which is 54 Å. We use the many-body GW electron and hole effective masses as 0.29m0 and 0.34m049, respectively, where m0 is the bare electron mass. We calculate the binding energy of XX− by subtracting the total energy of the exciton and trion from the total energy of XX−.
Data availability
The datasets generated and analysed during the current study are available from the corresponding author on reasonable request.
References
Chernikov, A. et al. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2. Phys. Rev. Lett. 113, 076802 (2014).
Wang, G. et al. Colloquium: excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Xiao, D., Liu, G.-B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other Group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 7, 494–498 (2012).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotechnol. 7, 490–493 (2012).
Sidler, M. et al. Fermi polaron-polaritons in charge-tunable atomically thin semiconductors. Nat. Phys. 13, 255–261 (2017).
Kogar, A. et al. Signatures of exciton condensation in a transition metal dichalcogenide. Science 358, 1314–1317 (2017).
Cotleţ, O., Zeytinoǧlu, S., Sigrist, M., Demler, E. & Imamoǧlu, A. Superconductivity and other collective phenomena in a hybrid Bose-Fermi mixture formed by a polariton condensate and an electron system in two dimensions. Phys. Rev. B 93, 054510 (2016).
Fogler, M. M., Butov, L. V. & Novoselov, K. S. High-temperature superfluidity with indirect excitons in van der Waals heterostructures. Nat. Commun. 5, 4555 (2014).
Jones, A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol. 8, 634–638 (2013).
Palacios-Berraquero, C. et al. Large-scale quantum-emitter arrays in atomically thin semiconductors. Nat. Commun. 8, 15093 (2017).
Branny, A., Kumar, S., Proux, R. & Gerardot, B. D. Deterministic strain-induced arrays of quantum emitters in a two-dimensional semiconductor. Nat. Commun. 8, 15053 (2017).
Palacios-Berraquero, C. et al. Atomically thin quantum light-emitting diodes. Nat. Commun. 7, 12978 (2016).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano. Lett. 10, 1271–1275 (2010).
Mak, K. F. et al. Tightly bound trions in monolayer MoS2. Nat. Mater. 12, 207–211 (2013).
Ross, J. S. et al. Electrical control of neutral and charged excitons in a monolayer semiconductor. Nat. Commun. 4, 1474 (2013).
Gourley, P. L. & Wolfe, J. P. Experimental determination of equilibrium constants for excitonic systems in stressed, ultrapure silicon. Phys. Rev. B 25, 6338–6348 (1982).
Kim, J. C., Wake, D. R. & Wolfe, J. P. Thermodynamics of biexcitons in a GaAs quantum well. Phys. Rev. B 50, 15099–15107 (1994).
You, Y. et al. Observation of biexcitons in monolayer WSe2. Nat. Phys. 11, 477–481 (2015).
Dey, P. et al. Biexciton formation and exciton coherent coupling in layered GaSe. J. Chem. Phys. 142, 212422 (2015).
Plechinger Gerd et al. Identification of excitons, trions and biexcitons in single‐layer WS2. Phys. Status Solidi —RRL 9, 457–461 (2015).
Sie, E. J., Frenzel, A. J., Lee, Y.-H., Kong, J. & Gedik, N. Intervalley biexcitons and many-body effects in monolayer MoS2. Phys. Rev. B 92, 125417 (2015).
Hao, K. et al. Neutral and charged inter-valley biexcitons in monolayer MoSe2. Nat. Commun. 8, 15552 (2017).
Nagler, P. et al. Zeeman splitting and inverted polarization of biexciton emission in monolayer WS2. Preprint at http://arXiv.org/abs/1801.09255 (2018).
Paradisanos, I. et al. Room temperature observation of biexcitons in exfoliated WS2 monolayers. Appl. Phys. Lett. 110, 193102 (2017).
Cadiz, F. et al. Excitonic linewidth approaching the homogeneous limit in MoS2-Based van der Waals heterostructures. Phys. Rev. X 7, 021026 (2017).
Tongay, S. et al. Defects activated photoluminescence in two-dimensional semiconductors: interplay between bound, charged, and free excitons. Sci. Rep. 3, 2657 (2013).
Mostaani, E. et al. Diffusion quantum Monte Carlo study of excitonic complexes in two-dimensional transition-metal dichalcogenides. Phys. Rev. B 96, 075431 (2017).
Szyniszewski, M., Mostaani, E., Drummond, N. D. & Fal’ko, V. I. Binding energies of trions and biexcitons in two-dimensional semiconductors from diffusion quantum Monte Carlo calculations. Phys. Rev. B 95, 081301 (2017).
Kidd, D. W., Zhang, D. K. & Varga, K. Binding energies and structures of two-dimensional excitonic complexes in transition metal dichalcogenides. Phys. Rev. B 93, 125423 (2016).
Mayers, M. Z., Berkelbach, T. C., Hybertsen, M. S. & Reichman, D. R. Binding energies and spatial structures of small carrier complexes in monolayer transition-metal dichalcogenides via diffusion Monte Carlo. Phys. Rev. B 92, 161404 (2015).
Van der Donck, M., Zarenia, M. & Peeters, F. M. Excitons, trions, and biexcitons in transition-metal dichalcogenides: magnetic-field dependence. Phys. Rev. B 97, 195408 (2018).
Zomer, P. J., Guimarães, M. H. D., Brant, J. C., Tombros, N. & van Wees, B. J. Fast pick up technique for high quality heterostructures of bilayer graphene and hexagonal boron nitride. Appl. Phys. Lett. 105, 013101 (2014).
Courtade, E. et al. Charged excitons in monolayer WSe2: experiment and theory. Phys. Rev. B 96, 085302 (2017).
Wang, G. et al. In-plane propagation of light in transition metal dichalcogenide monolayers: optical selection rules. Phys. Rev. Lett. 119, 047401 (2017).
Zhou, Y. et al. Probing dark excitons in atomically thin semiconductors via near-field coupling to surface plasmon polaritons. Nat. Nanotechnol. 12, 856–860 (2017).
Plechinger, G. et al. Trion fine structure and coupled spin-valley dynamics in monolayer tungsten disulfide. Nat. Commun. 7, 12715 (2016).
Jones, A. M. et al. Excitonic luminescence upconversion in a two-dimensional semiconductor. Nat. Phys. 12, 323 (2016).
Aivazian, G. et al. Magnetic control of valley pseudospin in monolayer WSe2. Nat. Phys. 11, 148–152 (2015).
Srivastava, A. et al. Valley Zeeman effect in elementary optical excitations of monolayer WSe2. Nat. Phys. 11, 141–147 (2015).
Robert, C. et al. Fine structure and lifetime of dark excitons in transition metal dichalcogenide monolayers. Phys. Rev. B 96, 155423 (2017).
Novoselov, K. S. et al. Two-dimensional atomic crystals. PNAS 102, 10451–10453 (2005).
Casiraghi, C. et al. Rayleigh imaging of graphene and graphene layers. Nano. Lett. 7, 2711–2717 (2007).
Zhao, W. et al. Lattice dynamics in mono- and few-layer sheets of WS2 and WSe2. Nanoscale 5, 9677–9683 (2013).
Zhao, W. et al. Evolution of electronic structure in atomically thin sheets of WS2 and WSe2. 7, 791–797 (2012).
Terrones, H. et al. New first order raman-active modes in few layered transition metal dichalcogenides. Sci. Rep. 4, 4215 (2014).
Needs, R. J., Towler, M. D., Drummond, N. D. & Ríos, P. L. Continuum variational and diffusion quantum Monte Carlo calculations. J. Phys. Condens. Matter 22, 023201 (2010).
Shi, H., Pan, H., Zhang, Y.-W. & Yakobson, B. I. Quasiparticle band structures and optical properties of strained monolayer MoS2 and WS2. Phys. Rev. B 87, 155304 (2013).
Acknowledgements
The authors thank Bernhard Urbaszek, Neil D. Drummond, Vladimir I. Fal’ko and Ioannis Paradisanos for useful discussions. We acknowledge funding from NSF DMR-1552220, Elemental Strategy Initiative conducted by the MEXT, Japan and the CREST (JPMJCR15F3), JST, EU Graphene Flagship, ERC Grants Hetero2D and PHOENICS, EPSRC Grants EP/509K01711X/1, EP/K017144/1, EP/N010345/1, EP/M507799/ 5101, and EP/L016087/1, Marie Skłodowska-Curie Actions Spin-NANO, Grant No. 676108, Quantum Technology Hub NQIT EP/M013243/1.
Author information
Authors and Affiliations
Contributions
M.B., A.C.F. and M.A. conceived and managed the project; K.W. and T.T. provided hBN crystals; H.L., B.C. and S.T. provided WSe2 crystals; M.B., A.R.C. and D.D. fabricated and characterised the devices; M.B., A.R.-P.M., D.M.K., C.P.-B., B.P. and M.A. performed the low-temperature PL measurements and analysed the results; E.M. performed the calculations. All authors participated in the discussion of the results and the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Barbone, M., Montblanch, A.RP., Kara, D.M. et al. Charge-tuneable biexciton complexes in monolayer WSe2. Nat Commun 9, 3721 (2018). https://doi.org/10.1038/s41467-018-05632-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05632-4
This article is cited by
-
Raman scattering excitation in monolayers of semiconducting transition metal dichalcogenides
npj 2D Materials and Applications (2024)
-
Two-dimensional materials for future information technology: status and prospects
Science China Information Sciences (2024)
-
Charged biexciton polaritons sustaining strong nonlinearity in 2D semiconductor-based nanocavities
Nature Communications (2023)
-
Excitonic Complexes in Two-Dimensional Transition Metal Dichalcogenides
Nature Communications (2023)
-
Photoluminescence imaging of single photon emitters within nanoscale strain profiles in monolayer WSe2
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.