Abstract
Monolayer transition-metal dichalcogenides (TMDCs) show a wealth of exciton physics. Here, we report the existence of a new excitonic species, the high-lying exciton (HX), in single-layer WSe2 with an energy of ~3.4 eV, almost twice the band-edge A-exciton energy, with a linewidth as narrow as 5.8 meV. The HX is populated through momentum-selective optical excitation in the K-valleys and is identified in upconverted photoluminescence (UPL) in the UV spectral region. Strong electron-phonon coupling results in a cascaded phonon progression with equidistant peaks in the luminescence spectrum, resolvable to ninth order. Ab initio GW-BSE calculations with full electron-hole correlations explain HX formation and unmask the admixture of upper conduction-band states to this complex many-body excitation. These calculations suggest that the HX is comprised of electrons of negative mass. The coincidence of such high-lying excitonic species at around twice the energy of band-edge excitons rationalizes the excitonic quantum-interference phenomenon recently discovered in optical second-harmonic generation (SHG) and explains the efficient Auger-like annihilation of band-edge excitons.
Similar content being viewed by others
Introduction
Optical transitions in atoms occur between different discrete electronic states. Coherent coupling can arise between transition pathways, giving rise to quantum-interference phenomena such as electromagnetically induced transparency (EIT)1,2. Analogous multilevel systems in semiconductor quantum wells—intersubband transitions—have opened up applications in the infrared and terahertz frequency range3. Further extension of such phenomena towards the visible spectral range is desirable, particularly in semiconductors that are promising for optoelectronic applications. In a semiconductor, at sufficiently low temperatures, an electron in the conduction band and a hole in the valence band can interact with each other to form a correlated state—an exciton. In monolayer TMDCs, excitons can exhibit large optical transition strengths, giving rise to radiative lifetimes on the order of 150 fs4—over 10,000 times shorter than those of atoms. These band-edge excitons can therefore interact strongly with incident radiation5,6. Promoting excitons into states at significantly higher energies—beyond their continuum limit—involves exciting the electron into high-lying conduction bands. If such transitions in a crystal occur vertically in momentum space, high-energy excitons would contribute to a multilevel excitonic structure that could support atom-like quantum interference. The common expectation would suggest that these excitons are resonant states in the two-particle continuum that relax quickly towards the optical band gap and therefore do not have appreciable coherence time. Recently, however, clear signatures of excitonic quantum interference have been observed in monolayer WSe2 when driven by a 140 fs laser pulse7. In addition, efficient Auger-like upconversion of luminescence in monolayer WSe2 has been attributed to electronic transitions to upper conduction bands8. These experiments suggest that the optically bright band-edge exciton can couple to a discrete metastable state of approximately twice the energy, located in the same region of momentum space. More surprisingly, the coherence time of such a metastable state was inferred from the excitonic quantum-interference experiments to be as long as that of the band-edge A-exciton7,9. If correct, monolayer WSe2 would comprise a multilevel excitonic energy structure reminiscent of that of dilute atomic-gas systems1,2.
Here, we probe this HX directly by upconverted photoluminescence (UPL) in the UV and identify its origin by ab initio GW-BSE calculations. The HX appears at an energy close to twice that of the band-edge exciton and features a linewidth as narrow as 5.8 meV, consistent with a coherence time of at least 100 fs as is necessary for the observed excitonic quantum interference phenomenon7,10. Such an exciton appears particularly unexpected when the independent-particle picture of interband transitions suggests that the only available electronic states with consistent energy and momenta arise from a conduction band of negative curvature6,11.
Results
Dipole-allowed transition from high-lying conduction bands
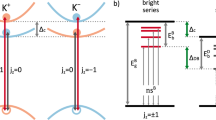
Figure 1a shows the ab initio GW quasiparticle band structure of monolayer WSe2 around the K-point in momentum space. The magnitude of the oscillator strength of the interband transition coupling the spin–orbit–split top valence band to the different conduction bands is coded in color. The full band structure is shown in Supplementary Fig. 1. The lowest-energy band-edge “A-exciton” is characterized by a dipole-allowed optical transition between the valence-band maximum and the upper spin-split conduction-band minimum at the K-point in the Brillouin zone. Besides the band-edge transition, our calculations in Fig. 1a indicate an additional dipole-allowed transition at the same K-point from a high-lying conduction band (CB+2−) to the top valence band (VB+)6,11, with approximately 4% of the oscillator strength of the band-edge transition (CB+ to VB+). Such higher-energy transitions happen to be located at around twice the band-edge transition energy (red double-headed arrows).
a Calculated GW band structure of bare monolayer WSe2. Higher (lower) energy spin-split bands are labeled by + (–) superscripts. The color indicates normalized oscillator strength of electrons making a transition from the top valence band (VB+) to the different conduction bands (CB, CB+1, and CB+2). Red double-headed arrows mark the exciton resonances invoked to explain quantum interference in optical second-harmonic generation (SHG)7. b Resonant pumping of band-edge A excitons (red arrow) results in momentum-selective excitation of higher-lying bands at the K-symmetry points. Electrons from the high-lying band recombine with holes from the valence band to emit UV light (blue arrow), measured as upconverted photoluminescence (UPL) spectra. Electrons in the first conduction band (CB) relax towards the K-points by emitting phonons, whereas electrons in the downwards-curved higher-lying conduction band relax away from the K-points (green curves). c PL spectrum of hBN-encapsulated monolayer WSe2 at 5 K under narrow-band continuous-wave (CW) excitation at 1.732 eV. The peak at 3.464 eV arises from SHG (purple), below which upconverted PL (UPL) from the HX (blue) is observed in the form of a set of 10 peaks. The bottom-left inset indicates the Auger-like process responsible for populating exciton states from the higher-lying conduction band, generating UPL. The intensity of the SHG (purple dots) co-polarized with the laser varies as the laser polarization is rotated with respect to the crystal lattice (right inset), whereas the HX luminescence (blue dots) does not. The top-left inset shows the UPL excitation (UPLE) spectrum of the HX (blue), which matches the band-edge A-exciton PL spectrum (red).
Probing the high-lying exciton by momentum-selective UPL
As illustrated in Fig. 1b, to selectively excite electron–hole pairs in the vicinity of the fundamental bandgap at the K-points (+K or −K-point), we use a linearly polarized narrow-band continuous-wave (CW) laser at 716 nm (1.732 eV), resonantly driving the A-exciton of monolayer WSe2 encapsulated in hexagonal boron nitride (hBN) (see Supplementary Fig. 3 for sample details). The process of Auger-like exciton–exciton annihilation8,12,13,14, indicated by the sketch in the bottom-left inset of Fig. 1c, can raise the electron to a higher band as momentum conservation localizes it around the K-points. The resulting UPL spectrum at 5 K in Fig. 1c shows two distinct features: a narrow peak at twice the excitation energy, i.e. at 3.464 eV; and a series of peaks beginning 60 meV lower in energy. The first peak, limited in width by the spectral resolution of the monochromator, arises from CW SHG15, which originates from the broken inversion symmetry of monolayer WSe2. The remaining peaks are reminiscent of excitonic luminescence. A total of ten narrow peaks are resolved with a mean linewidth of 11.4 meV. The SHG and excitonic UPL are easily discriminated by measuring the change in emission intensity co-polarized with the laser as the laser polarization is rotated with respect to the WSe2 crystal16. The right inset of Fig. 1c shows the characteristic six-fold symmetry of the SHG, arising from the three-fold rotational crystal symmetry. In contrast, the polarization dependence of copolarized UPL appears as a circle. Since the UPL arises at energies that are independent of the excitation energy (Supplementary Fig. 4b), the emission cannot be attributed to hyper-Raman scattering and is not related to the phonon cascades recently observed in Raman scattering from monolayer WSe217. We label this UV emissive species the “high-lying exciton” HX. The linewidth of the dominant HX peak can be as narrow as 5.8 meV at low pump fluences (see Supplementary Fig. 3d), and therefore places a lower limit on the exciton coherence time of ~100 fs.
Narrow linewidth and in-plane dipole orientation of the HX
Resolving such narrow discrete luminescence peaks at almost twice the bandgap is unexpected since the excitonic linewidth usually increases with excitation or emission energy as shown in Fig. 2a and Supplementary Table 1; higher-lying transitions such as the B and C excitons18 are subject to a broader range of non-radiative relaxation channels which limit their lifetime. The relationship between the HX UPL and the A-exciton transition is identified by sweeping the laser energy over the A-exciton resonance while recording the HX luminescence intensity, i.e. performing PL excitation (PLE) spectroscopy as shown in Supplementary Fig. 4b. The top-left inset of Fig. 1c shows the PL spectrum of the fundamental band-edge exciton (red line) in comparison to the PLE spectrum of the integrated HX emission (blue dots); PL and PLE spectra are virtually identical. As we demonstrate in Supplementary Fig. 5, the HX luminescence shows characteristics of in-plane transition-dipole orientation analogous to that of the A-exciton, but unlike the spin-forbidden dark exciton which has an out-of-plane transition dipole5.
a Energies and linewidths (full width at half maximum) of the prominent excitonic states seen in the PL of hBN encapsulated monolayer WSe2. The PL linewidth increases with transition energy until the HX breaks the trend. A summary of the data is given in Supplementary Table 1. The error bars were obtained from peak fitting. b HX UPL peak positions as a function of peak number. The error bars were obtained from multi-peak fitting and are below the diameter of the spheres. The fitted slope of 15.5 ± 0.1 meV corresponds to the calculated longitudinal acoustic (LA) phonon energy (orange arrows) near the K-points, which allows inelastic scattering of electronic states between +K and −K-points. Inset: the momentum change from \(\Gamma\) to +K (gray arrow) equals that from +K to −K (orange arrow). c and d The spin (black arrows) sublevels of conduction and valence bands of single-layer WSe2 are non-degenerate at the K-points. Momentum-conserving electron–phonon scattering (orange arrows) can involve either one phonon and a spin flip (c), or a spin-conserving two-phonon double-resonance transition (d). e Calculated GW band structure of monolayer WSe2 of CB+2− around the K-point. The color code of the band structure shows the expectation values of the spin operator on the spinor wavefunctions in the out-of-plane direction, i.e., 〈Sz〉, in units of \(\hslash\). The curved arrows illustrate the energy associated with LA-phonon scattering.
Phonon progression in the HX UPL
Figure 2b shows the energy of the HX luminescence peaks as fitted in Supplementary Fig. 6c. The 10 peaks are spaced equally, suggesting that they result from cascaded electron–phonon scattering at a phonon energy of 15.5 ± 0.1 meV. Such a phonon progression is known from PLE spectra19,20 and Raman scattering17,21 of monolayer TMDCs, but it is very unusual to find it so prominently in their PL spectra, with 10 peaks resolved. Calculations of the phonon dispersion in monolayer WSe2 (Supplementary Fig. 1b) suggest that the progression interval corresponds exactly to the emission of a longitudinal acoustic (LA) phonon close to the M and K-points of the Brillouin zone, where the phonon density of states is the largest22. With increasing temperature, the phonon occupancy (and consequently the electron–phonon interaction) increases and the intensity of the higher-order phonon progression peaks, therefore, increases (Supplementary Fig. 7). We propose that strong inelastic resonant electron–phonon scattering occurs between +K and −K-valleys23,24, as sketched in Fig. 2c, d. Such intervalley scattering can occur in <100 fs25,26,27, while the radiative decay of the band-edge A-exciton in monolayer WSe2 takes ~150 fs4. Given that the oscillator strength of the HX is expected (and confirmed in our GW-BSE calculations) to be much smaller than that of the A-exciton, the radiative decay of the HX is presumably slower.
As in previous studies of monolayer TMDCs, our GW band-structure calculations of monolayer WSe2 in Supplementary Fig. 1a reveal that all the conduction and valence bands around the K-points are spin split because of spin–orbit coupling. The combination of mirror-plane and time-reversal symmetry suggests that spin in the out-of-plane direction, Sz, is a good quantum number with opposite orientations in the +K and −K-valleys28,29. Figure 2e shows the CB+2− band, color-coded by the calculated 〈Sz〉 expectation value. Two different phonon-scattering processes between valleys are thus conceivable to move an electron of the high-lying exciton downwards in energy in two distinct ways: one-phonon scattering (Fig. 2c), which requires a spin–flip30,31; and a double-resonance two-phonon mechanism (Fig. 2d)23 conserving spin. The spin-conserving two-photon process should be favored in luminescence over the one-phonon mechanism. Indeed, the spectrum in Fig. 1c demonstrates that even-numbered peaks are more intense than odd-numbered ones, implying a higher transition probability for the two-phonon processes. However, we note that the helicity of the excitation can be destroyed by the fast exchange interaction32,33 arising during the Auger-like population process of the HX state so that the luminescence is not necessarily expected to be circularly polarized.
As illustrated in Fig. 1b, repeated electron–phonon scattering in a band of negative curvature should move the electron lower in energy, away from the K-symmetric points. Spin-valley locking is then relaxed, which, for higher-lying bands, persists only over a limited region of momentum space close to the K-point (see Fig. 2e). The alternation in peak intensity in the HX PL is pronounced up to peak number 5. Inspection of the Brillouin zone of single-layer WSe2, inset in Fig. 2b, in conjunction with the phonon progression observed, supports the assertion that the HX PL originates from the K-symmetric points. If the radiative state were instead formed around the Γ or M points, which lack significant spin-valley locking, there would be no obvious reason for the peak intensity to alternate in the progression. It is conceivable that the HX phonon progression could be interpreted in the context of polaronic excitons, which may provide an explanation for the extraordinarily narrow linewidth of the luminescence. The question of whether the progression is best rationalized in terms of bound excitons which emit phonons, or as polaronic excitons which form into split subbands24, is primarily a matter of the electron–phonon coupling strength, offering challenges for future study.
p-like HX state in two-photon PL excitation spectroscopy
A signature of the excitonic nature of optical transitions in TMDC monolayers is the existence of a series of excited states with different selection rules5,34. Besides Auger-like excitation, two-photon absorption (TPA) may also populate a dark excitonic state that subsequently converts to the radiative HX state. As sketched in Fig. 3a, for systems undergoing dipole-allowed interband transitions with winding number zero34, TPA probes odd-parity “p-like” excitonic states, while one-photon absorption and emission correspond to transitions involving even-parity “s-like” states34,35,36. For the excitation formed by TPA to relax to the radiative HX, the TPA energy must be no lower than the HX zero-phonon transition energy, i.e. around 3.4 eV. There is no need for TPA to occur at exactly twice the energy of the A-exciton, i.e. to overlap with the one-photon resonant Auger-like mechanism identified in the PLE in Fig. 1c. Figure 3b plots emission spectra as a function of excitation energy for a high pump fluence of 35 kW/cm2, revealing a clear cut-off just below the transition energy of the A-exciton. TPA (orange arrow) sets in when the laser energy is just below the A-exciton transition (green marker). The diagonal line stems from the SHG. Auger and TPA mechanisms are clearly distinguished by their respective power dependencies shown in the inset of Fig. 3c: the intensity of two-photon PL (orange) scales quadratically with excitation power, whereas the Auger-like process (green) shows a sublinear dependence because of bleaching of the A-exciton transition at high powers8. Although the two PLE features are not degenerate, the PL spectra from TPA and Auger-like excitation are identical (panel c). The lower part of Fig. 3b illustrates the pump-power dependence of the PLE spectra, obtained from the integrated HX PL intensity as a function of excitation energy. At low powers, only one PLE peak is seen, corresponding to the PL spectrum of the A-exciton and implying Auger-assisted upconversion to the HX as described in Fig. 1c. At high powers, this feature broadens, presumably because of electron–electron scattering and increased screening of the excitonic electron–hole pair, and an additional peak appears due to TPA. This narrow PLE peak has a linewidth of ~12 meV, virtually identical to the average linewidth of the HX PL transitions in Fig. 3c, thus suggesting that TPA and PL transitions arise from excitonic states of similar nature. The complete evolution of the PLE spectrum with pump power is shown in Supplementary Fig. 4. As we discuss in Supplementary Fig. 2, the energy of the non-emissive p-like HX state probed by TPA (3.43 eV) matches perfectly with the energy at which the transparency dip is observed in SHG (3.423 eV) due to the excitonic quantum interference effect7. This coincidence also implies that the HX cannot arise from a localized defect in the WSe2 monolayer crystal37,38.
a The HX can be formed either by two-photon absorption (TPA) involving a virtual level (dashed) or by Auger-like exciton-exciton annihilation (black arrows) of the A-exciton AX. TPA populates a dark p-like HX state, which subsequently relaxes (gray arrow) to the bright s-like HX state. b Change of the UPL spectrum with a photon energy of the CW laser at an irradiance of 35 kW/cm2, showing TPA (arrow) below the onset of the Auger-like double-exciton process. The diagonal line stems from SHG from the WSe2 monolayer. The spectrally integrated HX UPL intensity is plotted as a function of excitation energy in the lower panel. TPA (2\({{{{{\rm{\omega }}}}}}\) resonance) is observed at a pump intensity of 35 kW/cm2, while only the one-photon (1\({{{{{\rm{\omega }}}}}}\)) resonance is observed at 0.35 kW/cm2. c The two excitation mechanisms are distinguished by their power dependencies (inset). For the Auger-like mechanism (green), excitation in resonance with the band-edge A-exciton at 1.732 eV gives a sublinear dependence of UPL intensity on excitation power because of bleaching of the A-exciton transition. The corresponding power-law exponent p is about 0.6. Sub-resonant excitation at 1.715 eV yields the parabolic power dependence characteristic of TPA (orange). The corresponding power-law exponent is close to 2.0. The HX PL spectrum is independent of the excitation pathway (green and orange lines).
Sample to sample variation of HX energy
To prove that the two-photon excitation and the one-photon emission of the HX do not simply originate from different phonon transitions of one and the same state, we also performed measurements on monolayer WSe2 encapsulated by hBN layers of different thicknesses. Changing the dielectric environment of the monolayer modifies the binding energy of excitons and thus the energy separation between excitonic states5, but should not affect intralayer phonons. As demonstrated in Supplementary Fig. 6 and Table 1, the separation between p-like HX states, probed by TPA, and s-like HX states, probed by HX PL, varies between 27 and 37 meV across samples. No such variation is seen in the spacing of the phonon progression, which is identical for all samples (Supplementary Table 2).
Ab initio GW-BSE calculation of the HX
To conclusively establish the contribution of higher-lying conduction bands to the HX, we performed ab initio GW-BSE calculations18,39,40, as implemented in the BerkeleyGW package41. Figure 4a shows the computed absorbance spectrum of monolayer WSe2. The calculation explains the salient features (which are shown theoretically to be excitonic transitions in the absorbance) of the experimental reflectance contrast of hBN-encapsulated WSe2 plotted in Fig. 4b. The minor difference between the calculated and measured energies of excitonic transitions stems mainly from the influence of the dielectric environment, i.e. the hBN encapsulation, which is not included in the calculation. We discuss the influence of the hBN layers on the calculated exciton transition energy in Supplementary Fig. 8. As seen from Fig. 4a, b, there are many features around 3.4 eV, i.e. in the range of the HX PL and TPA. These features contain different transitions involving different bands and K-points throughout the Brillouin zone. Given that the interband transition from a high-lying conduction band (CB+2−) to the top valence band (VB+) at the K-point has only ~4% of the oscillator strength of the interband transition of the band-edge A-exciton transition (CB+ to VB+), the narrow-linewidth HX is not expected to be discernible in conventional absorption or reflectance measurements. We emphasize that this multitude of transitions arises because both the calculated absorbance and the experimental reflectance probe the entire Brillouin zone and therefore sample different bands. Resonant pumping of A-excitons in UPL, however, selectively populates excitons, including the HX, around the K-valleys. Figure 4c plots the entire UPL spectrum, showing the narrow HX feature together with several broader excitonic features at lower energies. To identify the HX in the calculation, we filter out excitons originating from transitions outside the K-valleys, retaining only those formed by transitions within a range of <0.2 Å−1 around the K-point as illustrated in Supplementary Fig. 1a. Since pumping A-excitons predominantly populates holes at the topmost valence band, we only include this band (VB+) in the calculation here for clarity. Excitons with contributions from both VB+ and VB− are shown in Supplementary Fig. 9. The resulting absorbance spectrum, restricted to transitions around the K-valleys, is plotted in Fig. 4d. The HX peak at 3.34 eV clearly stands out in the calculation at the UV range, with no comparable peaks apparent within the ±0.5 eV energy range.
We also show calculated absorbance spectra when the transitions include only a subset of the conduction bands: only CB (red), only CB+1 (yellow), or only CB+2 (blue). The calculation restricted to only CB+2 closely reproduces the HX feature obtained when all CBs are included. The contributions of individual conduction bands to the wavefunction of the excitons with different energy in the K-valleys are examined further shown in Fig. 4e, where the area of each disk plotted is proportional to the integrated oscillator strength of the different band components (see Supplementary Methods and Notes for details). From these analyses, it is evident that the optical strength of the high-lying feature HX arises primarily from the dominant contribution of the downcurved conduction band CB+2−, offering a clear rationalization of the experimental observations in Fig. 1. As we discuss in detail in Supplementary Fig. 10, the HX also contains an admixture of the CB+1 bands. This constituent is non-emissive (hence does not show up clearly in Fig. 4e) and may, therefore, contribute to the narrow linewidth exhibited by the HX PL. The lower conduction bands have a much smaller contribution to the HX peak due to the relatively large energy separation between higher (CB+2) and lower conduction bands (CB and CB+1) in the K-valley.
a Calculated absorbance spectrum of bare monolayer WSe2, accounting for transitions over the entire Brillouin zone. The dominant low-energy excitonic transitions are indicated. b Experimental reflectance contrast of monolayer WSe2 encapsulated by hBN on a sapphire substrate at 5 K. c UPL spectrum (solid line) measured under resonant pumping of the A-exciton. The dashed line shows the same spectrum multiplied by 0.02 at the corresponding energy range. d The calculated absorbance spectrum of bare monolayer WSe2, restricted to transitions around the K-points (within 6% of the Brillouin-zone area) from the topmost VB+ to only the lower conduction bands (CB, red), only the CB+1 bands (yellow), only the CB+2 bands (blue), or all bands (gray). The HX feature at 3.34 eV appears only when contributions from CB+2 are included. The inset shows the square of the HX envelope function in reciprocal space centered around K (black dot), with a scale bar of 0.2 \({\rm A} ^{-1}\). e Contributions of the different spin-split conduction bands to the excitonic optical strength of the different peaks in (d), indicated by the size of the disk area. The dominant contribution to HX comes from transitions from the VB+ to the negative-mass band CB+2−. The disk area within the gray box is rescaled by a factor of 0.02.
Excitons comprising negative-mass electrons
The band structure in Fig. 1a and Supplementary Fig. 1a shows that CB+2− corresponds to an electron of negative mass. The inset in Fig. 4d shows the envelope function of the HX wavefunction in momentum space, which is to be compared with the A-exciton wavefunction in Supplementary Fig. 10. In Supplementary Fig. 10e we project the HX exciton envelope function onto the quasiparticle band structure to demonstrate that the HX is indeed localized around the K-points, where the effective-mass approximation remains valid. An effective two-band model as shown in Supplementary Fig. 11 gives the same conclusion that the HX really can reside around the K-points in momentum space instead of spreading out to local minima of the high-lying conduction band. The HX has a calculated exciton radius5 of 1.2 nm, which is smaller than the 1.5-nm radius of the 1s A-exciton. This reduction is consistent with a heavier reduced exciton mass arising from an electron in a band of negative curvature, i.e. of negative effective mass.
Discussion
The idea of a stable exciton involving a negative-mass electron may seem counterintuitive. However, such a complex is indeed possible within a simple effective-mass hydrogenic model, provided that the hole mass \({m}_{{{{{{\rm{h}}}}}}}^{\ast }\) is positive and smaller in magnitude than the negative electron mass \({m}_{{{{{{\rm{e}}}}}}}^{\ast }\) (see Supplementary Fig. 12) so that the reduced mass of the exciton (\(1/\mu =1/{m}_{{{{{{\rm{h}}}}}}}^{\ast }+1/{m}_{{{{{{\rm{e}}}}}}}^{\ast }\)) remains positive. Then, the total mass of the exciton (\(M={m}_{{{{{{\rm{h}}}}}}}^{\ast }+{m}_{{{{{{\rm{e}}}}}}}^{\ast }\)) becomes negative. Drawing an analogy to classical orbital motion, the semiclassical motion of the electron and hole may then be thought of as joint orbiting around a common center which does not lie geometrically between the two particles, so that, as indicated on the top right side of Fig. 1b, the electron accelerates in the same direction as the hole. It is important to stress that, because the HX forms around the K-point, such an exciton is not related to the so-called “camel’s back exciton” formed due to a local camel-back-like structure in the conduction band42, or the somewhat more controversial so-called “bielectron” state43,44,45. In this proposed bound bielectron model, a negative-mass electron and a positive-mass electron from different conduction bands are bound together under the condition of the negative-mass electron being lighter.
The observation of an alternating peak intensity in the HX phonon progression (Fig. 1c) is consistent with the involvement of a negative-mass electron undergoing a cascaded phonon emission away from the K-points as sketched in Fig. 1b. If, instead, the HX were formed by positive-mass electrons, phonon emission would move electrons towards the K-points, where the spin-valley locking is more pronounced. The alternating behavior in the intensity of the phonon peaks would then appear stronger with increasing peak order, in conflict with the observation in Fig. 1c. Direct experimental evidence for the negative total mass of this peculiar excitonic species remains subject to further research. Studies of their ultrafast dynamics, diffusion and magneto-optical characteristics promise to be particularly insightful in this regard.
Since the electronic structure of many semiconducting monolayer TMDCs is qualitatively comparable6,11 and the efficient upconversion process has been observed in both monolayer MoSe2 and MoTe214, narrowband high-lying excitons in the free-particle continuum are expected to be a generic feature of TMDCs. Our results unveil the rich physics of complex many-body excitations in monolayer TMDCs, which emerges not only in the formation of various excitons and exciton complexes but, more importantly, in the coherent coupling and interference between excitonic transitions. In comparison to band-edge excitons, high-lying excitons appear to have larger orbital contributions from the chalcogenide atoms and are therefore much more sensitive to band hybridization with an adjacent layer in multilayer structures46. As we recently proved in twisted-bilayer WSe2, the HX energy can be tuned over a broad range by twist angle, with an average twist-angle susceptibility of 8.1 meV/°. Correspondingly, the excitonic quantum interference can be turned on and off by twisting46. High-lying excitons combined with band-edge excitons, therefore, form an atomic-like excitonic multilevel system, setting the basis for future exploration of quantum excitonics.
Methods
Sample preparation
We exfoliated the monolayer WSe2 and thin layers of hBN from bulk crystals (WSe2, HQ Graphene; hBN, NIMS) on PDMS films (Gel-Pak, Gel-film® X4) using Nitto tape (Nitto Denko, SPV 224P)47. We stamp-transferred the hBN and monolayer WSe2 flakes layer by layer onto either Si/SiO2, sapphire, or diamond substrates while heating the substrate to 65 °C. The hBN-encapsulated WSe2 samples were annealed under a high vacuum at 150 °C for 5 h.
Optical spectroscopy
The setup is illustrated in Supplementary Fig. 13a. We used an objective of 0.6 numerical aperture (Olympus, LUCPLFLN) to focus the laser onto the sample and collect the signal. The sample was placed under a vacuum on the cold finger of a helium-flow cryostat (Janis, ST-500). We used a grating of 1200, 600 or 150 grooves mm−1 to disperse the signals, and a CCD camera (Princeton Instruments, PIXIS 100) to record the spectra. A 50:50 beam splitter was used to separate excitation and detection pathways. The photon-energy-dependent instrument response in Supplementary Fig. 13b was measured with a calibration light source (LS-1-CAL, Ocean Optics) placed in front of the objective. The original spectra are shown in the main text and the Supplementary Information, without correction for the instrument response. We measured the photoluminescence (PL) of monolayer WSe2 by exciting samples with an argon-ion laser (Spectra Physics, 2045E) at 488 nm and filtering out the laser line from the signal with a 488 nm long-pass edge filter. The reflectance contrast of monolayer WSe2 was measured using a broad-band Xenon lamp (EQ-99X, Energetiq). We measured the upconverted PL and SHG of monolayer WSe2 by exciting samples with a tunable CW laser (Sirah, Matisse CR) and filtering out the laser line using a 680 nm short-pass filter.
Data availability
The raw data that support the plots within this paper and the other findings of this study are available from the corresponding authors upon reasonable request.
References
Lukin, M. D. & Imamoğlu, A. Controlling photons using electromagnetically induced transparency. Nature 413, 273–276 (2001).
Fleischhauer, M., Imamoglu, A. & Marangos, J. P. Electromagnetically induced transparency: optics in coherent media. Rev. Mod. Phys. 77, 633–673 (2005).
Weber, E. R., Willardson, R. K., Liu, H. C. & Capasso, F. Intersubband Transitions in Quantum Wells: Physics and Device Applications (Elsevier Science, 1999).
Poellmann, C. et al. Resonant internal quantum transitions and femtosecond radiative decay of excitons in monolayer WSe2. Nat. Mater. 14, 889 (2015).
Wang, G. et al. Colloquium: excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Liu, G.-B., Xiao, D., Yao, Y., Xu, X. & Yao, W. Electronic structures and theoretical modelling of two-dimensional group-VIB transition metal dichalcogenides. Chem. Soc. Rev. 44, 2643–2663 (2015).
Lin, K.-Q., Bange, S. & Lupton, J. M. Quantum interference in second-harmonic generation from monolayer WSe2. Nat. Phys. 15, 242–246 (2019).
Manca, M. et al. Enabling valley selective exciton scattering in monolayer WSe2 through upconversion. Nat. Commun. 8, 14927 (2017).
Moody, G. et al. Intrinsic homogeneous linewidth and broadening mechanisms of excitons in monolayer transition metal dichalcogenides. Nat. Commun. 6, 8315 (2015).
Lin, K.-Q., Martin, R., Bange, S. & Lupton, J. M. Polymer coatings tune electromagnetically induced transparency in two-dimensional semiconductors. ACS Photonics 6, 3115–3119 (2019).
Kormányos, A. et al. k·p theory for two-dimensional transition metal dichalcogenide semiconductors. 2D Mater. 2, 022001 (2015).
Mouri, S. et al. Nonlinear photoluminescence in atomically thin layered WSe2 arising from diffusion-assisted exciton–exciton annihilation. Phys. Rev. B 90, 155449 (2014).
Danovich, M., Zólyomi, V., Fal’ko, V. I. & Aleiner, I. L. Auger recombination of dark excitons in WS2 and WSe2 monolayers. 2D Mater. 3, 035011 (2016).
Han, B. et al. Exciton states in monolayer MoSe2 and MoTe2 probed by upconversion spectroscopy. Phys. Rev. X 8, 031073 (2018).
Yao, K. et al. Continuous wave sum frequency generation and imaging of monolayer and heterobilayer two-dimensional semiconductors. ACS Nano 14, 708–714 (2020).
Seyler, K. L. et al. Electrical control of second-harmonic generation in a WSe2 monolayer transistor. Nat. Nanotechnol. 10, 407 (2015).
Paradisanos, I. et al. Efficient phonon cascades in WSe2 monolayers. Nat. Commun. 12, 538 (2021).
Qiu, D. Y., da Jornada, F. H. & Louie, S. G. Optical spectrum of MoS2: many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 216805 (2013).
Shree, S. et al. Observation of exciton–phonon coupling in MoSe2 monolayers. Phys. Rev. B 98, 035302 (2018).
Chow, C. M. et al. Phonon-assisted oscillatory exciton dynamics in monolayer MoSe2. NPJ 2D Mater. Appl. 1, 33 (2017).
Gołasa, K. et al. Multiphonon resonant Raman scattering in MoS2. Appl. Phys. Lett. 104, 092106 (2014).
Zhu, H. et al. Observation of chiral phonons. Science 359, 579–582 (2018).
Carvalho, B. R. et al. Intervalley scattering by acoustic phonons in two-dimensional MoS2 revealed by double-resonance Raman spectroscopy. Nat. Commun. 8, 14670 (2017).
Kang, M. et al. Holstein polaron in a valley-degenerate two-dimensional semiconductor. Nat. Mater. 17, 676–680 (2018).
Bertoni, R. et al. Generation and evolution of spin-, valley-, and layer-polarized excited carriers in inversion-symmetric WSe2. Phys. Rev. Lett. 117, 277201 (2016).
Jin, Z., Li, X., Mullen, J. T. & Kim, K. W. Intrinsic transport properties of electrons and holes in monolayer transition-metal dichalcogenides. Phys. Rev. B 90, 045422 (2014).
Selig, M. et al. Excitonic linewidth and coherence lifetime in monolayer transition metal dichalcogenides. Nat. Commun. 7, 13279 (2016).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014).
Kurpas, M., Faria Junior, P. E., Gmitra, M. & Fabian, J. Spin-orbit coupling in elemental two-dimensional materials. Phys. Rev. B 100, 125422 (2019).
Wang, Z. et al. Intravalley spin–flip relaxation dynamics in single-layer WS2. Nano Lett. 18, 6882–6891 (2018).
Kioseoglou, G. et al. Valley polarization and intervalley scattering in monolayer MoS2. Appl. Phys. Lett. 101, 221907 (2012).
Yu, T. & Wu, M. W. Valley depolarization due to intervalley and intravalley electron–hole exchange interactions in monolayer MoS2. Phys. Rev. B 89, 205303 (2014).
Glazov, M. M. et al. Exciton fine structure and spin decoherence in monolayers of transition metal dichalcogenides. Phys. Rev. B 89, 201302 (2014).
Cao, T., Wu, M. & Louie, S. G. Unifying optical selection rules for excitons in two dimensions: band topology and winding numbers. Phys. Rev. Lett. 120, 087402 (2018).
Ye, Z. et al. Probing excitonic dark states in single-layer tungsten disulphide. Nature 513, 214 (2014).
He, K. et al. Tightly bound excitons in monolayer WSe2. Phys. Rev. Lett. 113, 026803 (2014).
Srivastava, A. et al. Optically active quantum dots in monolayer WSe2. Nat. Nanotechnol. 10, 491–496 (2015).
Zhang, S. et al. Defect structure of localized excitons in a WSe2 monolayer. Phys. Rev. Lett. 119, 046101 (2017).
Hybertsen, M. S. & Louie, S. G. Electron correlation in semiconductors and insulators: band gaps and quasiparticle energies. Phys. Rev. B 34, 5390–5413 (1986).
Rohlfing, M. & Louie, S. G. Electron–hole excitations and optical spectra from first principles. Phys. Rev. B 62, 4927–4944 (2000).
Deslippe, J. et al. BerkeleyGW: a massively parallel computer package for the calculation of the quasiparticle and optical properties of materials and nanostructures. Comput. Phys. Commun. 183, 1269–1289 (2012).
Altarelli, M., Sabatini, R. A. & Lipari, N. O. Camel’s back excitons in GaP. Solid State Commun. 25, 1101–1104 (1978).
Gross, E., Perel, V. & Shekhmamet’ev, R. Inverse hydrogenlike series in optical excitation of light charged particles in a bismuth iodide (BiI3) crystal. Sov. J. Exp. Ther. Phys. Lett. 13, 229 (1971).
Petroff, Y., Yu, P. Y. & Shen, Y. R. Absorption, photoluminescence, and resonant Raman scattering in Bil3. Phys. Status Solidi (b) 61, 419–427 (1974).
Czaja, W. et al. On the existence of bielectrons in BiI3. Solid State Commun. 13, 1445–1449 (1973).
Lin, K.-Q. et al. Twist-angle engineering of excitonic quantum interference and optical nonlinearities in stacked 2D semiconductors. Nat. Commun. 12, 1553 (2021).
Castellanos-Gomez, A. et al. Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping. 2D Mater. 1, 011002 (2014).
Acknowledgements
The authors thank R. Huber, M.M. Glazov, and P. Merkl for many helpful discussions, and S. Krug for technical support. Financial support is gratefully acknowledged from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) SFB 1277 (Project-ID 314695032) projects B03, B04, B05 and B11, SPP 2244 (Project-ID LI 3725/1-1, 443378379), and the Emmy-Noether Grant CH 1672/1 (Project-ID: 287022282), and the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter ct.qmat (EXC 2147, Project-ID: 390858490); P.E.F.J. was supported by a Capes-Humboldt Research Fellowship of the Alexander von Humboldt Foundation (Grant No. 99999.000420/2016-06). D.Y.Q. was supported by the National Science Foundation (NSF) under grant number DMR-2114081. The work at the Lawrence Berkeley National Lab was supported by the van der Waals Heterostructures Program through the Office of Science, Office of Basic Energy Sciences, U.S. Department of Energy under Contract No. DE-AC02-05CH11231, which provided the formulation of the theory and theoretical analyses; and by the National Science Foundation under Grant No. DMR-1926004, which provided for the GW and GW-BSE calculations; advanced software and codes were provided by the Center for Computational Study of Excited-State Phenomena in Energy Materials (C2SEPEM) at the Lawrence Berkeley National Laboratory, which is funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC02-05CH11231, as part of the Computational Materials Sciences Program. Computational resources were provided by the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, and the Texas Advanced Computing Center (TACC) at The University of Texas at Austin. B.P. and B.M. were supported by the Gianna Angelopoulos Program for Science, Technology, and Innovation and the Winton Program for the Physics of Sustainability. Growth of hexagonal boron nitride crystals was supported by the Elemental Strategy Initiative conducted by the MEXT, Japan (Grant Number JPMXP0112101001) and JSPS KAKENHI (Grant Numbers 19H05790 and JP20H00354).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
K.-Q.L. conceived the project and carried out the measurements with the support of S.B.; J.D.Z., K.-Q.L., J.Z., C.B., N.P., C.S. and A.C. contributed to the fabrication of samples; C.S.O., P.E.F.J., B.P., B.M., J.F., D.Y.Q. and S.G.L. contributed to the theoretical calculations; K.W. and T.T. provided hBN crystals; K.-Q.L., S.B. and J.M.L. analyzed the data and wrote the paper with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lin, KQ., Ong, C.S., Bange, S. et al. Narrow-band high-lying excitons with negative-mass electrons in monolayer WSe2. Nat Commun 12, 5500 (2021). https://doi.org/10.1038/s41467-021-25499-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-25499-2
This article is cited by
-
Excitons stabilize above the band gap in bilayer WSe2
Nature Nanotechnology (2024)
-
Ultraviolet interlayer excitons in bilayer WSe2
Nature Nanotechnology (2024)
-
High-lying valley-polarized trions in 2D semiconductors
Nature Communications (2022)
-
Unconventional excitonic states with phonon sidebands in layered silicon diphosphide
Nature Materials (2022)
-
Excitonic resonances control the temporal dynamics of nonlinear optical wave mixing in monolayer semiconductors
Nature Photonics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.