Introduction

In low-dimensional systems, the reduction of the screening and the consequent enhancement of Coulomb interaction leads to fascinating many-body phenomena. Of particular interest is the formation of charged and neutral exciton complexes such as excitons, trions, and biexcitons due to the strong electron–hole interaction. Two-dimensional transition metal dichalcogenides (2D TMDCs) with their stability, ease of fabrication, and unique light–matter interaction properties offer a distinctive platform to study such many-body effects1,2,3,4,5,6 and open the doors for new technological applications7,8.

Biexcitons or exciton molecules have been studied extensively in quantum wells and quantum dots due to their potential applications in quantum information devices as building blocks for logic gates or entangled photon sources9,10. Moreover, biexcitons lasing in quantum dots and solution-processed quantum wells11,12 has also been a major driving force toward studying biexciton. From a theoretical perspective, the study of biexciton formation and dynamics is an essential step toward a better understating of exciton–exciton interaction and, more generally, the electron–hole plasma and related many-body phenomena that are relevant for modern optoelectronic applications13,14,15,16,17. In 2D TMDCs, biexcitons have attracted increasing attention because of their high binding energy, which is one order of magnitude larger than its counterparts in conventional quantum well and quantum dots18. The spin-valley locking and the possible control of optical excitations via polarized light in 2D TMDCs19,20,21,22,23 make biexcitons of particular interest in these materials. Therefore, it is worth speculating about promising upcoming technological applications based on biexcitons in 2D TMDCs (see, e.g., magnetic field tuning of biexcitons in ref. 24).

Although many experimental efforts have been made to study biexcitons in 2D TMDCs, only few first-principles theoretical calculations have been reported in the field. This is due to the large configurational space of biexcitons (as compared to excitons and trions) in which two electrons and two holes have to be distributed over conduction and valence bands, making the ab initio simulation prohibitively expensive. This also explains why most of the previous theoretical simulations of biexcitons are based on the effective mass approach25,26,27,28. We emphasize that the important advantage of the ab initio approaches over previous effective mass models is the inclusion of the electron–hole exchange interaction, which is of primordial importance in determining biexciton valley character and fine structure (FS) as discussed later in this communication. Already at the exciton level, the electron–hole exchange interaction is known to play a key role in the valley dynamics of bright excitons and the lifting of the valley degeneracy of dark excitons29,30,31. Recently, Steinhoff et al.32 successfully incorporated this interaction in an ab initio description of biexciton in WSe2 and mentioned its importance. In ref. 32, the authors studied the coherent optical absorption of biexcitons in resonant pump–probe experiments from first principles using the dynamics-controlled truncation scheme14,33. In this coherent process, the pump and probe pulses are tuned at the exciton resonance and only bright–bright (BB) biexciton states are of interest. The role of exciton spin-dark states (called shortly here dark states) is hence absent. On the other hand, in incoherent biexciton formation (e.g., in photoluminescence (PL) experiments), the material is first excited above the band gap and then relaxes to low-laying exciton and biexciton states after the emission of optical phonons. In such a process, the dark states (being low in energy) play an important role as revealed by recent PL and magneto-PL measurements which demonstrate a fundamental biexciton transition that originates from a dark–bright (DB) biexciton state3,5. Other important aspects of biexcitons such as their valley character and FS, as well as non-equilibrium effects, are still open questions of primary importance, which require an ab initio investigation.

In this work, the previous questions are addressed in the case of WSe2 monolayer using first-principle methods. This includes configuration interaction and many-body perturbation theory approaches, which have been recently proposed to treat charged and neutral excitations in semiconductors34. A brief discussion of our approach is given in the “Methods” section together with the explicit form of the biexciton Hamiltonian. The full derivation of the latter is given in the Supplementary Information (see Supplementary Note 1). Upon diagonalization of the biexciton Hamiltonian, it has been found that the low-laying biexciton eigenstates can be classified from low to high energy into dark–dark (DD), DB, and BB states depending on the spin orientation of the constituent electrons and holes. The first bright biexciton state is found to be an intervalley combination of dark and bright exciton state formed at the Brillouin zone (BZ) edges (at the K and \({{\bf{K}}}^{\prime}\) points), in good agreements with recent PL and magneto-PL experiments3,5. At low peak broadening, the first biexciton peak shows a clear FS splitting of 2.8 meV in agreement with recent PL measurements31. Furthermore, by examining the effects of the electron–hole exchange interaction, it has been found that this biexciton FS is a pure intervalley electron–hole exchange effect and it is mainly due to the FS of the exciton dark state (the final state of the recombination process). Finally, by calculating biexciton transitions from high-laying states (excited DB and BB states), it has been found that although the BB states lay above the DB ones due to the large conduction band splitting, biexciton transitions from the BB states are below the transition from the first DB state. We explain this counterintuitive effect by a simple electron–hole exchange analysis. The observation of these transitions is shown to be a signature of non-thermalized biexciton population.

Results

Optical spectra and binding energies

The diagonalization of the biexciton Hamiltonian discussed in the “Methods” section yields the optical spectra shown in Fig. 1a and the binding energies depicted in Table 1. For comparison, we have also performed excitons and trions calculation using the same methodology as in ref. 34. As shown in Fig. 1a, the biexciton peak is located between the exciton and the negative trion (called here simply trion) peaks with a binding energy of 20 meV, which is in a very good agreement with recent PL and electroluminescence experimental measurements2,3,4,5,6, and also with previous ab initio and effective mass approaches25,26,27,28,32. Furthermore, the biexciton peak shows a clear FS of 2.8 meV, which will be discussed in the next section. It is noteworthy that the first observation of biexciton reported in earlier works1 shows a biexciton peak below the fundamental exciton and trion peaks with a binding energy of 50 meV. However, recent works1,2,3,4,5,6 attributed this early observation to charged biexcitons. The trion binding energy is found to be 50 meV in our calculation, which is slightly higher than the experimental value of 40 meV1,2. This difference can be attributed to the environmental screening (e.g., h-BN encapsulation), which is not included in our calculation and which is known to reduce the binding energies of the photo-generated species, as it reduces the Coulomb interaction between quasiparticles35,36. The difference can also stem from the dissimilarity between the experimental and theoretical doping levels as discussed recently in refs. 37,38 due to the finite k-mesh sampling used in theoretical simulations.

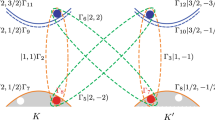
Fig. 1: Exciton, trion, and biexciton optical spectra and eigenstates.
figure 1

a Biexciton spectrum (biexciton to exciton recombination) in blue together with trion and exciton spectra in red and black, respectively. b Exciton, trion, and biexciton eigenvalue manifolds. The dark–dark (DD) manifold indicates a series of dark biexciton states. The DB1 and the BB1 states are the first dark–bright (DB) and bright–bright (BB) states in the spectrum, respectively. For exciton, D and B are the dark and bright states, whereas for trion, S and T are the singlet and triplet states, respectively. The biexciton peaks XX1,2 originate from the DB1 → D transition with a fine structure determined mainly by the lifted double degeneracy in the D state under the electron–hole exchange interaction. On the other hand, for trions, the fine structure results from the splitting of the first bright trion state into S and T states, which recombine to the conduction band minimum (CBM). c Schematics of the main configurations entering the formation of the many-body states introduced in b. Dark circles indicate a dark exciton state, whereas gray circles indicate a bright one.

Full size image
Table 1 Binding energy of trions and biexcitons in WSe2.
Full size table

By analyzing the configurational composition of the biexciton eigenstates (see Supplementary Note 3) within 100 meV above the lowest eigenvalue, it has been found that the eigenstates are of three types: DD, DB, and BB (see Fig. 1c). DD states are formed by two dark exciton states at the K and \({{\bf{K}}}^{\prime}\) valleys, and, hence, are optically inactive due to their spin configuration. In contrast to excitons and trions, the biexciton spectrum starts with several dark states (the DD manifold in Fig. 1b), which span almost 60 meV above the lowest biexciton eigenvalue. Excitons and trions, on the other hand, have only two quasi-degenerate dark states below the first optically active one as shown in Fig. 1b). The existence of optically dark states strongly alters the optical properties of materials in general. For excitons, this includes the PL quantum efficiency at low temperatures and the ultra narrow linewidth of the PL emission, among other properties39,40. For biexcitons, we expect the same alteration, as the lifetime of dark excitons or biexcitons are orders of magnitude longer than for their bright counterparts at low temperature31. In particular, for biexcitons, a large DD manifold with many dark states may hinder the observation of the biexciton signal due to the high related relaxation probability to dark states. This may explain the need to use higher light density in PL experiments to observe biexcitons as compared to the one needed to observe trions and excitons.

Above the DD manifold, optically active states start to appear, namely the DB and BB states, which start with DB1 and BB1 states, respectively. The DB (BB) states are formed by one dark (bright) exciton state at the K valley and one bright exciton state at the \({{\bf{K}}}^{\prime}\) valley as shown in Fig. 1c. The BB states lay always above the DB states due to the large conduction band maximum (CBM) spin–orbit splitting ΔCBM = 37 meV. The biexciton peaks XX1 and XX2 shown in Fig. 1a results from the radiative recombination of the first DB biexciton state, denoted by DB1 in Fig. 1b, to the dark exciton state and constitute the biexciton FS, which is discussed in the next section. Recent magneto-PL measurement3 and the simple model analysis of Li et al.5 have shown that the observed biexciton peak is indeed a DB combination of exciton states.

Fine structure

If the peaks broadening is reduced below 3 meV, a clear FS is then observed in the calculated biexciton spectrum (see Fig. 1a and Table 2), with two constituent subpeaks, XX1 and XX2, energetically separated by 2.8 meV. Due to the required low peak broadening, which is close to the radiative limit41, this FS is hard to observe. Nevertheless, Barbone et al.6 recently reported a biexciton FS of 2.5 meV in WSe2 monolayer, a value which is very close to the theoretical calculation reported here. This FS is found in our calculation to be a pure electron–hole exchange effect, as it vanishes when the electron–hole exchange interaction is neglected (see Supplementary Note 4 for a comparison between the biexciton spectrum with and without the electron–hole exchange). In the case where the electron–hole exchange interaction is ignored in the biexciton Hamiltonian, the DB1 biexciton state and the D exciton state are doubly degenerate due to time-reversal symmetry or valley degeneracy. This degeneracy refers simply to the two possibilities in placing the dark exciton state either at the K or \({{\bf{K}}}^{\prime}\) valleys. In that case, no FS is observed in the biexciton spectrum and the DB1 → D biexciton transition is simply four times degenerate. When the electron–hole exchange interaction is included, the DB1 state splits by 0.3 meV (not shown in Fig. 1b due to the large energy scale) and the D state splits by 2.5 meV (magnified in Fig. 1b). Hence, it is the sum of the two splitting in the DB1 and D states that gives rise to the total FS of the biexciton peak with the largest contribution (90%) stemming from the splitting of the exciton dark state under the electron–hole exchange interaction. In a recent work by Robert et al.31, the dark exciton FS in WSe2 was measured and found to be around 0.6 meV, a value which is smaller than the 2.5 meV FS reported here. We attribute this difference to the environmental screening. From a theoretical point of view, it is prohibitively expensive to include the environmental screening in an ab initio way (e.g., by adding few layer of h-BN to the simulation cell). However, using screening models to simulate the environmental screening35,36, it has been found that the additional screening by the substrate or the encapsulation always lower the binding energies of photoexcitations and their splitting due to the reduction of the Coulomb interaction. Hence, it is highly expected that in a measurement where the monolayer is freestanding without additional screening, the dark exciton FS will be larger than the one reported by Robert et al.31. An important consequence of the fact that the biexciton FS is mainly due to the exciton dark state FS is that the intervalley (not the intravalley) electron–hole exchange interaction is the component controlling the biexciton FS. Recall that the intravalley exchange component is only present for the bright exciton formed at the valence band maximum (VBM) and the CBM + 1 for a given valley because of the parallel spin orientation of these bands in W-based TMDCs as shown in Fig. 1c. The intervalley exchange component, on the other hand, is present for the dark exciton state and is therefore responsible for its splitting, which dominates the biexciton FS. In fact, it is known theoretically and experimentally as well, that the intervalley exchange interaction, which couples the two valleys, lift the valley degeneracy and split the exciton dark state42,43. Therefore, it is the intervalley electron–hole exchange interaction that is responsible for the exciton and biexciton FS.

Table 2 Fine structure of trions and biexcitons in WSe2 monolayer (meV).
Full size table

The mechanism giving rise to the biexciton FS is different from that of the trion FS (shown in Fig. 1a, red curve), despite that both have the same origin, being the intervalley electron–hole exchange interaction. The trion FS has been extensively studied lately from both theoretical and experimental sides5,29,34,36,44 where it has been shown that the trions FS is the result of the splitting of the first optical active trion state into singlet and triplet under the intervalley exchange interaction (see Fig. 1b). This is also found in our ab initio calculation with a trion FS of 16 meV slightly higher than the experimental value of 10 meV (see Table 2). Although for trions the FS is due to a splitting in the trion state (initial state of the recombination), for biexcitons the FS is mainly due to the splitting in the final dark exciton state under the intervalley electron–hole exchange interaction.

Non-equilibrium effects

The biexciton spectrum shown in Fig. 1a includes recombinations from all biexciton states up to the the first optically active one (i.e., the DB1 state) without thermal equilibrium effects. It is straightforward to include thermal equilibrium effects through a simple Boltzmann weight; however, it has been realized recently that exciton and trion populations are out of thermal equilibrium at least for the first 10 ps after the pump pulse45. This timescale is larger than the exciton lifetime which is around 1 ps only46,47,48. This suggests that radiative recombination from high-laying states is possible. Indeed, this effect manifests itself prominently for trions where it is clear that if the trion population were fully thermalized into an equilibrium Boltzmann distribution, the trion FS would not be observable at low-temperature measurements due to the large singlet–triplet splitting (experimentally determined to be 10 meV, see Table 2) as compared to the thermal energy (0.33 meV at 4 K).

By analogy to the trion case, for biexciton, transitions from non-thermalized states can give rise to extra peaks in the biexciton spectrum. These states are basically the excited bright DB and BB states, which would recombine, if enough time would be given, to the final D or B exciton states. The full treatment of equilibrium effects including, e.g., phonon relaxation is beyond the scope of this communication. However, an optical signature of a non-thermalized biexciton population might be derived in this work by analyzing which peak would arise if the biexciton population would be out of thermal equilibrium. This can be achieved by calculating the biexciton spectrum when high-laying states, beyond the DB1 state, are involved. In Fig. 2, the biexciton spectrum is shown each time a new peak arises when high-laying states (up to 100 meV above the lowest biexciton state) are progressively included in the calculation of the spectrum. The blue curve in Fig. 2 contains the first biexciton peak at 1.96 eV arising from the DB1 state reached at around 58 meV above the fundamental biexciton state. At around 13 meV (29 meV) above the DB1 state, a new peak arises at 1.975 eV (1.986 eV), which corresponds to a transition from an excited DB state, called here as DB2 (DB3), to the final D exciton state. At 42 meV above the DB1 state, we see the appearance of the first BB biexciton transition at around 1.931 eV or equivalently 30 meV below the XX1 peak. This transition originates from the first BB biexciton state (BB1) in the biexciton spectrum (see Fig. 1b). As for the trions, the observation of these peaks would offer an optical signature of a non-thermalized biexciton population.

Fig. 2: Biexciton spectra calculated with increasing number of biexciton states.
figure 2

The labels above the peaks denote the biexciton state from which the peak originates. The black curve represents the exciton peak and the blue one the biexciton double peak at 1.96 eV, which originate from the dark–bright DB1 state. The dashed green curve is the calculated biexciton spectrum including all the states up to 13 meV above the DB1 state. At this energy, the DB2 peak appears. The red dotted-dashed (cyan dotted) curve is the biexciton spectrum with the new peak from the DB3 (respectively the bright–bright BB1) biexciton state reached at 29 meV (respectively 42 meV) above the DB1.

Full size image

It is relatively surprising to observe the biexciton peak arising from the radiative recombination of the BB1 state (the XX3 peak at 1.931 eV in Fig. 2) below the XX1 peak originating from the first bight biexciton state (DB1), as for trions and excitons, transitions from states above the first bright one are always above the fundamental transition from the lowest bright state in the spectrum. This counterintuitive fact is explained in details in Supplementary Note 5.

Discussion

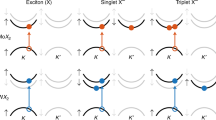
As mentioned in the “Introduction,” the configurational space of biexcitons is large. However, for the bright low-laying states, spin–orbit splitting and symmetry constraints reduce the main contributions to the biexciton eigenstates to only few configurations. First, the large VBM spin–orbit splitting, ΔVBM = 340  meV, forces the two holes forming the biexciton low-laying states to occupy the VBM at K or \({{\bf{K}}}^{\prime}\) points in the BZ. Moreover, for zero biexciton center of mass momentum, translational symmetry forces the bright configurations to be either of intervalley on intravalley character only (see Fig. 3a–d). The electron–hole exchange interaction favors, however, the intervalley configurations over the intravalley ones as explained in the following.

Fig. 3: Schematic comparison of electron–hole exchange interactions entering the formation of inter- and intravalley configurations.
figure 3

In a and b, the comparison is between the intervalley (a) and intravalley (b) configurations for the dark–bright DB1 state. In c and d, the same comparison is shown for the bright–bright BB1 state. In all these plots, only the interactions that are present in one configuration and not the other are shown for comparison. Moreover, we neglect the electron–electron exchange interaction in this figure. The positions of electrons and holes in the intravalley configuration are exaggerated for visibility.

Full size image

First, we have compared the strength of the inter and intravalley electron–hole exchange interaction in monolayer WSe2. Recall that the intervalley exchange controls the exciton dark state splitting, whereas the intravalley exchange controls the extra splitting between the dark and bright exciton states when the exchange interaction is included. Therefore, to perform the comparison, we have calculated the exciton eigenstates with and without the electron–hole exchange. It has been found that the dark exciton state splitting (as mentioned earlier) is 2.5 meV, whereas the DB splitting due to exchange is 10 meV. This implies that the intervalley exchange is smaller than the intravalley one. Second, in a single configuration picture as shown in Fig. 3 for a DB state, the intervalley configuration in Fig. 3a have an inter-valley electron–hole exchange contribution, whereas the intravalley configuration in Fig. 3b have an intravalley exchange contribution. According to the comparison made previously, the biexciton DB intervalley configuration is favorable (lower in energy) over the intravalley one. The previous analysis can be repeated for the BB state where the two electron–hole pairs occupy the spin bright configurations as shown in Fig. 3c, d (i.e., the two electrons belongs to the CBM + 1 and the two holes to the VBM). In the intervalley BB configuration (Fig. 3c), the excitons pairs are located at the K and \({{\bf{K}}}^{\prime}\) points, and are no longer coupled by the electron–hole exchange interaction due to the spin configuration of the electrons and holes (recall that only Fermions with parallel spins can feel an exchange interaction). On the other hand, the intravalley BB configuration (Fig. 3d) has two extra intravalley exchange interactions, making it higher in energy. Thus, for the BB state, the intervalley configuration is again favorable.

It is worthy to contrast the previous single configuration picture to our actual many-body calculation. The configurational analysis (Supplementary Note 3) of the the DB1 (BB1) many-body wavefunction indicates that the main contribution to its weight stems from the DB1 (BB1) intervalley configuration (left panels of Fig. 3), which confirms the previous single configuration picture. However, one should stress on the fact that the previous analysis does not exclude the intravalley configurations from entering the formation of biexciton states but rather to have a small contribution.

At the difference to excitons and trions, biexciton states are relatively more delocalized over the configurational space. This simply means that the weight of the biexciton wavefunction is not stemming in a large portion from one single configuration only (see Supplementary Note 3). For trions and excitons, up to 30% of the total wavefunction weight is stemming from the the single configurations shown in Fig. 1c (the D, B configurations for exciton and the S, T configurations for trion). However, for the DB1 biexciton state, up to 5% only of its weight is stemming from its main configuration (the DB1 configuration in Fig. 1c). The same result is observed for the BB1 state. This delocalized character of the biexciton wavefunctions is essential to understand the small splitting of the DB1 state under the electron–hole exchange interaction as compared to the dark exciton state. Recall that this splitting is 0.3 meV for the biexcitons and 2.5 meV for the excitons, although both splitting have the same origin being the intervalley electron–hole exchange interaction. In fact, the exciton dark state wavefunction has 30% of its weight localized on the dark exciton configuration shown in Fig. 1c, which is the most sensitive configuration to the electron–hole exchange interaction. On the other hand, the biexciton DB1 state has only 5% of its weight stemming from the intervalley configuration shown in Fig. 3a, which is basically the configuration that is mostly sensitive to the electron–hole exchange interaction. This implies that the splitting of the DB1 biexciton state should be smaller than the splitting of the exciton D state and, as a consequence, the biexcitons FS is mainly controlled by the FS of the dark exciton state, as previously discussed.

In conclusion, we have shown that biexcitons in 2D TMDCs are complex bound states with rich physical properties. We have demonstrated the importance of the electron–hole exchange interaction in controlling the valley character of biexciton states and their FS. Moreover, it has been shown that non-thermalized biexciton population leads to the appearance of new biexciton peaks, which can be used to study non-equilibrium effects. Finally, we should stress that in this work, biexciton transitions from non-vanishing crystal momentum state have been ignored. These transitions are as important as the ones treated in this work and can also be bright if the final exciton state has the same momentum as the initial biexciton state restoring, therefore, the conservation of momentum. However, they are expected to be higher in energy than the DB1 state, as they are formed by the electron and hole states above the band edges. Moreover, this work only focused on WSe2 monolayer. We believe that, despite the similarities between different TMDCs, it is not fully justified to extrapolate the present results to other monolayers. The reason behind that is the difference in the spin character of the CBM and its spin–orbit splitting between different TMDCs. For instance, we expect biexciton in MoS2 monolayer to have different valley character then in WSe2 and therefore to have different optical selection rules under circularly polarized light.

Method

Biexciton Hamiltonian

Although for trions and excitons explicit Hamiltonians have been proposed in the literature34,49, for biexcitons a Hamiltonian that includes all inter-particles direct and exchange interactions (see below) has not been reported to the best of our knowledge. It is noteworthy that the approach of Steinhoff et al.32 uses an equation of motion without explicit reference to the many-body biexciton Hamiltonian. Moreover, the equation of motion does not include all the electron–hole interaction terms due to fermionic permutations as discussed below. In this work, the biexciton Hamiltonian Hxx is derived following the generalized approach of Torche et al.34. In this approach, biexcitons are defined as the eigenstates of the many-body Hamiltonian when the latter is diagonalized in the subspace of doubly excited determinants. The projection of the many-body Hamiltonian into this space leads, therefore, to the biexciton Hamiltonian whose final form reads (see Supplementary Note 1 for a full derivation)

$$H_{\mathrm{xx}}= H_{\mathrm{o}}+H_{\mathrm{ee}}+ H_{\mathrm{hh}} + H_{\mathrm{eh}},$$

with H0, Hee, Hhh, Heh referring, respectively, to the free electron–hole, electron–electron, hole–hole, and electron–hole Hamiltonians with matrix elements given by:

$$\left\langle kl\gamma \delta \right|{H}_{\text{0}}\left|ij\alpha \beta \right\rangle = \; ({\epsilon }_{i}+{\epsilon }_{j}-{\epsilon }_{\alpha }-{\epsilon }_{\beta })\ {\delta }_{ki}{\delta }_{lj}{\delta }_{\gamma \alpha }{\delta }_{\delta \beta }\\ \left\langle kl\gamma \delta \right|{H}_{\text{ee}}\left|ij\alpha \beta \right\rangle = \left[\left\langle kl\right|W\left|ij\right\rangle -\left\langle kl\right|W\left|ji\right\rangle \right]{\delta }_{\gamma \alpha }{\delta }_{\delta \beta }\\ \left\langle kl\gamma \delta \right|{H}_{\text{hh}}\left|ij\alpha \beta \right\rangle = \left[\left\langle \gamma \alpha \right|W\left|\delta \beta \right\rangle -\left\langle \gamma \alpha \right|W\left|\beta \delta \right\rangle \right]{\delta }_{ki}{\delta }_{lj}\\ \left\langle kl\gamma \delta \right|{H}_{\text{eh}}\left|ij\alpha \beta \right\rangle = \left[\left\langle k\alpha \right|v\left|\gamma i\right\rangle -\left\langle k\alpha \right|W\left|i\gamma \right\rangle \right]{\delta }_{lj}{\delta }_{\delta \beta }\\ +\,\text{all} \,\,{16} \,\,{Fermionic} \,\,{permutations}$$

Where:

$$\left\langle ij\right|W\left|kl\right\rangle =\int d{{\bf{r}}}_{1}d{{\bf{r}}}_{2}\ {\phi }_{i}^{* }({{\bf{r}}}_{1}){\phi }_{j}^{* }({{\bf{r}}}_{2})W({{\bf{r}}}_{1},{{\bf{r}}}_{2}){\phi }_{k}({{\bf{r}}}_{1}){\phi }_{l}({{\bf{r}}}_{2}),$$

and

$$\left\langle ij\right|v\left|kl\right\rangle =\int d{{\bf{r}}}_{1}d{{\bf{r}}}_{2}\ {\phi }_{i}^{* }({{\bf{r}}}_{1}){\phi }_{j}^{* }({{\bf{r}}}_{2})v({{\bf{r}}}_{1},{{\bf{r}}}_{2}){\phi }_{k}({{\bf{r}}}_{1}){\phi }_{l}({{\bf{r}}}_{2}).$$

In the previous set of equations, \(\left|i\right\rangle\) (equivalently ϕi) and ϵi are a set of eigenvectors and eigenvalues from a GW calculation and W (v) is the static screened (bare) Coulomb interaction. The biexciton configurations \(\left|ij\alpha \beta \right\rangle\) are a set of doubly excited determinants build from the ground state of the system where two electrons are promoted from the valence bands α and β to the conduction bands i and j (see Supplementary Note 1 for an exact definition). The indexes i, j, α, and β in the previous notations are combined indexes for both bands and crystal momenta quantum numbers, e.g., i: = n, kn. A full derivation of the previous Hamiltonian and the explicit 16 fermionic permutations are provided in the Supplementary Note 1.

The difference between the previous biexciton Hamiltonian and the one used in the work of Steinhoff et al.32 can be summarized in two points. First, the electron–hole interaction term Heh in our derivation comprises all fermionic permutations of electrons and holes with a total of 16 terms. These terms refer simply to all the possible scattering processes from an initial biexciton state to a final one via the electron–hole interaction. In fact, one can form four independent initial electron–hole pairs from the initial biexciton state with two electrons and two holes. These four initial pairs are to be scattered into the four final pairs from the biexciton final state. Hence, there will be 16 different processes (see Supplementary Note 1 for an exact derivation). Our derivation suggests that all these terms are of equal importance, as they are all derived from the same Hamiltonian Heh. The second difference resides in the electron–electron and hole–hole exchange terms in Hee and Hhh, which are screened in our biexciton Hamiltonian. We believe that if the electron–electron (hole–hole) direct interaction is screened, then the exchange interaction should also be screened. According to the derivation of the biexciton Hamiltonian provided in Supplementary Note 1, for the electron–electron (hole–hole) terms, both interactions (direct and exchange) are derived from the same entity, namely the Coulomb interaction, by simple fermionic permutation, which suggests that if one is screened the other one should also be screened. This should not be confused with the electron–hole direct and exchange terms, which are not derived from the same physical entity. In the Bethe–Salpeter equation50, the electron–hole exchange is derived from the exchange part of the electron self-energy (and thus should not be screened), whereas the direct electron–hole interaction is derived from the correlation part of the self-energy and should, therefore, be screened. Thus, the electron–electron (hole–hole) and electron–hole exchange interactions have different origins and screening (or not) one of them does not imply that the other should be (or should not be) screened.

Computational details

All the calculation reported in this communication are based on fully relativistic density functional theory calculation at the  Perdew-Burke-Ernzerhof (PBE) level using norm-conserving pseudopotentials from the pseudo-dojo library51. For quasi-particle energies, the G0W0 method was used for band gap correction followed by a scissor shift of all conduction bands. The G0W0 scissor correction of the bands was 0.96 eV. The scissor approximation is well justified near the band gap in TMDCs. G0W0 calculations were performed using the plasmon-pole model of Godby and Needs52 with 1000 empty bands used in the sum over empty states for the calculation of the screening function. Furthermore, a 2D-truncated Coulomb interaction was used to eliminate periodic image effects in response calculation. The treatment of the singular term in the screened Coulomb interaction was performed following Ismail–Beigi’s scheme53.

To reduce the computational load, the biexciton configurations \(\left|ij\alpha \beta \right\rangle\) are restricted to those having a vanishing biexciton momentum q = ki + kj − kα − kβ = 0. Moreover, we have restricted the single-particle wavefunctions entering the formation of a generic biexciton configuration \(\left|ij\alpha \beta \right\rangle\) to the states near the K and \({{\bf{K}}}^{\prime}\) points in the BZ and to the VBM, VBM + 1 and CBM, CBM + 1 only. Previous ab initio calculations have found that, although having an exceptionally large binding energy, excitons, trions, and biexcitons wavefunctions in monolayer TMDCs are largely of the Wannier type, meaning that they are well localized in momentum space to a small neighborhood around the K and \({{\bf{K}}}^{\prime}\) points in the BZ32,34. The extent of the included single-particle state is determined by a circle of radius r around the K and \({{\bf{K}}}^{\prime}\) points. Convergence studies (see Supplementary Note 2) show that a radius of 0.25 Å is enough to converge the biexciton binding energy within 1 meV accuracy. Furthermore, the convergence of the biexciton binding energy with respect to the BZ sampling shows that (see Supplementary Note 2) a grid of 39 × 39 is sufficient to converge the biexciton binding energy within 2 meV accuracy. The restricted BZ sampling technique used here to calculate the low-laying biexciton states has already been used in previous works32,34 and has been proven to give reliable results. The calculation of the optical spectra follows the methodology developed in ref. 34 with a reduced phenomenological broadening full width at half maximum (FWHM) of 2 meV to make the biexciton FS more clear. Finally, density functional theory and screening calculations have been performed using the Abinit package54, whereas the diagonalization of the biexciton Hamiltonian has been performed using the SLEPc library55.