Main

The transition from a fluid to a rigid, or jammed, state occurs and is of interest in a wide variety of condensed matter, with glasses, granular packings and colloidal suspensions being well-known examples. Understanding the transition, occurring variously when temperature or applied stress is lowered, or the density raised, requires knowledge of interconnected changes in structure, thermodynamics, dynamics of structural relaxation and rheology. A unified and definitive picture of this jamming transition, has been an actively pursued goal with implications in diverse areas of research6. Random packings of frictionless hard and soft spheres have been studied in this general context6,7,8,9, and in particular as an idealized or reference model for granular materials. Much attention has been focused on behaviour as the jamming point, identified7,8 to occur as a packing fraction of about 64%, is approached. Although the density at which random close packing occurs is understood not to be unique (see, for example, refs 6,9,10 and references therein), many aspects of behaviour suggesting the jamming point (denoted henceforth as φJ) to be a critical point11, are robust6. Real granular materials studied experimentally inevitably deviate from this idealization, and how these deviations influence their jamming behaviour has been an active subject of recent research1,2,3,4,5,12. In particular, jamming of frictional grains under shear deformation, or shear jamming, has been shown to arise3 over a range of stresses, and of densities below φJ, resulting in a density–stress phase diagram that is substantially different from the frictionless case13. An extended range of jamming densities has also been discussed earlier in the context of random loose packing7,8,14, protocol dependence and memory effects15,16, and specifically for frictional packings1,2. Given that the structural changes and organization resulting from the shear deformation, as well as friction are likely to play an important role in generating shear-jammed packings, elucidating the role of each of these factors is central to understanding shear jamming. We address this issue here, through a computational study of sheared configurations of frictionless soft spheres.

We study a system of N = 2,000 equal-sized frictionless spheres interacting with a harmonic repulsive potential10,11 over a wide range of densities, from a packing fraction of 0.26–0.627, generated (for high densities) by rapid compression of fluid configurations or decompression of jammed configurations. Shear deformation is applied through an athermal quasistatic procedure13, by incrementing strain γxz in small steps (typically of dγ = 5 × 10−5, but as low as dγ = 5 × 10−12 in cases indicated), followed by energy minimization at each step. The procedure is applied until a steady state in which the shear stress σxz (which remains very small) and the average number of contacts Z reach stable values. Further details concerning the simulations and analysis are presented in the Methods and Supplementary Information.

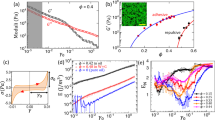
We monitor the evolution of the structure under shear by considering the pair correlation function g(r), the distribution of the number of contacts each sphere has, and the free-volume distribution, each of which exhibit unique signatures near the jamming point for frictionless sphere packings: the pair correlation function exhibits a near-contact power-law singularity g(r) ∼ ((r/σ) − 1)−α with α ∼ 0.45, and singularities in the (split) second peak17,18. The contact number distribution, which we compute with and without considering rattlers (rattlers are spheres with fewer than four contact neighbours), is peaked at Z = 6, the value required by the isostaticity condition. The free volumes of individual spheres are computed using an exact algorithm that employs the Voronoi tessellation, and the free-volume distribution exhibits a distinct power-law tail for nearly jammed packings, as described in ref. 19 and references therein. This feature of the free-volume distribution has also been observed for sheared configurations in two and three dimensions at high densities close to the jamming point20. In Fig. 1, we show how these features evolve, for sheared configurations at different values of strain for packing fraction φ = 0.58. It is seen that the g(r) develops a near-contact power law17,18, initially absent, as shear strain is increased (Fig. 1a), and the split-second peak develops the characteristic twin singularities (Fig. 1b)18. The peak of the distribution of contact numbers, initially at zero, evolves to larger values. Finally, the free-volume distribution, initially exhibiting a form typical of the fluid, develops a power-law tail characteristic of nearly jammed packings19. Thus, sheared fluid configurations at φ = 0.58 develop, by all of these measures, characteristics of jammed configurations. Figure 2 shows the same quantities in the steady state, for the range of densities studied, demonstrating the same behaviour at all densities. Whereas the near-contact power law in the g(r) is very similar in all cases, the sub-peak at smaller r in the second peak, as may be expected from packing considerations, becomes sharper as density increases. The average number of contacts moves from values less than 4 towards 6 as density increases. Table 1 summarizes information on contact numbers. The exponent in the free-volume distribution changes slightly with density, as does the exponent describing the near contact in g(r). Although these variations require explanation, the main point is clear: with an increase of shear strain, initially fluid configurations over a broad range of densities evolve structures that bear strong resemblance to jammed configurations.

Figure 1: Evolution of structure with shear strain.
figure 1

a, Evolution of radial distribution function g(r) for φ = 0.58 with strain (γ). For γ = 0.41, the system has reached the steady state and has a power law in g(r) extending over five decades. b, Radial distribution function showing changes in the second peak as the system is strained. As we move from the bottom curve to the top curve, the direction of increase in strain, the discontinuity in the second peak develops and becomes stronger. Each curve is shifted by 1 from the previous curve along the y axis for clarity. c, Distribution of contact number as a function of strain. At zero strain, there are no contact neighbours and after γ = 0.1, particles begin to have contact neighbours. d, Evolution of the free-volume distribution with strain. The power-law tail in f(Vf) develops around the same strain value for which contact neighbour distribution develops a peak at a non-zero value of Z. Data for nearly jammed configurations at 0.639 are shown in all panels for comparison (thick green lines).

Full size image
Figure 2: Structure in the steady state as a function of density.
figure 2

a, Power-law divergence in g(r) for sheared configurations in the steady state. The power-law exponent value depends slightly on density and is about 0.45 for the nearly jammed case. b, Singularities in the second peak of the g(r) are observed at all densities at and 2σ, with the feature at becoming stronger as density increases. c, Distribution of contact number. d, Free-volume distributions. The exponent of the power-law tail indicated by fit lines depends slightly on density. Data for nearly jammed configurations at 0.639 are shown in all panels for comparison (thick green lines).

Full size image
Table 1 Statistics of steady-state structural features of sheared packings.
Full size table

We consider next the statistics of the number of contacts and the distribution of forces between spheres. In Fig. 3a, we show the parametric relationship between the mean contact number and the density that we have of our sheared configurations of frictionless spheres. The mean contact number decreases from a 6 at the isotropic frictionless jamming density of ∼0.64, to a value of 4 at a density ∼0.55. Interestingly, the relationship shown by our data closely matches those of refs 1,2, for frictional jammed packings. The presence of a threshold density of 0.55 is further supported by the distribution of contact forces normalized to their mean value, P(f), shown in Fig. 3b. These distributions show a peak at finite values above φ = 0.55, a previously identified characteristic of jammed packings21,22,23. These results together indicate the presence of a threshold density 0.55, and a similarity between the sheared configurations of frictionless spheres we generate and frictional jammed packings. This observation has resonance with a number of other past suggestions, including the occurrence of a glass transition24, shear thickening25, onset of dilatancy and random loose packing14. The last of these, random loose packing, however, is a feature of frictional packings, and we have so far dealt with frictionless packings. An appealing picture, which we explore below, is that shear deformation, even in the absence of friction, serves to induce structures26 at densities above 0.55, and considerably below φJ, which may be stabilized by friction, when present, to produce shear-jammed packings.

Figure 3: Structural and mechanical indicators suggesting frictional jamming above φ = 0.55.
figure 3

a, Parametric plot showing the average contact number versus density for sheared configurations, compared with that of frictional packings obtained in refs 1,2. The average contact number becomes greater than 4 for φ ≥ 0.55. b, Distributions of contact forces for different densities, which exhibit a peak at finite values for φ ≥ 0.55. c, Configurations subjected to the Lubachevsky–Stillinger jamming protocol at different compression rates. Plotted are the resulting densities of jammed configurations indicating a change of behaviour for φ > 0.58. Compression rates in the legend are indicated by ‘CR’. d, Percolation of jammed (Z ≥ 2D) spheres in the sheared configurations indicating a percolation threshold at φ = 0.585, shown for different system sizes.

Full size image

Before we consider the role of friction, we consider the jamming properties of the sheared frictionless packings themselves, by applying the Lubachevsky–Stillinger27 jamming procedure (see Methods) for a range of compression rates to the configurations generated at different densities. For slow compression rates, for all initial densities, the resulting jammed configurations have densities close to φ = 0.64, as seen in Fig. 3c. However, at high compression rates, we note a difference in behaviour across φ ∼ 0.58. At higher initial densities, configurations jam at roughly the same density, but at lower initial densities, the jammed densities are higher. The possibility of generating jammed configurations above a density of 0.58, albeit at high compression rates, seems to be related to the percolation of locally stable structures. In Fig. 3d we show the percolation probability of spheres with contact number Z ≥ 2D = 6, for different system sizes N = 256, 2,000, 5,000, 20,000. The connected clusters of such spheres percolate at ∼0.58. The suggested possibility of 0.58 being a threshold that is distinct from that at density 0.55, and the analysis of other percolation characteristics that may elucidate the limiting density of 0.55 suggested by other results above, deserve further analysis but are not pursued further here. Percolation of D + 1 coordinated spheres occurs at a much lower density, data for which are shown in the Supplementary Information for completeness.

To assess whether sheared frictionless spheres can jam in the presence of friction, we perform simulations including frictional contact forces using the discrete-element method (DEM). We subject the steady-state sheared configurations to a strain step (dγ = 5 × 10−5) in addition to slight compression (see Methods and Supplementary Information), and evolve them using DEM, varying the friction coefficient μ and the damping coefficients ζn and ζt (see Methods and Supplementary Information), and monitor the evolution of the structure. We initially choose damping coefficients ζn = ζt = 0. Although the spheres do not move significantly during any of these simulations (with mean squared displacements less than 10−4), for small enough friction coefficients at any density, the shear stress and the average contact number decay rapidly to zero indicating that the structure is unjammed (see Supplementary Information). The threshold friction coefficient is identified at each density beyond which the sheared configurations remain jammed. For densities above φ = 0.58, sheared configurations remain jammed, but below, the configurations unjam for the studied range of friction coefficients. Figure 4a shows the threshold friction coefficients obtained, which compare reasonably well to values obtained in isotropic frictional simulations in ref. 2. Figure 4b shows the fraction of initial contacts that survive as a function of time, for large friction coefficients well above the threshold value, with steady-state configurations generated with dγ = 10−12. It is seen that most of the contacts remain intact for densities above φ = 0.57, but they decay to 0 below. A closer agreement with isotropic frictional simulations in ref. 2 is obtained by the inclusion of damping (as done in ref. 2), as shown in Fig. 4a. For ζn = 3 and 30 (ζt = (1/2)ζn) respectively, frictional jamming occurs down to φ = 0.58 and 0.57. The mean contact number Z, at the lower density limit to frictional jamming reaches 4 in all of these cases as shown in Fig. 4c. With a suitable procedure, we therefore expect the lower density limit to frictional jamming to be φ = 0.55, at which we obtain sheared frictionless packings with Z = 4. Thus, the sheared configurations of frictionless spheres we generate jam in the presence of friction above a threshold friction coefficient that closely matches those of isotropic frictional packings2, above the threshold density of 0.55. Shear-jammed configurations form from sheared steady-state configurations with negligible rearrangement, in contrast to isotropic frictional jamming, and are anisotropic, as shown in Fig. 4d. The anisotropy (defined from the fabric tensor; see Methods) of the shear-jammed configurations is identical to the sheared steady-state configurations in the range of densities where we obtain shear jamming. As an independent test, to be described elsewhere, we solve the force balance equations for the steady-state configurations using forces generated by DEM simulations as initial guesses, to obtain forces needed for force balance from geometric information alone.

Figure 4: Frictional jamming of sheared steady-state configurations.
figure 4

a, Threshold friction coefficient as a function of the density, beyond which sheared steady-state structures jam, for damping coefficients ζn = 0,3,30. Also shown for comparison are results for frictional packings obtained in ref. 2. b, Fraction of contact pairs initially present that survive as a function of time, for friction coefficients above the threshold (for density φ ≥ 0.57; for φ = 0.55 and 0.58 the friction coefficient is 100), and ζn = 3, η = 3. c, Comparison of coordination number Z of the initial structure and the final structure obtained from frictional dynamics after applying a strain of Δγ = 5 × 10−5. Curves labelled ζn = 0,3,30 are for steady-state configurations with dγ = 10−5, just above the threshold friction coefficient, and no solvent friction, whereas configurations for the curve labelled ζn = 3, η = 3 are obtained with dγ = 10−12, for friction coefficients well above the threshold, and finite solvent friction η. The contact number is close to, but different from, the initial value for densities above φ = 0.57, whereas they are zero for lower densities (except the case ζn = 3, η = 3, where overdamping results in cessation of particle motion before all contacts are lost). d, Fabric anisotropy as a function of packing density for steady-state (SS), shear-jammed (SJ) and isotropic frictional jammed (ISO) configurations. The anisotropy of steady-state and shear-jammed packings is the same.

Full size image

Although many questions are suggested from the results above that must be investigated further, they show that shear deformation of spheres even in the absence of friction at densities well below the isotropic jamming point leads to the emergence of geometric features resembling jammed packings, with a threshold density that may be identified with the random-loose-packing limit that may be identified with the case of infinite friction. The force distributions and the relationship between the packing fraction and contact number in the steady state support the comparison of the sheared configurations above the threshold density with frictional jammed packings with varying friction. Our results thus serve to disentangle the role of structure formation under shear and friction in the generation of shear jamming phenomenology. They also identify the lower limit of shear jamming with random loose packing. Whether the same kind of structure formation can arise in isotropic compression12 rather than shear, analysis of the anisotropies in sheared structures, and the role of finite shear rates present some obvious questions to pursue in future work. It is also of interest to investigate further the similarities and differences between our results and those for shear-jammed states obtained in frictionless packings16 above a limit density for isotropic jamming.

Methods

The model system we study is composed of N = 2,000 frictionless spheres interacting with soft harmonic repulsive potential, v(r) = (ε/2)(1 − (r/σ))2, where ε and σ, the interaction strength and size of the spheres, define the reduced units used throughout. The initial configurations are hard-sphere configurations, obtained at high densities in two ways: starting from an equilibrated hard-sphere fluid at initial density 0.45, a fast initial compression is effected using a Monte Carlo simulation until the desired density is reached for the initial configurations; starting from packings at φj, obtained by the Lubachevsky–Stillinger jamming protocol27, lower density configurations are obtained by rescaling the simulation box size. The Lubachevsky–Stillinger procedure involves event-driven molecular dynamics of hard spheres, whose radii are inflated at a specified rate. The procedure terminates when the radii cannot be increased by any finite amount without the next collision of a pair of spheres intervening, or when the collision rate diverges. In practice, the procedure is terminated when the sphere radii do not change by more than 10−10 between successive collisions.

Athermal quasistatic simulations are performed using LAMMPS (ref. 28), which involves the following steps: affine transformation of coordinates by a small step with dγ = 5 × 10−5; energy minimization using the conjugate-gradient method, employing Lees–Edwards periodic boundary conditions. This procedure is used until steady states are reached. We also use a strain step of dγ = 5 × 10−12 to shear steady-state configurations further to validate our contact definition (see below), to evaluate contact forces and to perform frictional simulations.

Data shown are averaged over 50–70 initial independent configurations, except those in Fig. 4, which are averaged over 10 configurations, Fig. 3b, which are averaged for 20 configurations, and Fig. 3d, which are averaged over 1,000 configurations.

We use a cutoff of ∼10−5, which is the distance at which g(r) deviates from the power law, to define contact neighbours to compute the contact number Z. This cutoff is a precision limit that is dependent on the strain step used in athermal quasistatic simulations, as we show in the Supplementary Information by considering various dγ down to 5 × 10−12. To have a consistent definition of contact, we compress configurations by rescaling the diameter of the spheres (by ∼10−5 when dγ = 5 × 10−5 and ∼10−12 when dγ = 5 × 10−12 and so on) so that all neighbour pairs identified as contact neighbours have finite contact forces. As this equivalence becomes more exact for smaller strain steps, we consider steady-state configurations with strain step dγ = 5 × 10−12 when evaluating forces between contact neighbours (Fig. 3b). The data for frictional simulations (Fig. 4) are for dγ = 5 × 10−5. Data shown in the Supplementary Information validate in detail the procedure we adopt.

To generate jammed configurations using the Lubachevsky–Stillinger procedure, the small overlaps in the sheared configurations are removed by decreasing the diameter by a small amount (∼10−9), which is then increased to unity through the Lubachevsky–Stillinger protocol with a fast compression rate of 0.1, involving negligible displacements of spheres (∼10−16). We use the steady-state configurations to calculate free volumes of the particles using the algorithm described in ref. 19.

To test the stability of steady-state sheared structures in the presence of friction, we use the discrete-element method29 to model contact interactions between particles through a repulsive linear spring–dashpot model. The model, described further in the Supplementary Information, involves normal and tangential spring constants κn, κt, damping coefficients ζn, ζt = (1/2)ζn, and the friction coefficient μ as parameters. The model parameters used are κn = κt = 2 and the normal contact damping ζn = 0,3,30. The contacts present when friction is turned on provide the initial condition for the contact history. Tangential forces, initially zero, are generated by subsequent tangential displacements during the time the contact remains unbroken. At each contact, the Coulomb yield criterion is obeyed; that is, Ft ≤ μFn, where μ is the friction coefficient, which is initially varied from 0.01 to 100 in multiples of 10 to bracket the threshold value beyond which configurations are jammed. Threshold μ values are refined further by considering a finer grid of values. Configurations identified as jammed exhibit a finite shear modulus, which we illustrate in one case in the Supplementary Information.

Anisotropy of initial and jammed structures for isotropic and sheared steady-state initial conditions is calculated, using the fabric tensor, defined as

where rij are distance vectors between contact neighbours. The normalized difference between the largest eigenvalue C1 to the smallest C3, (C1 − C3)/(C1 + C2 + C3) defines the fabric anisotropy. The normalization (C1 + C2 + C3) equals the mean number of contacts per sphere.