Abstract
The spin Hall effect and its inverse have key roles in spintronic devices as they allow conversion of charge currents to and from spin currents. The conversion efficiency strongly depends on material details, such as the electronic band structure and the nature of impurities. Here we show an anomaly in the inverse spin Hall effect in weak ferromagnetic NiPd alloys near their Curie temperatures with a shape independent of material details, such as Ni concentrations. By extending Kondo's model for the anomalous Hall effect, we explain the observed anomaly as originating from the second-order nonlinear spin fluctuation of Ni moments. This brings to light an essential symmetry difference between the spin Hall effect and the anomalous Hall effect, which reflects the first-order nonlinear fluctuations of local moments. Our finding opens up a new application of the spin Hall effect, by which a minuscule magnetic moment can be detected.
Similar content being viewed by others
Introduction
Spintronics has provided an impetus for the intensive development of techniques to generate or detect spin currents, such as nonlocal spin injection1, spin pumping2 and spin light emission devices3. The spin Hall effect (SHE)4, which converts a charge current to a spin current, and its inverse have been widely explored in semiconductors3,4,5 and nonmagnetic metals2,6,7 by using such techniques. Although most of the work has concentrated on the phenomenon and mechanism of the SHE itself, Uchida et al. have used the SHE as a detector of a spin-dependent chemical potential arising from the spin Seebeck effect8,9. Further applications of the SHE are, however, still lacking. Recently, the doping of gold with individual iron impurities was considered as a mechanism to enhance the SHE through spin fluctuations of the iron moments10. This raises the question whether the SHE might be sensitive to collective fluctuations, in particular, close to a magnetic phase transition where the fluctuations are strong. As for the anomalous Hall effect (AHE) in a pure ferromagnetic metal such as Fe11 and Ni11,12, a sharp peak of the Hall resistivity (ρH) appears only below the Curie temperature (TC). This can be understood as an effect of fluctuations of local magnetic moments13.
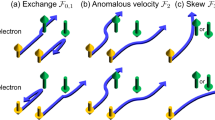
In this report, we demonstrate experimentally, and provide a theoretical argument, that the inverse SHE (ISHE) also shows an anomaly, but that it is substantially different from that of the AHE. Figure 1 shows schematic images of the AHE and the ISHE of a weak ferromagnetic material near TC. In the AHE, a charge current is injected into the ferromagnetic material, and the difference of the skew scattering probabilities for spin-up and spin-down electrons results in a Hall voltage. In the ISHE, on the other hand, a spin current is injected and both spin-up and spin-down electrons are deflected to the same side, which also results in a Hall voltage. Contrary to the AHE, however, we observe a dip and peak in the ISHE for weak ferromagnetic NiPd alloys below and above TC, respectively. As the quantity of the involved Ni ions are very small, the present system could be used for sensitive magnetometry.
(a) AHE (incident charge current JC) and (b) ISHE (incident spin current JS). The green and pink spheres represent the conduction electrons (that is, −|e|) and localized ones, and the grey arrows show the directions of spins. The fluctuation of the localized spins near TC is indicated by the longer grey arrows with shades. The skew scattering probabilities for spin-up and spin-down conduction electrons, resulting in anomalous Hall or inverse spin Hall voltage, are represented by red and blue arrows, respectively.
Results
AHE and ISHE of NiPd alloys
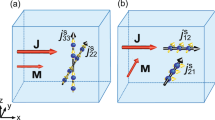
We measured the SHE of a weakly ferromagnetic NiPd nanowire with 7, 8 and 9% Ni using the nonlocal spin injection technique14,15,16 at 5–50 K. Figure 2a,b shows the schematic structure and scanning electron microscopic image of the lateral spin valve with the NiPd middle wire. The NiPd alloy is a weak ferromagnet when the Ni concentration is larger than 2.3% (ref. 17). Depending on the Ni concentration, its TC varies from a few K to hundreds of K. To characterize the magnetic property of NiPd wires in our devices, AHE measurements were performed for the reference NiPd Hall bars prepared at the same time as the SHE devices. A representative AHE resistance Rxy for Ni0.08Pd0.92, which is proportional to the magnetization, is shown in Fig. 3a. We note that in the AHE measurements, the external field H was applied perpendicularly to the plane, which is different from the ISHE measurements (see Fig. 2b). At T=5 K, a hysteresis loop of the magnetization can be clearly seen. With increasing temperature, the magnetization continually decreases to zero and Rxy simply shows the ordinary Hall resistance above 30 K. The Curie temperature TC for Ni0.08Pd0.92 can be determined to be about 21 K by plotting the remnant magnetization Mr and coercive field Hc versus temperature (Fig. 3b), which is lower than the value for the bulk alloy18. This is presumably due to the imperfect distribution of Ni in our alloy, prepared by the ion implantation technique, compared with bulk alloys (see Methods). We also performed the same measurements for the other two concentrations where TC for Ni0.07Pd0.93 and Ni0.09Pd0.91 are 16 and 32 K, respectively.
(a) Schematic image of the device. The green spheres with the red and blue arrows correspond to spin-up and spin-down electrons, respectively. JC and JS are the charge and spin current, respectively. The thinner red and blue arrows indicate the spin-up and spin-down electron motion, respectively. (b) Scanning electron microscopic image of the device consisting of two Py wires and a NiPd middle wire bridged by a Cu wire. The arrow for the magnetic field H represents the positive direction in the case of ISHE measurement.
(a) AHE resistance Rxy at different temperatures. The remnant magnetization Mr and coercive field Hc correspond to Rxy at H=0 Oe and the x-intercept of Rxy curve, respectively. (b) Temperature dependence of Mr and Hc. From both plots, TC can be determined to be 21 K. (c) Representative RISHE curves of Ni0.08Pd0.92 measured at 10, 20, 22 and 30 K. At 20 and 22 K, RISHE at high fields is reduced and enhanced, respectively. (d) A typical anisotropic magnetoresistance of Py1 measured at 10 K. (e) Three-dimensional plot of RISHE as a function of temperature (15–25 K) and magnetic field, represented by both height and colour.
The ISHE is based on the spin to charge current conversion, which follows the vector product as below: JC  JS × sC, where JC and JS are the charge and spin current density, sC is the spin orientation of the conduction electron. Our device configuration is depicted in Fig. 2a. The charge current flows from one of two Ni0.81Fe0.19 (hereafter Py) wires, that is, Py1 to the left hand side of the Cu wire. As the spin–orbit (SO) interaction of Cu is quite weak, it works as a transmitter of the generated spin current at the Cu/Py1 interface to the right hand side of the Cu wire. The spin current is preferentially absorbed into the NiPd middle wire below the Cu wire because of its strong SO interaction. This absorption is confirmed by a reduction of the nonlocal spin valve signal detected at the second Py electrode Py2, as detailed in refs 15 and 16. In the case of Ni0.08Pd0.92, the nonlocal spin valve signal is reduced to 0.25 compared with the value without the NiPd middle wire, and the spin diffusion length is estimated to be 10 nm. The absorbed spin-up and spin-down electrons with the orientation sC parallel to the hard direction of the Py wires are scattered by Ni impurities in Pd, resulting in the Hall voltage VISHE. From the field variation, the overall change of ISHE resistance RISHE (equal to VISHE divided by the charge current) can be observed.
JS × sC, where JC and JS are the charge and spin current density, sC is the spin orientation of the conduction electron. Our device configuration is depicted in Fig. 2a. The charge current flows from one of two Ni0.81Fe0.19 (hereafter Py) wires, that is, Py1 to the left hand side of the Cu wire. As the spin–orbit (SO) interaction of Cu is quite weak, it works as a transmitter of the generated spin current at the Cu/Py1 interface to the right hand side of the Cu wire. The spin current is preferentially absorbed into the NiPd middle wire below the Cu wire because of its strong SO interaction. This absorption is confirmed by a reduction of the nonlocal spin valve signal detected at the second Py electrode Py2, as detailed in refs 15 and 16. In the case of Ni0.08Pd0.92, the nonlocal spin valve signal is reduced to 0.25 compared with the value without the NiPd middle wire, and the spin diffusion length is estimated to be 10 nm. The absorbed spin-up and spin-down electrons with the orientation sC parallel to the hard direction of the Py wires are scattered by Ni impurities in Pd, resulting in the Hall voltage VISHE. From the field variation, the overall change of ISHE resistance RISHE (equal to VISHE divided by the charge current) can be observed.
We show representative ISHE resistance RISHE curves for Ni0.08Pd0.92 as a function of the magnetic field at various temperatures in Fig. 3c, where all curves are shifted for clarity. Generally, RISHE increases linearly with the magnetic field up to 2,000 Oe and then becomes flat. This is consistent with the saturation of the magnetization of Py1, indicated by the anisotropic magnetoresistance curve of Py1 shown in Fig. 3d. In the following, we focus on RISHE with saturated magnetization of Py1 (that is, |H|>2,000 Oe). For temperatures far below (10 K; black curve) and above (30 K; pink curve) TC, RISHE is completely flat at high enough fields, which is as expected in the ISHE for nonmagnetic systems. The values of RISHE are much larger than those for pure Pd, where an intrinsic mechanism should apply16,19,20 and we will argue that this increase comes from the extrinsic effect of the Ni impurities.
For temperatures near TC, in contrast, anomalous behaviour can be clearly seen. At 20 K just below TC (≈21 K), RISHE decreases with increasing the magnetic field (|H|) up to 8,000 Oe and then flattens out (see the red curve in Fig. 3c). Just above TC, at 22 K, on the other hand, RISHE has a positive slope versus magnetic field even above 2,000 Oe and is not yet saturated at our maximum field. By making many similar scans for a full temperature range from 10 to 30 K, we can display this behaviour more clearly seen in the three-dimensional plot shown in Fig. 3e. The x and y axes are the magnetic field and temperature, respectively, whereas both the z axis and colour represent RISHE. When the temperature crosses TC, a reduction first appears at 20 K as a light blue peak at negative fields or a light-yellow dip at positive fields (see red triangles in Fig. 3e); then an enhancement appears at 22 K as a dark blue dip at negative fields or a red peak at positive fields (see blue stars in Fig. 3e). Such a behaviour of RISHE is observed below and above but only in the vicinity of TC. As already mentioned, RISHE for a nonmagnetic metal should be completely flat at any temperature. It is thus unambiguous that the observed change in RISHE of the NiPd alloys near TC is correlated to the magnetic phase transition of the NiPd wire (see Fig. 3b). On the other hand, such an anomaly near TC is not observed in the temperature dependence of the spin absorption rate or the spin diffusion length of NiPd. This is because the spin diffusion length depends simply on the resistivity and the SO interaction of the NiPd wire, whereas the ISHE signal is strongly affected by the type of scattering mechanisms, that is, skew scattering, side-jump or band structure.
Anomaly in ISHE of NiPd alloys near the Curie temperature
To better quantify the contribution to the ISHE intrinsic to the NiPd wire, we define the change in RISHE as ΔRISHE≡[RISHE (Hmax)−RISHE (−Hmax)]/2, as shown in Fig. 3c. As a maximum field Hmax, we chose 8,800 Oe in this work. Certainly, RISHE at 22 K is not fully saturated even at 8,800 Oe, which is different from RISHE at 20 K. This is related to the fact that it is much more difficult to align the localized magnetic moments of Ni impurities above TC compared with those below TC even if high magnetic fields are applied. In Fig. 4a, we plot ΔRISHE of Ni0.08Pd0.92 (shown by red dots) as a function of temperature. The anomaly of ΔRISHE near TC is clearly seen. Below 18 K, ΔRISHE is almost constant with temperature. Only in the vicinity of TC, however, it shows a dip and peak structure at 20 and 21.5 K, respectively. As ΔRISHE varies little with temperature except near TC, it can be separated into the temperature-independent background  and the anomalous part δΔRISHE, as
and the anomalous part δΔRISHE, as  . The results for NiPd with 7% and 9% of Ni are plotted with black squares and blue triangles, respectively. The increase of
. The results for NiPd with 7% and 9% of Ni are plotted with black squares and blue triangles, respectively. The increase of  with the doping concentration suggests the extrinsic contribution induced by the Ni impurities. Thus,
with the doping concentration suggests the extrinsic contribution induced by the Ni impurities. Thus,  comes from both the extrinsic SHE of Ni impurities and the intrinsic SHE of Pd16. Despite the fact that
comes from both the extrinsic SHE of Ni impurities and the intrinsic SHE of Pd16. Despite the fact that  depends strongly on the Ni concentrations, δΔRISHE does so primarily via a shift to be near the corresponding TC. We emphasize that such critical behaviour was reproducible for each of at least three samples at each Ni concentration—thus our arguments are based on more than ten complete data sets, of which only one is shown in Fig. 3e.
depends strongly on the Ni concentrations, δΔRISHE does so primarily via a shift to be near the corresponding TC. We emphasize that such critical behaviour was reproducible for each of at least three samples at each Ni concentration—thus our arguments are based on more than ten complete data sets, of which only one is shown in Fig. 3e.
(a) Inverse spin Hall resistance ΔRISHE of NixPd1-x middle wires with Ni concentration x=0.07 (black square), 0.08 (red dot) and 0.09 (blue triangle) as a function of temperature. The anomaly of ΔRISHE for each Ni concentration appears only near its TC. (b) The anomalous component δΔRISHE for Ni concentration equal to x=0.07 (black square), 0.08 (red dot) and 0.09 (blue triangle) plotted as a function of normalized temperature (T−TC)/TC. For comparison, we also show the uniform second-order nonlinear susceptibility χ2uni (black solid line).
For the three concentrations, δΔRISHE are plotted as a function of the reduced temperature (T−TC)/TC in Fig. 4b. Note that each curve corresponds to one full data set: for example, the red line represents a reduction of all of Fig. 3e. Although the three devices have different TC and  , the anomalous behaviour appears to be universal near TC: the three curves almost scale onto one. The amplitudes of the dip and peak are about 5 μΩ. The anomalous behaviour disappears when the reduced temperature differs from TC by 10%. These results are obviously different from the case of the AHE13, where the anomaly of the Hall resistivity ρH appears only below TC.
, the anomalous behaviour appears to be universal near TC: the three curves almost scale onto one. The amplitudes of the dip and peak are about 5 μΩ. The anomalous behaviour disappears when the reduced temperature differs from TC by 10%. These results are obviously different from the case of the AHE13, where the anomaly of the Hall resistivity ρH appears only below TC.
Discussion
What is the origin of the anomaly of δΔRISHE observed only in the vicinity of TC? Resistive anomalies near magnetic critical points TC have been studied for a long time. The anomaly near TC in the longitudinal resistivity appears within the first Born approximation from quadratic fluctuations  (Mi−
(Mi− Mi
Mi )(Mj−
)(Mj− Mj
Mj )
) in the moments Mi and Mj of localized spins at sites i and j, where contributions come only when i and j are within a certain cutoff distance21. The resistivity then depends on a linear local magnetic susceptibility
in the moments Mi and Mj of localized spins at sites i and j, where contributions come only when i and j are within a certain cutoff distance21. The resistivity then depends on a linear local magnetic susceptibility  , which is a summation of short-range fluctuations up to this distance. To simplify notation we shall denote the sum of such short-range correlations as ∑
, which is a summation of short-range fluctuations up to this distance. To simplify notation we shall denote the sum of such short-range correlations as ∑ (M−
(M− M
M )2
)2 , omitting the site subscripts, and we shall use similarly abbreviated notations for higher-order moments. As mentioned in the introduction, the anomaly of ρH in the AHE near TC was explained by Kondo13. Note that the quantities r1 and r2 in ref. 13 correspond to a first-order nonlinear susceptibility
, omitting the site subscripts, and we shall use similarly abbreviated notations for higher-order moments. As mentioned in the introduction, the anomaly of ρH in the AHE near TC was explained by Kondo13. Note that the quantities r1 and r2 in ref. 13 correspond to a first-order nonlinear susceptibility  and a second-order nonlinear susceptibility
and a second-order nonlinear susceptibility  , respectively. We change notation for simplicity, and also to emphasize that Kondo makes a strictly local approximation, whereas we extend the theory to include nearby correlations between atomic moments. The anomaly of ρH in the AHE appears from the first-order fluctuation of local moments
, respectively. We change notation for simplicity, and also to emphasize that Kondo makes a strictly local approximation, whereas we extend the theory to include nearby correlations between atomic moments. The anomaly of ρH in the AHE appears from the first-order fluctuation of local moments  . The second-order spin fluctuation
. The second-order spin fluctuation  is also defined in ref. 13, but made no contribution to the AHE. This will be explained below; we first note that the
is also defined in ref. 13, but made no contribution to the AHE. This will be explained below; we first note that the  and
and  terms appear in the s-d Hamiltonian to the same order with respect to the SO coupling constant λ of the localized moment. The term in
terms appear in the s-d Hamiltonian to the same order with respect to the SO coupling constant λ of the localized moment. The term in  changes sign for spin-up or -down electrons, whereas
changes sign for spin-up or -down electrons, whereas  does not. Thus, the scattering amplitudes for spin-up and -down conduction electrons are different and proportional to
does not. Thus, the scattering amplitudes for spin-up and -down conduction electrons are different and proportional to  and
and  , respectively13. As illustrated in Fig. 1, in the case of the AHE configuration, spin-up and -down conduction electrons are scattered to opposite directions. As a result, ρH is proportional to the difference of scattering amplitudes between spin-up and -down electrons, that is,
, respectively13. As illustrated in Fig. 1, in the case of the AHE configuration, spin-up and -down conduction electrons are scattered to opposite directions. As a result, ρH is proportional to the difference of scattering amplitudes between spin-up and -down electrons, that is,  . On the other hand, in the ISHE configuration, both spin-up and -down electrons are scattered to the same side. Unlike the AHE, the obtained RISHE is proportional to the sum of scattering amplitudes between spin-up and -down electrons, that is,
. On the other hand, in the ISHE configuration, both spin-up and -down electrons are scattered to the same side. Unlike the AHE, the obtained RISHE is proportional to the sum of scattering amplitudes between spin-up and -down electrons, that is,  . The effect of such terms has been hidden for 50 years13. However, it is naturally expected that the contributions related to
. The effect of such terms has been hidden for 50 years13. However, it is naturally expected that the contributions related to  can survive if the incident current is the spin current, which is exactly the case for the ISHE.
can survive if the incident current is the spin current, which is exactly the case for the ISHE.
To make a comparison between theory and experiment, we should, in principle, calculate  , which is integrated over the Fermi surface. This
, which is integrated over the Fermi surface. This  should be proportional to the experimental δΔRISHE. However, the integration depends essentially on the Fermi wave vector, which acts as a cutoff to any divergence. To avoid including material-dependent parameters, we compare with a quantity, the uniform second-order nonlinear susceptibility
should be proportional to the experimental δΔRISHE. However, the integration depends essentially on the Fermi wave vector, which acts as a cutoff to any divergence. To avoid including material-dependent parameters, we compare with a quantity, the uniform second-order nonlinear susceptibility  , which is independent of cutoff.
, which is independent of cutoff.  is the response of the moments on all the sites to a uniform magnetic field and is the sum of correlations over all distances without any cutoff (see Supplementary Discussion). In Fig, 4b we superimpose on the experimental data a mean-field calculation of
is the response of the moments on all the sites to a uniform magnetic field and is the sum of correlations over all distances without any cutoff (see Supplementary Discussion). In Fig, 4b we superimpose on the experimental data a mean-field calculation of  . It diverges with opposites signs above and below TC. We interpret the dip and peak observed in the experimental data as a smearing of such a divergence. In a full calculation the theoretical spin Hall resistance should also be smeared: the divergence is cutoff, just as for the longitudinal resistance21. To confirm the above scenario, we have performed Monte Carlo simulations for
. It diverges with opposites signs above and below TC. We interpret the dip and peak observed in the experimental data as a smearing of such a divergence. In a full calculation the theoretical spin Hall resistance should also be smeared: the divergence is cutoff, just as for the longitudinal resistance21. To confirm the above scenario, we have performed Monte Carlo simulations for  where the contribution of nearest-neighbour correlations is taken into account. As can be seen in Supplementary Fig. S1, the smearing of the divergence of
where the contribution of nearest-neighbour correlations is taken into account. As can be seen in Supplementary Fig. S1, the smearing of the divergence of  at TC is well reproduced. Thus, we argue that neither the full theory nor the experiments should diverge at TC.
at TC is well reproduced. Thus, we argue that neither the full theory nor the experiments should diverge at TC.
Finally, we note that the anomaly of ρH in the AHE in pure Fe11 and Ni11,12 may alternatively be explained by Karplus and Luttinger's theory, which is based on band effects22. In this theory, ρH would be proportional to ρxx2 M
M where ρxx is the longitudinal resistivity and
where ρxx is the longitudinal resistivity and  M
M is the averaged magnetization. As
is the averaged magnetization. As  M
M is zero above TC, the sign change of RISHE below and above TC seems to preclude explanation by such band effects.
is zero above TC, the sign change of RISHE below and above TC seems to preclude explanation by such band effects.
In conclusion, we have demonstrated a characteristic behaviour of the SHE at the magnetic phase transition of the weak ferromagnetic NiPd near its Curie temperature TC. It can be explained by the fluctuation contributions to skew scattering via SO interactions, and appears as the second-order nonlinear spin fluctuation  . Considering the small volume of NiPd wire (10−16 cm3) and the magnetic moment of NiPd, the total magnetic moment involved in the experiment is extremely small: <10−14 emu. Such a tiny moment is far below the sensitivity of magnetometer (for instance, 10−8 emu for SQUID). The successful extractions of the contribution of higher-order spin fluctuations in our experiments prove the extremely high sensitivity of our method. This technique could be very useful to understand more complex spin textures such as spin-glasses and spin-ice. For those systems, the linear magnetic susceptibility
. Considering the small volume of NiPd wire (10−16 cm3) and the magnetic moment of NiPd, the total magnetic moment involved in the experiment is extremely small: <10−14 emu. Such a tiny moment is far below the sensitivity of magnetometer (for instance, 10−8 emu for SQUID). The successful extractions of the contribution of higher-order spin fluctuations in our experiments prove the extremely high sensitivity of our method. This technique could be very useful to understand more complex spin textures such as spin-glasses and spin-ice. For those systems, the linear magnetic susceptibility  has been well studied so far but there have been almost no experimental studies of the higher-order spin fluctuations, where some important physics might be still hidden. The present method constitutes a novel approach to detect high-order nonlinear fluctuations with an extremely high sensitivity, which is impossible to achieve by a direct measurement. This will broaden the application of the SHE from potential devices to a means of measuring higher-order spin fluctuations, particularly in the critical region.
has been well studied so far but there have been almost no experimental studies of the higher-order spin fluctuations, where some important physics might be still hidden. The present method constitutes a novel approach to detect high-order nonlinear fluctuations with an extremely high sensitivity, which is impossible to achieve by a direct measurement. This will broaden the application of the SHE from potential devices to a means of measuring higher-order spin fluctuations, particularly in the critical region.
Methods
Sample preparation
The spin Hall devices were fabricated on a thermally oxidized silicon substrate using electron beam lithography on poly(methyl methacrylate) resist and a subsequent lift-off process. Here we used a lateral spin valve structure, which consists of two Py wires (30-nm thick and 100-nm wide) with a separation distance of 1 μm and a NiPd middle wire (20-nm thick and 100-nm wide) bridged by a Cu wire (100-nm thick and 100-nm wide) as is detailed in Fig. 2 in the main text. A Pd wire was first deposited by electron beam evaporation using a 99.999% purity source. To form the NiPd alloy wire with a Ni content of 7, 8 and 9%, we implanted a suitable amount of Ni+ into the Pd wire using an Ion Implanter (NH-20SR) with an acceleration voltage of 30 kV. As is mentioned in the main text, the prepared NiPd alloy is not perfectly homogenous and nickel is distributed over ~10 nm below the Cu/NiPd interface in 20 nm thick Pd wires. This nickel distribution would lower the TC compared with bulk NiPd alloys. However, the spin diffusion length of NiPd of about 10 nm corresponds to the maximum distribution of Ni in Pd. That is why we could still observe the spin fluctuation of Ni moment. The two Py wires were deposited by electron beam evaporation, whereas the Cu bridge was fabricated by a Joule heating evaporator. Before the Cu evaporation, a careful Ar ion beam milling with a beam current of 12 mA and beam voltage of 600 V was performed for 30 s to clean the surfaces of Py and NiPd wires and to obtain highly transparent contacts.
Additional information
How to cite this article: Wei, D.H. et al. The spin Hall effect as a probe of nonlinear spin fluctuations. Nat. Commun. 3:1058 doi: 10.1038/ncomms2063 (2012).
References
Jedema, F. J., Heersche, H. B., Filip, A. T., Baselmans, J. J. A. & van Wees, B. J. Electrical detection of spin precession in a metallic mesoscopic spin valve. Nature 416, 713–716 (2002).
Saitoh, E., Ueda, M., Miyajima, H. & Tatara, G. Conversion of spin current into charge current at room temperature: inverse spin-Hall effect. Appl. Phys. Lett. 88, 182509 (2006).
Wunderlich, J., Kaestner, B., Sinova, J. & Jungwirth, T. Experimental observation of the spin Hall effect in a two-dimensional spin-orbit coupled semiconductor system. Phys. Rev. Lett. 94, 047204 (2005).
Dyakonov, M. I. & Perel, V. I. Current-induced spin orientation of electrons in semiconductors. Phys. Lett. A 35, 459–460 (1971).
Kato, Y. K., Myers, R. C., Gossard, A. C. & Awschalom, D. D. Observation of the spin Hall effect in semiconductors. Science 306, 1910–1913 (2004).
Valenzuela, S. O. & Tinkham, M. Direct electronic measurement of the spin Hall effect. Nature 442, 176–179 (2006).
Kimura, T., Otani, Y., Sato, T., Takahashi, S. & Maekawa, S. Room-temperature reversible spin Hall effect. Phys. Rev. Lett. 98, 156601 (2007).
Uchida, K. et al. Observation of the spin Seebeck effect. Nature 455, 778–781 (2008).
Uchida, K. et al. Spin Seebeck insulator. Nat. Mater. 9, 894–897 (2010).
Gu, B. et al. Quantum renormalization of the spin Hall effect. Phys. Rev. Lett. 105, 086401 (2010).
Jan, J.-P. Effet Hall et température dans les conducteurs ferromagnétiques. Helv. Phys. Acta. 25, 677–700 (1952).
Lavine, J. M. Extraordinary Hall-effect measurements on Ni, some Ni alloys, and ferrites. Phys. Rev. 123, 1273–1277 (1961).
Kondo, J. Anomalous Hall effect and magnetoresistance of ferromagnetic metals. Prog. Theor. Phys. 27, 772–792 (1962).
Vila, L., Kimura, T. & Otani, Y. Evolution of the spin Hall effect in Pt nanowires: size and temperature effects. Phys. Rev. Lett. 99, 226604 (2007).
Niimi, Y. et al. Extrinsic spin Hall effect induced by iridium impurities in copper. Phys. Rev. Lett. 106, 126601 (2011).
Morota, M. et al. Indication of intrinsic spin Hall effect in 4d and 5d transition metals. Phys. Rev. B 83, 174405 (2011).
Murani, A. P., Tari, A. & Coles, B.R. Critical concentration for the onset of ferromagnetism in Pd-Ni alloys. J. Phys. F Metal Phys. 4, 1769–1781 (1974).
Liechtenstein, A. I., Katsnelson, M. I., Antropov, V. P. & Gubanov, V. A. Local spin density functional approach to the theory of exchange interactions in ferromagnetic metals and alloys. J. Magn. Magn. Mater. 67, 65–74 (1987).
Guo, G. Y., Murakami, S., Chen, T.-W. & Nagaosa, N. Intrinsic spin Hall effect in platinum: first-principles calculations. Phys. Rev. Lett. 100, 096401 (2008).
Tanaka, T. et al. Intrinsic spin Hall effect and orbital Hall effect in 4d and 5d transition metals. Phys. Rev. B 77, 165117 (2008).
Fisher, M. E. & Langer, J. S. Resistive anomalies at magnetic critical points. Phys. Rev. Lett. 20, 665–668 (1968).
Karplus, R. & Luttinger, J. M. Hall effect in ferromagnetics. Phys. Rev. 95, 1154–1160 (1954).
Acknowledgements
We thank Y. Iye and S. Katsumoto for the use of the lithography facilities. T.Z. also thanks the Advanced Science Research Center of the JAEA for support via the REIMEI program. This work was supported by KAKENHI and a Grant-in-Aid for Scientific Research in Priority Area from MEXT.
Author information
Authors and Affiliations
Contributions
D.H.W. and Y.N. designed the experiments and fabricated devices. D.H.W. collected the data and carried out the analysis. B.G., T.Z. and S.M. developed the theoretical analysis. B.G. developed the detailed equations in Supplementary Information. Y.O. planned and supervised the project. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figure S1, Supplementary Discussion and Supplementary References (PDF 68 kb)
Rights and permissions
About this article
Cite this article
Wei, D., Niimi, Y., Gu, B. et al. The spin Hall effect as a probe of nonlinear spin fluctuations. Nat Commun 3, 1058 (2012). https://doi.org/10.1038/ncomms2063
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2063
This article is cited by
-
Critical enhancement of the spin Hall effect by spin fluctuations
npj Quantum Materials (2024)
-
Paramagnon-Enhanced Spin Currents in a Lattice near the Curie Point
Scientific Reports (2018)
-
A new pathway towards all-electric spintronics: electric-field control of spin states through surface/interface effects
Science China Physics, Mechanics and Astronomy (2013)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.