Anomalous spin Hall and inverse spin Hall effects in magnetic systems

Abstract

Spin current is a very important tensor quantity in spintronics. However, the well-known spin-Hall effect (SHE) can only generate a few of its components whose propagating and polarization directions are perpendicular with each other and to an applied charge current. It is highly desirable in applications to generate spin currents whose polarization can be in any possible direction. Here anomalous SHE and inverse spin-Hall effect (ISHE) in magnetic systems are predicted. Spin currents, whose polarisation and propagation are collinear or orthogonal with each other and along or perpendicular to the charge current, can be generated, depending on whether the applied charge current is along or perpendicular to the order parameter. In anomalous ISHEs, charge currents proportional to the order parameter can be along or perpendicular to the propagating or polarization directions of the spin current.

Introduction

The terminology and recent escalating research activities on spin Hall effect (SHE), originally proposed by Dyakonov and Perel¹, are largely due to the rediscovery of the effect by Hirsch² and due to the subsequent experimental verifications of the effect in semiconductor devices^3,4. SHE is widely used to generate spin current, and inverse SHE (ISHE) is for spin current detection. Similar to electric currents in electronics that perform all kinds of tasks, spin currents can carry and process information in spintronics. Different from an electric current that is the flow of charges, a scalar, a spin current is the flow of angular momenta, a vector. In the Cartesian coordinates, spin current is a tensor of rank two with nine components, instead of a vector for electric currents. A spin current passing through a magnetic material can exert a torque on spins or on magnetic moments. This torque is component sensitive and useful as a control knob for spin manipulation in nanodevices^5,6,7,8,9,10.

The well-known SHE says that a charge current J in a material with spin–orbit interaction can generate a spin current ${j}_{ij}^{{\rm{s}}}$, here i and j denote respectively spin flowing direction $\hat{{\rm{i}}}$ and spin polarizing direction $\hat{{\rm{j}}}$. $\hat{{\rm{i}}}$, $\hat{{\rm{j}}}$, and J are mutually perpendicular to each other. Thus, in the Cartesian coordinate this spin current is ${j}_{ij}^{{\rm{s}}}\,=\,{\theta }_{0}\hslash /(2e){\epsilon }_{ijk}{J}_{k}$, where ϵ_ijk is the Levi-Civita symbol and the Einstein summation convention is applied. θ₀ is a material parameter called spin Hall angle whose value is an issue of recent debates. Like all effects having inverse effects, the inverse effect of SHE is called ISHE^11,12,13 that says a spin current can generate a charge current of ${J}_{k}\,=\,\theta ^{\prime} (2e)/(\hslash ){\epsilon }_{ijk}{j}_{ij}^{{\rm{s}}}$. $\theta ^{\prime}$ is called inverse spin Hall angle, and $\theta ^{\prime} ={\theta }_{0}$ due to the Onsager reciprocity. From the application point of view, one shortcoming of the spin current from the conventional SHE is that spin current polarization must be perpendicular to the spin current propagation direction. In this paper, three anomalous SHEs and ISHEs in magnetic materials are predicted based on general tensor requirement of a physical quantity¹⁴ and the assumption that charge-spin interconversion involves order parameters, magnetization M for ferromagnets and the Neel order n for anti-ferromagnets. Specifically, spin currents ${j}_{ii}^{{\rm{s}}}$ are converted from a charge current collinear with the order parameter where $\hat{{\rm{i}}}$ is perpendicular to the charge current. When a charge current flows perpendicularly to the order parameter, two spin currents ${j}_{ij}^{{\rm{s}}}$ are generated, where directions $\hat{{\rm{i}}}$ and $\hat{{\rm{j}}}$ are either respectively along electric current and order parameter or respectively along the order parameter and electric current. In the anomalous ISHE, a charge current along the order parameter is generated when a spin current ${j}_{ii}^{{\rm{s}}}$ with its polarization and propagation collinear flow perpendicularly to the order parameter. A charge current along either the spin current flow direction or polarization direction is generated by a spin current ${j}_{ij}^{{\rm{s}}}$ when $\hat{{\rm{i}}}$ and $\hat{{\rm{j}}}$ are mutually perpendicular to each other, and either $\hat{{\rm{i}}}$ or $\hat{{\rm{j}}}$ is along the order parameter.

Results

Consider a piece of ferromagnetic or anti-ferromagnetic metal with an applied charge current density J. A ferromagnet is used as an example below.

Anomalous SHE when the charge current is along M

Without losing generality, let J and M be along the $\hat{{\rm{x}}}$ direction. From Eqs. (5), (6), and (7) (see “Methods” section), the general SHE in magnetic materials is

$${j}_{ij}^{{\rm{s}}}\,=\,\frac{\hslash }{2e}[{\theta }_{0}{\epsilon }_{ij1}\,+\,({\theta }_{1}\,+\,{\theta }_{2}){\delta }_{ij\ne 1}M]J.$$

(1)

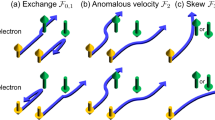
Spin current ${j}_{22}^{{\rm{s}}}$ and ${j}_{33}^{{\rm{s}}}$ proportional to MJ are generated. Figure 1a is the schematic diagram of the anomalous SHE, where the thicker and thinner red arrowed lines denote respectively the charge current source and magnetization. The black arrowed lines denote two spin currents whose polarization are indicated by smaller golden arrows. Clearly, the conventional SHE cannot generate such a spin current.

Fig. 1: Schematics of anomalous spin Hall effect.

a The charge current J (the thicker red arrowed line) and magnetization M (the thinner red arrowed line) are along the x direction. Two anomalous spin current ${j}_{22}^{{\rm{s}}}$ and ${j}_{33}^{{\rm{s}}}$ (the black arrowed lines) proportional to M (magnitude of M) and J (magnitude of J) are generated. b The charge current J (the thicker red arrowed line) and magnetization M (the thinner red arrowed line) are respectively along the $\hat{{\rm{x}}}$ and the $\hat{{\rm{y}}}$ directions. Two spin currents ${j}_{12}^{{\rm{s}}}$ and ${j}_{21}^{{\rm{s}}}$ (the black arrowed lines decorated with golden arrows) proportional to MJ are generated.

Anomalous SHE when J is perpendicular to M

Without losing generality, J and M are respectively assumed along the $\hat{{\rm{x}}}$ and the $\hat{{\rm{y}}}$ directions. From Eqs. (5–7), we have

$${j}_{ij}^{{\rm{s}}}\,=\,\frac{\hslash }{2e}({\theta }_{0}{\epsilon }_{ij1}\,+\,{\theta }_{1}{\delta }_{i1}{\delta }_{j2}M\,+\,{\theta }_{2}{\delta }_{i2}{\delta }_{j1}M)J.$$

(2)

Equation (2) says that spin current ${j}_{12}^{{\rm{s}}}$ and ${j}_{21}^{{\rm{s}}}$, proportional to the magnetization M and propagating respectively along the $\hat{{\rm{x}}}$ and the $\hat{{\rm{y}}}$ directions, are generated. This is different from the conventional SHE that does not allow a spin current polarized or propagating along the charge current direction. The schematic diagram of the anomalous SHE is shown in Fig. 1b.

Anomalous ISHE due to spin current of ${j}_{33}^{{\rm{s}}}$

If spin current ${j}_{33}^{{\rm{s}}}$ is applied, following electric currents are generated according to Eqs. (8) and (9) (see “Methods” section),

$${J}_{k}\,=\,\frac{2e}{\hslash }({\theta }_{1}^{\prime}\,+\,{\theta }_{2}^{\prime}){\delta }_{ki\ne 3}{M}_{i}\,{j}_{33}^{{\rm{s}}}.$$

(3)

In this case, the theory predicts that a charge current of $\frac{2e}{\hslash }({\theta }_{1}^{\prime}\,+\,{\theta }_{2}^{\prime}){j}_{33}^{{\rm{s}}}{{\bf{M}}}_{\perp }$ is generated, where M_⊥ is the projection of the magnetization vector in the xy-plane. The charge current should be zero if the magnetization is parallel to the spin current propagation direction. The schematic of this anomalous ISHE is shown in Fig. 2a, b.

Fig. 2: Schematic of anomalous inverse spin Hall effect.

a The flow of a spin current ${j}_{33}^{{\rm{s}}}$ (the red arrowed line decorated with golden arrows) generates a charge current J (the black arrowed line) along M_⊥ (the thinner red arrowed line), the projection of M in the xy-plane. b No charge current can be generated when M is along the $\hat{{\rm{z}}}$. The flow of a spin current ${j}_{12}^{{\rm{s}}}$ (the red arrowed lines decorated with golden arrows) generates a charge current (the black arrow) along the $\hat{{\rm{x}}}$ and proportional to the y component of the magnetization (c) and a charge current (the black arrow) along the $\hat{{\rm{y}}}$ and proportional to the x component of the magnetization (d).

Anomalous ISHE due to spin current of ${j}_{12}^{{\rm{s}}}$

The charge current from the ISHE of Eqs. (8) and (9) is

$${J}_{k}\,=\,\frac{2e}{\hslash }{j}_{12}^{{\rm{s}}}[{\theta }_{0}^{\prime}{\delta }_{k3}\,+\,{\theta }_{1}^{\prime}{M}_{2}{\delta }_{k1}\,+\,{\theta }_{2}^{\prime}{M}_{1}{\delta }_{k2}].$$

(4)

Interestingly, beside of charge current $\frac{2e}{\hslash }{j}_{12}^{{\rm{s}}}{\theta }_{0}^{\prime}{\bf{z}}$ along the $\hat{{\rm{z}}}$ direction from the conventional ISHE, there are two more charge currents $\frac{2e}{\hslash }{j}_{12}^{s}{\theta }_{1}^{\prime}{M}_{2}\hat{{\rm{x}}}$ and $\frac{2e}{\hslash }{j}_{12}^{s}{\theta }_{2}^{\prime}{M}_{1}\hat{{\rm{y}}}$ along the $\hat{{\rm{x}}}$ and $\hat{{\rm{y}}}$ directions, respectively. This two anomalous ISHEs are illustrated in Fig. 2c, d.

Possible experimental verification

Figure 3 illustrates an experimental setup for verifying predicted effects. A FM1/NM/FM2 multilayer system lays in the xy-plane, and a charge current J is applied to the bottom ferromagnetic layer FM2 whose magnetization M is collinear with J. NM is a non-magnetic-spacing layer that can be metal or thin insulating film. The charge current whose direction is chosen as the $\hat{{\rm{x}}}$ direction generates two spin currents ${j}_{33}^{{\rm{s}}}\,=\,({\theta }_{1}\,+\,{\theta }_{2})\frac{\hslash }{2e}MJ$ and ${j}_{32}^{{\rm{s}}}\,=\,{\theta }_{0}\frac{\hslash }{2e}J$ (two arrowed lines decorated with small arrows) propagating perpendicularly to the layers. One of them ${j}_{32}^{{\rm{s}}}$ is the spin current from the conventional SHE. The other ${j}_{33}^{{\rm{s}}}$ is from the anomalous SHE. The two spin currents pass thought the spacing layer and enter the top ferromagnetic metal layer FM1. If magnetization M₁ in FM1 is along the $\hat{{\rm{z}}}$ direction, ${j}_{33}^{{\rm{s}}}$ generates no charge current from the anomalous ISHE illustrated in Fig. 2b or from the conventional ISHE (because the propagation and polarization of the spin current are collinear). Spin current ${j}_{32}^{{\rm{s}}}$ can generate two charge current in FM1. One of them ${{\bf{J}}}_{1}\,=\,{\theta }_{2}^{\prime}\frac{2e}{\hslash }{M}_{1}{j}_{32}^{{\rm{s}}}$ proportional to M₁ is from the anomalous ISHE illustrated in Fig. 2d and flows along the $\hat{{\rm{y}}}$ direction. The other ${{\bf{J}}}_{2}\,=\,{\theta }_{0}^{\prime}\frac{2e}{\hslash }{j}_{32}^{{\rm{s}}}$ is from the conventional ISHE, and flows along the x direction.

Fig. 3: (Color online) Proposed setup for experimental verification.

A multilayer film lying in the xy-plane consists of a ferromagnetic metal layer 1 (FM1) on the top, a non-magnetic layer (NM) in the middle, and a ferromagnetic metal layer 2 (FM2) on the bottom. The magnetization of FM2 is M (the thinner red arrowed line). Applied charge current J (the thicker red arrowed line) is collinear with M and is along the $\hat{{\rm{x}}}$ direction. FM1 is for spin current detection whose magnetization M₁ is along the $\hat{{\rm{z}}}$ direction. Spin currents ${j}_{33}^{{\rm{s}}}$ and ${j}_{32}^{{\rm{s}}}$ (the black arrowed lines decorated with smaller arrows) are respectively generated by the anomalous (${j}_{33}^{{\rm{s}}}$) and conventional spin Hall effect. The two spin currents passing thought the spacing layer and enter into the top ferromagnetic metal layer FM1. J₁ and J₂ are two charge currents respectively from the anomalous inverse spin Hall effect and the conventional inverse spin Hall effect. A voltage drop V_y across the $\hat{{\rm{y}}}$ direction in FM1 is generated by J₁. a A setup for NM being a thin insulating spacing. b For NM being a metal, FM1 is replaced by a Hall bar along the $\hat{{\rm{y}}}$ direction.

For an open circuit in the $\hat{{\rm{y}}}$ direction on the top layer (FM1), J₁ shall generate a voltage drop cross the $\hat{{\rm{y}}}$ direction as denoted by V_y in Fig. 3. V_y shall change sign when M₁ reverses its direction. Both the existence of a non-zero V_y and its sign change are the features of the anomalous ISHE. Ideally, one would like to eliminate closed circuit in the $\hat{{\rm{x}}}$ direction on the top layer in order to eliminate possible contribution of usual anomalous Hall contribution to V_y. This can be achieved either by using a thin insulating spacing or by using a Hall bar as denoted by Fig. 3b. Obviously, the charge current along the $\hat{{\rm{y}}}$ direction is a unique feature of the anomalous ISHE in this theory because no known effect give a M₁ dependence of V_y.

Discussions

The tensor requirements of physical quantities allow anomalous SHEs and ISHEs. However, the magnitudes of these effects for a given material is not known. Thus, a compelling evidence for their existence would be highly desirable and would give the experimentalists guidance as to where they can begin their search for these effects. Here, I provide two possible mechanisms for the anomalous SHEs. One is trivial and the other has the same origin as that of the anomalous Hall effect. Let us consider an electric current J flowing along the $\hat{{\rm{x}}}$ direction in a magnet whose magnetization M points to the $\hat{{\rm{z}}}$ direction. In the trivial mechanism, a spin current of magnitude of ${j}_{13}^{{\rm{s}}}\,=\,a\hslash J/(2e)$ shall accompany the charge current due to the spin polarization of itinerant electrons, where a is the spin polarizability of itinerant electrons.

In a non-trivial mechanism related to the anomalous Hall effect, an electric field will build up along the $\hat{{\rm{y}}}$ direction due to the open boundary condition along the $\hat{{\rm{y}}}$ direction in a normal setup. According to the anomalous Hall effect, the field is E = ρ₁MJ, where ρ₁ is anomalous Hall resistivity, normally much bigger than the normal Hall resistivity. Under this field, a charge current σ_yyE along the $\hat{{\rm{y}}}$ direction is generated that cancels the deflected charge current along the $\hat{{\rm{x}}}$ direction due to the anomalous Hall effect, where σ_yy is the longitudinal conductivity along the $\hat{{\rm{y}}}$ direction. However, in general the spin polarization of two currents are not the same in magnetic materials. As a result, there is no net charge current along the $\hat{{\rm{y}}}$ direction, but there is a spin current flowing along the $\hat{{\rm{y}}}$ direction, i.e., ${j}_{23}^{{\rm{s}}}$. The magnitude of this current is order of aσ_yyE, where a is a material-dependent number of order of 1 measuring the polarizability. Interestingly, the predicted SHEs and ISHEs may have already been observed in recent experiments^15,16. Non-local measurements used in those experiments can be used to test anomalous SHE and ISHE. It should also be pointed out that the anomalous Hall effect induced anomalous SHE proposed here is different from the anomalous Hall effect induced spin-transfer torque in literature¹⁷.

The anomalous SHEs and ISHEs described above work also for the interconversion of charge-spin in an anti-ferromagnet involving the Neel order parameter n. One needs simply to replace the magnetization M by n. The anomalous SHEs and ISHEs may have already been observed in ferromagnet¹⁸, in anti-ferromagnets^19,20,21 and in two-dimensional Weyl semimetals^22,23. Unfortunately, those experiments did not look at their data in terms of anomalous SHE and ISHE, but as unusual spin torques in ferromagnetic resonance or spin-torque ferromagnetic resonances.

According to the anomalous SHE and ISHE described above, a charge current along the $\hat{{\rm{x}}}$ directions in a ferromagnetic or anti-ferromagnetic metal, whose order parameter is collinear with the current, can generate ${j}_{yy}^{{\rm{s}}}$ and ${j}_{zz}^{{\rm{s}}}$. Since the $\hat{{\rm{y}}}$ and $\hat{{\rm{z}}}$ direction is open and no sustainable spin current exist, a spin accumulation of <s_z> and <s_y> will occur on the two surface respectively in the $\hat{{\rm{z}}}$ and $\hat{{\rm{y}}}$ directions. Thus this direction-dependent spin accumulation is another fingerprints of the present theory. Of course, this spin accumulation is hidden in the main order parameter pointing to the $\hat{{\rm{x}}}$ direction, and how to observe it may be an issue. It may be easier to observe the spin accumulation in an anti-ferromagnet because of zero net magnetization everywhere in the absence of a current.

So far, the predictions are based on the tensor requirement of physical quantities¹⁴, instead of deriving them from a microscopic Hamiltonian. In some sense, similar to energy spectrum analysis in group theory, our theory does not provide the actual possible strengths of the anomalous SHEs and ISHEs, θ₁, ${\theta }_{1}^{\prime}$, θ₂, and ${\theta }_{2}^{\prime}$. To find these strengths, one needs to compute all possible spin (charge) current conversion from a given microscopic model when an external charge (spin) current is applied. Such a microscopic theory is surely important and necessary although it is foreseeable difficult because of necessity of including electron–electron interactions and the nature of non-conservation of spin current. It might be interesting to point out that the tensor analysis, though not a traditional approach in condensed matter physics from a microscopic Hamiltonian, have been used to understand the anisotropic magnetoresistance²⁴ and generalized Ohm’s law in magnetic material²⁵. One should not confuse the tensor requirement on physical quantities with the symmetry restriction on physical quantities²⁶.

In summary a theory of anomalous SHEs and anomalous ISHEs in magnetic materials is presented when the charge-spin interconversion involves the order parameters, such as the magnetization in ferromagnetic materials and the Neel order in anti-ferromagnetic materials. In particular, spin current ${j}_{ii}^{{\rm{s}}}$ can be generated by a charge current collinear with the order parameter and propagating perpendicularly to $\hat{{\rm{i}}}$. Inversely, a charge current can be generated by a spin current of ${j}_{ii}^{{\rm{s}}}$ along the projection of order parameter perpendicular to $\hat{{\rm{i}}}$. In other words, no charge current can be generated when the spin current flow along the order parameter in this case. Two anomalous spin currents proportional to the magnitude of order parameter can be generated by an applied charge current when it is perpendicular to the order parameter. One of them propagates along the order parameter and is polarized along the charge current direction. The other propagates along the charge current direction and is polarized along the order parameter. For an applied spin current with mutually perpendicular propagation and polarization directions, a charge current along the spin current propagation direction is generated if the order parameter is collinear with the polarization of the spin current. Also, a charge current along the polarization of spin current is generated if the order parameter is collinear with the propagation direction of the spin current. Experimental verifications are also proposed. A possible mechanism for the anomalous SHE is also discussed. In terms of applications, one of the great advantages of anomalous SHE is that one can control the generated spin or charge current by controlling the magnetization or the Neel order in the magnetic materials.

Methods

Derivation of anomalous SHE

A spin current ${j}_{ij}^{{\rm{s}}}$ is generated by J. Since spin current is a tensor of rank 2 and J a tensor of rank 1, the most general relationship between ${j}_{ij}^{{\rm{s}}}$ and J, in the linear response region, is

$${j}_{ij}^{s}\,=\,\frac{\hslash }{2e}{\theta }_{ijk}^{{\rm{SH}}}{J}_{k},$$

(5)

where ${\theta }_{ijk}^{{\rm{SH}}}$ is the spin Hall angle tensor of rank 3 that does not depend on current J (trivial spin current aJM + bMJ that accompanies a polarized charge current is not included). In three dimension, i, j, k = 1, 2, 3 stand for respectively the $\hat{{\rm{x}}}$, $\hat{{\rm{y}}}$, and $\hat{{\rm{z}}}$ directions. In the absence of magnetic field, the only available non-zero rank tensors (other than the electric current) are order parameter M or n for a ferromagnet or an anti-ferromagnet, as well as the Levi-Civita symbol of ϵ_ijk = 1 for (i, j, k) = (1, 2, 3), (2, 3, 1), (3, 1, 2), ϵ_ijk = − 1 for (i, j, k) = (1, 3, 2), (2, 1, 3), (3, 2, 1), and ϵ_ijk = 0 for any other choices of (i, j, k). If the order parameter can also participate in the SHE, and if we restrict ourselves upto the first-order interaction between the order parameter and spin current generation, or linear anomalous SHE and ISHE in M or n (in the case of anti-ferromagnet), one possible rank 3 tensor does not contain M and can only be the Levi-Civita symbol. This is exactly the conventional SHE. Other possible rank 3 tensors linear in M contain two Levi-Civita symbols so that one can have three free indices by contracting two pairs indices out of total seven indices (adding more Levi-Civita symbols would not generate any new terms). There are two distinct ways of contracting two pair indices so that the most general ${\theta }_{ijk}^{{\rm{SH}}}$ in the case of ferromagnet is

$${\theta }_{ijk}^{{\rm{SH}}}\,=\,{\theta }_{0}{\epsilon }_{ijk}\,+\,{\theta }_{1}{M}_{l}{\epsilon }_{iln}{\epsilon }_{jnk}\,+\,{\theta }_{2}{M}_{l}{\epsilon }_{ink}{\epsilon }_{jln},$$

(6)

where θ₀ is the usual spin Hall angle that does not interact with M, θ_α (α = 1, 2) are anomalous SHE coefficients. It is straight forward to see that the last two terms can be recast as

$$[({\theta }_{1}\,+\,{\theta }_{2}){\delta }_{ij}{\delta }_{kl\ne i}\,+\,{\theta }_{1}{\delta }_{ik}{\delta }_{jl\ne i}\,+\,{\theta }_{2}{\delta }_{il}{\delta }_{jk\ne i}]{M}_{l}.$$

(7)

From perturbation point view, terms with more than one order parameters are higher-order interactions. In general the response is much weaker. Thus, it is only meaningful to consider them only when the prediction in this manuscript is firmly established.

Derivation of anomalous ISHE

Similar to spin current generation by a charge current, an external spin current ${j}_{ij}^{{\rm{s}}}$ passing through a ferromagnet can in principle generate a charge current J. By the same arguments as above, the most general expression for J is

$${J}_{k}\,=\,\frac{2e}{\hslash }{\theta }_{ijk}^{{\rm{ISH}}}{j}_{ij}^{{\rm{s}}}$$

(8)

where ${\theta }_{ijk}^{{\rm{ISH}}}$ is the inverse spin Hall angle tensor of rank 3 that does not depend on spin current ${j}_{ij}^{{\rm{s}}}$. For a ferromagnet whose magnetization can also participant in the generalized ISHE, the most general ${\theta }_{ijk}^{{\rm{ISH}}}$, up to the linear term in M, is

$${\theta }_{ijk}^{{\rm{ISH}}}\,=\,{\theta }_{0}^{\prime}{\epsilon }_{ijk}\,+\,{\theta }_{1}^{\prime}{M}_{l}{\epsilon }_{iln}{\epsilon }_{jnk}\,+\,{\theta }_{2}^{\prime}{M}_{l}{\epsilon }_{ink}{\epsilon }_{jln},$$

(9)

${\theta }_{0}^{\prime}$ is the usual inverse spin Hall angle that does not interact with M, ${\theta }_{\alpha }^{\prime}$ (α = 1, 2) are coefficients that characterize the anomalous ISHEs linear in M.