Critical enhancement of the spin Hall effect by spin fluctuations

Abstract

The spin Hall (SH) effect, the conversion of the electric current to the spin current along the transverse direction, relies on the relativistic spin-orbit coupling (SOC). Here, we develop a microscopic theory on the mechanisms of the SH effect in magnetic metals, where itinerant electrons are coupled with localized magnetic moments via the Hund exchange interaction and the SOC. Both antiferromagnetic metals and ferromagnetic metals are considered. It is shown that the SH conductivity can be significantly enhanced by the spin fluctuation when approaching the magnetic transition temperature of both cases. For antiferromagnetic metals, the pure SH effect appears in the entire temperature range, while for ferromagnetic metals, the pure SH effect is expected to be replaced by the anomalous Hall effect below the transition temperature. We discuss possible experimental realizations and the effect of the quantum criticality when the antiferromagnetic transition temperature is tuned to zero temperature.

Introduction

The spin Hall (SH) effect^1,2,3 and its reciprocal effect, the inverse SH effect⁴, are among the most important components for the spintronic application⁵ because they allow the electrical conversion between charge current and pure spin current, where electrons with opposite spin components flow along opposite directions with zero net charge current. Based on these effects, a variety of phenomena have been envisioned^6,7. The SH effect and the anomalous Hall (AH) effect⁸ are both rooted in the relativistic spin-orbit coupling (SOC), and these effects are traditionally understood as arising from intrinsic mechanisms, i.e., band effects^9,10, or extrinsic mechanisms, i.e., impurity/disorder effects^{11,12,13,14,15,16} and interfaces¹⁷.

There have appeared a number of proposals of the extrinsic mechanisms of the SH effect utilizing excitations or fluctuations in solids, such as phonons^18,19,20. Identifying new mechanisms thus opens up a new research avenue and hereby helps to improve the efficiency of the SH effect, which remains small for practical applications²¹. Recently, the current authors proposed extrinsic mechanisms focusing on the spin fluctuation (SF) in nearly ferromagnetic (FM) disordered systems²². In these mechanisms, the critical SF associated with the zero-temperature FM quantum critical point (QCP) plays a fundamental role. It was predicted that the SH conductivity σ_SH is maximized at nonzero temperature when approaching the QCP. When the FM transition temperature T_C is finite, the pure SH effect is replaced by the AH effect below T_C, thus limiting the operation temperature range of the SH effect. This limitation could be lifted when the antiferromagnetic (AFM) SF is considered because the net magnetic moment is absent even below the AFM transition temperature T_N. From the study of itinerant electron magnetism²³, it has been recognized that the FM SF and the AFM SF provide qualitatively different behavior in electronic specific heat, conductivity, etc^24,25,26. Thus, the SH effect could be another example that highlights the difference between FM SF and AFM SF.

While the SH effect due to the FM critical SF has not been experimentally examined, yet, refs. ^27,28,29 examined the SH effect in FM alloys with finite T_C. In ref. ²⁷, Wei et al. reported that the temperature dependence of the inverse SH resistance of Ni-Pd alloys follows the uniform second-order nonlinear susceptibility χ₂, but the inverse SH resistance has peaks above and below the Curie temperature and changes its sign at T_C. This behavior is consistent with the theoretical prediction in ref. ³⁰, which used a static mean field approximation to the model proposed by Kondo³¹. On the other hand in ref. ²⁸, Ou et al. reported that the inverse SH effect of Fe-Pt alloys is maximized near T_C as if it follows the uniform linear susceptibility. More recently, Wu et al. reported similar effects using Ni-Cu alloys²⁹. For AFM systems, early work on Cr has already reported the large SH effects^32,33. Recently, Fang and coworkers found that the SH conductivity in metallic Cr is enhanced when temperature is approaching the Néel temperature T_N³⁴, suggesting the AFM SF as the main mechanism of the SH effect. However, the effect of AFM SF to the SH effect has not been theoretically addressed.

The main purpose of this work is to develop the theoretical description of the SH effect in magnetic metallic systems by the SF when the magnetic transition temperature (T_C or T_N) is finite. Our theory is based on a microscopic model describing the coupling between itinerant electrons and localized magnetic moments by Kondo³¹ and the self-consistent renormalization theory describing the fluctuation of localized moments by Moriya²³. The main difference between AFM systems and FM systems is that the AFM ordering or correlation is characterized by the nonzero magnetic wave vector Q. Thus, itinerant electrons scattered by the AFM SF gain or lose corresponding momentum. Our theory takes into account this momentum conservation appropriately. Despite this difference, it is demonstrated that the SH conductivity is enhanced as temperature is approaching T_C for FM systems or T_N for AFM systems. The result for the AFM systems strongly supports the conjecture made in ref. ³⁴. We highlight the qualitatively different behavior between the AFM SF and the FM SF near the finite-temperature phase transition and near the QCP.

For magnetic metallic systems, intrinsic mechanisms could also contribute to a variety of Hall effects, such as the AH effect by the Berry curvature and the topological Hall effect induced by chiral spin ordering. This work, however, does not cover these effects because these are band effects and do not show diverging behavior.

Results

In this section, we present our main results. The first subsection is devoted to setting up our theoretical tools. We introduce the s-d Hamiltonian, which is modified from the original form developed by Kondo³¹. Based on this model, the scattering mechanism for the SH conductivity will be clarified. Then, we set up the Gaussian action, which describes the SF based on the self-consistent renormalization theory by Moriya²³. In the second subsection, theoretical results of the SH conductivity will be presented.

Theoretical model and formalism

In this work, we consider three-dimensional systems. The s-d Hamiltonian is written as H = H₀ + H_K. Here, the non-interacting itinerant electron part is described by ${H}_{0}={\sum }_{{{{\bf{k}}}},\nu }{\varepsilon }_{{{{\bf{k}}}}}{a}_{{{{\bf{k}}}}\nu }^{{\dagger} }{a}_{{{{\bf{k}}}}\nu }$, where ε_k is an energy eigenvalue at momentum k given by ${\varepsilon }_{{{{\bf{k}}}}}=\frac{{\hslash }^{2}{k}^{2}}{2m}-{\varepsilon }_{{{{\rm{F}}}}}$ with the Fermi energy ε_F and the carrier effective mass m, and ${a}_{{{{\bf{k}}}}\nu }^{({\dagger} )}$ is an annihilation (creation) operator of an electron at momentum k with the spin index ν. We chose the simplest-possible band structure as it allows detailed analytical calculations. This electronic part of the Hamiltonian is assumed to be unrenormalized²³. However, as discussed briefly later, going beyond this assumption is necessary especially near the non-zero critical temperature. The s-d coupling term in the original model has a mixed representation of momentum of conduction electrons and real-space coordinate of localized magnetic moments (see ref. ³¹ and Supplementary Note 1 for details). For magnetic metallic systems, where localized magnetic moments form a periodic lattice and conduction electrons hop through the same lattice sites, it is more convenient to express the model Hamiltonian entirely in the momentum space as

$$\begin{array}{lll}{H}_{{{{\rm{K}}}}}\,=\,-\frac{1}{\sqrt{N}}\mathop{\sum}\limits_{{{{\bf{k}}}},{{{{\bf{k}}}}}^{{\prime} }}\mathop{\sum}\limits_{\nu ,{\nu }^{{\prime} }}{a}_{{{{\bf{k}}}}\nu }^{{\dagger} }{a}_{{{{{\bf{k}}}}}^{{\prime} }{\nu }^{{\prime} }}\left[2({{{{\bf{J}}}}}_{{{{\bf{k}}}}-{{{{\bf{k}}}}}^{{\prime} }}\cdot {{{{\bf{s}}}}}_{\nu {\nu }^{{\prime} }})\right.\\ \qquad\quad\times\, \{{{{{\mathcal{F}}}}}_{0}+2{{{{\mathcal{F}}}}}_{1}({{{\bf{k}}}}\cdot {{{{\bf{k}}}}}^{{\prime} })\}+{{{\rm{i}}}}{{{{\mathcal{F}}}}}_{2}{{{{\bf{J}}}}}_{{{{\bf{k}}}}-{{{{\bf{k}}}}}^{{\prime} }}\cdot ({{{{\bf{k}}}}}^{{\prime} }\times {{{\bf{k}}}})\\ \qquad\quad+\,\frac{{{{\rm{i}}}}}{\sqrt{N}}{\sum }_{{{{\bf{p}}}}}{{{{\mathcal{F}}}}}_{3}\left\{({{{{\bf{J}}}}}_{{{{\bf{p}}}}}\cdot {{{{\bf{s}}}}}_{\nu {\nu }^{{\prime} }})({{{{\bf{J}}}}}_{{{{\bf{k}}}}-{{{{\bf{k}}}}}^{{\prime} }-{{{\bf{p}}}}}\cdot ({{{{\bf{k}}}}}^{{\prime} }\times {{{\bf{k}}}}))\right.\\ \quad\qquad+\,({{{{\bf{J}}}}}_{{{{\bf{p}}}}}\cdot ({{{{\bf{k}}}}}^{{\prime} }\times {{{\bf{k}}}}))({{{{\bf{J}}}}}_{{{{\bf{k}}}}-{{{{\bf{k}}}}}^{{\prime} }-{{{\bf{p}}}}}\cdot {{{{\bf{s}}}}}_{\nu {\nu }^{{\prime} }})\\ \qquad\quad-\,\frac{2}{3}({{{{\bf{J}}}}}_{{{{\bf{p}}}}}\cdot {{{{\bf{J}}}}}_{{{{\bf{k}}}}-{{{{\bf{k}}}}}^{{\prime} }-{{{\bf{p}}}}})({{{{\bf{s}}}}}_{\nu {\nu }^{{\prime} }}\cdot ({{{{\bf{k}}}}}^{{\prime} }\times {{{\bf{k}}}}))\left.\right\}\left.\right].\end{array}$$

(1)

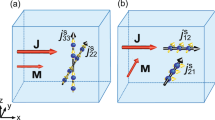
Here, ${{{{\bf{s}}}}}_{\nu {\nu }^{{\prime} }}=\frac{1}{2}{{{{\boldsymbol{\sigma }}}}}_{\nu {\nu }^{{\prime} }}$ is the spin of a conduction electron with the Pauli matrices σ. N is the total number of lattice sites. J_p is the Fourier transform of a local spin moment J_n at position R_n defined by ${{{{\bf{J}}}}}_{{{{\bf{p}}}}}=\frac{1}{\sqrt{N}}{\sum }_{n}{{{{\bf{J}}}}}_{n}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}{{{\bf{p}}}}\cdot {{{{\bf{R}}}}}_{n}}$. Parameters ${{{{\mathcal{F}}}}}_{l}$²² are related to F_l defined in ref. ³¹. ${{{{\mathcal{F}}}}}_{0,1}$ terms correspond to the standard s-d exchange interaction or Hund coupling as depicted in Fig. 1a. Note that the ${{{{\mathcal{F}}}}}_{0,1}$ terms represent ferromagnetic coupling. With these leading terms, the behavior of the theoretical model is less exotic than that with antiferromagnetic coupling often used in the context of heavy fermions^35,36. The subleading ${{{{\mathcal{F}}}}}_{2,3}$ terms represent the exchange of angular momentum between a conduction electron and a local moment. These terms are odd (linear or cubic)-order in J_n and s and induce the electron deflection depending on the direction of J_n or s. More precisely, the ${{{{\mathcal{F}}}}}_{2}$ term and the ${{{{\mathcal{F}}}}}_{3}$ term generate the side-jump and the skew-scattering contributions to the SH conductivity, respectively, as depicted in Fig. 1b, c. From Eq. (1) and the position operator r, the velocity operator is obtained as v = (i/ℏ)[H_K, r]. The anomalous velocity, the main source of the side-jump contribution, arises from the ${{{{\mathcal{F}}}}}_{2}$ term (see Supplementary Note 1 for details).

Fig. 1: Schematic view of the Kondo model.

a Spin dependent scattering by ${{{{\mathcal{F}}}}}_{0,1}$ terms, b anomalous velocity induced by ${{{{\mathcal{F}}}}}_{2}$ terms, and c skew scattering by ${{{{\mathcal{F}}}}}_{3}$ terms. Yellow arrows indicate conduction electrons, and green arrows indicate local moments. In the ${{{{\mathcal{F}}}}}_{2(3)}$ scattering processes, the electron deflection depends on the direction of the local moment (the electron spin), leading to the side-jump (skew-scattering) contribution to σ_SH. Adapted from Okamoto, S., Egami, T. & Nagaosa, N. Phys. Rev. Lett. 123, 196603 (2019).

From Eq. (1), one can notice the main difference from FM alloy systems²². Since itinerant electrons and localized moments share the same lattice structure, their coupling does not have a phase factor such as ${{{{\rm{e}}}}}^{{{{\rm{i}}}}{{{\bf{p}}}}\cdot ({{{{\bf{R}}}}}_{n}-{{{{\bf{R}}}}}_{{n}^{{\prime} }})}$, where R_n is the position of the localized moment J_n. Therefore, the SF could contribute to the SH effect even if it has characteristic momentum Q ≠ 0, such as in AFM systems, without introducing destructive effects. Otherwise, averaging over the lattice coordinate would lead to zero SH effect as $\langle {{{{\rm{e}}}}}^{{{{\rm{i}}}}{{{\bf{Q}}}}\cdot ({{{{\bf{R}}}}}_{n}-{{{{\bf{R}}}}}_{{n}^{{\prime} }})}\rangle \,\approx\, 0$.

To describe the fluctuation of localized moments J_n, we adopt a generic Gaussian action given by^{23,37,38,39,40},

$${A}_{{{{\rm{Gauss}}}}}=\frac{1}{2}\mathop{\sum}\limits_{{{{\bf{p}}}},l}{D}_{{{{\bf{p}}}}}^{-1}({{{\rm{i}}}}{\omega }_{l})\,{{{{\bf{J}}}}}_{{{{\bf{p}}}}}({{{\rm{i}}}}{\omega }_{l})\cdot {{{{\bf{J}}}}}_{-{{{\bf{p}}}}}(-{{{\rm{i}}}}{\omega }_{l})$$

(2)

with

$${D}_{{{{\bf{p}}}}}({{{\rm{i}}}}{\omega }_{l})=\frac{1}{\delta +A| {{{\bf{p}}}}-{{{\bf{Q}}}}{| }^{2}+| {\omega }_{l}| /{\Gamma }_{{{{\bf{p}}}}}}.$$

(3)

Here, J_p(iω_l) is a space and imaginary-time τ Fourier transform of J_n(τ), where we made the τ dependence explicit, and ω_l = 2lπT is the bosonic Matsubara frequency. Parameter A is introduced as a constant so that A∣p − Q∣² has the unit of energy, and δ is the distance from the magnetic transition temperature and is related to the magnetic correlation length as ξ ∝ δ^−1/2 at T > T_N,C and to the ordered magnetic moment as M(T) ∝ δ^1/2 at T < T_N,C. Γ_p represents the Landau damping, whose momentum dependence is neglected for AFM systems, Γ_p = Γ, since it is weak near the magnetic wave vector Q. For FM systems with Q = 0, the damping term has a momentum dependence as Γ_p = Γp. With impurity scattering or disorder, Γ_p remains finite below a cutoff momentum ∣p∣ ≤ q_c as Γ_p = Γq_c.

While the above Gaussian action can be derived by solving an interacting electron model, it is a highly nontrivial problem and dependent on the detail of theoretical model and the target material. Instead, we adopt a conventional approach, where the material dependence is described by a small number of parameters and derive the spin Hall conductivity arising from the spin fluctuation and the subleading terms of Eq. (1). In fact, theoretical analyses based on this Gaussian action have been successful to explain many experimental results on itinerant magnets²³. In principle, δ depends on temperature and is determined by solving self-consistent equations for a full model including non-Gaussian terms^{23,37,38,39,40,41}. However, the temperature dependence of δ is known for the following three cases in three dimension. I: δ ∝ T − T_N,C at T ≳ T_N,C, II: δ ∝ M²(T) ∝ T_N,C − T at T ≲ T_N,C, and III: δ ∝ T^3/2 at T ~ 0 when T_N → 0, i.e., approaching the QCP. For FM with impurity scattering or disorder δ ∝ T^3/2 at T ~ 0 when T_C → 0, while for clean FM δ ∝ T^4/3.

Spin-Hall conductivity

With the above preparations, we analyze the SH conductivity using the Matsubara formalism, by which one can take the dynamical SF into account via a diagramatic technique. Here, the frequency-dependent SH conductivity is considered as σ_SH(iΩ_l). Ω_l is the bosonic Matsubara frequency, which is analytically continued to real frequency as iΩ_l → Ω + i0⁺ at the end of the analysis, and then the DC limit, Ω → 0, is taken to obtain σ_SH. Based on the diagrammatic representations in Figs. 2 and 3, σ_SH is expressed in terms of electron Green’s function G and the propagator D of the longitudinal SF. While the transverse SFs or spin wave excitations exist below the magnetic transition temperature, the scattering of electrons by such SFs does not show a critical behavior^42,43, and its contribution is expected to be small. Therefore, for our analysis, we consider only longitudinal SFs below T_N,C.

Fig. 2: Diagrammatic representation for the side-jump contribution.

Solid (wavy) lines are the electron Green’s functions (the SF propagators). Squares (circles) are the spin (charge) current vertices, with filled symbols representing the velocity correction with ${{{{\mathcal{F}}}}}_{2}$, i.e., side jump. Filled triangles are the interaction vertices with ${{{{\mathcal{F}}}}}_{0,1}$. Adapted from Okamoto, S., Egami, T. & Nagaosa, N. Phys. Rev. Lett. 123, 196603 (2019).

Fig. 3: Diagrammatic representation for the skew-scattering contribution.

Filled pentagons are the interaction vertices with ${{{{\mathcal{F}}}}}_{3}$. The definitions of the other symbols or lines are the same as in Fig. 2. Adapted from Okamoto, S., Egami, T. & Nagaosa, N. Phys. Rev. Lett. 123, 196603 (2019).

We first focus on the SH effect by the AFM SF. By carrying out the Matsubara summations, the energy integrals and the momentum summations as detailed in Supplementary Note 2, we find

$${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\approx \frac{{e}^{2}m{\tau }_{{{{\bf{k}}}}}}{2{\pi }^{3}{\hslash }^{4}| {{{\bf{Q}}}}| }\,{A}_{{{{\rm{AFM}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\,{\tilde{I}}_{{{{\rm{AFM}}}}}(T,\delta )$$

(4)

for the side-jump contribution and

$${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scat.}}}}}\approx \frac{{e}^{2}{\tau }_{{{{\bf{k}}}}}^{2}\,\Gamma \,\delta }{2{\pi }^{2}{\hslash }^{3}| {{{\bf{Q}}}}| }\,{A}_{{{{\rm{AFM}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scat.}}}}}\,{I}_{{{{\rm{AFM}}}}}^{2}(T,\delta )$$

(5)

for the skew-scatting contribution. Here, e is the elementary charge. In both cases, τ_k is the carrier lifetime on the Fermi surface at special momenta k that satisfies the nesting condition. Such momenta k form loops on the Fermi surface. With the parabolic band, the carrier lifetime due to the AFM SF along such loops is independent of momentum as detailed in Supplementary Note 4. The momentum dependence of the carrier lifetime due to other effects, such as disorder and phonons, is weak. Thus, we assume that τ_k is a constant. The functions ${\tilde{I}}_{{{{\rm{AFM}}}}}(T,\delta )$ and I_AFM(T, δ) defined in Supplementary Note 2 represent the coupling between conduction electrons and the dynamical SF. ${A}_{{{{\rm{AFM}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ and ${A}_{{{{\rm{AFM}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ are constants defined by the integrals over the azimuth angle of momentum k measured from the direction of Q as described in Supplementary Note 2. Since the angle integrals give only geometrical factors of ${{{\mathcal{O}}}}(1)$, ${A}_{{{{\rm{AFM}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\approx {{{{\mathcal{F}}}}}_{0}{{{{\mathcal{F}}}}}_{2}{k}_{{{{\rm{F}}}}}^{2}$ and ${A}_{{{{\rm{AFM}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}\approx {{{{\mathcal{F}}}}}_{0}^{2}{{{{\mathcal{F}}}}}_{3}{k}_{{{{\rm{F}}}}}^{4}$.

Similarly, the SH conductivity due to the FM SF is obtained (for details, see Supplementary Note 3) as

$${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\approx \frac{2{e}^{2}{\tau }_{{{{\bf{k}}}}}}{m}\,{A}_{{{{\rm{FM}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\,{I}_{{{{\rm{FM}}}}}(T,\delta )$$

(6)

for the side-jump contribution and

$${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scat.}}}}}\approx \frac{4{e}^{2}\hslash {\tau }_{{{{\bf{k}}}}}^{2}}{{m}^{2}}\,{A}_{{{{\rm{FM}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scat.}}}}}\,{I}_{{{{\rm{FM}}}}}^{2}(T,\delta )$$

(7)

for the skew-scatting contribution. Here, τ_k is the carrier lifetime on the Fermi surface, and the constants ${A}_{FM}^{side\,jump}$ and ${A}_{FM}^{skew\,scatt.}$ are given by ${A}_{{{{\rm{FM}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\approx \frac{m{k}_{{{{\rm{F}}}}}^{3}}{{\pi }^{2}\hslash }{{{{\mathcal{F}}}}}_{0}{{{{\mathcal{F}}}}}_{2}$ and ${A}_{{{{\rm{FM}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}\approx \frac{m{k}_{{{{\rm{F}}}}}^{5}}{{\pi }^{2}{\hslash }^{2}}{{{{\mathcal{F}}}}}_{0}^{2}{{{{\mathcal{F}}}}}_{3}$, respectively. The function I_FM(T, δ) is defined in Supplementary Note 3.

Temperature dependence of the Spin-Hall conductivity

Reflecting the temperature dependence of spin dynamics, σ_SH by the SF could show a strong temperature dependence. This is governed by the functions ${\tilde{I}}_{{{{\rm{AFM}}}}}(T,\delta )$, I_AFM(T, δ), and I_FM(T, δ), and the carrier lifetime τ_k. τ_k has several contributions, such as the disorder or impurity effects τ_dis, which T dependence is expected to be small, the electron-electron interactions τ_ee, the electron-phonon interactions τ_ep, and the scattering due to the SF τ_sf. Within the current model, ${\tau }_{{{{\rm{sf}}}}}\approx \frac{\hslash }{2}{{{{\mathcal{F}}}}}_{0}^{-2}{I}_{{{{\rm{AFM,FM}}}}}^{-1}(T,\delta )$ (see Supplementary Note 4 for details).

In addition to the different momentum dependencies in the damping term Γ_p, the AFM SF and the FM SF have fundamentally different characters due to the momentum conservation during scattering events. For the AFM case, electrons scattered by the SF gain or lose momentum Q. As a result, ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ in Eq. (5) has extra δ [for comparison, see Eq. (7)]. Furthermore, ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ has ${\tilde{I}}_{{{{\rm{AFM}}}}}(\delta ,T)$, whose temperature dependence somewhat differs from I_AFM(δ, T). ${\tilde{I}}_{{{{\rm{AFM}}}}}(\delta ,T)$ has the same temperature dependence of the scattering rate due to the AFM SF as reported by ref. ⁴³. While the result of ref. ⁴³ was obtained by loosening the momentum conservation by averaging the electron self-energy over the Fermi surface, the momentum dependence is explicitly considered in our ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$. These differences in the scattering process lead to the different temperature dependence in σ_SH by the AFM SF and the FM SF.

Supplementary Table I summarizes the T dependence of δ and T-δ dependence of ${\tilde{I}}_{{{{\rm{AFM}}}}}(T,\delta )$, I_AFM(T, δ), and I_FM(T, δ) in three T regimes I–III and in the vicinity of the magnetic phase transition at T_N,C between regimes I and II. By including the T dependence of δ, the full T dependence of ${\tilde{I}}_{{{{\rm{AFM}}}}}(T,\delta )$ and I_AFM,FM(T, δ) is fixed as follows: In the regimes I and II, ${\tilde{I}}_{{{{\rm{AFM}}}}}(T,\delta )$, I_AFM(T, δ), and I_FM(T, δ) are enhanced as T → T_N,C as ${\tilde{I}}_{{{{\rm{AFM}}}}}(T,\delta )\propto {\delta }^{-1/2}\propto 1/\sqrt{| T-{T}_{{{{\rm{N}}}}}| }$, I_AFM(T, δ) ∝ δ⁻¹ ∝ 1/∣T − T_N∣, and I_FM(T, δ) ∝ δ⁻¹ ∝ 1/∣T − T_C∣, respectively. While the divergence of ${\tilde{I}}_{{{{\rm{AFM}}}}}(T,\delta )$ is cutoff at T_N, the 1/∣T − T_N,C∣ divergence of I_AFM,FM(T, δ) at T_N,C is weakened to the logarithmic divergence $-\ln | T-{T}_{{{{\rm{N}}}}}|$ or the smaller power $1/\sqrt{|T-T_{\rm C}|}$. Note however that this behavior of I_AFM,FM(T, δ) right at T_N,C is a result of the current treatment which does not include the feedback between the carrier lifetime and the SF spectrum. We anticipate that including such feedback effects will cutoff these divergences. Since this requires one to solve the full Hamiltonian, including electron-electron interactions self-consistently, such a treatment is left for the future study. The SH angle Θ_SH = σ_SH/σ_c, where σ_c is the charge conductivity, is expected to be much smaller than 1, even though Θ_SH could be enhanced at the critical temperature, because σ_SH and σ_c are both proportional to the carrier lifetime. On the other hand, the behavior near the QCP, the regime III, is qualitatively reliable. This is because, the scattering rate ${\tau }_{{{{\bf{k}}}}}^{-1}$ for the pure case and I_AFM,FM(T, δ) approach 0 with T → 0 and, and fulfill the self-consistency condition between them. In this regime, however, τ_k diverges with T → 0 without disorder effects. This could leads to the pathological divergence of σ_SH. We will not consider such a situation in the main text, and give a brief discussion in Supplementary Note 5.

The temperature dependence of σ_SH coming from δ, ${\tilde{I}}_{{{{\rm{AFM}}}}}$, and I_AFM,FM is summarized in Table 1. Reflecting the diverging behavior of ${\tilde{I}}_{{{{\rm{AFM}}}}}$ and I_AFM,FM, σ_SH is sharply enhanced as T → T_N,C in the regimes I and II, as displayed in Fig. 4 for the AFM case and Fig. 5 for the FM case. Here, the approximate inverse carrier lifetime appropriate in these T regimes is considered as ${\tau }_{{{{\bf{k}}}}}^{-1}={r}_{{{{\rm{dis}}}}}+{r}_{{{{\rm{ee}}}}}{T}^{2}+{r}_{{{{\rm{sf}}}}}{T}^{3}/| T-{T}_{{{{\rm{N,C}}}}}|$, where r_dis, r_ee, and r_sf terms correspond to the disorder effect, electron-electron interaction⁴⁴, and the SF, respectively. Focusing on the low T behavior, we ignored the electron-phonon coupling, which would contribute to the carrier lifetime at high temperatures close to the Debye temperature^45,46. In the current theory, there are three energy units; the Fermi energy ε_F ≈ ℏv_F/a, the spin stiffness A/a² and magnetic transition temperature T_N,C. The temperature dependence of ${\sigma }_{{{{\rm{AFM,FM}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ and ${\sigma }_{{{{\rm{FM}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ is from I_AFM,FM(T, δ), and therefore T is scaled by ε_F, while ${\sigma }_{{{{\rm{AFM}}}}}^{{{{\rm{sidejump}}}}}$ is from ${\tilde{I}}_{{{{\rm{AFM}}}}}(T,\delta )$ and T is scaled by A/a². For the analytical plots, we use the dimensionless unit for temperature, where T is scaled by these energy units, and T_N,C = 1 for the T regimes I and II. With this convention, r_dis, r_ee, r_sf have the unit of inverse time.

Table 1 T dependence of σ_SH

Fig. 4: Schematic temperature dependence of the SH conductivity of antiferromagnets in the T regimes I and II with nonzero T_N.

The side-jump contribution ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ is shown in a and the skew-scattering contribution ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ is shown in b. The carrier lifetime is modeled as ${\tau }_{{{{\bf{k}}}}}^{-1}={r}_{{{{\rm{dis}}}}}+{r}_{{{{\rm{ee}}}}}{T}^{2}+{r}_{{{{\rm{sf}}}}}{T}^{3}/| T-{T}_{{{{\rm{N}}}}}|$, with r_dis, r_ee, and r_sf terms representing the disorder and impurity effects, electron-electron interaction, and the AFM SF, respectively. r_sf is varied with fixing r_dis = r_ee = 1. Shaded areas indicate where the current treatment breaks down, requiring the self-consistent treatment.

Fig. 5: Schematic temperature dependence of the SH conductivity ferromagnets in the T regimes I and II with nonzero T_C.

The side-jump contribution ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ is shown in a and the skew-scattering contribution ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ is shown in b. The carrier lifetime is modeled as ${\tau }_{{{{\bf{k}}}}}^{-1}={r}_{{{{\rm{dis}}}}}+{r}_{{{{\rm{ee}}}}}{T}^{2}+{r}_{{{{\rm{sf}}}}}{T}^{3}/| T-{T}_{{{{\rm{C}}}}}|$, with r_dis, r_ee, and r_sf terms representing the disorder and impurity effects, electron-electron interaction, and the FM SF, respectively. r_sf is varied with fixing r_dis = r_ee = 1. Shaded areas indicate where the current treatment breaks down, requiring the self-consistent treatment.

Despite the diverging trend as T → T_N, ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ and ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ sharply drop to zero in the vicinity of T_N with nonzero r_sf. This is caused by the suppression of τ_k due to the SF as ${\tau }_{{{{\bf{k}}}}}\approx {r}_{{{{\rm{sf}}}}}^{-1}| T-{T}_{{{{\rm{N}}}}}| /{T}^{3}$. We anticipate that a self-consistent treatment of the original interacting electron model kills this entire suppression, leading to a smooth T dependence of σ_SH.

${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ and ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ have stronger T dependence than the AFM counterparts, leading to the divergence with T approaches T_C with r_sf = 0. Nonzero r_sf suppresses the divergence in ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ and ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ in the vicinity of T_C, leading to sharp cusps. However, similar to the AFM case, we anticipate that a self-consistent treatment of the original model leads to a smooth T dependence of σ_SH across T_C.

Because of the competition between the divergence of I_AFM,FM(T, δ) and the suppression of τ_k, it might be challenging to deduce the precise temperature scaling of the SH conductivity at T_N,C. Nevertheless, our result summarized in Table 1 will be helpful to analyze experimental SH conductivity because the two contributions are separated.

For the quantum critical regime III, the carrier lifetime has the temperature dependence as ${\tau }_{{{{\bf{k}}}}}^{-1}={r}_{{{{\rm{dis}}}}}+{r}_{{{{\rm{ee}}}}}{T}^{2}+{r}_{{{{\rm{sf}}}}}{T}^{3/2}$ for the AFM case and the FM with disorder effects. The temperature dependence of σ_SH is strongly influenced by that of τ_k. Thus, here we discuss the cases with disorder effect which make τ_k finite at T = 0. Special cases, where the disorder effect is absent and τ_k becomes infinity at T = 0, will be briefly discussed in Supplementary Note 5.

The schematic temperature dependence of σ_AFM,SH and σ_FM,SH is shown in Figs. 6 and 7, respectively. With nonzero r_dis, all σ_SH approach 0 with T goes to 0 but with different T scaling; ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\propto {T}^{3/2}$, ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}\propto {T}^{9/2}$, ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\propto {T}^{3/2}$, and ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}\propto {T}^{3}$. For the latter two cases, different power laws of T were predicted in ref. ²² as described in Supplementary Note 3.

Fig. 6: Schematic temperature dependence of the SH conductivity of antiferromagnets in the T regime III with T_N → 0.

The side-jump contribution ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ is shown in a, and the skew-scattering contribution ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ shown in b. The carrier lifetime is modeled as ${\tau }_{{{{\bf{k}}}}}^{-1}={r}_{{{{\rm{dis}}}}}+{r}_{{{{\rm{ee}}}}}{T}^{2}+{r}_{{{{\rm{sf}}}}}{T}^{3/2}$, and r_dis is varied with fixing r_ee = 1 and r_sf = 0.0(0.1) for solid (dashed) lines.

Fig. 7: Schematic temperature dependence of the SH conductivity of ferromagnets in the T regime III with T_C → 0.

The side-jump contribution ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ is shown in (a), and the skew-scattering contribution ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ shown in (b). The carrier lifetime is modeled as ${\tau }_{{{{\bf{k}}}}}^{-1}={r}_{{{{\rm{dis}}}}}+{r}_{{{{\rm{ee}}}}}{T}^{2}+{r}_{{{{\rm{sf}}}}}{T}^{3/2}$, and r_dis is varied with fixing r_ee = 1 and r_sf = 0(0.1) for solid (dashed) lines.

Interestingly, ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ and ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ show formally the same leading T dependence because the divergence of the SF propagator has a cutoff by ∣Q∣ in the former and q_c in the latter. On the other hand, ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ and ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ show contrasting T dependence; the former continuously decreases with decreasing T while the latter first increases, shows maximum, and finally goes to zero with decreasing T because of the competition between τ_k and I_FM(T, δ).

Discussion

We have seen that the SH effect in magnetic metallic systems induced by spin fluctuations has different contributions with different temperature scaling. In this section, we consider remaining questions regarding the relative strength between different contributions as well as the experimental/materials realization of our theory.

When the FM critical fluctuation is dominant in the carrier lifetime in the temperature regime III, the carrier lifetime is given by ${\tau }_{{{{\rm{sf}}}}}\approx \hslash /2{\{{F}_{0}+2{F}_{1}{k}_{{{{\rm{F}}}}}^{2}\}}^{2}{I}_{{{{\rm{FM}}}}}(T,\delta )$, and therefore the ratio between the maximum ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ and the maximum ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ is estimated as ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}/{\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\approx {\varepsilon }_{{{{\rm{F}}}}}{{{{\mathcal{F}}}}}_{3}/{{{{\mathcal{F}}}}}_{0}{{{{\mathcal{F}}}}}_{2}$ (see, Eqs. (6) and (7) and the discussion in ref. ²²). From the typical interaction strengths ${{{\mathcal{F}}}}{{{\rm{s}}}}$ and the Fermi energy ε_F, the maximum of ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ is expected to be 1 to 2 orders of magnitude larger than that of ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$. This relation is expected be hold for the FM case with finite T_C.

When disorder effects or electron-electron scattering becomes dominant in the carrier lifetime, the magnitude of τ_k and I_FM(T, δ) has to be explicitly considered. Using the asymptotic form of I_FM(T, δ) near δ ~ 0 in the T regimes of I, II, and III, ${I}_{{{{\rm{FM}}}}}(T,\delta )\approx \frac{1}{8\pi }{(\frac{aT}{\hslash {v}_{{{{\rm{F}}}}}})}^{3}\frac{1}{\delta }$ (see Supplementary Note 3 for details) the ratio between ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ and ${\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ is estimated as

$$\frac{{\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}}{{\sigma }_{{{{\rm{FM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}}\approx \frac{{k}_{{{{\rm{F}}}}}^{2}}{4\pi m}{\tau }_{{{{\bf{k}}}}}{{{{\mathcal{F}}}}}_{0}\frac{{{{{\mathcal{F}}}}}_{3}}{{{{{\mathcal{F}}}}}_{2}}{\left(\frac{aT}{\hslash {v}_{{{{\rm{F}}}}}}\right)}^{3}\frac{1}{\delta }.$$

(8)

Because of the factor of 1/δ, this ratio diverges when δ goes to zero as T approaches T_C as long as τ_k is finite. Thus, the skew-scattering mechanism is expected to become dominant near the critical temperature. On the other hand near the FM QCP, the side-jump contribution may grow with lowering temperature when the carrier lifetime is dominated by other mechanisms than the SF.

In the AFM-fluctuation case, the situation is more complicated. This is because the side-jump contribution and the skew-scattering contribution have different temperature dependence, ${\tilde{I}}_{{{{\rm{AFM}}}}}(T,\delta )$ vs. I_AFM(T, δ), while they show similar enhancement near the magnetic transition temperature. Therefore, the microscopic parameters determining the SF come into play. To see this, first consider the temperature regimes I and II, where the leading temperature dependence of ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ and ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}$ is given by

$${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\approx \frac{{e}^{2}m}{32{\pi }^{2}{\hslash }^{4}}\frac{{\tau }_{{{{\bf{k}}}}}}{| {{{\bf{Q}}}}| }\,{{{{\mathcal{F}}}}}_{0}{k}_{{{{\rm{F}}}}}^{2}{{{{\mathcal{F}}}}}_{2}\,\frac{{T}^{2}}{\Gamma \sqrt{\delta {(A/{a}^{2})}^{3}}}$$

(9)

and

$${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}\approx \frac{{e}^{2}}{128{\pi }^{3}{\hslash }^{3}}\frac{{\tau }_{{{{\bf{k}}}}}^{2}}{| {{{\bf{Q}}}}| }\,{{{{\mathcal{F}}}}}_{0}^{2}{k}_{{{{\rm{F}}}}}^{2}{{{{\mathcal{F}}}}}_{3}\,{\left(\frac{T}{{\varepsilon }_{{{{\rm{F}}}}}}\right)}^{6}\frac{\Gamma }{\delta },$$

(10)

respectively. Here, we approximate k_F ≈ 1/a (inverse lattice constant), so that ℏv_F/a ≈ ε_F. The ratio between these two contributions leads to

$$\frac{{\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}}{{\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}}\approx \frac{1}{2\pi }\frac{{\tau }_{{{{\bf{k}}}}}}{\hslash }\,{\Gamma }^{2}{{{{\mathcal{F}}}}}_{0}\frac{{{{{\mathcal{F}}}}}_{3}}{{{{{\mathcal{F}}}}}_{2}}\frac{{T}^{4}}{{\varepsilon }_{{{{\rm{F}}}}}^{5}}\sqrt{\frac{{(A/{a}^{2})}^{3}}{\delta }}.$$

(11)

Thus, the relative strength depends on both electronic properties and the SF. On the electronic part, (i) longer lifetime τ_k, (ii) larger ${{{{\mathcal{F}}}}}_{3}$ than ${{{{\mathcal{F}}}}}_{2}$, and (iii) smaller Fermi energy ε_F prefer the skew-scattering mechanism over the side jump. On the SF part, (iv) larger A, corresponding to spin stiffness or magnetic exchange, (v) larger damping ratio Γ, which is a dimensionless parameter here but is proportional to the electron density of states at the Fermi level, and (vi) smaller δ prefer the skew-scattering contribution.

Near the AFM QCP (the T regime III), ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ is modified as

$${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}\approx \frac{{e}^{2}m}{2{\pi }^{3}{\hslash }^{4}}\frac{{\tau }_{{{{\bf{k}}}}}}{| {{{\bf{Q}}}}| }\,{{{{\mathcal{F}}}}}_{0}{k}_{{{{\rm{F}}}}}^{2}{{{{\mathcal{F}}}}}_{2}\,\frac{{T}^{3/2}}{\Gamma \sqrt{{(A/{a}^{2})}^{3}}}.$$

(12)

Hence, with δ = T^3/2, the ratio between the two contributions becomes

$$\frac{{\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{skew}}}}\,{{{\rm{scatt.}}}}}}{{\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}}\approx \frac{\pi }{32}\frac{{\tau }_{{{{\bf{k}}}}}}{\hslash }\,{\Gamma }^{2}{{{{\mathcal{F}}}}}_{0}\frac{{{{{\mathcal{F}}}}}_{3}}{{{{{\mathcal{F}}}}}_{2}}\frac{{T}^{3}}{{\varepsilon }_{{{{\rm{F}}}}}^{5}}\sqrt{{(A/{a}^{2})}^{3}}.$$

(13)

Thus, ${\sigma }_{{{{\rm{AFM,SH}}}}}^{{{{\rm{side}}}}\,{{{\rm{jump}}}}}$ is expected to become progressively dominant as T → 0. This could be seen in the contrasting T dependence of σ_AFM,SH as plotted in Fig. 6.

In this work, we first considered the SH effect by the AFM SF, which is relevant to AFM metallic Cr. As early studies have reported, metallic Cr shows large SH effect^32,33. With the small SOC for a 3d element, this indicates additional contributions to the SH effect. Recent study used high-quality single crystal of Cr and revealed the detailed temperature dependence of the SH conductivity³⁴. Their electric resistivity data does not show a strong anomaly at T_N. This indicates that the carrier lifetime is influenced by magnetic ordering and the AFM SF only weakly and, thus, the system is in the perturbative regime, corresponding to very small r_sf in the plots of Fig. 4. Thus, the strong enhancement in the SH conductivity could be ascribed to the mechanisms developed in this work. The remaining question is which mechanism provides the main contribution to the SH effect in Cr, the side-jump mechanism or the skew-scattering mechanism. This will be answered when the SF fluctuation spectrum is carefully analyzed. Such analyses will also be helpful to understand and predict other AFM metallic systems for the SH effect.

At this moment, we are unaware of experimental reports of the SH effect in the vicinity of the AFM QCP. It might be worth investing the SH effect using CeCu_6−xAu_x⁴⁷ and other Ce compounds⁴⁸. The temperature dependence of the SH conductivity might provide further insight into the nature of their QCP.

The SH effect near the FM critical temperature appears to depend on the material. Early studies on Ni-Pd alloys²⁷ reported that the temperature dependence of the SH effect is analogous to that of the uniform second-order nonlinear susceptibility χ₂, with a positive peak above T_C and a negative peak below T_C, thus showing the sign change across T_C. Such a behavior is qualitatively reproduced by a theoretical work by Gu et al.³⁰, which adopted a static mean field approximation to the Kondo’s model³¹. The current work, on the other hand, predicts that the SH effect of FM metals is maximized at T_C, while the same model is used as Gu et al. An experimental study by Ou et al. reported the sharp enhancement of the SH effect near T_C of Fe-Pt alloys²⁸, the behavior resembles our prediction. A more recent experimental study by Wu et al. also reported a similar but weaker enhancement of the SH effect of Ni-Cu alloys²⁹. How the SH effect depends on the material, changing sign or maximizing at T_C, remains an open question. One possible scenario is that the spin dynamics in Ni-Pd alloys is ‘classical’ in nature, while that in Fe-Pt and Ni-Cu alloys is more ‘quantum’, so that the theoretical analysis presented in this work is more relevant to the latter. Detailed experimental analysis on the spin dynamics of these FM metallic alloys using inelastic neutron scattering would settle this issue.

It is not obvious which SF generates the larger spin Hall effect, AFM or FM, because the detail of the materials property is involved. From the leading temperature dependence, the FM SF gives a stronger temperature dependence of the spin Hall conductivity when approaching T_C from higher temperature than the AFM fluctuation when approaching T_N. For FM metals, the spin Hall effect is expected to be replaced by the anomalous Hall effect below T_C, which is not the scope of the current study, while for AFM metals the spin Hall effect should persist down to low temperatures. Thus, both systems could be useful for the spintronic application depending on the temperature range.

To summarize, we developed the comprehensive theoretical description of the spin Hall effect in magnetic metallic systems due to the spin fluctuation. The special focus is paid to the antiferromagnetic spin fluctuation with nonzero Néel temperature T_N and T_N = 0, and the FM SF with nonzero Curie temperature T_C. In contrast to the spin Hall effect due to the ferromagnetic critical fluctuation, where the skew-scattering mechanism is one or two orders of magnitude stronger than the side-jump mechanism, the relative strength of the mechanisms could be altered depending on the detail of the spin-fluctuation spectrum and temperature. In particular, for antiferromagnetic metals, the skew-scattering mechanism becomes progressively dominant when approaching the magnetic transition temperature T_N, while the side-jump contribution becomes dominant by lowering temperature below T_N. The crossover from the skew scattering to the side jump also appears in a quantum critical system, where T_N is tuned to zero temperature. Aside from the absolute magnitude of the spin Hall conductivity, antiferromagnetic metals and ferromagnetic metals could be complementary in nature. This work thus provides an important component in antiferromagnetic spintronics⁴⁹. Many magnetic metallic systems have been reported to show a variety of Hall effects, for example the anomalous Hall effect in Fe₃GeTe₂⁵⁰, induced by the nontrivial band topology due to the orbital complexity, the spin-orbit coupling, as well as magnetic ordering. In the presence of such complexities, the predicted scaling law of the spin Hall effect could be modified, while the critical enhancement would not be entirely eliminated. Such an interplay will be an exciting research area, but left for future study.