Abstract
The van der Waals interaction in vertical heterostructures made of two-dimensional (2D) materials relaxes the requirement of lattice matching, therefore enabling great design flexibility to tailor novel 2D electronic systems. Here we report the successful growth of MoSe2 on single-layer hexagonal boron nitride (hBN) on the Ru(0001) substrate using molecular beam epitaxy. Using scanning tunnelling microscopy and spectroscopy, we found that the quasi-particle bandgap of MoSe2 on hBN/Ru is about 0.25 eV smaller than those on graphene or graphite substrates. We attribute this result to the strong interaction between hBN/Ru, which causes residual metallic screening from the substrate. In addition, the electronic structure and the work function of MoSe2 are modulated electrostatically with an amplitude of ∼0.13 eV. Most interestingly, this electrostatic modulation is spatially in phase with the Moiré pattern of hBN on Ru(0001) whose surface also exhibits a work function modulation of the same amplitude.
Similar content being viewed by others
Introduction
The emergence of semiconducting transition metal dichalcogenides (TMDs) as two-dimensional (2D) electronic materials has triggered intensive research activities1,2,3,4. In conjunction with graphene (a semi-metal) and hBN (a large gap insulator), they form a diverse tool set for tailoring novel 2D electronic systems. One particularly powerful approach is stacking different types of van der Waals (vdW) materials to form vdW heterostructures5. Many conceptual demonstrations of vdW heterostructures have been achieved by using mechanical exfoliations of vdW layers and then stacking them together using transfer methods6,7,8. This exfoliation/transferring approach, however, is not scalable. An attractive and scalable approach is the direct epitaxial growth of 2D heterostructures, which has recently been shown in several systems using ambient chemical vapour deposition (CVD)9,10,11,12,13,14,15. Nevertheless, achieving atomic scale control of contamination using ambient CVD is quite challenging. As an ultra-high-vacuum (UHV)-based growth technique, molecular beam epitaxy (MBE) should provide better control of interface formation16, although the number of 2D heterostructure systems demonstrated is more limited17,18,19,20,21.
Single-layer hBN on transition metal surfaces, including Ru(0001), is a very interesting platform with very rich phenomena22,23,24. It had been used as a platform to grow graphene/hBN heterostructures25,26,27,28 and moreover, such heterostructures can be separated from the Ru(0001) substrate by using electrochemical exfoliation29,30. Owing to the slight lattice mismatch between the hBN and Ru(0001) surfaces, a so-called nanomesh Moiré pattern forms22,23. Such a Moiré pattern introduces not only height corrugation on hBN (ref. 23) but also periodic modulation in the local work function31,32,33. These properties make the single-layer hBN/Ru(0001) and related systems an ideal platform for investigating how the local work function impacts the electronic structure of the overlayer on top of hBN/Ru(0001) substrate.
In this paper, we report the MBE growth and scanning tunnelling microscopy/spectroscopy (STM/STS) investigation of MoSe2 on single-layer hBN on Ru(0001). We not only demonstrate the feasibility of growing MoSe2/hBN heterostructure using MBE but also illustrate a convincing case of electronic structure tuning of TMDs. We find the strong interaction between hBN and Ru(0001) makes hBN inseparable from the underlying Ru. The interaction arising from the local atomic registry between the layers and the resulting charge transfer are verified by first-principles calculations. The hBN/Ru(0001) system as a whole has a strong electrostatic screening effect on the band structure of MoSe2, reducing the MoSe2 quasi-particle gap by 0.25 eV compared with that of MoSe2 on graphene or graphite substrates34. Furthermore, we show that the local work function modulation on single-layer hBN results in a rigid shift of the band structure of MoSe2 without changing the bandgap, indicating a pure electrostatic effect. Moreover, the modulation of the MoSe2 band edges is about 0.13 eV, quantitatively similar to the local work function modulation amplitude in hBN. In addition, the work function in MoSe2 shows the same modulation, illustrating a convincing case of real-space electrostatic tuning of the band profile.
Results
Growth and characterization of MoSe2/hBN/Ru(0001)
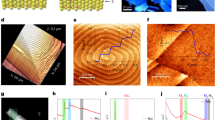
MoSe2/hBN/Ru(0001) heterostructures are synthesized in an all-UHV approach. First, single-layer hBN is prepared on Ru(0001) following the standard UHV-CVD procedure22,23. Put briefly, hBN forms by the catalytic dehydrogenation of borazine molecules on the Ru(0001) surface at proper vapour pressure and temperature. The high quality of hBN is confirmed by in situ reflection high-energy electron diffraction (RHEED) and STM. Shown in Fig. 1a is the RHEED pattern after the hBN growth on Ru(0001), with sharp spots indicating perfect crystallinity of the sample surface. Note that there are six dots arranged at hexagon corners surrounding each bright spot on the first Laue ring, reflecting the existence of a Moiré pattern. Figure 1b shows a typical large-scale STM image of continuous single-domain hBN. A nanomesh Moiré pattern is clearly seen. The full coverage of single-domain hBN observed here agrees with the spotty characteristic of RHEED. After a full coverage of single-layer hBN, additional exposure to borazine molecule would not lead to additional growth suggesting that borazine molecules no longer have access to the catalytic Ru(0001) surface. The zoomed-in image of the nanomesh shown in Fig. 1c reveals that the periodicity of the nanomesh pattern is 3.2 nm, in agreement with the periodicities of 13 × 13 hBN and 12 × 12 Ru(0001) lattices23,35. Meanwhile, two distinct topography features on the nanomesh are seen: the lower and strongly bound regions assigned as holes; and the higher and loosely bound regions assigned as wires. This uneven binding causes the corrugation of the hBN, with an average amplitude of about 0.1 nm.
(a) RHEED pattern of epitaxial single-layer hBN on the Ru(0001) substrate. (b) Large-scale STM image (−2 V, 5 pA, 215 nm × 215 nm) shows the uniform high-quality single-layer hBN on Ru(0001). (c) The upper panel is the high-resolution STM image (−2 V, 5 pA, 20 nm × 20 nm) of the hBN nanomesh (Moiré pattern), and the lower panel is the height profile along the red dashed line. The periodicity and corrugation of the nanomesh are about 3.2 and 0.1 nm, respectively. (d) RHEED pattern of the single-layer MoSe2 thin film grown on hBN/Ru(0001). The sharp and uniform streaks (indicated by red arrows) reflect the successful synthesis of the MoSe2 film. (e) Large-scale STM image (−2 V, 5 pA, 215 nm × 215 nm) shows the successful fabrication of nanoscale MoSe2 islands. The bright lines in the single-layer MoSe2 regions are domain boundaries. (f) The top panel is the STM image of a typical MoSe2 island, and the inset reveals the atomic resolution of the MoSe2 layer. The bottom panel is the height profile along the red dashed line. The corrugation amplitude of the MoSe2 surface is about 0.8 Å and is completely in phase with that of the underlying hBN, indicating that the periodic structure on the island is actually a transparent pattern from the nanomesh (corrugation amplitude of ∼1.3 Å) through the single-layer MoSe2, instead of a Moiré pattern formed by MoSe2 and the underlying hBN.
After confirming the high quality of hBN/Ru(0001), we transferred this sample in situ to the MBE system for MoSe2 growth. This all-UHV approach produces a heterostructure with a clean and sharp interface. Additional sharp and uniform RHEED streaks (indicated by red arrows) in Fig. 1d reflect the successful formation of flat crystalline MoSe2 layers. In Fig. 1e, the large-scale STM image shows MoSe2 islands with diameters from tens to hundreds of nanometres and the bright clusters in the centre of islands are double-layer MoSe2. The apparent sharp lines within the MoSe2 are domain boundaries, which looks brighter because of the extra finite local density of states (LDOS) in the bandgap36,37. In Fig. 1f, the top panel shows a typical MoSe2 island, the inset shows an atomic resolution image taken from single-layer MoSe2, and the lower panel displays the height profile along the red dashed line. From the grid in the upper panel and the height profile in the lower panel, it is evident that the superstructure of the MoSe2 island has the same periodicity, corrugated amplitude and phase as the underlying hBN. Surprisingly, the expected Moiré pattern of MoSe2 and hBN, whose periodicity is ∼1 nm, is not observed here. Rather the superstructure visible on the MoSe2 is just a replication of the Moiré pattern from the underlying hBN, evident by the match in phase and periodicity of spatial modulation.
Bandgap renormalization of MoSe2/hBN/Ru(0001)
The renormalization of the bandgap in 2D materials due to the substrate is an intriguing concept that receives a lot of attentions recently10,17,34,38,39. It has been shown that single-layer MoS2 grown on Au(111) has a significantly lower bandgap than that grown on graphite10,38,39. In the case of MoSe2, earlier study suggested that MoSe2 on graphite has a smaller gap than MoSe2 on bilayer graphene17. However, later investigations indicated that the two cases have identical bandgaps34. The availability of hBN/Ru(0001) as the substrate that provides an excellent opportunity to revisit this important issue because hBN is a large gap insulator, which is anticipated to provide better isolation of the screening effect.
In Fig. 2a we show tunnelling conductance spectra with a fixed tip–sample distance, denoted as dI/dV, of MoSe2/hBN/Ru(0001), together with that of MoSe2/HOPG and MoSe2/graphene/SiC for comparison. In these spectra, one can identify positions of the valence band state at the Γ point (labelled as EΓ), the valence band maximum (VBM; at K point) EV (located at ∼0.4 eV above EΓ) and the conduction band minimum (CBM) EC. The quasi-particle bandgap is the energy difference between EV and EC. The spectra show that single-layer MoSe2 on graphene or on HOPG have a similar quasi-particle bandgap of 2.15 eV while single-layer MoSe2 on hBN/Ru(0001) has a smaller quasi-particle bandgap of 1.90 eV. The results show that the quasi-particle bandgap of single-layer MoSe2 indeed depends on the supporting substrate. Nevertheless, how it is renormalized does not follow the intuition that hBN should provide a better electronic isolation of MoSe2 from the substrate. Also shown in Fig. 2b is the tunnelling spectrum acquired on hBN with a relatively large sample stabilization voltage of −4 V (implying a relatively large sample-to-tip distance). Interestingly, significant conductance is still present in the expected gap region of hBN, reflecting remnant metallic characteristics. In Fig. 2c, we show statistical distributions of the results from 102 individual tunnelling spectra measured from different locations. The mean value and the s.d. of the quasi-particle bandgap of the single-layer MoSe2/hBN/Ru(0001) is 1.90±0.07 eV. Moreover, the dI/dV spectrum taken on top of a double-layer MoSe2 also shows the bandgap is about 1.58 eV (Supplementary Fig. 1), smaller than the gap of double-layer MoSe2 on graphene by 0.22 eV (ref. 34).
(a) Logarithm of dI/dV spectra for single-layer MoSe2 grown on different substrates. MoSe2/hBN/Ru(0001), MoSe2/graphene/SiC and MoSe2/HOPG are shown in black, red and blue, respectively. The MoSe2 layer on hBN has a smaller quasi-particle bandgap (by about 0.25 eV) than that of the MoSe2 on graphene or graphite substrates. (b) Logarithmic dI/dV of hBN/Ru(0001) shows the remnant metallic characteristics, due to the strong interaction between single-layer hBN and Ru(0001). (c) Statistical distribution (from 102 individual dI/dV spectra) of the quasi-particle bandgap measured for MoSe2/hBN. Mean value: 1.90 eV; s.d.: 0.07 eV.
Thus, our study convincingly demonstrates the concept of band structure renormalization in TMDs. Nevertheless, the actual manifestation of renormalization is probably more complex than an intuitive interpretation of the substrate electrostatic screening and is discussed further below.
Work function modulation of MoSe2/hBN/Ru(0001)
Besides the bandgap renormalization discussed above, we have also observed a periodic modulation of the band profile, which is associated with the work function modulation of the nanomesh Moiré pattern. Location-specific STS measurements are shown in Fig. 3. The typical dI/dV spectra taken from MoSe2 hole (red curves) and wire (blue curves) regions are plotted in both the linear scale (upper panel) and the logarithmic scale (lower panel) in Fig. 3a. We use the dI/dV spectra in the logarithmic scale to determine the CBM, the VBM and the energy of the Γ point in the valance band, ΓV (or EΓ). While the bandgap values and the energy differences between ΓV and the CBM are the same for both the hole and wire regions, there is a rigid offset for the absolute values of the CBM, VBM and ΓV. Such an offset in the band structure is illustrated more drastically in dI/dV mappings carried out at different tip–sample bias. Figure 3b,c is the topography of the same area at −2.15 and −2.0 V, which are close to ΓV of holes ( ) and wires (
) and wires ( ), respectively, and they look the same. However, the corresponding dI/dV mappings taken simultaneously in Fig. 3e,f have a completely reversed contrast; at −2.15 V the wire regions, which are brighter in the topography images, have a lower LDOS, while at −2 V the hole regions, darker in topography, have lower LDOS. This phenomenon confirms the existence of the modulation of the MoSe2 band structure. An alternative spectroscopy technique, tip-to-sample distance Z versus bias sweep at constant current mode, is used to determine the Γ point values. The (∂Z/∂V)I spectra taken over an ensemble of 120 holes and wires (Supplementary Fig. 2) statistically determine that
), respectively, and they look the same. However, the corresponding dI/dV mappings taken simultaneously in Fig. 3e,f have a completely reversed contrast; at −2.15 V the wire regions, which are brighter in the topography images, have a lower LDOS, while at −2 V the hole regions, darker in topography, have lower LDOS. This phenomenon confirms the existence of the modulation of the MoSe2 band structure. An alternative spectroscopy technique, tip-to-sample distance Z versus bias sweep at constant current mode, is used to determine the Γ point values. The (∂Z/∂V)I spectra taken over an ensemble of 120 holes and wires (Supplementary Fig. 2) statistically determine that  =−2.14±0.03 eV,
=−2.14±0.03 eV,  =−2.01±0.02 eV and therefore the amplitude of the periodic modulation of band profile is 0.13±0.05 eV.
=−2.01±0.02 eV and therefore the amplitude of the periodic modulation of band profile is 0.13±0.05 eV.
(a) The dI/dV spectra taken on the single-layer MoSe2 flake. The tunnelling conductance dI/dV (with arbitrary unit) is plotted in both the linear scale (upper panel) and the logarithmic scale (lower panel). The black dashed arrows indicate the energy locations of the Γ points, and we observed a rigid shift of the whole band structures (by about 0.13 eV) on hole and wire locations. (b,c) Topography for the corrugated single-layer MoSe2. (d,e) Corresponding dI/dV images for b and c, respectively. Scale bar, 2 nm. (f) Field emission resonance (FER) spectroscopy measured on the MoSe2 wire (blue) and MoSe2 hole (red). (g) FER spectroscopy measured on the hBN wire (blue) and hBN hole (red).
In addition, the (∂Z/∂V)I spectra in the field emission region are used, and the sample bias for the first field emission resonance (FER) peak is considered a good approximation of the work function of the sample32,33. Figure 3f,g shows the local work function modulation of hBN/Ru(0001) is 0.14 eV, and for the MoSe2 overlayer such modulation is 0.16 eV, both in excellent agreement with the periodic band offset observed on MoSe2. From this consistency, one can conclude that the band offset in MoSe2 is purely an electrostatic effect.
Discussion
The bonding and resulting change in the electronic structure of hBN on Ru(0001) can be understood by first-principles calculations. The observed Moiré pattern in hBN/Ru(0001) corresponds to roughly 13 × 13 hBN on 12 × 12 Ru(0001), which is too large for a thorough theoretical analysis using plane waves. Instead, we used a supercell with √67 × √67 hBN on √57 × √57 Ru(0001) and a small rotational angle of 5.6°, as shown in Fig. 4a, which provides the essential collection of different atomic registries between the layers and reliable electronic properties for them because the strain (0.45%) is very small. The relaxed atomic configuration is shown in Fig. 4b, indicating that a certain portion of the hBN layer is moved closer to the Ru substrate. This happens in the region near the black circle in Fig. 4a, in which the N atoms are approximately located right above the Ru atoms and strong bonding occurs, giving rise to a calculated interlayer reduction as large as 1.6 Å, in agreement with calculated results obtained previously with different supercells, basis sets and exchange-correlation functionals40,41,42. The bonding can be seen by the iso-surfaces of charge transfer shown in Fig. 4c. In contrast, the green and purple circles mark the regions in which Ru atoms are located right below the B atoms and the centre of the B–N hexagons, respectively. The interlayer interaction is weak, and these two regions are at about 3.7 Å above the Ru plane, a reasonable distance for the vdW interaction.
(a) Top view and (b) side view of the atomic structure of √67 × √67 hBN on √57 × √57 Ru(0001). The red, blue and grey spheres are N, B and Ru atoms, respectively. The black, pink and green circles indicate the regions with N atoms at the top, face-centred cubic and hexagonal close-packed sites, respectively, with respect to the Ru(0001) substrate. The average distance between the hBN and the surface Ru layers is about 3.73 Å in the regions indicated by both the green and pink circles and 2.14 Å in the region of the black circle, with a maximal height difference of about 1.67 Å for the hBN layer. (c) Charge density difference induced by the interaction, with the yellow (blue) iso-surfaces indicating an increase (decrease) in the charge density. (d) Calculated electrostatic potential variations at the height of 4.9 Å above the hBN layer, which corresponds to average of the interlayer distances of hBN and MoSe2. The potential at the centre of the vacuum region is set at zero. The profile along the black dashed line is also shown below in which the upper (lower) red dashed line indicates the minimum at the wire (hole) region.
If we evaluate the electrostatic potential at 4.9 Å above the hBN layer (the average of the vdW layer separations of hBN and MoSe2), the value in the hole region is clearly lower than that in the wire region by 0.14 eV, as shown in Fig. 4d. This is in excellent agreement with the relative band edge shift of single-layer MoSe2 between the two regions as observed in the experiment. The projected density of states shown in Supplementary Fig. 3 confirms that the significant interaction between hBN and the Ru substrate in the hole region induces states in the hBN gap, giving rise to a metallic characteristic.
Our observation of a bandgap reduction of 0.25 eV for MoSe2 on hBN/Ru(0001) proposes interesting possibilities of bandgap renormalization in 2D materials. One probable origin is the extra screening by the states in the gap of hBN arising from the strong interaction with the substrate metal. Keeping this remnant screening effect in mind, one still need to reconcile with the fact that the wire region has a weaker interaction and thus should have a weaker screening (relative to the hole region). Yet we do not observe any difference in the electronic structures between the hole and wire region, except for the electrostatic modulation. One possibility is that the corrugation of the Moiré pattern observed on MoSe2 is smaller than that corrugation of hBN Moiré pattern by about 0.5 Å (Fig. 1f), which suggests a modulation of vdW gap distance by the same amount (smaller vdW gap in the wire region). Such a vdW gap modulation would provide a compensation effect. Nevertheless, STM topography does not necessarily reflect the structural contrast quantitatively and thus this explanation is tentative at best. Another possible reason is the significant corrugation (about 0.08 nm) of single-layer MoSe2 as shown in Fig. 1f. In planar single-layer MoSe2 the VBM (CBM) is the dxy and  orbitals from Mo. Any local distortion away from the perfect flatness will break the planar symmetry and induce additional hybridization between these d orbitals. A bandgap reduction is an entirely plausible result in this situation.
orbitals from Mo. Any local distortion away from the perfect flatness will break the planar symmetry and induce additional hybridization between these d orbitals. A bandgap reduction is an entirely plausible result in this situation.
In summary, we have demonstrated the successful MBE growth of single-layer MoSe2 islands on top of hBN/Ru(0001). Our STM/STS results have revealed that MoSe2 on the strongly coupled hBN/Ru(0001) has a quasi-particle bandgap of 1.90±0.07 eV, 0.25 eV smaller than the results on graphite and graphene. These results on the one hand affirm the concept of band structure renormalization due to the substrate, but on the other hand shows that the renormalization is far more complex than a simple consideration of the metallicity of the substrate and call for more thorough theoretical/experimental investigations. In addition, we show that the local work function modulation on the hBN/Ru(0001) nanomesh structure creates a periodic template of potential modulation, where the band profile of the MoSe2 mimics this potential modulation precisely.
Methods
Growth of MoSe2/hBN/Ru(0001) heterostructures
The clean Ru(0001) surface was obtained on a piece of Ru single crystal by multiple cycles of Xe+ sputtering and annealing at 1,000 °C. Hexagonal boron nitride formed on Ru when the single crystal was heated to 1,000 °C and exposed to a borazine vapour of 1 × 10−6 torr for about 5 min, then the sample was slowly cooled down to room temperature. The quality of the hBN was checked by STM and RHEED. Then this hBN/Ru(0001) sample was transferred in situ to a MBE chamber for the MoSe2 growth. The high-purity Mo (99.95%) and Se (99.999%) elemental sources were evaporated from an e-beam evaporator and an effusion cell, respectively, with a ratio of 1:30. Single-layer MoSe2 with a coverage of about 30% formed after 45 min of deposition with a substrate temperature of 420 °C, followed by 30 min of annealing at the same temperature with the Se flux maintained.
Scanning tunnelling microscopy and spectroscopy
All STM investigations reported here were acquired at 77 K in UHV (base pressure is better than 6 × 10−11 mbar). A tungsten tip was used. The bias voltage was applied to the sample. The conventional STS, dI/dV, was acquired at a constant tip-to sample distance (Z) with the feedback loop off. The (∂Z/∂V)I spectrum was acquired when the tip-to-sample distance Z changes corresponding to the scanning of bias V to keep the constant current.
First-principles calculations
We have performed first-principles calculations with density functional theory as implemented in the Vienna Ab initio Simulation Package43. We used the projector augmented wave method44 to treat core electrons, and the Perdew–Burke–Ernzerhof (PBE) form45 for the exchange-correlation functional with a plane-wave cutoff energy of 300 eV. The periodic slabs contain three Ru layers as the substrate and a vacuum region of about 13 Å. The bottom of the three Ru layers is fixed, while the rest two Ru layers and the hBN layer are allowed to relax during the geometry optimization.
Data availability
The data that support the findings of this study are available from the corresponding author on request.
Additional information
How to cite this article: Zhang, Q. et al. Bandgap renormalization and work function tuning in MoSe2/hBN/Ru(0001) heterostructures. Nat. Commun. 7, 13843 doi: 10.1038/ncomms13843 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263–275 (2013).
Butler, S. Z. et al. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 7, 2898–2926 (2013).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2 . Nano Lett. 10, 1271–1275 (2010).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Haigh, S. J. et al. Cross-sectional imaging of individual layers and buried interfaces of graphene-based heterostructures and superlattices. Nat. Mater. 11, 764–767 (2012).
Kretinin, A. V. et al. Electronic properties of graphene encapsulated with different two-dimensional atomic crystals. Nano Lett. 14, 3270–3276 (2014).
Rivera, P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2–WSe2 heterostructures. Nat. Commun. 6, 7242 (2015).
Behura, S., Nguyen, P., Che, S., Debbarma, R. & Berry, V. Large-area, transfer-free, oxide-assisted synthesis of hexagonal boron nitride films and their heterostructures with MoS2 and WS2 . J. Am. Chem. Soc. 137, 13060–13065 (2015).
Shi, J. et al. All chemical vapor deposition synthesis and intrinsic bandgap observation of MoS2/graphene heterostructures. Adv. Mater. 27, 7086–7092 (2015).
Wang, S., Wang, X. & Warner, J. H. All chemical vapor deposition growth of MoS2:h-BN vertical van der Waals heterostructures. ACS Nano 9, 5246–5254 (2015).
Yan, A. et al. Direct growth of single- and few-layer MoS2 on h-BN with preferred relative rotation angles. Nano Lett. 15, 6324–6331 (2015).
Fu, L. et al. Direct growth of MoS2/h-BN heterostructures via a sulfide-resistant alloy. ACS Nano 10, 2063–2070 (2016).
Chiu, M.-H. et al. Determination of band alignment in the single-layer MoS2/WSe2 heterojunction. Nat. Commun. 6, 7666 (2015).
Lin, Y.-C. et al. Atomically thin heterostructures based on single-layer tungsten diselenide and graphene. Nano Lett. 14, 6936–6941 (2014).
Koma, A. & Yoshimura, K. Ultrasharp interfaces grown with Van der Waals epitaxy. Surf. Sci. 174, 556–560 (1986).
Ugeda, M. M. et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 13, 1091–1095 (2014).
Bradley, A. J. et al. Probing the role of interlayer coupling and coulomb interactions on electronic structure in few-layer MoSe2 nanostructures. Nano Lett. 15, 2594–2599 (2015).
Miwa, J. A. et al. Van der Waals epitaxy of two-dimensional MoS2–graphene heterostructures in ultrahigh vacuum. ACS Nano 9, 6502–6510 (2015).
Liu, X. et al. Rotationally commensurate growth of MoS2 on epitaxial graphene. ACS Nano 10, 1067–1075 (2016).
Zhang, C. et al. Visualizing band offsets and edge states in bilayer-monolayer transition metal dichalcogenides lateral heterojunction. Nat. Commun. 7, 10349 (2016).
Corso, M. et al. Boron nitride nanomesh. Science 303, 217–220 (2004).
Goriachko, A. et al. Self-assembly of a hexagonal boron nitride nanomesh on Ru(0001). Langmuir 23, 2928–2931 (2007).
Laskowski, R., Blaha, P., Gallauner, T. & Schwarz, K. Single-layer model of the hexagonal boron nitride nanomesh on the Rh(111) surface. Phys. Rev. Lett. 98, 106802 (2007).
Sutter, P., Cortes, R., Lahiri, J. & Sutter, E. Interface formation in monolayer graphene-boron nitride heterostructures. Nano Lett. 12, 4869–4874 (2012).
Roth, S., Matsui, F., Greber, T. & Osterwalder, J. Chemical vapor deposition and characterization of aligned and incommensurate graphene/hexagonal boron nitride heterostack on Cu(111). Nano Lett. 13, 2668–2675 (2013).
Liu, M. et al. Quasi-freestanding monolayer heterostructure of graphene and hexagonal boron nitride on Ir(111) with a zigzag boundary. Nano Lett. 14, 6342–6347 (2014).
Yang, W. et al. Epitaxial growth of single-domain graphene on hexagonal boron nitride. Nat. Mater. 12, 792–797 (2013).
Lu, J. et al. Order–disorder transition in a two-dimensional boron–carbon–nitride alloy. Nat. Commun. 4, 2681 (2013).
Sutter, P., Huang, Y. & Sutter, E. Nanoscale integration of two-dimensional materials by lateral heteroepitaxy. Nano Lett. 14, 4846–4851 (2014).
Dil, H. et al. Surface trapping of atoms and molecules with dipole rings. Science 319, 1824–1826 (2008).
Joshi, S. et al. Boron nitride on Cu(111): an electronically corrugated monolayer. Nano Lett. 12, 5821–5828 (2012).
Schulz, F. et al. Epitaxial hexagonal boron nitride on Ir(111): a work function template. Phys. Rev. B 89, 235429 (2014).
Zhang, C. et al. Probing critical point energies of transition metal dichalcogenides: surprising indirect gap of single layer WSe2 . Nano Lett. 15, 6494–6500 (2015).
Sutter, P., Lahiri, J., Albrecht, P. & Sutter, E. Chemical vapor deposition and etching of high-quality monolayer hexagonal boron nitride films. ACS Nano 5, 7303–7309 (2011).
Liu, H. et al. Dense network of one-dimensional midgap metallic modes in monolayer MoSe2 and their spatial undulations. Phys. Rev. Lett. 113, 066105 (2014).
Liu, H. et al. Line and point defects in MoSe2 bilayer studied by scanning tunneling microscopy and spectroscopy. ACS Nano 9, 6619–6625 (2015).
Miwa, J. A. et al. Electronic structure of epitaxial single-layer MoS2. Phys. Rev. Lett. 114, 046802 (2015).
Krane, N., Lotze, C., Läger, J. M., Reecht, G. & Franke, K. J. Electronic structure and luminescence of quasi-freestanding MoS2 nanopatches on Au(111). Nano Lett. 16, 5163–5168 (2016).
Laskowski, R. & Blaha, P. Ab initio study of h-BN nanomeshes on Ru(001), Rh(111), and Pt(111). Phys. Rev. B 81, 075418 (2010).
Brugger, T. et al. Comparison of electronic structure and template function of single-layer graphene and a hexagonal boron nitride nanomesh on Ru(0001). Phys. Rev. B 79, 045407 (2009).
Gómez Díaz, J. et al. Hexagonal boron nitride on transition metal surfaces. Theor. Chem. Acc. 132, 1–17 (2013).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
This research was supported with grants from the Welch Foundation (F-1672), and the US National Science Foundation (DMR-1306878 and EFMA-1542747). C.-R.P. and M.-Y.C. acknowledge support from Academia Sinica. C.Z. acknowledges the National Basic Research Program of China (Grant No. 2014CB921102).
Author information
Authors and Affiliations
Contributions
Q.Z. and Y.C. carried out the growth of heterostructures and STM/S measurements; Q.Z., Y.C. and C. Zhang carried out the data analysis; C.-R.P. and M.-Y.C. carried out the first-principles calculation; C.-K.S. and C. Zeng advised on the experiment and provided input on the data analysis; Q.Z., Y.C. and C.-K.S. wrote the paper with input from other co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures and Supplementary References (PDF 835 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, Q., Chen, Y., Zhang, C. et al. Bandgap renormalization and work function tuning in MoSe2/hBN/Ru(0001) heterostructures. Nat Commun 7, 13843 (2016). https://doi.org/10.1038/ncomms13843
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13843
This article is cited by
-
Electronic gap characterization at mesoscopic scale via scanning probe microscopy under ambient conditions
Nature Communications (2022)
-
Selective self-assembly of 2,3-diaminophenazine molecules on MoSe2 mirror twin boundaries
Nature Communications (2019)
-
Tuning the Electronic Structures of Atomic Layer MoS2 on Different Substrates Using Scanning Tunneling Microscopy/Spectroscopy
Journal of Electronic Materials (2019)
-
Hexagonal MoTe2 with Amorphous BN Passivation Layer for Improved Oxidation Resistance and Endurance of 2D Field Effect Transistors
Scientific Reports (2018)
-
First-principles study of nonmetal doped monolayer MoSe2 for tunable electronic and photocatalytic properties
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.