Introduction

A haplotype, generally described by a DNA sequence, is a single genetic constituent of an individual chromosome inherited from the father or mother. Haplotype information is invaluable for various gene-based studies and applications, e.g., gene-disease association studies, evolutionary genetics, personalized medicine, and drug development (Risch and Merikangas 1996; Hodge et al. 1999; Johnson et al. 2001). Because of current technological limitations, however, homologous chromosomes in a pair are usually determined in mixed form. That is, the diplotype cannot be determined with certainty from multilocus genotype information. Even though experimental haplotyping is technically possible (Tost et al. 2002; Ding and Cantor 2003), it is too difficult, expensive, and time-consuming. Statistical and computational methods are alternatively used to infer diplotypes from the set of genotype data for a population. Personalized medicine is one of the most important applications of haplotype inference because humans have a wide variety of polymorphic sites (Venter et al. 2001; Daly et al. 2001).

Various methods have been proposed for haplotype inference (Clark 1990; Excoffier and Slatkin 1995; Stephens et al. 2001; Niu et al. 2002; Qin et al. 2002; Scheet and Stephens 2006; Xing et al. 2007). The probabilistic model of haplotype frequencies or of individual diplotypes mainly consists of heredity and selection. Two major models have been proposed; the first is Hardy–Weinberg equilibrium (HWE) based, and the second is coalescence based. HWE could be the simplest model to define all of them. Moreover, the only parameters are the haplotype frequencies in the population. The expectation-maximization (EM) algorithm is usually used to determine the optimal solution with this model (Excoffier and Slatkin 1995). The EM algorithm guarantees convergence to a locally optimal solution and, depending on the initial values, converges to one of several globally optimal solutions with high probability. Furthermore, it provides a sufficiently accurate result even if the HWE assumption is violated (Niu et al. 2002). However, it cannot handle more than about 20 heterozygous loci because of the exponentially increasing cost of calculation. The coalescence model is also widely used and can explain more about heredity—recombination and point mutation. Although this is considered to be appropriate for stable populations, it is less suitable for those that are unstable. Because the model has a great deal of redundancy, even small deviations in the samples from the true distribution of the population easily result in an over-fitted inference to a given data set. Moreover, it is not easy to find the optimal solution using this model. The Markov-chain Monte Carlo (MCMC) method, which is usually employed to determine an optimal guess for this model, neither guarantees local nor global optimality and is not quick to converge. Intrinsically, its solution is an approximation, and its accuracy depends on the number of Monte Carlo steps. Some approximation is generally introduced to save calculation cost.

We propose a method that combines a grouping preprocess and the EM algorithm (the “GrEM” method) to reduce the cost of calculation, and that produces a solution that is theoretically equivalent to the EM solution without any approximation. The cost is reduced by making use of the symmetrical and inclusive haplotype relationships in the likelihood function. If a haplotype group is found in which every haplotype is equivalent to every other haplotype in the sense of haplotype frequency likelihood, these haplotypes are handled as one group. If a constant superiority–inferiority relationship is found between two haplotypes in the sense of haplotype frequency likelihood, the inferior one is dropped. This simple preprocessing greatly reduces the number of haplotype and diplotype candidates that are considered when the EM algorithm is subsequently run. The optimal solution in some data sets may not be unique. Even in these cases, the GrEM method can find the solution in the form of two optimal haplotype groups and not in the form of two optimal haplotypes for each subject.

Materials and methods

Probabilistic model

The data available are assumed to be on non-genealogical unphased multilocus genotypes such as those on single nucleotide polymorphism (SNP), on short tandem repeat polymorphism, or on a variable number of tandem repeats in a single haplotype block. This assumption is reasonable given that these data, especially the SNP data, represent the most frequent forms of human genetic variations and are less expensive to obtain than genealogical data and phased data. Moreover, SNP data have a higher density and are less mutable (Wang et al. 1998; Kruglyak 1999). The International HAPMAP Project has collected and stored a great deal of SNP data in a database for use in developing a haplotype map of the human genome (Altshuler et al. 2005; Frazer et al. 2007).

The data model and inference framework are as follows. The given data set consists of data for I subjects, and the data for the ith subject, g i , specifies a sequence of observed genotypes of N polymorphic loci. What we infer is the most probable diplotype for each subject, \( \user2{d}_{i} \equiv \left( {d_{{i,1}} ,d_{{i,2}} } \right), \) where each d i,j denotes haplotype identification. To prevent permutation symmetry, d i,1 and d i,2 are always sorted in a certain order; this has been written as d i,1 ≤ d i,2 here. We carry out inference using the maximum likelihood (ML) inference of the haplotype frequencies θ:

$$ \user2{\hat \theta } \equiv \mathop {\arg \max }\limits_{\varvec{\theta}} P\left( {\left\{ {g_{i} } \right\}\left|\varvec{\theta}\right.} \right), $$
(1)
$$ \left\{ {\user2{\hat d}_{i} } \right\} \equiv \mathop {\arg \max }\limits_{{\left\{ {\user2{d}_{i} } \right\}}} P\left( {\left\{ {\user2{d}_{i} } \right\}\left| {\left\{ {g_{i} } \right\}} \right.,\user2{\hat \theta }} \right). $$
(2)

For simplicity, we have limited the given data to those for SNP, but extension to more general polymorphism data would be easy.

The model assumes HWE,

$$ P\left( {\left\{ {g_{i} } \right\},\left\{ {\user2{d}_{i} } \right\}\left|\varvec{\theta}\right.} \right) \equiv \prod\limits_{i}^{I} {\delta _{{d_{{i,1}} \le d_{{i,2}} ,\;d_{{i,1}} \oplus d_{{i,2}} = g_{i} }} \left( {1 + \delta _{{d_{{i,1}} \ne d_{{i,2}} }} } \right)\theta _{{d_{{i,1}} }} \theta _{{d_{{i,2}} }} } , $$
(3)

where δ denotes an indicator function, which yields 1 when the given condition is true and 0 otherwise. HWE implies that the relationship between any two haplotypes is primarily equal. In other words, recombination and point mutation are not explicitly considered.

The specific EM algorithm in this inference problem is given by the following update equation starting from randomly set θ (0):

$$ \begin{aligned}\varvec{\theta}^{{\left( {t + 1} \right)}} & \equiv \mathop {\arg \max }\limits_{\varvec{\theta}} \sum\limits_{{\left\{ {\user2{d}_{i} } \right\}}} {P\left( {\left\{ {\user2{d}_{i} } \right\}\left| {\left\{ {g_{i} } \right\}} \right.,\varvec{\theta}^{{\left( t \right)}} } \right)\ln P\left( {\left\{ {g_{i} } \right\},\left\{ {\user2{d}_{i} } \right\}\left|\varvec{\theta}\right.} \right)} \\ & = \frac{1}{{2I}}\sum\limits_{i}^{I} {\frac{{\sum\nolimits_{{d_{{i,1}} \le d_{{i,2}} ,\;d_{{i,1}} \oplus d_{{i,2}} = g_{i} }} {\theta _{{d_{{i,1}} }}^{{\left( t \right)}} \theta _{{d_{{i,2}} }}^{{\left( t \right)}} \left( {\delta _{{d_{{i,1}} = h}} + \delta _{{d_{{i,2}} = h}} } \right)} }}{{\sum\nolimits_{{d_{{i,1}} \le d_{{i,2}} ,\;d_{{i,1}} \oplus d_{{i,2}} = g_{i} }} {\theta _{{d_{{i,1}} }}^{{\left( t \right)}} \theta _{{d_{{i,2}} }}^{{\left( t \right)}} } }}} . \\ \end{aligned} $$
(4)

However, this approach in the EM algorithm quickly breaks down due to the huge number of candidate diplotypes.

Methods

Here we explain the symmetrical and inclusive relationship between haplotypes regarding the likelihood function. By exploiting this relationship, candidate haplotypes can be grouped or dropped, hopefully resulting in a small number of haplotype groups that concern the succeeding EM algorithm.

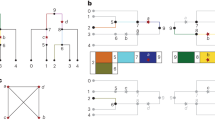
We start with the simplest case shown in Fig. 1a, in which only one subject is in a data set. “g 1: [1112]” represents observed genotype data consisting of four SNP loci with this subject, and “[1112]” within the circle of g 1 represents all possible haplotype(s) this subject may have. The genotype datum for each SNP locus could be two major alleles “1”, two minor alleles “2”, both alleles “3”, or missing “0”. The haplotype datum for each SNP locus could be a major allele “1” or a minor allele “2”. The bidirectional arrow represents a possible haplotype combination, or simply a diplotype, this subject may have. In this case, there is no other possibility than this subject having two identical haplotypes [1112].

Fig. 1
figure 1

Four examples of data sets shown by Venn diagrams of haplotypes. [1111], [1112], [1121], [1122], [1211], [1212], [1221], [1222], and [2111] represent haplotypes with four SNP loci. g 1:[1333] represents genotype data of the first subject enclosing all possible haplotypes the subject may have. Each bidirectional arrow represents a diplotype of a subject specifying two haplotypes. Only one subject is in a data set. a The subject has no heterozygous loci, so the diplotype is [1112] and [1112]. b The subject has one heterozygous locus, so the diplotype is [1111] and [1112]. c The subject has three heterozygous loci, and there are four equally possible diplotypes. d Two subjects are in a data set. Only the haplotype [1111] has the possibility of being shared by two subjects. The paired haplotype with [1111] regarding the first subject, [1222], and the one regarding the second subject, [2111], are also special haplotypes in the sense of the likelihood. The paired haplotypes have been enclosed by dashed borderlines for convenience

Full size image

In Fig. 1b, only subject g 1 has genotype data of [1113], which means this subject has only one possibility regarding diplotypes, i.e., [1111] and [1112].

In Fig. 1c, also, only subject g 1 has genotype data of [1333], which means this subject has four possibilities regarding diplotypes, (1) [1111] and [1222], (2) [1112] and [1221], (3) [1121] and [1212], and (4) [1122] and [1211]. These four possible diplotypes are also represented by the bidirectional arrows. In this case, the likelihood function is given by

$$ P\left( {\left\{ {g_{i} } \right\}\left|\varvec{\theta}\right.} \right) = \theta _{{[1111]}} \theta _{{[1222]}} + \theta _{{[1112]}} \theta _{{[1221]}} + \theta _{{[1121]}} \theta _{{[1212]}} + \theta _{{[1122]}} \theta _{{[1211]}} , $$
(5)

and there are four ML solutions, i.e., \( \left( {\theta _{{[1111]}} ,\theta _{{[1222]}} ,\theta _{{[1112]}} ,\theta _{{[1221]}} ,\theta _{{[1121]}} ,\theta _{{[1212]}} ,\theta _{{[1122]}} ,\theta _{{[1211]}} } \right) \) is (1) (1/2, 1/2, 0, 0, 0, 0, 0, 0), (2) (0, 0, 1/2, 1/2, 0, 0, 0, 0), (3) (0, 0, 0, 0, 1/2, 1/2, 0, 0), and (4) (0, 0, 0, 0, 0, 0, 1/2, 1/2). Here, note two characteristics of the likelihood function: the first is that four possible diplotypes are symmetrical, e.g., the exchange of two sets of theta values, \( \left( {\theta _{{[1111]}} ,\theta _{{[1222]}} } \right) \Leftrightarrow \left( {\theta _{{[1112]}} ,\theta _{{[1221]}} } \right) \) does not affect the likelihood under any arbitrary θ. Neither do exchanges of \( \left( {\theta _{{[1111]}} ,\theta _{{[1222]}} } \right) \Leftrightarrow \left( {\theta _{{[1121]}} ,\theta _{{[1212]}} } \right), \) \( \left( {\theta _{{[1112]}} ,\theta _{{[1221]}} } \right) \Leftrightarrow \left( {\theta _{{[1121]}} ,\theta _{{[1212]}} } \right), \) etc. This characteristic is obvious due to the symmetry of diplotypes in the likelihood function. The second characteristic is that optimal solutions are only given when three diplotype possibilities are zero, e.g., \( \left( {\theta _{{[1112]}} ,\theta _{{[1221]}} } \right) = \left( {\theta _{{[1121]}} ,\theta _{{[1212]}} } \right) = \left( {\theta _{{[1122]}} ,\theta _{{[1211]}} } \right) = \left( {0,0} \right). \) This characteristic is also easily proven using simple inequality

$$ \begin{aligned} & \theta _{{[1111]}} \theta _{{[1222]}} + \theta _{{[1112]}} \theta _{{[1221]}} + \theta _{{[1121]}} \theta _{{[1212]}} + \theta _{{[1122]}} \theta _{{[1211]}} \\ & \quad \le \left( {\theta _{{[1111]}} + \theta _{{[1112]}} + \theta _{{[1121]}} + \theta _{{[1122]}} } \right)\left( {\theta _{{[1222]}} + \theta _{{[1221]}} + \theta _{{[1212]}} + \theta _{{[1211]}} } \right) \\ & \quad \; + 0 \times 0 + 0 \times 0 + 0 \times 0, \\ \end{aligned} $$
(6)

which always holds (the equality mainly holds when three diplotype possibilities are zero). These two characteristics suggest that the concentration of haplotype frequencies to one of diplotypes, e.g.,

$$ \begin{gathered} \theta _{{[1111]}} \leftarrow \theta _{{[1111]}} + \theta _{{[1112]}} + \theta _{{[1121]}} + \theta _{{[1122]}} , \hfill \\ \theta _{{[1222]}} \leftarrow \theta _{{[1222]}} + \theta _{{[1221]}} + \theta _{{[1212]}} + \theta _{{[1211]}} , \hfill \\ \theta _{{[1112]}} \leftarrow 0,\;\theta _{{[1121]}} \leftarrow 0,\;\theta _{{[1122]}} \leftarrow 0, \hfill \\ \theta _{{[1221]}} \leftarrow 0,\;\theta _{{[1212]}} \leftarrow 0,\;\theta _{{[1211]}} \leftarrow 0, \hfill \\ \end{gathered} $$
(7)

is always necessary to obtain an optimal solution. We have called this type of concentration intra-group concentration. After this intra-group concentration, the EM algorithm can derive the best values for not-zero-assigned thetas (θ [1111] and θ [1222]). If we remember that an occasionally chosen diplotype (θ [1111] and θ [1222]) represents all four diplotypes, we can reconstruct four optimal solutions after the EM algorithm is run.

Next, let consider the case of two subjects in Fig. 1d. Here, the likelihood function is given as

$$ P\left( {\left\{ {g_{i} } \right\}\left|\varvec{\theta}\right.} \right) = \left( {\theta _{{[1111]}} \theta _{{[1222]}} + \theta _{{[1112]}} \theta _{{[1221]}} + \theta _{{[1121]}} \theta _{{[1212]}} + \theta _{{[1122]}} \theta _{{[1211]}} } \right) \times \left( {\theta _{{[1111]}} \theta _{{[2112]}} } \right), $$
(8)

and there is only one ML solution, i.e., \( \left( {\theta _{{[1111]}} ,\theta _{{[1222]}} ,\theta _{{[2111]}} } \right) = \left( {1/2,1/4,1/4} \right) \) where other unspecified haplotype frequencies are zero. Here, also note two characteristics: the first is that regarding g 1, concentrating haplotype frequencies to the diplotype [1111] and [1222] is always a better strategy than concentrating them to other diplotypes [1112] and [1221], [1121] and [1212], or [1122] and [1211]. This is because haplotype [1111] is the one both subjects may have, and this shared haplotype is always a better choice than non-shared haplotypes. More rigorously, the following inequality

$$ \begin{aligned} & \left[ {\theta _{{[1111]}} \theta _{{[1222]}} + \theta _{{[1112]}} \theta _{{[1221]}} + \theta _{{[1121]}} \theta _{{[1212]}} + \theta _{{[1122]}} \theta _{{[1211]}} } \right] \times \left[ {\theta _{{[1111]}} \theta _{{[2112]}} } \right] \\ & \;\; \le \left[ {\left( {\theta _{{[1111]}} + \theta _{{[1112]}} + \theta _{{[1121]}} + \theta _{{[1122]}} } \right)\left( {\theta _{{[1222]}} + \theta _{{[1221]}} + \theta _{{[1212]}} + \theta _{{[1211]}} } \right)} \right] \times \left[ {\theta _{{[1111]}} \theta _{{[2112]}} } \right], \\ \end{aligned} $$
(9)

always holds (the equality mainly holds when thetas of \( \theta _{{[1112]}} ,\theta _{{[1221]}} ,\theta _{{[1121]}} ,\theta _{{[1212]}} ,\theta _{{[1122]}} ,\;{\text{and}}\;\theta _{{[1211]}} \) are zero). The second characteristic is that if some haplotype is shared, the paired haplotype regarding each subject is also an important haplotype, i.e., the paired haplotypes of [1222] regarding g 1 and those of [2111] regarding g 2. These two characteristics suggest that the concentration of haplotype frequencies to the diplotype involving the shared haplotype,

$$ \begin{gathered} \theta _{{[1111]}} \leftarrow \theta _{{[1111]}} + \theta _{{[1112]}} + \theta _{{[1121]}} + \theta _{{[1122]}} , \hfill \\ \theta _{{[1222]}} \leftarrow \theta _{{[1222]}} + \theta _{{[1221]}} + \theta _{{[1212]}} + \theta _{{[1211]}} , \hfill \\ \theta _{{[1112]}} \leftarrow 0,\;\theta _{{[1121]}} \leftarrow 0,\;\theta _{{[1122]}} \leftarrow 0, \hfill \\ \theta _{{[1221]}} \leftarrow 0,\;\theta _{{[1212]}} \leftarrow 0,\;\theta _{{[1211]}} \leftarrow 0, \hfill \\ \end{gathered} $$
(10)

is always necessary to obtain an optimal solution. We call this type of concentration inter-group concentration. After inter-group concentration, the EM algorithm can derive the best values for not-zero-assigned thetas (θ [1111], θ [1222], and θ [2111]).

These two types of concentrations can be combined into a grouping preprocess of haplotypes. Consider the case of two subjects shown in Fig. 2a. Here, there are two ML solutions, i.e., \( \left( {\theta _{{[1111]}} ,\theta _{{[1222]}} ,\theta _{{[2112]}} } \right) = \left( {1/2,1/4,1/4} \right) \) and \( \left( {\theta _{{[1112]}} ,\theta _{{[1221]}} ,\theta _{{[2111]}} } \right) = \left( {1/2,1/4,1/4} \right). \) where unspecified haplotype frequencies are zero. We determine these ML solutions as follows. First, we draw a borderline to distinguish haplotypes the first subject may have from the other haplotypes. Similarly, we draw borderlines (solid lines) for every subject. Each borderline defines each territory. Some territories are overlapped; the haplotypes in such areas are haplotypes shared by more than one subject. We also define such overlapped areas as new territories. Second, we also draw borderlines to distinguish paired haplotypes regarding each subject. Specifically, if the territory of the first subject includes some other territory, we draw a new borderline to distinguish the paired haplotypes. We also define such areas as new territories. Similarly, we draw complete borderlines (dashed lines) for every subject. Note that any overlapped haplotype groups and any paired haplotype groups also form new territories, so a new territory may produce another new territory, one after another. This manipulation usually takes a lot of time. Last, we delete every territory that includes any other territories or is intersected by any other territories. In another words, we leave only the most nested territories.

Fig. 2
figure 2

An example of a data set showing a a Venn diagram of haplotypes, and b the resulting three territories the grouping preprocess determines. The territory [1113] is shared by two subjects. [1223] and [2113] correspond to the paired territories with [1113] regarding the first and second subjects, respectively

Full size image

The grouping preprocess above finally yields the three territories shown in Fig. 2b. According to inter-group concentration, only the most nested territories are interesting. According to intra-group concentration, every haplotype is equal in a territory and one of these haplotypes should be left if that territory has more than one haplotype. Consequently, the grouping preprocess precisely determines all territories that are worth leaving. After the grouping preprocess, we run the EM algorithm with only three territories, i.e., three thetas corresponding to each territory, which are the so-to-speak territory frequencies, to determine the optimal values. Compared to the original EM algorithm that needs to deal with numerous haplotypes (ten haplotypes in this case), the number of territories is usually quite smaller. The EM algorithm will derive the territory frequencies as \( \left( {\theta _{{[1113]}} ,\theta _{{[1223]}} ,\theta _{{[2113]}} } \right) = \left( {1/2,1/4,1/4} \right). \) Then, we can easily determine there are two ML solutions:\( \left( {\theta _{{[1111]}} ,\theta _{{[1222]}} ,\theta _{{[2112]}} } \right) = \left( {1/2,1/4,1/4} \right) \) and \( \left( {\theta _{{[1112]}} ,\theta _{{[1221]}} ,\theta _{{[2111]}} } \right) = \left( {1/2,1/4,1/4} \right) \) by referring to the given genotypes data. However, we do not want to carry out this expansion because it is too verbose and a territory occasionally includes numerous haplotypes. The most probable diplotypes for each subject can also be easily determined by using inferred territory frequencies.

From the computational point of view, each territory is expressed like genotype data, e.g., [1113], which means a set of haplotypes [1111] and [1112]. This single-sequence expression greatly reduces the computational cost because a territory sometimes includes an exponential number of haplotypes. If some territory happens to include [1111] and [1122], it is not convex and we cannot express this area as a single sequence, but this is never the case. This is because the initial territory of each subject is convex and an intersection of any two convex territories is also convex. Also, any paired territory is convex if the referred-to territory is convex.

One exception should be noted regarding intra-group concentration here. Consider the case in Fig. 3a, in which the third subject has been added to the previous case. The grouping preprocess derives the territories in Fig. 3b, where three territories ([1113], [1223], and [2113]) form a loop through the three bidirectional arrows. In such loopy cases, especially when the number of the territories is odd in a loop, intra-group concentration is not fully possible. This problem is like a Möbius strip. If we concentrate haplotype frequencies to [1111] in the territory of [1113], we should also concentrate haplotype frequencies to [1222] in the territory of [1223], and consequently, [2111], [1112], [1221], and [2112] through the bidirectional arrows in Fig. 3a. Therefore, we cannot concentrate haplotype frequencies to one haplotype in each territory; at least two haplotypes in each territory are needed. Fortunately, finding the territories forming a loop with an odd number of territories is computationally easy, and we can effectively manage to solve this problem.

Fig. 3
figure 3

An example of a data set showing a a Venn diagram of haplotypes and b the resulting four territories the grouping preprocess determines. Only the diplotypes the third subject may have are indicated by the dotted bidirectional arrows for convenience. The territories [1113], [1223], and [2113] form a loop through three bidirectional arrows

Full size image

The grouping preprocess is also effective where a genotype data set includes some missing values. Consider the case in Fig. 4a, in which the first subject has one missing value. Here, regarding the first subject, the paired haplotype with [1111] corresponds to either [1222] or [1221] because of the ambiguity of the missing value. By using the symmetry between these two paired haplotypes, we find they are equal and we do not need to distinguish them. Therefore, the paired territory with [1111] is [1223]. After the grouping preprocess with this extended definition of the paired territory, we obtain the result in Fig. 4b. The succeeding EM algorithm will derive \( \left( {\theta _{{[1111]}} ,\theta _{{[1223]}} ,\theta _{{[2111]}} } \right) = \left( {1/2,1/4,1/4} \right), \) and we can determine there are two ML solutions:\( \left( {\theta _{{[1111]}} ,\theta _{{[1222]}} ,\theta _{{[2111]}} } \right) = \left( {1/2,1/4,1/4} \right) \) and \( \left( {\theta _{{[1111]}} ,\theta _{{[1221]}} ,\theta _{{[2111]}} } \right) = \left( {1/2,1/4,1/4} \right). \)

Fig. 4
figure 4

An example of a data set showing a a Venn diagram of haplotypes and b the resulting three territories the grouping preprocess determines. Because the fourth SNP datum of the first subject is missing, either [1221] or [1222] corresponds to the paired haplotype with [1111]

Full size image

Regarding validation, we compared how well the GrEM method performed against both the original EM and other conventional methods using real and artificial data sets. First, we compared the number of candidate diplotypes between the GrEM method and the original EM algorithm. Note that the GrEM method combined the grouping preprocess and the original EM algorithm, so we could evaluate the performance of the grouping preprocess itself. Also note that the number of candidate diplotypes was more appropriate for evaluating the computational cost than that of the candidate haplotypes (see Eq. 4). Second, we compared the diplotype likelihood or error rates of inferred diplotypes for real data sets and artificial data sets, respectively. Note that the diplotype likelihood is a useful estimate when the correct answer is not available in real data sets. We used rather small data sets for the comparison with the original EM so that it could handle them. We used rather large data sets for the comparisons with the conventional methods, i.e., SNPHAP (see Clayton Website), PL-EM (Qin et al. 2002), fastPHASE (Scheet and Stephens 2006), PHASE (Scheet and Stephens 2003), 2SNP (Brinza and Zelikovsky 2006), HaploRec (Eronen et al. 2006) and Beagle (Browning and Browning 2007). SNPHAP, PL-EM, and HaploRec were roughly based on the HWE and EM algorithm, while fastPHASE was based on the coalescence model and the MCMC method (Stephens and Donnelly 2003; Marchini et al. 2006). PHASE uses a prior distribution based on the coalescence model with a Gibbs sampler while PL-EM and SNPHAP are based on a uniform Dirichlet prior. Beagle uses a hidden Markov model (HMM) and implements the EM algorithm to fit the model. 2SNP is based on the consideration of two haplotypes. Third, we measured the coincidence rates of inferred diplotypes between the GrEM method and the conventional methods and all running times.

Materials and computer system

The real data sets we used were sampled from the Tokyo Women’s Medical University with the approval of their Ethical Review Board and with appropriate informed consent by the subjects (Kamatani et al. 2004). Autosomal SNP data from 1,032 normal volunteers were used, and DNA samples were obtained from 752 randomly selected subjects. We chose 21 regions (R01-21) for the SNPs, each of which was considered to be a single or a few haplotype block(s).

The artificial data sets were created according to Niu et al. (2002), i.e., we generated the data sets by using HWE, single point mutation, and recombination criteria. More specifically, we first randomly prepared each allele of 30 ancestors and then mated them randomly to create successive generations with a point mutation rate of 10−5 a single miosis and a crossing-over rate of 10−3 a single miosis (it may happen between every neighboring SNP loci). The growth rate for the first two generations was 2.0, and that for the remaining generations was 1.05. Each artificial data set was constructed by random sampling from the 101st generation.

The computer system we used had an Intel® Core™ 2 Duo T7200 (2.0 GHz and 4-MB cache) CPU and a 2-GB main memory. The program was developed using C# language in the.NET Framework 2.0 environment under a Microsoft® Windows® OS.

Results

The GrEM method successfully reduced the number of candidate diplotypes (Fig. 5). The geometrical average ratios of the numbers of candidate diplotypes were 0.139 for small real data sets and 0.236 for small artificial data sets. The GrEM method reduced the numbers for large data sets, which the original EM algorithm could not handle. The reduction in the rate of haplotype candidates by using the GrEM method was roughly the same as that of the diplotype candidates.

Fig. 5
figure 5

Number of candidate diplotypes in a real data sets (R01-15) and b artificial data sets including A101-200 in Table 1. Every artificial data set consists of 256 subjects and has 1.0% missing values. The error bars indicate ±1 standard deviation. The averages and error bars were calculated on a logarithmic scale over 100 independent artificial data sets

Full size image

The GrEM method generally performed as well as the EM algorithm (Table 1) for both the small real data sets and the small artificial data sets regarding diplotype likelihood and error rates, respectively. More specifically, the GrEM method slightly outperformed the EM algorithm, which will be discussed later.

Table 1 Comparison with EM results
Full size table

The GrEM method also generally performed as well as the conventional methods (Table 2) for both the real data sets and the artificial data sets. More precisely, it performed slightly better and this will also be discussed later.

Table 2 Comparison with results using conventional methods
Full size table

The results for the average coincidence rate between the GrEM method and the conventional methods reveal that the inferred diplotypes were roughly the same, but about 1% were different (Table 3) although both 2SNP and HaploRec showed large differences from other methods. The running times for the GrEM method were generally longer than those for the conventional methods (Table 3). More precisely, PL-EM sometimes showed memory overflow in the real data sets. Also, PHASE sometimes showed program errors in the artificial data sets. PHASE and fastPHASE took a slightly longer time than the GrEM method in the real data sets.

Table 3 Average coincidence rates and running times
Full size table

Discussion

We propose a haplotype inference approach, the GrEM method, which combines a grouping preprocess with the expectation-maximization (EM) algorithm. It reduces the cost of calculation and produces a solution theoretically equivalent to that of the EM algorithm based on the HWE model. Although the EM algorithm was demonstrated to be accurate in identifying common haplotypes, it could not handle large data sets. The grouping preprocess in the GrEM method extended the application of the EM algorithm without the need for any approximation. Therefore, the GrEM method can be used as an alternative to the EM algorithm. In testing, the GrEM method actually reduced the cost of calculation and output equivalent results to those of the EM algorithm. In short, the GrEM method reduced the limitations of the EM algorithm without degrading performance. This result strongly supports its alternative use to the EM algorithm.

The effects of inter-group concentration were usually more dominant than those of intra-group concentration. This is because the remaining territories with the grouping preprocess answers tended to include only one haplotype. The effect of inter-group concentration can generally be considered to be dominant when the territories of numerous subjects are overlapped, while the effect of intra-group concentration can be considered to be dominant when the territories of subjects are rarely overlapped. Thus, both the concentrations are considered to be important.

The slightly better results with the GrEM method than the original EM in artificial data sets could be due to the generative model of the artificial data sets. We specifically adopted recombination hot spots between all neighboring SNP loci with a constant recombination rate, while in real data sets we chose a haplotype block or a few haplotype blocks. Due to this difference, there were many similar but not exactly the same local maxima considered to be included in the artificial data sets, while there were many exactly the same local maxima considered to be included in real data sets. This could be because the parameter space the EM algorithm had to explore was reduced with the grouping preprocess, making it easier to find one of the ML solutions with a smaller number of EM algorithm trials.

In the field of haplotype inference, both the probabilistic model and the cost of calculation have been significant issues. The actual situation is that finding the optimal solution is quite difficult, even with the HWE model, which is one of the simplest. The GrEM method makes this less difficult, and roughly extends the feasible number of SNP loci from 20 to 40 loci. In other probabilistic models used by other conventional methods, finding the optimal solution could be more difficult. We found there was about a 1% difference between the diplotypes inferred by the GrEM method and the conventional methods. This suggests that the conventional methods infer diplotypes that differ from those in the maximum likelihood (ML) solution based on HWE. The reasons explaining these differences need to be clarified in detail. These differences might arise from the differences in probabilistic models or some deviation from the optimal inferences by using approximation. Excepting two quite different methods, 2SNP and HaploRec, the inferred diplotypes by fastPHASE were generally different from others; this might arise from the difference of the probabilistic models: the coalescence model and HWE model. Among SNPHAP, PL-EM, and the GrEM method, there were less differences in inferring diplotypes. This could be because of being based on the same HWE model, and slight differences could be due to the differences of the adopted approximations. Similarities of the GrEM result to those of PHASE and Beagle are hard to explain because they adopt different models and different optimizations.

Also, the slightly better results of diplotype likelihood with the GrEM method than with the conventional methods in real data sets could have been because the GrEM method was aimed at maximizing the diplotype likelihood through maximizing the haplotype likelihood, while the conventional methods adopted different cost functions or various approximations. The slightly lower error rates with the GrEM method than with the conventional methods could be because of using no approximation and/or the better fitness of the probabilistic model to the artificial data sets, although the data sets were not created to fit the model intentionally. The differences in the number of candidate diplotypes between real and artificial data sets might also have arisen from the constant recombination rate of each recombination hot spot.

Feasibility testing demonstrated that the GrEM method could run even on ordinary laptop computers although we occasionally encountered unreasonable calculation costs or memory overflows for large data sets. Because the grouping preprocess does not use any approximation, the running time depends on the complexity of the data set used. The limitation in data set size is estimated to be about 40 loci from 250 subjects with 1% missing values; this largely depends on variations in the corresponding haplotype block and especially the rate of missing values. From another point of view, the variety of human genomes is not infinite; it is at most twice the whole human population. Consequently, testing the GrEM method using more powerful 64-bit CPUs or super computers with large amount of memory could be worthwhile. Regarding the feasibility of the conventional methods, they were apparently capable of inferring haplotypes in these data sets. However, the unreasonable cases in PL-EM and the longer running times of PHASE and fastPHASE than the GrEM method in the real data sets suggest both the limitations of these methods and the difficulty of the haplotype inference problem.