Introduction

Quantitative trait locus (QTL) analysis maps quantitative phenotypic variation to chromosomal regions using marker and pedigree information. In contrast to QTL mapping, association mapping does not require pedigree information as it is based on whole population analysis of historical recombinations. Experimental design, quality of the marker map, and methodology determine the success of a QTL mapping study. Both design and methodology are relatively simple with controlled inbred line crosses. But even if a study using inbred lines successfully identified QTL, extension to the base population is difficult: because numbers of available inbred lines are generally low and relationships of lines to each other may be unknown, statistical inference to the base population is unreliable. Hence, even for organisms where inbred lines are available, outbred pedigrees may be more appropriate.

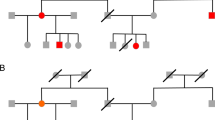
For most long-lived organisms, insufficient numbers of inbred lines are available and mapping must be carried out with available pedigrees. Mapping QTL in complex pedigrees is a daunting task; the combinatorial complexity is enormous. For a pedigree of N individuals and F founders, each of the 2(N − F) meioses has two states, resulting in a total of 22(N−F) states. The totality of the meiotic states defines the allele flow relationship between individuals. Other terms used for this are segregation pattern, inheritance pattern, set of meiosis indicators, or ‘descent-graph’ (Sobel and Lange, 1996). Furthermore, the ordered diploid genotype of each founder, prior to observing the data, may have any combination of alleles. The combination of ordered founder genotypes and the descent-graph is called the ‘descent-state’ (Sobel and Lange, 1996) (see Figure 1). It completely determines the ordered genotype of each indivual in the pedigree. Because of the combinatorial complexity, exact methods for calculation of the likelihood or the posterior distribution are only available for simple models and relatively short pedigrees (eg, Kruglyak et al, 1996). Stochastic simulation using Markov chain Monte Carlo (MCMC) integration of the posterior distribution (Gelman et al, 1995) offers more flexibility.

Figure 1
figure 1

Descent state representation of a pedigree with ordered genotypes at a single locus. The numbers represent the ordered founder genotypes and the arrows the descent graph.

Full size image

With MCMC, an approximate sample from a distribution is obtained by cyclically updating sets of parameters conditional on the current values of these and/or other parameters and the data. For instance, the posterior mean and variance of a normally distributed data set may be obtained by cyclically alternating between (i) sampling the mean conditional on the variance and the data and (ii) sampling the variance conditional on the mean and the data. Importantly, a complex problem can be thus subdivided into smaller manageable units. MCMC can be employed for integration of both the likelihood or posterior distribution, ie, in both a frequentist as well as a Bayesian context. But it fits more naturally into a Bayesian scheme, because it is based on updating conditonal distributions rather than maximizing the log-likelihood. We therefore adopt a fully Bayesian approach and supply (non-informative or weakly informative) prior distributions.

As the first part in the MCMC sampler, consider updating the marker genotypic information. For obtaining the descent-state, ie, the descent-graph or inheritance pattern and the genotypic founder configurations, many MCMC schemes are available (reviewed in Hoeschele, 2001). One such scheme proceeds individual by individual and locus by locus, conditional on the parameter settings of all other individuals and loci (Kong, 1991). This can be done relatively simply using a Gibbs sampler (Gelman et al, 1995), ie, by sampling directly from the conditional distribution. But it has been demonstrated that this approach may get stuck locally: with multiallelic loci, legal states may not communicate through a finite chain of single steps, such that it is impossible to reach a (potentially) more probable state; with biallelic loci, the sampler gets stuck locally for long times (Hoeschele, 2001). Expressed in MCMC jargon (Gelman et al, 1995), the approach suffers greatly from poor mixing (it is ‘sticky’) and problems of reducibility (it does not reach some possible parameter regions at all). To avoid this pitfall, more complex updating methods have been devised (reviewed in Hoeschele, 2001): genotypes of many or all individuals in a pedigree are updated jointly instead of sequentially, eg, the ‘peeling’ (Elston and Stewart, 1971; Fernando et al, 1993) and ‘reverse peeling’ (Ott, 1989; Heath, 1997) algorithms. Although these procedures are relatively slow and complicated to implement, they are successful where applicable. But unfortunately not all pedigrees are ‘peelable’.

Sobel and Lange (1996) presented a flexible method applicable to arbitrary pedigrees, ie, also to those where peeling is impossible, called the ‘descent-graph sampler’. With the descent-graph sampler, the probability of an inheritance pattern (descent-graph) is evaluated by summing over the probabilities of all compatible founder genotypes. Thus the sample space is reduced compared with the above-mentioned methods: instead of sampling the descent state, ie, the descent-graph and the founder genotypes, only the descent-graph is sampled.

Compared with sampling marker genotypes, updating the QTL genotypes conditional on the flanking loci, QTL effects, and phenotypic information is relatively easy. Since the number of QTL alleles in an outbred population is generally unknown, we treat the effect of each diploid combination of two founder alleles as a normally distributed random variable with mean zero and only estimate the variance of these effects. This is called the random model approach (Xu and Atchley, 1995). As another step in the cycle of MCMC updating, we jointly update location, genotypes, and effects, for each QTL in turn.

With a Bayesian approach, the number of QTL can be treated as a random variable, ie, the posterior probability of models with zero, one, or more QTL on a linkage group may be evaluated. For this technically demanding step in the MCMC cycle, we use the reversible jump algorithm developed by Green (1995) and employed to advantage in the context of QTL mapping (eg, Satagopan et al, 1996; Stephens and Fisch, 1998; Sillanpää and Arjas, 1998, 1999).

Herein, we develop a Bayesian method to map QTL using the descent-graph sampler of marker inheritance patterns for arbitrarily complex mating designs and incomplete marker information. The Bayesian method is implemented via an MCMC algorithm. The number of QTL on a linkage group is assumed to be variable. The algorithm allows for the simultaneous estimation of number, locations, and effects of QTL. We evaluate the efficacy of the algorithm by computer simulations and compare it with other methods for QTL mapping in outbred populations.

Model

Let individuals in the mapping population be indexed by i with 1 ≤ i ≤ N and let F be the number of founder individuals. Let marker loci be indexed by l with 1 ≤ l ≤ L. Denote the proportion of allele a of locus l by pla and let P = {pla}L,Al=1, a=1, where A is the number of alleles of locus l in the population. (Note that P is not a matrix because the number of alleles may vary between loci.) Let M represent the marker information and let the vector y represent the phenotypic values of the N individuals.

Let the QTL be indexed by q with 1 ≤ q ≤ Q and located at positions λq = {λq}Qq=1. Let the diploid genotypic value of locus q, ie, the sum of the maternal and the paternal additive genetic and the dominance effects, be represented by the vector gq = {gqr}2F(F+1)r=1. We employ the constraint that one of the gq is set to zero. For a particular pedigree, only a limited set of founder allelic combinations may be realized, such that the dimension of gq may effectively be much smaller than 2F(F + 1). Let G = {g1, . . ., gQ}. We assume that the genotypic effects G depend on the underlying genetic variances σ2g = {σ2gq}Qq=1, ie, we assume a random model approach (Xu and Atchley, 1995). Let σ2e represent the environmental variance.

For each marker locus or QTL, the descent-graph specifies the allele flow relationship between individuals and, thus, consists of two parts: the pedigree relationship and the 2(N − F) meiosis indicators, which we will represent as a vector zq. The meiosis indicators can take on a value of 0 or 1 depending on whether the maternal or paternal allele is inherited. Let the matrix of meiosis indicators for the L marker loci plus Q QTL be represented as Z = {z1}(L+Q)k=1. If a particular (focal) locus is referred to, let its vector of meiosis indicators be represented as z and that of the previous and next loci be represented as z− and z+, respectively. Whether the focal locus is a QTL or a marker locus will be clear from the context. We assume the Haldane mapping function.

For partitioning the phenotypic variation, we employ the following statistical model:

where X is the design matrix of the fixed effects b and Wq = Wq(zq) is the design matrix of the genetic effects; Wq is a deterministic function of the random variables zq. The gq are the genetic effects and the vector e represents the environmental effects. In this formula, each allele is traced back to its founder alleles, ie, the model is written in the form of a reduced animal model (Hoeschelc, 2001).

Next we focus on the posterior distribution. Let the variables be represented by θ = {b, G, σ2g, λ, Z, σ2e. To complete a Bayesian model, prior distributions must be chosen. For Z and λ, we assume flat (or uninformative) prior distributions, ie, every possible parameter value has the same prior probability. For the QTL effects G, we chose rather uninformative priors of the same functional form as the likelihood (conjugate priors Gelman et al, 1995). Conjugate priors are often very reasonable and facilitate the mathematical analysis. For the environmental variance σe and the prior QTL variances, we also chose conjugate priors: independent inverse chi-square distributions with prior variances fractions of the observed phenotypic variance and prior degrees of freedom of two. Combining all the independent prior and conditional distributions, the posterior distribution of the variables conditional on the data for a given number of QTL is given by

We model the number of QTL on a linkage group as a random variable. Following other authors (eg, Satagopan et al, 1996; Stephens and Fisch, 1998; Sillanpää and Arjas, 1998, 1999), we choose a truncated Poisson distribution as prior for QTL number.

Implementation

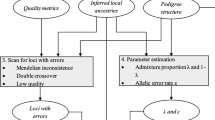
An approximation of the posterior distribution is obtained by cyclically switching between the following steps: (i) sampling of the marker descent-graph for all marker loci, (ii) joint sampling of position, meiosis indicators, and QTL effects for all QTL, (iii) separate sampling of QTL meiosis indicators, (iv) sampling of phenotypic mean and genetic and environmental variances, and (v) birth or death of a QTL.

Sampling of the marker descent-graph for all marker loci

The marker genotype sampler employed is an implementation of the Sobel and Lange (1996) descent-graph sampler. Central to the algorithm is the evaluation of the likelihood of the data given the descent-graph, ie, the allelic inheritance pattern for each independent extended family. For this, the probability of the data must be evaluated conditional on all possible allelic states and the descent-graph and then summed, such that the probability of the data conditional on the descent-graph is obtained. Recursing naively through all possible allelic states requires evaluation of A(2F) states for a locus with A alleles.

To speed up this step, Sobel and Lange (1996) divide the descent graph into non-communicating compartments (‘founder-tree graphs’). This requires much computational overhead and may not be successful in some pedigrees. We therefore employed a different algorithm: the path of each founder allele (the ‘founder-tree’ in the terminology of Sobel and Lange (1996)) is traversed in its entire length and the set of possible alleles is restricted to the intersection of the alleles of all typed individuals it passes through. If the path passes through at least one individual with complete marker phenotypic information, the number of compatible alleles is at most two. For the simulated data sets we used, it is usually reduced to just a single allele. This allows for swift recursion through possible states.

Note that this algorithm can handle dominant markers, which are generally biallelic. But since the population allele frequency of dominant markers is usually unknown, this would require a change of the model.

For running the descent-graph MCMC chain, a Metropolis-Hastings algorithm (Gelman et al, 1995) must be used: a new state of the descent-graph is sampled conditional on the old state from a jumping or proposal distribution; this new state is then accepted or rejected in favor of the old state with a certain probability (see the Appendix for an example). Choice of appropriate proposal distributions is an art as well as a science: if the proposal is too similar to the old values, speed of mixing may be unacceptably slow even though most proposals are accepted; if the proposal is too different from the old values, mixing may be slow because proposals are nearly never accepted.

In our implementation of the marker sampler, we deviate only in minor details from the proposal distributions used by Sobel and Lange (1996): for convenience, we strictly base our implementation on the full-sib family. In each round of updating, the number of full-sib families is a random variable sampled from a Poisson distribution truncated at the maximum number of available families. Conditional on this number, a set of families are chosen randomly.

Within the chosen family or families, we suggest three types of switches. The simplest switch is a source switch (eg, Figure 2a): the origin of the arrow connecting a parental allelic node with the child is changed from the parental paternal node to the parental maternal node (Sobel and Lange (1996) transition rule T0). Each of the four possible combinations of source switches, two paternal and two maternal ones, are proposed with equal probability.

Figure 2
figure 2

An example of the three move types: (a) a source switch, (b) a phase switch, and (c) a parent switch (with a phase switch). The focal family, where the switch happens, is always indicated with filled circles.

Full size image

The second switch (eg, Figure 2b), corresponding to transition rule T1 of Sobel and Lange (1996), is most easily understood as a switch of the phase in a parent. The origin of all outgoing arrows from a single individual are switched, such that a child that before the switch inherited the maternal allele inherits the paternal one, and vice versa. We also include the possibility of switching the phases of both parents in a nuclear family.

The third switch (eg, Figure 2c), corresponding to transition rule T2 of Sobel and Lange (1996), is more complicated than the previous two. It can be most easily thought of as swapping the contribution of the parents in the focal family. After swapping, however, paternally derived genes flow to maternal ones and vice versa. To correct for this illegal flow, requires further rearrangement in the next generation. We also consider a concurrent change of phase in the parents as exemplified in Figure 2c.

These three transition types combine randomly in the selected families to update the old state z in a compound switch, ie, a new set of meiosis indicators z*. Acceptance or rejection of z* over the old state z is determined locus by locus conditional on the neighboring loci (z+ and z−) using a Metropolis-Hastings step. As Metropolis- Hastings samplers are generally rather insensitive to minor changes in the proposal distribution (eg, Richardson and Green, 1997), the differences between the Sobel and Lange (1996) implementation and ours will be negligible.

Loci on a single chromosome are updated in a correlated fashion: a compound switch proposed for a certain marker locus will, with probability p, also be proposed for the next locus; with probability 1 − p a different, independently sampled switch will be proposed. With this choice of proposal distribution the probability of proposal of multilocus descent-graph B given multilocus descent-graph A is the same as proposal of A given B, ie, j(A|B) = j(B|A). Hence, correction of differences in proposal probability is not required in the acceptance ratio of the Metropolis step. Especially for tightly linked loci, such as those considered in the simulations later on, this correlated updating of loci improves mixing.

Joint sampling of position, meiosis indicators, and QTL effects for all QTL

For updating of QTL variables, we note that the diploid genotypic effects of all the 2F(F+1) genotypic combinations of each QTL will, generally, be different from each other. Furthermore, none of the 2F(F+1) QTL genotypes can be excluded with certainty using the phenotypic data, although different genotypes are differently probable. Hence, the descent-graph algorithm we used for marker data is unavailable. We, thus, update QTL descent-states and other QTL parameters as follows: a new position λ*q is proposed from a uniform distribution symmetric around the old position. Conditional on the new position and the meiosis indicators of the neighboring loci (z+, z−), the new meiosis indicators z* for the focal QTL are sampled using Haldane’s mapping function.

Conditional on these meiosis indicators the fixed effects and the variances and z*, a vector of the QTL-effects gq needs to be sampled. This would be difficult using the usual parametrization in additive and dominance effects. Instead, we parametrize the model using diploid genotypic effects. With this parametrization, the effect of each particular combination of two founder alleles is independently normally distributed with mean zero and the same genetic variance. Furthermore, the variance-covariance matrix of the genotypic effects (Wang et al 1993) (WTqWq/σ2g + I/σ2e)−1 is diagonal and inversion is trivial. This makes it possible to sample directly from the conditional distribution for updating QTL effects and variances, ie, to use a relatively simple Gibbs sampling scheme. All new variables are accepted or rejected with a single Metropolis-Hastings step (see the Appendix for equations).

Separate sampling of QTL meiosis indicators

It turned out that mixing is improved with an additional step: a proposal for the QTL-meiosis indicators is sampled conditional on the neighboring loci and accepted or rejected with a Metropolis-Hastings step using the ratio of the old and new probabilities calculated from Pr(y|b, G, Z, σ2e).

Sampling of phenotypic mean and genetic and environmental variances

The phenotypic mean is drawn from a Normal distribution using a Gibbs sampler. Environmental and genetic variances are drawn from an inverse chi-square distribution using a Gibbs sampler.

Birth or death of a QTL

We will not go into the details of the reversible jump algorithm, but refer the reader to Green (1995) for a general mathematical introduction and to, eg, Satagopan et al (1996), Stephens and Fisch (1998), Sillanpää and Arjas (1998), Sillanpää and Arjas (1999), and Vogl and Xu (2000) for applications to linkage mapping. The posterior distribution of number of QTL is obviously influenced by the parameters of the truncated Poisson prior distribution but also by the prior genetic QTL variance. For small prior variances, more and smaller QTL, are placed along the chromosome; for large prior variances, fewer and larger QTL are placed along the chromosome. Mixing between different numbers of QTL is more effective for small prior variances. As speed of computation is proportional to number of QTL, the prior variance influences practical computation too. We had good results when truncating the prior Poisson distribution at four QTL per chromosome and setting the mean prior QTL variance to 0.03 the phenotypic variance.

Simulation study

We simulated one chromosome of length 1M; markers were equally and rather tightly spaced in 0.1M intervals. For checking the marker sampler, we simulated a single fullsib family of variable size and employed the following test: the marker sampler is started both from the true descent-graph as well as from a set of random descent-graphs drawn independently for each marker locus. Initially, runs started from the true value have much lower values of imputed recombination rates between adjacent loci than runs started randomly. The test consists in monitoring the convergence rate of the difference in the sum of the log of the recombination probability for all loci and individuals between these two sets of runs; the better the sampler mixes the faster the convergence.

For checking both the marker and the QTL sampler, the environmental variance was always set to one; two QTL were always present; their genotypic effects were sampled from a normal distribution with a genotypic variance of one at locations 0.15 and 0.65. Whether the effects are in coupling or repulsion (if the effects are mainly additive) or exhibit more complicated patterns (if the dominance component is large) in a certain extended family depends on chance. We refrained from analysing QTL on different linkage groups, because it is very time-consuming and does not pose any theoretical or practical challenges.

We present in detail three types of simulations: (i) 13 full sib families with 40 offspring each; (ii) 24 pedigrees, each with two unrelated founder families that gave rise to one sire and two dams, which were crossed reciprocally with the other family to give rise to four families with 10 offspring each; (iii) similar to the second simulation, but with 35 pairs of families and with one dam less in the middle generation and thus only 20 offspring in the last generation. Note that in the latter two pedigrees nearly all information is contained in the third and last generation. Marker genotype information was simulated as either present in all individuals or missing from half the founders. We also performed trial runs with more complicated pedigrees. In all cases, we assumed that phenotypic information was missing from the founders.

A consistent descent-graph was sampled for each marker using the algorithm of Sobel et al (1995) and zero QTL were assumed to be present initially. Before starting regular alternation between the marker and QTL sampler, 5000 rounds of marker sampling were performed. The first 5000 rounds of the marker plus QTL sampler were discarded to allow for approximate convergence to the posterior distribution, while the next 10000 were sampled.

A second test of the marker sampler in conjunction with the QTL sampler is comparison of the posterior distribution of inferred QTL locations with the simulated true positions and effects; this also tests the QTL sampler.

Descent-graph (marker) sampler

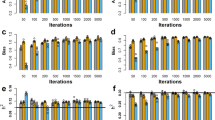
The number of individuals in a full sib family influences the speed of convergence of the difference between runs started from the true multilocus descent-graph and from a random multilocus descent-graph (Figure 3). With 40 individuals, approximate convergence is achieved after less than 1000 iterations, while for 100 individuals 10000 iterations was not enough.

Figure 3
figure 3

Dependence of the convergence speed (as difference in the log-likelihood of runs from different starting conditions depending on time) of the marker sampler on the number of offspring in a fullsib family. Solid line: 100 offspring; coarsely broken line: 80 offspring; finely broken line: 60 offspring dotted line: 40 offspring.

Full size image

For more complicated pedigrees, convergence speed was slightly slower than for a single fullsib family of comparable size (data not shown). The limit of the capability of our sampler is thus between about 50 to 100 individuals in a single extended family. We did not try to more accurately determine this limit as it varies with pedigree structure and is likely implementation dependent. Applicability of our algorithm to an extended family with over 50 members should be ascertained with computer simulations.

QTL sampler

Results of the simulations of the three pedigrees with full or missing founder marker information are presented in Figure 4 (i) corresponding to a and b; (ii) corresponding to c and d; (iii) corresponding to e and f. As expected results are better with full information, (a), (c), and (e), and clearly indicate presence of two major QTL in about the right locations. If information is missing, (b), (d), and (f), the posterior distributions are a bit more erratic. Only for pedigree (iii), the mode of the QTL at 0.15 is appreciably lower for the pedigree with full information (e) than for the one with missing information (f). This is probably a statistical fluke.

Figure 4
figure 4

QTL intensity for pedigrees (i) (a and b), (ii) (c and d), and (iii) (e and f), with full founder information (a, c, and e) and with partially missing founder information (b, d, and f). Solid line: QTL intensity (intensity); broken line: average QTL variance.

Full size image

Discussion

Mapping QTL in large, arbitrary pedigrees is a complex task. Exact methods (eg, Kruglyak et al, 1996) are only available for simple pedigrees. For larger pedigrees, approximate samples from the likelihood or posterior distribution can be obtained by MCMC integration. Published MCMC methods differ in the strategy for sampling marker meiosis indicators and in model assumptions for QTL, mainly whether a biallelic fixed effects model (eg, Heath, 1997; Sillanpää and Arjas, 1999) or a multiallelic random effects model (eg, Xu and Atchley, 1995; Yi and Xu, 2000) is assumed.

Herein, we implement the descent-graph sampler (Sobel and Lange, 1996) for updating marker inheritance indicators. With the descent-graph sampler, a modified descent-graph (pattern of meiosis indicators) is suggested conditionally on the old pattern and the pedigree but unconditionally on the observed marker phenotypes. This allows for great flexibility; it can handle arbitrary pedigrees and is unaffected by missing marker data. From our simulations it seems, however, that if the number of meioses is larger than 50 to 100, approximation to the posterior distribution is slow.

Running the descent-graph sampler requires rapid calculation of the probability of a particular descent-graph conditional on the marker data and population allele frequencies. Naively, this would require recursing through all possible marker states for each of the 2F founder alleles. This strategy is prohibitively slow and needs to be sped up significantly. Instead of partitioning the space into independent units (the founder-tree graph approach of Sobel and Lange (1996)), we traverse the path of each founder allele to limit the number of possible allelic combinations. With this modification, speed of calculation of the probability of a particular descent-graph conditional on the marker data and population allele frequencies is not rate limiting any more. We note, as an aside, that the descent-graph sampler has the ability to handle dominant loci as well.

For modeling the QTL effects, we employ the random effect model (eg, Xu and Atchley, 1995; Yi and Xu, 2000). Instead of the usual parametrization using additive and dominance effects, we sample diploid genotypic effects. This makes sampling of genotypic effects much simpler than separate sampling of additive and dominance effects. If the genotypic effects and the (diagonal) design matrix are stored, additive and dominance variances can be calculated after the MCMC run has finished. Thus, partitioning of variances can be performed a posteriori without affecting MCMC speed. The only remaining disadvantage of our parametrization is that it is not possible to choose independent priors for additive and dominance effects.

All methods for mapping in complex pedigrees advanced so far involve trade-offs: exact methods are available only for short pedigrees; individual by individual and locus by locus sampling gets trapped locally; summation over genotypes via the peeling algorithm is only possible for certain pedigrees (all reviewed in Hoeschele, 2001). Furthermore, an allele-dropping algorithm where, starting from the founders, offspring alleles are sampled sequentially conditional on the parental genotypes, requires that at least complete founder allelic information is available (eg, Yi and Xu, 2000). But since allelic information of especially the founder individuals is often unavailable, this will rule out analysis of many data sets.

The descent-graph method (Sobel and Lange, 1996), employed herein, can handle arbitrarily complex pedigrees and allows for missing marker information, but is prohibitively slow in too large pedigrees (pedigrees with more than about 50 members) because the sampler mixes poorly. Hence, for large but regular pedigrees, eg, a collection of large nuclear families, other, less flexible methods may be more successful. For extremely large and complicated (unpeelable) pedigrees, no method is currently available.

Outbred pedigrees that necessitate the complicated approaches discussed above usually arise with long-lived lifestock or trees, and in human populations. If at least some influence on the experimental design is possible, eg, in livestock and tree breeding, the method of analysis may be chosen first and the pedigree fitted to it. Otherwise choice of method requires careful evaluation of their relative merits.