Abstract
Berry’s approach on “transitionless quantum driving” shows how to set a Hamiltonian which drives the dynamics of a system along instantaneous eigenstates of a reference Hamiltonian to reproduce the same final result of an adiabatic process in a shorter time. In this paper, motivated by transitionless quantum driving, we construct shortcuts to adiabatic passage in a three-atom system to create the Greenberger-Horne-Zeilinger states with the help of quantum Zeno dynamics and of non-resonant lasers. The influence of various decoherence processes is discussed by numerical simulation and the result proves that the scheme is fast and robust against decoherence and operational imperfection.
Similar content being viewed by others
Introduction
“Shortcuts to adiabatic passage (STAP)”1,2 which are a set of techniques to speed up a slow quantum adiabatic process usually through a non-adiabatic route, have attracted a great deal of attention in recent years. They can overcome the harmful effects caused by decoherence, noise or losses because of a long operation time. Quantum science also greatly desires fast and robust theoretical methods since high repetition rates contribute to the achievement of better signal-to-noise ratios and better accuracy. Therefore, in the last several years, STAP have been applied in a wide range of systems in theory and experiment3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23. Various reliable, fast and robust methods and schemes have been proposed to implement quantum information processing (QIP), such as fast population transfer5,6,7, fast entanglement generation6,8, fast implementation of quantum phase gates9.
To construct shortcuts to speed up adiabatic processes effectively, two methods which are in fact strongly related and even potentially equivalent to each other24: are invariant-based inverse engineering based on Lewis-Riesenfeld invariant10,25 and Berry’s approach named “transitionless quantum driving” (TQD)26,27,28,29. Whereas, each of the two methods also has its own characteristics, for example, using Lewis-Riesenfeld invariants to construct shortcuts usually does not have to break down the form of the original Hamiltonian H0(t), so that the possibility of designing a Hamiltonian H(t) very difficult or impossible to implement in practice is avoided5,12. However, the invariants always have fixed forms which lead to that shortcut methods based on Lewis-Riesenfeld invariants might be limited or even hopeless in some cases to construct shortcuts to implement QIP rapidly5. For example, in the paper8 proposed by Chen et al., they had no choice but to make one of the atoms to be a control qubit or use auxiliary levels for the atoms to generate entangled states.
There is still plenty to do to make wide applications of STAP for fast QIP in some experimental systems, for example, the cavity quantum electronic dynamics (QED) systems. It is worth noting that, TQD provides a very effective method to construct the “counter-diabatic driving” (CDD) Hamiltonian H(t) which accurately drives the instantaneous eigenstatees of H0(t). Nevertheless, it is almost always found that the designed CDD Hamiltonian is hard to be directly implemented in practice2,30,31,32,33,34, especially in multiparticle systems. Examples of ways to overcome this problem may be found in refs 34, 35, 36, 37, 38. Also, in a large detuning limit, Lu et al.6 have found a simplified effective Hamiltonian equivalent to H(t). This idea inspires us that finding an alternative physically feasible (APF) Hamiltonian which is effectively equivalent to H(t). However, the approximation in ref. 6 is too complex to be generalized to N-qubit entanglement cases. It is known to all that, entanglement of more qubits shows more nonclassical effects and is more useful for quantum applications. For example, one of the two kinds of three-qubit entangled states named the Greenberger-Horne-Zeilinger (GHZ) states provide a possibility for testing quantum mechanics against local hidden theory without using Bell’s inequality39,40. Therefore, great interest has arisen regarding the significant role of the GHZ states in the foundations of quantum mechanics measurement theory and quantum communication. In view of that we wonder if it is possible to use TQD to construct shortcuts for one-step generation of multi-qubit entanglement, i.e., the three-atom GHZ states, without abandoning any of the atoms or using auxiliary levels.
In this scenario, motivated by refs 5, 6, 7, 8, we use TQD to construct STAP to generate the three-atom GHZ states effectively and rapidly in one step. It would be a promising idea of applying STAP to realize multi-qubit entanglement generation in cavity QED systems. Different from ref. 6, we use the quantum Zeno dynamics41,42 to simplify the system first and then under the large detuning conditon, we obtain the effective Hamiltonian which is equivalent to the corresponding CDD Hamiltonian to speed up the evolution process. Therefore, the adiabatic process for a multi-qubit system is speeded up and the STAP is easy to be achieved in experiment. Comparing with ref. 8, we use TQD in this paper so that the laser pulses are not strongly limited and we do not need to use auxiliary levels or multi-step operations to generate the three-atom GHZ states. Moreover, we find that any quantum system whose Hamiltonian is possible to be simplified into the form in eq. (15), the corresponding APF Hamiltonian can be built and the STAP can be constructed with the same approach presented in this paper. The above advantages mean the present scheme is much more useful in dealing with the fast and noise-resistant generation of multi-qubit entanglement or even other QIP.
Basic theories
Transitionless quantum driving
Consider an arbitrary time-dependent Hamiltonian H0(t), with instantaneous eigenstates and energies given by

When this system satisfies the adiabatic condition, H0(t) will drive the system into

where

To find the Hamiltonian H(t) that drives the eigenstates  , we define a unitary operator
, we define a unitary operator

which obeys

Then the Hamiltonian H(t) is obtained

The simplest choice is  , for which the bare states
, for which the bare states  , with no phase factors, are driven by26
, with no phase factors, are driven by26

reflecting

Quantum Zeno dynamics
The quantum Zeno dynamics was named by Facchi and Pascazio in 200242. It is derived from the quantum Zeno effect which describes a phenomenon that the system can actually evolve away from its initial state while it still remains in the so-called Zeno subspace determined by the measurement when frequently projected onto a multidimensional subspace. According to von Neumann’s projection postulate, the quantum Zeno dynamics can be achieved via continuous coupling between the system and an external system instead of discontinuous measurements42. In general, we assume that a dynamical evolution process is governed by the Hamiltonian

where  is the Hamiltonian of the quantum system investigated, K is a coupling constant and
is the Hamiltonian of the quantum system investigated, K is a coupling constant and  is viewed as an additional interaction Hamiltonian performing the measurement. In the “infinitely strong measurement” limit
is viewed as an additional interaction Hamiltonian performing the measurement. In the “infinitely strong measurement” limit  41,42, The Hamiltonian for the whole system is nearly equivalent to
41,42, The Hamiltonian for the whole system is nearly equivalent to

whit Pn being the nth orthogonal projection onto the invariant Zeno subspace  and the eigenspace of
and the eigenspace of  belonging to the eigenvalue εn, i.e.,
belonging to the eigenvalue εn, i.e.,  .
.
Model
We consider three Λ-type atoms are trapped in a bimodal-mode cavity as shown in Fig. 1. Atoms 1, 2 and 3 have three sets of ground states  ,
,  and
and  , respectively and each of them has an excited state
, respectively and each of them has an excited state  . The atomic transition
. The atomic transition  is driven resonantly through classical laser field with time-dependent Rabi frequency Ω(t), transition
is driven resonantly through classical laser field with time-dependent Rabi frequency Ω(t), transition  is coupled resonantly to the left-circularly polarized mode of the cavity with coupling λl and transition
is coupled resonantly to the left-circularly polarized mode of the cavity with coupling λl and transition  is coupled resonantly to the right-circularly polarized mode of the cavity with coupling λr. Under the rotating-wave approximation (RWA), the interaction Hamiltonian for this system reads
is coupled resonantly to the right-circularly polarized mode of the cavity with coupling λr. Under the rotating-wave approximation (RWA), the interaction Hamiltonian for this system reads  :
:

where HAL denotes the coupling between the atoms and the laser pulses and HAC denotes the coupling between the atoms and the cavities, al and ar are the left- and right-circularly annihilation operators of the cavity modes and β means the two Rabi frequencies are β-dephased from each other. If we assume the initial state is  , the system will evolve within a single-excitation subspace with basis states
, the system will evolve within a single-excitation subspace with basis states

In light of quantum Zeno dynamics, we rewrite the Hamiltonian HI in eq. (11) as Hre through the relation 
 and
and  , where
, where

Here  ,
,  ,
,  ,
,  and
and  are the eigenvectors of HAC corresponding eigenvalues
are the eigenvectors of HAC corresponding eigenvalues  ,
,  ,
,  ,
,  and
and  , respectively. And we obtain (we set
, respectively. And we obtain (we set 

Through performing the unitary transformation  and neglecting the terms with high oscillating frequency by setting the condition
and neglecting the terms with high oscillating frequency by setting the condition  (the Zeno condition), we obtain an effective Hamiltonian
(the Zeno condition), we obtain an effective Hamiltonian

which can be seen as a simple three-level system with an excited state  and two ground states
and two ground states  and
and  . For this effective Hamiltonian, its eigenstates are easily obtained
. For this effective Hamiltonian, its eigenstates are easily obtained

corresponding eigenvalues  ,
,  , respectively, where
, respectively, where  and
and  . When the adiabatic condition
. When the adiabatic condition  is fulfilled, the initial state
is fulfilled, the initial state  will follow
will follow  closely and when
closely and when  and
and 
 , we obtain the GHZ states:
, we obtain the GHZ states:  . When β = π, it shows the most common form:
. When β = π, it shows the most common form:  . However, this process will take quite a long time to obtain the target state, which is undesirable.
. However, this process will take quite a long time to obtain the target state, which is undesirable.
Using TQD to construct shortcuts to adiabatic passage
The instantaneous eigenstates 
 for the effective Hamiltonian
for the effective Hamiltonian  above do not satisfy the Schrödinger equation
above do not satisfy the Schrödinger equation  . According to Berry’s general transitionless tracking algorithm26, from
. According to Berry’s general transitionless tracking algorithm26, from  , one can reverse engineer H(t) which is related to the original Hamiltonian
, one can reverse engineer H(t) which is related to the original Hamiltonian  but drives the eigenstates exactly. From refs 6,11,12, we learn the simplest Hamiltonian H(t) is derived in the form
but drives the eigenstates exactly. From refs 6,11,12, we learn the simplest Hamiltonian H(t) is derived in the form

Substituting eq. (16) in eq. (17), we obtain

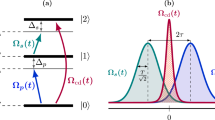
where  . Similar to ref. 6, for this three-atom system in a real experiment, the Hamiltonian H(t) is hard or even impossible to be implemented in practice. We should find an APF Hamiltonian whose effect is equivalent to H(t). The model used for the APF Hamiltonian is similar to that in Fig. 1 with three atoms trapped in a cavity and the atomic level configuration is shown in Fig. 2: the transition
. Similar to ref. 6, for this three-atom system in a real experiment, the Hamiltonian H(t) is hard or even impossible to be implemented in practice. We should find an APF Hamiltonian whose effect is equivalent to H(t). The model used for the APF Hamiltonian is similar to that in Fig. 1 with three atoms trapped in a cavity and the atomic level configuration is shown in Fig. 2: the transition  is non-resonantly driven by classical field with time-dependent Rabi frequency
is non-resonantly driven by classical field with time-dependent Rabi frequency  and detuning Δ, the transition
and detuning Δ, the transition  is coupled non-resonantly to the cavity with coupling λl (λr) and detuning Δ. The rotating-frame Hamiltonian reads
is coupled non-resonantly to the cavity with coupling λl (λr) and detuning Δ. The rotating-frame Hamiltonian reads

where  is the phase difference between
is the phase difference between  and
and  . Then similar to the approximation for the Hamiltonian from eq. (11) to eq. (15), we also obtain an effective Hamiltonian for the present non-resonant system43
. Then similar to the approximation for the Hamiltonian from eq. (11) to eq. (15), we also obtain an effective Hamiltonian for the present non-resonant system43

By adiabatically eliminating the state  under the condition
under the condition  , we obtain the final effective Hamiltonian
, we obtain the final effective Hamiltonian

Choosing  , the first two terms of eq. (21) can be removed and the Hamiltonian becomes
, the first two terms of eq. (21) can be removed and the Hamiltonian becomes

where  . This effective Hamiltonian is equivalent to the CDD Hamiltonian H(t) in eq. (18) when
. This effective Hamiltonian is equivalent to the CDD Hamiltonian H(t) in eq. (18) when

Hence, the Rabi frequencies for the APF Hamiltonian are designed

where  .
.
Fast and noise-resistant generation of the three-atom GHZ states with STAP
We will show that the creation of a three-atom GHZ state governed by  is much faster than that governed by HI. To satisfy the boundary condition of the fractional stimulated Raman adiabatic passage (STIRAP),
is much faster than that governed by HI. To satisfy the boundary condition of the fractional stimulated Raman adiabatic passage (STIRAP),

the Rabi frequencies  and
and  in the original Hamiltonian HI(t) are chosen as
in the original Hamiltonian HI(t) are chosen as

where Ω0 is the pulse amplitude, tf is the operation time and t0, tc are some related parameters. In order to create a three-atom GHZ state, the finial state  should be
should be  according to eq. (16). Therefore, we have tanα = 1. By choosing parameters for the laser pulses suitably to fulfill the boundary condition in eq. (25), the time-dependent
according to eq. (16). Therefore, we have tanα = 1. By choosing parameters for the laser pulses suitably to fulfill the boundary condition in eq. (25), the time-dependent  and
and  are gotten as shown in Fig. 3 with parameters
are gotten as shown in Fig. 3 with parameters  and
and  . For simplicity, we set β = 0 in the following discussion. Fig. 4 shows the relationship between the fidelity of the generated three-atom GHZ state (governed by the APF Hamiltonian
. For simplicity, we set β = 0 in the following discussion. Fig. 4 shows the relationship between the fidelity of the generated three-atom GHZ state (governed by the APF Hamiltonian  and two parameters Δ and tf when
and two parameters Δ and tf when  satisfying the Zeno condition, where the fidelity for the three-atom GHZ state is given through
satisfying the Zeno condition, where the fidelity for the three-atom GHZ state is given through  (
( is the density operator of the whole system when
is the density operator of the whole system when  ). We find that there is a wide range of selectable values for parameters Δ and tf to get a high fidelity of the three-atom GHZ state. The fidelity increases with the increasing of tf while decreases with the increasing of Δ. It is not hard to understand, putting eq. (26) into eq. (24) and setting
). We find that there is a wide range of selectable values for parameters Δ and tf to get a high fidelity of the three-atom GHZ state. The fidelity increases with the increasing of tf while decreases with the increasing of Δ. It is not hard to understand, putting eq. (26) into eq. (24) and setting  , we can find
, we can find

where  is the amplitude of
is the amplitude of  . That means, in order to satisfy the Zeno condition
. That means, in order to satisfy the Zeno condition  and the large detuning condition
and the large detuning condition  , the ratio Δ/tf should be small enough. Moreover, this relationship also explains the phenomenon in Fig. 4 that to achieve a high fidelity with a larger detuning Δ, a longer interaction time tf is required. Then to prove the operation time required for the creation of the three-atom GHZ state governed by
, the ratio Δ/tf should be small enough. Moreover, this relationship also explains the phenomenon in Fig. 4 that to achieve a high fidelity with a larger detuning Δ, a longer interaction time tf is required. Then to prove the operation time required for the creation of the three-atom GHZ state governed by  is much shorter than that governed by HI, we contrast the performances of population transfer from the initial state
is much shorter than that governed by HI, we contrast the performances of population transfer from the initial state  governed by the APF Hamiltonian
governed by the APF Hamiltonian  and that governed by the original Hamiltonian HI in Fig. 5 with
and that governed by the original Hamiltonian HI in Fig. 5 with  . The time-dependent population for any state
. The time-dependent population for any state  is given by the relationship
is given by the relationship  , where ρ(t) is the corresponding time-dependent density operator. The comparison of Fig. 5(a,b) shows that with this set of parameters, the APF Hamiltonian
, where ρ(t) is the corresponding time-dependent density operator. The comparison of Fig. 5(a,b) shows that with this set of parameters, the APF Hamiltonian  can govern the evolution to achieve a near-perfect three-atom GHZ state from state
can govern the evolution to achieve a near-perfect three-atom GHZ state from state  in short interaction time while the original Hamiltonian
in short interaction time while the original Hamiltonian  can not. In fact, through solving the adiabatic condition
can not. In fact, through solving the adiabatic condition  , we obtain
, we obtain

where f(t) is a wave function whose amplitude is irrelevant to tf. The result shows when Ω0 is a constant, the longer the operation time tf is, the better the adiabatic condition is satisfied. This is proved in Fig. 6. Figure 6 reveals the relationship between G(tf) and λtf, where  . From this figure, we discover that even with
. From this figure, we discover that even with  which does not meet the Zeno condition, the operation time required for the three-atom GHZ state generation in an adiabatic system is longer than 100/λ (when
which does not meet the Zeno condition, the operation time required for the three-atom GHZ state generation in an adiabatic system is longer than 100/λ (when  ,
,  ). We also plot the fidelities of the evolved states governed by
). We also plot the fidelities of the evolved states governed by  and
and  (in different cases) in Fig. 7, with respect to the target three-atom GHZ state. Shown in the figure, even with a large laser intensity, say,
(in different cases) in Fig. 7, with respect to the target three-atom GHZ state. Shown in the figure, even with a large laser intensity, say,  , the interaction time required for creation of the three-atom GHZ state via adiabatic passage is still much longer than that via STAP. Generally speaking, the adiabatic condition is satisfied much better with a relatively larger laser intensity, while, the system would be very sensitive to the decoherence caused by the cavity decay with a relatively large laser intensity. This will be proved in the following.
, the interaction time required for creation of the three-atom GHZ state via adiabatic passage is still much longer than that via STAP. Generally speaking, the adiabatic condition is satisfied much better with a relatively larger laser intensity, while, the system would be very sensitive to the decoherence caused by the cavity decay with a relatively large laser intensity. This will be proved in the following.
Once the dissipation is considered, the evolution of the system can be modeled by a master equation in Lindblad form,

where Lk’s are the Lindblad operators. For both the resonant and non-resonant systems, there are eight Lindblad operators governing the dissipation:

where  and
and  are the decays of the cavity modes and γn
are the decays of the cavity modes and γn  are the spontaneous emissions of atoms. For simplicity, we assume
are the spontaneous emissions of atoms. For simplicity, we assume  and
and  . Figure 8(a) shows the fidelity of the three-atom GHZ state governed by the APF Hamiltonian
. Figure 8(a) shows the fidelity of the three-atom GHZ state governed by the APF Hamiltonian  versus these two noise resources with
versus these two noise resources with  ,
,  and
and  . It turns out that the present shortcut scheme with this set of parameters is much more sensitive to the cavity decays than the spontaneous emissions. Ref. 5 contributes to understanding this phenomenon, in fact, with this set of parameters, the Zeno condition for the non-resonant system is not ideally fulfilled because shortening the time implies an energy cost12,24 (in this system, the energy cost denotes requiring relative-large laser intensities). Known from ref. 5, destroying the Zeno condition slightly is also helpful to achieve the target state in a much shorter interaction time. However, if the Zeno condition has not been satisfied very well, the intermediate states including the cavity-excited states would be populated during the evolution, which causes that the system is sensitive to the cavity decays. However, we can find in Fig. 8(b) which shows fidelity of the three-atom GHZ state governed by original Hamiltonian HI with
. It turns out that the present shortcut scheme with this set of parameters is much more sensitive to the cavity decays than the spontaneous emissions. Ref. 5 contributes to understanding this phenomenon, in fact, with this set of parameters, the Zeno condition for the non-resonant system is not ideally fulfilled because shortening the time implies an energy cost12,24 (in this system, the energy cost denotes requiring relative-large laser intensities). Known from ref. 5, destroying the Zeno condition slightly is also helpful to achieve the target state in a much shorter interaction time. However, if the Zeno condition has not been satisfied very well, the intermediate states including the cavity-excited states would be populated during the evolution, which causes that the system is sensitive to the cavity decays. However, we can find in Fig. 8(b) which shows fidelity of the three-atom GHZ state governed by original Hamiltonian HI with  and
and  in the presence of decoherence, with large laser intensities, the adiabatic scheme is also sensitive to the cavity decays as we mentioned above. The comparison of these two figures drops a result that the present shortcut scheme is almost the same with the adiabatic one in restraining the decoherence.
in the presence of decoherence, with large laser intensities, the adiabatic scheme is also sensitive to the cavity decays as we mentioned above. The comparison of these two figures drops a result that the present shortcut scheme is almost the same with the adiabatic one in restraining the decoherence.
The robustness against operational imperfection is also a main factor for the feasibility of the scheme because most of the parameters are hard to accurately achieve in experiment. Therefore, we define  as the deviation of any parameter x, where
as the deviation of any parameter x, where  is the actual value and x is the ideal value. Then in Fig. 9(a) we plot the fidelity of the GHZ state versus the variations in total operation time T
is the actual value and x is the ideal value. Then in Fig. 9(a) we plot the fidelity of the GHZ state versus the variations in total operation time T  and laser amplitude
and laser amplitude  and in Fig 9(b) we plot the fidelity of the GHZ state versus the variations in coupling λ and detuning Δ. As shown in the figures, the scheme is robust against all of these variations. Any deviation
and in Fig 9(b) we plot the fidelity of the GHZ state versus the variations in coupling λ and detuning Δ. As shown in the figures, the scheme is robust against all of these variations. Any deviation 
 causes a reduction less than 3% in the fidelity.
causes a reduction less than 3% in the fidelity.
In a real experiment, the cesium atoms which have been cooled and trapped in a small optical cavity in the strong-coupling regime44,45 can be used in this scheme. We take the hyperfine states of  as the excited sates and the hyperfine states of
as the excited sates and the hyperfine states of  as the ground sates. With a set of cavity QED parameters
as the ground sates. With a set of cavity QED parameters  MHz,
MHz,  MHz and
MHz and  MHz in strong-coupling regime46,47,48, the fidelity of the three-atom GHZ state in this paper is 98.24%. Thus, the scheme is robust and might be promising within the limits of current technology.
MHz in strong-coupling regime46,47,48, the fidelity of the three-atom GHZ state in this paper is 98.24%. Thus, the scheme is robust and might be promising within the limits of current technology.
Conclusion
We have presented a promising method to construct shortcuts to adiabatic passage (STAP) for a three-atom system to generate GHZ states in the cavity QED system. Through using quantum Zeno dynamics and “transitionless quantum driving”, we are free to simplify a complicated Hamiltonian and choose the laser pulses to construct shortcuts in multi-qubit system to implement the fast quantum information processing. Numerical simulation demonstrates that the scheme is fast and robust against the decoherence caused by both atomic spontaneous emission, photon leakage and operational imperfection. The deficiency is that the present scheme might be sensitive to the cavity decays because of some inevitable factors. Compared with the previous shortcut methods, this method obviously works better at entanglement generation in multi-qubit systems. In fact, any quantum system whose Hamiltonian is possible to be simplified into the form in eq. (15), the shortcut can be constructed with the same method presented in this paper. For example, similar to refs 49,50 for the generation of the multiparticle GHZ states in an atom-fiber-cavity combined system, we can shorten the operation time using the same method in the following steps: (1) We consider the Hamiltonian HAL (the Hamiltonian describing the interaction between atoms and lasers) as Hobs in eq. (9) and the rest of the total Hamiltonian (the interaction between atoms and cavities and the interaction between cavities and fibers) as  in eq. (9). Then, choosing the “dark Zeno subspace”, that means
in eq. (9). Then, choosing the “dark Zeno subspace”, that means  in eq. (10), we can obtain an effective Hamiltonian named the Zeno Hamiltonian
in eq. (10), we can obtain an effective Hamiltonian named the Zeno Hamiltonian  . (2) For this effective Hamiltonian, by using TQD, we construct the CDD Hamiltonian H(t) that speeds up the adiabatic process. (3) Similar to the GHZ state generation, we find out the corresponding non-resonant system (the APF Hamiltonian) whose effective Hamiltonian
. (2) For this effective Hamiltonian, by using TQD, we construct the CDD Hamiltonian H(t) that speeds up the adiabatic process. (3) Similar to the GHZ state generation, we find out the corresponding non-resonant system (the APF Hamiltonian) whose effective Hamiltonian  has the form in eq. (22). (4) Making
has the form in eq. (22). (4) Making  , the parameters for the APF Hamiltonian are determined and the shortcut is constructed. Then the APF Hamiltonian would govern the system to achieve the same final result as the adiabatic process governed by the original Hamiltonian with a much shorter operation time. Similar idea can be generalized to generate other multi-qubit quantum entangled states, for example, Bell states, W states, singlet states and so on. This might lead to a useful step toward realizing fast and noise-resistant quantum information processing for multi-qubit systems in current technology.
, the parameters for the APF Hamiltonian are determined and the shortcut is constructed. Then the APF Hamiltonian would govern the system to achieve the same final result as the adiabatic process governed by the original Hamiltonian with a much shorter operation time. Similar idea can be generalized to generate other multi-qubit quantum entangled states, for example, Bell states, W states, singlet states and so on. This might lead to a useful step toward realizing fast and noise-resistant quantum information processing for multi-qubit systems in current technology.
Additional Information
How to cite this article: Chen, Y.-H. et al. Shortcuts to adiabatic passage for fast generation of Greenberger-Horne-Zeilinger states by transitionless quantum driving. Sci. Rep. 5, 15616; doi: 10.1038/srep15616 (2015).
References
Chen, X., Lizuain, I., Ruschhaupt, A., Guéry-Odelin, D. & Muga, J. G. Shortcut to adiabatic passage in two- and three-level atoms. Phys. Rev. Lett. 105, 123003 (2010).
Torrontegui, E. et al. Chapter 2 - Shortcuts to Adiabaticity. Adv. Atom. Mol. Opt. Phys. 62, 117–169 (2013).
del Campo, A. Shortcuts to adiabaticity by counterdiabatic driving. Phys. Rev. Lett. 111, 100502 (2013).
Masuda, S. & Nakamura, K. Acceleration of adiabatic quantum dynamics in electromagnetic fields. Phys. Rev. A 84, 043434 (2011).
Chen, Y. H., Xia, Y., Chen, Q. Q. & Song, J. Efficient shortcuts to adiabatic passage for fast population transfer in multiparticle systems. Phys. Rev. A 89, 033856 (2014).
Lu, M., Xia, Y., Shen, L. T., Song, J. & An, N. B. Shortcuts to adiabatic passage for population transfer and maximum entanglement creation between two atoms in a cavity. Phys. Rev. A 89, 012326 (2014).
Lu, M., Xia, Y., Shen, L. T. & Song, J. An effective shortcut to adiabatic passage for fast quantum state transfer in a cavity quantum electronic dynamics system. Laser Phys. 24, 105201 (2014).
Chen, Y. H., Xia, Y., Chen, Q. Q. & Song, J. Shortcuts to adiabatic passage for multiparticles in distant cavities: applications to fast and noise-resistant quantum population transfer, entangled states’ preparation and transition. Laser Phys. Lett. 11, 115201 (2014).
Chen, Y. H., Xia, Y., Chen, Q. Q. & Song, J. Fast and noise-resistant implementation of quantum phase gates and creation of quantum entangled states. Phys. Rev. A 91, 012325 (2015).
Muga, J. G., Chen, X., Ruschhaup, A. & Guéry-Odelin, D. Frictionless dynamics of Bose-Einstein condensates under fast trap variations. J. Phys. B 42, 241001 (2009).
Chen, X. et al. Fast optimal frictionless atom cooling in harmonic traps: Shortcut to adiabaticity. Phys. Rev. Lett. 104, 063002 (2010).
Chen, X. & Muga, J. G. Transient energy excitation in shortcuts to adiabaticity for the time-dependent harmonic oscillator. Phys. Rev. A 82, 053403 (2010).
Schaff, J. F., Capuzzi, P., Labeyrie, G. & Vignolo, P. Shortcuts to adiabaticity for trapped ultracold gases. New J. Phys. 13, 113017 (2011).
Torrontegui, E. et al. Fast atomic transport without vibrational heating. Phys. Rev. A 83, 013415 (2011).
Chen, X., Torrontegui, E., Stefanatos, D., Li, J. S. & Muga, J. G. Optimal trajectories for efficient atomic transport without final excitation. Phys. Rev. A 84, 043415 (2011).
Torrontegui, E. et al. Fast transport of Bose-Einstein condensates. New J. Phys. 14, 013031 (2012).
Li, Y., Wu, L. A. & Wang, Z. D. Fast ground-state cooling of mechanical resonators with time-dependent optical cavities. Phys. Rev. A 83, 043804 (2011).
del Campo, A. Frictionless quantum quenches in ultracold gases: A quantum-dynamical microscope. Phys. Rev. A 84, 031606(R) (2011); Fast frictionless dynamics as a toolbox for low-dimensional Bose-Einstein condensates. Eur. Phys. Lett.96, 60005 (2011).
Ruschhaupt, A., Chen, X., Alonso, D. & Muga, J. G. Optimally robust shortcuts to population inversion in two-level quantum systems. New J. Phys. 14, 093040 (2012).
Schaff, J. F., Song, X. L., Vignolo, P. & Labeyrie, G. Fast optimal transition between two equilibrium states. Phys. Rev. A 82, 033430 (2010).
Schaff, J. F., Song, X. L., Capuzzi, P., Vignolo, P. & Labeyrie, G. Shortcut to adiabaticity for an interacting Bose-Einstein condensate. Eur. Phys. Lett. 93, 23001 (2011).
Walther, A. et al. Number-theoretic nature of communication in quantum spin systems. Phys. Rev. Lett. 109, 050502 (2012).
Tseng, S. Y. & Chen, X. Engineering of fast mode conversion in multimode waveguides. Opt. Lett. 37, 5118–5120 (2012).
Chen, X., Torrontegui, E. & Muga, J. G. Lewis-Riesenfeld invariants and transitionless quantum driving. Phys. Rev. A 83, 062116 (2011).
Lewis, H. R. & Riesenfeld, W. B. An exact quantum theory of the time-dependent harmonic oscillator and of a charged particle in a time-dependent electromagnetic field. J. Math. Phys. 10, 1458–1473 (1969).
Berry, M. V. Transitionless quantum driving. J. Phys. A 42, 365303 (2009).
Bason, M. G. et al. High-fidelity quantum driving. Nat. Phys. 8, 147–152 (2012).
Demirplak, M. & Rice, S. A. Adiabatic population transfer with control fields. J. Phys. Chem. A 107, 9937–9945 (2003).
Demirplak, M. & Rice, S. A. On the consistency, extremal and global properties of counterdiabatic fields. J. Chem. Phys. 129, 154111 (2008).
del Campo, A., Rams, M. M. & Zurek, W. H. Assisted Finite-Rate adiabatic passage across a quantum critical point: Exact solution for the quantum ising model. Phys. Rev. Lett. 109, 115703 (2012).
Takahashi, K. Transitionless quantum driving for spin systems. Phys. Rev. E 87, 062117 (2013).
Takahashi, K. How fast and robust is the quantum adiabatic passage. J. Phys. A 46, 315304 (2013).
Muga, J. G., Chen, X., Ibáñez, S. Lizuain, I. & Ruschhaupt, A. Transitionless quantum drivings for the harmonic oscillator. J. Phys. B 43, 085509 (2010).
Ibáñez, S., Chen, X., Torrontegui, E., Muga, J. G. & Ruschhaupt, A. Multiple schrödinger pictures and dynamics in shortcuts to adiabaticity. Phys. Rev. Lett. 109, 100403 (2012).
Martínez-Garaot, S., Torrontegui, E., Chen, X. & Muga, J. G. Shortcuts to adiabaticity in three-level systems using Lie transforms. Phys. Rev. A 89, 053408 (2014).
Torrontegui, E., Martínez-Garaot, S. & Muga, J. G. Hamiltonian engineering via invariants and dynamical algebra. Phys. Rev. A 89, 043408 (2014).
Opatrný, T. & Mølmer, K. Partial suppression of nonadiabatic transitions. New J. Phys. 16, 015025 (2014).
Saberi, H., Opatrny, T., Mølmer, K. & del Campo, A. Adiabatic tracking of quantum many-body dynamics. Phys. Rev. A 90, 060301(R) (2014).
Greenberger, D. M., Horne, M. A., Shimony, A. & Zeilinger, A. Bells theorem without inequalities. Am. J. Phys. 58, 1131–1143 (1990).
Zheng, S. B. One-step synthesis of multiatom Greenberger-Horne-Zeilinger states. Phys. Rev. Lett. 87, 230404 (2001).
Kwiat, P., Weinfurter, H., Herzog, T., Zeilinger, A. & Kasevich, M. A. Interaction-free measurement. Phys. Rev. Lett. 74, 4763–4766 (1995).
Facchi, P. & Pascazio, S. Quantum Zeno subspaces. Phys. Rev. Lett. 89, 080401 (2002).
Chen, Y. H., Xia, Y. & Song, J. Deterministic generation of singlet states for N-atoms in coupled cavities via quantum Zeno dynamics. Quantum inf. Process. 13, 1857–1877 (2014).
Ye, J., Vernooy, D. W. & Kimble, H. J. Trapping of single atoms in cavity QED. Phys. Rev. Lett. 83, 4987–4990 (1999).
McKeever, J. et al. State-insensitive cooling and trapping of single atoms in an optical cavity. Phys. Rev. Lett. 90, 133602 (2003).
Spillane, S. M. et al. Ultrahigh-Q toroidal microresonators for cavity quantum electrodynamics. Phys. Rev. A 71, 013817 (2005).
Hartmann, M. J., Brandão, F. G. S. L. & Plenio, M. B. Strongly interacting polaritons in coupled arrays of cavities. Nat. Phys. 2, 849–855 (2006).
Brennecke, F. et al. Cavity QED with a Bose-Einstein condensate. Nature 450, 268–271 (2007).
Li, W. A. & Wei, L. F. Controllable entanglement preparations between atoms in spatially-separated cavities via quantum Zeno dynamics. Opt. Express 20, 13440–13450 (2012).
Hao, S. Y., Xia, Y., Song, J. & An, N. B. One-step generation of multiatom Greenberger-Horne-Zeilinger states in separate cavities via adiabatic passage. J. Opt. Soc. Am. B 30, 468–474 (2013).
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grants No. 11575045 and No. 11374054, the Foundation of Ministry of Education of China under Grant No. 212085 and the Major State Basic Research Development Program of China under Grant No. 2012CB921601.
Author information
Authors and Affiliations
Contributions
Y.H.C. and Y.X. came up with the initial idea for the work and performed the simulations for the model. J.S. performed the calculations for the model. Y.H.C. and Q.Q.C. performed all the data analysis and the initial draft of the manuscript. All authors participated in the writing and revising of the text.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chen, YH., Xia, Y., Song, J. et al. Shortcuts to adiabatic passage for fast generation of Greenberger-Horne-Zeilinger states by transitionless quantum driving. Sci Rep 5, 15616 (2015). https://doi.org/10.1038/srep15616
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep15616
This article is cited by
-
Shortcuts to Adiabatic Passage for Fast Generation of Entangled States in Directly Coupled Bimodal-Mode Cavitieseee
International Journal of Theoretical Physics (2021)
-
Fast and robust implementation of quantum gates by transitionless quantum driving
Quantum Information Processing (2021)
-
Preparation of three-atom GHZ states based on deep reinforcement learning
Quantum Information Processing (2021)
-
Preparing Greenberger-Horne-Zeilinger States by Lypunov Control
International Journal of Theoretical Physics (2021)
-
One-step implementation of a robust Fredkin gate based on path engineering
Quantum Information Processing (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

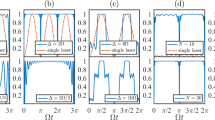




 versus the interaction time λtf and the detuning Δ/λ.
versus the interaction time λtf and the detuning Δ/λ.
 and
and  with
with  , tf = 35/λ and Δ = 2.2λ, (a) governed by the APF Hamiltonian
, tf = 35/λ and Δ = 2.2λ, (a) governed by the APF Hamiltonian  , (b) governed by the original Hamiltonian HI(t).
, (b) governed by the original Hamiltonian HI(t).

 and the original Hamiltonian HI(t).
and the original Hamiltonian HI(t).
 when
when  ,
,  and
and  . (b) Dependences on κ/λ and
. (b) Dependences on κ/λ and  of the fidelity of the three-atom GHZ state governed by the original Hamiltonian HI(t) when
of the fidelity of the three-atom GHZ state governed by the original Hamiltonian HI(t) when  and
and  .
.
 . (b) λ and Δ.
. (b) λ and Δ.