Abstract
We theoretically and numerically analyze thermal invisibility based on the concept of scattering cancellation and mantle cloaking. We show that a small object can be made completely invisible to heat diffusion waves, by tailoring the heat conductivity of the spherical shell enclosing the object. This means that the thermal scattering from the object is suppressed and the heat flow outside the object and the cloak made of these spherical shells behaves as if the object is not present. Thermal invisibility may open new vistas in hiding hot spots in infrared thermography, military furtivity and electronics heating reduction.
Similar content being viewed by others
Introduction
The realization of electromagnetic invisibility cloaks1,2,3,4 is undoubtedly one of the most exciting and challenging applications of metamaterials5. In the previous decades, thanks to the astonishing development of micro- and nano-fabrication and 3D printing, this goal has got closer to reality. In 2005, Alù and Engheta proposed a transparency device that relies on the so-called scattering cancellation technique (SCT)6. This mechanism consists of using a low or negative electric permittivity cover to cancel the different scattering multipoles of the object to hide. This class of cloaking devices has been shown to be quite robust to changes in the geometry of objects and the frequency of operation7,8,9. Moreover, a recent experimental study has shown that these cloak designs can actually be realized at microwave frequencies10. Applications in furtivity, non-invasive sensing and probing can be envisaged11,12, opening new directions in medicine, defense and telecommunications. Recent findings also suggest that objects can be made invisible using the mantle cloaking technology, where a metasurface can produce similar effects with a simpler and thinner geometry. This is achieved by tailoring the surface current on the metasurface and consequently the phase of re-radiated fields13,14,15,16. It should also be mentioned here that other cloaking techniques have been put forward in the recent years based on various concepts such as conformal mapping1, transformation optics2,3,17, homogenization of multistructures18,19, active plasmonic cloaks20, anomalous localized resonances21 and waveguide theory22.
The concept of invisibility has been extended to other realms of physics. Cloaks capable of hiding objects from acoustic waves23,24,25, surface water waves26, flexural bending waves27, seismic waves28,29, quantum matter waves30,31 and even diffusive light propagation32,33 have been developed. And more recently, after the seminal work of Guenneau et al.34, invisibility cloaks for heat waves has become another exciting venue for cloaking applications35,36,37. Thermal cloak designs inspired by transformation optics2 have been subsequently proposed38,39,40 to control the flow of heat in metamaterial structures. Their experimental validation followed shortly41,42,43,44. Thermal cloaking may find interesting applications in modern electronics. It can be used to reduce the heat diffused from computers or to protect a specific nano-electronic component by re-directing the flow of heat. This technique can also be used for isolation in buildings to reduce the consumption of energy required in heating or cooling.
In this paper, we propose to use the concept of scattering cancellation to generate the invisibility effect for heat diffusion waves. The peculiarity of our cloak is that, unlike earlier designs, we consider both static and time-harmonic dependence (note that time-harmonic heat sources can be generated using pulsating lasers45). This scenario requires cancellation of two scattering orders for small objects, i.e. the monopole and dipole ones, corresponding to the specific heat capacity and the heat conductivity, respectively. Numerical simulations confirm that a scattering reduction of over 40 dB can be obtained for optimized cloak parameters. Additionally, it is shown that the proposed cloak suppresses both the near and far heat fields. We also demonstrate that coating an object with an ultra-thin layer or thermal metasurface is a viable way for scattering reduction (mantle cloaking).
Results
Heat diffusion waves and their dispersion relation
Using the first principle of thermodynamics in a closed system46, one can show that in the absence of radiation and convection, the temperature of a physical system obeys the Fourier relation 
. Here, 
, 
and 
represent the density of heat flux (heat flow per unit surface per unit time), the density of the fluid and the temperature field, respectively. 
is the specific heat capacity and 
denotes the heat energy generated per unit volume per unit time (Fig. 1). Using the Fourier law, i.e. the linear and instantaneous relation 
, where 
is the heat conductivity of the medium, one can derive,
For a constant conductivity and in the absence of heat sources, Eq. (1) simplifies to 
. To solve this equation, one can assume that 
, with 
, where 
is the wave number of the pseudo diffusion plane wave and 
its angular frequency. This ansatz is valid, only because Eq. (1) is a linear equation, meaning that 
is a solution, if and only if, 
is a solution. The dispersion relation of heat diffusion waves is thus 
. If one assumes that 
is real, then 
, with 
. The general solutions are thus attenuated diffusing plane waves. Now, under the assumption of time-harmonic dependence 
, generated for instance by a pulsating laser and constant conductivity, Eq. (1) simplifies to
For the structure in Fig. 1, Eq. (1) is supplied with two boundary conditions that should be satisfied at the surface of both spherical object and the cloak. Across the boundaries 
and 
, we have the continuity of the temperature and the density of heat flux, i.e. 
and 
, where the signs + and − refer respectively to the inner and outer regions and 
denotes the normal derivative, which only depends upon the radial coordinate in the case of circular objects. Here, 
and 
are the inner and outer radii of the shell. Moreover, 
represent the conductivity, fluid density, heat capacity and wave number in the background medium (
), object (
) and shell (
), respectively.
Thermal scattering problem.
(a) Cross-sectional view of the heat transfer scenario, with the object to cloak in the middle. (b) Cross-sectional view of the cloaked object.
Scattering cancellation technique for heat diffusion waves: static regime
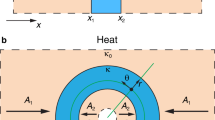
The aim of this study is to show that scattering from various spherical objects can be reduced drastically by carefully choosing the values of the shell conductivity and the specific heat capacity. First, a spherical object centered at the origin of a spherical coordinate system is considered. Two parallel plates set at different temperatures 
, generate a heat flux (plane heat diffusion wave) that impinges on the scattering object [Fig. 1(a)]. In this first section, the case of static (steady-state) regime is considered, i.e. 
. So Eq. (1) is simplified to 
. The scalar temperature field 
in the different regions of space can be expressed in spherical coordinates (Fig. 1) as,
where 
represents the Legendre polynomial of order 
. For 
, 
, therefore 
and all the other coefficients 
are zero. The remaining coefficients are obtained by solving the linear system
which is obtained by applying the continuity conditions at the boundaries 
and 
. The scattering cancellation condition is obtained by enforcing that the first scattering coefficient 
is zero,
where 
. Solving Eq. (7) for 
yields the value of the shell conductivity, which ensures that there is no temperature perturbation with a uniform temperature gradient, as if the object does not exist,
Scattering cancellation technique for heat diffusion waves: time-harmonic regime
The scattering coefficients relate the scattered fields to the incident ones and depend on the geometry of the object and the frequency 
. Moreover, for a given size 
of the object, only contributions up to a given order 
are relevant, since the amplitude of the scattering coefficients changes as 
. The incident heat excitation is an oblique plane diffusion wave, of incidence angle 
and is of the form 
. In a spherical coordinate system, it can be expressed as
where 
denotes the 
spherical Bessel function and 
is the amplitude of the incident temperature field. The scattered field (
) can be expressed in a spherical coordinate system as
where 
are the complex scattering coefficients and 
are spherical Hankel functions of the first kind. Therefore, the temperature field can be expressed in the different regions of space as
with 
and (
) complex coefficients of the temperature field inside the object and the shell, respectively. Applying the continuity conditions at the boundaries 
and 
yields the different coefficients. In particular, 
. Here 
and 
are given by the determinants
and
The scattering cross-section (SCS) 
is a measure of the overall visibility of the object to external observers. It is obtained by integrating the scattering amplitude 
, defined such that 
, for 
,
Here, 
is the incremental solid angle, in spherical coordinates, 
and 
is expressed as
Inserting Eq. (17) into Eq. (16) yields
In the quasistatic limit (long diffusion length 
), only few scattering orders contribute to the overall scattering cross-section, namely the first two orders (
for the monopole and 
for the dipole mode, unlike in the electrodynamic case, where the first dominant mode is the dipole one). In this scenario, one has
Consequently, canceling these two modes, i.e. 
and 
, will ensure that 
and the thermal scattering from the object will be suppressed. Namely, the SCT conditions on the parameters of the cloaking shell 
, 
and 
are
and
The monopole SCT condition in Eq. (20), depends only on the product of the density and the specific heat of the shell and the ratio of radii of the object and the shell 
. Similarly, the condition in Eq. (21) depends only on the conductivity of the shell and 
. By enforcing these two conditions, the total scattering from the spherical object can be suppressed in the quasistatic limit.
Figures 2(a) and 2(b) illustrate numerical solutions to Eqs. (20) and (21), where the variation of the relative specific heat capacity 
and the relative heat conductivity 
are plotted versus 
and 
and 
, respectively. From the solution of Eq. (20), given in Fig. 2(a), one can see that the relative specific heat capacity of the shell 
, given here in logarithmic scale, takes positive and negative values, depending on 
and the heat capacity of the object. The red line represents the curve obeying the equation 
implying 
. The specific heat capacity takes negative (positive near-zero) values above (below) this curve. From the solution of Eq. (21), given in Fig. 2(b), it can be seen that the required relative heat conductivity of the shell 
needs to be almost always negative, for varying 
and 
. However, for an object with small heat conductivity and small radius [lower part of Fig. 2(b), in blue color], the required shell conductivity is close to zero. In fact, from Eq. (21), one can derive that for the negative solution of Eq. (21)
where 
. It can be clearly seen that for positive conductivities of the object, the condition 
has to be satisfied to achieve the optimal heat cloaking effect.
Optimal cloaking parameters.
(a) Relative specific heat capacity of the shell 
in logarithmic scale, versus the ratio 
and the relative specific heat capacity of the object 
. The color bar denotes the plot of 
. (b) Relative heat conductivity of the shell 
in logarithmic scale, versus the ratio 
and the relative heat conductivity of the object 
. The color bar denotes the plot of log 
and the dashed black line represents log 
.
Let us move now to the analysis of a specific scenario, where the heat scattering of a spherical object is characterized. The relative specific heat capacity of the object is 
and its relative conductivity is 
. The radius of the object 
and the wave numbers are normalized to 
. The free space wave number is chosen as 
. This object is coated with a shell of outer radius 
. 
of the total object-shell structure, defined in Eqs. (16)–(18), is normalized to the SCS of the bare object and plotted against varying values of 
and 
. The result is shown in Fig. 3(a) in logarithmic scale. The blue regions correspond to significant scattering reduction, whereas red regions correspond to enhanced scattering from the structure. It can be noticed that ranges of 
between 1 and 4 and 
between 0.05 and 0.5, are best for thermal scattering cancellation (now using the positive solution of Eq. (21), for practical realizations). The white dot has coordinates (3.1, 0.15) that correspond to the theoretical SCT condition obtained from Eqs. (20) and (21). It is also interesting to note that numerical simulations taking into account many scattering orders, give scattering reduction of 40 dB, sensibly around the same point.
Thermal scattering reduction.
(a) Normalized (analytical) SCS 
in logarithmic scale, versus the relative heat conductivity 
and the relative specific heat capacity 
. The white dot represents the position of optimized scattering reduction, with a value of 40 dB. The color bar denotes the plot of 
, where the subscripts 1 and 2 refer to the scattering cross-section of the obstacle and cloaked structure, respectively. (b) Normalized SCS versus the relative heat conductivity for various values of the specific heat capacity 
. (c) Normalized SCS versus the relative specific heat capacity 
for various values of the relative heat conductivity 
.
These results show the importance of taking into account both the shell conductivity and specific heat capacity, in contrast to previous studies that only considered the effect of conductivity through the static analysis. This can be better understood from Figs. 3(b) and 3(c), where the normalized SCS is plotted versus 
for various values of 
and versus 
for various values of 
, respectively. The sensitivity to variations in 
is more evident from these figures, since a small variation from the optimum value results in fast deterioration of the scattering reduction: when 
is equal to 1 or 5, there is no dip in the SCS and the scattering is high, as can be seen from Fig. 3(c). The sensitivity to variations in 
is less important, as can be seen from Fig. 3(b), but it is important to choose values around those predicted by Eqs. (20) and (21). On the other hand, when 
, peaks corresponding to modal resonances start appearing in the scattering cross-section (related to Fano-like response of the system due to interference between dark and bright scattering modes)47.
To better illustrate the efficiency of the proposed cloak, the far-field scattering patterns, i.e. the heat scattering amplitude 
in polar coordinates, in the 
−
plane, are shown in Figs. 4(a) and 4(b). These figures demonstrate that the object is almost undetectable at all angles with scattering amplitude orders of magnitude lower than that of the bare object. As a result, there is no temperature perturbation around the object immersed in the thermal fields. To further demonstrate the functionality of the cloak, Figs. 4(c) and 4(d) plot the amplitude distribution of the scattered thermal field when the heat from the infinite sheet of oscillating heat source is impinging from left to right on the structure, without and with the cloaking shell, respectively. When the object is cloaked, the field amplitude is constant everywhere in space in contrast to the case of the object without the cloak.
Near and far-field characterization.
Analytical scattering amplitude 
, given by Eq. (17), in polar coordinates and in logarithmic scale (a) for the bare object with 
and (b) for the cloaked object, with 
. Amplitude of the oscillating temperature in the near-field of (c) the same bare object of Fig. 4(a) and (d) the same cloaked object of Fig. 4(b) for 
. Arrows show the direction of 
and the color bar denotes the plot of 
.
Discussion
Mantle cloaking for heat diffusion waves
As stated in the introduction, recent findings suggest that objects can be made invisible using the surface cloaking technology, where a metasurface may produce similar cloaking effects in a simpler and thinner geometry14,15,16. The ultrathin mantle cloak with an averaged surface reactance metasurface13 reduces the scattering from the hidden object, comparable to bulk metamaterial cloaks. The setup of the problem is similar to the previous section, except for the fact that scattering cancellation is achieved by a surface, instead of a shell. This is illustrated in the inset of Fig. 5(a). The impedance boundary condition results in jumps in the radial component of the density of heat flux, on the interface between the two media.
Thermal mantle cloaking.
Normalized (analytical) SCS 
versus 
for the object with normalized radius 
and relative heat conductivity 
for various values of the ratio 
. (b) Normalized SCS 
versus normalized frequency for the same object with 
and 
for values of the ratio 
and 
. The inset of Fig. 5(a) illustrates the object coated with a thermal metasurface, projected in the 
−
plane. Amplitude of the temperature field on the 
−
plane for the same object (c) with mantle cloak with 
and (d) without the cloak. The color bar denotes the plot of 
.
In what follows it is shown that the scattering from various spherical objects can be drastically reduced by choosing the appropriate surface impedance and thus their visibility to heat diffusion waves can be suppressed.
To design a mantle cloak, we keep the boundary conditions at 
same as those in the previous sections, while we replace the boundary conditions at 
with
Eq. (24) is a surface impedance condition that implies a jump in the density of heat flux. Here, 
is the averaged surface impedance that relates the temperature to the density of heat flux on the surface.
Following the procedure described in the previous section, with these new boundary conditions, one can show that the 
th spherical scattering harmonic can be suppressed, provided that the following determinant is canceled,
It should be noted that for the mantle cloak design considered here, 
and 
. In Eq. (25), the dimensionless function 
is defined as
For 
, the spherical Bessel functions take a simpler polynomial form and the approximate cloaking condition in this limit can be written as
This clearly shows that by properly choosing the thermal surface reactance (expressed in units of J = (m2K)), it is possible to suppress the dominant multipolar scattering in the quasistatic limit.
Figure 5(a) plots the SCS versus 
for cloaked objects with various 
. The SCS of a bare object is plotted for comparison. For 
, we notice that the metasurface does not reduce the scattering, consistent with the limit of no-surface. For specific values of 
, however, a relevant scattering reduction is achieved and this may be obtained for different values of 
, even in the limit of a cloak winding conformal to the object (
).
Figure 5(b) plots the SCS versus the frequency for cloaked objects with 
(conformal) and 
. We suppose here that the surface reactance does not vary with frequency and is given with 
for 
and 
for 
. The SCS of uncloaked objects with radius 
and 
are plotted for comparison. It is evident that excellent scattering reduction may be achieved over a large range of frequencies for both cases.
Figures 5(c) and 5(d) plot the amplitude of the temperature field scattered by a cloaked and uncloaked object, on the 
−
plane at a time instant, respectively. When the object is cloaked, both forward and backward scattering almost vanish. This reduction of scattering is achieved due to the proper choice of the surface impedance, which restores almost uniform amplitude all around the cloak.
Summary
In conclusion, we have proposed an original route towards designing thermal cloaks based on the scattering cancellation technique. This technique is inspired by the plasmonic cloaking, which makes use of shells with induced negative polarization to suppress scattered electromagnetic fields. And contrary to invisibility cloaks based on transformation optics, SCT offers simple cloaking designs (without the need of anisotropy and inhomogeneity of the physical parameters).
One may envision that using this design may further make the thermal cloaking closer to its practical and feasible realization. We believe that such a structured cloak could be manufactured within current technology, having in mind some potential applications in invisibility, sensing and thermography. The range of industrial applications is vast and our proof of concept should foster research efforts in this emerging area of thermal cloaks and metamaterials.
Methods
Analytical methods based on scattering Mie theory of spherical thermal scatterers are used to obtain the results presented in Figs. 2, 3, 4(a), 4(b) and 5. In the quasistatic limit, where the size of the object is much smaller than the wavelength and only the lowest-order Mie coefficients are kept, analytical formulas are obtained [Eqs. (20) and(21)]. Those give results similar to the ones obtained from full Mie series solutions [Fig. 3(a)]. The results given in Figs. 4(c) and 4(d) are obtained using COMSOL Multiphysics software, which solves Eq. (2) with proper boundary conditions using a finite element scheme.
Change history
21 January 2016
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has not been fixed in the paper.
21 January 2016
We theoretically and numerically analyze thermal invisibility based on the concept of scattering cancellation and mantle cloaking. We show that a small object can be made completely invisible to heat diffusion waves, by tailoring the heat conductivity of the spherical shell enclosing the object. This means that the thermal scattering from the object is suppressed, and the heat flow outside the object and the cloak made of these spherical shells behaves as if the object is not present. Thermal invisibility may open new vistas in hiding hot spots in infrared thermography, military furtivity, and electronics heating reduction.
References
Leonhardt, U. Optical conformal mapping. Science 312, 1777–1780 (2006).
Pendry, J. B., Schurig, D. and Smith, D. R. Controlling electromagnetic fields. science 312, 1780–1782 (2006).
Schurig, D. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006).
Guenneau, S. et al. The colours of cloaks. J. Opt. 13, 024014 (2011).
Sihvola, A. Metamaterials in electromagnetics. Metamaterials 1, 2–11 (2007).
Alù, A. and Engheta, N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 72, 016623 (2005).
Alù, A. and Engheta, N. Plasmonic materials in transparency and cloaking problems: mechanism, robustness and physical insights. Opt. Express 15, 3318–3332 (2007).
Mühlig, S., Farhat, M., Rockstuhl, C. and Lederer, F. Cloaking dielectric spherical objects by a shell of metallic nanoparticles. Phys. Rev. B 83, 195116 (2011).
Mühlig, S. et al. A self-assembled three-dimensional cloak in the visible. Sci. Rep. 3, 2328 (2013).
Rainwater, D. et al. Experimental verification of three-dimensional plasmonic cloaking in free-space. New J. Phys. 14, 013054 (2012).
Alù, A. and Engheta, N. Cloaking a sensor. Phys. Rev. Lett. 102, 233901 (2009).
Alù, A. and Engheta, N. Cloaked near-field scanning optical microscope tip for noninvasive near-field imaging. Phys. Rev. Lett. 105, 263906 (2010).
Munk, B. A. Frequency Selective Surfaces: Theory and Design. (John Wiley & Sons., 2005).
Alù, A. Mantle cloak: Invisibility induced by a surface. Phys. Rev. B 80, 245115 (2009).
Chen, P. -Y., Farhat, M., Guenneau, S., Enoch, S. and Alù, A. Acoustic scattering cancellation via ultrathin pseudo-surface. Appl. Phys. Lett. 99, 191913 (2011).
Farhat, M., Chen, P. -Y., Guenneau, S., Enoch, S. and Alù, A. Frequency-selective surface acoustic invisibility for three-dimensional immersed objects. Phys. Rev. B 86, 174303 (2012).
Cai, W., Chettiar, U. K., Kildishev, A. V. and Shalaev, V. M. Optical cloaking with metamaterials. Nature photon. 1, 224–227 (2007).
Farhat, M., Guenneau, S., Movchan, A. and Enoch, S. Achieving invisibility over a finite range of frequencies. Opt. Express 16, 5656–5661 (2008).
Farhat, M. et al. A homogenization route towards square cylindrical acoustic cloaks. New J. Phys. 10, 115030 (2008).
Vasquez, F. G., Milton, G. W. and Onofrei, D. Active exterior cloaking for the 2d laplace and helmholtz equations. Phy. Rev. Lett. 103, 073901 (2009).
Nicorovici, N., Milton, G. W., McPhedran, R. C. and Botten, L. C. Quasistatic cloaking of two-dimensional polarizable discrete systems by anomalous resonance. Opt. Express 15, 6314–6323 (2007).
Smolyaninov, I. I., Smolyaninova, V. N., Kildishev, A. V. and Shalaev, V. M. Anisotropic metamaterials emulated by tapered waveguides: application to optical cloaking. Phy. Rev. Lett. 102, 213901 (2009).
Torrent, D. and Sánchez-Dehesa, J. Acoustic cloaking in two dimensions: a feasible approach. New J. Phys. 10, 063015 (2008).
Cummer, S. A. et al. Scattering theory derivation of a 3d acoustic cloaking shell. Phy. Rev. Lett. 100, 024301 (2008).
Norris, A. N. Acoustic cloaking theory. Proc. R. Soc. A-Math. Phys. Eng. Sci. 464, 2411–2434 (2008).
Farhat, M., Enoch, S., Guenneau, S. and Movchan, A. Broadband cylindrical acoustic cloak for linear surface waves in a fluid. Phy. Rev. Lett. 101, 134501 (2008).
Farhat, M., Guenneau, S. and Enoch, S. Ultrabroadband elastic cloaking in thin plates. Phy. Rev. Lett. 103, 024301 (2009).
Brun, M., Guenneau, S. and Movchan, A. B. Achieving control of in-plane elastic waves. Appl. Phy. Lett. 94, 061903 (2009).
Brûlé, S., Javelaud, E., Enoch, S. and Guenneau, S. Experiments on seismic metamaterials: Molding surface waves. Phys. Rev. Lett. 112, 133901 (2014).
Zhang, S., Genov, D. A., Sun, C. and Zhang, X. Cloaking of matter waves. Phy. Rev. Lett. 100, 123002 (2008).
Greenleaf, A., Kurylev, Y., Lassas, M. and Uhlmann, G. Approximate quantum cloaking and almost-trapped states. Phy. Rev. Lett. 101, 220404 (2008).
Schittny, R., Kadic, M., Bueckmann, T. and Wegener, M. Invisibility cloaking in a diffusive light scattering medium. Science 345, 427–429 (2014).
Schittny, R. et al. Transient behavior of invisibility cloaks for diffusive light propagation. Optica 2, 84–87 (2015).
Guenneau, S., Amra, C. and Veynante, D. Transformation thermodynamics: cloaking and concentrating heat flux. Opt. Express 20, 8207–8218 (2012).
Alù, A. Thermal cloaks get hot. Physics 7, 12, Feb (2014).
Maldovan, M. Sound and heat revolutions in phononics. Nature 503, 209–217 (2013).
Leonhardt, U. Applied physics: Cloaking of heat. Nature 498, 440–441 (2013).
Chen, T., Weng, C. -N. and Chen, J. -S. Cloak for curvilinearly anisotropic media in conduction. Appl. Phys. Lett. 93, 114103 (2008).
Guenneau, S. and Amra, C. Anisotropic conductivity rotates heat fluxes in transient regimes. Opt. Express 21, 6578–6583 (2013).
Moccia, M., Castaldi, G., Savo, S., Sato, Y. and Galdi, V. Independent manipulation of heat and electrical current via bifunctional metamaterials. Phys. Rev. X 4, 021025 (2014).
Narayana, S. and Sato, Y. Heat flux manipulation with engineered thermal materials. Phys. Rev. Lett. 108, 214303 (2012).
Schittny, R., Kadic, M., Guenneau, S. and Wegener, M. Experiments on transformation thermodynamics: molding the flow of heat. Phys. Rev. Lett. 110, 195901 (2013).
Han, T. et al. Experimental demonstration of a bilayer thermal cloak. Phys. Rev. Lett. 112, 054302 (2014).
Xu, H., Shi, X., Gao, F., Sun, H. and Zhang, B. Ultrathin three-dimensional thermal cloak. Phys. Rev. Lett. 112, 054301 (2014).
Shendeleva, M. L. Thermal wave reflection and refraction at a plane interface: Two-dimensional geometry. Phys. Rev. B 65, 134209 (2002).
Reif, F. Fundamentals of statistical and thermal physics. (Waveland Press., 2009).
Argyropoulos, C., Chen, P. -Y., Monticone, F., D'Aguanno, G. and Alù, A. Nonlinear plasmonic cloaks to realize giant all-optical scattering switching. Phys. Rev. Lett. 108, 263905 (2012).
Acknowledgements
This work is partially funded by King Abdulaziz City for Science and Technology (KACST) TIC (Technology Innovation Center) for Solid-state Lighting at KAUST. P.-Y.C. would like to acknowledge fruitful discussion with David Piech. S.G. would like to acknowledge a funding of the European Research Council through ERC grant ANAMORPHISM.
Author information
Authors and Affiliations
Contributions
M.F. and P.-Y.C conceived the idea of this study. M.F. performed numerical simulations and wrote the manuscript. P.Y.C., H.B., C.A., S.G. and A.A. contributed to the analysis of the results and reviewed the manuscript. S.G. and A.A. supervised the project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Farhat, M., Chen, PY., Bagci, H. et al. Thermal invisibility based on scattering cancellation and mantle cloaking. Sci Rep 5, 9876 (2015). https://doi.org/10.1038/srep09876
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep09876
This article is cited by
-
Exploring localized ENZ resonances and their role in superscattering, wideband invisibility, and tunable scattering
Scientific Reports (2024)
-
Diffusion metamaterials
Nature Reviews Physics (2023)
-
Conformal and polarization adjustable cloaking metasurface utilizing graphene with low radar cross section for terahertz applications
Optical and Quantum Electronics (2022)
-
Active Cloaking of a Non-Uniform Scatterer
Scientific Reports (2020)
-
Review: recent progress in metal-less metasurfaces and metamaterials
Applied Physics A (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
