Abstract
The dynamics of neural networks is often characterized by collective behavior and quasi-synchronous events, where a large fraction of neurons fire in short time intervals, separated by uncorrelated firing activity. These global temporal signals are crucial for brain functioning. They strongly depend on the topology of the network and on the fluctuations of the connectivity. We propose a heterogeneous mean–field approach to neural dynamics on random networks, that explicitly preserves the disorder in the topology at growing network sizes and leads to a set of self-consistent equations. Within this approach, we provide an effective description of microscopic and large scale temporal signals in a leaky integrate-and-fire model with short term plasticity, where quasi-synchronous events arise. Our equations provide a clear analytical picture of the dynamics, evidencing the contributions of both periodic (locked) and aperiodic (unlocked) neurons to the measurable average signal. In particular, we formulate and solve a global inverse problem of reconstructing the in-degree distribution from the knowledge of the average activity field. Our method is very general and applies to a large class of dynamical models on dense random networks.
Similar content being viewed by others
Introduction
Topology has a strong influence on phases of dynamical models defined on a network. Recently, this topic has attracted the interest of both theoreticians and applied scientists in many different fields, ranging from physics, to biology and social sciences1,2,3,4,5,6. Research has focused in two main directions. The direct problem aims at predicting the dynamical properties of a network from its topological parameters7. The inverse problem is addressed to the reconstruction of the network topological features from dynamic time series8,9,10,11. The latter approach is particularly interesting when the direct investigation of the network is impossible or very hard to be performed.
Neural networks are typical examples of such a situation. In local approaches to inverse problems8,9,10,11, the network is reconstructed through the knowledge of long time series of single neuron dynamics, a methods that applies efficiently to small systems only. Actually, the signals emerging during neural time evolution are often records of the average synaptic activity from large regions of the cerebral cortex – a kind of observable likely much easier to be measured than signals coming from single neuron activities12,13. Inferring the topological properties of the network from global signals is still an open and central problem in neurophysiology. In this paper we investigate the possibility of formulating and solving such a global version of the inverse problem, reconstructing the network topology that has generated a given global (i.e. average) synaptic-activity field. The solution of such an inverse problem could also imply the possibility of engineering a network able to produce a specific average signal.
As an example of neural network dynamics, we focus on a system of leaky integrate–and–fire (LIF) excitatory neurons, interacting via a synaptic current regulated by the short–term plasticity mechanism14,15. This model is able to reproduce synchronization patterns observed in in vitro experiments16,17,18. As a model for the underlying topology we consider randomly uncorrelated diluted networks made of N nodes. In general N is considered quite a large number, as is the number of connections between pairs of neurons. This suggests that the right framework for understanding large–population neural networks should be a mean–field approach, where the thermodynamic limit, N → ∞, is expected to provide the basic ingredients for an analytic treatment. On the other hand, the way such a thermodynamic limit is performed may wipe out any relation with the topological features that are responsible, for finite N, of relevant dynamical properties.
In Erdös–Renyi directed networks, where each neuron is randomly and uniformly connected to a finite fraction of the other neurons (massive or dense connectivity), the fluctuations of the degree determine a rich dynamical behavior, characterized in particular by quasi-synchronous events (QSE). This means that a large fraction of neurons fire in a short time interval of a few milliseconds (ms), separated by uncorrelated firing activity lasting over some tens of ms. Such an interesting behavior is lost in the thermodynamic limit, as the fluctuations of the connectivity vanish and the “mean-field-like” dynamics reduces to a state of fully synchronized neurons (e.g., see19). In order to maintain the QSE phenomenology in the large N limit, we can rather consider the sequence of random graphs that keep the same specific in-degree distribution  , where
, where  is the fraction of incoming neurons connected to neuron i for any finite N, similarly to the configuration models20. This way of performing the thermodynamic limit preserves the dynamical regime of QSE and the difference between synchronous and non-synchronous neurons according to their specific in-degree
is the fraction of incoming neurons connected to neuron i for any finite N, similarly to the configuration models20. This way of performing the thermodynamic limit preserves the dynamical regime of QSE and the difference between synchronous and non-synchronous neurons according to their specific in-degree  . By introducing explicitly this N → ∞ limit in the differential equations of the model, we obtain a heterogeneous mean–field (HMF) description, similar to the one recently introduced in the context of epidemiological spreading on networks2,3,21,22. Such mean–field like or HMF equations can be studied analytically by introducing the return maps of the firing times. In particular, we find that a sufficiently narrow distributions of
. By introducing explicitly this N → ∞ limit in the differential equations of the model, we obtain a heterogeneous mean–field (HMF) description, similar to the one recently introduced in the context of epidemiological spreading on networks2,3,21,22. Such mean–field like or HMF equations can be studied analytically by introducing the return maps of the firing times. In particular, we find that a sufficiently narrow distributions of  is necessary to observe the quasi–synchronous dynamical phase, which vanishes on the contrary for broad distributions of
is necessary to observe the quasi–synchronous dynamical phase, which vanishes on the contrary for broad distributions of  .
.
More importantly, these HMF equations allow us to design a “global” inverse–problem approach, formulated in terms of an integral Fredholm equation of the first kind for the unknown  23. Starting from the dynamical signal of the average synaptic-activity field, the solution of this equation provides with good accuracy the
23. Starting from the dynamical signal of the average synaptic-activity field, the solution of this equation provides with good accuracy the  of the network that produced it. We test this method for very different uncorrelated network topologies, where
of the network that produced it. We test this method for very different uncorrelated network topologies, where  ranges from a Gaussian with one or several peaks, to power law distributions, showing its effectiveness even for finite size networks.
ranges from a Gaussian with one or several peaks, to power law distributions, showing its effectiveness even for finite size networks.
The overall procedure applies to a wide class of network dynamics of the type

where the vector wi represents the state of the site i, F(wi, 0) is the single site dynamics, g is the coupling strength, G(wj) is a suitable coupling function and  is the adjacency matrix of the directed uncorrelated dense network, whose entries are equal to 1 if neuron j fires to neuron i and 0 otherwise.
is the adjacency matrix of the directed uncorrelated dense network, whose entries are equal to 1 if neuron j fires to neuron i and 0 otherwise.
Results
The LIF model with short term plasticity
Let us introduce LIF models, that describe a network of N neurons interacting via a synaptic current, regulated by short–term–plasticity with equivalent synapses16. In this case the dynamical variable of the neuron i is wi = (vi, xi, yi, zi) where vi is the rescaled membrane potential and xi, yi and zi represent the fractions of synaptic transmitters in the recovered, active and inactive state, respectively (xi + yi + zi = 1). Eq. (1) then specializes to:



The function Sj(t) is the spike–train produced by neuron j,  , where tj(m) is the time when neuron j fires its m-th spike. Notice that we assume the spike to be a δ function of time. Whenever the potential vi(t) crosses the threshold value vth = 1, it is reset to vr = 0 and a spike is sent towards its efferent neurons. The mechanism of short–term plasticity, that mediates the transmission of the field Sj(t), was introduced in14,15 to account for the activation of neurotransmitters in neural dynamics mediated by synaptic connections. In particular, when neuron i emits a spike, it releases a fraction of neurotransmitters uxi(t) (see the second term in the r.h.s. of Eq. (3)) and the fraction of active resources yi(t) is increased. Between consecutive spikes of neuron i, the use of active resources determines the exponential decrease of yi(t), on a time scale τin, thus yielding the increment of the fraction of inactive resources zi(t) (see the first term on the r.h.s. of Eq. (4)). Simultaneously, while zi(t) decreases (see the second term on the r.h.s. of Eq. (4)), the fraction of available resources is recovered over a time scale τr: in fact, from Eq.s (3) and (4) one readily obtains
, where tj(m) is the time when neuron j fires its m-th spike. Notice that we assume the spike to be a δ function of time. Whenever the potential vi(t) crosses the threshold value vth = 1, it is reset to vr = 0 and a spike is sent towards its efferent neurons. The mechanism of short–term plasticity, that mediates the transmission of the field Sj(t), was introduced in14,15 to account for the activation of neurotransmitters in neural dynamics mediated by synaptic connections. In particular, when neuron i emits a spike, it releases a fraction of neurotransmitters uxi(t) (see the second term in the r.h.s. of Eq. (3)) and the fraction of active resources yi(t) is increased. Between consecutive spikes of neuron i, the use of active resources determines the exponential decrease of yi(t), on a time scale τin, thus yielding the increment of the fraction of inactive resources zi(t) (see the first term on the r.h.s. of Eq. (4)). Simultaneously, while zi(t) decreases (see the second term on the r.h.s. of Eq. (4)), the fraction of available resources is recovered over a time scale τr: in fact, from Eq.s (3) and (4) one readily obtains  . We assume that all parameters appearing in the above equations are independent of the neuron indices and that each neuron is connected to a macroscopic number,
. We assume that all parameters appearing in the above equations are independent of the neuron indices and that each neuron is connected to a macroscopic number,  , of pre-synaptic neurons: this is the reason why the interaction term is divided by the factor N. In all data hereafter reported we have used phenomenological values of the rescaled parameters: τin = 0.2, τr = 133τin, a = 1.3, g = 30 and u = 0.519.
, of pre-synaptic neurons: this is the reason why the interaction term is divided by the factor N. In all data hereafter reported we have used phenomenological values of the rescaled parameters: τin = 0.2, τr = 133τin, a = 1.3, g = 30 and u = 0.519.
The choice of the value of the external current, a, is quite important for selecting the dynamical regime one is interested to reproduce. In fact, for a > vth = 1, neurons are in a firing regime, that typically gives rise to collective oscillations19,24,25,27. These have been observed experimentally in mammalian brains, where such a coherent rythmic behavior involves different groups of neurons26. On the other hand, it is also well known that in many cases neurons operate in the presence of a subthreshold external current18. In this paper, we aim to present a method that works irrespectively of the choice of a. For the sake of simplicity, we have decided to describe it for a = 1.3, i.e. in a strong firing regime.
Numerical simulations can be performed effectively by transforming the set of differential equations (2)–(4) into an event–driven map19,28,29. On Erdös–Renyi random graphs, where each link is accepted with probability p, so that the average in-degree 〈k〉 = pN, the dynamics has been analyzed in detail19. Neurons separate spontaneously into two different families: the locked and the unlocked ones. The locked neurons determine quasi-synchronous events (QSE) and exhibit a periodic dynamics. The unlocked ones participate in the uncorrelated firing activity and exhibit a sort of irregular evolution. Neurons belong to one of the two families according to their in-degree ki. In this topology, the thermodynamic limit can be simply worked out. Unfortunately, this misses all the interesting features emerging from the model at finite N. Actually, for any finite value of N, the in–degree distribution P(k) is centered around 〈k〉, with a standard deviation  . The effect of disorder is quantified by the ratio σk/〈k〉, that vanishes for N → ∞. Hence the thermodynamic limit reproduces the naive mean–field like dynamics of a fully coupled network, with rescaled coupling g → pg, that is known to eventually converge to a periodic fully synchronous state19.
. The effect of disorder is quantified by the ratio σk/〈k〉, that vanishes for N → ∞. Hence the thermodynamic limit reproduces the naive mean–field like dynamics of a fully coupled network, with rescaled coupling g → pg, that is known to eventually converge to a periodic fully synchronous state19.
The LIF model on random graphs with fixed in–degree distribution
At variance with the network construction discussed in previous sections, uncorrelated random graphs can be defined by different protocols, that keep track of the in-degree inhomogeneity in the thermodynamic limit. In our construction, we fix the normalized in–degree probability distribution  , so that σk/〈k〉 is kept constant for any N20. Accordingly,
, so that σk/〈k〉 is kept constant for any N20. Accordingly,  is a normalized distribution defined in the interval
is a normalized distribution defined in the interval  (while the number of inputs k ∈ (0, N]). In particular, if
(while the number of inputs k ∈ (0, N]). In particular, if  is a truncated Gaussian distribution, the dynamics reproduces the scenario observed in19 for an Erdös–Renyi random graph. In fact, also in this case neurons are dynamically distinguished into two families, depending on their in–degree. Precisely, neurons with
is a truncated Gaussian distribution, the dynamics reproduces the scenario observed in19 for an Erdös–Renyi random graph. In fact, also in this case neurons are dynamically distinguished into two families, depending on their in–degree. Precisely, neurons with  in between two critical values,
in between two critical values,  and
and  , are locked and determine the QSE: they fire with almost the same period, but exhibit different (
, are locked and determine the QSE: they fire with almost the same period, but exhibit different ( -dependent) phases. All the other neurons are unlocked and fire in between QSE displaying an aperiodic behavior. Notice that the range
-dependent) phases. All the other neurons are unlocked and fire in between QSE displaying an aperiodic behavior. Notice that the range  corresponds to the left tail of the truncated Gaussian distribution; accordingly, the large majority of unlocked neurons is found in the range
corresponds to the left tail of the truncated Gaussian distribution; accordingly, the large majority of unlocked neurons is found in the range  (see Fig. 1). In order to characterize the dynamics at increasing N, we consider for each neuron its inter-spike-interval (ISI), i.e. the lapse of time in between consecutive firing events. In Fig. 2 we show the time-average of ISI vs
(see Fig. 1). In order to characterize the dynamics at increasing N, we consider for each neuron its inter-spike-interval (ISI), i.e. the lapse of time in between consecutive firing events. In Fig. 2 we show the time-average of ISI vs  , or
, or  . One can clearly observe the plateau of locked neurons and the crossover to unlocked neurons at the critical values
. One can clearly observe the plateau of locked neurons and the crossover to unlocked neurons at the critical values  and
and  .
.
Raster plot representation of the dynamics of a network of N = 500 neurons with a Gaussian in-degree distribution 
 .
.
Black dots signal single firing events of neurons at time t. Neurons are naturally ordered along the vertical axis according to the values of their in-degree. The global field Y (t) (red line) is superposed to the raster plot for comparison (its actual values are multiplied by the factor 103, to make it visible on the vertical scale).
Time average of inter-spike intervals  vs
vs  from a Gaussian distribution with
from a Gaussian distribution with  and
and  and for three networks with N = 500 (blue triangles), N = 5000 (red diamonds), N = 20000 (green squares).
and for three networks with N = 500 (blue triangles), N = 5000 (red diamonds), N = 20000 (green squares).
For each size, the average is taken over 8 different realizations of the random network. We have also performed a suitable binning over the values of  , thus yielding the numerical estimates of the critical values
, thus yielding the numerical estimates of the critical values  and
and  . In the inset we show a zoom of the crossover region close to
. In the inset we show a zoom of the crossover region close to  . Black dots are the result of simulations of the mean field dynamics (see Eq.s (6)–(8)) with M = 307.
. Black dots are the result of simulations of the mean field dynamics (see Eq.s (6)–(8)) with M = 307.
Remarkably, networks of different sizes (N = 500, 5000 and 20000) feature the same  for locked neurons and almost the same values of
for locked neurons and almost the same values of  and
and  . There is not a sharp transition from locked to unlocked neurons, because for finite N the behavior of each neuron depends not only on its
. There is not a sharp transition from locked to unlocked neurons, because for finite N the behavior of each neuron depends not only on its  , but also on neighbor neurons sending their inputs. Nevertheless, in the inset, the crossover appears to be sharper and sharper for increasing N, as expected for true critical points. Furthermore, the fluctuations of
, but also on neighbor neurons sending their inputs. Nevertheless, in the inset, the crossover appears to be sharper and sharper for increasing N, as expected for true critical points. Furthermore, the fluctuations of  over different realizations, by
over different realizations, by  , of three networks of different size exhibit a peak around
, of three networks of different size exhibit a peak around  and
and  , while they decrease with N as ~ N−1/2 (data not shown). Thus, the qualitative and quantitative features of the QSE at finite sizes are expected to persist in the thermodynamic limit, where fluctuations vanish and the dynamics of each neuron depends only on its in–degree.
, while they decrease with N as ~ N−1/2 (data not shown). Thus, the qualitative and quantitative features of the QSE at finite sizes are expected to persist in the thermodynamic limit, where fluctuations vanish and the dynamics of each neuron depends only on its in–degree.
Heterogeneous mean field equations
We can now construct the Heterogeneous Mean–Field (HMF) equations for our model by combining this thermodynamic limit procedure with a consistency relation in Eqs. (2)–(4). The input field received by neuron i is  , where I(i) is the set of ki neurons transmitting to neuron i. For very large values of N the average field generated by presynaptic neurons of neuron i, i.e.
, where I(i) is the set of ki neurons transmitting to neuron i. For very large values of N the average field generated by presynaptic neurons of neuron i, i.e.  , can be approximated with
, can be approximated with  , where the second sum runs over all neurons in the network (mean–field hypothesis). Accordingly, we have
, where the second sum runs over all neurons in the network (mean–field hypothesis). Accordingly, we have  : as a consequence in the thermodynamic limit the dynamics of each neuron depends only on its specific in–degree. In this limit,
: as a consequence in the thermodynamic limit the dynamics of each neuron depends only on its specific in–degree. In this limit,  becomes a continuous variable independent of the label i, taking values in the interval (0,1]. Therefore, all neurons with the same in–degree
becomes a continuous variable independent of the label i, taking values in the interval (0,1]. Therefore, all neurons with the same in–degree  follow the same dynamical equations and we can write the dynamical equations for the class of neurons with in–degree
follow the same dynamical equations and we can write the dynamical equations for the class of neurons with in–degree  . Finally, we can replace Yi with
. Finally, we can replace Yi with  , where
, where

The HMF equations, then, read



where  ,
,  and
and  are the membrane potential, fraction of active and inactive resources of the class of neurons with in–degree
are the membrane potential, fraction of active and inactive resources of the class of neurons with in–degree  , respectively. Despite this set of equations cannot be solved explicitly, they provide a great numerical advantage with respect to direct simulations of large systems. Actually, the basic features of the dynamics of such systems can be effectively reproduced (modulo finite–size corrections) by exploiting a suitable sampling of
, respectively. Despite this set of equations cannot be solved explicitly, they provide a great numerical advantage with respect to direct simulations of large systems. Actually, the basic features of the dynamics of such systems can be effectively reproduced (modulo finite–size corrections) by exploiting a suitable sampling of  . For instance, one can sample the continuous variable
. For instance, one can sample the continuous variable  into M discrete values
into M discrete values  in such a way that
in such a way that  is kept fixed (importance sampling). Simulations of Equations (5)–(8) show that the global field field Y (t) is periodic and the neurons split into locked and unlocked. Locked neurons feature a firing time delay with respect the peak of Y (t) and this phase shift depends on the in–degree
is kept fixed (importance sampling). Simulations of Equations (5)–(8) show that the global field field Y (t) is periodic and the neurons split into locked and unlocked. Locked neurons feature a firing time delay with respect the peak of Y (t) and this phase shift depends on the in–degree  . As to unlocked neurons, that typically have an in-degree
. As to unlocked neurons, that typically have an in-degree  , they follow a complex dynamics with irregular firing times. In Fig. 2 (black dots) we compare
, they follow a complex dynamics with irregular firing times. In Fig. 2 (black dots) we compare  , obtained from the HMF equations for M = 307, with the same quantity computed by direct simulations of networks up to size N = 2 × 104. The agreement is remarkable evidencing the numerical effectiveness of the method.
, obtained from the HMF equations for M = 307, with the same quantity computed by direct simulations of networks up to size N = 2 × 104. The agreement is remarkable evidencing the numerical effectiveness of the method.
The direct problem: stability analysis and the synchronization transition
In the HMF equations, once the global field Y (t) is known, the dynamics of each class of neurons with in-degree  can be determined by a straightforward integration and we can perform the stability analysis that Tsodyks et al. applied to a similar model30. As an example, we have considered the system studied in Fig. 2. The global field Y (t) of the HMF dynamics has been obtained using the importance sampling for the distribution
can be determined by a straightforward integration and we can perform the stability analysis that Tsodyks et al. applied to a similar model30. As an example, we have considered the system studied in Fig. 2. The global field Y (t) of the HMF dynamics has been obtained using the importance sampling for the distribution  . We have fitted Y (t) with an analytic function of time Yf(t), continuous and periodic in time, with period T. Accordingly, Eq. (6) can be approximated by
. We have fitted Y (t) with an analytic function of time Yf(t), continuous and periodic in time, with period T. Accordingly, Eq. (6) can be approximated by

Notice that, by construction, the field Yf(t) features peaks at times t = nT, where n is an integer. In this way we can represent Eq. (9) as a discrete single neuron map. In practice, we integrate Eq.(9) and determine the sequence of the (absolute value of the) firing time–delay,  , of neurons with in–degree
, of neurons with in–degree  with respect to the reference time nT. The return map
with respect to the reference time nT. The return map  of this quantity reads
of this quantity reads

In Fig. 3 we plot the return map of the rescaled firing time–delay  for different values of
for different values of  . We observe that in-degrees
. We observe that in-degrees  corresponding to locked neurons (e.g., the brown curve) have two fixed points
corresponding to locked neurons (e.g., the brown curve) have two fixed points  and
and  , i.e. two points of intersection of the curve with the diagonal. The first one is stable (the derivative of the map
, i.e. two points of intersection of the curve with the diagonal. The first one is stable (the derivative of the map  is <1) and the second unstable (the derivative of the map
is <1) and the second unstable (the derivative of the map  is >1). Clearly, the dynamics converges to the stable fixed point displaying a periodic behavior. In particular, the firing times of neurons
is >1). Clearly, the dynamics converges to the stable fixed point displaying a periodic behavior. In particular, the firing times of neurons  are phase shifted of a quantity
are phase shifted of a quantity  with respect the peaks of the fitted global field. The orange and violet curves correspond to the dynamics at the critical in-degrees
with respect the peaks of the fitted global field. The orange and violet curves correspond to the dynamics at the critical in-degrees  and
and  where the fixed points disappear (see Fig. (2)). The presence of such fixed points influences also the behavior of the unlocked component (e.g., the red and light blue curves). In particular, the nearer
where the fixed points disappear (see Fig. (2)). The presence of such fixed points influences also the behavior of the unlocked component (e.g., the red and light blue curves). In particular, the nearer  is to
is to  or to
or to  , the closer is the return map to the bisector of the square, giving rise to a dynamics spending longer and longer times in an almost periodic firing. Afterwards, unlocked neurons depart from this almost periodic regime, thus following an aperiodic behavior. As a byproduct, this dynamical analysis allows to estimate the values of the critical in–degrees. For the system of Fig. 1,
, the closer is the return map to the bisector of the square, giving rise to a dynamics spending longer and longer times in an almost periodic firing. Afterwards, unlocked neurons depart from this almost periodic regime, thus following an aperiodic behavior. As a byproduct, this dynamical analysis allows to estimate the values of the critical in–degrees. For the system of Fig. 1,  and
and  , in very good agreement with the numerical simulations (see Fig. 2).
, in very good agreement with the numerical simulations (see Fig. 2).
Still in the perspective of the direct problem, the HMF equations provide further insight on how the network topology influences the dynamical behavior. We have found that, in general, the fraction of locked neurons increases as  becomes sharper and sharper, while synchronization is eventually lost for broader distributions. In Fig. 4 we report the fraction of locked neurons,
becomes sharper and sharper, while synchronization is eventually lost for broader distributions. In Fig. 4 we report the fraction of locked neurons,  , as a function of the standard deviation deviation
, as a function of the standard deviation deviation  , for different kinds of
, for different kinds of  (single or double–peaked Gaussian, power law) in the HMF equations. For the truncated power law distribution, we set
(single or double–peaked Gaussian, power law) in the HMF equations. For the truncated power law distribution, we set  . In all cases, there is a critical value of
. In all cases, there is a critical value of  above which fl vanishes, i.e. QSE disappear. The generality of this scenario points out the importance of the relation between
above which fl vanishes, i.e. QSE disappear. The generality of this scenario points out the importance of the relation between  and the average synaptic field Y(t).
and the average synaptic field Y(t).
The fraction of locked neurons, fl, as a function of the standard deviation  of the distributions: truncated Gaussian with
of the distributions: truncated Gaussian with  (black dots); truncated superposition of two Gaussians (both with standard deviation 0.03), one centered at
(black dots); truncated superposition of two Gaussians (both with standard deviation 0.03), one centered at  and the other one at a varying value
and the other one at a varying value  , that determines the overall standard deviation
, that determines the overall standard deviation  (blue squares); truncated power law distribution with
(blue squares); truncated power law distribution with  (red diamonds).
(red diamonds).
In the last case the value of the standard deviation is changed by varying the exponent α, while the average  changes accordingly. Lines have been drawn to guide the eyes.
changes accordingly. Lines have been drawn to guide the eyes.
The inverse problem
The HMF approach allows to implement the inverse problem and leads to the reconstruction of the distribution  from the knowledge of Y(t). If the global synaptic activity field Y(t) is known, each class of neurons of in-degree
from the knowledge of Y(t). If the global synaptic activity field Y(t) is known, each class of neurons of in-degree  evolves according to the equations:
evolves according to the equations:



Notice that the variable v(t), y(t), z(t) can take values that differ from the variables generating the field Y(t), i.e. v(t), y(t), z(t), as they start from different initial conditions. However, the self consistent relation for the global field Y(t) implies:

If Y(t) and  are known, this is a Fredholm equation of the first kind in
are known, this is a Fredholm equation of the first kind in  23. In the general case of Eq. (1), calling E(t) the global measured external field, the evolution equations corresponding to Eq.s (11)–(13) read
23. In the general case of Eq. (1), calling E(t) the global measured external field, the evolution equations corresponding to Eq.s (11)–(13) read

and the Fredholm equation for the inverse problem is

In the case of our LIF model, as soon as a locked component exists, Eq. (14) can be solved by a functional Montecarlo minimization procedure applied to a sampled  . At variance with the direct problem,
. At variance with the direct problem,  is the unknown function and, accordingly, we have to adopt a uniform sampling of the support of
is the unknown function and, accordingly, we have to adopt a uniform sampling of the support of  . A sufficiently fine sampling has to be used for a confident reconstruction of
. A sufficiently fine sampling has to be used for a confident reconstruction of  (See Methods section).
(See Methods section).
To check our inverse method, we choose a distribution  , evolve the system and extract the global synaptic field Y(t). We then verify if the procedure reconstructs correctly the original distribution
, evolve the system and extract the global synaptic field Y(t). We then verify if the procedure reconstructs correctly the original distribution  . In panels (a), (b) and (c) of Fig. 5 we show examples in which Y(t) has been obtained from the simulation of the HMF with different
. In panels (a), (b) and (c) of Fig. 5 we show examples in which Y(t) has been obtained from the simulation of the HMF with different  (Gaussian, double peak Gaussian and power law). We can see that the method determines confidently the original distribution
(Gaussian, double peak Gaussian and power law). We can see that the method determines confidently the original distribution  . Notice that the method fails as soon as the locked component disappears, as explained in the methods section. Remarkably, the method can recognize the discontinuity of the distribution in
. Notice that the method fails as soon as the locked component disappears, as explained in the methods section. Remarkably, the method can recognize the discontinuity of the distribution in  and the value of the exponent of the power law α = 4.9. Finally, in panel (d) of Fig. 5, we show the result of the inverse problem for the distribution
and the value of the exponent of the power law α = 4.9. Finally, in panel (d) of Fig. 5, we show the result of the inverse problem for the distribution  obtained from a global signal generated by a finite size realization with N = 500 and 〈k〉 = 350. The significant agreement indicates that the HMF and its inverse problem are able to infer the in–degree probability distribution
obtained from a global signal generated by a finite size realization with N = 500 and 〈k〉 = 350. The significant agreement indicates that the HMF and its inverse problem are able to infer the in–degree probability distribution  even for a realistic finite size network. This last result is particularly important, as it opens new perspectives for experimental data analysis, where the average neural activity is typically measured from finite size samples with finite but large connectivity.
even for a realistic finite size network. This last result is particularly important, as it opens new perspectives for experimental data analysis, where the average neural activity is typically measured from finite size samples with finite but large connectivity.
Inverse problem for  from the global field Y(t).
from the global field Y(t).
Panels (a), (b) and (c) show three distributions of the kind considered in Fig. (4) (black continuous curves) for the HMF equations and their reconstructions (circles) by the inverse method. The parameters of the three distributions are  ,
,  and α = 4.9. In panel (d) we show the reconstruction (crosses) of P
and α = 4.9. In panel (d) we show the reconstruction (crosses) of P (black continuous line) by the average field Y(t) generated by the dynamics of a finite size network with N = 500.
(black continuous line) by the average field Y(t) generated by the dynamics of a finite size network with N = 500.
Discussion
The direct and inverse problem for neural dynamics on random networks are both accessible through the HMF approach proposed in this paper. The mean-field equations provide a semi–analytic form for the return map of the firing times of neurons and they allow to evidence the effects of the in-degree distribution on the synchronization transition. This phenomenology is not limited to the LIF model analyzed here and it is observed in several neural models on random networks. We expect that the HMF equations could shed light on the nature of this interesting, but still not well understood, class of synchronization transitions24,25,31. The mean field nature of the approach does not represent a limitation, since the equations are expected to give a faithful description of the dynamics also in networks with finite but large average in-degree, corresponding to the experimental situation observed in many cortical regions32.
The inverse approach, although tested here only on numerical experiments, gives excellent results on the reconstruction of a wide class of in-degree distributions and it could open new perspectives on data analysis, allowing to reconstruct the main topological features of the neural network producing the QSE. The inversion appears to be stable with respect to noise, as clearly shown by the effectiveness of the procedure tested on a finite realization, where the temporal signals of the average synaptic activity is noisy. We also expect our inverse approach to be robust with respect to the addition of limited randomness in leaky currents and also with respect to a noise compatible with the signal detection from instruments. Finally, the method is very general and it can be applied to a wide class of dynamical models on networks, as those described in Eq. (1).
Further developments will allow to get closer to real experimental situations. We mention the most important, i.e. the introduction of inhibitory neurons and the extension of our approach by taking into account networks with degree correlations3, that are known to characterize real structures and sparse networks. The HMF equations appear to be sufficiently flexible and simple to allow for these extensions.
Methods
Montecarlo approach to the inverse problem
In this section we provide details of the algorithmic procedure adopted for solving the inverse problem, i.e. reconstructing the distribution  from Eq. (14). In the HMF formulation, the field Y(t) is generated by an infinite number of neurons and
from Eq. (14). In the HMF formulation, the field Y(t) is generated by an infinite number of neurons and  is a continuous variable in the interval (0, 1]. In practice, we can sample uniformly this unit interval by L disjoint subintervals of length 1/L, labelled by the integer i. This corresponds to an effective neural index i, that identifies the class of neurons with in-degree
is a continuous variable in the interval (0, 1]. In practice, we can sample uniformly this unit interval by L disjoint subintervals of length 1/L, labelled by the integer i. This corresponds to an effective neural index i, that identifies the class of neurons with in-degree  . In this way we obtain a discretized definition converging to Eq.(14) for L → ∞:
. In this way we obtain a discretized definition converging to Eq.(14) for L → ∞:

In order to improve the stability and the convergence of the algorithm by smoothing the fluctuations of the fields  , it is convenient to consider a coarse–graining of the sampling by approximating Y(t) as follows
, it is convenient to consider a coarse–graining of the sampling by approximating Y(t) as follows

where  is the average of L/L′ synaptic fields of connectivity
is the average of L/L′ synaptic fields of connectivity  . This is the discretized Fredholm equation that one can solve to obtain
. This is the discretized Fredholm equation that one can solve to obtain  from the knowledge of
from the knowledge of  and Y(t). For this aim we use a Monte Carlo (MC) minimization procedure, by introducing at each MC step, n, a trial solution,
and Y(t). For this aim we use a Monte Carlo (MC) minimization procedure, by introducing at each MC step, n, a trial solution,  , in the form of a normalized non-negative in-degree distribution. Then, we evaluate the field Yn(t) and the distance
, in the form of a normalized non-negative in-degree distribution. Then, we evaluate the field Yn(t) and the distance  defined as:
defined as:


The time interval [t1, t2] has to be taken large enough to obtain a reliable estimate of  . For instance, in the case shown in Fig. 1, where Y(t) exhibits an almost periodic evolution of period T ≈ 1 in the adimensional units of the model, we have used t2 − t1 = 10. The overall configuration of the synaptic fields, at iteration step n + 1, is obtained by choosing randomly two values
. For instance, in the case shown in Fig. 1, where Y(t) exhibits an almost periodic evolution of period T ≈ 1 in the adimensional units of the model, we have used t2 − t1 = 10. The overall configuration of the synaptic fields, at iteration step n + 1, is obtained by choosing randomly two values  and
and  and by defining a new trial solution
and by defining a new trial solution  , so that, provided both
, so that, provided both  and
and  are non-negative, we increase and decrease
are non-negative, we increase and decrease  of the same amount,
of the same amount,  , in
, in  and
and  respectively. A suitable choice is
respectively. A suitable choice is  . Then, we evaluate
. Then, we evaluate  : If
: If  the step is accepted i.e.
the step is accepted i.e.  , otherwise Pn+1 = Pn. This MC procedure amounts to the implementation of a zero temperature dynamics, where the cost function
, otherwise Pn+1 = Pn. This MC procedure amounts to the implementation of a zero temperature dynamics, where the cost function  can only decrease. In principle, the inverse problem in the form of Eq.(18) is solved, i.e.
can only decrease. In principle, the inverse problem in the form of Eq.(18) is solved, i.e.  , if
, if  . In practice, the approximations introduced by the coarse-graining procedure do not allow for a fast convergence to the exact solution, but
. In practice, the approximations introduced by the coarse-graining procedure do not allow for a fast convergence to the exact solution, but  can be considered a reliable reconstruction of the actual
can be considered a reliable reconstruction of the actual  already for
already for  . We have checked that the results of the MC procedure are quite stable with respect to different choices of the initial conditions
. We have checked that the results of the MC procedure are quite stable with respect to different choices of the initial conditions  , thus confirming the robustness of the method. We give in conclusion some comments on the very definition of the coarse-grained synaptic field
, thus confirming the robustness of the method. We give in conclusion some comments on the very definition of the coarse-grained synaptic field  . Since small differences in the values of
. Since small differences in the values of  reflect in small differences in the dynamics, for not too large intervals
reflect in small differences in the dynamics, for not too large intervals  the quantity
the quantity  can be considered as an average over different initial conditions. For locked neurons the convergence of the average procedure defining
can be considered as an average over different initial conditions. For locked neurons the convergence of the average procedure defining  is quite fast, since all the initial conditions tend to the stable fixed point, identified by the return map described in the previous subsection. On the other hand, the convergence of the same quantity for unlocked neurons should require an average over a huge number of initial conditions. For this reason, the broader is the distribution, i.e. the bigger is the unlocked component (see Fig. 4), the more computationally expensive is the solution of the inverse problem. This numerical drawback for broad distributions emerges in our tests of the inversion procedure described in Fig. 5. Moreover, such tests show that the procedure works insofar the QSE are not negligible, but it fails in the absence of the locking mechanism. In this case, indeed, the global field Y(t) is constant and also
is quite fast, since all the initial conditions tend to the stable fixed point, identified by the return map described in the previous subsection. On the other hand, the convergence of the same quantity for unlocked neurons should require an average over a huge number of initial conditions. For this reason, the broader is the distribution, i.e. the bigger is the unlocked component (see Fig. 4), the more computationally expensive is the solution of the inverse problem. This numerical drawback for broad distributions emerges in our tests of the inversion procedure described in Fig. 5. Moreover, such tests show that the procedure works insofar the QSE are not negligible, but it fails in the absence of the locking mechanism. In this case, indeed, the global field Y(t) is constant and also  become constant, when averaging over a sufficiently large number of samples. This situation makes Eq.(18) trivial and useless to evaluate
become constant, when averaging over a sufficiently large number of samples. This situation makes Eq.(18) trivial and useless to evaluate  . We want to observe that, while in general
. We want to observe that, while in general  , one can reasonably expect that
, one can reasonably expect that  is a very good approximation of
is a very good approximation of  . This remark points out the conceptual importance of the HMF formulation for the possibility of solving the inverse problem.
. This remark points out the conceptual importance of the HMF formulation for the possibility of solving the inverse problem.
References
Wang, X. F. Synchronization in small-world dynamical networks. Int. J. Bifurcation Chaos 12, 885 (2002).
Barrat, A., Barthelemy, M. & Vespignani, A. Dynamical Processes on Complex Networks. Cambridge University Press, Cambridge, UK (2008).
Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Critical phenomena in complex networks. Rev. Mod. Phys. 80, 1275 (2008).
Cohen, R. & Havlin, S. Complex Networks: Structure, Robustness and Function. Cambridge University Press, Cambridge, UK, (2010).
Arenas, A., Díaz-Guilera Kurths, J., Moreno, Y. & Zhou, C. Synchronization in complex networks. Phys. Rep. 469, 93 (2008).
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M. & Hwanga, D. U. Complex networks: Structure and dynamics. Phys. Rep. 424, 175 (2006).
Donetti, L., Hurtado, P. I. & Muñoz, M. A. Entangled networks, synchronization and optimal network topology. Phys. Rev. Lett. 95, 188701 (2005).
Shneidman, E., Berry, M. J., Segev, R. & Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 440, 1007 (2006).
Cocco, S., Leibler, S. & Monasson, R. Neuronal couplings between retinal ganglion cells inferred by efficient inverse statistical physics methods. Proc. Natl. Acad. Sci. USA 106, 14058 (2009).
Shandilya, S. G. & Timme, M. Inferring network topology from complex dynamics. New J. Phys. 13, 013004 (2011).
Zheng, H. L., Alava, M., Aurell, E., Hertz, J. & Roudi, Y. Maximum likelihood reconstruction for Ising models with asynchronous updates. Phys. Rev. Lett. 110, 210601 (2013).
Niedermeyer, E. & Lopes da Silva, F. H. Electroencephalography: Basic Principles, Clinical Applications and Related Fields. Lippincott Williams & Wilkins, (2005).
Huettel, S. A., Song, A. W. & McCarthy, G. Functional Magnetic Resonance Imaging. Sunderland, MA: Sinauer Associates, (2009).
Tsodyks, M. & Markram, H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc. Natl. Acad. Sci. USA 94, 719 (1997).
Tsodyks, M., Pawelzik, K. & Markram, H. Neural networks with dynamic synapses. Neural Comput. 10, 821 (1998).
Tsodyks, M., Uziel, A. & Markram, H. Synchrony Generation in Recurrent Networks with Frequency-Dependent Synapses. The Journal of Neuroscience 20, 1–5 (2000).
Volman, V., Baruchi, I., Persi, E. & Ben-Jacob, E. Generative modelling of regulated dynamical behavior in cultured neuronal networks. Physica A 335, 249 (2004).
di Volo, M. & Livi, R. The influence of noise on synchronous dynamics in a diluted neural network. J. of Chaos Solitons and Fractals 57, 54 (2013).
di Volo, M., Livi, R., Luccioli, S., Politi, A. & Torcini, A. Synchronous dynamics in the presence of short-term plasticity. Phys. Rev. E 87, 032801 (2013).
Chung, F. & Lu, L. Complex Graphs and Networks, CBMS Series in Mathematics, AMS (2004).
Pastor–Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200 (2001).
Vespignani, A. Modelling dynamical processes in complex socio-technical systems. Nature Physics 8, 39 (2012).
Kress, R. Linear Integral equations, Applied numerical sciences. 82, Springer-Verlag, New York, (1999).
Olmi, S., Livi, R., Politi, A. & Torcini, A. Collective oscillations in disordered neural networks. Phys. Rev. E 81, 046119 (2010).
Luccioli, S., Olmi, S., Politi, A. & Torcini, A. Collective dynamics in sparse networks. Phys. Rev. Lett. 109, 138103 (2012).
Buzsaki, G. Rhythms of the Brain. Oxford University Press, New York (2006).
Richardson, M., Brunel, N. & Hakim, V. From Subthreshold to Firing-Rate Resonance. J. Neurophysiol. 89, 2538 (2003).
Brette, R. Exact simulation of integrate–and–fire models with synaptic conductances. Neural Comput. 18, 2004 (2006).
Zillmer, R., Livi, R., Politi, A. & Torcini, A. Stability of the splay state in pulse-coupled networks. Phys. Rev. E 76, 046102 (2007).
Tsodyks, M., Mitkov, I. & Sompolinsky, H. Pattern of synchrony in inhomogeneous networks of oscillators with pulse interactions. Phys. Rev. Lett. 71, 1280 (1993).
Mohanty, P. K. & Politi, A. A new approach to partial synchronization in globally coupled rotators. J. Phys. A: Math. Gen. 39, L415 (2006).
Deco, G., Ponce-Alvarez, A., Mantini, D., Romani, G. L., Hagmann, P. & Corbetta, M. Resting-State Functional Connectivity Emerges from Structurally and Dynamically Shaped Slow Linear Fluctuations,. The Journal of Neuroscience. 33, 11239 (2013).
Acknowledgements
This work is partially supported by the Centro Interdipartimentale per lo Studio delle Dinamiche Complesse (CSDC) of the Universita' di Firenze and by the Istituto Nazionale di Fisica Nucleare (INFN).
Author information
Authors and Affiliations
Contributions
R.B., M.C., M.d.V., R.L. and A.V. contributed to the formulation of the problem, to its solution, to the discussions and to the writing of the paper. M.d.V. performed the simulations and produced all the plots.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Burioni, R., Casartelli, M., di Volo, M. et al. Average synaptic activity and neural networks topology: a global inverse problem. Sci Rep 4, 4336 (2014). https://doi.org/10.1038/srep04336
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04336
This article is cited by
-
Optimal responsiveness and information flow in networks of heterogeneous neurons
Scientific Reports (2021)
-
Reconstruction scheme for excitatory and inhibitory dynamics with quenched disorder: application to zebrafish imaging
Journal of Computational Neuroscience (2021)
-
Synchronization transition in neuronal networks composed of chaotic or non-chaotic oscillators
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


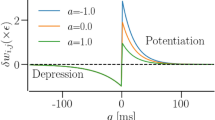



 in Eq.
in Eq. for different values of
for different values of  , corresponding to lines of different colors, according to the legend in the inset: the black line is the bisector of the square.
, corresponding to lines of different colors, according to the legend in the inset: the black line is the bisector of the square.
