Introduction

The characterization of material mechanical properties at their building-block scales has been receiving increased attention in the recent years. In this regard, the ideal single crystal properties can provide the baseline data that can be used to evaluate the behavior for defective structures or material behavior at higher spatial-scales where the response is usually confounded by a myriad of factors, such as vacancies, substitutions, grain boundaries, micro-structures, defects and contaminants at free boundaries and other defects and their interactions. However, experimental determination of the multi-axial stress-strain-strength behavior of perfect single crystals is extremely difficult for reasons ranging from the fabrication of such ideal samples to the challenges associated with testing and the interpretation of the test results. Although indentation experiments, that by nature include nonlinear deformations, have been performed recently on single crystal, such as that of HAP1,2, the data interpretation to extract the complete nonlinear stress-strain-strength behavior requires a priori assumptions of some mechanical constitutive models and the solution of boundary value problems in solid mechanics3,4. For complex multi-component crystal this could require a priori knowledge of material anisotropy and its evolution with loading and numerous assumptions related to anisotropic damage or yield functions and how these evolve with loading.

On the other hand, with recent advances in computational capabilities, it is now possible to investigate the theoretical mechanical behavior of complex multi-atom systems using large atomic models (of the order of 1000 atoms) and ab initio methods5,6,7,8. In this article, we report the results of extensive multi-axial tensile simulation of stoichiometric HAP crystal using a highly accurate ab initio technique. The focus of the present work is on nonlinearity, loading-path dependence and strength of the ideal HAP crystal. Hydroxyapatite (HAP) and its variant formed by various substitutions are an important class of bioceramics that compose most mineralized biological tissues in which they often occur in their basic crystal habit. These bioceramics are finding increasing applications in tissue engineered materials and implants of various types9. Consequently, the mechanical behavior of HAP and other equally complex materials, such as calcium silicate hydrates (CSH), materials is of intense interest, particularly at their unit-cell or single crystal scales. Our results reveal complex local structural changes in these crystals as they are subjected to different multi-axial loading. We find the stress-strain behavior to be highly nonlinear and load-path dependent. We also find that the HAP elastic anisotropy is significantly different from the anisotropy near crystal strength. Further we find it expedient to reduce the multi-axial strength properties in the tensile regime to a single “failure envelope index” that can be used for comparing similar materials. These findings have profound significance with respect to how we classify materials based upon their stress-strain response, how we describe their strength or yield behavior and how we formulate effective continuum or atomistic methods for large-scale simulations.

Results

Figure 1 shows four different projections of the relaxed structure of the orthorhombic HAP supercell used in the simulation. A large number of ‘theoretical’ experiments were performed by deforming the supercell along specified strain paths in a stepwise manner (details in the Methods section). Here, we illustrate the nonlinear loading-path dependent mechanical behavior of HAP crystal under three types of stress conditions: (1) triaxial, wherein the three principal stress components are similar, that is σ1 ≈ σ2 ≈ σ3, (2) equi-biaxial, wherein two principal stress components are similar and larger than the third, that is σ1 ≈ σ2≫σ3 ≈ 0 and (3) uniaxial, wherein σ1 ≫ σ2 ≈ σ3 ≈ 0. These three stress conditions represent behavior from regions of stress-space that lie (1) close to the interior of the tensile octant, (2) on the three planes that border the tensile octant and (3) on the three tensile stress axes, respectively. We have selected a subset of simulations (out of the total of 175 loading paths) that satisfy the above three stress condition criteria. The deformation energies for the three conditions are shown in Figure 2 plotted against strain measure defined as the square root of sum of squares . We observe from Figure 2 that the deformation energies deviate from a quadratic relationship at small strains, indicating that the stress-strain behavior for single crystals is linear only under very small deformations. Furthermore, the deformation energies vary considerably under different loading conditions. The largest deformation energy at the yield/failure point (defined as the strain at which the stress is maximum) occurs in case 1 wherein the supercell experiences an equiaxial (or pressure) loading.

Figure 1
figure 1

Projections of the supercell structure of HAP: (a) x-y plane, (b) x-z plane, (c) y-z plane and (d) perspective (with PO4 tetrahedra shown as yellow-brown, Ca ions as green and OH group as red-white).

Full size image
Figure 2
figure 2

Deformation energy versus strain of HAP supercell for selected simulations corresponding to the three stress conditions: triaxial (a) and (d), biaxial (b) and (e) and uniaxial (c) and (f), respectively.

Curves in (a), (b) and (c) are in the arithmetic scale and (d), (e) and (f) are in logarithmic scale. The log-scale curves show the departure from quadratic behavior after initial two loading steps indicating the onset of non-linear behavior.

Full size image

Stress-strain behavior

The stress-strain curves that correspond to the deformation energy plots are shown in Figure 3(a) through 3(c). For simplicity of visualization, these curves are plotted in terms of the square root of sum of squares of the three calculated stress and applied strain components. Further, in Figures 3(d) through (f) we have plotted the calculated stress components against the applied strain for one example simulation chosen from each of the Figures 3(a)–(c) for the three stress conditions – (1) equi-triaxial or pressure loading, wherein the three principal stress components are approximately equal, that is σ1 = σ2 = σ3, (2) equi-biaxial, wherein two principal stress components are approximately equal and the third is close to zero, that is σ1 = σ2≫σ3 ≈ 0 and (3) uniaxial, wherein σ1 ≫ σ2 ≈ σ3 ≈ 0. These stress conditions are typically used in laboratory testing of mechanical properties of materials at large spatial scales. The stress-strain curves have distinct differences partly due to the different loading paths and partly due to the inherent as well as loading induced crystal anisotropy. The nonlinear stress-strain behavior and the evolution of anisotropy with loading can be more clearly seen from Figures 3(d) through (f). Under an approximately equiaxial loading in Figure 3(d), we note that the x- and y-stress components reach a peak and commence to soften, while the z- stress is still growing, albeit at a smaller rate. Similar, nonlinear behavior is observed in Figures 3(e) and 3(f), where the stress-components do not evolve in a proportional manner.

Figure 3
figure 3

Stress-strain behavior of HAP supercell: (a), (b) and (c) give curves for selected simulations corresponding to the three stress conditions – triaxial, biaxial and uniaxial, respectively and (d), (e) and (f) give stress components for one example simulation chosen from (a)–(c).

Full size image

We observe that the stress-strain curves under different loading conditions exhibit a range of behavior in terms of nonlinearity and strength. The initial portion (<2% strain) can be described as approximately linear. Beyond that, there is an onset of non-linearity that either (1) reaches an abrupt failure with a post-peak softening or an asymptotic behavior (labeled as case 1 in Figure 3(b)), or (2) progresses gradually to a peak followed by softening or asymptotic behavior (labeled as case 2 in Figure 3(a)), or (3) exhibits an abrupt yield followed by hardening behavior (labeled as case 3 in Figure 3(a)). Consequently, the stress-strain behavior cannot be classified into the classical notions of ‘brittle’ and ‘ductile’ and the material cannot be classified on the basis of ‘strength’ and ‘toughness’ as done classically10. Different loading-paths result in different attributes for the same material.

Strength and evolving anisotropy

The deformation energy at peak or asymptotic stress (considered to be failure/yield point) can be interpreted as a measure of material toughness. In Figure 4(a) we have plotted the failure deformation energy envelope in the strain space. For visualization, the projections viewed from x-, y- and z-axes are shown along with the 3D plot in Figure 4(a). This 3D envelope is constructed by plotting the failure deformation energy as the radial distance corresponding to the direction cosines for each of the simulated strain paths. The resulting point cloud is then interpolated to obtain a smooth envelope. We can see from the Figure 4(a) that the failure deformation energy is highly directional, dependent both on the crystal orientation and the applied loading directions. We further note that the diversity of stress-strain behavior implies likelihood of different mechanism by which ‘yield’ or ‘failure’ occur. Consequently, the failure process does not fit into the well-known failure/yield theory of von Mises, Tresca or Mohr-Coulomb and so on11,12. Therefore, a single failure/yield criterion is difficult to devise for any particular material. As discussed in our previous paper8, we can consider the HAP crystal to have failed when the major principal stress reaches either a peak or a “yield” value under the various applied loading conditions to conform to a uniaxial failure criterion. Alternatively, other failure criterion may be specified, such as the peak or yield in the stress invariants, particularly the 2nd invariant, albeit none satisfactorily or universally. Here for simplicity, we have chosen to define failure as a significant or abrupt change in the slope of stress-strain curves shown in Figures 3(a)–(c).

Figure 4
figure 4

Failure envelopes: column (a) failure energy plotted in the strain-space (axis are in eV), column (b) failure strain plotted in the strain-space (axis are in % strain) and column (c) failure stress plotted in the stress-space (axis are in GPa).

The rows correspond to the 3D, x-, y- and z-axis projections, respectively. The color bar for each column is shown alongside the 3D projection.

Full size image

To elucidate the directional nature of the strength behavior we have constructed failure envelopes in Figures 4(b) and 4(c) by plotting the applied strain or the calculated stress corresponding to the above failure criterion in the strain-space and stress-space, respectively, for all the simulated loading paths based on 175 data points. The resultant point cloud is fitted using a smooth surface to obtain the failure envelopes in the purely tensile octant of the strain- and the stress-space. Figures 4(b) and 4(c) give the projections viewed from x-, y- and z-axes as well as the 3D plot of the failure envelopes. As expected the strain- and strain space failure envelopes show a highly anisotropic behavior. In the stress-space, the smallest radial distance to the failure envelope is along the x-direction indicating that the crystal is weakest under uniaxial-stress loading in the x-direction. In the strain-space such a preferential direction is not observed, although that is likely a consequence of the assumed failure criterion. We also observe that in the strain-space, the crystal fails at higher strains under equi-biaxial and equi-triaxial condition. In comparison in the stress-space, the equi-triaxial condition results in the highest stress at failure. Clearly, the direction-dependence of failure is different in the stress and strain-spaces.

Limited experimental studies using nanoindentation performed on the side and basal planes of single HAP crystals have also indicated significant direction dependence in the hardness and fracture toughness1,2. It is also interesting to note that the reported hardness values (6.41–14.8 GPa) have similar order of magnitudes as the uniaxial strength predicted by our calculations (6.5, 10.1 and 8.4 GPa in the x-, y- and z-directions, respectively). However, experimental data can never produce the entire failure envelope that can be obtained from simulation as shown in Figure 4. Furthermore, it should be emphasized that the indentation process has to be interpreted as a boundary value problem in continuum mechanics; therefore it does not directly provide the crystal stress-strain behavior under a single strain or stress loading-path. The data interpretation to extract material properties, such as indentation modulus or toughness, requires assumptions of some constitutive relations, which are typically taken as linear elastic or some form of elasto-plastic constitutive laws3,4. The stress and strain condition in an indentation experiments are quite complex and depend upon the local material properties. Moreover, the presence of small defects in the bulk or at free boundaries (such as vacancies, contaminants or boundary defects) could act as initiators of localized deformation modes that can propagate to the free boundaries resulting in underestimation of ideal properties. Indeed a key challenge in determining fundamental 3D stress-strain-strength properties of materials at their building block scales through experimental methods is the lack proper constitutive models, which in traditional continuum mechanics are formulated from experimental data. This gives rise to the proverbial chicken-egg problem. To our knowledge loading-path dependent behavior of perfect single crystals, such as reported here, has not been determined using experimental methods. The approach used in this paper to determine the 3D stress-strain behavior under multi-axial loading through atomistic computational methods remains, arguably, the only feasible option for determination of the stress-strain-strength behavior for a perfect single crystal.

We also observe that while the failure envelope provides a visualization of the crystal strength and its anisotropy, the size of the failure envelope, defined in terms of the volume it contains or its surface area, can function as a simple quantitative index measure of relative strength behavior of different materials or same material system with defects. For stronger material system the failure envelope is expected to be larger, hence its volume and surface area would be larger. However, for materials whose failure envelope has the same volume, the surface area provides a measure of anisotropy, since for isotropic systems the failure envelope is an octant of a sphere. Table 1 gives this “failure envelope index” in terms of stress, strain and energy for the HAP crystal. The “failure envelope index” can be used for comparison of the relative strengths and toughness of the different material, especially when one wants to evaluate the effects of small changes, such as effects of substitutions for example in fluorapatite (FAP) and vacancies, upon the mechanical behavior of single crystals. To this end, it would be desirable to develop a database of this index for classification based upon material intrinsic strength.

Table 1 Failure envelope index
Full size table

We further note that the anisotropy of the strength response does not coincide with the elastic anisotropy of HAP crystal due to the loading-path dependent nature of the stress-strain behavior. The elastic properties of HAP crystal are isotropic in the x-y plane which corresponds to the a–b crystallographic plane of the hexagonal HAP unit cell8. However, the strength response in the x-y plane is highly anisotropic as shown in Figure 4. Moreover, the degree of anisotropy appears to be different depending upon the adopted strength criterion. Clearly the material response to the imposed loading is to adjust the electronic-structure and consequently the atomic-structure to the most stable state. These equilibrium structures are different under different loading conditions and depend upon the path taken to arrive at a particular loading condition. The strength response reflects the atomic structure under the loading condition.

Local structure evolution

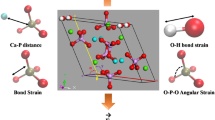
In this regards we note that the nonlinear loading-path dependent behavior of these multi-atom complex crystals that comprise of ionic, covalent and hydrogen bonds stems from different deformation mechanisms that are triggered and persist under different loading paths. For the HAP crystal, the primary deformation mechanisms consist of rotation of the rigid PO4 tetrahedral units, the repositioning of the Ca ions and the alignment of OH group. We note that the P-O and O-H bonds undergo very small deformations (<0.5% strain) over the entire loading process that deforms the crystal by >10% strain. Figure 5 gives examples of the local structures in the undeformed crystal and at failure under the three loading conditions. We note that the rotation magnitudes and directions of the PO4 tetrahedral units are remarkably different depending upon the loading conditions. As the lattice is distorted in each loading case, the interatomic interactions likely change as a result of the repositioning of the Ca ions and the rotation of the PO4 tetrahedral units to their minimal local energies. It is also interesting that when the loading is such that the stresses in the x-directions dominate, the OH group loses its alignment along the z-axis (c-axis) as seen from the OH group structure in the last column of Figure 5. The atomic relaxations and changes in interatomic distances from Figure 5 allude to potential changes in interatomic bonding. Further quantitative analyses, such as overlap population or bond order calculations13,14 could be used to investigate the variations in bonding characteristics with variations in atomic-scale structures under deformation.

Figure 5
figure 5

Typical changes in the local structures that manifest under different loading path.

These local deformation mechanisms contribute to the nonlinearity and evolving anisotropy of the stress-strain-failure response.

Full size image

Discussion

The diverse load-path dependent stress-strain-strength behavior clearly suggests that the failure or yield behavior of HAP is unlikely to be predicted by its elastic properties. This observation is in contrast with the current classification of material strength or toughness that are mostly based on parameters such as the bulk modulus, the shear modulus, Poisson’s ratio or their ratios which are defined for polycrystals under linear elasticity assumption15,16,17,18,19. The loading path dependent deformation mechanism also have direct impact on development of both continuum and atomistic approaches that can be applied to larger scale modeling of complex materials, such as HAP. From the continuum viewpoint, the modeling of experimental data from techniques such as nanoindentation using classical approaches may be inadequate. Under indentation, these various deformation mechanisms will be active in different locations of the indented crystal in response to the local loading path. Continuum theories that account for local mechanisms, such as micro-polar or gradient theories [see for example20,21,22 and references therein, see also23,24], need to be developed for adequate characterization. Furthermore, the loading path dependent change in local structures implies that the interatomic interactions, particularly those involving Ca are exceptionally complex. These complexities will impact the development of realistic/accurate potential functions for use in classical molecular dynamics or molecular mechanics approaches to simulation of HAP and its interactions at grain boundaries or with other organic/inorganic molecules. We expect similar conclusions to be true for other equally or more complex materials, such as calcium silicate hydrate (CSH) crystals. In our opinion, ab initio simulations which do not depend upon parameterized potential functions or atomistic methods that derive force fields from ab initio simulations are the only viable approach to obtain reliable data in understanding the complex mechanical behavior.

Finally, we note that the results presented here are for a perfect crystal. Defects such as substitutions, partial occupancies, vacancies that occur in real materials and their interaction with the local deformation mechanism leading to dislocations or disclinations will further complicate the behavior. The combination of these complexities, the loading-path dependent behavior of perfect crystal and the local structural changes indicate the difficulty of developing classical continuum and molecular dynamics (mechanics) approaches for multi-atom crystals that comprise of ionic, covalent and hydrogen bonds. The absence of robust large scale methods confounds the proper interpretation of the experimental data. Therefore, new theoretical methods, computational techniques and more powerful supercomputers will be needed for such studies as these behaviors cannot be determined directly from experimental methods.

Methods

The crystal structure of HAP has been well determined and fully described in the previous calculations25,26. The primitive cell of HAP in the hexagonal lattice has 44 atoms. This structure was doubled and translated into an orthorhombic cell in the previous simulation8. In the present study of strength behavior of HAP, it is desirable to have an even larger supercell. We note that although we are dealing with crystalline materials under periodic boundary conditions, the internal deformation is not guaranteed to be linear or even periodic within the supercell. The larger supercell is chosen to reduce the boundary effects and allow for greater degree of freedom for the internal structures, such that the atomic displacements are not overly constrained by the periodic boundary conditions. Accordingly, we further enlarged the previous model in x and z directions, resulting in a supercell of 352 atoms. The model is then fully relaxed using VASP (Vienna Ab initio Simulation Package)27,28 with high accuracy. We used the PAW-PBE potential29 and a single k-point at Γ which is sufficient due to the enlarged supercell. The energy cut-off of 600 eV is adopted and the convergence criteria for the total energy and force per atom are set at 0.0001 eV and 0.001 eV/Å, respectively. The dimensions of the supercell used in the simulation was = 19.0915 Å, = 16.5330 Å and = 13.7833 Å. Supercell of this size is sufficiently large to accommodate the structural deformation under applied strains.

The supercell was deformed according to the following loading-path: , and , where the strains are incremented stepwise while keeping constant the proportion εxx:εyy:εzz and the maximum of the three strain increments, max(Δεxx:Δεyy:Δεzz), as 1%. Proportional loading was employed such that we can probe the anisotropic behavior of the supercell by loading in various directions. With this choice we can also ensure sufficiently uniform coverage of the tensile octant of the strain- and stress-spaces. During each extension step, the atomic positions in the supercell were fully relaxed using VASP. The extension steps were repeated for the next strain until the stress reaches the maximum and beyond. It should be pointed out that the relaxation at each strain level to obtain stable stress components of the cell requires a large number of iterations to reach convergence for a large complex supercell, especially after the maximum of the stress has been reached which typically takes a minimum of 12–13 steps along a loading path.

The focus of our simulations was on loading paths that resulted in primarily tensile action on the supercell so that we can study loading induced nonlinearity and strength. Simulations under primarily compressive loading resulting in material densification are not of concern here as these do not lead to failure of perfect crystals. Sufficient numbers of loading-paths were simulated to ensure that smooth failure envelopes can be constructed in the tensile octant of the stress-space. In the present study for HAP, a total of 175 multi-axial loading-paths were simulated by choosing different proportionality constants for the proportion εxx:εyy:εzz. We note that in the strain controlled simulations precise stress conditions cannot be maintained. In contrast, performing stress-controlled simulations with ab initio method are generally very difficult. Therefore, to obtain results close to the boundaries, that is in the xy-, yz- and xz- planes, of the tensile octant of the stress space, a number of loading-paths were simulated in which both tensile and compressive (negative εii) components were specified. By specifying mixed tensile and compressive strain components we were able to obtain close-to biaxial (in which one of the three principal stress component is close to zero) and uniaxial stress conditions (in which two of the three principal stress components are close to zero). Tensile triaxial stress conditions were typically obtained for the loading paths with purely tensile strain components.