Abstract
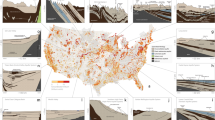
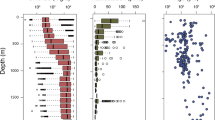
Groundwater is important for energy and food security, human health and ecosystems. The time since groundwater was recharged—or groundwater age—can be important for diverse geologic processes, such as chemical weathering, ocean eutrophication and climate change. However, measured groundwater ages range from months to millions of years. The global volume and distribution of groundwater less than 50 years old—modern groundwater that is the most recently recharged and also the most vulnerable to global change—are unknown. Here we combine geochemical, geologic, hydrologic and geospatial data sets with numerical simulations of groundwater and analyse tritium ages to show that less than 6% of the groundwater in the uppermost portion of Earth’s landmass is modern. We find that the total groundwater volume in the upper 2 km of continental crust is approximately 22.6 million km3, of which 0.1–5.0 million km3 is less than 50 years old. Although modern groundwater represents a small percentage of the total groundwater on Earth, the volume of modern groundwater is equivalent to a body of water with a depth of about 3 m spread over the continents. This water resource dwarfs all other components of the active hydrologic cycle.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Change history
11 June 2018
In the version of this Article originally published, the wrong article was listed as ref. 33; it should have been "Oki, T. & Kanae, S. Global hydrological cycles and world water resources. Science 313, 1068–1072 (2006)." This has been corrected in the online versions of the Article.
References
Sturchio, N. C. et al. One million year old groundwater in the Sahara revealed by krypton-81 and chlorine-36. Geophys. Res. Lett. 31, L05503 (2004).
McCallum, J. L., Cook, P. G. & Simmons, C. T. Limitations of the use of environmental tracers to infer groundwater age. Groundwater 53, 56–70 (2014).
Weissmann, G. S., Zhang, Y., LaBolle, E. M. & Fogg, G. E. Dispersion of groundwater age in an alluvial aquifer system. Wat. Resour. Res. 38, 1198 (2002).
Bethke, C. M. & Johnson, T. M. Groundwater age and groundwater age dating. Annu. Rev. Earth Planet. Sci. 36, 121–152 (2008).
Kazemi, G., Lehr, J. & Perrochet, P. Groundwater Age (Wiley-Interscience, 2006).
Alley, W. M., Healy, R. W., LaBaugh, J. W. & Reilly, T. E. Flow and storage in groundwater systems. Science 296, 1985–1990 (2002).
Foster, S. S. D. & Chilton, P. J. Groundwater: The processes and global significance of aquifer degradation. Phil. Trans. R. Soc. Lond. B 358, 1957–1972 (2003).
Taylor, R. G. et al. Ground water and climate change. Nature Clim. Change 3, 322–329 (2013).
Moore, W. S. Large groundwater inputs to coastal waters revealed by 226Ra enrichments. Nature 380, 612–614 (1996).
Maher, K. & Chamberlain, C. P. Hydrologic regulation of chemical weathering and the geologic carbon cycle. Science 343, 1502–1504 (2014).
Lehner, B., Verdin, K. & Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos 89, 93–94 (2008).
Gruber, S. Derivation and analysis of a high-resolution estimate of global permafrost zonation. Cryosphere 6, 221–233 (2012).
Garmonov, I. V., Konoplyantsev, A. A. & Lushnikova, N. P. in The World Water Balance and Water Resources of the Earth (ed. Korzun, K. I.) 48–50 (Hydrometeoizdat, 1974).
Chahine, M. T. The hydrological cycle and its influence on climate. Nature 359, 373–380 (1992).
Schneider, U. et al. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 115, 15–40 (2014).
L’ Vovich, M. I. in World Water Resources and their Future (ed. Nace, R. L.) 13–23 (American Geophysical Union, 1979); http://onlinelibrary.wiley.com/book/10.1029/SP013
Nace, R. L. in Water, Earth, and Man: A Synthesis of Hydrology, Geomorphology, and Socio-Economic Geography (ed. Chorley, R. J.) 31–42 (Methuen and Co., 1969).
Holland, H. D. & Turekian, K. K. (eds) in Treatise on Geochemistry 2nd edn (Pergamon, 2003); http://www.sciencedirect.com/science/referenceworks/9780080983004
Fan, Y., Li, H. & Miguez-Macho, G. Global patterns of groundwater table depth. Science 339, 940–943 (2013).
USSR Committee for the International Hydrologic Decade World Water Balance and Water Resources of the Earth (UNESCO, 1978).
Gleeson, T., Moosdorf, N., Hartmann, J. & vanBeek, L. P. H. A glimpse beneath Earth’s surface: GLobal HYdrogeology MaPS (GLHYMPS) of permeability and porosity. Geophys. Res. Lett. 41, 3891–3898 (2014).
Cardenas, M. B. Potential contribution of topography-driven regional groundwater flow to fractal stream chemistry: Residence time distribution analysis of Tóth flow. Geophys. Res. Lett. 34, L05403 (2007).
Lerner, D. N. in Geochemical Processes, Weathering and Groundwater Recharge in Catchments (eds Saether, O. M. & de Caritat, P.) 109–150 (Balkema, 1997).
Scanlon, B., Healy, R. & Cook, P. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 10, 18–39 (2002).
Scanlon, B. R. et al. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 20, 3335–3370 (2006).
Döll, P. & Fiedler, K. Global-scale modeling of groundwater recharge. Hydrol. Earth Syst. Sci. 12, 863–885 (2008).
Giordano, M. Global groundwater? Issues and solutions. Annu Rev. Environ. Resour. 34, 153–178 (2009).
Morris, B. L. et al. Groundwater and its Susceptibility to Degradation: A Global Assessment of the Problem and Options for Management (UNEP Early Warning and Assessment Report Series RS 03-3, 2003).
Fleckenstein, J. H., Krause, S., Hannah, D. M. & Boano, F. Groundwater-surface water interactions: New methods and models to improve understanding of processes and dynamics. Adv. Water Resour. 33, 1291–1295 (2010).
Nicot, J.-P., Scanlon, B. R., Reedy, R. C. & Costley, R. A. Source and fate of hydraulic fracturing water in the Barnett Shale: A historical perspective. Environ. Sci. Technol. 48, 2464–2471 (2014).
Wada, Y., van Beek, L. P. H. & Bierkens, M. F. P. Nonsustainable groundwater sustaining irrigation: A global assessment. Wat. Resour. Res. 48, W00L06 (2012).
Athy, L. F. Density, porosity, and compaction of sedimentary rocks. AAPG Bull. 14, 1–24 (1930).
Oki, T. & Kanae, S. Global hydrological cycles and world water resources. Science 313, 1068–1072 (2006).
Ehrenberg, S. N. & Nadeau, P. H. Sandstone vs. carbonate petroleum reservoirs: A global perspective on porosity-depth and porosity-permeability relationships. Am. Assoc. Petrol. Geol. Bull. 89, 435–445 (2005).
Hartmann, J. & Moosdorf, N. The new global lithological map database GLiM: A representation of rock properties at the Earth surface. Geochem. Geophys. Geosyst. 13, Q12004 (2012).
Laske, G. & Masters, G. A global digital map of sediment thickness. Eos 78, F483 (1997).
Zhang, Y., Ye, S. & Wu, J. A modified global model for predicting the tritium distribution in precipitation, 1960–2005. Hydrol. Process. 25, 2379–2392 (2011).
Begemann, F. & Libby, W. F. Continental water balance, ground water inventory and storage times, surface ocean mixing rates and world-wide water circulation patterns from cosmic-ray and bomb tritium. Geochim. Cosmochim. Acta 12, 277–296 (1957).
Clark, I. & Fritz, P. Environmental Isotopes in Hydrogeology (Lewis, 1997).
Kotzer, T. G., Kudo, A., Zheng, J. & Workman, W. Natural and anthropogenic levels of tritium in a Canadian Arctic ice core, Agassiz Ice Cap, Ellesmere Island, and comparison with other radionuclides. J. Glaciol. 46, 35–40 (2000).
Tóth, J. A theoretical analysis of groundwater flow in small drainage basins. J. Geophys. Res. 68, 4795–4812 (1963).
Jiang, X.-W., Wan, L., Cardenas, M. B., Ge, S. & Wang, X.-S. Simultaneous rejuvenation and aging of groundwater in basins due to depth-decaying hydraulic conductivity and porosity. Geophys. Res. Lett. 37, L05403 (2010).
Jiang, X.-W., Wan, L., Wang, X.-S., Ge, S. & Liu, J. Effect of exponential decay in hydraulic conductivity with depth on regional groundwater flow. Geophys. Res. Lett. 36, L24402 (2009).
Cardenas, M. B. & Jiang, X. W. Groundwater flow, transport, and residence times through topography-driven basins with exponentially decreasing permeability and porosity. Wat. Resour. Res. 46, W11538 (2010).
Bernabé, Y., Mok, U. & Evans, B. Permeability-porosity relationships in rocks subjected to various evolution processes. Pure Appl. Geophys. 160, 937–960 (2003).
Goode, D. J. Direct simulation of groundwater age. Wat. Resour. Res. 32, 289–296 (1996).
Acknowledgements
T.G. and E.L. were supported by the NSERC and a CIFAR Junior Fellowship. M.B.C. and K.M.B. were supported by the NSF (EAR-0955750) and the Geology Foundation at the University of Texas at Austin. K.M.B. and S.J. were supported by American Geophysical Union Horton Research Grants.
Author information
Authors and Affiliations
Contributions
T.G. conceived and led the project and the writing of the paper. K.M.B. led and conducted the modelling, geomatic analysis and model-related calculations as well as developed the mathematical methods for calculating the metrics. S.J. conducted the tritium data collection and analysis. E.L. derived the original geomatic data and a method for coupling geomatic data to models, as well as conducted the data analysis of total groundwater storage. M.B.C. brainstormed ideas and analysed results. All authors co-developed the methods, wrote text for their respective sections, and heavily discussed and edited all drafts of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 2975 kb)
Rights and permissions
About this article
Cite this article
Gleeson, T., Befus, K., Jasechko, S. et al. The global volume and distribution of modern groundwater. Nature Geosci 9, 161–167 (2016). https://doi.org/10.1038/ngeo2590
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/ngeo2590
This article is cited by
-
Global peak water limit of future groundwater withdrawals
Nature Sustainability (2024)
-
Delineating groundwater potential zones with GIS and analytic hierarchy process techniques: the case of Great Ruaha River catchment, Tanzania
Hydrogeology Journal (2024)
-
Data driven of underground water level using artificial intelligence hybrid algorithms
Scientific Reports (2023)
-
Offshore freshened groundwater in the Pearl River estuary and shelf as a significant water resource
Nature Communications (2023)
-
Groundwater deeper than 500 m contributes less than 0.1% of global river discharge
Communications Earth & Environment (2023)