Abstract
The distribution of groundwater age is useful for evaluating the susceptibility and sustainability of groundwater resources. Here, we compute the aquifer-scale cumulative distribution function to characterize the age distribution for 21 Principal Aquifers that account for ~80% of public-supply pumping in the United States. The aquifer-scale cumulative distribution function for each Principal Aquifer was derived from an ensemble of modeled age distributions (~60 samples per aquifer) based on multiple tracers: tritium, tritiogenic helium-3, sulfur hexafluoride, chlorofluorocarbons, carbon-14, and radiogenic helium-4. Nationally, the groundwater is 38% Anthropocene (since 1953), 34% Holocene (75 – 11,800 years ago), and 28% Pleistocene (>11,800 years ago). The Anthropocene fraction ranges from <5 to 100%, indicating a wide range in susceptibility to land-surface contamination. The Pleistocene fraction of groundwater exceeds 50% in 7 eastern aquifers that are predominately confined. The Holocene fraction of groundwater exceeds 50% in 5 western aquifers that are predominately unconfined. The sustainability of pumping from these Principal Aquifers depends on rates of recharge and release of groundwater stored in fine-grained layers.
Similar content being viewed by others
Introduction
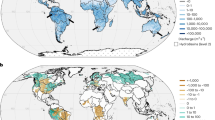
Knowing the distribution of groundwater age in a sample, or in an aquifer, is important for assessing the susceptibility of groundwater to anthropogenic and geogenic contamination, and for understanding the potential impacts of water-level declines due to overdraft and changes in recharge1. The presence of Anthropocene2 water (i.e., water that entered an aquifer as recharge since 1953) can be indicative of susceptibility to anthropogenic contamination, and the presence of Holocene or Pleistocene water can be indicative of groundwater mining. The distribution of age in a sample can be obtained if multiple age tracers are measured, but not from a single tracer. For example, if the only available tracer is tritium (3H), then groundwater could be classified as young, mixed, or old3 but the age would remain unknown. Alternatively, if only carbon-14 (14C) is available as a tracer, then one could compute an age, but not its distribution. Information obtained from a single tracer has proven useful, particularly when one has an ensemble of samples; for example, the vulnerability of groundwater supply has been evaluated at a global scale based on a single tracer in each sample4,5. However, the age distribution provides a more complete picture of the ages present in groundwater, particularly when both Anthropocene (since 1953) and Pleistocene (>11,800 yrs) water are present in a sample. The full age distribution, therefore, provides more detailed information that is needed for understanding groundwater resources. This paper evaluates the distribution of groundwater age, not only in samples, but also in large regional aquifers, known as Principal Aquifers6 (PAs). The 21 PAs evaluated here account for 80% of the groundwater used for public supply in the continental United States (US)7 (Fig. 1).
Sites from the Glacial aquifer system are symbolized with a triangle and sites from the Basin and Range carbonates are symbolized with an upside-down triangle to differentiate them from sites in other aquifers (circles). Principal Aquifers that have been combined or separated are indicated in parentheses.
The groundwater age distribution in a sample can span years, decades, or millennia. Sometimes the age distribution is unimodal, for example a Gaussian distribution, but it can also be bimodal or even multi-modal. Here, we compute the full age distributions in groundwater samples collected at 1279 sites used for public supply distributed across the 21 PAs. At each well, we collected multiple tracers8 with overlapping and complementary dating ranges. Tritium (3H), chlorofluorocarbons (CFCs), sulfur hexafluoride (SF6), and tritiogenic helium-3 (3Hetrit) were collected because they are useful for identifying groundwater recharged during the Anthropocene. Carbon-14 (14C) and radiogenic helium-4 (4Herad) were collected because they are useful for identifying Holocene and Pleistocene water. 14C is also useful as a tracer of Anthropocene water because concentrations were elevated in the atmosphere due to above ground nuclear weapons testing. Nearly all sites had at least two tracers, and 72% had 3 or more. Lumped parameter models (LPMs) were fit to the measured concentrations, which provide an age distribution for each sample9,10,11,12. Age distributions computed from LPMs are similar to distributions computed from more resource intensive, numerical groundwater flow models13,14.
The sampling design used for this study provides a spatially unbiased estimate of groundwater age at the scale of individual PAs and at the scale of continental US. Each PA was divided into a grid of equal-area cells, typically 60, and one public-supply well per cell was selected for sampling15. This design ensures that the wells are spatially distributed across a PA and that the ensemble of wells is statistically representative of the area used for public supply in the PA16. We use an aquifer scale cumulative distribution function (ACDF) to represent the distribution of groundwater age in a PA. The ACDF is computed as a simple linear combination of the cumulative distribution functions (CDFs) of the individual samples in the ensemble17. Given the ACDF, the proportion of groundwater in a PA that is Anthropocene (since 1953), Holocene (75–11,800 yrs), or Pleistocene (>11,800 yrs) can then be computed. These proportions cannot be computed accurately from a CDF of the mean ages of the samples or from ages derived from results for a single tracer. The distribution of groundwater ages in the continental US is an area-weighted combination of the ACDFs for the PAs.
The 21 PAs6 were grouped into six classes: Western unconsolidated, Coastal clastic, Interior sandstone and sandstone-carbonates, Glacial, Carbonate, and Igneous and metamorphic (Fig. 1; Supplementary Fig. 1; Supplementary Table 1). These groupings provide context for evaluating the distribution of groundwater age at the continental scale. The Western unconsolidated class includes six PAs that are primarily alluvium, and the climate is primarily semi-arid to arid. The Coastal clastic class is comprised of five PAs that consist of thick sequences of unconsolidated to semi-consolidated sediment, that are located along the humid Gulf and Atlantic coasts. The Interior sandstone-carbonate class includes three aquifers that are either entirely sandstone or interbedded sandstone-carbonates. The Glacial aquifer system covers ~25% of the northern US and is relatively thin compared to the other classes. The Carbonate class includes six PAs extending from the arid west (Basin and Range carbonates) to the humid east (Floridan and Biscayne). The Igneous and metamorphic class comprises two fractured rock aquifers, one in the northwest and one in the east.
Here, we show that groundwater age in aquifers used for public supply systematically varies across the US. Groundwater is primarily Holocene in the unconsolidated aquifers of the western US, Pleistocene in the semi-consolidated aquifers in the Gulf and Atlantic Coasts, and Pleistocene in the Interior sandstone-carbonates. Groundwater age in the carbonate PAs ranges from primarily Anthropocene to primarily Pleistocene, varying systematically as a function of climate and degree of confinement. Groundwater is primarily Anthropocene in the relatively thin Glacial aquifer system and in the eastern fractured crystalline-rock PA. Groundwater in the western, fractured crystalline-rock PA is primarily Holocene, reflecting the aridity of the climate. The different age distributions observed across the PAs present different challenges for understanding and managing the susceptibility and sustainability of the resource. These distinctions would be lost if all the data were treated as a single ensemble.
Results and discussion
Modeled ages of groundwater samples
The mean age of groundwater computed for each sample is shown in Fig. 1 and given in table 2 of the USGS Data Release8. Mean age ranges from one to ~750,000 years, with a median of ~2500 years. Roughly half of all samples consist of groundwater that is pre-Anthropocene, whereas ~20% of the samples are Anthropocene.
Thirty percent of all samples are bimodal mixtures of Anthropocene and pre-Anthropocene groundwater (Supplementary Fig. 2). Wells with bimodal age distributions have tracer concentrations that reflect a mixture of water with disparate ages. For example, 60% of samples had 14C concentrations less than 90 pmC, and the mean age of groundwater for these samples would be greater than 1000 years based on 14C alone (Supplementary Fig. 3). However, about one-fourth of these samples had detectable levels of 3H (>0.1 TU). The presence of 3H in these samples indicate that the 14C concentration is a mixture of elevated 14C from atmospheric nuclear weapons testing and lower 14C from older groundwater. These samples have fractions of Anthropocene water and Holocene or Pleistocene water that would not be identified without multiple tracers and modeling the age distribution (Supplementary Discussion 1).
Errors associated with mean age, which are computed by the fitting algorithm, were generally within 10%. The median error of the mean age was 9%, and the interquartile range was 5–25%. Errors of 5–25% generally have small effect on the estimated fractions of Anthropocene, Holocene, and Pleistocene groundwater. Larger errors are generally associated with bimodal models. The algorithm for fitting age distributions to tracer concentrations incorporates uncertainties associated with each tracer: 3H, 3Hetrit, SF6, CFCs, 14C, and 4Herad. The methods for correcting tracer concentrations for gas solubility, excess air, sources of 14C-free carbon, and mantle helium, and their uncertainties are discussed in the Methods section and Supplementary Information.
Mean groundwater ages for samples are positively correlated with well depth (Spearman’s correlation p value < 0.05) in all but two aquifers (BNRC, PDBR) (Supplementary Fig. 4). The positive correlation is consistent with the expectation that groundwater age increases with depth11. The positive correlation with depth can also arise in aquifers where groundwater flow is predominately lateral, and formations dip downward away from recharge areas, as they do in the coastal PAs. The absence of correlation in the BNRC and PDBR PAs reflects the dominance of flow through fractures, and in the case of the BNRC, also reflects the occurrence of the PA as outcrops across discontinuous mountain highlands6. These correlations, and lack thereof, are consistent with the general understanding of the hydrology of the PAs.
Travel time through the unsaturated zone is important for understanding the age distribution of a sample that is predominantly Anthropocene. In aquifers of the western US, about a third of the samples were predominantly Anthropocene; in these samples, travel times through the unsaturated zone ranged from 1 to 10 years in about half the samples, and 10–25 years in the other half (Supplementary Fig. 5). These results show that the unsaturated zone, which is often ignored, can be an important contributor to the age of Anthropocene groundwater. Travel time through the unsaturated zone is not an important factor for understanding the age distribution of groundwater that is Holocene or Pleistocene, because it is short in comparison.
Distribution of groundwater age in Principal Aquifers used for public supply
The distribution of groundwater age in a PA is characterized by its ACDF (Fig. 2). The ACDF is the spatially averaged ensemble of all individual sample age distributions in a PA and is not the expected age distribution of an individual well in a PA. The ACDF is the average fraction in each age-bin (1-year increment) across the spectrum of ages in a PA17. The ACDF preserves the full spectrum of ages present in individual samples that could be lost if the CDF was based on the mean age (Supplementary Discussion 2). Steeper slopes indicate a narrower range of ages are present in the PA whereas gradual slopes indicate a broad range of ages are present. Plateaus indicate the ACDF is bimodal where ages are absent. Plateaus can arise from the aggregation of samples with bimodal age distributions or from the aggregation of unimodal samples of disparate age. The ACDFs are interpreted in the context of the hydrology of the PA.
The ACDF is the composite of all individual sample age distributions. Lines are labeled in descending order. The Principal Aquifers and their abbreviations are defined in Fig. 1.
In the Western unconsolidated PAs, groundwater is predominately Holocene (Fig. 3; Supplementary Table 2), reflecting low rates of natural recharge under arid conditions (Supplementary Fig. 1). The largest proportions of Anthropocene groundwater in the unconsolidated PAs, as indicated by the ACDFs, are found in the CACB, CVAL, and HPAQ (Fig. 2). These unconsolidated PAs are the most affected by human activity that accelerates the hydrologic cycle. For example, in CVAL14 and HPAQ18, agricultural irrigation and pumping has caused Anthropocene groundwater to move downward rapidly, displacing Holocene groundwater that was present prior to agricultural development. Consequently, many samples in these PAs have bimodal age distributions that reflect the capture of natural and human-impacted groundwater. In areas dominated by engineered recharge, such as the Los Angeles Coastal Plain19,20 in CACB, Anthropocene groundwater is moving laterally outward from managed recharge facilities, replacing the older groundwater currently extracted by public-supply wells located downgradient from the recharge facilities. At the century(s) timescale, the Anthropocene fraction is likely to become the largest component of these PAs. To the extent that Anthropocene groundwater contains contaminants like nitrate and volatile organic compounds, these PAs are at increasing risk with time.
Blue bars represent Anthropocene proportions, yellow bars represent Holocene proportions, and red bars represent Pleistocene proportions. The Principal Aquifers and their abbreviations are defined in Fig. 1.
Groundwater in the Coastal PAs, in contrast to the Western unconsolidated PAs, is predominately Pleistocene (Fig. 3). In addition, the ACDFs for these PAs are similar to one another21 (Fig. 2). The Coastal PAs are confined over most of their areal extent, with unconfined conditions limited to a narrow inland outcrop belt. The small amount of Anthropocene groundwater, evident in the ACDFs, is found in these inland recharge areas. As the PAs dip and deepen towards the coast, groundwater age increases as it moves laterally. Although the climate is humid along the Atlantic and Gulf coasts, most of the groundwater is Pleistocene because of the large lateral travel distances. Although the groundwater is primarily Pleistocene, and there may be some concern that the resource is being mined, groundwater extractions may be sustainable due to vertical leakage into the aquifer from overlying and underlying fine-grained confining layers22,23,24,25.
Groundwater in the Interior sandstone-carbonate PAs, like the Coastal PAs, has a relatively small proportion of Anthropocene groundwater (Fig. 3). The ACDFs for the Interior PAs are different from one another (Fig. 2). In all three Interior PAs, groundwater is recharged in upland unconfined areas flowing laterally towards downgradient discharge areas. Anthropocene groundwater generally occurs only in the upland areas. In the COPL, groundwater is mostly Holocene, and in the EDTR and CMOR, groundwater is mostly Pleistocene. The oldest groundwater in the US, as identified in this study, occurs in the deeply buried parts of the CMOR; more than 25% of groundwater is older than 100 ka. Like the Coastal PAs, pumping from the Interior-sandstone PAs may be sustainable due to vertical leakage from adjacent confining layers. Additional analytical tools, such as groundwater modeling26, can be used to address whether the hydrologic system is balanced or is being mined.
Groundwater in the Glacial PA is generally young: 60% Anthropocene, 30% Holocene, and 10% Pleistocene (Fig. 3). The groundwater is generally young because the PA is mostly located in the humid east, the deposits are relatively thin27, and the topography is hummocky. These conditions lead to active groundwater flow over short distances, and a large proportion of Anthropocene water. Older groundwater in the Glacial PA tends to occur where the deposits are thicker17. Although the rates of pumping may be sustainable due to high rates of recharge, groundwater in the Glacial PA may be susceptible to contamination from anthropogenic activities.
The six Carbonate PAs are characterized by a diverse set of climatic and hydrogeologic conditions. Consequently, the ACDFs differ amongst the PAs. With the exception of the BISC, the ACDFs are bimodal (Fig. 2), reflecting the dual porosity of these carbonate aquifers. The oldest groundwater occurs in the two PAs that are predominately confined—OZRK and FLOR—and the youngest groundwater occurs in the four PAs that are predominately unconfined (Fig. 3). The predominance of Holocene and Pleistocene groundwater in the OZRK and FLOR, both of which are in humid climates, illustrates the importance of confinement. Amongst the four unconfined PAs, groundwater is oldest in the BNRC, located in the arid west, and youngest in the BISC, located in the humid east, reflecting the importance of climate. The contrast in age between the confined FLOR and the unconfined BISC, both of which are in Florida, further demonstrates the importance of confinement. The diversity of ACDFs for the Carbonate PAs exemplifies the utility of ACDFs for distinguishing hydrologic characteristics of PAs.
The age of groundwater in the two fractured-rock PAs reflects the importance of climate. The CLPT basalts are in the arid West (Supplementary Fig. 1) and the groundwater is primarily Holocene (Fig. 3). The PDBR is in the humid east and the groundwater is primarily Anthropocene (Fig. 3). The difference in age between the PAs may also partly reflect groundwater flow through deep rubble and interflow zones that underlie less permeable basalt flows in the CLPT.
Nationally, the fraction of Anthropocene groundwater, based on area weighting of PAs, is 38%, Holocene is 34%, and Pleistocene is 28%. These results indicate that groundwater used for public supply in the US was recharged mostly during the Holocene and Pleistocene, which is consistent with recent assessments of the distribution of groundwater age in aquifers globally5.
Implications
ACDFs are useful for evaluating the susceptibility of groundwater resources to contamination. PAs with a large fraction of Anthropocene groundwater may be susceptible to anthropogenic contamination. For example, groundwater in the BISC is 100% Anthropocene and pesticides were detected across the entire PA, albeit at low concentrations28. In contrast, groundwater in the PDBR is 95% Anthropocene, but pesticides were detected in only ~55% of the PA. The difference in pesticide prevalence reflects land use (Supplementary Table 1): the BISC is completely developed whereas the PDBR is 45% developed (Supplementary Table 1). The presence of Anthropocene water does not necessarily indicate the presence of anthropogenic contaminants but does indicate the groundwater is susceptible to contamination from human activities at the land surface.
PAs with a large fraction of Holocene or Pleistocene groundwater may be susceptible to geogenic contamination. Over long timescales, groundwater evolves geochemically as it moves along a flowpath. High concentrations of geogenic contaminants often occur from changes in pH, redox, and ionic composition29. For example, in the CMOR, high radium concentrations occur in Holocene and Pleistocene groundwater but not in Anthropocene groundwater30. Likewise, in the four Coastal PAs, high concentrations of arsenic and fluoride occur only in Pleistocene groundwater31. But it is not always the case that elevated concentrations of geogenic contaminants occur only in Holocene or Pleistocene water; geology of the PA is also important. For example, in the Glacial PA, high concentrations of arsenic and manganese occur in Anthropocene groundwater. The high concentrations are related to high organic carbon that leads to reduced geochemical conditions32,33. In the Western unconsolidated PAs, Anthropocene groundwater can contain uranium that was mobilized by anthropogenic activities at the land-surface34.
The distribution of groundwater age in a PA is also useful for understanding the sustainability of groundwater extractions1. For example, in the High Plains (HPAQ), where water levels are being lowered over large areas due to pumping, groundwater is predominately Holocene. Groundwater is being mined in the HPAQ35,36. In contrast, in the Los Angeles Coastal Basin, Holocene groundwater has been pumped from the aquifer for several decades, but the hydrologic balance is maintained by enhanced recharge that emplaces Anthropocene groundwater at rates equal to pumping20. The LA example demonstrates that the removal of Holocene groundwater is not necessarily mining. Ongoing monitoring of groundwater age can be an important component for groundwater management.
Methods
Collection of environmental tracer data
In this study, 1279 groundwater sites used for public supply were sampled over a 15-year period (2004–2018)8. Sites in each PA were sampled over a short period, usually a few months. Most sites were wells; ten were springs. Wells used for public supply have construction characteristics that vary by PA, but typically have deep construction depths and long screen lengths (Supplementary Table 1; Supplementary Fig. 4). Wells had construction depths greater than 60 m (200 ft) in more than 80% of public supply wells, and most wells had screen lengths or open intervals that spanned more than 20 m (60 ft). Groundwater samples were collected from sample points that discharge raw, untreated groundwater. USGS sampling protocols are designed to obtain samples that represent conditions in the aquifer37,38.
Samples were analyzed for dissolved and noble gases (nitrogen, helium, neon, argon, krypton, and xenon), helium isotopes (3Hetrit, 4Herad), 3H, 14C, SF6, and CFCs8. Not all tracers were sampled at every well. In California, 166 wells were sampled by the USGS for the California State Water Resources Control Board’s Groundwater Ambient Monitoring and Assessment Priority Basin Project (2004–2011). Wells sampled by the GAMA-PBP did not always include SF6 or CFCs. Groundwater samples from 1,113 sites were collected by the U.S. Geological Survey’s National Water-Quality Assessment Project (NAWQA; 2012–2018). Sites sampled by NAWQA primarily collected SF6 in preference to CFCs. At least one tracer of Anthropocene water (3H, 3Hetrit, SF6 mainly) and one tracer of pre-Anthropocene water (14C mainly) was collected at more than 95% of sites. Analytical methods are described in Supplementary Methods 1. Limits for the detection or absence of 3H, SF6, CFC-11, CFC-12, CFC-113, 14C, and 4Herad were 0.1 TU, 1 TU, 0.5 pptv, 10 pptv, 50 pptv, 5 pptv, 0.1 pmC, and 9.0 × 10−8.
Processing of environmental tracer concentrations
Environmental tracer data need to be processed to be used for computing groundwater age distributions.
Carbon 14
Measured 14C concentrations were corrected for geochemical dilution by 14C-dead sources of carbon using three methods: analytical correction models39,40, geochemical codes41,42, or by scaling the atmospheric 14C record (Supplementary Methods 2). In general, PAs that were predominantly pre-Anthropocene had 14C-corrections using inverse geochemical models and analytical correction models. In PAs that were predominantly Anthropocene, scaling the 14C-record was preferred because the other two methods tend to over-correct the 14C values of Anthropocene water. Overcorrection is particularly a problem where open-system dissolution of carbonates or silicates are the primary sources of dissolved inorganic carbon43,44,45. In these cases, multiple tracers of Anthropocene water (3H, 3Hetrit, and SF6) were used to provide an estimate of the 14C-correction factor. The correction factor was estimated by scaling the 14C record between zero and one until the predicted 14C concentrations were consistent with the other tracers of Anthropocene water (Supplementary Fig. 7). The scaling factor, based on the Anthropocene fraction, was also used for computing ages of pre-Anthropocene water. The use of the scaling factor can underestimate the potential carbon dilution experienced by older groundwater and can lead to an older estimate of age than the actual age. However, dilution factors computed from the scaling method are similar to other simple methods based on rock type or changes in δ13C46 (Supplementary Methods 2).
Although correction of 14C for dilution by dead carbon does introduce uncertainty into the 14C data, it is preferred over the use of uncorrected 14C data. The magnitude of the 14C corrections is generally 30-46 pmC and has the effect of making the apparent age of the groundwater younger. The magnitude of the correction is greater than the estimated uncertainty in the correction (<20%), which means corrected 14C are generally closer to the “true” 14C than the uncorrected values would be.
Gas tracers
The environmental tracers SF6, CFCs, 3Hetrit, and 4Herad, were corrected for contributions due to solubility equilibrium, excess air, gas fractionation, and terrigenic helium affecting 3Hetrit using the computer program DGMETA47. DGMETA uses standard methods for these corrections, and additionally incorporates model and analytical uncertainties into the correction calculations. The 3He/4He ratio of terrigenic helium, which is needed to compute 3Hetrit, was estimated for each PA by evaluating the 3He/4He of groundwater with 3H < 0.5 TU. Terrigenic helium can be entirely from radiogenic, 4Herad, decay of uranium and thorium in the Earth’s crust but can also be from mantle sources. These two sources have distinct 3He/4He ratios that were identified graphically in DGMETA. 4Herad concentrations were not used to compute age distributions when the PA had large fractions of mantle-derived helium present (>10%). For some PAs, diffusion of 4Herad from the crust can cause 4Herad ages to appear older than the actual age. Corrections for a crustal flux was estimated by matching 14C- and 4Herad- depth profiles of aquifers48,49 (Supplementary Methods 3).
Modeling groundwater age distributions of samples
Groundwater age, as defined here, is the time elapsed since water infiltrated the land surface. Travel time through the unsaturated zone was considered in models of Anthropocene groundwater. Groundwater age distributions were computed by inverse model calibration of LPMs with measured tracer concentrations using the computer program TracerLPM12. LPMs are steady-state, analytical distribution functions of idealized tracer transport in aquifers9,10,11,12. Tracer concentrations from an LPM are computed by convolution of the LPM age distribution (Supplementary Methods 4; equation 2) with each tracer’s history in recharge. The modeled age distribution of the sample is then found by varying the model parameters (mean age) of the LPM until the error between output tracer concentrations and the measured tracer concentrations, relative to the measured tracer error, is minimized. The best-fit model parameters and their errors are determined from an inverse method similar to the one described by Johnson and Faunt50. Errors associated with the fitted parameters, mean age for example, are taken from the diagonal terms of the variance–covariance matrix.
Goodness-of-fit was evaluated using the chi-square test statistic, which is a sum of the squared differences between modeled and measured tracer concentrations weighted by the squared tracer error. The errors associated with each tracer were assigned different values to reflect the uncertainty associated with correcting or estimating the concentrations of the different tracers. Generally, 3H errors were set to 10% of the measured value because the only error is associated with its analysis. The other tracers were set to 20% of their measured value to reflect the additional uncertainty with the processing of the data. The assignment of a lower error to 3H than to the other tracers gives more weight to 3H in fitting the model. Models were accepted when the chi-square was less than 10. A chi-square less than 10 indicates that the mean predicted concentration is within 10% of the measured value.
Ninety seven percent of the models had chi-square values less than 10, which is an indicator of a good fit to the tracer data. However, chi-square values less than 1 could also indicate that a model is under-constrained; ~80% had chi-square values less than 1. For samples that were under-constrained, we computed a set of multiple solutions that fit the data and selected the median mean age of the set to represent the sample. Less than 3% of the models had chi-square values greater than 10, which is an indicator of a poor fit. A poor fit could result from complicated tracer mixtures or poor model selections.
LPM tracer concentrations are computed by convolution of the age distribution with each tracer’s regional atmospheric history. Most regional records, except for 4Herad, are available in the program TracerLPM12. 3H in precipitation for each site is from Michel et al.51 based on each site’s latitude-longitude position. The 3H record is also used to compute 3Hetrit concentrations. Northern Hemisphere atmospheric mixing ratios of SF6 and CFCs were from the U.S. Geological Survey Groundwater Dating Laboratory52. Atmospheric records of 14C over the last 50,000 years were constructed by combining the international calibration curve, NH_IntCal1353 with modern tropospheric 14C data for northern Hemisphere zones (zones 1, 2, or 3)54. For some samples, the atmospheric history of 3H was scaled to match tracer relationships of Anthropocene water for groups of samples in the same area. Dilution of the 3H record can occur near eastern coastlines or can be concentrated in areas where 3H deposition is more strongly affected by precipitation events that originate at northern latitudes. Scaling factors for each sample are indicated in Table 4 of the data release accompanying this paper8.
4Herad concentrations in water were calculated from the helium production rate equation of Andrews and Lee55. The helium production rate was computed from average abundances of uranium and thorium (in ppm) in surficial rocks56 of outcrop areas of the PAs, porosity values from Manger57, and a bulk density of 2.2.
Models of groundwater age can be non-unique, so a consistent approach was implemented for a set of samples in a PA. Each sample was visually inspected to guide model selection, and to evaluate tracer concentrations for degradation, contamination, and dilution (Supplementary Methods 5). All modeling results are listed in Table 4 of the data release8. Table 4 contains all model information necessary to verify the model results in TracerLPM: measured tracer concentrations, modeled tracers, model name, tracer history used to compute LPM concentrations, scaling factors of tracer history, unsaturated zone travel time treatment, and helium-4 calculation parameters.
For most samples, a single dispersion model (DM) or a bimodal mixing model composed of two dispersion models (BMM-DM-DM) was used to model groundwater age distributions. The dispersion model is a one-dimensional analytical solution to the advection-dispersion equation58 (Supplementary Methods 4; equation 3). In general, a single DM was used when groundwater was either solely recharged since 1953 (Anthropocene) (Fig. 4; blue line) or solely recharged before 1953 (pre-Anthropocene) (Fig. 4; yellow line). In ~40% of samples, the concentrations of Anthropocene tracers were below detection levels.
a The age distribution and b Cumulative age distribution for samples of Anthropocene (since 1953) (blue line), Holocene (yellow), and mixed Anthropocene and Holocene (green) groundwater. A single dispersion model (DM) was used for Anthropocene and Holocene samples and a binary dispersion model (BMM-DM-DM) was used for the mixed age sample (green). The dispersion models were parameterized with a dispersion parameter of 0.01. The mean age of the unimodal distributions were 25 years and 150 years. For the binary dispersion model, the mean age of the first component was 10 years and the mean age of the second component was 196.5 years. The mean age of the bimodal distribution is 150 years.
A bimodal mixing model was used when tracer concentrations indicated the presence of both Anthropocene and pre-Anthropocene groundwater (Fig. 4; green line). Thirty percent of the samples had detectable concentrations of both Anthropocene and pre-Anthropocene water. In some cases, particularly the fractured- and carbonate-rock PAs (VRPD, PDBR), the bimodal model was also used when there were two components of Anthropocene groundwater (samples 1b and 3 in Supplementary Methods 5).
In some aquifers, alternative LPMs to the DM were used to model the age distributions of samples but the general approach to modeling samples as unimodal or bimodal distributions was the same. LPMs can often correspond to different well and aquifer geometries that make some LPMs more appealing than others. Jurgens et al.14 showed that multiple LPMs often give similar age distributions when fit to the same tracer data. The fitting of LPMs to tracer data often identify parts of the age distribution shared by various LPMs that most explain the measured tracer data. Consequently, assessments of age based other LPMs will yield similar results.
Errors of mean age were generally less than 10%. The median error of the mean age was 9%, the first quartile was 5% and the third quartile was 25%. Higher mean age errors are generally associated with bimodal models that point to a large range of potential ages. A 10% shift in the mean age would typically result in a change in the fraction of Anthropocene, Holocene, or Pleistocene water of less than 5%.
Data availability
All site information, locations, calculations of tracer concentrations from their analytical measurements, and model output are provided in the publicly available USGS Data Release Jurgens et al.8 (https://doi.org/10.5066/P9W7T0DN). Analytical measurements of dissolved gases, CFCs, SF6, 3H, and 14C and site information are also publicly available online through the USGS National Water Information System (NWIS, https://waterdata.usgs.gov/nwis).
Code availability
All map figures were made with ESRI ArcMap software (10.4). The baselayers are publicly available from the USGS: the hillshade is at https://www.sciencebase.gov/catalog/item/544172ece4b0b0a643c73c75; and the Principal Aquifers are at https://water.usgs.gov/GIS/metadata/usgswrd/XML/aquifers_us.xml and https://water.usgs.gov/GIS/metadata/usgswrd/XML/alluvial_and_glacial_aquifers.xml. The groundwater ages and age distributions for samples were computed using publicly available USGS software programs DGMETA and TracerLPM. Versions of these programs are available at web sites listed in the references and available at https://github.com/bcjurgens/TracerLPM or by the author upon request. The ACDFs in Fig. 2 can be generated using TracerLPM, but for convenience is also provided as Supplementary Data.
References
Ferguson, G., Cuthbert, M. O., Befus, K., Gleeson, T. & McIntosh, J. C. Rethinking groundwater age. Nat. Geosci. 13, 592–594 (2020).
Zalasiewicz, J. et al. The Working Group on the Anthropocene: summary of evidence and interim recommendations. Anthropocene 19, 55–60 (2017).
Lindsey, B. D., Jurgens, B. C., & Belitz, K. Tritium as an indicator of modern, mixed, and premodern groundwater age: U.S. Geological Survey Scientific Investigations Report 2019–5090, 18 p. https://doi.org/10.3133/sir20195090 (2019).
Gleeson, T., Befus, K. M., Jasechko, S., Luijendijk, E. & Cardenas, M. B. The global volume and distribution of modern groundwater. Nat. Geosci. 9, 161–167 (2016).
Jasechko, S. et al. Global aquifers dominated by fossil groundwaters but wells vulnerable to modern contamination. Nat. Geosci. 10, 425–429 (2017).
Miller, J. A. Ground Water Atlas of the United States: Introduction and national summary, https://doi.org/10.3133/ha730A (1999)
Lovelace, J. K. et al. Estimated groundwater withdrawals from principal aquifers in the United States, 2015 (ver. 1.2, October 2020): U.S. Geological Survey Circular 1464, 70 p. https://doi.org/10.3133/cir1464 (2020).
Jurgens, B. C. et al. Data for distribution of groundwater age in aquifers used for public supply, United States. U.S. Geological Survey Data Release, https://doi.org/10.5066/P9W7T0DN (2022).
Małoszewski, P. & Zuber, A. Determining the turnover time of groundwater systems with the aid of environmental tracers. J. Hydrol. 57, 207–231 (1982).
Cook, P. G. & Böhlke, J. K. Determining timescales for groundwater flow and solute transport. In: Cook, P. G. & Herczeg, A. L. (eds) Environmental Tracers in Subsurface Hydrology. Springer, Boston, MA. https://doi.org/10.1007/978-1-4615-4557-6_1 (2000)
Kazemi, G. A., Lehr, J. H. & Perrochet, P. Groundwater age: Kazemi/Groundwater Age. (John Wiley & Sons, Inc., 2006). https://doi.org/10.1002/0471929514.
Jurgens, B. C., Böhlke, J. K., & Eberts, S. M. TracerLPM (Version 1): An Excel® workbook for interpreting groundwater age distributions from environmental tracer data. U.S. Geological Survey Techniques and Methods Report 4-F3, 60 p. https://pubs.usgs.gov/tm/4-f3/pdf/tm4-F3.pdf (2012).
Eberts, S. M., Böhlke, J. K., Kauffman, L. J. & Jurgens, B. C. Comparison of particle-tracking and lumped-parameter age-distribution models for evaluating vulnerability of production wells to contamination. Hydrogeol. J. 20, 263–282 (2012).
Jurgens, B. C., Böhlke, J. K., Kauffman, L. J., Belitz, K. & Esser, B. K. A partial exponential lumped parameter model to evaluate groundwater age distributions and nitrate trends in long-screened wells. J. Hydrol. 543, 109–126 (2016).
Scott, J. C., Computerized stratified random site‐selection approaches for design of a ground‐water quality sampling network, U.S. Geological Survey Water Resources Investigations Report 90–4101, 109 p. https://doi.org/10.3133/wri90410 (1990).
Belitz, K., Jurgens, B., Landon, M. K., Fram, M. S. & Johnson, T. Estimation of aquifer scale proportion using equal area grids: assessment of regional scale groundwater quality: equal area grids and aquifer scale proportion. Water Resour. Res. 46, https://doi.org/10.1029/2010WR009321 (2010).
Solder, J. E., Jurgens, B., Stackelberg, P. E. & Shope, C. L. Environmental tracer evidence for connection between shallow and bedrock aquifers and high intrinsic susceptibility to contamination of the conterminous U.S. glacial aquifer. J. Hydrol. 583, 124505 (2020).
McMahon, P. B., Böhlke, J. K., & Carney, C. P. Vertical gradients in water chemistry and age in the northern High Plains aquifer, Nebraska, 2003. U.S. Geological Survey Scientific Investigations Report 2006–5294, 58 p. https://doi.org/10.3133/sir20065294 (2007)
Shelton, J. L. et al. Low-level volatile organic compounds in active public supply wells as ground-water tracers in the Los Angeles Physiographic Basin, California, 2000. U.S. Geological Survey Water-Resources Investigations Report 2001-4188, 35 p. https://doi.org/10.3133/wri20014188 (2001).
Reichard, E. G. et al. Geohydrology, geochemistry, and ground-water simulation-optimization of the central and west coast basins, Los Angeles County, California. U.S. Geological Survey Water Resources Investigations Report 2003-4065, 196 p. https://doi.org/10.3133/wri034065 (2003).
Solder, J. E. Groundwater age and susceptibility of south Atlantic and Gulf Coast principal aquifers of the contiguous United States: U.S. Geological Survey Scientific Investigations Report 2020–5050, 46 p. https://doi.org/10.3133/sir20205050 (2020).
Bredehoeft, J. D. Neuzil, C. E., & Milly, P. C. Regional flow in the Dakota aquifer; a study of the role of confining layers. U.S. Geological Survey Water Supply Paper 2237, 45 https://doi.org/10.3133/wsp2237 (1983).
Williamson, A. K., & Grubb, H. F. Groundwater flow in the Gulf Coast aquifer systems, south-central United States. U.S. Geological Survey Professional Paper 01-1416, Chapter F, 173 p. https://doi.org/10.3133/pp1416F (2001).
Clark, B. R., Westerman, D. A., & Fugitt, D. T. Enhancements to the Mississippi Embayment Regional Aquifer Study (MERAS) groundwater-flow model and simulations of sustainable water-level scenarios: U.S. Geological Survey Scientific Investigations Report 2013–5161, 29 p. http://pubs.usgs.gov/sir/2013/5161/ (2013).
Masterson, J. P. et al. Documentation of a groundwater flow model developed to assess groundwater availability in the Northern Atlantic Coastal Plain aquifer system from Long Island, New York, to North Carolina (ver. 1.1, December 2016): U.S. Geological Survey Scientific Investigations Report 2016–5076, 70 p. https://doi.org/10.3133/sir20165076 (2016).
Mandle, R. J. & Kontis, A. L. Simulation of regional ground-water flow in the Cambrian-Ordovician aquifer system in the norther Midwest, United States: in Regional aquifer-system analysis, U.S. Geological Survey Professional Paper 1405-C, 97 p. https://doi.org/10.3133/pp1405C (1992).
Yager, R. M. et al. Characterization and occurrence of confined and unconfined aquifers in Quaternary sediments in the glaciated conterminous United States (ver. 1.1, February 2019): U.S. Geological Survey Scientific Investigations Report 2018–5091, 90 p. https://doi.org/10.3133/sir20185091 (2019).
Bexfield, L. M., Belitz, K., Lindsey, B. D., Toccalino, P. L. & Nowell, L. H. Pesticides and pesticide degradates in groundwater used for public supply across the United States: occurrence and human-health context. Environ. Sci. Technol. 55, 362–372 (2021).
Appelo, C. A. J., Postma, D. & Appelo, C. A. J. Geochemistry, Groundwater and Pollution, Second Edition. (CRC Press, 2004).
Stackelberg, P. E., Szabo, Z. & Jurgens, B. C. Radium mobility and the age of groundwater in public-drinking-water supplies from the Cambrian-Ordovician aquifer system, north-central USA. Appl. Geochem. 89, 34–48 (2018).
Degnan, J. R., Lindsey, B. D., Levitt, J. P. & Szabo, Z. The relation of geogenic contaminants to groundwater age, aquifer hydrologic position, water type, and redox conditions in Atlantic and Gulf Coastal Plain aquifers, eastern and south-central USA. Sci. Total Environ. 723, 137835 (2020).
Erickson, M. L., Yager, R. M., Kauffman, L. J. & Wilson, J. T. Drinking water quality in the glacial aquifer system, northern USA. Sci. Total Environ. 694, 133735 (2019).
Levitt, J. P., Degnan, J. R., Flanagan, S. M. & Jurgens, B. C. Arsenic variability and groundwater age in three water supply wells in southeast New Hampshire. Geosci. Front. 10, 1669–1683 (2019).
Burow, K. R., Belitz, K., Dubrovsky, N. M. & Jurgens, B. C. Large decadal-scale changes in uranium and bicarbonate in groundwater of the irrigated western U.S. Sci. Total Environ. 586, 87–95 (2017).
Scanlon, B. R. et al. Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley. Proc. Natl Acad. Sci. 109, 9320–9325 (2012).
Konikow, L. F. Long-term groundwater depletion in the United States. Groundwater 53, 2–9 (2015).
U.S. Geological Survey National field manual for the collection of water-quality data: U.S. Geological Survey Techniques of Water-Resources Investigations, book 9, chaps. A1-A10, (Variously dated) available online at http://pubs.water.usgs.gov/twri9A
Koterba, M. T., Wilde, F. D. & Lapham, W. W. Ground-water data-collection protocols and procedures for the National Water-Quality Assessment Program—Collection and documentation of water-quality samples and related data. U.S. Geological Survey Open-File Report 95-399., 113. https://doi.org/10.3133/ofr95399 (1995).
Tamers, M. A. Validity of radiocarbon dates on ground water. Geophys. Surv. 2, 217–239 (1975).
Han, L.-F. & Plummer, L. N. Revision of Fontes & Garnier’s model for the initial 14C content of dissolved inorganic carbon used in groundwater dating. Chem. Geol. 351, 105–114 (2013).
Plummer, L. N., Prestemon, E. C. & Parkhurst, D. L. An interactive code (NETPATH) for modeling NET geochemical reactions along a flow PATH, version 2.0: U.S. Geological Survey Water-Resources Investigations Report 94-4169, 130 p. http://pubs.er.usgs.gov/usgspubs/wri/wri944169 (1994).
Parkhurst, D. L. & Charlton, S. R. NetpathXL—An Excel® interface to the program NETPATH: U.S. Geological Survey Techniques and Methods 6-A26, 11 p. https://doi.org/10.3133/tm6A26 (2008).
Cartwright, I., Fifield, L. K. & Morgenstern, U. Using 3H and 14C to constrain the degree of closed-system dissolution of calcite in groundwater. Appl. Geochem. 32, 118–128 (2013).
Cartwright, I., Currell, M. J., Cendón, D. I. & Meredith, K. T. A review of the use of radiocarbon to estimate groundwater residence times in semi-arid and arid areas. J. Hydrol. 580, 124247 (2020).
Seltzer, A. M. et al. Groundwater residence time estimates obscured by anthropogenic carbonate. Sci. Adv. 7, eabf3503 (2021).
Ingerson, E. & Pearson, F. J. Estimation of age and rate of motion of groundwater by the 14C-method. Recent researches in the fields of atmosphere, hydrosphere and nuclear geochemistry 263-283 (1964).
Jurgens, B. C. et al. DGMETA (Version 1): dissolved gas modeling and environmental tracer analysis computer program. U.S. Geological Survey Techniques and Methods Report 4-F5, 50 p. https://doi.org/10.3133/tm4F5 (2020).
Stute, M., Sonntag, C., Deák, J. & Schlosser, P. Helium in deep circulating groundwater in the Great Hungarian Plain: Flow dynamics and crustal and mantle helium fluxes. Geochim. Cosmochim. Acta 56, 2051–2067 (1992).
Kulongoski, J. T., Hilton, D. R. & Izbicki, J. A. Source and movement of helium in the eastern Morongo groundwater Basin: the influence of regional tectonics on crustal and mantle helium fluxes. Geochim. Cosmochim. Acta 69, 3857–3872 (2005).
Johnson, M. L. & Faunt, L. M. Parameter estimation by least-squares methods, in: Methods in Enzymology, Numerical Computer Methods. Academic Press, pp. 1–37, https://doi.org/10.1016/0076-6879(92)10003-V (1992).
Michel, R. L., Jurgens, B. C. & Young, M. B. Tritium deposition in precipitation in the United States, 1953 – 2012, U.S. Geological Survey Scientific Investigations Report 2018-5086, 11 p. https://doi.org/10.3133/sir20185086 (2018).
U.S. Geological Survey. CFC and SF6 Air Curves (2016) U.S. Geological Survey Web Site, https://water.usgs.gov/lab/software/air_curve/index.html.
Reimer, P. J. et al. IntCal13 and marine13 radiocarbon age calibration curves 0–50,000 years cal BP. Radiocarbon 55, 1869–1887 (2013).
Hua, Q., Barbetti, M. & Rakowski, A. Z. Atmospheric radiocarbon for the period 1950–2010. Radiocarbon 55, 2059–2072 (2013).
Andrews, J. N. & Lee, D. J. Inert gases in groundwater from the Bunter Sandstone of England as indicators of age and palaeoclimatic trends. J. Hydrol. 41, 233–252 (1979).
Phillips, J. D., Duval, J. S. & Ambroziak, R. A. National geophysical data grids; gamma-ray, gravity, magnetic, and topographic data for the conterminous United States: U.S. Geological Survey Digital Data Series DDS-9, https://doi.org/10.3133/ds9 (1993).
Manger, G. E. Porosity and bulk density of sedimentary rocks, in: U.S. Geological Survey Bulletin 1144-E, 55 p. https://doi.org/10.3133/b1144E (1963).
Kreft, A. & Zuber, A. On the physical meaning of the dispersion equation and its solutions for different initial and boundary conditions. Chem. Eng. Sci. 33, 1471–1480 (1978).
Acknowledgements
This work was part of the U.S. Geological Survey’s National Water-Quality Assessment Project. We thank the many water purveyors and well owners that gave us access to their wells. We thank the editors, two anonymous reviewers, and Ian Cartwright for their reviews of the manuscript. Early versions of this manuscript also improved from comments from Ward Sanford, Justin Kulongoski, John Solder, and Marylynn Musgrove.
Author information
Authors and Affiliations
Contributions
B.C.J. and K.B. conceived the idea, led the study, and wrote the manuscript. K.F. and P.B.M. contributed data analysis and reviewed early versions of the manuscript. A.G.H., G.C., and M.B.Y conducted oversaw the laboratory analyses of tracers.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Ian Cartwright, Jürgen Sültenfuß and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Rahim Barzegar, Joe Aslin.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jurgens, B.C., Faulkner, K., McMahon, P.B. et al. Over a third of groundwater in USA public-supply aquifers is Anthropocene-age and susceptible to surface contamination. Commun Earth Environ 3, 153 (2022). https://doi.org/10.1038/s43247-022-00473-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-022-00473-y
This article is cited by
-
Modern groundwater reaches deeper depths in heavily pumped aquifer systems
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.