Abstract
Recognizing direct relationships between variables connected in a network is a pervasive problem in biological, social and information sciences as correlation-based networks contain numerous indirect relationships. Here we present a general method for inferring direct effects from an observed correlation matrix containing both direct and indirect effects. We formulate the problem as the inverse of network convolution, and introduce an algorithm that removes the combined effect of all indirect paths of arbitrary length in a closed-form solution by exploiting eigen-decomposition and infinite-series sums. We demonstrate the effectiveness of our approach in several network applications: distinguishing direct targets in gene expression regulatory networks; recognizing directly interacting amino-acid residues for protein structure prediction from sequence alignments; and distinguishing strong collaborations in co-authorship social networks using connectivity information alone. In addition to its theoretical impact as a foundational graph theoretic tool, our results suggest network deconvolution is widely applicable for computing direct dependencies in network science across diverse disciplines.
Similar content being viewed by others
Main
Network science has been widely adopted in recent years in diverse settings, including molecular and cell biology1, social sciences2, information science3, document mining4 and other data mining applications. Networks provide an efficient representation for variable interdependencies, represented as weighted edges between pairs of nodes, with the edge weight typically corresponding to the confidence or the strength of a given relationship. Given a set of observations relating the values that elements of the network take in different conditions, a network structure is typically inferred by computing the pairwise correlation, mutual information or other similarity metrics between each pair of nodes.
The resulting edges include numerous indirect dependencies owing to transitive effects of correlations. For example, if there is a strong dependency between nodes 1 and 2, and between nodes 2 and 3 in the true (direct) network, high correlations will also be visible between nodes 1 and 3 in the observed (direct and indirect) network, thus inferring an edge from node 1 to node 3, even though there is no direct information flow between them (Fig. 1a). Moreover, even if a true relationship exists between a pair of nodes, its strength may be over-estimated owing to additional indirect relationships, and distinguishing the convolved direct and indirect contributions is a daunting task. As the size of networks increases, a very large number of indirect edges may be due to second-order, third-order and higher-order interactions, resulting in diffusion of the information contained in the direct network, and leading to inaccurate network structures and network weights in many applications1,5,6,7,8,9,10,11.
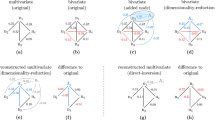
(a) Direct edges in a network (solid blue arrows) can lead to indirect relationships (dashed red arrows) as a result of transitive information flow. These indirect contributions can be of length 2 (e.g., 1→2→3), 3 (e.g., 1→2→3→5) or higher, and can combine both direct and indirect effects (e.g., 2→4), and multiple indirect effects along varying paths (e.g., 2→3→5, 2→4→5). Self-loops are excluded from networks. Network deconvolution seeks to reverse the effect of transitive information flow across all indirect paths in order to recover the true direct network (blue edges, Gdir) based on the observed network (combined blue and red edges, Gobs). (b) Algebraically, the transitive closure of a network can be expressed as an infinite sum of the true direct network and all indirect effects along paths of increasing lengths, which can be written in a closed form as an infinite-series sum. Network deconvolution exploits this closed form to express the direct network Gdir as a function of the observed network Gobs. (c) To efficiently compute this inverse operation, we express both the true and observed networks Gdir and Gobs by decomposition into their eigenvectors and eigenvalues, which enables each eigenvalue λidir of the original network to be expressed as a nonlinear function of a single corresponding eigenvalue λiobs of the convolved observed network. (d,e) Network deconvolution assumes that indirect flow weights can be approximated as the product of direct edge weights, and that observed edge weights are the sum of direct and indirect flows. When these assumptions hold (d), network deconvolution removes all indirect flow effects and infers all direct interactions and weights exactly. Even when these assumptions do not hold (e), network deconvolution infers 87% of direct edges, showing robustness to nonlinear effects.
Several approaches have been proposed to infer direct dependencies among variables in a network. For example, partial correlations have been used to characterize conditional relationships among small sets of variables12,13,14, and probabilistic approaches, such as maximum entropy models, have been used to identify informative network edges10,15,16. Other works use graphical models and message-passing algorithms to characterize direct information flows in a network17,18, or variations of Granger causality19 to capture the dynamic relationships among variables20,21,22. Alternative approaches formulated the problem of separating direct from indirect dependencies as a general feature-selection problem23,24,25, using Bayesian networks26,27,28, or using an information-theoretic approach to eliminate indirect information flow in the network29. These methods are limited to relatively low-order interaction terms29, or are computationally very expensive12,13,14, or are designed for specific applications10,15,16,17,30,31, thus limiting their applicability.
In this paper, we formulate the problem of network deconvolution in a graph-theoretic framework. Our goal is a systematic method for inferring the direct dependencies in a network, corresponding to true interactions, and removing the effects of transitive relationships that result from indirect effects. When the matrix of direct dependencies is known, all transitive relationships can be computed by summing this direct matrix and all its powers, corresponding to the transitive closure of a weighted adjacency matrix, which convolves all direct and indirect paths at all lengths (Fig. 1b). Given an observed matrix of correlations that contains both direct and indirect effects, our task is to recover the original direct matrix that gave rise to the observed matrix. For a weighted network where edge weights represent the confidence, mutual information or correlation strength relating two elements in the network, the inverse problem seeks to recognize the fraction of the weight of each edge attributable to direct versus indirect contributions, rather than to keep or remove unit-weight edges. This inverse problem is dramatically harder than the forward problem of transitive closure, as the original matrix is not known.
We introduce an algorithm for network deconvolution that can efficiently solve the inverse problem of transitive closure of a weighted adjacency matrix, by use of decomposition principles of eigenvectors and eigenvalues, and by exploiting the closed form solution of infinite Taylor series. We demonstrate the effectiveness of this approach and our algorithm in several large-scale networks from different domains and with different properties (Supplementary Table 1). First, we seek to distinguish likely direct targets in gene regulatory networks as a post-processing step for diverse gene network inference methods, and show that network deconvolution improves both global and local network quality. Second, we show the effectiveness of network deconvolution in distinguishing directly interacting amino-acid residues based on pairwise mutual information data in multispecies protein alignments. Third, we apply network deconvolution to a social network setting using a co-authorship network that contains solely connectivity information, and show that the resulting edge weights are able to distinguish strong and weak ties independently inferred based on the number of joint papers and additional co-authors. The wide applicability of network deconvolution suggests that such a closed-form solution is not only of important theoretical use in reversing the effect of matrix transitive closure, but also of wide practical applicability in a diverse set of real-world networks.
Results
Resolving direct and indirect dependencies in a graph
Mathematically, we model the weights of an observed network Gobs, whose diagonal is set to zero, as the sum of both direct weights in the true network Gdir, and indirect weights due to indirect paths of increasing length in  ,
,  and others (Fig. 1a). The inverse problem of inferring the direct network from the observed network is seemingly intractable, as the direct information has now diffused through the observed network beyond recognition. However, expressing Gobs as an infinite sum of the exponentially decreasing contributions of increasingly indirect paths leads to a closed form solution for Gobs as a function of Gdir using an infinite-series summation (Fig. 1b). Moreover, by decomposing the observed network into its eigenvalues and eigenvectors, which provide a factorization of the connectivity matrix into its canonical form, we can express each eigenvalue of the direct matrix as a function of the corresponding eigenvalue of the observed matrix (Fig. 1c). This decomposition leads to a simple closed-form solution for Gdir and provides a framework for an efficient globally optimal algorithm to deconvolve the contributions of direct and indirect edges given an observed network (Online Methods and Supplementary Note, 1).
and others (Fig. 1a). The inverse problem of inferring the direct network from the observed network is seemingly intractable, as the direct information has now diffused through the observed network beyond recognition. However, expressing Gobs as an infinite sum of the exponentially decreasing contributions of increasingly indirect paths leads to a closed form solution for Gobs as a function of Gdir using an infinite-series summation (Fig. 1b). Moreover, by decomposing the observed network into its eigenvalues and eigenvectors, which provide a factorization of the connectivity matrix into its canonical form, we can express each eigenvalue of the direct matrix as a function of the corresponding eigenvalue of the observed matrix (Fig. 1c). This decomposition leads to a simple closed-form solution for Gdir and provides a framework for an efficient globally optimal algorithm to deconvolve the contributions of direct and indirect edges given an observed network (Online Methods and Supplementary Note, 1).
The resulting network deconvolution algorithm can be viewed as a nonlinear filter over eigenvalues of a locally observed network to compute global edge significance, removing indirect flow effects for each eigenvalue by computing the inverse of a Taylor series expansion (Supplementary Fig. 1). This results in the decrease of large positive eigenvalues of the observed dependency matrix that are inflated owing to indirect effects. The eigenvalue/eigenvector matrix decomposition holds for all symmetric matrices, including all correlation or information-based matrices, and also for some asymmetric input matrices, such as those in Supplementary Note, 1.4.1. For nondecomposable matrices, we present an iterative conjugate gradient descent approach for network deconvolution that converges to a globally optimal solution by convex optimization (Supplementary Note, 1.4.2 and Supplementary Fig. 2).
Our formulation of network deconvolution has two underlying modeling assumptions: first that indirect flow weights can be approximated as the product of direct edge weights, and second, that observed edge weights are the sum of direct and indirect flows. When these assumptions hold, network deconvolution provides an exact closed-form solution for completely removing all indirect flow effects and inferring all direct interactions and weights exactly (Fig. 1d). We show that network deconvolution performs well even when these assumptions do not hold, by inclusion of nonlinear effects through simulations when the direct edges are known (Fig. 1e and Supplementary Note, 1.3) and by application to diverse real-world biological and social networks where additional properties can be independently evaluated. Our Taylor series closed-form solution assumes that all eigenvalues of the direct dependency matrix are between –1 and 1, which leads to a geometric decrease in the contributions of indirect paths of increasing lengths (Supplementary Note, 1.2). This assumption can be achieved for any matrix by scaling the observed input network by a function of the magnitude of its eigenvalues (Supplementary Note, 1.6 and Supplementary Fig. 4).
We also provide a useful generalization of network deconvolution when the observation dependency matrix is itself noisy (Supplementary Note, 1.5). Although direct dependency weights cannot be recovered exactly from the noisy observations, we show that the resulting estimates are close to true weights for moderate noise levels in the input data sets (Supplementary Fig. 3). We also present two extensions of the network deconvolution algorithm (Supplementary Note, 1.7) that make it scalable to very large networks: the first exploits the sparsity of eigenvalues of low rank networks, and the second parallelizes network deconvolution over potentially overlapping subgraphs of the network (Supplementary Fig. 5).
We next apply our network deconvolution approach to three settings: (i) inferring gene regulatory networks, (ii) inferring protein structural constraints and (iii) inferring weak and strong ties in social networks.
Application to gene regulatory networks
We first apply our network deconvolution algorithm to gene regulatory networks, which are pervasively used in molecular biology to describe regulatory relationships between transcription factors (regulators) and their target genes1. Regulatory network inference from high-throughput gene expression data1,6,32, or by integrating complementary types of data sets33,34,35, is a well-studied problem in computational molecular biology26,29,36,37, enabling us to benefit from available data sets and community efforts for direct method comparisons1,6. Perhaps the largest such comparison is the recently published network inference challenge part of the Dialogue on Reverse Engineering Assessment and Methods (DREAM) project5.
In the DREAM5 network inference challenge5, different methods were applied to reconstruct networks for the bacterium Escherichia coli and the single-celled eukaryote Saccharomyces cerevisiae based on experimental data sets, and to reconstruct an in silico network based on simulated data sets (Supplementary Note, 2.1 and Supplementary Fig. 6). True positive interactions were defined as a set of experimentally validated interactions from the RegulonDB database for E. coli38, and a high-confidence set of interactions supported by genome-wide transcription-factor binding data (ChIP-chip) and evolutionarily conserved binding motifs for S. cerevisiae39. All methods were evaluated using the same four performance evaluation metrics: (i) the area under the precision-recall curve; (ii) the area under the receiver operating characteristic curve; (iii) a combined per-network score that utilizes both previous metrics for each individual network; and (iv) an overall per-method score that summarizes the combined performance across all three networks (Online Methods and Supplementary Note, 2.3). The DREAM5 challenge provides an ideal benchmark for evaluating network deconvolution, given the uniform benchmarks for network reconstruction used, and the participation of many of the research teams at the forefront of network inference research, with a total of 35 different prediction methods applied across a wide array of methodologies.
Given that network deconvolution is designed as a way to eliminate indirect edge weights in mutual information–based and correlation-based networks, we first applied it to the networks predicted by the top-scorers of such methods, including CLR37, ARACNE29 and basic mutual information (relevance networks)40. In all cases, we found that network deconvolution substantially improved the performance of each method according to all metrics used and for all networks tested in DREAM5 (Fig. 2a). The average per-method score increased by 66%, and the per-network scores increased by 61%, 78% and >300-fold in the in silico, E. coli and S. cerevisiae networks, respectively, (the strong S. cerevisiae improvements are due to low scores for all methods). It is notable that ARACNE, which seeks to remove transitive edges by studying feed-forward loops directly, showed a 87% improvement by network deconvolution, indicating that these indirect effects are not always detectable at the local level but instead require a global network deconvolution approach. As information theory methods are among the most widely used network inference approaches5,6, their use in combination with network deconvolution can be of great general use.
(a) Network deconvolution applied to the inferred networks of top-scoring methods from DREAM5 leads to consistent improvements for mutual information (MI) and correlationbased methods (average performance increase, 66%). Network deconvolution also improves other top-scoring methods (11% on average), including the best-performing method of the DREAM5 challenge (GENIE3), thus leading to a new overall highest performance. Moreover, the community network obtained by integrating network predictions from individual methods (1–9) before network deconvolution is outperformed by the community network based on deconvolved networks by ∼25%. The bottom panel shows the performance of network deconvolution for eigenvalue scaling parameter (beta) 0.5 and 0.9 in the corresponding application (DREAM5), showing our results are robust to the choice of this parameter (Supplementary Note 1.6 and Supplementary Fig. 4). b Network motif analysis showing the relative performance of inference methods for cascades (casc.) and feed-forward loops (FFL) before and after network deconvolution. Red and blue corresponds to increased and decreased prediction accuracy, respectively, of the two motif types relative to the overall performance of the method before network deconvolution (measured by AUROC; Supplementary Note, 2.4). The original methods (before network deconvolution, left side) have different relative performances for cascades and FFLs, for example, MI–based network inference tends to include feed-forward edges (red arrow), resulting in higher accuracy for FFLs but lower accuracy for cascades, whereas the opposite is true for the Inferelator and ANOVerence. The deconvolved networks (after network deconvolution, right side) show significantly higher accuracy (AUROC) for true cascade network motifs for all methods, and moderately improved accuracy for FFLs on average, showing that network deconvolution successfully eliminates spurious indirect feed-forward edges for true cascade motifs, without sacrificing accuracy for true FFLs.
We next applied network deconvolution to other top-performing inference methods that are not based on mutual information or correlation. These include ANOVerence41 that uses a nonparametric nonlinear similarity metric between transcription factors and target genes, GENIE3 (ref. 23) that uses regression and a tree-based ensemble method, TIGRESS42 that uses a sparse regression formulation and feature selection, and Inferelator32 that uses regression and variable selection based on expression data. We found that network deconvolution was effective even when applied to these methods, leading to an overall performance increase of 11% on average using the same metric. The performance was increased for three of the four methods, including for the top-performing method (GENIE3), which increased by 13%. As GENIE3 was the overall top-performing method, this suggests that the combination of GENIE3 and network deconvolution provides the new top-performing method, outperforming all other 35 methods that were assessed in the DREAM5 challenge5. We also applied network deconvolution in combination with the community prediction method from DREAM5 (ref. 5). We found that community prediction after network deconvolution showed 25% greater performance than community prediction on the original networks, suggesting that network deconvolution maintains the complementary aspects of these networks important in community prediction approaches. We note that the community prediction approach is not the best predictor here, with or without network deconvolution, probably owing to the insufficiently diverse nature of the original networks. Overall, these results suggest that despite the ability of even the best-performing methods to recover high-quality networks, strong indirect effects remain, which can be reduced by use of network deconvolution.
We next studied how network deconvolution affects the prediction of local network connectivity patterns. We specifically focused on the ability to correctly predict feed-forward loops, that truly contain both an indirect A→B→C path and a feed-forward A→C edge, and regulatory cascades, for which A and C are only connected through B (Supplementary Note, 2.4). Consistent with previous studies5, we found that network inference methods tend to perform better on one or the other network motif, based on their approach for dealing with indirect information (Fig. 2b). For example, mutual information–based network inference (MI) is biased toward including feed-forward edges, leading to increased accuracy for feed-forward loops, but many spurious transitive edges for cascades, whereas the Inferelator and ANOVerence are biased toward excluding feed-forward edges, leading to increased accuracy for cascades but many missing feed-forward edges in feed-forward loops. Notably, the ARACNE algorithm, which seeks to directly remove transitive edges, shows a decreased performance for feed-forward loops relative to MI, highlighting the difficulty of distinguishing transitive edges from true feed-forward edges. If network deconvolution can accurately identify spurious indirect edges but preserve true feed-forward edges, we should expect substantially increased accuracy for cascades, and no decrease in accuracy for feed-forward edges. Indeed, we found that deconvolved networks lead to improved prediction accuracy for true cascades for each method, thus correctly eliminating spurious A → C edges (Fig. 2b). Importantly, the improved performance on cascades did not lead to an increased error rate on feed-forward loops, where prediction accuracy remained similar or improved in most deconvolved networks, with the exception of TIGRESS, which was also the only method where network deconvolution did not lead to an improved overall performance. Taken together, these results show that network deconvolution effectively distinguishes direct from indirect edges, improving the predictions of a wide range of gene regulatory network inference approaches.
Application to protein structural constraints
We next applied ND to infer structural constraints between pairs of amino-acids for protein structure prediction43,44,45. Prior work used evolutionary information to reveal pairs of amino acid residues that are proximal in the three-dimensional protein structure. However, the pairwise evolutionary correlation matrix may contain many transitive relationships between pairs of residues7,8,9,10,17,31,46,47,48,49. For example, if two amino-acid residues both interact with an intermediate residue, but are not directly interacting with each other, they will show high mutual information owing to indirect effects. One approach to remove transitive noise is to use a probabilistic maximum entropy solution10 that is specifically designed for inferring directly interacting residues15,16,30. Our aim here is to demonstrate effectiveness of using network deconvolution as a general method to infer directly interacting residues over protein contact networks.
As strong clusters of high mutual information have been shown to hinder identification of directly interacting residues, we reasoned that network deconvolution may be able to break up these clusters and reveal directly interacting residues, by distinguishing those correlations that can be explained by transitive relationships. Here, we build on an approach which uses comparative genomics information of residue co-variation across evolutionarily diverged species.
We applied network deconvolution to predict contact maps on fifteen proteins in different folding classes with sizes ranging from 50 to 260 residues15 (Supplementary Table 2). In our input network, the nodes represent amino acid residues, and each edge between a pair of residues represents their co-variation across multiple sequence alignments spanning 2,000–72,000 sequences, quantified by their mutual information. Applying network deconvolution to a mutual information network leads to a systematic and substantial increase in the discovery rate of interacting amino-acids, based on non-adjacent amino-acid contact maps for known structures (Fig. 3a and Supplementary Fig. 7). High mutual information residue pairs contain both physically interacting residues and non-interacting residues, presumably owing to indirect interactions. Application of network deconvolution reduces the scores of non-interacting pairs and facilitates distinguishing directly interacting ones (Fig. 3b).
(a) Applying network deconvolution to predict experimentally determined residue contacts (gray dots) based on amino-acid sequence alignments on 15 proteins in different folding classes with sizes ranging from 50 to 260 residues in human. We applied network deconvolution to networks derived by mutual information (MI) and direct information15 (DI). Each plot shows the full residue contact map twice, with the lower left triangle showing network deconvolution (ND) applied to MI, and upper right triangle showing ND applied to DI. Arrows highlight distinct residue interactions captured by each method, highlighting the improvement over both MI and DI. (b) Cumulative distributions of graph weights for interacting and noninteracting amino acid pairs, for both MI (blue) and network deconvolution (ND, red), of all proteins except 1hzx as all methods have very low performance prior to network deconvolution, possibly due to its poor sequence alignment. Network deconvolution assigns higher weights to true-positive edges and lower weights to false negatives, leading to sevenfold higher discrimination between true contacts and indirect ones for the 10% of edges with highest scores.
We also applied network deconvolution to a weighted interaction network based on direct information15. Although using network deconvolution over direct information led to a small improvement over the top predictions, which was especially consistent for non-redundant interacting pairs (Supplementary Fig. 7b), a robust performance assessment requires comparison of predicted proteins 3D structures, which is beyond the scope of this study (Supplementary Figs. 8–10).
Application to co-authorship collaboration relationships
We next applied our network deconvolution approach to a social network of co-authorship information50 to distinguish strong and weak collaborations, that can play different key roles in social networks11,51,52,53. Given the recent surge of social networks like Facebook or ResearchGate, recognizing weak and strong ties is increasingly important for recommending friends or colleagues, recognizing conflicts of interest or evaluating an author's contribution to a team. Previous approaches have defined strong ties using shared indirect contacts54, edges that increase network distance upon removal or edges connecting nodes within the same module52. In co-authorship networks, strong ties have been defined by using additional information beyond network connectivity (Supplementary Note, 4), including the number of co-authored papers and the number of other co-authors of these papers50,55.
We used an unweighted input network of 1,589 scientists working in the field of network science50, in which two authors are connected by an edge if they have co-authored at least one paper. We then applied our network deconvolution approach directly on the edges provided by the co-authorship network, to recognize whether network connectivity information alone is sufficient to capture additional information about strong and weak ties previously computed on the same network. Our assumption is that edges resulting from indirect paths likely correspond to weak collaborations, diluted over many other co-authors, whereas edges with low indirect contributions are more likely to correspond to meaningful collaborations. Application of network deconvolution to this unit-weight network led to a weighted network whose transitive closure most closely captures the input network information, and whose weights represent the inferred strength of likely direct interactions. We then ranked all co-authorship edges according to the weight assigned to each by the network deconvolution approach.
We found that the resulting edge weights indeed capture co-authorship tie strengths previously computed by summing the number of co-authored papers and down-weighting each paper by the number of additional co-authors55. We defined true strong ties based on Newman's weight ≥ 0.5 (36% of edges) that incorporates additional publication information, and our predictions based on the network deconvolution weight corresponding to the same fraction of edges (network deconvolution weight ≥ 0.64). We found that network deconvolution correctly recovered 77% of strong co-authorship ties solely by use of the network topology, demonstrating that additional information about collaboration strength lies within network connectivity information, and that network deconvolution is very well-suited for discovering it (Fig. 4a). Beyond the binary classification of edges into strong and weak, we found a strong overall agreement between the rank obtained by the true collaboration strength and the rank provided by the network deconvolution weight (correlation coefficient R2 = 0.74, Fig. 4b). The exception was a population of edges that had strong collaboration scores but weak network deconvolution weights, likely due to the number of co-authored publications that factors in the collaboration score but is not available in the network deconvolution network input. Indeed, collaborators connected by a strong edge that were incorrectly predicted by network deconvolution had on average co-authored sixfold more papers per author than collaborators correctly predicted as weak, suggesting a very strong additional bias beyond the information provided by the topology. With the widespread availability of social networks and the current interest in predicting strong and weak social ties, we expect that network deconvolution will be widely useful in many social network applications beyond co-authorship.
(a) Use of network deconvolution to distinguishing strong ties from weak ties in the largest connected component of a co-authorship network containing 379 authors. True collaboration strengths were computed by summing the number of co-authored papers and down-weighting each paper by the number of additional co-authors. Network deconvolution only had access to unweighted co-authorship edges, but exploiting transitive relationships to weigh down weak ties resulting in 77% accurate predictions (solid lines) and only 23% inaccurate predictions (dashed lines), demonstrating that this information lies within the network edges, and that network deconvolution is well-suited for discovering it. (b) Beyond the binary classification of strong and weak ties, we found a strong correlation (R2 = 0.74) across all 2,742 edges connecting 1,589 authors, between the weights assigned by network deconvolution (ND) and the true collaboration strengths obtained using additional publication details.
Discussion
Network deconvolution provides a general framework for computing direct dependencies in a network by use of observed similarities. It can recognize and remove spurious transitive edges due to indirect effects, decrease edge weights that are overestimated owing to indirect relationships, and assign edge weights corresponding to direct dependencies to the remaining edges. Thereby, network deconvolution can improve the quality of a broad range of observed networks that are tainted by indirect edge weights because of transitive effects. We introduced an efficient and scalable algorithm for deconvolving an observed network based on a nonlinear filter computing the inverse of a Taylor series expansion over each eigenvalue. We demonstrated that network deconvolution is effective for gene regulatory network inference, protein contact prediction based on protein sequence alignment and inference of collaboration strength from co-authorship social networks. In each case, even though we did not use domain-specific knowledge, network deconvolution was effective, illustrating the generality and wide applicability of the approach.
The problem of indirect spurious edges has been widely recognized in network inference, but characterized mostly at the local level. In particular, even top-performing network inference methods have been shown to contain many false transitive edges in cascade network motifs, and efforts to remedy this situation lead to incorrect removal of true edges in feed-forward loops5. At this local level, we have shown that network deconvolution has the ability to correctly remove spurious transitive edges in true cascade network motifs, while maintaining true feed-forward edges in feed-forward network motifs. In contrast to previous methods that make well-documented tradeoffs in sensitivity versus specificity for these transitive edges5, network deconvolution reduces the number of false positives on indirect interactions, while maintaining true positives in feed-forward loops.
However, network deconvolution has a much broader effect than simply removing local indirect edges. In contrast to previous approaches that study local patterns of dependencies to recognize potential indirect edges, network deconvolution takes a global approach by directly inverting the transitive closure of the true network. Previous algorithms29 have sought local approximations to the removal of indirect effects which have been limited to indirect paths of only limited lengths (typically of length 2), owing to the computational complexity of enumerating and evaluating all higher-order paths, and the lack of a systematic way to compute their combined effects. By exploiting eigenvector decomposition and Taylor series closed form solutions, network deconvolution provides four advantages over local approaches: (i) it leads to a much more computationally efficient solution, (ii) it has the power to remove indirect effects over paths with arbitrary lengths, (iii) it can remove the combined effects of arbitrarily many indirect paths between two nodes and (iv) it eliminates the need for iterative network refinement. These advantages are due to the fact that network deconvolution is essentially a single global operation to subtract the transitive effects of all powers of an adjacency matrix, rather than testing only pair-wise relationships or small network motifs one at a time.
Moreover, we showed that network deconvolution can be applied to networks with very different properties. The networks used here were of different size, density, clustering coefficient or network centrality, showing that network deconvolution is robust to these parameters. The input networks were also based on different properties, including mutual information and correlation that network deconvolution was designed for, but also networks based on regression, tree-based ensemble methods, feature selection approaches and other nonlinear similarity metrics. We also applied network deconvolution to both weighted and unweighted networks, and used the results both for reweighing of edges and for edge classification, demonstrating the discrete and continuous applications of the approach. More generally, network deconvolution is not just about edge inclusion or removal, but about probabilistic weighing of individual edges to reveal direct interactions based on observed relationships across the complete network.
We believe that the network deconvolution algorithm introduced here will serve as a foundational graph theoretic tool for computing direct dependencies in many problems in network science and other fields. Although the forward problem of repeated matrix multiplication, also known as network convolution or matrix interpolation in applied fields, has been a key graph theoretical tool, the inverse problem has received relatively little attention. Matrix interpolation has been used in protein-protein interaction networks to propagate functional information through the network56, in movies and shopping applications to make recommendations for users based on previous actions57 and in social networks to make friend recommendations. We similarly expect network deconvolution to lead to a rich set of applications in network science, molecular and cell biology and many other fields.
Methods
Network deconvolution.
Network deconvolution framework is outlined in Figure 1 (full description in Supplementary Note, 1). A perennial challenge to inferring networks is that, observed similarity weights are the sum of both direct and indirect relationships. A direct information flow modeled by an edge in Gdir can give rise to two or higher level indirect flows. Such indirect flows are captured in Gindir:

where the power associated with each term in Gindir corresponds to the number of edges of indirect paths. Gdir + Gindir together capture both direct and indirect dependencies, which in fact comprise the observed dependencies. Note that, the observed dependency matrix is linearly scaled so that the largest absolute eigenvalue of Gdir < 1. Therefore, the effects of indirect information flows decrease exponentially with the length of indirect paths (Supplementary Notes, 1.2 and 1.6). Self-loops of observed dependency network are excluded by setting its diagonal components to zero.
Suppose Gobs represents the matrix of observed dependencies: a properly scaled similarity matrix between variables (nodes in the network). Gobs can be derived by use of different pairwise similarity metrics, such as correlation or mutual information, and scaled linearly, based on the largest absolute eigenvalue of the unscaled similarity matrix. The observed dependency matrix captures both direct and indirect effects; that is, Gobs = Gdir + Gindir. Note that, the indirect dependency matrix, Gindir, is a function of another unknown Gdir. The main question is how to compute Gdir by using the tainted observed similarities Gobs.
Although Gindir may at first appear intractable because it is an infinite sum, one may note that, similarly to Taylor series expansions, under mild conditions (Supplementary Notes, 1.1 and 1.2) that are generally present in the setting that we consider, we have:

The above observation leads to a simple closed-form expression for Gdir (Fig. 1b):

For symmetric input matrices and some asymmetric ones, we show that, the observed dependency matrix Gobs can be decomposed to its eigenvalues and eigenvectors (Supplementary Note, 1.4). Say U and Σobs represent the matrix of eigenvectors and a diagonal matrix of eigenvalues of matrix Gobs. The i-th diagonal component of the matrix Σobs represents the i-th eigenvalue  of the observed dependency matrix Gobs. Then, by using the eigen decomposition principle, we have Gobs = UΣobsU−1.
of the observed dependency matrix Gobs. Then, by using the eigen decomposition principle, we have Gobs = UΣobsU−1.
In this framework, an optimal solution to compute direct dependencies can be computed in the following steps, which comprise the main parts of the proposed network deconvolution algorithm (Fig. 1c):
Step 1 (decomposition step). Decompose the observed dependency matrix Gobs to its eigenvalues and eigenvectors such that Gobs = UΣobsU−1.
Step 2 (deconvolution step). Form a diagonal matrix Σdir whose i-th diagonal component is

Then, the output direct dependency matrix is Gdir = UΣdirU−1.
We show that this algorithm finds a globally optimal direct dependency matrix without error (Supplementary Note, 1.2).
Performance metrics for gene regulatory networks.
A detailed description of gene regulatory network performance metrics is given in Supplementary Note, 2.3. Network predictions were evaluated as binary classification tasks where edges were predicted to be present or absent. Then, standard performance metrics from machine learning were used: precision-recall (PR) and receiver operating characteristic (ROC) curves. Similar to DREAM5 (ref. 5), only the top 100,000 edge predictions were accepted. Then, AUROC and AUPR were separately transformed into P-values by simulating a null distribution for 25,000 random networks. To compute an overall score that summarizes the performance over the three networks with available gold standards (E. coli, S. cerevisiae and in silico), we used the same metric as in the DREAM5 project, which is defined as the mean of the (log-transformed) network-specific P-values:



Accession codes.
All code and data sets are available at <http://compbio.mit.edu/nd> and in Supplementary Data.


References
De Smet, R. & Marchal, K. Advantages and limitations of current network inference methods. Nat. Rev. Microbiol. 8, 717–729 (2010).
Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 45, 167–256 (2003).
Koetter, R. & Médard, M. An algebraic approach to network coding. IEEE/ACM Trans. Netw. 11, 782–795 (2003).
Witten, I.H., Frank, E. & Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques (Morgan Kaufmann, 2011).
Marbach, D. et al. Wisdom of crowds for robust gene network inference. Nat. Methods 9, 796–804 (2012).
Marbach, D. et al. Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci. USA 107, 6286–6291 (2010).
Dunn, S.D., Wahl, L.M. & Gloor, G.B. Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics 24, 333–340 (2008).
Burger, L. & van Nimwegen, E. Disentangling direct from indirect co-evolution of residues in protein alignments. PLoS Comput. Biol. 6, e1000633 (2010).
Giraud, B.G., Heumann, J.M. & Lapedes, A.S. Superadditive correlation. Phys. Rev. 59, 4983–4991 (1999).
Lapedes, A.S., Giraud, B.G., Liu, L. & Stormo, G.D. Correlated mutations in models of protein sequences: phylogenetic and structural effects. IMS Lecture Notes-Monograph Series 33, 236–256 (1999).
Friedkin, N.E. Information flow through strong and weak ties in intra-organizational social networks. Soc. Networks 3, 273–285 (1982).
de la Fuente, A., Bing, N., Hoeschele, I. & Mendes, P. Discovery of meaningful associations in genomic data using partial correlation coefficients. Bioinformatics 20, 3565–3574 (2004).
Hemelrijk, C.K. A matrix partial correlation test used in investigations of reciprocity and other social interaction patterns at group level. J. Theor. Biol. 143, 405–420 (1990).
Veiga, D.F.T., Vicente, F.F.R., Grivet, M., De la Fuente, A. & Vasconcelos, A.T.R. Genome-wide partial correlation analysis of Escherichia coli microarray data. Genet Mol. Res. 6, 730–742 (2007).
Marks, D.S. et al. Protein 3D structure computed from evolutionary sequence variation. PLoS ONE 6, e28766 (2011).
Hopf, T.A. et al. Three-dimensional structures of membrane proteins from genomic sequencing. Cell 149, 1607–1621 (2012).
Weigt, M., White, R.A., Szurmant, H., Hoch, J.A. & Hwa, T. Identification of direct residue contacts in protein-protein interaction by message passing. Proc. Natl. Acad. Sci. USA 106, 67–72 (2009).
Wainwright, M.J. & Jordan, M.I. Graphical models, exponential families, and variational inference. Found. Trends Mach. Learn. 1, 1–305 (2008).
Seth, A. Granger causality. Scholarpedia 2, 1667 (2007).
Quinn, C.J., Coleman, T.P., Kiyavash, N. & Hatsopoulos, N.G. Estimating the directed information to infer causal relationships in ensemble neural spike train recordings. J. Comput. Neurosci. 30, 17–44 (2011).
Ding, M., Truccolo, W.A. & Bressler, S.L. Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biol. Cybern. 157, 145–157 (2001).
Pearl, J. Causality: Models, Reasoning, and Inference (Cambridge Univ Press, 2000).
Huynh-Thu, V.A., Irrthum, A., Wehenkel, L. & Geurts, P. Inferring regulatory networks from expression data using tree-based methods. PLoS ONE 5, e12776 (2010).
Meinshausen, N. & Bühlmann, P. High dimensional graphs and variable selection with the Lasso. Ann. Stat. 34, 1436–1462 (2006).
Pinna, A., Soranzo, N. & de la Fuente, A. From knockouts to networks: establishing direct cause-effect relationships through graph analysis. PLoS ONE 5, e12912 (2010).
Friedman, N., Linial, M., Nachman, I. & Pe'er, D. Using Bayesian networks to analyze expression data. J. Comput. Biol. 7, 601–20 (2000).
Friedman, N. Inferring cellular networks using probabilistic graphical models. Science 303, 799–805 (2004).
Hartemink, A., Gifford, D., Jaakkola, T.S. & Young, R.A. Using graphical models and genomic expression to statistically validate models of genetic regulatory networks. Pac. Symp. Biocomput. 6, 422–433 (2001).
Margolin, A.A. et al. ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics 7, S7 (2006).
Marks, D.S., Hopf, T.A. & Sander, C. Protein structure prediction from sequence variation. Nat. Biotechnol. 30, 1072–1080 (2012).
Jones, D., Buchan, D., Cozzetto, D. & Pontil, M. PSICOV: precise structural contact prediction using sparse inverse covariance estimation on large multiple sequence alignments. Bioinformatics 28, 184–190 (2012).
Bonneau, R. et al. The Inferelator: an algorithm for learning parsimonious regulatory networks from systems-biology data sets de novo. Genome Biol. 7, R36 (2006).
Bar-Joseph, Z. et al. Computational discovery of gene modules and regulatory networks. Nat. Biotechnol. 21, 1337–1342 (2003).
Reiss, D.J., Baliga, N.S. & Bonneau, R. Integrated biclustering of heterogeneous genome-wide datasets for the inference of global regulatory networks. BMC Bioinformatics 7, 280 (2006).
Greenfield, A., Madar, A., Ostrer, H. & Bonneau, R. DREAM4: Combining genetic and dynamic information to identify biological networks and dynamical models. PLoS ONE 5, e13397 (2010).
di Bernardo, D. et al. Chemogenomic profiling on a genome-wide scale using reverse-engineered gene networks. Nat. Biotechnol. 23, 377–383 (2005).
Faith, J.J. et al. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 5, e8 (2007).
Gama-Castro, S. et al. RegulonDB version 7.0: transcriptional regulation of Escherichia coli K-12 integrated within genetic sensory response units (Gensor Units). Nucleic Acids Res. 39, D98–D105 (2011).
MacIsaac, K.D. et al. An improved map of conserved regulatory sites for Saccharomyces cerevisiae. BMC Bioinformatics 7, 113 (2006).
Butte, A.J. & Kohane, I.S. Mutual information relevance networks: functional genomic clustering using pairwise entropy measurements. Pac. Symp. Biocomput. 426, 418–429 (2000).
Küffner, R., Petri, T., Tavakkolkhah, P., Windhager, L. & Zimmer, R. Inferring gene regulatory networks by ANOVA. Bioinformatics 28, 1376–1382 (2012).
Haury, A.C., Mordelet, F., Vera-Licona, P. & Vert, J.P. TIGRESS: trustful inference of gene regulation using stability selection. BMC Syst. Biol. 6, 145 (2012).
Altschuh, D., Lesk, A., Bloomer, A. & Klug, A. Correlation of co-ordinated amino acid substitutions with function in viruses related to tobacco mosaic virus. J. Mol. Biol. 193, 693–707 (1987).
Göbel, U., Sander, C., Schneider, R. & Valencia, A. Correlated mutations and residue contacts in proteins. Proteins 18, 309–317 (1994).
Neher, E. How frequent are correlated changes in families of protein sequences? Proc. Nat. Acad. Sci. USA 91, 98–102 (1994).
Nugent, T. & Jones, D.T. Accurate de novo structure prediction of large transmembrane protein domains using fragment-assembly and correlated mutation analysis. Proc. Natl. Acad. Sci. USA 109, E1540–E1547 (2012).
Morcos, F. et al. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. USA 108, E1293–E1301 (2011).
Lapedes, A., Giraud, B. & Jarzynski, C. Using sequence alignments to predict protein structure and stability with high accuracy. Preprint at 〈http://arXiv.org/abs/1207.2484〉 (2012).
Ekeberg, M., Lövkvist, C., Lan, Y., Weigt, M. & Aurell, E. Improved contact prediction in proteins: using pseudolikelihoods to infer Potts models. Phys. Rev. E 87, 012707 (2013).
Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 74, 036104 (2006).
Granovetter, M. The strength of weak ties: a network theory revisited. Sociol. Theory 1, 201–233 (1983).
Ferrara, E., De Meo, P., Fiumara, G. & Provetti, A. The role of strong and weak ties in Facebook: a community structure perspective. Preprint at http://arXiv.org/abs/1203.0535 (2012).
Tang, J., Sun, J., Wang, C. & Yang, Z. Social influence analysis in large-scale networks. Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining KDD '09, 807–816. 〈doi:10.1145/1557019.1557108〉 (2009).
Shi, X. Networks of strong ties. Physica A 378, 33–47 (2007).
Newman, M.E.J. Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys. Rev. E 64, 016132 (2001).
Sharan, R., Ulitsky, I. & Shamir, R. Network-based prediction of protein function. Mol. Syst. Biol. 3, 88 (2007).
Song, X., Tseng, B.L., Lin, C.-Y. & Sun, M.-T. Personalized recommendation driven by information flow. Proceedings of the 29th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval SIGIR '06, 509–516 〈doi:10.1145/1148170.1148258〉 (2006).
Acknowledgements
We thank B. Holmes for suggestions on the initial aspects of this work, M. Bansal on the protein structural constraints, Y. Liu for initial analysis of DREAM5 networks and R. Küffner for discussions and code used for network motif analysis. The work was supported by US National Institutes of Health grants R01 HG004037 and HG005639 to M.K., a Swiss National Science Foundation fellowship to D.M. and National Science Foundation CAREER award 0644282 to M.K.
Author information
Authors and Affiliations
Contributions
S.F. and M.K. developed the method, analyzed results and wrote the paper. D.M. contributed to DREAM5 data sets, gene network inference and network motif analysis. M.M. contributed to correctness proof and robustness analysis.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Text and Figures
Supplementary Note, Supplementary Figures 1–10 and Supplementary Tables 1–2 (PDF 2800 kb)
Supplementary Data
NB code and datasets (ZIP 428749 kb)
Rights and permissions
About this article
Cite this article
Feizi, S., Marbach, D., Médard, M. et al. Network deconvolution as a general method to distinguish direct dependencies in networks. Nat Biotechnol 31, 726–733 (2013). https://doi.org/10.1038/nbt.2635
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nbt.2635
This article is cited by
-
Widening the landscape of transcriptional regulation of green algal photoprotection
Nature Communications (2023)
-
Earth microbial co-occurrence network reveals interconnection pattern across microbiomes
Microbiome (2020)
-
Single-cell transcriptional networks in differentiating preadipocytes suggest drivers associated with tissue heterogeneity
Nature Communications (2020)
-
Protist Interactions and Seasonal Dynamics in the Coast of Yantai, Northern Yellow Sea of China as Revealed by Metabarcoding
Journal of Ocean University of China (2020)
-
Using Machine Learning to Measure Relatedness Between Genes: A Multi-Features Model
Scientific Reports (2019)