Abstract
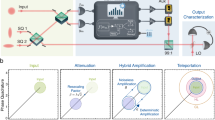
Quantum teleportation1 allows for the transfer of arbitrary unknown quantum states from a sender to a spatially distant receiver, provided that the two parties share an entangled state and can communicate classically. It is the essence of many sophisticated protocols for quantum communication and computation2,3,4,5. Photons are an optimal choice for carrying information in the form of ‘flying qubits’, but the teleportation of photonic quantum bits6,7,8,9,10,11 (qubits) has been limited by experimental inefficiencies and restrictions. Main disadvantages include the fundamentally probabilistic nature of linear-optics Bell measurements12, as well as the need either to destroy the teleported qubit or attenuate the input qubit when the detectors do not resolve photon numbers13. Here we experimentally realize fully deterministic quantum teleportation of photonic qubits without post-selection. The key step is to make use of a hybrid technique involving continuous-variable teleportation14,15,16 of a discrete-variable, photonic qubit. When the receiver’s feedforward gain is optimally tuned, the continuous-variable teleporter acts as a pure loss channel17,18, and the input dual-rail-encoded qubit, based on a single photon, represents a quantum error detection code against photon loss19 and hence remains completely intact for most teleportation events. This allows for a faithful qubit transfer even with imperfect continuous-variable entangled states: for four qubits the overall transfer fidelities range from 0.79 to 0.82 and all of them exceed the classical limit of teleportation. Furthermore, even for a relatively low level of the entanglement, qubits are teleported much more efficiently than in previous experiments, albeit post-selectively (taking into account only the qubit subspaces), and with a fidelity comparable to the previously reported values.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993)
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998)
Gottesman, D. & Chuang, I. L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 402, 390–393 (1999)
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001)
Raussendorf, R. & Briegel, H. J. A one-way quantum computer. Phys. Rev. Lett. 86, 5188–5191 (2001)
Bouwmeester, D. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997)
Boschi, D., Branca, S., De Martini, F., Hardy, L. & Popescu, S. Experimental realization of teleporting an unknown pure quantum state via dual classical Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 80, 1121–1125 (1998)
Kim, Y.-H., Kulik, S. P. & Shih, Y. Quantum teleportation of polarization state with a complete Bell state measurement. Phys. Rev. Lett. 86, 1370–1373 (2001)
Marcikic, I., de Riedmatten, H., Tittel, W., Zbinden, H. & Gisin, N. Long-distance teleportation of qubits at telecommunication wavelengths. Nature 421, 509–513 (2003)
Pan, J.-W., Gasparoni, S., Aspelmeyer, M., Jennewein, T. & Zeilinger, A. Experimental realization of freely propagating teleported qubits. Nature 421, 721–725 (2003)
Ma, X.-S. et al. Quantum teleportation over 143 kilometres using active feed-forward. Nature 489, 269–273 (2012)
Lütkenhaus, N., Calsamiglia, J. & Suominen, K.-A. Bell measurements for teleportation. Phys. Rev. A 59, 3295–3300 (1999)
Pan, J.-. et al. Multiphoton entanglement and interferometry. Rev. Mod. Phys. 84, 777–838 (2012)
Vaidman, L. Teleportation of quantum states. Phys. Rev. A 49, 1473–1476 (1994)
Braunstein, S. L. & Kimble, H. J. Teleportation of continuous quantum variables. Phys. Rev. Lett. 80, 869–872 (1998)
Furusawa, A. et al. Unconditional quantum teleportation. Science 282, 706–709 (1998)
Hofmann, H. F., Ide, T., Kobayashi, T. & Furusawa, A. Information losses in continuous-variable quantum teleportation. Phys. Rev. A 64, 040301(R) (2001)
Polkinghorne, R. E. S. & Ralph, T. C. Continuous variable entanglement swapping. Phys. Rev. Lett. 83, 2095–2099 (1999)
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information 380–386 (Cambridge Univ. Press, 2000)
Braunstein, S. L. & Kimble, H. J. A posteriori teleportation. Nature 394, 840–841 (1998)
Yonezawa, H., Braunstein, S. L. & Furusawa, A. Experimental demonstration of quantum teleportation of broadband squeezing. Phys. Rev. Lett. 99, 110503 (2007)
Ide, T., Hofmann, H. F., Kobayashi, T. & Furusawa, A. Continuous-variable teleportation of single-photon states. Phys. Rev. A 65, 012313 (2001)
Lee, N. et al. Teleportation of nonclassical wave packets of light. Science 332, 330–333 (2011)
Takeda, S. et al. Generation and eight-port homodyne characterization of time-bin qubits for continuous-variable quantum information processing. Phys. Rev. A 87, 043803 (2013)
Bowen, W. P. et al. Experimental investigation of continuous-variable quantum teleportation. Phys. Rev. A 67, 032302 (2003)
Jia, X. et al. Experimental demonstration of unconditional entanglement swapping for continuous variables. Phys. Rev. Lett. 93, 250503 (2004)
Mišta, L., Jr, Filip, R. & Furusawa, A. Continuous-variable teleportation of a negative Wigner function. Phys. Rev. A 82, 012322 (2010)
Jozsa, R. Fidelity for mixed quantum states. J. Mod. Opt. 41, 2315–2323 (1994)
Massar, S. & Popescu, S. Optimal extraction of information from finite quantum ensembles. Phys. Rev. Lett. 74, 1259–1263 (1995)
Zavatta, A., D’Angelo, M., Parigi, V. & Bellini, M. Remote preparation of arbitrary time-encoded single-photon ebits. Phys. Rev. Lett. 96, 020502 (2006)
Acknowledgements
This work was partly supported by PDIS, GIA, G-COE, APSA and FIRST, commissioned by MEXT (Japan); by the SCOPE programme commissioned by MIC (Japan); and by ASCR-JSPS. S.T. and M.F. acknowledge financial support from ALPS. We thank L. Mišta Jr, H. Yonezawa and J. Kimble for comments.
Author information
Authors and Affiliations
Contributions
A.F. planned and supervised the project. P.v.L. and S.T. theoretically defined the scientific goals. S.T. and T.M. designed and performed the experiment, and acquired the data. S.T. and M.F. developed the electronic devices. S.T., T.M. and M.F. analysed the data. S.T. and P.v.L. wrote the manuscript with assistance from all other co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains a Supplementary Discussion, Supplementary Data, Supplementary References, Supplementary Figures 1-2 and Supplementary Tables 1-2. (PDF 1994 kb)
Rights and permissions
About this article
Cite this article
Takeda, S., Mizuta, T., Fuwa, M. et al. Deterministic quantum teleportation of photonic quantum bits by a hybrid technique. Nature 500, 315–318 (2013). https://doi.org/10.1038/nature12366
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature12366
This article is cited by
-
Continuous variable quantum teleportation and remote state preparation between two space-separated local networks
Science China Information Sciences (2024)
-
Parity-encoding-based quantum computing with Bayesian error tracking
npj Quantum Information (2023)
-
A quantum-bit encoding converter
Nature Photonics (2023)
-
Quantum Teleportation of the Entangled Superconducting Qubits via LC Resonators
International Journal of Theoretical Physics (2023)
-
Improving the probabilistic quantum teleportation efficiency of arbitrary superposed coherent state using multipartite even and odd j-spin coherent states as resource
Applied Physics B (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.