A pure likelihood approach to the analysis of genetic association data: an alternative to Bayesian and frequentist analysis

Abstract

Investigators performing genetic association studies grapple with how to measure strength of association evidence, choose sample size, and adjust for multiple testing. We apply the evidential paradigm (EP) to genetic association studies, highlighting its strengths. The EP uses likelihood ratios (LRs), as opposed to P-values or Bayes’ factors, to measure strength of association evidence. We derive EP methodology to estimate sample size, adjust for multiple testing, and provide informative graphics for drawing inferences, as illustrated with a Rolandic Epilepsy (RE) fine-mapping study. We focus on controlling the probability of observing weak evidence for or against association (W) rather than type I errors (M). For example, for LR⩾32 representing strong evidence, at one locus with n=200 cases, n=200 controls, W=0.134, whereas M=0.005. For n=300 cases and controls, W=0.039 and M=0.004. These calculations are based on detecting an OR=1.5. Despite the common misconception, one is not tied to this planning value for analysis; rather one calculates the likelihood at all possible values to assess evidence for association. We provide methodology to adjust for multiple tests across m loci, which adjusts M and W for m. We do so for (a) single-stage designs, (b) two-stage designs, and (c) simultaneously controlling family-wise error rate (FWER) and W. Method (c) chooses larger sample sizes than (a) or (b), whereas (b) has smaller bounds on the FWER than (a). The EP, using our innovative graphical display, identifies important SNPs in elongator protein complex 4 (ELP4) associated with RE that may not have been identified using standard approaches.

Introduction

Three general statistical paradigms are available to analyze genetic association data: the Frequentist paradigm, the Bayesian paradigm^{1, 2} (or quasi-Bayesian paradigm³), and the pure likelihood or evidential paradigm (EP).^{4, 5, 6, 7, 8, 9} In each paradigm, the likelihood ratio, LR=f₁(x)/f₀(x), has a central role, where f₁(x) and f₀(x) are the probability functions for the random variable x under H₁ and H₀, respectively. The Law of Likelihood^{5, 10, 11} informs us how to interpret the LR, stating that the LR measures the strength of evidence favoring H₁ over H₀.

Under the Frequentist paradigm, the most powerful Frequentist test of H₀ rejects in favor of H₁ for sufficiently large values of the LR, using the Neyman–Pearson lemma; thus the LR dictates which test statistic to use. Although this is not a direct use of the LR for interpreting evidence strength, and the appropriateness of using a hypothesis test or P-value to represent evidence strength has been questioned,^{2, 5, 12} the LR remains integral to the hypothesis-testing framework of the frequentist paradigm.

The Bayes Factor (BF) is the Bayesian paradigm's alternative to the P-value.¹ The BF can be interpreted as the factor by which the prior odds of association are changed in light of the data to produce the posterior odds of association. The parameters are integrated out of the likelihood function with a weighting given by the prior distribution on the parameters. When θ₁ and θ₀, the parameters of the prior distributions, reflect two simple hypotheses, the BF=LR. The BF provides an attractive alternative to the P-value for genetic association studies,^{1, 2, 3} yet it too has limitations: ‘It is well understood that the priors on the parameters of the model can have a non-negligible impact on the value of the Bayes’ factor even as the amount of data gets large.’¹ (Supplementary Methods).

The EP takes the Law of Likelihood literally, and uses the LR itself rather than P-values or BFs to plan/design, analyze, and interpret genetic association studies. For the planning stage, the EP provides error probabilities analogous to type I and type II error rates based on LRs. These can be used to estimate sample size and to ensure that the probability of obtaining weak association evidence is low. For the analysis stage, likelihood functions take the central role, with LRs measuring the strength of evidence vis-à-vis two simple hypotheses, LR=f₁(x)/f₀(x).

In this study, we will delineate the planning, analysis, and multiple-testing approaches of the EP for use in genetic association studies, and highlight the advantages of using this paradigm. This represents an extension of our previous work, applying the EP to linkage analysis.^{7, 8} In the subsequent sections we provide definitions and the conceptual framework; show how evidential studies are planned for single tests of association; provide an application using a published fine-mapping study of Rolandic Epilepsy (RE);¹³ and then address the issue of multiple hypothesis testing. The methodology presented here is also applicable to candidate gene and whole genome association studies.

Definitions and conceptual framework

Using the LR as a measure of evidence

For the association studies discussed here we assume an underlying logistic regression model:

We define π_i=E(y_i), where y_i is equal to 1 when subject i has the disease and zero otherwise, and x_i=1 if the ith subject has the genotype of interest, and zero otherwise. The null hypothesis of no association implies that β₁=0, or, equivalently, that the OR is 1 (since β₁=log(OR)), whereas under the alternative we will take $e^{{\text{β}}_1^{*}}$ equal to some value greater than 1, without loss of generality.

Let L(β^*₁; x) represents the likelihood function for the data x, when the $\text{OR = }{e}^{{\text{β}}_1^{*}}$, whereas L(β₁=0; x) is the likelihood under the null hypothesis for the OR. Assume further that β₀ is a nuisance parameter that has been removed from the likelihood function using conventional methods (see section ‘Calculating error probabilities for a case/control association study: study planning’). Let

The LR in (2) is then the ratio of the two likelihoods, free of the nuisance parameter, and provides a measure of the relative evidence for a specified OR value versus OR=1. Common practice is to plot the likelihood as a function of $e^{{\text{β}}_1^{*}}$ (see section ‘Genetic association study of RE’); this will then provide a graphical representation of all possible LRs. Association can be determined by investigating the ratio of any two points on the curve, which correspond to two simple hypotheses.

To plan a study, an investigator needs to specify several values including an alternatively hypothesized OR value, $e^{{\text{β}}_1^{*}}$, which represents the minimum important effect size to detect (eg, OR=1.2 in a genome-wide association study); and some value of k>1 that is chosen to represent strong, convincing evidence favoring one hypothesis value over another. Possible choices for k may be 8, 32, 1000, and so on, with k=32 a commonly used benchmark in the evidential literature^{4, 5} and k=1000 (or even higher), a commonly used critical value in genome-wide linkage studies.¹⁴ A discussion on benchmarks can be found in Royall^{5, 6} and Edwards.¹⁵ The choice of k dictates the observed LR value at which one would declare strong evidence favoring one OR value over another. That is

represent strong evidence favoring H₁ and H₀, respectively. An LR falling between k and 1/k represents weak evidence, indicating that there is insufficient evidence in the data to strongly favor either hypothesis.

Error probabilities and bounds

The failure of the conditions in Equation (3) to occur when H₁ and H₀ are true, respectively, are considered errors, and their probabilities are defined in detail elsewhere.^{4, 5, 9} Briefly, two types of errors can occur under each simple hypothesis: The first of these occurs when the data yield strong evidence supporting the wrong hypothesis; for these we define the probabilities of misleading evidence,⁶

under H₀ and H_1, respectively, where n represents the total sample size in the study (cases and controls). M₀(n,k) is analogous to a type I error, yet is not fixed by design at α. M_i(n,k) i=0,1 are allowed to vary but are bounded: there is an absolute but crude upper bound of 1/k that holds for all sample sizes.^{4, 5, 6, 10} Furthermore, under general regularity conditions a large-sample bound of exists,⁶ where Φ is the cumulative normal probability distribution. This asymptotic bound holds for fixed-dimensional vector parameters (eg, the two degree of freedom association model) even when one uses profile likelihoods to construct the LR. These bounds ensure small error probabilities (well below 0.05 for reasonable k) in quite general situations.

The second error type occurs when the data yield only weak evidence. For this the probabilities of weak evidence are defined as

under H₀ and H_1, respectively. As n gets large, M_i(n,k) and W_i(n,k) converge to 0. Although the convergence of W_i(n,k) with n is monotonic for continuous response data, the convergence of M_i(n,k) is not:⁶ M_i(n,k) generally reaches a maximum (although this maximum is itself generally small) at sample sizes where W_i(n,k) is very large, and then converges to 0. By the time W_i(n,k) is reasonably small, M_i(n,k) is well below its maximum.⁶

Finally, the probabilities of strong evidence are

Minimizing the probabilities of misleading and weak evidence will necessarily maximize the probabilities of strong evidence, since

S₁(n,k) in Equation (6) is analogous to the frequentist concept of power. There is no frequentist analogue to W_i(n,k), outside the context of sequential testing.¹⁶

As M_i(n,k) has natural bounds that ensure it remain small, it is W_i(n,k) that must be controlled to ensure S_i(n,k) is high. The value of W_i(n,k) varies as a function of three quantities: sample size; the minimum important effect size for the parameter of interest (ie, in our case the OR); and the criterion k.

Calculating error probabilities for a case/control association study: study planning

Planning an evidential association study entails ensuring that M_i(n,k) and W_i(n,k) are small, i=0,1 and, as a consequence, S_i(n,k), are high. This is accomplished by determining the required sample size as a function of minor allele frequency (MAF) and effect size, where effect size (eg, OR=1.5) and MAF are generally determined by study design. Error probabilities (Equations (4–5)) can then be calculated using a likelihood free of nuisance parameters. (Note that one is not restricted to these pre-specified parameter values for analysis, the specification is merely for planning.)

The logistic regression model (Equation (1)) contains a nuisance parameter, β₀, whereas our interest is in the $\text{OR = }{e}^{{\text{β}}_1^{*}}$. Two options to eliminate the nuisance parameter are to condition on an appropriate statistic or to profile the nuisance parameter out. In section ‘Conditional likelihood’ we will provide analytical formulas for the error probabilities using the conditioning approach. For profile likelihoods, in contrast, we will use simulation to calculate the error probabilities (section ‘Profile likelihood’). Each option has its advantages: Using a profile likelihood we can incorporate many covariates into the model, and these covariates can be coded in any way allowing for additive, dominant, or any other coding for the genetic model; on the other hand, the conditional approach provides analytical formulas that are easier to interpret, yet allow for only a single dichotomous covariate. The error probabilities between the two approaches may differ slightly for the logistic regression model, but not substantially.

Conditional likelihood

We can use a conditional likelihood to eliminate the nuisance parameter, β₀, in Equation (1), and calculate the planning probabilities. The derivation of the likelihood and the closed form solutions for the error probabilities are in Appendix S.1 in Supplementary Material. We illustrate some error probabilities and sample sizes resulting for H₁:exp(β^*₁)=1.5 and 2 versus H₁:exp(β^*₁)=1, and for representative MAFs (or at-risk genotype frequencies, depending on the assumed genetic disease model) and for k=32. Figure 1 shows M_i(n,k) and W_i(n,k) plotted against the sample size needed in each group (n₁=n₂) for k=32 and for an at-risk genotype frequency, t₀/n, of 0.2, assuming we are in complete linkage disequilibrium with the disease allele. Under a recessive model this would correspond to an MAF=0.45. In Figure 1, the left column of plots gives M₀(n,k) and W₀(n,k), that is, the probabilities when H₀ is true, whereas the right column shows M_i(n,k) and W_i(n,k), that is, the probabilities when the true OR is 1.5 (or 2, for the dotted lines). Note how small the probabilities of misleading evidence, Mi(n,k), are even for this relatively low criterion of k=32.

Figure 1

Probabilities of weak and misleading evidence using a conditional likelihood, to detect an OR≥1.5 with at-risk genotype frequency=0.2, k=32. These results are based on exact calculations.

M_i(n,k) and W_i(n,k) are smaller for larger alternatively hypothesized ORs (compare OR=1.5 versus OR=2 in Figure 1), indicating that larger sample sizes are required to detect smaller alternatively hypothesized ORs, as one would expect. As the genotype frequency increases, the error rates decrease for a given sample size (data not shown). These observations suggest that sample size estimation be based on the smallest MAF to be analyzed and the smallest OR one wishes to detect. Notice also that for sample sizes where W_i(n,k) is small, M_i(n,k) is very small. This observation highlights that planning should be based on ensuring small W_i(n,k)s. As k increases, the M_i(n,k) decrease slightly, but the W_i(n,k) get disproportionately larger, indicating that it is counterproductive to decrease M_i(n,k) by raising the criterion for strong evidence, k (see Equation (A.1.3) and Supplementary Figure S.1 in Supplementary Methods).

Table 1 provides sample size estimates, through exact calculations, for given weak evidence bounds (ie, the sample size choice to ensure that both W₁(n,k) and W₀(n,k) are below the value in column 1) when t₀/n=0.2, 0.3, k=32, H₀: OR=1 versus H₁: OR=2. The maximum probability of misleading evidence, over all n, (max(M_i) ∀n), is also presented; despite being quite small, these values occur at sample sizes for which weak evidence would be too large to consider for a study.

Table 1 Sample size choices for given weak evidence bounds and maximum probability of misleading evidence over all n=n₁+n₂ (max(M_i) ∀n) when genotype frequency is 0.2, 0.3, and H₀: OR=1, H₁: OR=2, k=32

In Table 1 misleading evidence is small when H₀:OR=1 and H₁:OR=2 for any n. Not surprisingly, the smaller the bound on the probabilities of weak evidence or the smaller the at-risk genotype frequency (or alternatively hypothesized OR (Figure 1)), the larger the sample size required. For comparison using frequentist methods, the number of cases (equal to controls) required to achieve 80% power at a nominal type I error rate of 0.05 to detect an OR=2 for genotype frequency of 0.3 would be 310. (See Strug et al⁹ for more general comparisons of evidential and frequentist sample size estimates, and section S.1 and Supplementary Table S.1 in Supplementary Methods for a power comparison.)

Profile likelihood

A profile likelihood replaces the nuisance parameter of the likelihood function by its maximum likelihood estimator (MLE) at each fixed value of the parameter of interest. Thus, given the joint likelihood, L(β_0,β₁), the profile likelihood for β₁ is where the maximization is conducted at fixed values of β₁. Then one can treat the profile likelihood as a regular likelihood function¹⁷ under weak regularity conditions. One can profile out a multidimensional nuisance parameter vector to assess the relative support for different genotypic effect sizes, after adjusting for the covariates (assuming minimal collinearity). In this study, we will assume a disease is inherited in an additive manner, and we can calculate M_i(n,k) and W_i(n,k) just as we did in the ‘Conditional likelihood’ section, but using simulation and the profile LR, LR_p=L_p(β^*₁)/L_p(β₁=0).

Specifying the MAF (P=0.3), the minimum important effect size to detect (OR=1.5), and the prevalence of disease in those with the wild-type genotype (0.002), we simulated equal numbers of cases and controls (n₁=n₀=1 ,…, 800), with the genotypes in controls in Hardy–Weinberg equilibrium. For each combination of input parameters we simulated 1000 data sets assuming there was association with true OR=1.5, and 1000 data sets assuming no association (OR=1). From each data set j=1, …, 1000, of a given size (n=2 ,…, 1600) we calculated the LR_pj for H₀: OR=1 versus H₁: OR=1.5. In each case, we calculated M_i(n,k) and W_i(n,k) by counting the number of times the LR_pj fell in the appropriate range, then dividing by 1000, for example,

Figure 2 provides the values for these error probabilities as a function of n.

Figure 2

Weak and misleading evidence probabilities calculated using profile likelihoods; to detect OR=1.5, k=8, 32, 100, MAF=0.3, disease prevalence is 3%. These results are based on simulations.

Note the scale of the M_i(n,k) plots in Figure 2, where for any sample size, even with k=8, the M_i(n,k) remain very small, and are not of concern. However, at sample sizes where the M_i(n,k) are small, the W_i(n,k) may still be very large for all k considered. This again highlights the need to control the W_i(n,k) during planning, rather than the M_i(n,k). It should also be noted that for the scenario in Figure 2, it is not until the study contains 300 cases, that W₁(n,k) drops as low as about 10%, even for k=8.

Genetic association study of RE

In this section, we illustrate an evidential analysis as applied to an earlier study of RE.¹³ In that work we conducted mapping studies of RE to assist in unraveling its complex genetic inheritance. We conducted genome-wide linkage analysis in 38 families, using a subclinical phenotype present in all RE probands and some unaffected relatives; then we fine-mapped the linkage region with 44 SNPs in 68 RE cases and 187 controls; we replicated our association evidence in a sample from Calgary, Canada with 40 cases and 120 controls. See Strug et al¹³ for clinical descriptions and details of those analyses. In this study, we use the RE study to illustrate how to conduct an evidential association study, both for single SNP (section ‘Single SNP association analysis: using likelihood plots’) and regional SNP (section ‘Extending likelihood plots to a region of typed SNPs’) analysis.

Single SNP association analysis: using likelihood plots

The likelihood function for the OR parameter at a given SNP graphically represents all the evidence about association in the data set. For a single SNP one can plot the likelihood, as a function of the interest parameter (eg, odds ratio, relative risk, hazard ratio, regression coefficient), under an assumed model (eg, dominant, recessive, additive, etc).

Figure 3 provides a simple example of an evidential analysis of genetic association at three SNPs, separately, and the presence of RE in independent cases (n₁=68) and controls (n₂=187), assuming an additive model for the genotype.

Figure 3

Profile likelihood function for the OR, under an additive model, for three SNPs, SG11S21 (a), SG11S30 (b), and SG11S39 (c). Vertical line represents OR=1; 1/8, and 1/32 likelihood intervals provided.

Figure 3 shows a profile likelihood for the odds ratio, profiling out the baseline odds. The likelihoods are standardized to have maximum value of 1 at the MLE. Each plot in Figure 3 provides objective evidence of what the data tell us about the interest parameter at that SNP. The two likelihood intervals (LIs) on each of the three plots represent values of the ORs that are consistent with the data, at a k=8 (1/8 LI) or k=32 (1/32 LI) level. LIs are analogous to confidence intervals. However, LIs do not have a long-run frequency interpretation; rather, they reflect the evidence about the OR in the given data set.

Figure 3(c) shows an association between SNP SG11S39 and RE at the k=8 level, where there are many alternative values of the OR around 1.79 that are better supported than an OR=1 by a factor of greater than 8 (see the vertical line at OR=1 to the left of the likelihood function), and with plausible OR values of 1.07–3.04 from the LI at the k=8 level. For k=32, the LI includes an OR=1 as a plausible value, and hence there is not strong evidence favoring any OR value over an OR=1 by a factor of 32 or more. The corresponding 95% confidence interval for the OR at this SNP is 1.07–2.94. The LI is relatively narrow, indicating substantial information available in the data.

Figure 3(a) and (b) show likelihood functions for two additional SNPs. The likelihoods provide a useful tool to assess which SNP has the most association evidence, in some sense. Although the LIs are a little wider for SNP SG11S 39, the relative support for different ORs versus OR=1 is greater than the others at and around the maximum, and the OR=1 vertical line is further to the left of the LIs in SG11S 39 than for the others. (Supplementary Methods’ section S.2 and Supplementary Table S.2 provide frequentist and Bayesian association measures at these SNPs).

Extending likelihood plots to a region of typed SNPs

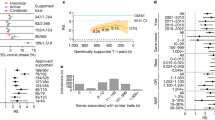
Looking at hundreds or thousands of likelihood functions for individual SNPs, side by side as in Figure 3, is not efficient or helpful when it comes to getting an idea of what is happening across the RE linkage region. Thus, we developed a plot that provides much of the information that is in an individual likelihood function plot, while also providing association evidence for multiple SNPs by base pair position. It does this by plotting the LIs for each SNP, graying out those where an OR=1 is considered a plausible value at some prespecified k, while identifying those that ‘light up’ in a given gene by plotting them in color. For illustrative purposes we reproduce one such figure from the original analysis¹³ (see Figure 4), to illustrate how the general methodology works.

Figure 4

Evidential analysis for association between SNPs in chromosome 11p and RE in 68 cases and 187 controls. LIs in color represent SNPs that pass the k=32 threshold for representing a SNP of interest. (Reprinted from Strug et al.¹³)

Figure 4 shows the evidential association plot across the region of 44 SNPs using the original sample of 68 RE cases and 187 controls. In this study, we used an additive disease model, a profile likelihood to eliminate the nuisance parameter from the likelihood function, and evidence strength of k=32 as a criterion to demarcate SNPs of interest (SoIs). To create these evidential figures we plot the SNPs by bp position on the x axis, and provide the OR on the y axis. The OR=1 line is plotted as a solid black horizontal line. Then, for each SNP the LIs for the ORs are plotted. These LIs are exactly the LIs provided in, for example, Figure 3. If association evidence exists at a given SNP (that is, if a SNP is flagged as a SoI because the 1/k LI excludes OR=1), the LI is presented in color, whereas, if no association evidence exists at the k-level specified, the LI is grayed out of the figure. The interpretation of an SoI is that there are alternative OR values that are favored by a factor of k or more over the likelihood at OR=1. Notice that the SoIs have LIs with three separate colors, navy blue, yellow, and turquoise. If the evidence strength is greater than 32 but less than 100 (ie, OR=1 is not in the 1/32 LI but is in the 1/100 LI) then just the navy blue portion of the LI is above the OR=1 horizontal line; if the evidence is greater than 100 but less than 1000, then the blue and yellow portions of the LI are above the OR=1 line; and if the evidence is greater than 1000, then the entire LI is above the OR=1 line, indicating that even at the k=1000 level, an OR=1 is not a plausible value. The small horizontal tick on each LI is the MLE, which provides information about the shape of the likelihood curve, and we can see from Figure 4 that the MLEs for the ORs at these three SoIs are approximately 2. The max LR for each SNP in color is also provided as text in the plot for calibration.

If the vertical LI colored line moves further above the horizontal OR=1 line with additional data rather than lower, then the additional dataset provides corroborating evidence that this SNP, with the same allele, is associated with increased risk of RE. Supplementary Figure S.2 in Supplementary Data provides the results from a joint analysis of the data in Figure 4 and a replication sample from Calgary, Canada of 40 cases and 120 controls, illustrating this principle. Table 2 lists the ORs, the 1/32 LIs, the max LRs, and the unadjusted P-values (for comparison) from the original (discovery sample) and the combined sample with Calgary. As can be seen in Table 2 (and Supplementary Figure S.2 in Supplementary Data), the LIs at all three SNPs of interest have become narrower, and moved further away from including an OR=1 as a plausible value. Interestingly, none of these three SNPs in the replication sample alone would show up as an SoI, highlighting the importance of analyzing samples jointly.

Table 2 The OR, the 1/32 LIs, max LR, and unadjusted P-values for the discovery analysis and joint analysis from the RE association study at SNPs in ELP4

Figure 4 (and Supplementary Figure S.2 in Supplementary Methods) indicate that only SNPs in the elongator protein complex 4 (ELP4) ‘light up,’ pointing to the role that ELP4 might be having in RE susceptibility. Furthermore, the same SNPs are providing corroborating evidence, although the strength of the evidence differs between SNPs and across the two datasets.

Accounting for multiple hypothesis testing in the EP

Methods to account for multiple hypothesis testing differ between the Bayesian, frequentist, and EPs. Frequentists must adjust their evidence measure, the P-value; Bayesians account for multiple tests by incorporating information into their prior probability;¹⁸ and in the EP we adjust our planning probabilities – but not the evidence measure itself – to account for the number of tests to be conducted. We discuss this evidential approach in detail.

The family-wise error rate and the generalized family-wise error rate

The most common error rate chosen to control for multiple hypothesis tests is the family-wise error rate (FWER). As presented in Table 3, the FWER is defined as P(V≥1).¹⁹ It reflects the probability of rejecting at least one true null hypothesis (or observing misleading evidence under the null for at least one SNP), assuming none of m loci is associated.

Table 3 Error rates defined under multiple testing

The EP, unlike the standard frequentist paradigm, decouples error rates from evidence measures.⁸ This is important for multiple test implications, as delineated in⁷. Briefly, when one conducts multiple SNP tests, the FWER increases with the number of tests conducted. In the frequentist paradigm, the FWER is always fixed at α (eg, α=0.05); therefore the significance criteria for any given test in a family of tests must be smaller (eg, α/m, m=number of tests). However, in the EP, M₀(n,k) is not fixed but rather is allowed to vary and is not tied to the value of the LR at which one declares strong association evidence. The FWER based on M₀(n,k) still increases with additional tests, so one must ensure in one's planning that over all tests, the FWER will remain at acceptable levels. However, the increase in the number of tests does not affect how we interpret the strength of the evidence itself, that is, the LR. We provide an upper bound on the FWER for the probability of misleading evidence:⁷

where M₀(n,k) is the probability of misleading evidence for one SNP test, as inEquation (4). This M₀(n,k) corresponds to the probability calculations before data collection as outlined in section ‘Calculating error probabilities for a case/control association study: study planning.’ Thus, for a fixed number of SNP tests (m), this upper bound can be made smaller by decreasing M₀(n,k) through sample size, k, MAF, or the pre-specified effect size. Increasing k is counterproductive, only minimally reducing M_i(n,k) whereas dramatically increasing W_i(n,k) (Equation (A.1.3) in Supplementary Methods); and the OR was chosen as the minimum important effect size to detect. If W_i(n,k) based on the minimum important effect size and specified k remain large, then these error calculations suggest we simply do not have a sufficiently large data set; here, increasing the sample size is the most desirable and appropriate course of action, when feasible.

Adding samples to ensure that the bound on the FWER remains small can be accomplished through Scheme (1) single-stage designs and Scheme (2) two-stage designs. In Scheme (1) one would plan a larger total sample size n at the beginning of the study through the simple calculation in Equation (8), varying n such that m × M₀(n,k) is sufficiently small. In Scheme (2) one adds the additional samples necessary from the calculation in Scheme (1) in a replication phase, which types only those SNPs or regions with strong evidence for association in the first stage. Scheme (2) results in a smaller bound on the FWER than Scheme (1) and may be more cost-effective, but S₁(n,k) may be smaller (see section ‘Probability of detecting true positives’, and Appendix S.3 in Supplementary Methods for a (conservative) lower bound on the two-stage probability of strong evidence). Note here that the increase in sample size (or the replication component) is the ‘adjustment’ for multiple hypothesis testing.

Controlling the FWER may be inappropriate for genome-wide association studies or large-scale fine-mapping endeavors. If one uses Scheme (1) or (2) above, one could relax the requirement that even one type I error is unacceptable. When m is large, we might choose to tolerate up to g−1 false positives. Specifically, consider the generalized FWER,²⁰ which can be expressed as gFWER=P(V≥g). The gFWER ensures a small probability of observing at least g misleading results in m tests if all are null. The value for g would be chosen depending on resources for follow-up. In this case,

when g=1, this quantity is approximately equal to m × M₀(n,k), M₀(n,k) small. Equation (9) shows that, for a given M₀(n,k), as g gets larger, the bound on the gFWER gets smaller. Thus, the larger the g, the smaller the sample size required. Moreover, the method derived to control the FWER in⁷ may also be used on the gFWER; that is, Equation (9) provides an upper bound on the gFWER, which can be used to plan larger studies or to implement the two-stage replication design to adjust for multiple hypothesis tests.

Probability of detecting true positives

Thus far, we have completely ignored the probability of detecting true positives, which should arguably be as important as, if not more important than, controlling false positives. It is straightforward to incorporate S₁(n,k) into the planning for multiple tests, ensuring that the probability of getting at least one true positive out of m loci is high. Following the notation of Table 3, suppose that of m marker loci, m₁ are truly associated with disease and the remaining m₀=m−m₁ are not associated. For each of the m₁ true markers the probability of being detected is P₁(LR_i≥k)=S₁(n,k), equal to the probability of strong evidence under the alternative hypothesis for one SNP test as in section ‘Calculating error probabilities for a case/control association study: study planning.’ Define PTP(m₁) as the probability of detecting at least one of the m₁ true positive loci. Several properties of PTP(m₁) can be noted regardless of whether the markers are independent (see Appendix S.2 in Supplementary Methods for derivation and calculations): (1) PTP(m₁) increases as the number of true positives increase; (2) the value of PTP(m₁) is independent of the number of false markers, m₀; and (3) PTP(m₁) is bounded below by S₁(n,k), the probability of strong evidence under the alternative in one SNP test. Thus, for any m₁, if S₁(n,k) is reasonably high for a single SNP analysis, then there is a good chance of identifying at least one true positive along with the false positives. For a single-stage design, S₁(n,k) is calculated as in section ‘Calculating error probabilities for a case/control association study: study planning’ with the expanded data set as the new sample size. For the two-stage design some additional calculation is required. The details are given in Appendix S.3 in Supplementary Methods. There, we see that in the two-stage design,

provides a lower bound on the probability of strong evidence under the alternative, where j₁ and j₂ represent the numbers of observations in the first and second stages, respectively, and n=j₁+j₂. Equation (10) implies that a larger total sample size is required for the two-stage design to achieve equally large strong evidence probabilities.

In summary, in an association study, one can adjust for multiple hypothesis testing by controlling the FWER or gFWER through a single- or two-stage design, while simultaneously ensuring a high probability of detecting at least one true positive by ensuring W₁(n,k) is small (or equivalently S₁(n,k) is large (Equation(7)).

Multiple testing applied to the RE example

We use the RE discovery sample and the Calgary replication sample to illustrate the evidential multiple-testing approach. We use a two-stage design to adjust for multiple hypothesis tests controlling the FWER. With 68 RE cases and 187 controls M₀(k=32) equals 0.002 to detect an OR=1.5 with MAF=0.30; thus for 44 SNP tests the FWER≤0.088 (by Equation (8)). Combining the data in a joint analysis with the Calgary sample, the FWER≤0.044 (with the two-stage design bound even smaller, depending on the number of markers chosen for follow-up).

Consequently, adding the Calgary data serves as our adjustment for conducting multiple SNP tests because it ensures that the FWER is controlled at acceptable levels – exactly the point of a multiple test adjustment.

The lower bound on the PTP(m₁) using the combined sample is S₁(415, 32)=0.04, and under the two-stage approach it equals S₁(255, 32)^*S₁(160, 1)=0.003, for OR=1.5 and MAF=0.30. Although this is only a lower bound, sample size should be much larger to ensure a reasonable bound on the probability of strong evidence. Section ‘Genetic association study of RE’ and Figure 4 illustrate that there was, however, strong evidence of association in one of the genes under the linkage peak, but at a larger OR value than the error probability calculations pre-specified. The a priori small strong evidence probability bound associated with the study does not detract from the strong conclusions of association we can make between RE and ELP4, we are just unable to unequivocally rule out the other genes in the region. From a planning perspective, it is best to have one's study characterized by a low probability of observing weak evidence and not to rely on good fortune.

Discussion

We have provided an alternative approach to analyzing genetic association studies, which does not require use of P-values, Bayes’ factors, or standard multiple test adjustments. These genetic association studies could involve either genome-wide analysis, fine-mapping linkage regions or candidate genes. In summary, we have shown that case–control genotype data can be analyzed for association using LRs; that when conducting association analyses across multiple SNPs one can adjust for multiple testing by using a replication sample (increasing sample size) and conducting a joint analysis; and that the evidential error probabilities are straightforward to compute and are useful and necessary when planning a study.

A replication study (or the use of additional samples) provides multiple test adjustments in the evidential framework. Replication studies are already a requirement by many journal editors for publication, by funding agencies, and policy makers. In addition, by planning a genetic association study evidentially through sample size choice and multiple test correction approaches, one can control the probability of obtaining weak association signals.

Evidential analysis evaluates evidence vis-à-vis all possible two simple hypotheses, and chooses SNPs of interest through LI criteria. LIs are more appropriate than confidence intervals for genetic association studies as they reflect what the collected dataset has to say about association rather than requiring a long-run frequency interpretation.

There is a common misconception concerning the role the simple alternative plays in evaluating the evidence in the EP: to be clear, the values one chooses for the simple hypotheses during planning are irrelevant for analysis; you are not tied to any particular pre-specified values when assessing evidence strength. For more on this topic, as well as a concrete example, see Strug and Hodge.⁸ Briefly, the specified alternative value of the OR should represent ‘the smallest meaningful difference’ from the null hypothesized value of OR=1. However, an alternative hypothesis is specified for planning purposes only; once the data have been observed, the value of β^*₁ has no role in interpreting the evidence, and the investigator can and should report the whole likelihood function (or LIs). The MLE never has the role of alternative hypothesis at the planning phase, for many reasons, one of which being that the MLE does not represent a simple hypothesis, and thus the universal and other bounds do not apply to the maximized LR.²¹

A limitation of the pure likelihood or evidential approach to analysis is its dependence on the correct choice of model. However, recent advances have provided methodology to ‘robustify’ likelihoods to guard against model misspecification^{22, 23} and this methodology is also available for use in genetic studies. Another perceived limitation is that evidential analysis requires larger sample sizes and a more stringent significance criteria than standard frequentist methodology,⁹ for a given SNP test. On the other hand, standard benchmarks for evidence strength are known to be anticonservative.²⁴

Our RE example highlights the ‘power’ one gains from a joint analysis, similar to results from other paradigms.²⁵ Yet even in a joint analysis using a P-value approach, a different, more stringent significance criterion must be applied because of multiple-testing penalties imposed by the frequentist paradigm. In the EP, we manage to avoid all evidence adjustments regardless of the design; rather, we adjust the error probabilities at the planning phase of the study through the sample size or by replication.

The RE example illustrates several other important differences between the two approaches as well: (1) rs986527 would not have been significant after Bonferroni correction in the original RE discovery sample, and so, depending on the scheme for follow-up, this SNP might not have been typed in a replication scheme; (2) if the Calgary samples had been analyzed separately using a P-value approach, only rs210426 would have been flagged as significant and this SNP did not appear important in the original sample; (3) depending on how one defines replication, many might conclude from a separate analysis that the Calgary sample did not replicate the original findings. In fact, this is not the case. We can see that the LIs at rs986527 and rs964112 favor ORs greater than 1.5 over an OR=1 in both samples, with the difference in strength easily attributed to factors such as differential LD patterns, varying MAFs, different sample sizes, and stochastic factors. Moreover, the fact that only SNPs in ELP4 ‘light up’ in the two analyses strongly suggests replication of ELP4.

Evian, an R package to conduct an EVIdential ANalysis and produce the illustrated evidential genetic association plots, is available at http://strug.ccb.sickkids.ca/evian. In this study, we advocate the use of evidential analysis for genetic association studies, highlight the multiple hypothesis-testing adjustment approaches, and illustrate how to plan evidentially. The multiple test adjustment approaches, that is, the addition of replication samples, are more consistent with the practice of science, and the field's move toward large-scale meta-analyses.