Abstract
To gain control over the diffusive heat flux in a given domain, one needs to engineer a thermal metamaterial with a specific distribution of the generally anisotropic thermal conductivity throughout the domain. Until now, the appropriate conductivity distribution was usually determined using transformation thermodynamics. By this way, only a few particular cases of heat flux control in simple domains having simple boundary conditions were studied. Thermal metamaterials based on optimization algorithm provides superior properties compared to those using the previous methods. As a more general approach, we propose to define the heat control problem as an optimization problem where we minimize the error in guiding the heat flux in a given way, taking as design variables the parameters that define the variable microstructure of the metamaterial. In the present study we numerically demonstrate the ability to manipulate heat flux by designing a device to concentrate the thermal energy to its center without disturbing the temperature profile outside it.
Similar content being viewed by others
Introduction
The control of the electromagnetic flux using metamaterials led to major innovations in electronics and communications1. Taking advantage of the analogies between electromagnetism and thermodynamics, some researchers developed materials with unprecedented thermal properties (the thermal “metamaterials”) for heat flux manipulation, for instance the heat flux inverter by Narayana and Sato2.
Compared to the advances in electromagnetism, the design of thermal metamaterials is an emerging research and development area. In a first approach, metamaterials can be empirically designed (e.g., the thermal shield of Narayana and Sato2). More sophisticated thermal metamaterials can be designed using the transformation thermodynamics concept (e.g., the inverter and the concentrator proposed by Narayana and Sato2 or the cloaking device of Schittny et al.3, inherited from electromagnetism4). A straightforward example of the application of ideas from electromagnetism in thermal problems is the heat flux inverter of Narayana and Sato2, derived from the device to rotate electromagnetic fields proposed by Chen and Chan5 to rotate electromagnetic fields.
The transformation-based approach has been applied to specific heat control problems. For general problems (i.e., having arbitrary prescribed magnitude and direction of the heat flux, geometry of the manipulating device, geometry and boundary conditions of the domain where the device is embedded) we propose a new, optimization-based approach for the design of thermal metamaterials. A variety of optimization algorithms have been used to design efficient metamaterials but only in the field of photonic6,7,8,9,10. Here we solve a nonlinear constrained optimization problem where the objective function to minimize is the error in the accomplishment of the given heat manipulation task, and the design variables characterize the spatial distribution of the metamaterial throughout the manipulating device.
We show the capability of the present method by designing a device for thermal concentration, as alternative to the transformation-based design of Chen and Lei11, using an interior point optimization algorithm.
Definition of the heat flux guidance problem
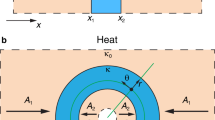
Let us consider the domain Ω in Fig. 1, with boundary ∂Ω divided in two non-overlapping portions: ∂Ωq (where the heat flux qwall is prescribed) and ∂ΩT (where the temperature Twall is prescribed). In steady state, the heat flux conduction in Ω is governed by the equation

and the boundary conditions:


where T is the temperature, s is the internal heat source, k is the (effective) thermal conductivity tensor, and n is the unit vector normal to and pointing outwards ∂Ω.
Using the finite element method (FEM), the temperature field in Ω is approximated as follows:

where Nj is the shape function associated to the node j of the finite elements mesh (discretized Ω) and Tj is the temperature at node j (unknown). Using a standard (Galerkin) FEM, the nodal temperature Tj is the solution of the algebraic system of equations

where Kij and Fi are the components of the global conductivity matrix and the nodal heat flux vector respectively, given by


The system of equations (5) is the FEM version of the heat conduction (1) subject to the boundary conditions (2) and (3). This is a classical FEM problem, whose solution has been extensively detailed in classical FEM literature, for instance in the book of Zienkiewicz and Taylor on the basics of FEM12.
Influence of the inhomogeneous microstructure on the macroscopic thermal response
Let the microstructure vary throughout Ω and be sampled at a series of points x(μ) ∈ Ω (μ = 1, …, N). Further, let the microstructure at any x(μ) be characterized by n parameters  , grouped in the vector p(μ). Then, the effective conductivity k at x(μ) is at last a function of p(μ), i.e.
, grouped in the vector p(μ). Then, the effective conductivity k at x(μ) is at last a function of p(μ), i.e.

The microstructure throughout Ω is characterized by the vector P = [p(1), …, p(N)]. Then, the global conductivity matrix K (whose components are given by equation (6)) is a function of P, and so they are the nodal temperatures Tj (solution of equation (5)) and the temperature field T (approximated by equation (4) for FEM).
Task accomplishment as an optimization problem
To design the microstructure in the macroscopic domain Ω consists of finding P such that Ω responds in a desired way. In this case, we aim to enforce the heat flux to take the magnitude as well as the direction of the vector  at a series of points x(q) ∈ Ω, q = 1, …, Q, as shown in Fig. 2. The heat flux at any x(q) is given by
at a series of points x(q) ∈ Ω, q = 1, …, Q, as shown in Fig. 2. The heat flux at any x(q) is given by

Then, we have to find P such that

Let us look for P within a space  of admissible solutions. Generally, the task (8) cannot be exactly satisfied by any
of admissible solutions. Generally, the task (8) cannot be exactly satisfied by any  . So, let us accomplish this task as well as possible by solving the nonlinear constrained optimization problem
. So, let us accomplish this task as well as possible by solving the nonlinear constrained optimization problem

where the objective function is the root mean square (RMS) error in the accomplishment of the task (8).
Application to a heat concentration and cloaking problem
Let us apply the proposed optimization-based approach to design a device for heat concentration as alternative to that designed by Chen and Lei11 based on transformation thermodynamics. This device, embedded in a plate with prescribed heat flux, is designed to concentrate the thermal energy at its center while keeping the outer flux unaltered (i.e., cloaking the device).
The Ω domain is the entire plate, a square of sides Lx = Ly = 14 cm subject to the following boundary conditions: T = Tmax = 100 °C for x = −Lx/2, T = Tmin = 0 °C for x = Lx/2, and q ⋅ n = 0 for y = ±Ly/2 (see Fig. 3). The heat flux normal to the plate is neglected. The plate is made of 40%-nickel steel with homogeneous and isotropic thermal conductivity kns = 10 W/(mK). Without the device, the heat flux in the plate is

The considered device is the ring Ωfree ⊂ Ω with inner and outer radii r = 1 cm and R = 5 cm, see Fig. 3. This ring is designed to thermally concentrate the heat flux in the region Ωfixint. A further design requirement on the device is to keep the heat flux outside it (i.e., in the remainder portion of the plate, Ωfixext) unaltered.
The domain Ω is discretized using a mesh of 70 × 70 bilinear rectangular finite elements, as shown in Fig. 4(a). Each blue element, belonging to the device Ωfree, has a microstructure sampling point. In the other elements, the material is nickel steel.
Regarding the mesh refinement, it is well known that it affects the optimal result, as it is widely discussed in the book of Bendsøe and Sigmund13. Normally, the finer the mesh, the more optimal the solution. The current choice was found to be a good deal between optimality and computational cost.
Definition of the metamaterial for anisotropic heat conduction
Following Narayana and Sato2, the anisotropy in the effective conductivity of the device Ωfree is achieved by using a stacked composite or laminate made of alternating sheets of materials A and B with different isotropic conductivities. As pointed out by Schittny et al.14, a laminate is a metamaterial because its effective conductivity, being anisotropic, goes beyond the conductivities of its constituents, which are isotropic.
Like Chen and Lei11, we adopted A = copper and B = polydimethylsiloxane (PDMS), with isotropic conductivities kcopper = 398 W/(mK) and kPDMS = 0.27 W/(mK). The use of laminates of materials with markedly distinct conductivity at the microstructural level leads to a highly anisotropic effective conductivity, which is a key issue for guiding the heat flux. Actually, it is a popular choice in the literature2,11,15,16.
As shown in Fig. 4(b), the representative volume element (RVE) of the microstructure of such composite at the sampling point x(μ) ∈ Ωfree is a unit square characterized by the vector p(μ) of components  (thickness of sheet of material A) and
(thickness of sheet of material A) and  (orientation of the sheets); the thickness of the sheet of material B is dB = lμ − dA, where lμ = 1 is the thickness of the RVE. The effective thermal conductivities at x(μ) in the direction of the sheets (λ) and normal to the sheets (τ) are17
(orientation of the sheets); the thickness of the sheet of material B is dB = lμ − dA, where lμ = 1 is the thickness of the RVE. The effective thermal conductivities at x(μ) in the direction of the sheets (λ) and normal to the sheets (τ) are17


These are principal conductivities, to be arranged in the matrix

Now, the matrix of tensorial components of the effective conductivity referred to the fixed Cartesian frame x-y at the point x(μ) can be computed as

where R is the rotation matrix

The equation (10) explicitly defines the effective conductivity at a point as a function of the microstructure at that point.
Optimization settings
To design the current device implies to solve the optimization problem given by equation (9). The cloaking task is prescribed by setting  at the center of the elements in Ω(1) and Ω(2), while the heat concentration task is forced by setting
at the center of the elements in Ω(1) and Ω(2), while the heat concentration task is forced by setting  at the center of elements in Ωfixint, with R/r = 5 in this case. Note that the vector P contains as variables only the vectors p(μ) characterizing the microstructure at the N = 1896 elements of Ωfree, with
at the center of elements in Ωfixint, with R/r = 5 in this case. Note that the vector P contains as variables only the vectors p(μ) characterizing the microstructure at the N = 1896 elements of Ωfree, with  and
and  , μ = 1, 2, … N.
, μ = 1, 2, … N.
For the chosen metamaterial, the current optimization problem is subject to the following box constraints:


Here, this nonlinear constrained optimization problem was solved using the IPOPT interior point algorithm18. Additional constraints may serve to avoid “complications”13: dependence on the finite element mesh, numerical instabilities, non-uniqueness of the solution, presence of multiple minima, etc. For the purpose of the current work, only the above box constraints are considered.
Results
The optimal solutions for dA (that is in fact the fraction of copper since the RVE was assumed to be a unit square) and θ (the orientation of the sheets) in the device are plotted in Fig. 5, together with the corresponding temperature distribution. Note that the device accomplished the combined task up to an RMS error equal to = 1.67 kW/m2 = 0.23||q0||.
Although we considered this error to be small enough, the solution is seriously affected by “checkerboard”-type instabilities, mainly in the orientation field (Fig. 5 at the center). This is a well-known and widely studied defect in material distribution problems (see the book of Bendsøe and Sigmund13 and references therein), which can be avoided using the density filter technique proposed by Sigmund19. The components of the vector P are still the design variables for the optimization problem (8), but the objective function in equation (9) as well as the constraints (11) and (12) are evaluated for the vector of physical or filtered parameters  . Then, the microstructure at the finite element e in Ωfree is actually characterized by the vector
. Then, the microstructure at the finite element e in Ωfree is actually characterized by the vector  , which is defined as
, which is defined as

where  is the filter radius (to be adopted), measured from the center of the finite element e, p(i) is the vector of design variables associated to the finite element i, Δei is the distance between the centers of the elements e and i, and 〈x〉 is the ramp function (〈x〉 = x for x > 0, and 〈x〉 = 0 for x ≤ 0).
is the filter radius (to be adopted), measured from the center of the finite element e, p(i) is the vector of design variables associated to the finite element i, Δei is the distance between the centers of the elements e and i, and 〈x〉 is the ramp function (〈x〉 = x for x > 0, and 〈x〉 = 0 for x ≤ 0).
Now, solving the optimization problem (9) using density filtering with  (i.e., five times the finite element size), we obtain the metamaterial distribution shown in Fig. 6, which is completely checkerboard-free. The so-obtained device Ωfree has a crosslike structure, with horizontal arms (parallel to q0) mostly made of highly-conductive copper and vertical arms (normal to q0) mostly made of poorly-conductive PDMS.
(i.e., five times the finite element size), we obtain the metamaterial distribution shown in Fig. 6, which is completely checkerboard-free. The so-obtained device Ωfree has a crosslike structure, with horizontal arms (parallel to q0) mostly made of highly-conductive copper and vertical arms (normal to q0) mostly made of poorly-conductive PDMS.
As consequence of the metamaterial distribution depicted in Fig. 6, the effective thermal conductivity varies inside the device as shown in Fig. 7, being generally anisotropic. Thanks to this conductivity distribution in the device, the temperature field in the whole plate is that shown in Fig. 8(a). There, it can be qualitatively realized how well the given combined cloaking and concentration task was accomplished: First, isotherms are almost parallel and equally spaced outside the device, as it would be the case without the device. Secondly, inside the device, the isotherms are significantly bent towards the inner region (Ωfixint), clearly demonstrating the strong energy concentration. This could be quantitatively appreciated in Fig. 8(b): The temperature along the center line y = 0, that where the heat flux is the most altered by the device, is slightly modified outside the device, while it has a gradient 4.58 times greater than the original one in the center of the device. Let us remark that, as solution of the optimization problem, the combined cloaking and concentration task was accomplished up to an RMS error equal to 2.04 kW/m2 = 0.29 ||q0||; individually, the RMS error for the concentration task in Ωfixint was 3.34 kW/m2 = 0.09 (R/r)||q0||, while the RMS error for the cloaking task in Ω(1) and Ω(2) was equal to 0.39 kW/m2 = 0.05 ||q0||. Although the minimization problem (9) accounts only for the portions Ω(1) and Ω(2) of Ωfixext, the heat flux is practically unaltered all around Ωfixext: it approaches q0 with a RMS error equal to 0.07 ||q0||.
Chen and Lei11 defined a concentration efficiency index as f = |(Tb − Tc)/(Ta − Td)|, where b and c are points located in the boundary of the heat concentration region Ωfixint, and a and d are points located at the outer boundary of the device Ωfree (see Fig. 8(b)). For the current device, we obtain f = 94.2%, close to the ideal f = 100%. Let us recall that the device designed by Chen and Lei based on the transformation approach, made of 100 radial copper-PDMS laminates, had a theoretical efficiency f = 96.3%, which fell to f = 88.1% for the finally fabricated device.
Comparing the current device to Chen and Lei’s one, it appears a crucial advantage of the current optimization-based design with respect to the transformation-based design: the device is designed just for the desired task (to manipulate an originally one-direction heat flux), avoiding to “oversize” it by performing unwanted or unprescribed tasks (in the case of Chen and Lei’s device, to manipulate the heat flux coming from any direction). Further, if the task is only to concentrate heat, the cloaking task is just a collateral result of applying the transformation-based approach.
Note that the current device can be seen as a neutral inclusion because of its cloaking effect. A priori, according to the theory of neutral inclusions (see chapter 7 in the book of Milton20 and references therein), it would be possible to determine in an analytical way a homogeneous isotropic material to make the cloaking device, a solution that is considerably more convenient than the current one using a heterogeneous metamaterial. However, let us remark that this trivial solution is not applicable to the current case. Actually, applying the Hashin-Shtrikman formula21 with the regions outside and enclosed by the device having the same isotropic conductivity kns, we determine that the only way of keeping the exterior flux unaltered is choosing the isotropic conductivity inside the device also equal to kns, which leads to completely ignore the heat flux concentration task.
Conclusions
We presented a novel method for designing metamaterials to control the diffusive heat flux in ways that were inconceivable using ordinary materials. This method consists in solving an optimization problem where the objective function to be minimized is the error in the accomplishment of a given heat flux control task, and the design variables define the microstructure in a heat flux manipulating device. Its potentiality was proved by designing a device for energy concentration that has close-to-ideal efficiency and, at the same time, leaves the external heat flux practically unaltered.
We expect these results may create opportunities to develop new advanced engineered materials for enhancing the efficiency of thermal devices in solar thermal collectors, for instance.
Future work will be devoted to ensure the manufacturability of these optimization-based designs.
Additional Information
How to cite this article: Peralta, I. et al. Optimization-based design of a heat flux concentrator. Sci. Rep. 7, 40591; doi: 10.1038/srep40591 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Maldovan, M. Sound and heat revolutions in phononics. Nature 503, 209–217 (2013).
Narayana, S. & Sato, Y. Heat flux manipulation with engineered thermal materials. Phys. Rev. Lett. 108, 214303 (2012).
Schittny, R., Kadic, M., Guenneau, S. & Wegener, M. Experiments on transformation thermodynamics: Molding the flow of heat. Phys. Rev. Lett. 110, 195901 (2013).
Pendry, J. B., Schurig, D. & Smith, D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006).
Chen, H. & Chan, C. T. Transformation media that rotate electromagnetic fields. Appl. Phys. Lett. 90, 241105 (2007).
Bor, E., Turduev, M. & Kurt, H. Differential evolution algorithm based photonic structure design: numerical and experimental verification of subwavelength λ/5 focusing of light. Sci. Rep. 6, 30871 (2016).
Jensen, J. S. & Sigmund, O. Topology optimization for nano-photonics. Laser Photon. Rev. 5, 308–321 (2011).
Sigmund, O. & Hougaard, K. Geometric properties of optimal photonic crystals. Phys. Rev. Lett. 100, 153904 (2008).
Jensen, J. S. & Sigmund, O. Systematic design of photonic crystal structures using topology optimization: low-loss waveguide bends. Appl. Phys. Lett. 84, 2022 (2004).
Frandsen, L. H. et al. Topology optimized mode conversion in a photonic waveguide fabricated in silicon-on-insulator material. Opt. Express 22, 8525–8532 (2014).
Chen, F. & Lei, D. Y. Experimental realization of extreme heat flux concentration with easy-to-make thermal metamaterials. Sci. Rep. 5 (2015).
Zienkiewicz, O. C. & Taylor, R. L. The finite element method vol. 1: The basis (Butterworth-Heinemann, 2000).
Bendsøe, M. P. & Sigmund, O. Topology optimization. Theory, methods, and applications (Springer-Verlag, 2003).
Schittny, R. et al. Invisibility cloaking in light-scattering media. Laser Photonics Rev. 10, 382–408 (2016).
Narayana, S., Savo, S. & Sato, Y. Transient heat flux shielding using thermal metamaterials. Appl. Phys. Lett. 102, 201904 (2013).
Vemuri, K. P., Canbazoglu, F. M. & Bandaru, P. R. Guiding conductive heat flux through thermal metamaterials. Appl. Phys. Lett. 105, 193904 (2014).
Kadic, M., Bückmann, T., Schittny, R. & Wegener, M. Metamaterials beyond electromagnetism. Rep. Prog. Phys. 76, 126501 (2013).
Wächter, A. & Biegler, L. T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. Ser. A 106, 25–57 (2006).
Sigmund, O. Morphology-based black and white filters for topology optimization. Struct. Multidisc. Optim. 33, 401–424 (2007).
Milton, G. W. The theory of composites (Cambridge University Press, 2004).
Hashin, Z. & Shtrikman, S. A variational approach to the theory of the effective magnetic permeability of multiphase materials. J. Appl. Phys. 33, 3125–3131 (1962).
Acknowledgements
We thank the following institutions for supporting this work: The European Research Council (ERC), through the project “Advanced Tools for Computational Design of Engineering Materials (COMP-DES-MAT)” (FP/2007-2013, ERC Grant Agreement 320815). The National Scientific and Technical Research Council (CONICET) from Argentina, through the project PIP 1105 “Computational Simulation of Multiphysics Problems. Application to Metal Solidification and Micromechanical Devices”.
Author information
Authors and Affiliations
Contributions
V.D.F. developed the optimization-based methodology for general thermomechanical problems, and I.P. applied it to design heat flux manipulating devices. A.A.C. collaborated in both tasks. All the work was done under the supervision of V.D.F., who is the tutor of I.P. (doctoral fellow) and A.A.C. (postdoctoral fellow).
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Peralta, I., Fachinotti, V. & Ciarbonetti, Á. Optimization-based design of a heat flux concentrator. Sci Rep 7, 40591 (2017). https://doi.org/10.1038/srep40591
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep40591
This article is cited by
-
Flexible and high precision thermal metasurface
Communications Materials (2021)
-
Topology optimization of thermal problems in a nonsmooth variational setting: closed-form optimality criteria
Computational Mechanics (2020)
-
Metamaterial for elastostatic cloaking under thermal gradients
Scientific Reports (2019)
-
Optimization-based design of an elastostatic cloaking device
Scientific Reports (2018)
-
Realization of a thermal cloak–concentrator using a metamaterial transformer
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




 denotes the desired heat flux at the point x(q)
denotes the desired heat flux at the point x(q) 




