Abstract
The estimation of the decoherence process of an open quantum system is of both theoretical significance and experimental appealing. Practically, the decoherence can be easily estimated if the coherence evolution satisfies some simple relations. We introduce a framework for studying evolution equation of coherence. Based on this framework, we prove a simple factorization relation (FR) for the l1 norm of coherence and identified the sets of quantum channels for which this FR holds. By using this FR, we further determine condition on the transformation matrix of the quantum channel which can support permanently freezing of the l1 norm of coherence. We finally reveal the universality of this FR by showing that it holds for many other related coherence and quantum correlation measures.
Similar content being viewed by others
Introduction
Quantum coherence, an embodiment of the superposition principle of states, lies at the heart of quantum mechanics and is also a major concern of quantum optics1. Physically, coherence constitutes the essence of quantum correlations (e.g., entanglement2 and quantum discord3) in bipartite and multipartite systems which are indispensable resources for quantum communication and computation tasks. It also finds support in the promising subject of thermodynamics4,5,6,7,8 and quantum biology9.
Clarifying the decoherence mechanism of an noisy system is an important research direction of quantum mechanics. But due to the lack of rigorous coherence measures, studies in this subject were usually limited to the qualitative analysis. Sometimes, coherence behaviors were also analyzed indirectly via various quantum correlation measures3. However, coherence and quantum correlations are in fact different. Very recently, the characterization and quantification of quantum coherence from a mathematically rigorous and physically meaningful perspective has been achieved10. This sets the stage for quantitative analysis of coherence, which were carried out mainly around the identification of various coherence monotones11,12,13,14,15,16 and their calculation17. Some other progresses about coherence quantifiers include their connections with quantum correlations18,19,20, their behaviors in noisy environments21,22, their local and nonlocal creativity23,24, their distillation25,26 and the role they played in the fundamental issue of quantum mechanics27,28,29,30.
One major goal of quantum theory is to find effective ways of maintaining the amount of coherence within a system. The reason is twofold. First, coherence represents a basic feature of quantum states and underpins all forms of quantum correlations1. Second, coherence itself is a precious resource for many new quantum technologies, but the unavoidable interaction of quantum devices with the environment often decoheres the input states and induces coherence loss, hence damage the superiority of these quantum technologies31.
Looking for general law determining the evolution equation of coherence can facilitate the design of effective coherence preservation schemes. Remarkably, the evolution equations for certain entanglement monotones (or their bounds)32,33,34,35,36,37,38,39,40 and geometric discords41 were found to obey the factorization relation (FR) for specific initial states. Then, it is natural to ask whether there exists similar FR for various coherence monotones. In this work, we aimed at solving this problem. We first classify the general d-dimensional states into different families and then prove a FR which holds for them. By employing this FR, we further identified condition on the quantum channel for freezing coherence. We also showed that this FR applies to many other coherence and correlation measures. These results are hoped to add another facet to the already rich theory of decoherence and shed light on revealing the interplay between structures of quantum channel and geometry of the state space, as well as how they determine quantum correlation behaviors of an open system.
Results
Coherence measures
By establishing rigorously the sets  of incoherent states which are diagonal in the reference basis {|i〉}i=1,…,d and incoherent operations Λ specified by the Kraus operators {El} which map
of incoherent states which are diagonal in the reference basis {|i〉}i=1,…,d and incoherent operations Λ specified by the Kraus operators {El} which map  into
into  , Baumgratz et al.10 presented the defining properties for an information-theoretic coherence measure C: (1) C(ρ) ≥ 0 for all states ρ and C(δ) = 0 iff
, Baumgratz et al.10 presented the defining properties for an information-theoretic coherence measure C: (1) C(ρ) ≥ 0 for all states ρ and C(δ) = 0 iff  . (2) Monotonicity under the actions of Λ, C(ρ) ≥ C(Λ(ρ)). (3) Monotonicity under selective incoherent operations on average, i.e.,
. (2) Monotonicity under the actions of Λ, C(ρ) ≥ C(Λ(ρ)). (3) Monotonicity under selective incoherent operations on average, i.e.,  , where
, where  and
and  is the probability of obtaining the outcome l. (4) Convexity,
is the probability of obtaining the outcome l. (4) Convexity,  , with pl ≥ 0 and
, with pl ≥ 0 and  .
.
There are several coherence measures satisfying the above conditions. They are the l1 norm and relative entropy10, the Uhlmann fidelity12, the intrinsic randomness14 and the robustness of coherence42. In this work, we concentrate mainly on the l1 norm of coherence, which is given by  in the basis {|i〉}i=1,…,d10 and will mention other coherence measures if necessary.
in the basis {|i〉}i=1,…,d10 and will mention other coherence measures if necessary.
FR for quantum coherence
Consider a general d-dimensional state in the Hilbert space  , with the density matrix
, with the density matrix

where  is the d × d identity matrix,
is the d × d identity matrix,  ,
,  , xi = Tr(ρXi) and Xi ∝ Ti. Here, {Ti} are generators of the Lie algebra SU(d). They can be represented by the d × d traceless Hermitian matrices which satisfy
, xi = Tr(ρXi) and Xi ∝ Ti. Here, {Ti} are generators of the Lie algebra SU(d). They can be represented by the d × d traceless Hermitian matrices which satisfy  , with fijk (dijk) being the structure constants that are completely antisymmetric (symmetric) in all indices43,44. If one arranges
, with fijk (dijk) being the structure constants that are completely antisymmetric (symmetric) in all indices43,44. If one arranges 
 , then
, then

where j, k ∈ {1, 2, …, d} with j < k and l ∈ {1, 2, …, d − 1}. Clearly, {Xi} satisfy  . Moreover, the notation i appeared in vjk is the imaginary unit.
. Moreover, the notation i appeared in vjk is the imaginary unit.
For ρ represented as Eq. (1),  can be derived as
can be derived as

where d0 = (d2 − d)/2 and xl related to wl which is diagonal in the basis {|i〉}i=1,…,d do not contribute to  .
.
To investigate evolution equation of coherence, we suppose the system S of interest interacts with its environment E, then by considering S and E as a whole for which their evolution is unitary, the reduced density matrix for S is obtained by tracing out the environmental degrees of freedom,  . In terms of the master equation description, the equation of motion of ρ can be written in a local-in-time form31
. In terms of the master equation description, the equation of motion of ρ can be written in a local-in-time form31

with  being the Louville super-operator which may be time independent or time dependent.
being the Louville super-operator which may be time independent or time dependent.
As it has been shown that for any master equation which is local in time, whether Markovian, non-Markovian, of Lindblad form or not, one can always construct a linear map which gives  (the opposite case may not always be true) and the linear map can be expressed in the Kraus-type representations45. If the map
(the opposite case may not always be true) and the linear map can be expressed in the Kraus-type representations45. If the map  is completely positive and trace preserving (CPTP), then one can explicitly construct the Kraus operators {Eμ} such that
is completely positive and trace preserving (CPTP), then one can explicitly construct the Kraus operators {Eμ} such that

where elements of  for
for  are given by
are given by  .
.
For convenience of later discussion, we turn to the Heisenberg picture to describe  via the map
via the map  , which gives
, which gives  . As an Hermitian operator
. As an Hermitian operator  on
on  can always be decomposed as
can always be decomposed as 
 ,
,  can be further characterized by the transformation matrix T defined via
can be further characterized by the transformation matrix T defined via

where  and here we denote by
and here we denote by  . Clearly, T00 = 1 and T0j = 0 for j ≥ 1. This further gives
. Clearly, T00 = 1 and T0j = 0 for j ≥ 1. This further gives  .
.
To present our central result, we first classify the states ρ into different families:  , with
, with

and  is a unit vector in
is a unit vector in  , while χ is a parameter satisfying
, while χ is a parameter satisfying  as
as  . By this classification scheme, different families of states are labeled by different unit vectors
. By this classification scheme, different families of states are labeled by different unit vectors  , while states belong to the same family are characterized by a common
, while states belong to the same family are characterized by a common  and can be distinguished by different multiplicative factors χ (see Fig. 1). That is to say,
and can be distinguished by different multiplicative factors χ (see Fig. 1). That is to say,  represents states with the characteristic vectors
represents states with the characteristic vectors  along the same or completely opposite directions but possessing different lengths.
along the same or completely opposite directions but possessing different lengths.
While  is fully described by
is fully described by  and the action of
and the action of  on it can be written equivalently as the map:
on it can be written equivalently as the map:  , a measure Q may only be function of
, a measure Q may only be function of  , i.e.,
, i.e.,  , with
, with  (α ≤ d2 − 1). Then as one can always make Qmax ≥ 1 (otherwise, one can normalize it by multiplying a constant to it), we have the following lemma.
(α ≤ d2 − 1). Then as one can always make Qmax ≥ 1 (otherwise, one can normalize it by multiplying a constant to it), we have the following lemma.
Lemma 1. For any quantum measure of  that can be factorized as
that can be factorized as  , and quantum channel
, and quantum channel  that gives the map
that gives the map  , the FR
, the FR

holds, where f(χ) and  are functionals of χ and
are functionals of χ and  , respectively, and
, respectively, and  is the probe state, with χp solution of the equation
is the probe state, with χp solution of the equation  .
.
The proof is given in Methods. Equipped with this lemma, we are now in position to present our central result.
Theorem 1. If the transformation matrix elements Tk0 = 0 for k ∈ {1, 2, …, d2 − d}, then the evolution of  obeys the following FR
obeys the following FR

with  the probe state, and
the probe state, and  .
.
The proof is left to the Methods. Here, we further show an implication of it. As Tk0 = 0 for k ∈ {1, 2, …, d2 − d}, we have  , hence
, hence  . On the other hand,
. On the other hand,  . This, together with Eq. (2), requires that all the nondiagonal elements of
. This, together with Eq. (2), requires that all the nondiagonal elements of  must be zero.
must be zero.
Corollary 1. If the operator  is diagonal, then the evolution of
is diagonal, then the evolution of  obeys the FR (9).
obeys the FR (9).
This corollary means that in addition to the usual completeness condition  of the CPTP map31, the FR (9) further requires
of the CPTP map31, the FR (9) further requires  to be diagonal. We denote this kind of channels
to be diagonal. We denote this kind of channels  . Clearly, they include the unital channel
. Clearly, they include the unital channel  [i.e.,
[i.e.,  ] as a special case.
] as a special case.
From a geometric perspective, Theorem 1 indicates that for all states of the same family  , namely, states with the characteristic vectors
, namely, states with the characteristic vectors  along the same or opposite directions, their coherence dynamics measured by the l1 norm can be represented qualitatively by that of the probe state
along the same or opposite directions, their coherence dynamics measured by the l1 norm can be represented qualitatively by that of the probe state  , as the magnitude of
, as the magnitude of  equals the product of the initial coherence
equals the product of the initial coherence  and the evolved coherence
and the evolved coherence  . This simplifies greatly the assessment of the decoherence process of an open system. Moreover, the FR (9) provides a strong link between amount of the coherence loss of a system and structures of the applied quantum channels. Particularly, as
. This simplifies greatly the assessment of the decoherence process of an open system. Moreover, the FR (9) provides a strong link between amount of the coherence loss of a system and structures of the applied quantum channels. Particularly, as  with the vectors
with the vectors  along the same or opposite directions fulfill the same decoherence law, the approach adopted here may offer a route for better understanding the interplay between geometry of the state space and various aspects of its quantum features. It might also provides a deeper insight into the effects of gate operation in quantum computing and experimental generation of coherent resources in noisy environments, as
along the same or opposite directions fulfill the same decoherence law, the approach adopted here may offer a route for better understanding the interplay between geometry of the state space and various aspects of its quantum features. It might also provides a deeper insight into the effects of gate operation in quantum computing and experimental generation of coherent resources in noisy environments, as  can specify the actions of environments, of measurements, or of both on the states
can specify the actions of environments, of measurements, or of both on the states  .
.
When some restrictions are imposed on the quantum channels, the FR (9) can be further simplified.
Corollary 2. If a channel  yields
yields  for
for  (β ≤ d2 − d), with q(t) containing information on
(β ≤ d2 − d), with q(t) containing information on  ’s structure, then the FR
’s structure, then the FR

holds for the family of states  .
.
The proof of this corollary is direct. As  , the parameters
, the parameters  for
for  are given by
are given by  . Therefore, by Eq. (3) we obtain
. Therefore, by Eq. (3) we obtain  . Clearly, its evolution is solely determined by the product of the initial coherence and a noise parameter |q(t)|.
. Clearly, its evolution is solely determined by the product of the initial coherence and a noise parameter |q(t)|.
There are many quantum channels satisfying the condition of Corollary 2. For instance, the Pauli channel  and Gell-Mann channel
and Gell-Mann channel  given in ref. 41 and the generalized amplitude damping channel
given in ref. 41 and the generalized amplitude damping channel  31. Notably,
31. Notably,  covers the bit flip, phase flip, bit-phase flip, phase damping and depolarizing channels which embody typical noisy sources in quantum information, while
covers the bit flip, phase flip, bit-phase flip, phase damping and depolarizing channels which embody typical noisy sources in quantum information, while  covers the structured reservoirs with Lorentzian and Ohmic-type spectral densities.
covers the structured reservoirs with Lorentzian and Ohmic-type spectral densities.
One can also construct quantum channel  under the action of which
under the action of which  obeys the FR (10) for arbitrary initial state. The Kraus operators describing
obeys the FR (10) for arbitrary initial state. The Kraus operators describing  are given by
are given by

with k ∈ {1, …, d2 − d} and l ∈ {d2 − d + 1, …, d2 − 1}, while q and q0 are time-dependent noisy parameters. Clearly,  reduces to the depolarizing channel when q0 = q.
reduces to the depolarizing channel when q0 = q.
N-qubit case
A general N-qubit state can be written as  , with
, with  , and
, and

here,  and σ1,2,3 are the usual Pauli matrices, while jk takes the possible values of {0, 1, 2, 3} other than the special case jk = 0 for all k. In the Methods section, we have proved that for every family of the N-qubit states
and σ1,2,3 are the usual Pauli matrices, while jk takes the possible values of {0, 1, 2, 3} other than the special case jk = 0 for all k. In the Methods section, we have proved that for every family of the N-qubit states  , with
, with  being a given unit vector, one can construct an auxiliary channel
being a given unit vector, one can construct an auxiliary channel  such that
such that  . This, together with Eq. (9), gives:
. This, together with Eq. (9), gives:
Corollary 3. For any N-qubit state ρN, there exists an auxiliary channel  such that
such that

with  ,
,  , d0 = (4N − 2N)/2, and
, d0 = (4N − 2N)/2, and  , with aij being determined by the transformation between {Yj} and {Xi}:
, with aij being determined by the transformation between {Yj} and {Xi}:  .
.
This corollary generalizes the FR (9) for the N-qubit states. It shows that coherence of the evolved state under the actions of two cascaded channels  is determined by the product of the coherence for the evolved probe state under the action of
is determined by the product of the coherence for the evolved probe state under the action of  and the coherence for the generated state by
and the coherence for the generated state by  . As every Yj can always be decomposed as linear combinations of the generators {Xi}, the above result applies also to the qudit states with d = 2N. As an explicit example, the transformation between {Yj} and {Xi} for N = 2 is given in the Methods section, from which
. As every Yj can always be decomposed as linear combinations of the generators {Xi}, the above result applies also to the qudit states with d = 2N. As an explicit example, the transformation between {Yj} and {Xi} for N = 2 is given in the Methods section, from which  and {aij} can be constructed directly.
and {aij} can be constructed directly.
Frozen coherence
By Theorem 1 we can also derive conditions on the quantum channel for which the l1 norm of coherence is frozen. To elucidate this, we return to Eq. (9), from which one can see that  is frozen if the coherence of the probe state remains constant 1 during the evolution, i.e.,
is frozen if the coherence of the probe state remains constant 1 during the evolution, i.e.,  . For later use, we denote by TS the submatrix of T consisting Tij with i ranging from 1 to d2 − d and j from 1 to d2 − 1. Then by Theorem 1 and the reasoning in its proof, we obtain the fourth corollary.
. For later use, we denote by TS the submatrix of T consisting Tij with i ranging from 1 to d2 − d and j from 1 to d2 − 1. Then by Theorem 1 and the reasoning in its proof, we obtain the fourth corollary.
Corollary 4. If Tk0 = 0 for k ∈ {1, 2, …, d2 − d}, and TS is a rectangular block diagonal matrix, with the main diagonal blocks

being orthogonal matrices, i.e.,  , the l1 norm of coherence for
, the l1 norm of coherence for  will be frozen during the entire evolution.
will be frozen during the entire evolution.
The proof is given in Methods. It enables one to construct channels  for which the l1 norm of coherence is frozen. As an explicit example, we consider the one-qubit case, with
for which the l1 norm of coherence is frozen. As an explicit example, we consider the one-qubit case, with  being described by
being described by  , i ∈ {0, 1, 2, 3} and
, i ∈ {0, 1, 2, 3} and  . Then by Corollary 4, one can obtain that when εi0 = εi3 = 0, and
. Then by Corollary 4, one can obtain that when εi0 = εi3 = 0, and
 , or when εi1 = εi2 = 0 and
, or when εi1 = εi2 = 0 and 
 , with Re(·) and Im(·) representing, respectively, the real and imaginary parts of a number, the l1 norm of coherence will be frozen. There are a host of {εij} that fulfill the requirements, e.g., ε01 = q(t),
, with Re(·) and Im(·) representing, respectively, the real and imaginary parts of a number, the l1 norm of coherence will be frozen. There are a host of {εij} that fulfill the requirements, e.g., ε01 = q(t),  , εk1 = εk2 = 0, or ε00 = q(t),
, εk1 = εk2 = 0, or ε00 = q(t),  , εk0 = εk3 = 0, with k ∈ {1, 2, 3} and q(t) contains the information on
, εk0 = εk3 = 0, with k ∈ {1, 2, 3} and q(t) contains the information on  ’s structure and its coupling with the system.
’s structure and its coupling with the system.
Moreover, for certain special initial states, the freezing condition presented in Corollary 4 may be further relaxed. In fact, for  with certain n2r−1 = 0 (or n2r = 0),
with certain n2r−1 = 0 (or n2r = 0),  simplifies to
simplifies to  (or
(or  ). For instance, when considering the channel
). For instance, when considering the channel  41, the l1 norm of coherence for
41, the l1 norm of coherence for  with n2 = 0 is frozen during the entire evolution when q1 = 1 (i.e., the bit flip channel). Similarly, for
with n2 = 0 is frozen during the entire evolution when q1 = 1 (i.e., the bit flip channel). Similarly, for  with n1 = 0, it is frozen when q2 = 1 (i.e., the bit-phase flip channel). These are in facts the results obtained in ref. 21. Needless to say, when
with n1 = 0, it is frozen when q2 = 1 (i.e., the bit-phase flip channel). These are in facts the results obtained in ref. 21. Needless to say, when  , the l1 norm of coherence is also frozen for
, the l1 norm of coherence is also frozen for  with certain n2r−1 = 0 or n2r = 0.
with certain n2r−1 = 0 or n2r = 0.
Outlook
The FR (9) presented here can be of direct relevance to other issues of quantum theory. For example, the l1 norm of coherence is a monotone of the entanglement-based coherence measure for one-qubit states12. Its logarithmic form  is lower bounded by the relative entropy of coherence Cr(ρ) which has a clear physical interpretation, while
is lower bounded by the relative entropy of coherence Cr(ρ) which has a clear physical interpretation, while  for arbitrary ρ has also been conjectured46. Further study shows that
for arbitrary ρ has also been conjectured46. Further study shows that  also bounds the robustness of coherence, i.e.,
also bounds the robustness of coherence, i.e.,  42. It is also connected to the success probability of state discrimination in interference experiments29 and the negativity of quantumness21,47. Thus, our results provide a route for inspecting the interrelations between decay behaviors of coherence, quantumness and entanglement.
42. It is also connected to the success probability of state discrimination in interference experiments29 and the negativity of quantumness21,47. Thus, our results provide a route for inspecting the interrelations between decay behaviors of coherence, quantumness and entanglement.
The FR also applies to other related coherence measures, as well as quantum correlations which are relevant to coherence. Some examples are as follows (see Methods section for their proof): (i) the coherence concurrence for one-qubit states14 and the trace norm coherence for one-qubit and certain qutrit states13,46; (ii) the genuine quantum coherence (GQC) defined via the Schatten p-norm for all states48, which is related to quantum thermodynamics and the resource theory of asymmetry; (iii) the robustness of coherence for the one-qubit states and d-dimensional states with X-shaped density matrix and its lower bound  which is a measure of the GQC for all states42; (iv) the K coherence defined based on the Wigner-Yanase skew information11, although it is problematic in the framework of coherence by Baumgratz et al.49, it may be a proper measure of the GQC48; (v) the purity of a state which is complementary with quantum coherence28; (vi) the geometric discord50,51,52,53,54 and measurement-induced nonlocality55,56; (vii) the maximum Bell-inequality violation57 and average fidelity of remote state preparation58 and quantum teleportation59. All these manifest the universality of the FR formulated in this paper and will certainly deepen our understanding of the already rich and appealing subject of quantum channels or the CPTP maps.
which is a measure of the GQC for all states42; (iv) the K coherence defined based on the Wigner-Yanase skew information11, although it is problematic in the framework of coherence by Baumgratz et al.49, it may be a proper measure of the GQC48; (v) the purity of a state which is complementary with quantum coherence28; (vi) the geometric discord50,51,52,53,54 and measurement-induced nonlocality55,56; (vii) the maximum Bell-inequality violation57 and average fidelity of remote state preparation58 and quantum teleportation59. All these manifest the universality of the FR formulated in this paper and will certainly deepen our understanding of the already rich and appealing subject of quantum channels or the CPTP maps.
Recently, Jing et al. studied quantum speed limits to the rate of change of quantumness measured by the non-commutativity of the algebra of observables60. We note that the coherence quantifiers can also be considered as a measure of quantumness, but it is different from the notion of quantumness considered in ref. 60 and references therein, although they both characterize global quantum nature of a state and are intimately related to quantum correlations such as discord. The coherence monotones characterize quantumness of a single state. It is basis dependent and vanishes for the diagonal states. The quantumness based on the non-commutativity relations measures the relative quantumness of two states. It is basis independent and vanishes only for the maximally mixed states. Of course, it is as well crucial to study evolution equation of it in future work.
Discussion
We have established a simple FR for the evolution equation of the l1 norm of coherence, which is of practical relevance for assessing coherence loss of an open quantum system. For a general d-dimensional state, we determined condition such that this FR holds. The condition can be described as a restriction on the transformation matrix, or on the operator  , of the quantum channel. By introducing an auxiliary channel, we further presented a more general relation which applies to any N-qubit state. With the help of the FR, we have also determined a condition the transformation matrix should satisfy such that the l1 norm of coherence for a general state is dynamically frozen and constructed explicitly the desired channels for one-qubit states. Finally, we showed that the FR holds for many other related coherence and quantum correlation measures. We hope these results may help in understanding the interplay between structure of the quantum channel, geometry of the state space and decoherence of an open system, as well as their combined effects on decay behaviors of various quantum correlations.
, of the quantum channel. By introducing an auxiliary channel, we further presented a more general relation which applies to any N-qubit state. With the help of the FR, we have also determined a condition the transformation matrix should satisfy such that the l1 norm of coherence for a general state is dynamically frozen and constructed explicitly the desired channels for one-qubit states. Finally, we showed that the FR holds for many other related coherence and quantum correlation measures. We hope these results may help in understanding the interplay between structure of the quantum channel, geometry of the state space and decoherence of an open system, as well as their combined effects on decay behaviors of various quantum correlations.
Methods
Proof of Lemma 1. As  gives the map
gives the map  and
and  fulfills
fulfills  , we have
, we have

Hence, it is evident that  when
when  .
.
If Qmax ≥ 1, the equation  with respect to χp is always solvable as
with respect to χp is always solvable as  . If Qmax < 1, one can normalize it by simply introducing a constant N such that
. If Qmax < 1, one can normalize it by simply introducing a constant N such that  , with Q′ obeying the FR of Eq. (8).
, with Q′ obeying the FR of Eq. (8).
Proof of Theorem 1. First, by using Eq. (3) and the fact that  , we obtain
, we obtain

which corresponds to  , with f(χ) = χ and
, with f(χ) = χ and  .
.
Second, when the transformation matrix elements Tk0 = 0 for k ∈ {1, 2, …, d2 − d}, we have

and therefore  .
.
From Eqs (16) and (17) one can see that both the l1 norm of coherence and the quantum channel  fulfill the requirements of Lemma 1 and the probe state
fulfill the requirements of Lemma 1 and the probe state  , with χp being solution of the equation
, with χp being solution of the equation  , which can be solved as
, which can be solved as  . This completes the proof.
. This completes the proof.
Proof of Corollary 3. Suppose  is described by the Kraus operators
is described by the Kraus operators  , with
, with  . Then, by employing the anticommutation relation of the Pauli operators σ1,2,3, we obtain
. Then, by employing the anticommutation relation of the Pauli operators σ1,2,3, we obtain

where  , with
, with  if vkμk(vk − μk) = 0 and
if vkμk(vk − μk) = 0 and  otherwise. This formula is equivalent to
otherwise. This formula is equivalent to  , with
, with  encoding the information of
encoding the information of  .
.
To solve εμ, we define coefficient matrix  and column vectors
and column vectors  ,
,  , then
, then  becomes
becomes  , hence ε can be derived as
, hence ε can be derived as  , with c−1 denoting the inverse matrix of c. Finally, by choosing
, with c−1 denoting the inverse matrix of c. Finally, by choosing  , we obtain
, we obtain  , thus completes the proof.
, thus completes the proof.
The transformation between generators {Yj} for the two-qubit states and {Xi} for the qudit states with d = 4 are as follows:

where  and elements
and elements  of
of  are arranged with (j1j2) in the sequence (01), (02), (03), (10), (11), (12), (13), …, (33).
are arranged with (j1j2) in the sequence (01), (02), (03), (10), (11), (12), (13), …, (33).
Proof of Corollary 4. As the submatrix TS is rectangular block diagonal, the elements Tij in the off-diagonal blocks are all zero. This, together with Tk0 = 0 for k ∈ {1, 2, …, d2 − d}, yields

for r ∈ {1, 2, …, d0}. Moreover, the requirement that  yields
yields

By using the above two equations, it is straightforward to see that  and therefore from Eq. (16) we have
and therefore from Eq. (16) we have  . This, together with Theorem 1, implies
. This, together with Theorem 1, implies  and hence completes the proof.
and hence completes the proof.
Frozen coherence of one qubit
Suppose the required channel  is described by the Kraus operators
is described by the Kraus operators  , with i ∈ {0, 1, 2, 3} and the values of
, with i ∈ {0, 1, 2, 3} and the values of  should satisfy certain constraints such that the requirement of Corollary 4 is satisfied. First, the completeness condition of the CPTP map, namely,
should satisfy certain constraints such that the requirement of Corollary 4 is satisfied. First, the completeness condition of the CPTP map, namely,  31, requires
31, requires

where  represents conjugation of εij and the notation i before εi2, Re(·) and Im(·) is the imaginary unit.
represents conjugation of εij and the notation i before εi2, Re(·) and Im(·) is the imaginary unit.
Second, Corollary 4 requires T10 = T20 = 0 and TS to be a rectangular block diagonal matrix which corresponds to T13 = T23 = 0. This yields

from which one can obtain

and

By comparing Eqs (22) and (24), one can note that the equalities are satisfied when εi0 = εi3 = 0,  , or when εi1 = εi2 = 0,
, or when εi1 = εi2 = 0,  . Under these two constraints, Eq. (25) simplifies, respectively, to
. Under these two constraints, Eq. (25) simplifies, respectively, to

and

Finally, the requirement that  , corresponds to
, corresponds to

and from Eqs (26) and (27), one can see that the third equality of Eq. (28) is always satisfied, while the first two equalities are equivalent. Therefore, to freeze the l1 norm of coherence, εij should satisfy one of the following two conditions:
(i) εi0 = εi3 = 0 for i ∈ {0, 1, 2, 3}, and

(ii) εi1 = εi2 = 0 for i ∈ {0, 1, 2, 3}, and

Other measures fulfilling the FR
(i) The coherence concurrence for the one-qubit states14 and the trace norm coherence for the one-qubit and certain qutrit states13,46, coincide with the l1 norm of coherence. Hence, the FR applies to them.
(ii) For the GQC measure  presented in ref. 48, we have
presented in ref. 48, we have

where  denotes full dephasing of ρ in the basis {|i〉}i=1,…,d. Thus,
denotes full dephasing of ρ in the basis {|i〉}i=1,…,d. Thus,  , with f(χ) = χ/2 and
, with f(χ) = χ/2 and  .
.
For the GQC measure  , the FR also holds as the optimal δ is given by Δ(ρ)48.
, the FR also holds as the optimal δ is given by Δ(ρ)48.
(iii) CRoC(ρ) for the one-qubit states and d-dimensional states with X-shaped density matrix, equals to the l1 norm of coherence and thus the FR holds.
(iv) The K coherence is defined as  11. As
11. As  can be decomposed as
can be decomposed as  53,
53,  is a function of
is a function of  , i.e.,
, i.e.,  , with
, with  . Then by using [X0, K] = 0, we obtain
. Then by using [X0, K] = 0, we obtain

thus  , with f(χ) = −χ2/2 and
, with f(χ) = −χ2/2 and  .
.
(v) For the quantifier  which is a monotonic function of the purity P(ρ) = Trρ2 of a state, we have the FR
which is a monotonic function of the purity P(ρ) = Trρ2 of a state, we have the FR  , with ρp bing the probe state for which
, with ρp bing the probe state for which  .
.
(vi) The general form of geometric quantum correlation measure can be written as

where  denotes the Schatten p-norm and opt represents the optimization over some class
denotes the Schatten p-norm and opt represents the optimization over some class  of the local measurements
of the local measurements  . This definition covers the geometric discord50,51,52 and measurement-induced nonlocality55,56. For these measures, as
. This definition covers the geometric discord50,51,52 and measurement-induced nonlocality55,56. For these measures, as  , we have
, we have

then by comparing with Lemma 1, we obtain f(χ) = (χ/2)p and  , i.e., the FR holds.
, i.e., the FR holds.
If ρ in Eq. (33) is replaced by  , then one obtains the Hellinger distance discord for p = 253,54. As
, then one obtains the Hellinger distance discord for p = 253,54. As  , with
, with  and
and  being the sets of Hermitian operators which constitute the orthonormal operator bases for the Hilbert space
being the sets of Hermitian operators which constitute the orthonormal operator bases for the Hilbert space  and
and  53 and
53 and  , the FR also holds for it.
, the FR also holds for it.
(vii) For two-qubit states, the maximum Bell-inequality violation Bmax(ρ)57, remote state preparation fidelity Frsp(ρ)58 and Nqt(ρ) which is a monotone of the average teleportation fidelity  59, are given by
59, are given by

where E1 ≥ E2 ≥ E3 are eigenvalues of the 3 × 3 matrix T†T and  . This gives
. This gives  for i ∈ {1, 2, 3}, which implies that all measures of Eq. (35) satisfy the requirement of Lemma 1.
for i ∈ {1, 2, 3}, which implies that all measures of Eq. (35) satisfy the requirement of Lemma 1.
Additional Information
How to cite this article: Hu, M.-L. and Fan, H. Evolution equation for quantum coherence. Sci. Rep. 6, 29260; doi: 10.1038/srep29260 (2016).
References
Ficek, Z. & Swain, S. Quantum interference and coherence: theory and experiments (Springer Series in Optical Sciences, 2005).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009).
Modi, K., Brodutch, A., Cable, H., Paterek, T. & Vedral, V. The classical-quantum boundary for correlations: discord and related measures. Rev. Mod. Phys. 84, 1655 (2012).
Åberg, J. Catalytic coherence. Phys. Rev. Lett. 113, 150402 (2014).
Lostaglio, M., Jennings, D. & Rudolph, T. Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 6, 6383 (2015).
Narasimhachar, V. & Gour, G. Low-temperature thermodynamics with quantum coherence. Nat. Commun. 6, 7689 (2015).
Lostaglio, M., Korzekwa, K., Jennings, D. & Rudolph, T. Quantum coherence, time-translation symmetry and thermodynamics. Phys. Rev. X 5, 021001 (2015).
Gour, G., Müller, M. P., Narasimhachar, V., Spekkens, R. W. & Halpern, N. Y. The resource theory of informational nonequilibrium in thermodynamics. Phys. Rep. 583, 1 (2015).
Lambert, N. et al. Quantum biology. Nat. Phys. 9, 10 (2013).
Baumgratz, T., Cramer, M. & Plenio, M. B. Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2014).
Girolami, D. Observable measure of quantum coherence in finite dimensional systems. Phys. Rev. Lett. 113, 170401 (2014).
Streltsov, A., Singh, U., Dhar, H. S., Bera, M. N. & Adesso, G. Measuring quantum coherence with entanglement. Phys. Rev. Lett. 115, 020403 (2015).
Shao, L. H., Xi, Z., Fan, H. & Li, Y. Fidelity and trace-norm distances for quantifying coherence. Phys. Rev. A 91, 042120 (2015).
Zhang, Y. R., Shao, L. H., Li, Y. & Fan, H. Quantifying coherence in infinite dimensional systems. Phys. Rev. A 93, 012334 (2016).
Yuan, X., Zhou, H., Cao, Z. & Ma, X. Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 92, 022124 (2015).
Rastegin, A. E. Quantum-coherence quantifiers based on the Tsallis relative α entropies. Phys. Rev. A 93, 032136 (2016).
Pires, D. P., Céleri, L. C. & Soares-Pinto, D. O. Geometric lower bound for a quantum coherence measure. Phys. Rev. A 91, 042330 (2015).
Yao, Y., Xiao, X., Ge, L. & Sun, C. P. Quantum coherence in multipartite systems. Phys. Rev. A 92, 022112 (2015).
Xi, Z., Li, Y. & Fan, H. Quantum coherence and correlations in quantum system. Sci. Rep. 5, 10922 (2015).
Ma, J., Yadin, B., Girolami, D., Vedral, V. & Gu, M. Converting coherence to quantum correlations. Phys. Rev. Lett. 116, 160407 (2016).
Bromley, T. R., Cianciaruso, M. & Adesso, G. Frozen quantum coherence. Phys. Rev. Lett. 114, 210401 (2015).
Zhang, Y. J., Han, W., Xia, Y. J., Yu, Y. M. & Fan, H. Role of initial system-bath correlation on coherence trapping. Sci. Rep. 5, 13359 (2015).
Mani, A. & Karimipour, V. Cohering and de-cohering power of quantum channels. Phys. Rev. A 92, 032331 (2015).
Hu, X., Milne, A., Zhang, B. & Fan, H. Quantum coherence of steered states. Sci. Rep. 6, 19365 (2016).
Chitambar, E. et al. Assisted distillation of quantum coherence. Phys. Rev. Lett. 116, 070402 (2016).
Winter, A. & Yang, D. Operational resource theory of coherence. Phys. Rev. Lett. 116, 120404 (2016).
Cheng, S. & Hall, M. J. W. Complementarity relations for quantum coherence. Phys. Rev. A 92, 042101 (2015).
Singh, U., Bera, M. N., Dhar, H. S. & Pati, A. K. Maximally coherent mixed states: complementarity between maximal coherence and mixedness. Phys. Rev. A 91, 052115 (2015).
Bera, M. N., Qureshi, T., Siddiqui, M. A. & Pati, A. K. Duality of quantum coherence and path distinguishability. Phys. Rev. A 92, 012118 (2015).
Du, S., Bai, Z. & Guo, Y. Conditions for coherence transformations under incoherent operations. Phys. Rev. A 91, 052120 (2015).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, 2000).
Konrad, T. et al. Evolution equation for quantum entanglement. Nat. Phys. 4, 99 (2008).
Faras, O. J., Latune, C. L., Walborn, S. P., Davidovich, L. & Ribeiro, P. H. S. Determining the dynamics of entanglement. Science 324, 1414 (2009).
Tiersch, M., de Melo, F. & Buchleitner, A. Entanglement evolution in finite dimensions. Phys. Rev. Lett. 101, 170502 (2008).
Gour, G. Evolution and symmetry of multipartite entanglement. Phys. Rev. Lett. 105, 190504 (2010).
Li, Z. G., Fei, S. M., Wang, Z. D. & Liu, W. M. Evolution equation of entanglement for bipartite systems. Phys. Rev. A 79, 024303 (2009).
Li, Z. G., Zhao, M. J., Fei, S. M. & Liu, W. M. Evolution equation for entanglement of assistance. Phys. Rev. A 81, 042312 (2010).
Yu, C. S., Yi, X. X. & Song, H. S. Evolution of entanglement for quantum mixed states. Phys. Rev. A 78, 062330 (2008).
Liu, Z. & Fan, H. Dynamics of the bounds of squared concurrence. Phys. Rev. A 79, 032306 (2009).
Mirafzali, S. Y., Sargolzahi, I., Ahanj, A., Javidan, K. & Sarbishaei, M. Factorization law for two lower bounds of concurrence. Phys. Rev. A 82, 032321 (2010).
Hu, M. L. & Fan, H. Evolution equation for geometric quantum correlation measures. Phys. Rev. A 91, 052311 (2015).
Napoli, C. et al. Robustness of coherence: an operational and observable measure of quantum coherence. Phys. Rev. Lett. 116, 150502 (2016).
Byrd, M. S. & Khaneja, N. Characterization of the positivity of the density matrix in terms of the coherence vector representation. Phys. Rev. A 68, 062322 (2003).
Kimura, G. The Bloch vector for N-level systems. Phys. Lett. A 314, 339 (2003).
Andersson, E., Cresser, J. D. & Hall, M. J. W. Finding the Kraus decomposition from a master equation and vice versa. J. Mod. Opt. 54, 1695 (2007).
Rana, S., Parashar, P. & Lewenstein, M. Trace-distance measure of coherence. Phys. Rev. A 93, 012110 (2016).
Nakano, T., Piani, M. & Adesso, G. Negativity of quantumness and its interpretations. Phys. Rev. A 88, 012117 (2013).
Streltsov, A. Genuine quantum coherence. arXiv:1511.08346 (2015).
Du, S. & Bai, Z. The Wigner-Yanase information can increase under phase sensitive incoherent operations. Ann. Phys. 359, 136 (2015).
Dakić, B., Vedral, V. & Brukner, Č. Necessary and sufficient condition for nonzero quantum discord. Phys. Rev. Lett. 105, 190502 (2010).
Luo, S. & Fu, S. Geometric measure of quantum discord. Phys. Rev. A 82, 034302 (2010).
Paula, F. M., de Oliveira, T. R. & Sarandy, M. S. Geometric quantum discord through the Schatten 1-norm. Phys. Rev. A 87, 064101 (2013).
Chang, L. & Luo, S. Remedying the local ancilla problem with geometric discord. Phys. Rev. A 87, 062303 (2013).
Girolami, D., Tufarelli, T. & Adesso, G. Characterizing nonclassical correlations via local quantum uncertainty. Phys. Rev. Lett. 110, 240402 (2013).
Luo, S. & Fu, S. Measurement-induced nonlocality. Phys. Rev. Lett. 106, 120401 (2011).
Hu, M. L. & Fan, H. Measurement-induced nonlocality based on the trace norm. New J. Phys. 17, 033004 (2015).
Horodecki, R., Horodecki, P. & Horodecki, M. Violating Bell inequality by mixed spin-1/2 states: necessary and sufficient condition. Phys. Lett. A 200, 340 (1995).
Dakić, B. et al. Quantum discord as resource for remote state preparation. Nat. Phys. 8, 666 (2012).
Horodecki, R., Horodecki, M. & Horodecki, P. Teleportation, Bell’s inequalities and inseparability. Phys. Lett. A 222, 21 (1996).
Jing, J., Wu, L. A. & del Campo, A. Fundamental speed limits to the generation of quantumness. arXiv:1510.01106 (2015).
Acknowledgements
This work was supported by NSFC (Grant Nos 11205121, 91536108), New Star Project of Science and Technology of Shaanxi Province (Grant No. 2016KJXX-27), Doctoral Fund of XUPT (Grant No. ZL2015) and CAS (Grant No. XDB01010000).
Author information
Authors and Affiliations
Contributions
M.-L.H. contributed the idea and performed the calculations. M.-L.H. and H.F. wrote the paper. All authors reviewed the manuscript and agreed with the submission.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hu, ML., Fan, H. Evolution equation for quantum coherence. Sci Rep 6, 29260 (2016). https://doi.org/10.1038/srep29260
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep29260
This article is cited by
-
Entanglement witness and linear entropy in an open system influenced by FG noise
Quantum Information Processing (2022)
-
Nonlocal advantage of quantum coherence and quantum discord versus internal energy in the Heisenberg chain
Quantum Information Processing (2021)
-
Thermal Nonlocal Advantage of Quantum Coherence in the Two-Site, Triangular, and Tetrahedral Lattices with Heisenberg Interactions
International Journal of Theoretical Physics (2021)
-
Quantum Coherence and Transfer of Quantum Information with a Kerr Medium Under Decoherence
International Journal of Theoretical Physics (2021)
-
Quantum coherence and its distribution in the extended Ising chain
Quantum Information Processing (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


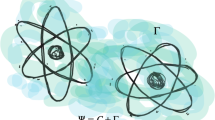

 are represented by the characteristic vectors
are represented by the characteristic vectors  along the same or opposite directions (left).
along the same or opposite directions (left). traverse a quantum channel
traverse a quantum channel  (right), their decoherence process can be described qualitatively by that of
(right), their decoherence process can be described qualitatively by that of  with the unit vector
with the unit vector  (the bottommost golden one).
(the bottommost golden one).