Abstract
Metal-dioxide & metal-dichalcogenide monolayers are studied by means of Density Functional Theory. For an accurate reproduction of the electronic structure of transition metal systems, the spin orbit interaction is considered by using fully relativistic pseudopotentials (FRUP). The electronic and spin properties of MX2 (M = Sc, Cr, Mn, Ni, Mo & W and X = O, S, Se & Te) were obtained with FRUP, compared with the scalar relativistic pseudopotentials (SRUP) and with the available experimental results. Among the differences between FRUP and SRUP calculations are giant splittings of the valence band, substantial band gap reductions and semiconductor to metal or non-magnetic to magnetic “transitions”. MoO2, MoS2, MoSe2, MoTe2, WO2, WS2 and WSe2 are proposed as candidates for spintronics, while CrTe2, with μ ~ 1.59 μB, is a magnetic metal to be experimentally explored.
Similar content being viewed by others
Introduction
The synthesis of single layer graphene in 20041 has been the trigger for a colossal amount of studies that uncovered the novel physical properties present in two dimensional (2D) materials2,3,4,5,6,7, which in turn evolved in a complete new branch of theoretical and experimental research within condensed matter physics8,9,10,11,12,13,14.
These works have led to significant advancements of emerging technologies with 2D materials6,8 such as: micro and nanoelectronics1,15,16,17, sensing18,19, energy storage20,21, energy conversion22,23,24, photonics25,26, optoelectronics7, magnetoresistance27 and spintronics/valleytronics28,29,30,31; motivating the search for new 2D semiconducting materials.
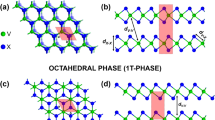
The effort to isolate different layered materials started almost simultaneous to the first isolation of single layer graphene3. The mechanical cleavage of MoS2 and NbSe2 2D crystals opened the research towards quasi-two dimensional transition-metal dichalcogenides (2D-MX2)32, materials with a nonzero band gap (Eg) and a doable architecture realization into electronic heterostructures33,34. For example, single layer MoS2, an hexagonal two dimensional transition metal dichalcogenide (Fig. 1a,b)3,9,29,30,35, presents a large intrinsic band gap of 1.8 eV, and has been proposed as a perfect transistor9 with potential application in spintronic devices28,29,36,37.
(a) H structure in a trigonal prismatic perspective and (b) xy plane view of the H structure. (c,d) correspond to the T structure in the octahedron perspective and in the xy view respectively. Blue circles represent the layer of metallic atoms sandwiched between top (light yellow circles) and bottom (dark yellow circles) layers of dichalcogenide atoms.
Although in some cases theoretical studies of 2D materials had preceded their physical isolation32,38,39, recently the experimental results incentivize addressing the subject by different theoretical approaches. In particular, the use of Density Functional Theory (DFT) has promptly contributed with suitable results on the electronic, vibrational and optical properties of several 2D materials, in particular of 2D-MX211,12,40.
The amount of DFT studies for 2D-MX2 in different configurations is vast, for example: studies of the physical properties of 2D-MX2 under dimensional confinement in the shape of ribbons41, the formation of 2D-MX2 heterostructures13, the effect of external electric fields42,43,44, the effect of defects in the morphology by atomic doping45, the alteration by chemical functionalization46,47 or the effect of applying mechanical strain40,48,49.
Experimentally, some studies report 2D-MX2 spintronics27,29,50,51,52,53,54,55,56,57,58,59, however only few computational works have explicitly considered the spin-orbit effect in selected compounds, i.e. MoS2, MoSe2, MoTe2, WS2, WSe2 and WTe230,49,54,59,60,61,62,63,64.
Theoretically and with DFT, the use of fully relativistic pseudopotentials, rather than of scalar ones, accuratelly predict the dispersion of transition metals d orbitals28,65,66,67, thus the importance of their use to calculate the electronic properties of 2D-MX2. A remarkable feature predicted by considering the spin orbit effects in non-magnetic semiconductors 2D-MX2 is the splitting of their valence bands, which cannot be observed with the common scalar pseudopotential approximations28. Furthermore, experiments with MoS2, MoSe2, MoTe2, WS2, WSe2 and WTe2 confirm the “giant” spin orbit effects, supporting the use of fully relativistic pseudopotentials and positioning them as candidates for valleytronics29,34,50,68,69. Specifically, MoTe2 has been recently proposed as an outstanding material for excitonic devices51,56.
Therefore, the main motivation of the present work is to present the most commonly reported 2D-MX2 semiconductors11 in the frame of fully relativistic calculations, unveiling the effects of the spin-orbit interaction, specifically in the following 2D-compounds: ScO2, ScS2, ScSe2, CrO2, CrS2, CrSe2, CrTe2, MnO2, NiO2, NiS2, NiSe2, MoO2, MoS2, MoSe2, MoTe2, WO2, WS2 and WSe2. In this text, the electronic properties of the selected materials are presented, emphasizing the difference between calculations with the spin orbit interaction and without it, and comparing with the available experimental results. Within the results, separate sections are dedicated to the magnetic and nonmagnetic semiconductors. A criterion of the spin orbit effect is reported in terms of the shrinkage of the band gap and the splitting of the valence band maximum (VBM).
Results
Although 2D-MX2 compounds could exist either in the honeycomb (H, trigonal prismatic), centered honeycomb (T, octahedral) or distorted honeycomb (T′)70 structures, in this work we performed calculations focusing in the semiconducting 2D-MX2, specifically in their more energetically stable forms according to theoretical DFT calculations. Thus the majority of the structures were studied in the H configuration, with the exception of MnO2 and NiX2 studied in the T configuration (Fig. 1). Additionally, a special mention is done to metallic WTe2 in its most stable T′ structure, for its relevance16,49.
Starting with the lattice parameters and the electronic band gaps as obtained by SRUP (after the benchmark with Vanderbilt pseudopotential calculations, as explained in the methodology), we compare our generalized gradient approximation (GGA) results with those reported in ref. 11 obtained with DFT within the local density approximation (LDA). The lattice parameters from our calculations are shown in Table 1 (all atomic coordinates are available in Supplementary Information, SI); they turned to be roughly 2% larger than those reported in ref. 11, a consequence from a finer cutoff thresholds used in our calculations, and from the underestimation of the LDA approach. In contrast, our values strictly reproduce the results obtained with the GGA approximation by Rasmussen et al.14 and Zibouche et al.64. In 2D systems, the electronic properties are highly sensitive to minor changes in the lattice parameters40, thus the cohesive energies (EC) and Egs in our work are slightly different to those reported by Ataca et al.11 and Kang et al.62. However our Egs are very close to the scalar relativistic results by Zibouche et al.64.
The general features of all the band structures calculated with SRUP closely reproduce those reported in refs 11, 14, 64 and 71; specifically the existence of a band gap and the presence of magnetism, as shown in Table 1. The ECs relative to the free constituent atoms calculated with SRUP are also presented in Table 1. There, EC[MX2] = ET[M] + 2ET[X] − ET[MX2], where ET[MX2] is the total energy of the MX2 and ET[M] and ET[X] the total energies of the corresponding free M and X atoms. Although in general, the presented ECs are slightly larger than those reported by Ataca et al.11 (due to the use of finer force and energy cutoff thresholds in the present work), the trend is preserved, i.e. the highest cohesive energy belongs to MO2, and it decreases for MS2, MSe2, with the lowest value for MTe2. After full geometry optimization relaxations performed with SRUP, the final atomic positions and cell parameters were used as input in the FRUP geometry optimization calculations. Neither the atomic positions, nor the cell parameters differ between FRUP and SRUP optimizations (all geometry data is available in SI).
Regarding the values of band gaps and magnetizations (μ), when the spin orbit is not taken into account (i.e. SRUP calculations), CrX2, NiX2, MoX2 and WX2 behave as nonmagnetic semiconductors, while MnO2 and ScX2 behave as magnetic, with μ values in good agreement with those reported in refs 11, 12, 14, 64 and 72 (see Table 1 and Fig. 2). Noncollinear calculations (i.e. FRUP calculations) are carried out in order to include the spin orbit effect. As a result, CrTe2 and NiSe2 present a change in their behavior from semiconductor to metal; moreover, CrTe2 turns from nonmagnetic to magnetic with a large μ of 1.59 μB, in clear contrast to the μ = 0 reported by Ataca et al.11 and Rasmussen et al.14.
A clear effect of FRUP calculations is the splitting of originally spin degenerated bands as calculated with SRUP (Fig. 3 and Table 2). In particular, this effect in the bands close to the band gap is reflected in the difference between SRUP and FRUP band gaps, here reported as  .
.
FRUP results are presented in the following subsections. The compounds are categorized according to their magnetic behavior as obtained with SRUP calculations, and sub classified according to their most stable structure, either belonging to the H or T families, i.e.: CrX2, MoX2 and WX2 (X = O, S, Se and Te) belong to the nonmagnetic H family, NiX2 (X = O, S and Se) to the nonmagnetic T family, ScX2 (X = S, Se and Te) belong to the magnetic H structures and finally MnO2 is the only member of the magnetic T family.
0.1 Nonmagnetic
In this section the compounds that calculated with SRUP resulted nonmagnetic are analyzed; first we present MX2 structures with M = Cr, Mo and W, which are more stable in the H configuration, followed by NiX2 with the mos stable configuration in the T structure.
All MX2s with X = O present indirect band gaps as calculated with SRUP (continuum blue lines in Fig. 2), with their Egs values increasing as the atomic number grows, i.e. from a value of 0.381 eV for CrO2 to a value of 0.898 eV for MoO2 and finally a value of 1.349 eV for WO2. The VBMs are situated in the Γ points, whereas the conduction band minimums (CBM), are at the K points. In contrast, when X = S, Se and Te, (and M = Cr, Mo and W), the band gaps are direct, reducing as the atomic number grows (see band gap reduction from left to right in Fig. 2). For all the direct semiconducting H structures, both VBMs and CBMs are located at the K points.
H structures
MO2
In general, MO2 structures present a small difference between bands calculated with FRUP and SRUP. Their ΔEgs are around a few meV (first column of Figs 2 and 3, and Table 2). However, the effect of the spin orbit inclusion is more noticeable around the K points, where locally flat VBMs calculated with SRUP split for FRUP calculations (e.g. the giant splitting = 556 meV for H-WO2 in Fig. 2 and Table 2). These locally flat bands -obtained with SRUP- result from an accumulation of d orbitals, emerging from the transition metals73 (see the density of states (DOS) in the SI Figs 1, 3 and 5, where narrow bands appear between −2.5 and −1.0 eV). In contrast, these bands disperse when the FRUP approximation is used73 (compare SI 1, 3 and 5 with SI 2, 4 and 6 respectively). Thus, it is required to consider the spin orbit interaction in order to obtain accurate electronic structures of systems involving transition metals65,66. Here WO2 is proposed as an experimental case of study in spintronic/valleytronics29,62.
CrX2 with X = S, Se and Te
Bulk CrS, CrSe and CrTe compounds, in contrast with their corresponding 2D nonmagnetic semiconductor structures, present magnetism74. The calculations for 2D CrX2 systems with FRUP yield a small effect due to the spin orbit interaction. For CrS2 and CrSe2, they remain as semiconductors (Figs 2 and 3). Differently, for CrTe2 the inclusion of spin orbit interaction turns it from a nonmagnetic semiconductor with a band gap of 0.534 eV, to a magnetic metal with a μ of 1.59 μB; in agreement with its metallic magnetic behavior reported by Lebegue et al.12. Looking at the local DOS (LDOS) in Fig. 4, it is clear that the principal contributions around the VBM and CBM, without spin-orbit effect, are mainly due to the contribution of the Cr 3d and Te 5p orbitals; specifically the  ,
,  and 3dxy orbitals that disperse in some degree when the fully relativistic approximation is considered60 (Figs 2 and 4). CrTe2 presents a ΔEg = 534 meV, the largest among all the systems reported in this work. CrS2 and CrSe2 present small VBM splittings, at the K points, of 69 and 95 meV respectively. In contrast CrTe2 presents a giant splitting of 2.32 eV, with the already mentioned magnetic moment of 1.59 μB.
and 3dxy orbitals that disperse in some degree when the fully relativistic approximation is considered60 (Figs 2 and 4). CrTe2 presents a ΔEg = 534 meV, the largest among all the systems reported in this work. CrS2 and CrSe2 present small VBM splittings, at the K points, of 69 and 95 meV respectively. In contrast CrTe2 presents a giant splitting of 2.32 eV, with the already mentioned magnetic moment of 1.59 μB.
 (dash brown),
(dash brown),  (solid yellow) and dxy (dash pink) are the main SRUP orbitals contributors from the VBM to the DOS (solid black). The major effect of the spin orbit reflects in the dispersion of these orbitals (solid blue). p and d orbitals are shifted for clarity. The arrows indicate the splitting of the VBM for the FRUP calculation for MoTe2.
(solid yellow) and dxy (dash pink) are the main SRUP orbitals contributors from the VBM to the DOS (solid black). The major effect of the spin orbit reflects in the dispersion of these orbitals (solid blue). p and d orbitals are shifted for clarity. The arrows indicate the splitting of the VBM for the FRUP calculation for MoTe2.
For the sake of completeness, we looked into the experimentally reported structures at the Inorganic Crystal Structure Database (ICSD), finding the existence of CrS2 (ICSD 75420)75, CrSe2 (ICSD 626718)76 and TlCrTe2 (ICSD 152836)77 as layered bulk materials, either in the T or T′ forms. From these information, 2D structures of CrS2, CrSe2 and CrTe2 were built in the T′, T and T forms respectively. The structures were geometry optimized and their electronic properties calculated (see band structures and DOSs in the SI Figs 16–21). For both approximations, SURP and FRUP the systems in the T or T′ structures are metallic. Regarding the cohesive energies, the structures in the T or T′ forms are ~1.65, 0.54, and 0.76 eV less stable than the above mentioned semiconducting H structures, respectively. The FRUP results for CrS2, CrSe2 and CrTe2 in the T and T′ structures present magnetism, with μ ~ 1.09, 0.08 and 0.33 μB respectively, in contrast with the non magnetic H CrS2 and CrSe2 semiconductors, and with the magnetic metal H CrTe2 with μ = 1.59 μB.
MoX2 with X = S, Se and Te
Now we present the results for some of the most studied metal-dichalcogenide monolayers; mainly MoS2 and MoSe23,6,7,8,9,10,11,12,13,29,34,50,64 and the emerging MoTe251,55,56,64. The effect of the spin orbit inclusion in their band gaps is shown in Fig. 3. For this group, the largest ΔEg is for MoS2 with a value of 155 meV. Experimentally available Egs shown in Table 2 present a fair agreement with the calculated values.
Considering the effect around the K point, the trend is the same as for Cr and W (Table 2); the VBMs split with the bands separation growing from S to Te as the atomic number increases. As mentioned before, with FRUP, the DOSs of the valence bands are disperse near the Fermi Energy (EF), in contrast to some narrow peaks present in DOSs obtained with SRUP (SI, Figs 3 and 4).
Theoretically, the splittings at the K point for MoS2, MoSe2 and MoTe2 are 151, 188 and 219 meV respectively (Table 2), data in a good agreement with refs 60, 61, 62 and 64, providing extra benchmarks for the used FRUP pseudopotentials. Experimentally, the energy differences between A and B excitons, attributed to the spin-orbit induced valence band splitting, measured via photoluminescence (PL) has been reported for MoS2, MoSe2 and MoTe2 as shown in Table 2 35,51,53,55,56,59,78,79. Calculated splittings are close to the experimental values attributed to the exciton binding energy in the case of MoS2 and MoSe2. For MoTe2, the calculated value of 219 meV is close to two of the experimentally reported values, and in contrast with a higher value of 580 meV in ref. 51.
The orbital-projected DOS for MoTe2 in Fig. 4 is presented in order to show the accumulation of Mo 4d orbitals close to the EF. Specifically the  ,
,  and 4dxy ones are the closest to the EF, and therefore, the orbitals where the splittings are expected to occur and actually occur, as shown in the MoTe2 panel of Fig. 2, where the VBM splits in two bands32,73 (Table 2).
and 4dxy ones are the closest to the EF, and therefore, the orbitals where the splittings are expected to occur and actually occur, as shown in the MoTe2 panel of Fig. 2, where the VBM splits in two bands32,73 (Table 2).
The giant spin-orbit-induced spin splitting supports the proposal of MoS2, MoSe2 and MoTe2 as candidates for their experimental valleytronics studies29,30,31.
WX2 with X = S and Se
Finalizing the nonmagnetic H compounds, the group of WX2 is analyzed. As in the previous cases, there is a growing tendency in ΔEg as the atomic number of the chalcogenide species increases (Fig. 3). The experimental and theoretical values of Egs are close.
Regarding the VBM splittings, the values are reported at the K points in Table 2. As for MoS2 and MoSe2, the results for WS2 and WSe2 are in agreement with those reported in refs 60, 61, 62 and 64, in both terms, of band gap and VBM splitting. Experimental value, from the energy difference between the A and B excitons for WS2 is reported in Table 2 in good agreement with the calculated one. Here WO2 is proposed as an experimental case of study in spintronic/valleytronics 29,62.
Since some theoretical studies report WTe2 system as a semiconductor in the H structure11,62,64, here we calculate it finding that the H structure is a metastable one with a bandgap of 1.060(0.649) eV for SRUP(FRUP) (See band structure and DOS in Fig. 15 of SI). This structure present a giant ΔEg of 411 eV and a VBM splitting at the K point of 609 meV. However, we also looked into the experimentally reported structures at the ICSD, finding the existence of WTe2 (ICSD 73323)80 as layered bulk material in the T′ form. We built the T′ structure, optimized it and found it ~0.03 eV more stable in terms of cohesive energy with respect to the meta stable H structure. Interestingly, the T′ WTe2 system is metallic from SRUP and FRUP calculations (see band structure and DOS in Figs 22 and 23 of SI), in agreement with the experimental and theoretical data in refs 16, 27 and 49.
T structure
NiX2 with X = O, S and Se
NiX2 systems are the only compounds in the energetically more stable T configuration of the nonmagnetic group (Fig. 1c,d). The VBM of NiO2 presents a bimodal behavior around the Γ point, whereas the CBM is located at 3/4 of the M − Γ path. In the case of NiS2 and NiSe2 the VBMs are closer to the Γ point and the CBMs locate in the Γ − K path, almost at the K point. All the band gaps for Ni systems are indirect.
Figure 2 shows that NiO2 and NiS2 are indirect semiconductor for both, SRUP and FRUP calculations. The spin orbit inclusion produces negligible alterations at their band structures with VBM splittings ~1 meV. Within this group, the case of interest is NiSe2, indirect semiconductor for SRUP and metallic when the spin orbit effect is considered41 (Fig. 2). A close up to the two highest SRUP valence bands (SI Fig. 9) reveals a degeneration for the VBM exactly at the Γ point. In contrast, FRUP brakes the degeneration with a giant band splitting of 302 meV, turning metallic as a result of the Fermi level crossing by the VBM.
0.2 Magnetic
In this last section we present all the compounds that calculated with SRUP are magnetic semiconductors in agreement with ref. 14, specifically T-MnO2, H-ScO2, H-ScS2 and H-ScSe2 (Fig. 5). After the inclusion of the spin orbit interaction the magnetic and semiconductor characters remain, with magnetization(band gap) of 2.98(1.23), 1.0(1.52), 0.97(0.72) and 0.84(0.45) μB(eV) respectively. To explore the effect of spin orbit, the focus is on the regions of the band structure where spin degeneration appears, as previously done for the NiSe2 band degeneration.
ScX2 with X = O, S and Se
This group presents the H structure as the energetically more stable configurations (Fig. 5 and Table 1). The VBMs and CBMs calculated with FRUP and SRUP coincide; however, the ante-penultimate and penultimate bands present some differences between FRUP and SRUP calculations. Zooming into the band structures allows to appreciate the effect of the inclusion of spin orbit (SI Fig. 14), with splitting of the referred bands ~10, 30 and 100 meV at the Γ point for ScO2, ScS2 and ScSe2 respectively. Furthermore, the SRUP (FRUP) energy difference between the ante-penultimate and the penultimate bands at the K point are 160(209) and 133(322) meV for ScS2 and ScSe2, respectively, i.e. band splittings ~50 and 190 meV. H ScO2 presents an Eg and a μ of 1.521 eV and 1μB respectively, in agreement with ref. 11 and in contrast with the work by Loh et al.81 reporting an antiferromagnetic metal behavior. Regarding ScS2, Zhang et al. have reported an Eg of 0.74 eV and a μ of 1 μB71, in perfect agreement with our SRUP calculations.
MnO2
A magnetic semiconductor with T structure, is the last compound presented in this work: MnO2, with an Eg of 1.23 eV and a μ = 2.98 μB, in good agreement with refs 14, 72 and 82 respectively (Fig. 5 and Table 1).
The inclusion of spin orbit for this compound is reflected at the bands below the VBM, specifically in the region close to the Γ point (SI, Fig. 11, from −1.4 to −1.0 eV). The band splitting with FRUP is 30 meV and its μ is not altered.
Discussion
With a benchmarking purpose, the present work addresses by means of fully relativistic DFT calculations, the effect of the spin orbit interaction in a thorough study of the electronic and spin properties for several semiconductor monolayer transition metal dioxide and dichalcogenides.
MoS2, MoSe2, MoTe2, WS2, WSe2 and WTe2 exist as van der Waals solids (their crystalline structure is presented in SI) and have been the focus of several experimental and theoretical works. In this paper the developed fully relativistic potentials were benchmarked by comparison with previous theoretical results, and more importantly, by comparing the VBM spin splitting with the experimentally available results from PL, confirming the validity of the potentials derived in this work.
Although the focus has been on the previous mentioned materials, we have also turn our attention towards those materials that could exist in 3D and can be exfoliated into 2D materials.
In particular, regarding the MO2 family, they exist in the rutile-like form and have not been yet experimentally reported, neither in the H or T forms. Therefore, our results for M = Sc, Cr, Mn, Ni, Mo and W in MO2 systems, were only compared with theoretical works, presenting, in general, a good agreement, unless the case of ScO2, which we found as a magnetic semiconductor in agreement with ref. 11 but in contrast with the metallic behavior reported in ref. 81.
The spin-orbit effects are presented with a growing tendency as the atomic number increases (Table 2). The general feature in the block of dioxide transition metal monolayers is an indirect band gap (from Γ to K), with orbitals around EF mainly due to presence of oxide p-orbitals. The metal d-obitals are not present around EF, and even that the valence bands split around the K-point, do not affect the values of the Egs. Motivating a future systematic study on the effects of spin-orbits in the rutile-like systems.
The giant spin-orbit effects found in several nonmagnetic semiconductors, supports the proposal of new materials as promising candidates for technological applications in valleytronics and spintronics (e.g. MoO2, MoTe2, NiSe2, WS2, WSe2 and WTe2)28,29,30,60,83. CrTe2 was found to behave as magnetic metal (with μ ~ 1.59 μB) when using FRUP versus its semiconductor behavior when calculated with SRUP.
Within the magnetic semiconductors FRUP calculations, for metallic dioxides, the results almost coincide with the calculations not considering the spin orbit effect.
Finally, metallic dichalcogenide magnetic semiconductors are not affected in their main features, only at their inner valence bands, specifically in the regions where SRUP calculations present points of degeneration, appearing shifts and splits of bands.
This work confirms the requirement of using a fully relativistic pseudopotential approximation in order to accurately predict properties in most of the monolayers involving transition metals.
Methods
Ab-initio calculations were performed with the Quantum ESPRESSO (QE)84 plane wave DFT and Density Functional Perturbation Theory code, available under the GNU Public License85. Spin polarized scalar relativistic calculations were performed for all the systems, and, in order to include the spin-orbit interaction, fully relativistic approximation was adopted65,66.
With the aim of using suitable pseudopotentials for transition metals, and generated by the same generation scheme, RRKJ pseudopotentials were chosen86. Scalar relativistic ultrasoft pseudopotentials (SRUP) and fully relativistic ultrasoft pseudopotentials (FRUP) for Mo, Ni, Se, S, O and Te, were accessible in the QE website repository84 within the RRKJ scheme. Meanwhile the pseudopotentials for Sc, Cr, Mn and W were not available and were generated through the ld1.x code, as implemented in QE84.
In order to benchmark the generated RRKJ pseudopotentials, the systems (MX2 with M = Sc, Cr, Mn and W, and X = O, S, Se and Te) were constructed and their lattice parameters and band structure calculated. Lattice parameters and band structures of all these structures were also calculated with the available pseudopotentials in the QE repository, specifically using PBE in the Vanderbilt scheme. The results from the RRKJ and the Vanderbilt pseudopotnentials were compared with perfect matching. Fully relativistic ultras of pseudopotentials (FRUP) were then built.
For the exchange-correlation, we used the Perdew-Burke-Ernzerhof (PBE) and GGA87,88. For the plane-wave basis sets, in all cases, we used converged energy cutoffs higher than 612 eV. The convergence energy parameter between consecutive self consistent field calculations was chosen as 10−7 eV. The maximum force acting on converged structures was smaller than 0.003 eV/Å, and the stress in the periodic direction was lower than 0.001 GPa. For the Brillouin-Zone integrations, Monkhorst-Pack grids89 of 16 × 16 × 1 k-points were used. The starting magnetization was randomly set to 1/2 μB on the metallic atoms.
Geometry optimization was performed using the conjugate gradient method, and the relaxed atomic positions and lattice parameters in the xy plane were obtained. For all H structures the relaxation was performed with symmetry constrains, providing the energetic minimum of the system. The size of the supercell in the z direction was fixed to 10 Å, providing enough distance to simulate 2D crystals, assuring isolation with the parallel adjacent supercell images.
Additional Information
How to cite this article: Reyes-Retana, J. A. and Cervantes-Sodi, F. Spin-orbital effects in metal-dichalcogenide semiconducting monolayers. Sci. Rep. 6, 24093; doi: 10.1038/srep24093 (2016).
References
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Katsnelson, M., Novoselov, K. & Geim, A. Chiral tunnelling and the klein paradox in graphene. Nat Phys 2, 620–625 (2006).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 102, 10451–10453, doi: 10.1073/pnas.0502848102 (2005).
Novoselov, K. et al. Two-dimensional gas of massless dirac fermions in graphene. Nature 438, 197–200 (2005).
Zhang, Y., Tan, Y.-W., Stormer, H. L. & Kim, P. Experimental observation of the quantum hall effect and berry’s phase in graphene. Nature 438, 201–204 (2005).
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat Chem 5, 263–275 (2013).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat Nanotechnol 7, 699–712 (2012).
Ferrari, A. C. et al. Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems. Nanoscale 7, 4598–4810, doi: 10.1039/C4NR01600A (2015).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nat Nanotechnol 6, 147–150 (2011).
Coleman, J. N. et al. Two-dimensional nanosheets produced by liquid exfoliation of layered materials. Science 331, 568–571, doi: 10.1126/science.1194975 (2011).
Ataca, C., Sahin, H. & Ciraci, S. Stable, single-layer MX2 transition-metal oxides and dichalcogenides in a honeycomb-like structure. J. Phys. Chem. C 116, 8983–8999, doi: 10.1021/jp212558p (2012).
Lebègue, S., Björkman, T., Klintenberg, M., Nieminen, R. & Eriksson, O. Two-dimensional materials from data filtering and ab initio calculations. Phys. Rev. X 3, 031002 (2013).
Terrones, H., López-Urías, F. & Terrones, M. Novel hetero-layered materials with tunable direct band gaps by sandwiching different metal disulfides and diselenides. Sci. Rep. 3, 1549, doi: 10.1038/srep01549 (2013).
Rasmussen, F. A. & Thygesen, K. S. Computational 2D materials database: Electronic structure of transition-metal dichalcogenides and oxides. J. Phys. Chem. C 119, 13169–13183, doi: 10.1021/acs.jpcc.5b02950 (2015).
Lu, W. & Lieber, C. M. Nanoelectronics from the bottom up. Nat Mater 6, 841–850 (2007).
Qian, X., Liu, J., Fu, L. & Li, J. Quantum spin hall effect in two-dimensional transition metal dichalcogenides. Science 346, 1344–1347, doi: 10.1126/science.1256815 (2014).
Fang, H. et al. High-performance single layered WSe2 p-FETs with chemically doped contacts. Nano Lett 12, 3788–3792 (2012).
Schwierz, F. Graphene transistors. Nat Nanotechnol 5, 487–496 (2010).
Fowler, J. D. et al. Practical chemical sensors from chemically derived graphene. ACS Nano 3, 301–306 (2009).
Chang, K. & Chen, W. L-cysteine-assisted synthesis of layered MoS2/graphene composites with excellent electrochemical performances for lithium ion batteries. ACS Nano 5, 4720–4728 (2011).
Bhandavat, R., David, L. & Singh, G. Synthesis of surface-functionalized WS2 nanosheets and performance as Li-ion battery anodes. J. Phys. Chem. Lett. 3, 1523–1530, doi: 10.1021/jz300480w (2012).
Beal, A., Hughes, H. & Liang, W. The reflectivity spectra of some group VA transition metal dichalcogenides. J. Phys. C Solid State 8, 4236 (1975).
Chandra, S., Singh, D., Srivastava, P. & Sahu, S. Electrodeposited semiconducting molybdenum selenide films. ii. optical, electrical, electrochemical and photoelectrochemical solar cell studies. J Phys D: Appl Phys 17, 2125 (1984).
Alharbi, F. et al. Abundant non-toxic materials for thin film solar cells: Alternative to conventional materials. Renew Energ 36, 2753–2758 (2011).
Gokus, T. et al. Making graphene luminescent by oxygen plasma treatment. ACS Nano 3, 3963–3968 (2009).
Eda, G. et al. Blue photoluminescence from chemically derived graphene oxide. Adv Mater 22, 505 (2010).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2 . Nature 514, 205–208 (2014).
Awschalom, D. & Samarth, N. Trend: Spintronics without magnetism. Physics 2, 50 (2009).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat Nanotechnol 7, 494–498 (2012).
Xiao, D., Liu, G.-B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802, doi: 10.1103/PhysRevLett.108.196802 (2012).
Cao, T. et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nat Commun 3, 887 (2012).
Mattheiss, L. F. Band structures of transition-metal-dichalcogenide layer compounds. Phys. Rev. B 8, 3719–3740, doi: 10.1103/PhysRevB.8.3719 (1973).
Geim, A. & Grigorieva, I. Van der waals heterostructures. Nature 499, 419–425 (2013).
Gong, Y. et al. Vertical and in-plane heterostructures from WS2/MoS2 monolayers. Nat Mater 13, 1135–1142, doi: 10.1038/nmat4091 (2014).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2 . Nano Lett 10, 1271–1275, doi: 10.1021/nl903868w (2010).
Dresselhaus, G. Spin-orbit coupling effects in zinc blende structures. Phys. Rev. 100, 580 (1955).
Bychkov, Y. A. & Rashba, E. I. Oscillatory effects and the magnetic susceptibility of carriers in inversion layers. J. Phys. C Solid State 17, 6039 (1984).
Duplock, E. J., Scheffler, M. & Lindan, P. J. Hallmark of perfect graphene. Phys. Rev. Lett. 92, 225502 (2004).
Nakada, K., Fujita, M., Dresselhaus, G. & Dresselhaus, M. S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 54, 17954 (1996).
Johari, P. & Shenoy, V. B. Tuning the electronic properties of semiconducting transition metal dichalcogenides by applying mechanical strains. ACS Nano 6, 5449–5456 (2012).
Reyes-Retana, J., Naumis, G. & Cervantes-Sodi, F. Centered honeycomb NiSe2 nanoribbons: Structure and electronic properties. J. Phys. Chem. C 118, 3295–3304, doi: 10.1021/jp409504f (2014).
Lu, N. et al. MoS2/MS2 heterobilayers: bandgap engineering via tensile strain or external electrical field. Nanoscale 6, 2879–2886 (2014).
Li, H.-M. et al. Metal-semiconductor barrier modulation for high photoresponse in transition metal dichalcogenide field effect transistors. Sci. Rep. 4 4041, doi: 10.1038/srep04041 (2014).
Santos, E. J. & Kaxiras, E. Electrically driven tuning of the dielectric constant in MoS2 layers. ACS Nano 7, 10741–10746 (2013).
Yue, Q., Chang, S., Qin, S. & Li, J. Functionalization of monolayer MoS2 by substitutional doping: a first-principles study. Phys. Lett. A 377, 1362–1367 (2013).
Ao, L. et al. Functionalization of a gase monolayer by vacancy and chemical element doping. Phys Chem Chem Phys 17, 10737–10748 (2015).
Voiry, D. et al. Covalent functionalization of monolayered transition metal dichalcogenides by phase engineering. Nat Chem 7, 45–49 (2015).
Guo, H., Lu, N., Wang, L., Wu, X. & Zeng, X. C. Tuning electronic and magnetic properties of early transition-metal dichalcogenides via tensile strain. J. Phys. Chem. C 118, 7242–7249 (2014).
Duerloo, K.-A. N., Li, Y. & Reed, E. J. Structural phase transitions in two-dimensional Mo-and W-dichalcogenide monolayers. Nat Commun 5, 4214, doi: 10.1038/ncomms5214 (2014).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nat Nanotechnol 7, 490–493 (2012).
Yang, J. et al. Robust excitons and trions in monolayer MoTe2 . ACS Nano 9, 6603–6609 (2015).
Zhao, Y., Zhang, Y., Yang, Z., Yan, Y. & Sun, K. Synthesis of MoS2 and MoO2 for their applications in H2 generation and lithium ion batteries: a review. Sci Technol Adv Mat 14, 043501 (2013).
Ji, Q. et al. Epitaxial monolayer MoS2 on mica with novel photoluminescence. Nano Lett 13, 3870–3877 (2013).
Tongay, S. et al. Thermally driven crossover from indirect toward direct bandgap in 2D semiconductors: MoSe2 versus MoS2 . Nano Lett 12, 5576–5580 (2012).
Ruppert, C., Aslan, O. B. & Heinz, T. F. Optical properties and band gap of single-and few-layer MoTe2 crystals. Nano Lett 14, 6231–6236 (2014).
Chen, B. et al. Environmental changes in MoTe2 excitonic dynamics by defects-activated molecular interaction. ACS Nano 9, 5326–5332, doi: 10.1021/acsnano.5b00985 (2015).
Hwang, W. S. et al. Transistors with chemically synthesized layered semiconductor WS2 exhibiting 105 room temperature modulation and ambipolar behavior. Appl Phys. Lett. 101, 013107 (2012).
Gutiérrez, H. R. et al. Extraordinary room-temperature photoluminescence in triangular WS2 monolayers. Nano Lett 13, 3447–3454 (2012).
Kozawa, D. et al. Photocarrier relaxation pathway in two-dimensional semiconducting transition metal dichalcogenides. Nat Commun 5, 4543, doi: 10.1038/ncomms5543 (2014).
Zhu, Z. Y., Cheng, Y. C. & Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 84, 153402, doi: 10.1103/PhysRevB.84.153402 (2011).
Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 86, 115409 (2012).
Kang, J., Tongay, S., Zhou, J., Li, J. & Wu, J. Band offsets and heterostructures of two-dimensional semiconductors. Appl Phys Lett 102, 012111 (2013).
Cheiwchanchamnangij, T. & Lambrecht, W. R. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2 . Phys. Rev. B 85, 205302 (2012).
Zibouche, N., Kuc, A., Musfeldt, J. & Heine, T. Transition-metal dichalcogenides for spintronic applications. Ann Phys 526, 395–401, doi: 10.1002/andp.201400137 (2014).
Dal Corso, A. & Conte, A. M. Spin-orbit coupling with ultrasoft pseudopotentials: Application to Au and Pt. Phys. Rev. B 71, 115106 (2005).
Smogunov, A., Dal Corso, A. & Tosatti, E. Magnetic phenomena, spin-orbit effects, and landauer conductance in Pt nanowire contacts: Density-functional theory calculations. Phys. Rev. B 78, 014423 (2008).
Roland, W. Spin-orbit coupling effects in two-dimensional electron and hole systems. Springer Tracts in Modern Physics, Springer, Berlin, Heidelberg 191 (2003).
Aivazian, G. et al. Magnetic control of valley pseudospin in monolayer WSe2 . Nat Phys, doi: 10.1038/nphys3201 (2015).
Srivastava, A. et al. Valley Zeeman effect in elementary optical excitations of monolayer WSe2 . Nat Phys, doi: 10.1038/nphys3203 (2015).
Augustin, J. et al. Electronic band structure of the layered compound Td- WTe2 . Phys. Rev. B 62, 10812 (2000).
Zhang, H., Lin, X. & Tang, Z.-K. Stable ScS2 nanostructures with tunable electronic and magnetic properties. Solid State Commun 220, 12–16 (2015).
Kwon, K. D., Refson, K. & Sposito, G. Defect-induced photoconductivity in layered manganese oxides: A density functional theory study. Phys. Rev. Lett. 100, 146601 (2008).
Goodenough, J. B. Spin-orbit-coupling effects in transition-metal compounds. Phys. Rev. 171, 466–479, doi: 10.1103/PhysRev.171.466 (1968).
Motizuki, K., Ido, H., Itoh, T. & Morifuji, M. Electronic structure and magnetism of 3d-transition metal pnictides. Springer Series in Materials Science, Springer, Berlin, Heidelberg 142 (2009).
Lafond, A., Deudon, C. & Meerschaut, A., A. and Sulpice. X-ray structure determination and magnetic properties of a new misfit layered compound: yttrium chromium sulfide; (Y0.93()0.07S)1.28CrS2 . Eur. J. Solid State Inorg. Chem. 31, 967.
Van Bruggen, C., Haange, R., Wiegers, G. & De Boer, D. CrSe2, a new layered dichalcogenide. Physica B + C 99, 166–172 (1980).
Ronneteg, S., Lumey, M.-W., Dronskowski, R. & Berger, R. The magnetic structure of TlCrTe2 . J. Alloy Compd. 403, 71–75 (2005).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805, doi: 10.1103/PhysRevLett.105.136805 (2010).
Ross, J. S. et al. Electrical control of neutral and charged excitons in a monolayer semiconductor. Nat Commun 4, 1474 (2013).
Mar, A., Jobic, S. & Ibers, J. A. Metal-metal vs tellurium-tellurium bonding in WTe2 and its ternary variants TaIrTe4 and NbIrTe4 . J. Am. Chem. Soc. 114, 8963–8971 (1992).
Loh, G. C. & Pandey, R. Versatile electronic properties of atomically layered ScO2 . J. Mater. Chem. C 3, 6627–6644, doi: 10.1039/C5TC01096A (2015).
Kan, M., Zhou, J., Sun, Q., Kawazoe, Y. & Jena, P. The intrinsic ferromagnetism in a MnO2 monolayer. J. Phys. Chem. Lett. 4, 3382–3386 (2013).
Datta, S. & Das, B. Electronic analog of the electro-optic modulator. Appl. Phys. Lett. 56, 665–667 (1990).
Giannozzi, P. et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J Phys: Condensed Matter 21, 395502 (2009).
License, G. G. P. Free software foundation. GNU Project URL http://www.fsf.org/copyleft/gpl.html Date of access:15/07/15 (1991).
Rappe, A. M., Rabe, K. M., Kaxiras, E. & Joannopoulos, J. D. Optimized pseudopotentials. Phys. Rev. B 41, 1227–1230, doi: 10.1103/PhysRevB.41.1227 (1990).
Perdew, J. P. et al. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 46, 6671–6687, doi: 10.1103/PhysRevB.46.6671 (1992).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868, doi: 10.1103/PhysRevLett.77.3865 (1996).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192, doi: 10.1103/PhysRevB.13.5188 (1976).
Acknowledgements
JARR is grateful with CONACYT for funding his postdoctoral research at Universidad Iberoamericana, Mexico City (UIA). FCS acknowledge funding from the Physics and Mathematics Department and the Research Division within UIA. Part of the computational work was performed at the Centro Nacional de Supercómputo (Thubat-Kaal) in San Luis Potosí, MX. Both authors acknowledge support from the Physics and Mathematics Department.
Author information
Authors and Affiliations
Contributions
J.R. proposed the idea and performed calculations. J.R. and F.C. discussed the results, contributed with ideas, wrote and revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Reyes-Retana, J., Cervantes-Sodi, F. Spin-orbital effects in metal-dichalcogenide semiconducting monolayers. Sci Rep 6, 24093 (2016). https://doi.org/10.1038/srep24093
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep24093
This article is cited by
-
Valley-optical absorption in planar transition metal dichalcogenide superlattices
Scientific Reports (2023)
-
Li adsorption and diffusion on the surfaces of molybdenum dichalcogenides MoX2 (X = S, Se, Te) monolayers for lithium-ion batteries application: a DFT study
Journal of Molecular Modeling (2023)
-
Gravitational Search Algorithm for Calculating Exciton Binding Energy in Monolayer Transition Metal Dichalcogenides
Journal of Electronic Materials (2021)
-
Modulation of Magnetoresistance Polarity in BLG/SL-MoSe2 Heterostacks
Nanoscale Research Letters (2020)
-
Electronic, optical and thermoelectric properties of the WS2–GaN interfaces: a DFT study
International Nano Letters (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.