Introduction

Cooperation behavior is ubiquitous in natural world and human society. Because of its great significance, understanding the cooperation, for example how cooperation emerges, what promotes cooperation, how cooperation behavior evolves and so on, has become a fundamental issue in evolutionary biology and attracted growing interest for long time1,2. Evolutionary game theory has offered a theoretical framework to study cooperation behavior among selfish individuals in interactive decision situations3,4,5,6,7. Among numerous game models, the prisoner’s dilemma (PD) game has attracted the most attention and become a classical and paradigmatic metaphor to study this issue8,9,10,11,12,13,14,15,16. Besides getting concerns from communities of classical game theory, this game model is also studied in the form of quantum version by physicists17. However, relative to the classical counterpart, quantum prisoner’s dilemma (QPD) game exhibits some completely different characteristics, one of which is that original dilemma can be resolved via quantum strategies. Though the respective evolution of PD and QPD has attracted much attention in previous studies18,19,20,21, the co-evolution of PD and QPD is rarely considered. With this regard, here classical and quantum PD will be coupled together to study the co-evolution of classical games and quantum games.

Up to now, a great number of factors promoting cooperation have been identified. Typical examples includes punishment and reward22,23,24, social diversity25, role assignation26,27, structured population8,28, age and memory29,30, heterogeneous activity31, to name but a few32,33,34,35. Recently, Nowak attribute all these scenarios to five well-known reciprocity mechanisms36: kin selection, direct reciprocity, indirect reciprocity, network reciprocity and group selection. Among them, network reciprocity, also known as spatial reciprocity, has been inspired the most research enthusiasm37,38,39,40. Generally, evolutionary games on networks can be classified into two categories based on the located interaction structure: evolutionary games on simplex networks and games on multilayer networks, respectively. The former mainly include scale-free networks41, small world networks42, etc. The multilayer networks, as a more flexible and versatile structure, have gained more and more attention recently43,44,45,46,47,48,49,50,51 (see a recent review52 for more details).

Among previous studies of coupled network games, game models are almost classical version where the quantum entanglement, representing an underlying connection among individuals, is not taken into consideration. The research paradigms are basically “classical games — classical games”, but not “classical games — quantum games” or “quantum games — quantum games”. In this paper, we turn our attention to the co-evolution of classical and quantum games. The PD, including two strategies cooperation (C) and defection (D), is used to model the interaction in macro world located on one network. The QPD, including three strategies cooperation (C), defection (D) and super cooperation (Q), is used to model the interaction in quantum world which is also located on another network. Like24,46, these two networks are coupled by utility functions and their coupling degree is measured by a coupling factor α (0 ≤ α ≤ 1). In QPD, an entanglement degree γ, where 0 ≤ γ ≤ π/2, is employed to represent the entanglement. Thus, we mainly study the impact of α and γ on the co-evolution of PD and QPD on the coupled networks.

Methods

Prisoner’s dilemma game and its quantum counterpart

The prisoner’s dilemma (PD) game is a simple and paradigmatic metaphor to study cooperation between unrelated individuals. In its basic version, there are two players who can choose either cooperation (C) or defection (D), respectively. In accordance with common practice8, the temptation of defection T = b determines the payoff received by a defector when meeting a cooperator, the reward for mutual cooperation is R = 1, the punishment for mutual defection is defined by P = 0 and the sucker’s payoff S = 0 is the payoff received by a cooperator if meeting a defector, where 1 < b < 2. It is clear that defection is the unique Nash equilibrium (NE) and evolutionarily stable strategy (ESS) of the PD. The payoff matrix of PD is expressed as

Quantum prisoner’s dilemma (QPD) game is an extension of classical PD by introducing quantum strategies and quantum entanglement. In the seminal work of Eisert et al.17, a widely used quantization scheme has been developed to extend classical PD into the quantum domain. In Eisert et al.’s scheme, the strategy of each player is in the form of unitary operator:

with 0 ≤ θ ≤ π and 0 ≤ ϕ ≤ π/2. Specifically, the identity operator and bit-flip operator correspond to the classical “cooperation” and “defection” strategies, respectively. In Eisert et al.’s scheme, there is another parameter γ which is a measure for the game’s entanglement, 0 ≤ γ ≤ π/2. For a separable game with γ = 0, strategy , namely , is the Nash Equilibrium (NE) and the QPD does not exhibit any features that go beyond PD. But for a maximally entangled quantum game with γ = π/2, a new strategy becomes the NE where the Pareto efficiency has been realized, in that sense the dilemma in the classical PD is removed.

Eisert et al.’s scheme is a little hard to be understood and accepted by the community of classical game theory because it involves some elusive quantum concepts and complicated computing. Li and Yong18 has simplified Eisert et al.’s scheme to a concise version by reducing the strategic space. In Li and Yong’s version of QPD, it consists of three strategies: cooperation (C), defection (D) and super cooperation (Q), given by , and , respectively. The payoff matrix is shown as below.

where γ is an entanglement degree, 0 ≤ γ ≤ π/2. In the simplified QPD, although there is only a quantum strategy Q, it still displays basic features of the quantum prisoner’s dilemma game: (1) If γ = 0, strategy Q collapses at C and the QPD degenerates to a classical PD; (2) If γ = π/2, quantum strategy Q is the unique NE which has realized Pareto efficiency; (3) If a Q meets a C, Q does not take advantage from C and they get the same payoffs cos2γ; (4) With the increase of γ, the Q gets more and more from the game playing against D and gradually becomes a dominant strategy with respect to D.

Evolutionary model of PD and QPD on coupled networks

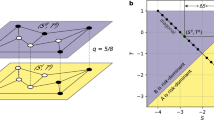
In this paper, we consider the co-evolution of classical PD and simplified QPD on coupled networks consisting of two-layer scale-free networks. The coupled network is constructed as follows. First, the Barabási-Albert algorithm53 is used to produce two identical scale-free networks G1 and G2 with size N1 = N2 = N. Then, we randomly select a node v1 from G1 and a node v2 from G2 to build an external link between them. Repeat this process for the remainder nodes of networks till each node on G1 has a corresponding partner on G2 and the converse is also true. As a result, the coupled structure is constructed by adding N external links to G1 and G2. The framework of this coupled infrastructure can get many kinds of explanations in the real world. For example, it can be seen as a real contacting network of people and its corresponding online social network. The key feature of the coupled networks is that each node has different connections on different layers. Although a corresponding relation is built between two networks G1 and G2, they are not physically connected, but are correlated by the utility function:

where x is a node on G1 and x′ is the coupled node on G2 and Px and Px′ are payoffs of x and x′ received from each network they belong to, respectively. Parameter α represents the coupling factor between G1 and G2, where 0 ≤ α ≤ 1. If α = 0, the two layers of coupled networks become completely independent.

In the evolutionary process, classical PD is placed on network G1 and the QPD is on G2. The evolutionary process of PD and QPD on the constructed coupled networks is simulated via the Monte Carlo simulation procedure comprising the following elementary steps. Initially, each player on G1 is randomly designated either as C or D and players on G2 are randomly designated as one role from C, D and Q. Then, every player from either G1 or G2 acquires its accumulated payoff by playing the game with all its linked neighbors on the same network (layer). More specifically, a player on G1 just plays games with its neighbors on G1 and the same to players on G2. Once players on G1 and G2 received their payoffs, the utility of each player is computed according to Eq. (4). Next, at each Monte carlo step (MCS) players update their strategies in an asynchronous manner: (i) we randomly select a player x from G1, then player x chooses a neighbor y on G1 at random and adopts the strategy sy from player y with a probability

where K = 0.1 denotes the uncertainty related to the strategy adoption process and its value does not qualitatively affect the evolutionary outcomes4; (ii) Similarly, execute operation (i) on network G2; (iii) Repeat (i) and (ii) N times, where N is the size of networks G1 and G2, so that each player on both G1 and G2 has a chance to change its strategy once on average during this MCS. Then the coupled networks go to next round of evolution.

In this paper, the simulation is performed on two identical scale-free networks G1 and G2 with size N1 = N2 = N = 5000 and average degree . The stationary fraction of each strategy is determined as the average within the last 1000 out of the total 5 × 104 MCS.

Simulation Results

We first investigate a special case of γ = 0 in which there dose not exist quantum entanglement so that the QPD degenerates to classical PD and the evolution on networks G1 and G2 is mainly affected by coupling factor α. Essentially, this case is equivalent to the evolution of PD on two-layer networks where layers are coupled by parameter α. It is easily found that the evolution on each network is completely irrelevant to the other one if α = 0. Figure 1 reveals the stationary fraction of different strategies as a function of b when γ = 0 on the coupled networks. Figure 1(a) corresponds to classical PD on G1, Fig. 1(b) is the case of QPD on G2. From Fig. 1(a), for the PD on G1: (i) despite the coupling factor α, the fraction of cooperators ρC drops with the increase of b; (ii) the smaller the value of α is, the better cooperators survive, such that when α = 0 representing networks G1 and G2 become completely independent, cooperation is promoted at the most extent. For the QPD on G2, as shown in Fig. 1(b), the obtained results are same with the case of PD on G1 because strategy Q collapses at strategy C and the QPD completely degenerates to classical PD when γ = 0. In summary, it is found that the coupling between networks G1 and G2 is not beneficial for cooperation when the entanglement is not taken into consideration.

Figure 1
figure 1

The stationary fraction of different strategies as a function of temptation of defect b when γ = 0.

(a) corresponds to the PD on network G1 and (b) is associated with the QPD on network G2. Each data presented is the average of 100 realizations.

Full size image

Next, to illustrate the impact of entanglement degree γ on the evolution of PD and QPD on the coupled networks, we fix the coupling factor α = 0.8 so as to observe the stationary fraction of different strategies when γ takes different values. For PD on G1, Fig. 2(a) shows ρC as a function of b under different γ, given α = 0.8. Correspondingly, for QPD on G2, Fig. 2(b–d) present the curves of ρC, ρD, ρQ, respectively. From Fig. 2(a), it is found that the ρC curve of PD on G1 basically does not show any changes regarding γ, which means the entanglement degree γ of QPD on G2 does not influence the evolution of PD on G1.

Figure 2
figure 2

Given α = 0.8, the stationary fraction of different strategies as a function of b when γ takes different values for PD and QPD.

(a) is the result of ρC of PD on network G1; (b–d) correspond to ρC, ρD and ρQ of QPD on network G2, respectively. Each data presented is the average of 100 realizations.

Full size image

For QPD on network G2, there are three kinds of strategies (i.e., cooperator C, defector D, super cooperator Q), from figures their stationary fractions change with γ, monotonously: with the rise of γ, ρC and ρD decline (see Fig. 2(b,c)), ρQ increases (see Fig. 2(d)). These results indicate that high entanglement degree is beneficial for Q and harmful to C and Q in the evolution of QPD on network G2. A theoretical analysis can be made to help understand the results. Let us recall the payoff matrix of QPD, as shown in Eq. (3). Li and Yong’s study18 shows that quantum strategy Q is the unique NE and ESS when . Meanwhile, if the population is well-mixed, with the process of evolution, C and D are going to be extinct and Q will gradually occupy the whole population. However, instead of a well-mixed population, in this paper the evolution of QPD is on a scale-free network which provides a structured population setting, so that in the end of evolution strategies coexist in the population and the stationary fraction of each strategy is varying with γ. In order to better understand what happens, let us decompose the payoff matrix Eq. (3) into pair-wise forms:

It is found that: (i) in the game GCD, D is strictly dominant compared with C, but C can get a certain amount of payoffs if a cluster of Cs has formed; (ii) in game GCQ, C and Q have equal status, anyone can not take advantage from the other and when γ ≠ 0 either C or Q must to cluster together to get the maximum payoff 1; (iii) in game GDQ, Q receives b sin2γ or 1, D obtains nothing or b cos2γ and with the increase of γ the expected payoff of D gets smaller and smaller until 0. By summarizing these points and noticing the population is located on a scale-free network, we get more understandings about the underlying mechanism of evolutionary QPD on G2: (i) with the rise of γ, Q can get more and more by exploiting D so that the payoff of Q exceeds that of C, as a result ρQ will be higher than ρC; (ii) Because the population is located on a scale-free network structure, C can form clusters to resist the invasion of D and to contend against Q; As γ gets bigger and bigger, the disadvantage of C becomes more and more obvious so that ρC has to go down until reaching the minimum when γ = π/2; (iii) As γ rises, on the one hand D gets less and less in the game against Q, on the other hand D fails to invade clusters of Cs, so that ρD declines and almost becomes 0 while γ = π/2.

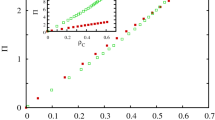
In Fig. 2(d), we have shown that strategy Q can not totally dominate network G2, the stationary fraction of Q, ρQ, just reaches a high level (but not 100%) even if the entanglement degree γ takes the maximum value π/2. This result is a little inconsistent with previous study shown in literature18. In Li and Yong’s study18, the authors drew a conclusion that super cooperator Q will emerge and basically dominates the whole population if and they verified the conclusion by using experiments evolved on random graphs. However, in our simulation, except of Q, at the end of evolution the population always contains a certain quantity of C. Someone may argue that in our simulation, shown in Fig. 2, the evolution of QPD occurred in two-layer coupled structures where the coupling factor α was set as 0.8, but not in a single-layered network. In order to eliminate the possible dispute, Fig. 3(a) shows the color map encoding ρQ on the b − γ parameter plane when α = 0.0. For the sake of comparison, the cases of α = 0.2 and α = 1.0 are also given in Fig. 3(b,c). Due to α = 0.0 in Fig. 3(a), this case is equivalent to the setting of QPD evolved on a single-layered network. From Fig. 3(a), it is found that: (i) on a scale-free network the fraction stationary of strategy Q is evidently less than 1 when γ is larger than , even when γ = π/2; (ii) if γ is obviously larger than , ρQ determined by the same γ is basically unchanged for any b; (iii) if γ is obviously smaller than , Q is gradually suppressed with the rise of the temptation of defect b. Therefore, through Fig. 3(a), we have clearly shown that Li and Yong’s conclusion is not fully satisfied on a scale free network. Although strategy Q is the unique NE and ESS of QPD when , but the feature only guarantees that in that condition Q will dominate all nodes of well-mixed populations or some random graphs whose heterogeneity are very low, as shown in Li and Yong’s study18. For high heterogeneous populations, such us scale free networks, our study shows that C can resist the invasion of evolutionarily stable and NE strategy Q so that C and Q coexist at the end of evolutionary QPD game. The result has provided a complement and perfection to previous study18. In addition, from Fig. 3(a–c), we also find that the low sensitivity of ρQ to b for the same γ which is obviously larger than is maintained and ρQ becomes bigger as α rises. And if γ is obviously smaller than , the negative correlation between ρQ and b is amplified with the increase of α.

Figure 3
figure 3

Color map encoding the fraction of strategy Q (i.e. ρQ) on the b − γ parameter plane.

(a–c) correspond to the cases of α = 0.0, α = 0.2 and α = 1.0, respectively. The curve on each map follows equation .

Full size image

Then, let us further study how the coupling factor α impacts the evolution of various strategies in PD and QPD games on the coupled networks. Similarly, we respectively consider the evolution of PD on G1 and QPD on G2. Figure 4 presents the stationary fraction of cooperators in evolutionary PD on network G1 as a function of temptation of defect b under different coupling factor α and entanglement degree γ. From Fig. 4, two main results are found as follows. Firstly, as same as Fig. 2(a), given a value of α, the entanglement degree γ basically does not have influences on ρC of evolutionary PD on G1. Secondly, the stationary fraction of cooperators ρC is increasing monotonously with the decline of α and it gets the maximum values when α = 0. The results show that low coupling factor is better to promote cooperation in classical PD in the coupled strructure.

Figure 4
figure 4

The stationary fraction of cooperators in evolutionary PD on network G1 as a function of b under different α and γ.

Each data presented is the average of 100 realizations.

Full size image

For QPD on network G2, it is a little complicated. Let us investigate the impact of γ and α on ρD, ρC, ρQ, ρ{C+Q}, respectively, as shown in Fig. 5. With respect to γ, herein we just consider two extreme cases γ = 0 and γ = π/2 because Fig. 2 has shown that the stationary fraction of each strategy changes monotonously with γ. First, from Fig. 5(a), it shows again that in the QPD strategy D basically can not survive in the case of maximum entanglement γ = π/2. And if there is no entanglement (i.e., γ = 0 so that the QPD degenerates to classical PD), the maximum coupling between G1 and G2 can best elevate the fraction of D in the evolutionary QPD on G2. Second, from Fig. 5(b) we find that the entanglement is not beneficial for C generally and despite of γ no coupling (i.e., α = 0) is always better to promote strategy C in the QPD on network G2. Moreover, we also notice that the strategy C does not go extinct even in the worst situation. Third, let us consider strategy Q according to Fig. 5(c). From Fig. 5(c), it is found that the coupling factor has different effects in the cases of maximum-entanglement and no-entanglement: If γ = π/2 meaning that it has the maximum entanglement in the QPD, the coupling plays a positive effect on boosting ρQ; However, if γ = 0 which means there is no entanglement so that strategy Q collapses at C, the coupling plays a negative effect on ρQ. Last, we go to study the sum of ρC and ρQ, namely ρ{C+Q}, under different γ and α, as shown in Fig. 5(d). According to Fig. 5(d), the effect of coupling on ρ{C+Q} becomes very small when γ = π/2 and at that case the population is basically composed by C and Q. When γ = 0 where Q collapses at C and the QPD degenerates to the PD, the coupling of α = 1 declines ρ{C+Q} to the greatest extent.

Figure 5
figure 5

The stationary fraction of strategies as a function of b in the evolutionary QPD on network G2 under different α and γ.

(a–d) correspond to results of ρD, ρC, ρQ and ρ{C+Q}, respectively. Each data presented is the average of 100 realizations.

Full size image

Now, based on the simulation results mentioned above, we can basically summarize the impacts of the coupling factor α and entanglement degree γ on the evolution of PD and QPD on two-layer coupling networks, as shown in Fig. 6. For the PD on G1: (i) the entanglement has no impacts on the evolution of strategies C and D; and (ii) despite γ, with the rise of coupling factor α the fraction of cooperators ρC is going down. However, for the QPD on G2: (i) either if α = 0 or α = 1, as the entanglement degree γ increases, strategies D and C are suppressed so that ρD and ρC decline, while ρQ gets a high increase which counteracts the decline of ρC so that ρ{C+Q} can also increase; (ii) if γ = 0, the increase of the coupling factor α makes ρD rising, ρC and ρQ declining; if γ gets the maximum value, the increase of α makes ρC declining and ρQ rising, but basically does not impact ρD and ρ{C+Q}.

Figure 6
figure 6

Summary of the evolution of PD and QPD on the two-layer coupled networks.

Symbols “↑”, “↓” and “−” represent ascending, declining and unchanged, respectively, when the entanglement degree γ or coupling factor α changes from 0 to maximum.

Full size image

In Fig. 5(c), we have simply shown that for the QPD the coupling factor α has positive effect on ρQ if γ = π/2 and negative effect on ρQ if γ = 0. Now let us deeply explore the impact of α on ρQ when the entanglement degree γ takes different values, as shown in Fig. 7. From Fig. 7(a) where γ = 0.0 ∗ π/2, it is found that: (i) on the one hand, ρQ is decreasing with the increase of the temptation of defect b; (ii) on the other hand, strategy Q is suppressed to the most degree when α gets the biggest value 1. However, as γ rises, these two points are challenged. If γ = 0.2 ∗ π/2 (see Fig. 7(b)), although ρQ declines barely as b increases, the effect of α becomes disordered so that the fraction of Q is not always the smallest when α = 1. Moreover, as shown in Fig. 7(c–e), starting from γ = 0.4 ∗ π/2, a new pattern is gradually built up that (i) as b increases, ρQ is either unchanging or boosted; (ii) strategy Q is promoted to the most degree when α gets the biggest value 1. At the most extreme case where α = 1.0 and γ = π/2, ρQ is 0.8270 at b = 1.0 and 0.8879 at b = 2.0, which shows that the rise of temptation of defect b does not restrain strategy Q. And at the case with γ = π/2 and b = 2.0, ρQ becomes 0.8095 at α = 0.0 and 0.8879 at α = 1.0, which means the increase of coupling factor α does not impede the super cooperator Q. These cases reflect that quantum strategy Q has many fantastic features which are obvious different from classical cooperation strategy Q that is always suppressed by the increase of b or α on single-layered or two-layer networks.

Figure 7
figure 7

The stationary fraction of super cooperators (Q) as a function of b in the evolutionary QPD on network G2 under different α, given that the entanglement degree γ takes different values.

(a–f) correspond to results of γ being 0.0 ∗ π/2, 0.2 ∗ π/2, 0.4 ∗ π/2, 0.6 ∗ π/2, 0.8 ∗ π/2, 1.0 ∗ π/2, respectively. Each data presented is the average of 100 realizations.

Full size image

Lastly, let us investigate how to increase the fraction of cooperators including C and Q on the whole two-layer coupled networks. Figure 8 shows the stationary fraction of all cooperators, including C on G1 and C, Q on G2, on the coupled networks as a function of α under different γ, given that the temptation of defect b takes different values. It is found that: (i) In any cases, the entanglement is forever beneficial to boosting the fraction of cooperators on the whole two-layer coupled networks. The bigger the value of γ, the more the cooperators on the coupled networks. (ii) If b gets a small value, such as 1.0 or 1.2 (see Fig. 8(a,b)), for different entanglement degree γ, the peak of the stationary fraction of all cooperators is located at an intermediate point of α belonging to [0, 1] but not at the smallest point of α, although at the peak point the fraction of cooperators is just slightly higher than that of others. (iii) If b gets a bigger value, for example 1.4 or 1.6 or 1.8 (see Fig. 8(c–e)), regardless of γ, the quantity of all cooperators will reach the maximum value when coupling factor α = 0.0. And in most cases the promotion for the fraction of cooperators at α = 0.0 is relatively obvious, in comparison of that with α = 1.0. (iiii) If b gets the maximum value 2.0 (see Fig. 8(f)), the reduction of α can not remarkably enhance cooperation when entanglement degree γ is high. Inspired by these observations mentioned above, in order to promote the cooperation level of the whole coupled structure as much as possible, therefore, we can adopt the following strategy: At first, if b is very large, for example b = 2.0, we’d better invest the most effort to increase the entanglement degree γ of QPD, which can most efficiently enhance the cooperation level of whole coupled networks; Second, if b is a little big, such as 1.4 < b < 1.8, we must simultaneously increase the entanglement degree γ and reduce the coupling factor α as much as possible; Third, if b is small, such as 1.0 < b < 1.2, in order to elevate the cooperation level of the whole network, we should, one the one hand enhance the entanglement degree γ, one the other hand find an appropriate value of the coupling factor α but not just reduce it.

Figure 8
figure 8

The stationary fraction of all cooperators, including C on G1 and C, Q on G2, on the whole two-layer coupled network as a function of α under different γ, given that the temptation of defect b takes different values.

(a–f) correspond to results of b being 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, respectively. Each data presented is the average of 100 realizations.

Full size image

Conclusion

In this paper we have shown the co-evolution of classical PD and simplified QPD on two-layer coupled networks. Different from previous studies of evolutionary games on multi-layer networks, in this work classical games and quantum games are coupled together. Classical prisoner’s dilemma and quantum prisoner’s dilemma are employed as the models of two different interactive environments and mechanisms, respectively. And two pivotal parameters, the entanglement degree γ in the quantum game and coupling factor α between classical games and quantum games, are taken into consideration. By means of numerous simulations, the main results in the evolution process are concluded basically. We hope this study can provide new insight in the evolutionary games on multilayer networks and understanding for the social dilemmas.

Additional Information

How to cite this article: Deng, X. et al. A novel framework of classical and quantum prisoner's dilemma games on coupled networks. Sci. Rep. 6, 23024; doi: 10.1038/srep23024 (2016).