Abstract
Real network data is often incomplete and noisy, where link prediction algorithms and spurious link identification algorithms can be applied. Thus far, it lacks a general method to transform network organizing mechanisms to link prediction algorithms. Here we use an algorithmic framework where a network’s probability is calculated according to a predefined structural Hamiltonian that takes into account the network organizing principles and a non-observed link is scored by the conditional probability of adding the link to the observed network. Extensive numerical simulations show that the proposed algorithm has remarkably higher accuracy than the state-of-the-art methods in uncovering missing links and identifying spurious links in many complex biological and social networks. Such method also finds applications in exploring the underlying network evolutionary mechanisms.
Similar content being viewed by others
Introduction
Link prediction algorithms aim at estimating the tendency of the existence of a link between two nodes, based on observed links, attributes of nodes, or dynamical correlations1,2,3. As our knowledge on many biological networks is very limited (e.g., most of the molecular interactions in cells are still unknown4), using predicting results to guide the laboratorial experiments rather than blindly checking all possible interactions will greatly reduce the experimental costs5,6. Besides, such predicting results for online social networks can be considered as friend recommendation7. Actually, how to recommend products to a target user in online e-commerce web sites is also a sub-problem of link prediction in bipartite networks where the prediction is for the target user8. Similar algorithms and techniques can be further applied in detecting spurious links under noisy environment9, in evaluating different network models by mapping evolving mechanisms into link prediction algorithms10 and more interestingly, in predicting the U.S. Supreme Court votes11.
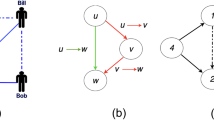
The missing link prediction problem1 and the spurious link identification problem9 are illustrated by Figs 1 and 2, respectively, which are networks of 4 nodes. In Supplementary Fig. 1 of the Supplementary Information (SI) we give the ensemble  of all four-node networks. The total number of four-node networks is 26 = 64, where 6 = 4 × 3/2 is the number of all possible links in the network of 4 nodes. For the missing link prediction, the task is to estimate the existence tendency of all the non-observed links based on the known network topology and nodes attributes (if we have such information). Specifically, consider an undirected network or graph G(V, E), where V is the set of
of all four-node networks. The total number of four-node networks is 26 = 64, where 6 = 4 × 3/2 is the number of all possible links in the network of 4 nodes. For the missing link prediction, the task is to estimate the existence tendency of all the non-observed links based on the known network topology and nodes attributes (if we have such information). Specifically, consider an undirected network or graph G(V, E), where V is the set of  nodes and E is the set of
nodes and E is the set of  links. Multiple links and self connections are not allowed. Denoted by U, the universal set contains all
links. Multiple links and self connections are not allowed. Denoted by U, the universal set contains all  possible links. Then, the set of nonexistent links is U − E. We assume that there are some missing links (or the links that will appear in the future) in the set U − E and the task of link prediction is to find out these links. Generally, we do not know which links are the missing or future links, otherwise we do not need to do prediction. Therefore, to test the algorithm’s accuracy, the observed links, E, is randomly divided into two parts: the training set, ET, is treated as known information, while the probe set (i.e., validation subset), EP, is used for testing and no information in this set is allowed to be used for prediction. Clearly,
possible links. Then, the set of nonexistent links is U − E. We assume that there are some missing links (or the links that will appear in the future) in the set U − E and the task of link prediction is to find out these links. Generally, we do not know which links are the missing or future links, otherwise we do not need to do prediction. Therefore, to test the algorithm’s accuracy, the observed links, E, is randomly divided into two parts: the training set, ET, is treated as known information, while the probe set (i.e., validation subset), EP, is used for testing and no information in this set is allowed to be used for prediction. Clearly,  and
and  . Take Fig. 1 as an example, the true network contains four nodes and four links, while the link (1, 3) is missing in the observed network AO. Then this missing link constitutes the probe set EP and the rest observed links constitute the training set ET. The set of non-observed links is U − ET.
. Take Fig. 1 as an example, the true network contains four nodes and four links, while the link (1, 3) is missing in the observed network AO. Then this missing link constitutes the probe set EP and the rest observed links constitute the training set ET. The set of non-observed links is U − ET.
For spurious link identification, the task is to evaluate the reliability of all the observed links based on the known network topology and nodes attributes (if we have such information). Specifically, consider an undirected network G(V, E), where V is the set of nodes and E is the set of links. Multiple links and self connections are not allowed. Then, the set of observed links is E. We assume that there are some spurious links in the set E and the task of spurious link identification is to find out these links. Of course, we do not know which links are the spurious link, otherwise we do not need to do identification. Therefore, to test the algorithm’s accuracy, we will randomly add some nonexistent links which will constitute the probe set EP and the given network (we may say it is the true network E) together with the probe set constitute the training set ET. Clearly, ET − EP = E and  . Take Fig. 2 as an example, the true network contains four nodes and four links, while the spurious link (1, 4) was added to the network to construct the training set. In reality, the training set can be considered as the real observed network which contains the errors and the true network presented here is actually unknown for us. However, to test the algorithm’s performance we assume that the given networks are all true, otherwise we cannot make any comparison.
. Take Fig. 2 as an example, the true network contains four nodes and four links, while the spurious link (1, 4) was added to the network to construct the training set. In reality, the training set can be considered as the real observed network which contains the errors and the true network presented here is actually unknown for us. However, to test the algorithm’s performance we assume that the given networks are all true, otherwise we cannot make any comparison.
Traditional methods or models for predicting missing links and identifying spurious links can be roughly divided into two classes: the probabilistic models and the similarity-based algorithms: the former include the probabilistic relational model12, the probabilistic entity relationship model13 and the relational model14, which usually require, in addition to the observed network structure, the information about node attributes; the latter assign a similarity score to every pair of nodes and rank all non-observed links according to their scores. How to define the similarity is a nontrivial challenge: it could be simple like the common-neighbor-based indices15,16,17 or complicated such as random-walk-based indices18,19 and iteratively defined indices20,21.
Recently, some novel algorithms related to the likelihood analysis were proposed9,22,23 and shown to be more accurate than many similarity-based methods. These algorithms usually presuppose certain organizing rules of networks. In despite of detailed differences, parameters associated with the organizing rules are often learned from the observed structure and then the network ensemble is built up, accordingly, a large number of networks could be sampled out to further determine the appearing probability of each link. Representative examples include the hierarchical structure model22, the stochastic block model9 and the Kronecker graphs model23.
This paper introduces an algorithmic framework where a network’s probability is calculated according to a predefined structural Hamiltonian and a non-observed link is scored by the conditional probability of adding the link to the network. The Hamiltonian is defined according to some reasonable organizing principles so that an observed network is usually of lower Hamiltonian than its randomized version. Here we consider a general principle called clustering mechanism, which declares that two nodes will have a high probability of making a link between them if they share some common neighbors or are connected by short paths. This mechanism gets direct supportive evidence from the high clustering coefficient of disparate networks24,25. In this paper, the clustering mechanism is explained as the high appearing probability of a link if its two nodes are connected by a large number of short paths and thus the corresponding Hamiltonian is defined according to the closed walk process. Numerical simulations on seven real networks showed remarkably higher accuracy of the proposed algorithm than the state-of-the-art methods in both uncovering missing links and detecting spurious links.
Results
Common neighbor similarity performs very well in many networks16,17, indicating that the three-order loops (i.e., triangles) are preferred in the network formation. We here generalize this idea to high-order loops and define a structural Hamiltonian:

where A is the N × N adjacency matrix of the network with  nodes and βk are the temperature parameters. When k > 2, the number of loops of length k that start and end at node i is
nodes and βk are the temperature parameters. When k > 2, the number of loops of length k that start and end at node i is  . Note that, a loop is counted several times since each of its nodes can be the starting node and given the starting node, it is counted twice by its two opposite directions. Since the loops counted here are not self-avoiding, it is more complex when a loop contains sub-loops. Roughly speaking, TrAk is 2k times the number of loops of length k, while to determine the exact number is not feasible. The approximated factor 2k can be taken into account by the parameter βk and the cases of k = 1 and k = 2 are trivial since TrA1 is 0 and TrA2 is simply twice the number of total links, so we only consider the terms TrAk for k ≥ 3. As k → ∞, TrAk+1/TrAk → λ1, i.e. TrAk grows exponentially with the leading eigenvalue λ1. Thus we take the logarithm to rescale each term in H(A) to the same magnitude.
. Note that, a loop is counted several times since each of its nodes can be the starting node and given the starting node, it is counted twice by its two opposite directions. Since the loops counted here are not self-avoiding, it is more complex when a loop contains sub-loops. Roughly speaking, TrAk is 2k times the number of loops of length k, while to determine the exact number is not feasible. The approximated factor 2k can be taken into account by the parameter βk and the cases of k = 1 and k = 2 are trivial since TrA1 is 0 and TrA2 is simply twice the number of total links, so we only consider the terms TrAk for k ≥ 3. As k → ∞, TrAk+1/TrAk → λ1, i.e. TrAk grows exponentially with the leading eigenvalue λ1. Thus we take the logarithm to rescale each term in H(A) to the same magnitude.
For a large k, the increase of TrAk is simply determined by the leading eigenvalue λ1 and TrAk contains less information about the local organizations, so we introduce a cutoff kc. Actually, even for large networks, usually the small-world property still holds and nodes may reach others within several steps26. Moreover, recent studies reveal that based only on some local information, it’s sufficient to reproduce closely many real world networks27. Thus a relatively small value of kc is usually sufficient for many networks. How to determine kc is introduced in S6 of SI and the present results correspond to the optimal kc.
The structural Hamiltonian can be rewritten as:

Note that we have rewritten the Hamiltonian in terms of the eigenvalues. Diagonalize the adjacency matrix as A = UTΛU, where U is the matrix with eigenvectors in each column and Λ the diagonal matrix of eigenvalues. Then we have  . Then the Hamiltonian in equation (2) can be obtained.
. Then the Hamiltonian in equation (2) can be obtained.
Given an ensemble  , where the observed network
, where the observed network  (here AO = A − AP and AP is the adjacency matrix of the probe set) and the probability of the appearance of AO is28,29:
(here AO = A − AP and AP is the adjacency matrix of the probe set) and the probability of the appearance of AO is28,29:

where  is the partition function. Such model is named exponential random graph model in social science literatures30. The parameters βk are then chosen to maximize the probability in equation (3), see more details in Supplementary Methods.
is the partition function. Such model is named exponential random graph model in social science literatures30. The parameters βk are then chosen to maximize the probability in equation (3), see more details in Supplementary Methods.
After determining the parameters βk, the score of a non-observed link (x, y) ∈ U − ET is assigned to be the conditional probability of the appearance of the link (x, y) based on the observed network:

where  is the observed network by adding the link (x, y) and Zxy is a normalization factor which defined as
is the observed network by adding the link (x, y) and Zxy is a normalization factor which defined as  . Here we assume adding the single link (x, y) to AO will not largely change the topological structure and thus the parameters βk for
. Here we assume adding the single link (x, y) to AO will not largely change the topological structure and thus the parameters βk for  is approximately the same to those for AO. Sxy can be regarded as a kind of similarity index, so all the non-observed links will be ranked by Sxy for prediction: links with higher scores are more likely to exist. Obviously, the partition function Zxy plays no role in producing the prediction.
is approximately the same to those for AO. Sxy can be regarded as a kind of similarity index, so all the non-observed links will be ranked by Sxy for prediction: links with higher scores are more likely to exist. Obviously, the partition function Zxy plays no role in producing the prediction.
In the spurious link identification problem, the score of a link (x, y) ∈ AO, to be spurious can be estimated by the conditional probability of the absence of this link, namely,

where  is the observed network AO by removing the link (x, y) and
is the observed network AO by removing the link (x, y) and 
 . Note that, different from the missing link prediction problem, here AO = A + AS, where AS is the adjacency matrix of the spurious set. Higher value of
. Note that, different from the missing link prediction problem, here AO = A + AS, where AS is the adjacency matrix of the spurious set. Higher value of  indicates a higher probability that the link (x, y) is a spurious link. The higher the value of
indicates a higher probability that the link (x, y) is a spurious link. The higher the value of  , the lower reliability this link (x, y) is. A summary of notations used for the method is shown in S3 of SI.
, the lower reliability this link (x, y) is. A summary of notations used for the method is shown in S3 of SI.
For comparison, we introduce some benchmark methods1, including similarity-based algorithms and likelihood models. The simplest similarity index is the Common Neighbors (CN) index15, where two nodes, x and y, are more likely to have a link if they have more common neighbors, namely,  , where Γ(x) denotes the set of neighbors of x. Two refined versions of CN are Adamic-Adar (AA) index31
, where Γ(x) denotes the set of neighbors of x. Two refined versions of CN are Adamic-Adar (AA) index31  and Resource Allocation (RA) index16,32
and Resource Allocation (RA) index16,32  . Very recently, Cannistraci, Alanis-Lobato and Ravasi6 simultaneously taked into account the number of common neighbors and the number of local community links (links connecting common neighbors) and proposed a series of similarity indices, including CAR, CPA, CAA, CRA and CJC indices (see details in Table 1 of ref. 6) for link prediction in brain connectomes and protein connectomes.
. Very recently, Cannistraci, Alanis-Lobato and Ravasi6 simultaneously taked into account the number of common neighbors and the number of local community links (links connecting common neighbors) and proposed a series of similarity indices, including CAR, CPA, CAA, CRA and CJC indices (see details in Table 1 of ref. 6) for link prediction in brain connectomes and protein connectomes.
Different from the aforementioned local similarity indices, Katz index33 makes use of global topological information by summing over the collection of paths with exponentially damping according to path lengths with a parameter α, which reads  and can be rewritten in a compact form, as S = (I − αA)−1 − I, where I is the identity matrix. In our experiments, the performance of Katz index corresponds to the optimal α.
and can be rewritten in a compact form, as S = (I − αA)−1 − I, where I is the identity matrix. In our experiments, the performance of Katz index corresponds to the optimal α.
We also consider two likelihood models, the Hierarchical Structural Model (HSM)22 and the Stochastic Block Model (SBM)9. HSM is based on the fact that many real networks are hierarchically organized, where nodes can be divided into groups, further subdivided into groups of groups and so forth. SBM is one of the most general network models, where nodes are partitioned into groups and the connecting probability of two nodes depends solely on the groups they belong to.
To quantify the accuracy of proposed methods, we adopt two standard metrics. The first one is called the area under the receiver operating characteristic curve (AUC value for short)34, which can be interpreted as the probability that a randomly chosen link in EP (i.e., a missing link that indeed exists but is not observed yet) is ranked higher than a randomly chosen link in U − E (i.e., a nonexistent link). If all the link scores are generated from an independent and identical distribution, the AUC value should be about 0.5. Therefore, the degree to which the value exceeds 0.5 indicates how much the algorithm performs better than pure chance. The second one is called precision35, which is defined as the ratio of relevant elements to the number of selected elements. That is to say, if we take the top-L links as predicted links, among which Lr links are right (i.e., there are Lr links in the probe set EP), then the precision equals Lr/L.
These two metrics can also be used to quantify the performance on detecting spurious links. In such a case, a number of spurious links are completely randomly generated that constitute the probe set EP (these links are also added to E). In contrast to the predicting algorithm, a detecting algorithm gives an ordered list of all observed links according to their scores. The AUC value in this task becomes the probability that a randomly chosen links in EP (i.e., a spurious link) is ranked lower than a randomly chosen link in E (i.e., an existing link). And if we pick up the last L links, among which Ls links are spurious, then the precision equals Ls/L. Calculations of AUC and precision for some simple illustrative networks are given in S2 of SI.
Seven different networks from various research fields are tested. (i) Jazz36: The network of Jazz musicians. (ii) Metabolic37: The metabolic network of the nematode worm C. elegans. (iii) C. elegans38: The neural network of C. elegans. (iv) US Air39: The network of the US air transportation system. (v) FWF40: The food web in Florida Bay during wet season. (vi) FWM41: The food web in Mangrove Estuary during wet season. (vii) Macaca42: cortical networks of the macaque monkey. The basic topological features of such networks are summarized in Table 1. The parameters of a network include the clustering coefficient C38 and the assortative coefficient r43.
For each of the seven networks, the training set ET contains 90% of the links and the remaining 10% of links constitutes the probe set EP. To calculate precision, we set  , which means the number of selected elements equals the number of relevant elements. Under this specific choice of L, precision is equal to another metric recall that is formally defined in35. All the data points are obtained by averaging over 10 implementations with independently random divisions of training set and probe set. The prediction accuracies measured by precision and AUC are shown in Tables 2 and 3, respectively. For each network, the bold number in the corresponding row emphasizes the highest accuracy. Very surprisingly, for all the seven real networks, our method performs best among all state-of-the-art algorithms, usually remarkably better than the second best. The standard deviations of the prediction accuracy can be found in SI. In Figs 3 and 4, we further show that such result is not sensitive to the size of the probe set, which is the fraction of
, which means the number of selected elements equals the number of relevant elements. Under this specific choice of L, precision is equal to another metric recall that is formally defined in35. All the data points are obtained by averaging over 10 implementations with independently random divisions of training set and probe set. The prediction accuracies measured by precision and AUC are shown in Tables 2 and 3, respectively. For each network, the bold number in the corresponding row emphasizes the highest accuracy. Very surprisingly, for all the seven real networks, our method performs best among all state-of-the-art algorithms, usually remarkably better than the second best. The standard deviations of the prediction accuracy can be found in SI. In Figs 3 and 4, we further show that such result is not sensitive to the size of the probe set, which is the fraction of  in Table 1.
in Table 1.
We next consider the identification of spurious links, where spurious links are those links being observed but not really existent, which may be resulted from experimental errors or data noise. Prediction of missing links and identification of spurious links are considered to be equally important and highly challenging in the reconstruction of networks9,44. The framework and method proposed in this paper can also be applied to identify spurious links.
To test the validity of the algorithms, we randomly add some links to each real network, which constitute the spurious set EP and the adjacency matrix of the spurious set is AS. Analogously, for spurious link identification, the AUC value can be interpreted as the probability that the spurious score of a randomly chosen link in EP is higher than that of a randomly chosen link in E. The precision is defined as the ratio of the successfully identified spurious links to the top-L selected links with the highest spurious scores. In the experiments, we set  and all the data points are averaged over 10 independent runs with different randomly generated spurious sets. The accuracies of spurious link identification measured by precision and AUC are shown in Tables 4 and 5, respectively (see SI for standard deviations). Again, our method is remarkably better than all other state-of-the-art methods and not sensitive to the size of training set, see Figs 5 and 6.
and all the data points are averaged over 10 independent runs with different randomly generated spurious sets. The accuracies of spurious link identification measured by precision and AUC are shown in Tables 4 and 5, respectively (see SI for standard deviations). Again, our method is remarkably better than all other state-of-the-art methods and not sensitive to the size of training set, see Figs 5 and 6.
Now we apply our method to analyze the network of macaque monkey brain, where nodes are the cortical areas and links are projections between them45. There are three kinds of links in the focal network, namely confirmed existing, confirmed absent and uncertain links. The reported links are based on neuroanatomical experiments and the uncertain links are owning to conflict reports in the literature. The original network is directed, we eliminate the directions of the link by treating a link as uncertain if it is bidirectional uncertain and as confirmed existing if it is confirmed in either direction. The undirected network consist of 32 nodes with 194 confirmed existing links, 90 confirmed absent links and 212 uncertain links. We then use our algorithm to estimate the probability of the uncertain links. To test the validity of the algorithm, we randomly hide 10% of the confirmed existing links as the probe set and the prediction task now is to find out these hidden confirmed existing links. When calculating the prediction accuracy, we consider both the case when uncertain links are included and excluded from the candidates of missing links.
As shown in Table 6, our method can successfully find out the hidden confirmed existing links. Notably, although the number of uncertain links is much greater than confirmed absent links, there is no significant drop of the accuracy when they are included. We find that the probability that a hidden confirmed link has a higher score than an uncertain link is 0.796, indicating that uncertain links are indeed less reliable generally. Besides, we also test that the probability that an uncertain link has a higher score than a confirmed absent link is 0.634, implying that there must be some missing links in the set of uncertain links.
Now an interesting problem arises, that is among the 212 uncertain links, which are more likely to be exist. Here we use the full knowledge of the confirmed links to make predictions, see the most likely latent links predicted by our method in Table 7. ref. 42 also gave a prediction on those uncertain links. After comparison, among the top-16 predicted links shown in Table 7 there are only two links are different—PIP-V3A and PIP-V4t—which are predicted to be absent by ref. 42. While with the new progress of the studies on macaque monkey brain, the data is increasingly extended and improved46. The data in ref. 46 provides us an opportunity to better evaluate the algorithms. Surprisingly, in the new data set, the two controversial links are shown to be confirmed. That is to say, our structural-based method give much accurate prediction than the spatial-based method proposed in ref. 42. Besides these two links, there are three links (emphasized by bold) are also confirmed by data in ref. 46, while the other 11 predicted links are waiting for the test by real experiments in the near future.
Discussion
Prediction is a core issue in network science, which is the only solid way to check whether our understanding of network evolution is right10. It covers a variety of problems, such as the prediction of missing links1, future links1, vanishing nodes47, reciprocal relationships48, spurious links9 and so on. In this paper, we used an algorithmic framework, where a network’s probability is estimated according to a predefined structural Hamiltonian and the existence score of a non-observed link is quantified by the conditional probability of adding the focal link to the network while the spurious probability of an observed link is quantified by the conditional probability of deleting the link.
Since the homophily49 and social recommendation50 mechanisms ruling the real network formation both exhibit local clustering property, we define a Hamiltonian according to the closed walk process that can well take into account the structural localization. For both missing link prediction and spurious link identification, the present method performs surprisingly well, much better than all state-of-the-art methods under consideration. Notice that, although this method can find applications in small networks or some small parts (e.g., communities) of a network, it is very time-consuming and cannot be directly applied to large-scale networks. One strategy to overcome this computational limit is to use parallel algorithms. Since individual runs of the matrix diagonalization are completely independent, parallelizing the algorithm is straightforward. And also, the diagonalization of symmetric matrices itself can be parallelized51. In addition, we found that when estimating the model parameters, it’s not necessary to toggle all matrix elements, but roughly a 10% is sufficient to obtain the same accuracy. After determining the parameters, matrix perturbation technics can be used to compute the scores of the links. We found that by using the perturbation approximations, the algorithm still gives good predictions for many networks.
The present method can be further used to explore underlying network evolving mechanisms. For example, we can transform different evolving mechanisms into different Hamiltonians to indirectly check which mechanism could best capture the network organization principle, with a potential assumption that the mechanism corresponding to the highest link prediction accuracy is the best. We can also fix the Hamiltonian to see whether there are some sudden changes in the evolving mechanism. Such changes usually occur in technological networks such as power grid and Internet driven by the applications of some new techniques, like the new Internet Protocol for AS (autonomous system) level routers, or in online social networks according to the changes of rules and interfaces in the web sites. In S7 of SI, we show successful applications in some artificial generated networks with sudden changes in network evolution.
Methods
Lacking an exact solution for the partition function, we apply the maximum pseudo-likelihood method52 to estimate the parameters βk. For any node pair (x, y), denoting Ac(x, y) the matrix with all elements the same as AO but the element  unknown, then the ratio of the conditional existence probability of the link (x, y) to the conditional nonexistence probability does not depend on the partition function, as
unknown, then the ratio of the conditional existence probability of the link (x, y) to the conditional nonexistence probability does not depend on the partition function, as

where  . So the conditional existence probability is:
. So the conditional existence probability is:  .
.
According to the Hammersley-Clifford Theorem53 we can replace the joint likelihood of the links of the network with the product over the conditional probability of each link, given the rest of the network. Then the temperature parameters βk can be estimated by maximizing the log-likelihood:

where the summation is over all node pairs. This is a convex optimization problem and we apply the gradient ascent method to estimate βk. Detailed steps of the parameter estimating algorithm are shown in the SI.
Additional Information
How to cite this article: Pan, L. et al. Predicting missing links and identifying spurious links via likelihood analysis. Sci. Rep. 6, 22955; doi: 10.1038/srep22955 (2016).
References
Lü, L. & Zhou, T. Link prediction in complex networks: A survey. Physica A 390, 1150 (2011).
Barzel, B. & Barabási, A.-L. Network link prediction by global silencing of indirect correlations. Nat. Biotech. 31, 720 (2013).
Lü, L., Pan, L., Zhou, T., Zhang, Y. C. & Stanley, H. E. Toward link predictability of complex networks. Proc. Acad. Natl. Sci. USA 112, 2325–2330 (2015).
Amaral, L. A. N. A truer measure of our ignorance. Proc. Acad. Natl. Sci. USA 105, 6795 (2008).
Serrano, M. Á. & Sagués, F. Network-based confidence scoring system for genome-scale metabolic reconstructions. BMC Syst. Biol. 5, 76 (2011).
Cannistraci, C. V., Alanis-Lobato, G. & Ravasi, T. From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complexnetworks. Sci. Rep. 3, 1613 (2013).
Aiello, L. M. et al. Friendship prediction and homophily in social media. ACM Trans. Web 6, 9 (2012).
Lü, L. et al. Recommender systems. Phys. Rep. 519, 1 (2012).
Guimerà, R. & Sales-Pardo, M. Missing and spurious interactions and the reconstruction of complex networks. Proc. Acad. Natl. Sci. USA 106, 22073 (2009).
Wang, W.-Q., Zhang, Q.-M. & Zhou, T. Evaluating network models: A likelihood analysis. EPL 98, 28004 (2012).
Guimerà, R. & Sales-Pardo, M. Justice Blocks and Predictability of US Supreme Court Votes. PLoS One 6, e27188 (2011).
Neville, J. & Jensen, D. J. Relational dependency networks. J. Machine Learning Res. 8, 653 (2007).
Heckerman, D., Meek, C. & Koller, D. Probabilistic Entity-Relationship Models, PRMs and Plate Models. In Introduction to Statistical Relational Learning (eds Getoor, L. & Taskar, B. ) 201–239 (Cambridge–Mass: MIT Press, 2007).
Yu, K. & Chu, W. Gaussian process models for link analysis and transfer learning. In Advances in Neural Information Processing Systems 1657–1664, Vancouver, Canada. Cambridge: MIT Press (2007, December).
Liben-Nowell, D. & Kleinberg, J. The link-prediction problem for social networks. J. Am. Soc. Inform. Sci. Technol. 58, 1019 (2007).
Zhou, T., Lü, L. & Zhang, Y.-C. Predicting missing links via local information. Eur. Phys. J. B 71, 623 (2009).
Lü, L., Jin, C.-H. & Zhou, T. Similarity index based on local paths for link prediction of complex networks. Phys. Rev. E 80, 046122 (2009).
Fouss, F., Pirotte, A., Renders, J.-M. & Saerens, M. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation. IEEE Trans. Knowl. Data. Eng. 19, 355 (2007).
Liu, W. & Lü, L. Link prediction based on local random walk. EPL 89, 58007 (2010).
Leicht, E. A., Holme, P. & Newman, M. E. J. Vertex similarity in networks. Phys. Rev. E 73, 026120 (2006).
Sun, D. et al. Information filtering based on transferring similarity. Phys. Rev. E 80, 017101 (2009).
Clauset, A., Moore, C. & Newman, M. E. J. Hierarchical structure and the prediction of missing links in networks. Nature 453, 98 (2008).
Kim, M. & Leskovec, J. The Network Completion Problem: Inferring Mising Nodes and Edges in Networks. In Proceedings of the 11th International Conference of Machine Learning 47–58, Boca Raton, Florida, USA. Mesa: SIAM/Omnipress (2011, December).
Szabó, G., Alava, M. & Kertész, J. Clustering in Complex Networks. Lect. Notes Phys. 650, 139 (2004).
Kossinets, G. & Watts, D. J. Empirical analysis of an evolving social network. Science 311, 88 (2006).
Backstrom, L., Boldi, P., Rosa, M., Ugander, J. & Vigna, S. Four degrees of separation. In Proceedings of the 4th International Conference on Web Science 33–42, Evanston, Illinois, USA. New York: ACM Press (2012, June).
Orsini, C. et al. Quantifying randomness in real networks. Nat. Commun. 6 (2015).
Newman, M. E. J. The Structure and Function of Complex Networks. SIAM Review 45, 167 (2003).
Park, J. & Newman, M. E. J. Statistical mechanics of networks. Phys. Rev. E 70, 066117 (2004).
Robins, G., Pattison, P., Kalish, Y. & Lusher, D. An introduction to exponential random graph (p*) models for social networks. Soc. Netw. 29, 173 (2007).
Adamic, L. A. & Adar, E. Friends and neighbors on the Web. Soc. Netw. 25, 211 (2003).
Ou, Q., Jin, Y.-D., Zhou, T., Wang, B.-H. & Yin, B.-Q. Power-law strength-degree correlation from resource-allocation dynamics on weighted networks. Phys. Rev. E 75, 021102 (2007).
Katz, L. A new status index derived from sociometric analysis. Psychometrika 18, 39 (1953).
Hanely, J. A. & McNeil, B. J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 143, 29 (1982).
Herlocker, J. L., Konstann, J. A., Terveen, K. & Riedl, J. T. Evaluating collaborative filtering recommender systems. ACM Trans. Inf. Syst. 22, 5 (2004).
Gleiser, P. & Danon, L. Community structure in Jazz. Adv. Complex Syst. 6, 565 (2003).
Duch, J. & Arenas, A. Community detection in complex networks using extremal optimization. Phys. Rev. E. 72, 027104 (2005).
Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440 (1998).
Batageli, V. & Mrvar, A. Pajek datasets. (2006) Available at: http://vlado.fmf.uni-lj.si/pub/networks/data/mix/USAir97.net. (Accessed: 20/11/2015).
Ulanowicz, R. E., Bondavalli, C. & Egnotovich, M. S. Network Analysis of Trophic Dynamics in South Florida Ecosystem, FY 97: The Florida Bay Ecosystem. Tech. Rep. CBL 98 (1998).
Baird, D., Luczkovich, J. & Christian, R. R. Assessment of Spatial and Temporal Variability in Ecosystem Attributes of the St Marks National Wildlife Refuge, Apalachee Bay, Florida. Estua. Coas. Shelf Sci. 47, 329 (1998).
da F. Costa, L., Kaiser, M. & Hilgetag, C. C. Predicting the connectivity of primate cortical networks from topological and spatial node properties. BMC Sys. Bio. 1, 16 (2007).
Newman, M. E. J. Assortative mixing in networks. Phys. Rev. Lett. 89, 208701 (2002).
Zeng, A. & Cimini, G. Removing spurious interactions in complex networks. Phys. Rev. E 85, 036101 (2012).
Felleman, D. J. & Van Essen, D. C. Distributed hierarchical processing in the primate cerebral cortex. Cerebral Cortex 1, 1 (1991).
Kaiser, M. & Hilgetag, C. C. Nonoptimal Component Placement, but Short Processing Paths, due to Long-Distance Projections in Neural Systems. PLoS Comput. Biol. 2, 95 (2006).
Dasgupta, K. et al. Social ties and their relevance to churn in mobile telecom networks. In Proceedings of the 11th International Conference on Extending Data Base Technology 668–677, Nantes, France. New York: ACM Press (2008, March).
Hopcroft, J., Lou, T. & Tang . Who will follow you back?: reciprocal relationship prediction. In Proceedings of the 20th ACM international conference on Information and Knowledge Management 1137–1146, Glasgow, United Kingdom. New York: ACM Press (2011, October).
McPherson, M., Smith-Lovin, L. & Cook, J. M. Birds of a feather: Homophily in social networks. Annual Rev. Sociology 27, 415 (2001).
Holme, P. & Kim, B. J. Growing scale-free networks with tunable clustering. Phys. Rev. E 65, 026107 (2002).
Cernuschi-Frias, B., Lew, S. E., Lez, H. N. & Pfefferman, J. D. A parallel algorithm for the diagonalization of symmetric matrices. In Proceedings of the 2000 IEEE International Symposium on Circuits and Systems 81–84, Geneva, Switzerland. IEEE (2000, May).
Anderson, C., Wasserman, S. & Crouch, B. A p* primer: logit models for social networks. Soc. Netw. 21, 37 (1999).
Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. Roy. Stat. Soc. Ser. B. 36, 192 (1974).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant Nos 11222543, 11075031, 11205042, 61433014). LL was supported by start-up fund of Hangzhou Normal University under Grant No. PE13002004039 and Zhejiang Provincial Natural Science Foundation of China under Grant No. LR16A050001. CKH was supported by Grants MOST 103-2112-M-001-016, 104-2112-M-001-002 and NCTS in Taiwan; he was thankful to USST where part of this work was done.
Author information
Authors and Affiliations
Contributions
L.P., T.Z., L.L. and C.-K.H. designed the research. L.P. performed the research. L.P., T.Z., L.L. and C.-K.H. analyzed the data. L.P., T.Z., L.L. and C.-K.H. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Pan, L., Zhou, T., Lü, L. et al. Predicting missing links and identifying spurious links via likelihood analysis. Sci Rep 6, 22955 (2016). https://doi.org/10.1038/srep22955
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep22955
This article is cited by
-
Missing link prediction using path and community information
Computing (2024)
-
Deep manifold matrix factorization autoencoder using global connectivity for link prediction
Applied Intelligence (2023)
-
A comprehensive framework for link prediction in multiplex networks
Computational Statistics (2023)
-
A Novel Link Prediction Framework Based on Gravitational Field
Data Science and Engineering (2023)
-
TRTCD: trust route prediction based on trusted community detection
Multimedia Tools and Applications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

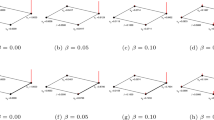

 nodes and
nodes and  links for predicting missing links.
links for predicting missing links.
 nodes and
nodes and  links for identifying spurious links.
links for identifying spurious links.


