Abstract
Within the framework of statistical learning, many behavioural studies investigated the processing of unpredicted events. However, surprisingly few neurophysiological studies are available on this topic and no statistical learning experiment has investigated electroencephalographic (EEG) correlates of processing events with different transition probabilities. We carried out an EEG study with a novel variant of the established statistical learning paradigm. Timbres were presented in isochronous sequences of triplets. The first two sounds of all triplets were equiprobable, while the third sound occurred with either low (10%), intermediate (30%), or high (60%) probability. Thus, the occurrence probability of the third item of each triplet (given the first two items) was varied. Compared to high-probability triplet endings, endings with low and intermediate probability elicited an early anterior negativity that had an onset around 100 ms and was maximal at around 180 ms. This effect was larger for events with low than for events with intermediate probability. Our results reveal that, when predictions are based on statistical learning, events that do not match a prediction evoke an early anterior negativity, with the amplitude of this mismatch response being inversely related to the probability of such events. Thus, we report a statistical mismatch negativity (sMMN) that reflects statistical learning of transitional probability distributions that go beyond auditory sensory memory capabilities.
Similar content being viewed by others
Introduction
Humans are sensitive to regularities within their environment and pick up statistical structures without explicit intent. This ability is explored within the frameworks of statistical learning1 and implicit learning2, both of which have been argued to investigate the same underlying learning phenomenon3,4. Although statistical learning appears to be domain-general5, it has most prominently been investigated in the context of language acquisition, especially word learning (for a review see ref. 6), as well as music7,8,9,10,11 (for reviews see refs 12, 13, 14). With regard to statistical learning paradigms, word learning has been argued to be grounded, at least in part, in sequence prediction: In a continuous stream of syllables, sequences of events linked with high statistical conditional probability likely correspond to words, whereas syllable transitions with low predictability may likely be indicative of word-boundaries14,15,16. Thus, tracking conditional probability relations between syllables has been regarded as highly relevant for the extraction of candidate word forms17,18.
In addition, integrating information across the extracted units eventually reveals distributional properties19,20. Extracted statistical properties provide an important basis for predictions which guide the processing of sensory information20,21,22. Stimuli that are hard to predict (e.g. the syllable after a word boundary) have been hypothesized to increase processing load21,22. Such an increase in processing load has been found to be reflected neurophysiologically in event-related brain potential (ERP) components such as the N100 and the N400: During successful stream segmentation, word-onsets evoke larger N100 and N400 ERPs compared to more predictable positions within the word in adults (e.g. refs 14,23, 24, 25, 26, 27) and similar ERP responses have been observed even in newborns28.
Although the statistical learning paradigm has been extensively used (typically using sequences of triplet stimuli), only few neurophysiological studies have varied the occurrence probability of single events within triplets29,30,31,32. A magnetoencephalograpic (MEG) study by Furl et al.31 used second-order Markov chains in which any pair of tones predicted the next tone with 90% probability. The remaining 10% of tones were, thus, unexpected (given successful learning of the second-order statistics). Such unexpected events elicited stronger magnetic fields than expected events in the time range between ~150–250 ms. An MEG study by Paraskevopoulos et al. used sequences of tone triplets, with triplet endings occurring with either high or low probability (thus, low and high probability triplets differed only with regard to the last tone of a triplet)32. Final tones with low probability elicited an enhanced P50m and a negativity around 150 ms (the latter was referred to by the authors as mismatch negativity, MMN). Finally, two MEG studies by Daikoku et al.31,32 used sequences in which sound pairs predicted a subsequent sound either with high (80%) or low probability (second-order Markov chains, similar to the study by Furl et al.)31. One study used sounds with different pitches29 and another study also used sounds with different phonemes, as well as pitches and phonemes combined30. In both studies, low-probability sounds elicited a stronger MEG response than high-probability sounds in the time-window from 100–220 ms, reminiscent of an MMN. Remarkably, these four MEG studies (refs 29, 30, 31, 32) are—to the best of our knowledge—the only studies reporting brain responses to low-probability items occurring instead of high-probability items within a statistical learning paradigm. This scarcity of studies is surprising, because processing of unexpected events, i.e. of events violating predictions based on prior (implicit) learning of statistical regularities, is a fundamental aspect of our everyday life.
Beyond the statistical learning paradigm, multiple types of predictive processes have been investigated and several types of early mismatch responses have been reported in response to unpredicted events: For example, violations of statistical regularities that are established on-line, on a moment-to-moment basis, elicit a mismatch negativity (MMN) and the regularities underlying the generation of the physical MMN33 and the abstract-feature MMN34 are thought to be represented mainly in sensory memory35,36,37,38. If local transition probabilities stored in auditory sensory memory change, the sensory representations of the new transition probabilities (and even of auditory feature contingencies) are dynamically updated, as reflected in MMN responses in the time range between ~100–200 ms39,40. By contrast, deviants in statistical learning paradigms, like those employed in the MEG studies described above29,30,31,32, require an extended period of learning and the mismatch response associated with statistical learning reflects the processing of local dependencies based on (implicit) knowledge about statistical regularities. That is, the mismatch response associated with statistical learning is based on memory representations beyond the capabilities of sensory memory.
Other early mismatch responses observed beyond statistical learning paradigms are (early) left anterior negativities41, the syntactic MMN42,43 and the early right anterior negativity (ERAN)44. The (early) left anterior negativities and the syntactic MMN have been reported in language-experiments and are taken to reflect syntactic processing including the processing of irregular local dependencies (e.g. morpho-syntactic irregularities such as “he come” and “we comes”). However, these ERP components have not been investigated in statistical learning experiments and they most probably do not only reflect processing of local dependencies, but also processing of syntactic (e.g. morpho-syntactic) information. The ERAN is evoked by music-syntactically irregular events within chord sequences or melodies. However, previous ERAN studies do not inform us about the processing of local dependencies comparable to those used in statistical learning paradigms, because in all previous ERAN studies using local irregularities, local irregularity confounded with hierarchically organized non-local dependencies45. For example, in a normal five-chord-cadence starting and ending on a tonic (as, e.g., in ref. 46), the final tonic following the penultimate dominant also hierarchically prolongs the initial tonic. Therefore, a final chord other than the tonic is not only locally less regular, but also violates the hierarchical organization of the harmonic sequence established by the first four chords.
To investigate ERP correlates of processing events that occur instead of predicted high-probability events within a statistical learning paradigm, we constructed auditory sequences using triplets of sounds. The triplets exhibited three different degrees of internal transition probability (see Fig. 1). They were randomly concatenated in a continuous stream and had endings with high, intermediate as well as low probability (see Fig. 1). Participants passively listened to this stream and our aim was to investigate the electrical brain responses evoked by the triplet endings (that is, ERPs evoked by triplet endings with high, intermediate and low probability). Thus, we employed a novel statistical oddball paradigm that advances the traditional statistical learning paradigm and the methods used in previous neurophysiological studies. Note that, similar to the above-mentioned MEG studies using statistical learning paradigms29,30,31,32, we were primarily interested in investigating brain responses to low probability items at a position with relatively low entropy, rather than triplet segmentation processes (used as a paradigm to investigate learning processes associated with word segmentation)14,23,24,25,26.
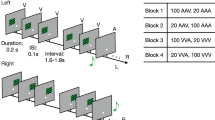
Arrangement of timbres into triplets and streams.
(A) Each of three triplet roots (AB, BC, CA) consisted of two timbres. Three different timbres were attached to each root (triplet endings: D, E, F), leading to nine timbre triplets. Across the exposition phase (duration ~1 h), triplets were presented with different frequencies of occurrence in a way that each root would be followed by a specific triplet ending with either high, intermediate, or low probability (numbers in circles indicate total number of presentations of a triplet during the exposition phase). (B) Timbre triplets were concatenated into a pause-free, pseudorandom stream. ERPs were calculated for triplet endings (i.e., for the final item of each triplet, indicated by the black squares) and for triplet roots (i.e., for the first two items of each triplet, indicated by the gray squares). Letters A to F refer to the six timbres used in this study; interm.: intermediate; p.: probability).
We used synthetic timbres as stimuli, instead of phonemes or pitches, because both Western tonal music and language exhibit a strong hierarchical organization47,48,49. Thus, it can be guaranteed that our stimuli exclude potential interference by long-term representations of hierarchically organized regularities (due to the lack of a pre-existing hierarchically organized rule system for our synthetic timbres).
We hypothesized that participants would incidentally establish a model of the transitional probability distribution over triplet endings. Because model predictions guide subsequent processing, endings with lower probability should be less expected and the effort to process items should be inversely related to the magnitude of their probability50. Using ERPs, we investigated the neurophysiological correlates of different magnitudes of probability (and thus of differences in processing load). Specifically, based on the results of the MEG studies on statistical learning described above29,30,31,32, we expected an early negativity in reaction to low probability triplet endings. In addition, we tested whether this negativity would have a larger amplitude when elicited by low compared to intermediate probability items. Thus, results were supposed to inform us about neurophysiological correlates of the processing of local dependencies, using a novel statistical learning paradigm and a hierarchy-free stimulus environment.
Materials and Methods
Participants
18 adults (9 females; mean age = 25.6 years, SD = 4.3) were recruited at the Freie Universität Berlin. All participants were right-handed (mean laterality quotient = 95.2,  according to the Edinburgh Handedness Inventory51. None of the participants had hearing impairment, absolute pitch, history of neurological disease, or musical training besides regular school lessons (according to self-report).
according to the Edinburgh Handedness Inventory51. None of the participants had hearing impairment, absolute pitch, history of neurological disease, or musical training besides regular school lessons (according to self-report).
Ethics Statement
The study was carried out in accordance with the guidelines of the Declaration of Helsinki and approved by the ethics committee of the Department of Educational Sciences and Psychology of the Freie Universität Berlin. Participants provided written informed consent before the experiment.
Stimuli
Timbre Triplets
Six timbre sounds were selected from a study by McAdams et al. (ref. 52). All sounds were equalized in pitch and loudness. Each sound had a duration of 300 ms, including a fadeout of 15 ms. Each timbre was followed by a 35 ms pause. The six timbres were reminiscent of Bassoon, Clarinet, Harpsichord, Trombone, Harp and Striano (bowed string/piano). We will refer to them with letters A to F (see also Fig. 1A).
The six timbre sounds (A to F) were combined into sound triplets (Fig. 1A), as decribed in the following. Timbres A, B and C were used for the first two timbres of each triplet: Each of these three timbres (A, B, C) appeared once in the first and once in the second position (AB, BC and CA, see also Fig. 1A). In the following, we will refer to the first two sounds of a triplet as “root”. Thus, three timbres (A, B, C) were used to create three roots (AB, BC, CA). The remaining timbres (D, E, F) served as triplet endings for each of the three roots, resulting in nine unique triplets (see also Fig. 1A).
Triplet Sets
The nine triplets were divided into three sets of triplets: one set with low frequency of occurrence (10%), one with intermediate frequency of occurrence (30%) and one with high frequency of occurrence (60%). E.g., the set with high frequency of occurrence comprised triplets ABD, BCE and CAF (see also Fig. 1A). Note that each set contained each root and each ending exactly once. Thus, constructing the triplet sets did not affect the presentation frequencies of individual timbres, roots or endings, as these were evenly distributed across sets. In other words, the transitional probability of a triplet ending, given the first two timbres of a triplet, depended on which of the three sets this specific triplet was in. Accordingly, we will refer to sets and triplet endings as low, intermediate and high probability sets and endings.
Triplet Streams
The triplets were concatenated to construct five pause-free timbre streams. Note that the interstimulus interval between two successive timbres was always 35 ms. Each stream consisted of 600 triplets and was 10 min long. Within each stream, triplets from the low, intermediate and high probability sets were presented with a ratio of 1:3:6. Concretely, each triplet was presented 20, 60 or 120 times, respectively (see Fig. 1B). The sequence of triplets within each stream was pseudorandomized: Triplets were never repeated directly and triplets from the low probability set were separated by at least three triplets from another set. Four additional timbres were used to create two completely random streams used only for demonstration and practice. They were edited like the six timbres used in the reqular streams. Each practice stream consisted of 90 sounds and was 30 s long.
Procedure
Participants sat in a sound attenuated room. An experimenter was present at all times. Participants were not informed about the intent of the study, nor the regularities within the stimuli. Sounds were presented via headphones at a normal comfortable intensity level (around 50 dB SPL). The experiment consisted of two parts, an exposition phase (~1 h) during which the electroencephalogram (EEG) was recorded and a behavioral task (~8 min).
Exposition Phase
The first part of the experiment was the exposition phase. The five timbre streams were presented as blocks, thus there were five blocks of stimuli (with a duration of 50 min in total). Between blocks there were pauses and the length of each pause was determined by the participant. During listening, participants watched a muted nature film (“Winged Migration”, Sony Pictures Classics, 2003), presented at ~60 cm distance within a horizontal visual angle of ~17°.
As a cover task and to control that participants processed the stimulus, 60 of the 9000 timbres (0.67%) were presented to one ear only. Participants were instructed to quickly press the space key in response to such acoustical deviants. The side of presentation was randomized. The acoustical deviants were only used for the cover task and excluded from the ERP data analysis. Before the exposition phase, the two practice streams were presented to familiarize participants with this task. Each practice stream contained three acoustical deviants.
Goodness-of-fit and Confidence Ratings
After the exposition phase (which lasted ~1 h), a behavioral test assessed the ability to differentiate triplet endings based on their frequency of occurrence with which they were presented during the exposition phase. Participants were presented with 36 trials. In each trial, participants were presented with two triplets (e.g. ABD and ABE). The first two sounds of these two triplets were the same (i.e., both triplets had the same root, e.g. AB), thus only the third sound (i.e., the triplet ending) differed between the two triplets. There was a 335 ms pause between the two triplets. Participants were asked which triplet-ending they “found to fit better” (two-alternative, forced-choice goodness-of-fit rating) and how confident they were with regard to their choice. The confidence ratings were obtained to assess whether participants were aware of any knowledge guiding their choices. Confidence ratings were obtained using a six-point scale, ranging from “guessing” to “absolutely certain”. The ending that had occurred more often during the exposition phase (see above) was defined as better fitting and thus as correct. Participants were rewarded with 10 cents for each correct choice. Feedback about the winnings was given after the last trial only. For each of the three roots (AB, BC, CA, see also Fig. 1A), three such comparisons were possible (high vs. intermediate, high vs. low. and intermediate vs. low probability endings). All of these nine comparisons of triplet endings were presented four times, in random order. Comparisons involving the same root were not repeated in consecutive trials and the order of presentation of the endings was counterbalanced.
Data Recording and Analysis
EEG recording
EEGs were recorded from 59 electrodes, cap-mounted in compliance with the extended 10-10 system (Fpz, Fp1, Fp2, AF3, AF4, AF7, AF8, Fz, F1, F2, F3, F4, F5, F6, F7, F8, FC1, FC2, FC3, FC4, FC5, FC6, FT7, FT8, Cz, C1, C2, C3, C4, C5, C6, T7, T8, CPz, CP1, CP2, CP3, CP4, CP5, CP6, TP7, TP8, Pz, P1, P2, P3, P4, P5, P6, P7, P8, POz, PO3, PO4, PO7, PO8, Oz, O1, O2), with additional electrodes placed on the right and left mastoids, as well as on the neck. The left mastoid electrode was used as reference and the neck electrode was used as ground. Horizontal and vertical electro-occulograms (EOGs) were recorded bipolarly with electrodes placed at the outer canthi of the eyes and above and below the right eye. Electrode impedance was kept below 5 kΩ. Signals were recorded using Brain Products Vision Recorder (Brain Products GmbH, Munich, Germany) with a 0.1 Hz to 1000 Hz bandpass filter and 500 Hz sampling rate.
EEG Data Analysis
EEG-data were analyzed using EEGLAB53. After data acquisition, EEG-data were re-referenced to the algebraic mean of the left and right mastoid electrodes and filtered with a 0.5 Hz high-pass filter (550 point, finite impulse response, Blackman) and a 30 Hz low-pass filter (2750 points, finite impulse response, Blackman). Epochs containing acoustical deviants or button presses were excluded from further analysis. Data containing artifacts were rejected by removing sampling points whenever the standard deviation within a 200 or 800 ms gliding window exceeded 25 μV at any electrode channel (including the EOG channels). Artifact rejections were visually controlled by the second author. Furthermore, Independent Component Analysis was used to remove eye and muscle artifacts. ERPs were calculated for low, intermediate and high probability triplet endings. In addition, to determine whether the triplet structure of the stimulus stream was represented in participants’ brain responses, ERPs were also calculated for triplet roots (i.e., the first two triplet items) for each block. All ERPs were computed using a 100 ms pre-stimulus baseline.
For statistical evaluation, electrodes were clustered into two regions of interest (ROIs), namely left anterior (FP1, AF3, AF7, F1, F3, F5, FC1, FC3, FC5) and right anterior (FP2, AF4, AF8, F2, F4, F6, FC2, FC4, FC6). The time windows used for statistical analyses (see below) were based on previous results (refs 29, 30, 31, 32, see Introduction) and visual inspection. Using SPSS 23.0 (IBM Corp., Armonk, NY, USA), ERPs elicited by triplet endings were statistically analyzed with a three-way repeated measures multivariate Analysis of Variance (MANOVA) with factors probability (low, intermediate and high probability ending), block (1 to 5) and hemisphere (left and right ROI) as within-subjects factors. Time windows were 70–130 ms and 130–220 ms. Significant effects of probability were investigated further using user-defined contrasts. ERPs elicited by triplet roots were statistically analyzed with a three-way repeated measures multivariate Analysis of Variance (MANOVA) with factors item position (first and second triplet item), block (1 to 5) and hemisphere (left and right ROI) as within-subjects factors. Time windows were 70–130 ms and 170 to 230 ms.
Behavioral Data Analysis
For the evaluation of the cover task (during the exposition phase), button presses within up to three sounds (i.e., 1.34 s) after acoustical deviants were regarded as hits. Choices in the goodness-of-fit ratings (after the exposition phase) were classified as correct if the chosen (“preferred”) triplet ending had higher probability than the rejected one. Otherwise choices were classified as incorrect. Mean correctness was calculated for each participant as the proportion of correct responses to the overall number of responses. Mean correctness was tested against chance level (two-tailed t-test,  . Correctness was also entered into an ANOVA with trial type (trials contrasting either high vs. low, high vs. intermediate, or low vs. intermediate endings) and repetition (four repetitions of nine comparisons of triplet endings) as within-subject factors. Factor repetition was included to guarantee that the frequencies of occurrence during the behavioral test did not modify the learned frequency distributions. In addition, Pearson’s product-moment correlation between goodness-of-fit and confidence ratings was calculated and tested for significance with a two-tailed t-test
. Correctness was also entered into an ANOVA with trial type (trials contrasting either high vs. low, high vs. intermediate, or low vs. intermediate endings) and repetition (four repetitions of nine comparisons of triplet endings) as within-subject factors. Factor repetition was included to guarantee that the frequencies of occurrence during the behavioral test did not modify the learned frequency distributions. In addition, Pearson’s product-moment correlation between goodness-of-fit and confidence ratings was calculated and tested for significance with a two-tailed t-test  for all trials and for each trial type separately. This analysis was carried out to determine whether participants with higher correctness rates would also be more confident in their judgements. Statistical evaluations of behavioral data were computed using R54.
for all trials and for each trial type separately. This analysis was carried out to determine whether participants with higher correctness rates would also be more confident in their judgements. Statistical evaluations of behavioral data were computed using R54.
Results
Acoustical Deviance Detection (Cover Task)
Participants discovered on average 98.9% of the 60 acoustical deviants in the cover task (SD = 1.3). No participant had more than two false alarms (M = 0.9, SD = 0.8). This indicates that participants perceived and responded to the acoustical stimuli despite watching the (muted) movie.
ERPs of Triplet Endings
Figure 2A shows that the triplet endings elicited a positive-going wave (P1) with a latency of ~100 ms, followed by a negative-going wave that was maximal at ~180 ms over frontal electrodes. The amplitude of this negativity varied with ending probability (see also dotted rectangle in Fig. 2A), being more negative for low than medium probability items and more negative for medium than high probability items (see also Fig. 2B and Table 1).
ERP results.
(A) Mean ERP waves of triplet endings (averaged across participants), recorded at Fz (−100–400 ms relative to the onset of the third triplet item). ERPs are shown separately for high (solid line), intermediate (dashed line) and low probability endings (dottes line). The area within the dotted rectangle indicates the time window used for statistical analysis (130–220 ms). The dotted vertical line indicates the onset of the subsequent timbre (i.e., the beginning of the next triplet). Compared to high probability triplet endings, endings with low and intermediate probability elicited a frontal negativity (this effect was larger for low than for intermediate probability endings). (B) Isopotential map showing the scalp distribution of the negativity evoked by low probability endings compared to high probability endings for the time window used for statistical analysis (difference potential: high subtracted from low probability endings). (C) Mean ERP waves of triplet roots (i.e., first and second items of triplets), recorded at Fz (−100–700 ms relative to the onset of the triplet root), separately for each of the five blocks. The dashed rectangle indicates the time window used for statistical analysis (170–230 ms). The dashed vertical lines indicate onsets of stimuli (i.e., onset of the second and third triplet item).
A MANOVA with factors probability (low, intermediate and high probability ending), block (1 to 5) and hemisphere (left and right ROI) for the time window from 130 to 220 ms after the onset of triplet endings showed a significant main effect of probability on mean ERP amplitudes  ,
,  ,
,  . Post-hoc tests using polynomial orthogonal contrasts revealed a significant linear trend
. Post-hoc tests using polynomial orthogonal contrasts revealed a significant linear trend  ,
,  ,
,  . This reflects an amplitude increase of the observed negativity from low over intermediate to high probability endings. Planned comparisons with user-defined contrasts confirmed this increase, revealing that the negativity differed significantly (and with large effect sizes) between low and high probability endings and between intermediate and high probability endings
. This reflects an amplitude increase of the observed negativity from low over intermediate to high probability endings. Planned comparisons with user-defined contrasts confirmed this increase, revealing that the negativity differed significantly (and with large effect sizes) between low and high probability endings and between intermediate and high probability endings  in each test, see Table 2 for details). The difference between low and intermediate probability endings was statistically not significant. Another main effect was observed for the factor block
in each test, see Table 2 for details). The difference between low and intermediate probability endings was statistically not significant. Another main effect was observed for the factor block  ,
,  ,
,  ; see Fig. 3). Polynomial contrasts revealed a linear trend
; see Fig. 3). Polynomial contrasts revealed a linear trend  ,
,  ,
,  . The interaction of the factors probability and block approached statistical significance
. The interaction of the factors probability and block approached statistical significance  ,
,  .
.
Mean amplitudes 130–220 ms elicited by triplet endings with different probabilities over the course of the experiment.
The mean amplitude changed over blocks, following a linear positive trend. Error bars indicate standard error. The amplitude scale is inverted to facilitate comparability with Fig. 2.
A MANOVA for the P1 effect with factors probability (low, intermediate and high probability ending), block (1 to 5) and hemisphere (left and right ROI) for the time window from 70 to 130 ms after the onset of triplet endings did not show a clear effect of probability on mean ERP amplitudes  , nor any interaction involving item probability.
, nor any interaction involving item probability.
ERPs of Triplet Roots
To determine whether the triplet structure of the stimulus stream was represented in participants’ brain responses, we also inspected the ERPs elicited by the first two triplet items (i.e., by the triplet roots, see also gray squares in Fig. 1B). Recall that the first two items were always a subset of the three timbres that could occur at positions one and two of each triplet (Fig. 1A). Therefore, any difference in brain responses between the first two triplet items could only be due to the fact that participants had a cognitive representation of the triplet structure of the stimulus stream. Figure 2C shows that both first and second triplet items elicited a positive-going wave (P1) at ~80 ms after stimulus onset, followed by an N1-like wave (indicated by the dashed rectangles) at ~200 ms and another (N2-like) negative wave peaking at ~310 ms. The N1-like wave clearly differed between the first and the second triplet items (whereas P1 and N2-like waves were similar for both triplet items). In addition, the N1-like wave increased systematically across blocks when elicited by the first, but not by the second item, probably reflecting developing word segmentation across blocks.
A MANOVA with factors item position (first and second triplet item), block (1 to 5) and hemisphere (left and right ROI) for the time window from 170 to 230 ms after the onset of the first and second triplet items showed significant effects of item position (reflecting that the amplitude of the N1-like wave differed between first and second triplet item,  ,
,  ,
,  , block (reflecting that the amplitude of the N1-like wave changed over the course of the experiment,
, block (reflecting that the amplitude of the N1-like wave changed over the course of the experiment,  ,
,  ,
,  and hemisphere (reflecting that the N1-like wave was right-lateralized,
and hemisphere (reflecting that the N1-like wave was right-lateralized,  ,
,  ,
,  . Moreover, the MANOVA indicated an interaction between block and hemisphere (reflecting that the lateralization of the N1-like wave was stronger at the beginning than at the end of the experiment,
. Moreover, the MANOVA indicated an interaction between block and hemisphere (reflecting that the lateralization of the N1-like wave was stronger at the beginning than at the end of the experiment,  ,
,  ,
,  . Despite a missing interaction between factors item position and block (
. Despite a missing interaction between factors item position and block ( , we carried out additional MANOVAs, separately for the first and second timbre (with factors block and hemisphere), justified by the large amplitude difference between the first and second triplet items (reflected in the large effect size of the main effect of item position). For the first item, the MANOVA indicated main effects of block
, we carried out additional MANOVAs, separately for the first and second timbre (with factors block and hemisphere), justified by the large amplitude difference between the first and second triplet items (reflected in the large effect size of the main effect of item position). For the first item, the MANOVA indicated main effects of block  ,
, 
 and hemisphere
and hemisphere  ,
,  ,
,  . The amplitude increase of the N1-like wave (reflected in the main effect of block) followed a clear linear trend
. The amplitude increase of the N1-like wave (reflected in the main effect of block) followed a clear linear trend  ,
,  ,
,  . For the second item, neither an effect of block
. For the second item, neither an effect of block  , nor an interaction between block and hemisphere was indicated
, nor an interaction between block and hemisphere was indicated  .
.
A MANOVA for the P1 effect with factors item position (first and second triplet item), block (1 to 5) and hemisphere (left and right ROI) for the time window from 70 to 130 ms after the onset of first and second triplet items did not indicate an effect of item position  , nor any interaction involving item position.
, nor any interaction involving item position.
Behavioral Effects of Ending Probabilities
In the goodness-of-fit ratings, participants’ preference for triplet endings (i.e., the correctness of their choices) was not systematically influenced by probability. The proportion of correct responses was not significantly different from chance—neither overall, nor when analyzing trial types separately (for details see Table 3 and Fig. 4). Accordingly, an ANOVA revealed no effect of trial type on preference (correctness) judgments. There was no effect of repetition, nor an interaction between trial type and repetition.
For trials with high vs. low triplets there was a significant correlation between correct responses and confidence ratings  ,
,  ,
,  . That is, in trials with high vs. low triplets subjects with higher numbers of correct responses also had higher confidence in their ratings. For the other trial types no such correlation was observed (see Table 3).
. That is, in trials with high vs. low triplets subjects with higher numbers of correct responses also had higher confidence in their ratings. For the other trial types no such correlation was observed (see Table 3).
Discussion
We used a statistical learning paradigm to compare the electroencephalographic and behavioral responses to acoustical events with high, intermediate and low transitional probability. Probabilities were determined by how frequently a stimulus succeeded the preceding context of two stimuli. Our stimuli had no inherent hierarchical organization and were unknown to the participants. Thus, we tested whether participants would track statistical properties, in particular transitional probabilities throughout the experiment. We expected participants to successfully acquire such information and form a predictive model of the stimulus environment. Because processing stimuli based on a predictive model should facilitate processing, we also hypothesized that a processing advantage for more probable stimuli and a relatively higher load for less probable stimuli, would be reflected in the electrical brain response to the final items (i.e., the endings) of the stimulus triplets. Correspondingly we found that items with lower probability elicited a stronger electrical brain response than items with high probability. This brain response had negative polarity, was distributed bilaterally over anterior scalp regions, had an onset at ~100 ms and was maximal between ~130 to 220 ms after the onset of the final item. This response to less probable stimuli is consistent with results of previous MEG studies on statistical learning29,30,31,32, showing differences in magnetic brain responses between more predictable and less predictable items in a similar latency range (i.e., between ~100 to 220 ms). One of these studies also reported an earlier effect at ~50 ms32, but neither the other three MEG studies29,31,32, nor our ERP results showed such an early effect.
The effect observed in our study is reminiscent of a family of perisylvian negativities that have been associated with the processing of irregularities in the auditory domain55, namely the physical Mismatch Negativity (MMN), abstract-feature MMN, Early Left Anterior Negativity (ELAN), syntactic MMN, Left Anterior Negativity (LAN) and Early Right Anterior Negativity (ERAN). As described in the Introduction, the physical MMN and the abstract-feature MMN are elicited when stimuli deviate from regularities represented in the auditory sensory memory56. Thus, with regard to physical and abstract-feature MMN, such regularities can be established on-line, on a moment-to-moment basis through invariance of stimulus features or more complex and abstract interstimulus relations (for reviews see refs 35,36,44, for special cases see refs 39,40). However, in our experiment the irregularity of an event was not of an acoustical nature. Instead, representations of regularity had to be established through an extended period of listening and (implicit) learning of information beyond auditory sensory memory capabilities. This suggests an analogy between the negativity observed in the present study on the one hand and the ERAN as well as the ELAN, the syntactic MMN and the LAN on the other, which all reflect the processing of syntactic irregularities represented in a long-term memory format. While ELAN, syntactic MMN and LAN are associated with syntax processing in language41,42,43, the ERAN is associated with music-syntactic processing (e.g., relating the function of a chord to its harmonic context)44. Thus, stimuli used in experiments investigating ELAN, music-syntactic MMN, LAN and ERAN also engage syntactic processing (such as morpho-syntactic processing) and possibly even hierarchical processing (due to the strong hierarchical organization of music and language)47,48,49. This makes it difficult to determine to which degree these ERP components reflect the pure processing of local dependencies (comparable to the processing of the statistical properties of stimuli in statistical learning paradigms), or also other cognitive processes. The negativity observed in the present study is purely due to the processing of local dependencies, i.e., purely due to the statistical properties of sounds, without any necessary contributions from hierarchical processing. Therefore, we suggest the term “statistical MMN” as a label for this mismatch response. However, this label comes with the note of caution that the MMN label is traditionally used for an effect elicited by irregularities that can be recognized on a moment-to-moment basis and stored in sensory memory (i.e., physical and abstract-feature MMN). It is likely that the sMMN does not only reflect higher processing load (e.g. due to the higher information content of unpredicted events), but also error signals (as, e.g., investigated within the framework of predictive coding)21,22,57. This issue remains to be specified.
Regarding the learning of the statistical properties of sounds across the exposition phase, ERPs elicited by the triplet root showed larger N1-like responses to the first than the second triplet item (cf. the dashed rectangles in Fig. 2C). Because the first and second triplet items were acoustically on average identical (see Fig. 1A), this observation indicates that participants had a cognitive representation of the triplet structure of the stimulus stream. Our data are consistent with data from adults (showing that ERP responses in the 100–200 ms range are more negative for the first than the second item of triplets, particularly in good learners)23 and newborns28. In addition, the N1-like response to the first (but not to the second) triplet item increased systematically across blocks. This increase probably reflects the development of word segmentation across blocks. Again, these observations are consistent with data showing enhanced N1 (and N400) ERP components in response to word onsets compared to random syllables (reviewed in ref. 26). With regard to effects of the learning of the statistical properties of the triplet endings across the experiment, we we found a trend for an interaction between block and probability (see also Fig. 3). This suggests that participants established representations of the statistical structure of the stream over the course of the exposition phase. Our observations of effects of statistical online learning are consistent with computational models of experimental data within the framework of implicit, or incidental learning11,58,59.
Incidental learning typically results in an intuition for the stimulus domain14. Therefore we hypothesized that the acquired knowledge about stimulus probability would invoke a gut feeling, strong enough to influence preference in a goodness-of-fit rating. This has been the case in previous studies11,60. However, our participants did not show such an effect. Similar dissociations between electrophysiological and behavioral results were also found in other studies25,30,40,61. In our experiment, participants learned incidentally, without instructions to do so and while watching a movie. Although behavioral effects have been shown under similar conditions62, others found that inattention compromises statistical learning63. In our case, the participants’ knowledge might just not have reached the necessary stability to be accessible to behavioural measures. Also, our stimuli were artificial sounds that differed only subtly in timbre. Other studies show that memorizing and discriminating timbres is a difficult task64 and a previous study found larger amplitudes of effects elicited by low-probability items in response to pitches than to timbres (phonemes)30. Therefore, for future studies on statistical learning with auditory stimuli the use of pitch information, rather than timbre, seems advisable.
Conclusions
Our study takes the statistical learning paradigm one step further: we constructed a new experimental setup to explore different degrees of intra-triplet probabilities within a continuous stream of triplets. We found an early negativity, referred to as “statistical MMN” (sMMN), that reflected probabilistic properties of sounds which were acquired through statistical learning under incidental learning conditions. Interestingly, the amplitude of the sMMN varied as a function of the frequency of occurrence (and thus the predictability) of the stimuli. Hence, our findings show that the sMMN reflects the detection of the degree of transition probability within the sequence. More specifically, our results indicate that representations of statistical regularities are reflected in a proportional neurophysiological response, the sMMN. Our findings are particularly interesting because, while being exposed to the stimulus, the participants were concurrently occupied with watching a movie and therefore likely applied only a minimal amount of attention. Nevertheless, the brain responses of participants revealed that they had established representations of complex interstimulus relations, even prior to the participants being consciously aware that they had learned something and even prior to clear behavioral evidence for learning, similar to a previous MEG study on statistical learning32 and similar to a study on abstract-feature contingencies39. Thus, our ERP results shed new light on the brain’s mechanisms involved in the acquisition and processing of statistical structures, as reflected in a statistical MMN.
Additional Information
How to cite this article: Koelsch, S. et al. Under the hood of statistical learning: A statistical MMN reflects the magnitude of transitional probabilities in auditory sequences. Sci. Rep. 6, 19741; doi: 10.1038/srep19741 (2016).
References
Saffran, J. R., Aslin, R. N. & Newport, E. L. Statistical learning by 8-month-old infants. Science 274, 1926–1928 (1996).
Cleeremans, A., Destrebecqz, A. & Boyer, M. Implicit learning: News from the front. Trends in cognitive sciences 2, 406–416 (1998).
Perruchet, P. & Pacton, S. Implicit learning and statistical learning: One phenomenon, two approaches. Trends in cognitive sciences 10, 233–238 (2006).
Dienes, Z. Conscious versus unconscious learning of structure. In Rebuschat, P. & Williams, J. (eds.) Statistical Learning and Language Acquisition 337–364 (2012).
Conway, C. M. & Christiansen, M. H. Modality-constrained statistical learning of tactile, visual and auditory sequences. Journal of Experimental Psychology: Learning, Memory and Cognition 31, 24 (2005).
Romberg, A. R. & Saffran, J. R. Statistical learning and language acquisition. Wiley Interdisciplinary Reviews: Cognitive Science 1, 906–914 (2010).
Saffran, J. R., Johnson, E. K., Aslin, R. N. & Newport, E. L. Statistical learning of tone sequences by human infants and adults. Cognition 70, 27–52 (1999).
Tillmann, B. & McAdams, S. Implicit learning of musical timbre sequences: statistical regularities confronted with acoustical (dis) similarities. Journal of Experimental Psychology: Learning, Memory and Cognition 30, 1131 (2004).
Schön, D. et al. Songs as an aid for language acquisition. Cognition 106, 975–983 (2008).
Loui, P. Statistical learning–what can music tell us. In P., R. & J., W. (eds.) Statistical Learning and Language Acquisition. Mouton de Gruyter 433–462 (Mouton de Gruyter, 2012).
Rohrmeier, M., Rebuschat, P. & Cross, I. Incidental and online learning of melodic structure. Consciousness and Cognition 20, 214–222 (2011).
Rohrmeier, M. & Rebuschat, P. Implicit learning and acquisition of music. Topics in cognitive science 4, 525–553 (2012).
Ettlinger, M., Margulis, E. H. & Wong, P. C. Implicit memory in music and language. Frontiers in psychology 2 (2011).
François, C. & Schön, D. Neural sensitivity to statistical regularities as a fundamental biological process that underlies auditory learning: the role of musical practice. Hearing research 308, 122–128 (2014).
Saffran, J. R., Newport, E. L. & Aslin, R. N. Word segmentation: The role of distributional cues. Journal of memory and language 35, 606–621 (1996).
Marcus, G. F., Vijayan, S., Rao, S. B. & Vishton, P. M. Rule learning by seven-month-old infants. Science 283, 77–80 (1999).
Saffran, J. R. Words in a sea of sounds: The output of infant statistical learning. Cognition 81, 149–169 (2001).
Hay, J. F., Pelucchi, B., Estes, K. G. & Saffran, J. R. Linking sounds to meanings: infant statistical learning in a natural language. Cognitive psychology 63, 93–106 (2011).
Hunt, R. H. & Aslin, R. N. Category induction via distributional analysis: Evidence from a serial reaction time task. Journal of memory and language 62, 98–112 (2010).
Thiessen, E. D., Kronstein, A. T. & Hufnagle, D. G. The extraction and integration framework: A two-process account of statistical learning. Psychological bulletin 139, 792 (2013).
Friston, K. & Kiebel, S. Predictive coding under the free-energy principle. Philosophical Transactions of the Royal Society B: Biological Sciences 364, 1211–1221 (2009).
Friston, K. The free-energy principle: a unified brain theory? Nature Reviews Neuroscience 11, 127–138 (2010).
Abla, D., Katahira, K. & Okanoya, K. On-line assessment of statistical learning by event-related potentials. Journal of Cognitive Neuroscience 20, 952–964 (2008).
Francois, C. & Schön, D. Musical expertise boosts implicit learning of both musical and linguistic structures. Cerebral Cortex 21, 2357–2365 (2011).
Schön, D. & François, C. Musical expertise and statistical learning of musical and linguistic structures. Frontiers in psychology 2 (2011).
Teinonen, T. & Huotilainen, M. Implicit segmentation of a stream of syllables based on transitional probabilities: An meg study. Journal of psycholinguistic research 41, 71–82 (2012).
François, C., Chobert, J., Besson, M. & Schön, D. Music training for the development of speech segmentation. Cerebral Cortex 23, 2038–2043 (2013).
Teinonen, T., Fellman, V., Näätänen, R., Alku, P. & Huotilainen, M. Statistical language learning in neonates revealed by event-related brain potentials. BMC neuroscience 10, 21 (2009).
Furl, N. et al. Neural prediction of higher-order auditory sequence statistics. Neuroimage 54, 2267–2277 (2011).
Paraskevopoulos, E., Kuchenbuch, A., Herholz, S. C. & Pantev, C. Statistical learning effects in musicians and nonmusicians: An MEG study. Neuropsychologia 50, 341–349 (2012).
Daikoku, T., Yatomi, Y. & Yumoto, M. Implicit and explicit statistical learning of tone sequences across spectral shifts. Neuropsychologia 63, 194–204 (2014).
Daikoku, T., Yatomi, Y. & Yumoto, M. Statistical learning of music-and language-like sequences and tolerance for spectral shifts. Neurobiology of learning and memory 118, 8–19 (2015).
Sams, M., Paavilainen, P., Alho, K. & Näätänen, R. Auditory frequency discrimination and event-related potentials. Electroencephalography and Clinical Neurophysiology 62, 437–448 (1985).
Paavilainen, P., Simola, J., Jaramillo, M. & Näätänen, R. Preattentive extraction of abstract feature conjunctions from auditory stimulation as reflected by the mmn. Psychophysiology 38, 359–365 (2001).
Näätänen, R., Kujala, T. & Winkler, I. Auditory processing that leads to conscious perception: a unique window to central auditory processing opened by the mismatch negativity and related responses. Psychophysiology 48, 4–22 (2011).
Schröger, E. et al. Predictive regularity representations in violation detection and auditory stream segregation: from conceptual to computational models. Brain topography 27, 565–577 (2014).
Czigler, I. & Winkler, I. Unconscious Memory Representations in Perception: Processes and mechanisms in the brain vol. 78 (John Benjamins Publishing, 2010).
Garrido, M. I., Kilner, J. M., Stephan, K. E. & Friston, K. J. The mismatch negativity: A review of underlying mechanisms. Clinical neurophysiology 120, 453–463 (2009).
Sussman, E. & Winkler, I. Dynamic sensory updating in the auditory system. Cognitive Brain Research 12, 431–439 (2001).
Bendixen, A., Prinz, W., Horv´ath, J., Trujillo-Barreto, N. J. & Schröger, E. Rapid extraction of auditory feature contingencies. Neuroimage 41, 1111–1119 (2008).
Friederici, A. D. Towards a neural basis of auditory sentence processing. Trends in Cognitive Sciences 6, 78–84 (2002).
Pulvermüller, F., Shtyrov, Y., Hasting, A. S. & Carlyon, R. P. Syntax as a reflex: Neurophysiological evidence for early automaticity of grammatical processing. Brain and language 104, 244–253 (2008).
Hasting, A. S., Kotz, S. A. & Friederici, A. D. Setting the stage for automatic syntax processing: the mismatch negativity as an indicator of syntactic priming. Journal of cognitive neuroscience 19, 386–400 (2007).
Koelsch, S. Music-syntactic processing and auditory memory: Similarities and differences between ERAN and MMN. Psychophysiology 46, 179–190 (2009).
Koelsch, S. Brain and music (Wiley, 2012).
Koelsch, S., Gunter, T. C., Wittfoth, M. & Sammler, D. Interaction between syntax processing in language and in music: An ERP study. Journal of Cognitive Neuroscience 17, 1565–1577 (2005).
Chomsky, N. Syntactic structures (Walter de Gruyter, 1957).
Lerdahl, F. & Jackendoff, R. A Generative Theory of Tonal Music (Cambridge, MA: MIT Press, 1983).
Rohrmeier, M. Towards a generative syntax of tonal harmony. Journal of Mathematics and Music 5, 35–53 (2011).
Pearce, M. T., Ruiz, M. H., Kapasi, S., Wiggins, G. A. & Bhattacharya, J. Unsupervised statistical learning underpins computational, behavioural and neural manifestations of musical expectation. NeuroImage 50, 302–313 (2010).
Oldfield, R. C. The assessment and analysis of handedness: The edinburgh inventory. Neuropsychologia 9, 97–113 (1971).
McAdams, S., Winsberg, S., Donnadieu, S., De Soete, G. & Krimphoff, J. Perceptual scaling of synthesized musical timbres: Common dimensions, specificities and latent subject classes. Psychological research 58, 177–192 (1995).
Delorme, A. & Makeig, S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. Journal of neuroscience methods 134, 9–21 (2004).
R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria (2008). URL http://www.R-project.org. ISBN 3-900051-07-0.
Koelsch, S. et al. Differentiating ERAN and MMN: An ERP-study. NeuroReport 12, 1385–1389 (2001).
Winkler, I. Interpreting the mismatch negativity. Journal of Psychophysiology 21, 147–163 (2007).
SanMiguel, I., Widmann, A., Bendixen, A., Trujillo-Barreto, N. & Schröger, E. Hearing silences: human auditory processing relies on preactivation of sound-specific brain activity patterns. The Journal of Neuroscience 33, 8633–8639 (2013).
Wiggins, G. A., Pearce, M. T. & Müllensiefen, D. et al. Computational modeling of music cognition and musical creativity. In Dean, R. T. (ed.) The Oxford Handbook of Computer Music (Oxford Univ Press: Oxford, 2009).
Rohrmeier, M. A. & Cross, I. Modelling unsupervised online-learning of artificial grammars: Linking implicit and statistical learning. Consciousness and cognition 27, 155–167 (2014).
Loui, P., Wessel, D. L. & Kam, C. L. H. Humans rapidly learn grammatical structure in a new musical scale. Music perception 27, 377 (2010).
Francois, C. & Schön, D. Learning of musical and linguistic structures: comparing event-related potentials and behavior. Neuroreport 21, 928–932 (2010).
Saffran, J. R., Newport, E. L., Aslin, R. N., Tunick, R. A. & Barrueco, S. Incidental language learning: Listening (and learning) out of the corner of your ear. Psychological science 8, 101–105 (1997).
Toro, J. M., Sinnett, S. & Soto-Faraco, S. Speech segmentation by statistical learning depends on attention. Cognition 97, B25–B34 (2005).
Golubock, J. L. & Janata, P. Keeping timbre in mind: Working memory for complex sounds that can’t be verbalized. Journal of Experimental Psychology: Human Perception and Performance 39, 399 (2013).
Acknowledgements
The authors would like to thank Stephen McAdams for providing the synthesized timbre sounds that were used as stimuli. The contribution of M.R. was in part generously supported by the Zukunftskonzept (ZUK 64) at TU Dresden supported by the Exzellenzinitiative of the Deutsche Forschungsgemeinschaft.
Author information
Authors and Affiliations
Contributions
S.K., M.R. and T.B., conceived the experiment, T.B. conducted the experiment, S.J. and T.B. analysed the results. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Koelsch, S., Busch, T., Jentschke, S. et al. Under the hood of statistical learning: A statistical MMN reflects the magnitude of transitional probabilities in auditory sequences. Sci Rep 6, 19741 (2016). https://doi.org/10.1038/srep19741
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep19741
This article is cited by
-
Seeking the neural representation of statistical properties in print during implicit processing of visual words
npj Science of Learning (2023)
-
Brain-correlates of processing local dependencies within a statistical learning paradigm
Scientific Reports (2022)
-
Electrophysiological and behavioral indicators of musical knowledge about unfamiliar music
Scientific Reports (2022)
-
Interaction within and between cortical networks subserving multisensory learning and its reorganization due to musical expertise
Scientific Reports (2022)
-
Single, but not dual, attention facilitates statistical learning of two concurrent auditory sequences
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.