Abstract
Chemically ordered hard magnetic L10-FeNi phase of higher grade than cosmic meteorites is produced artificially. Present alloy design shortens the formation time from hundreds of millions of years for natural meteorites to less than 300 hours. Electron diffraction detects four-fold 110 superlattice reflections and a high chemical order parameter (S  0.8) for the developed L10-FeNi phase. The magnetic field of more than 3.5 kOe is required for the switching of magnetization. Experimental results along with computer simulation suggest that the ordered phase is formed due to three factors related to the amorphous state: high diffusion rates of the constituent elements at lower temperatures when crystallizing, a large driving force for precipitation of the L10 phase and the possible presence of L10 clusters. Present results can resolve mineral exhaustion issues in the development of next-generation hard magnetic materials because the alloys are free from rare-earth elements and the technique is well suited for mass production.
0.8) for the developed L10-FeNi phase. The magnetic field of more than 3.5 kOe is required for the switching of magnetization. Experimental results along with computer simulation suggest that the ordered phase is formed due to three factors related to the amorphous state: high diffusion rates of the constituent elements at lower temperatures when crystallizing, a large driving force for precipitation of the L10 phase and the possible presence of L10 clusters. Present results can resolve mineral exhaustion issues in the development of next-generation hard magnetic materials because the alloys are free from rare-earth elements and the technique is well suited for mass production.
Similar content being viewed by others
Introduction
Iron meteorites with Widmannstaetten type of structure are mainly composed of iron and nickel. This structure is formed through an extremely slow cooling rate of about one Kelvin per million years in the universe1. The Widmannstaetten structure observed in Octahedrite-type meteorites is peculiar and results from the apparent phase separation of the α-phase (bcc-FeNi with a mineral name: kamacite) and γ-phase (fcc-FeNi: taenite) at the FeNi interface. The taenite phase lamellae observed in the meteorite have varying Ni concentration zones (28–50%)2. Both the disordered fcc and ordered L10 phases of Fe-Ni were detected. Interestingly, the L10 FeNi phase, which is also known as tetrataenite is a hard magnetic with a high saturation magnetization (Ms ~ 1270 emu cm−3) and a large uniaxial magneto-crystalline anisotropy (Ku ~ 1.3 × 107 erg cm−3)3,4,5. The theoretical maximum magnetic energy product of L10 FeNi (~42 MG Oe) is close to the best rare-earth-based hard magnets recently developed6.
Due to shortage of rare-earth elements, which are currently used to produce high-grade permanent magnets, magnets free of rare-earth elements must be developed (i.e., hard magnets based on L10 FeNi). Practically, it is impossible to produce L10 FeNi magnet similar to meteorites industrially because the order-disorder transition temperature of L10 FeNi is too low 320 °C2,6. The diffusion coefficients of Fe and Ni are extremely low around this temperature and in reality, no diffusion takes place, which is why the ordered L10 FeNi phase requires billions of years to form in cosmic products (meteorites). Since the discovery of the L10 FeNi phase in the 1960 s, several attempts (which might trigger atomic migration) such as irradiation with high-energy beams7, a nanoparticle technique8, mechanical alloying9, thin films comprised of mono-layered atoms10 and high-pressure torsion technique11 have been tried to artificially produce this phase. However, L10 FeNi-based hard magnets with high degree of chemical order have yet to be produced.
It seems that the production of L10 FeNi-based hard magnets via conventional material synthesis utilizing atomic diffusion in the crystalline state is extremely difficult, if not impossible. The high stability of crystalline phase and the extremely low diffusivity of the atoms around the order-disorder transition temperature (~320 °C) in crystalline alloys are the biggest hurdles. A high diffusivity of atoms at lower temperatures may successfully form the L10 FeNi phase, but it is difficult to achieve. Although high-pressure torsion and high-energy ball-milling techniques can increase the diffusivity of atoms11, the increase is insufficient. A high atomic diffusivity is possible at low temperatures, such as the transformation from an amorphous state to a stable crystalline state. Distribution of elements in the amorphous alloy is similar to the initial state of meteorites (chondrule). At the dawn of the universe, chondrules were formed by the condensation of solar nebula and melting of condensed mineral clumps. A liquid like state in an amorphous alloy (similar to chondrule) can exist at room temperature. The major difference in approaching a stable crystalline state from the amorphous state is the drastic increase in diffusivity at the transition temperature (i.e., crystallization temperature), whereas cooling molten alloys decreases the diffusivity at the transition temperature. If an alloy based on ~Fe50Ni50 can be made into an amorphous state with a crystallization temperature close to the order-disorder transition temperature, then L10 FeNi-based magnets may be realized.
Results
Various Fe-based amorphous alloys have been developed12. Generally, the crystallization temperature of these alloys is much higher (>450 °C) than the order-disorder transition temperature of the L10 FeNi phase. Recently, we have developed new high magnetic flux density FeSiBPCu-based nanocrystalline soft magnetic alloys13,14. The initial state of the FeSiBPCu alloy is amorphous, but it crystallizes into nano-crystalline α-Fe in the remaining amorphous matrix below 400 °C. Crystallization of this amorphous alloy is very rapid (i.e., the atomic diffusivity of the constituent elements is very high)15. Additionally this alloy also contains Phosphorus (P), which is also present in the NWA 6259 meteorite6. These characteristics are very promising for developing L10 FeNi-based hard magnets.
Therefore, we replaced Ni with Fe in the FeSiBPCu alloy. The results suggest that the Fe42Ni41.3Si8B4P4Cu0.7 alloy is the best among the investigated compositions. It should be noted that we also investigated crystalline FeNi binary alloys, but the formation of L10 FeNi could not be detected. In Fe42Ni41.3SixB12–xP4Cu0.7 (x = 2 to 8 at.%) alloys, a higher Si content is better for the formation of the L10 FeNi phase.
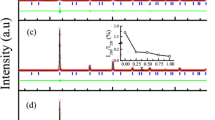
The as-quenched state of the Fe42Ni41.3Si8B4P4Cu0.7 alloy is amorphous and its crystallization temperature measured by differential scanning calorimetry (DSC) is ~400 °C (at a heating rate of 40 °C/minute). Figure 1 shows the X-ray diffraction (XRD) pattern of the Fe42Ni41.3Si8B4P4Cu0.7 ribbon crystallized at 400 °C for 288 hours. The diffraction peaks corresponding to the ordered L10 FeNi phase (inset of Fig. 1) along with α-Fe and Fe3B phases are also detected.
Experimental (black) and calculated X-ray diffraction patterns (red) of the L10 phase.
Right inset is a magnified graph at 2θ ranging from 20 to 30 degrees for the (001) super-lattice diffraction. Left inset demonstrates the atomic arrangements of the L10 phase with Fe (blue) and Ni (red) atoms drawn with lattice parameters of a = 3.560 and c = 3.615 Å.
The experimental X-ray diffraction pattern was fit to the L10 FeNi phase. The lattice constants, a and c, were evaluated to be 0.3560 and 0.3615 nm, respectively, which agree well with a natural meteorite (a = 0.3582 nm and c = 0.3607 nm)16. The intensity of the superlattice reflections is weak because Fe and Ni have similar atomic scattering factors. The calculated intensity of the (001) superlattice reflection is 0.3% of the (111) fundamental reflection, which is much lower than the experimentally observed value (~1.7%), suggesting that the ribbon has a texture in the out-of-plane direction i.e. c-axis.
Figure 2a shows a bright-field (BF) scanning transmission electron microscope (STEM) image of the Fe42Ni41.3Si8B4P4Cu0.7 alloy after annealing at 400 °C for 288 hours. The microstructure is composed of 30-50 nm sized polycrystalline grains. Elemental mapping by energy dispersive X-ray spectroscopy (EDX) using STEM reveals that these grains include at least three phases: an Fe-rich phase, a Ni-rich phase and a nearly equi-atomic Fe50Ni50 alloy phase (Fig. 2b). It should be mentioned that Si and P were detected in the Ni-rich grains, but not in the Fe-rich or FeNi grains. Detection of Fe3B phase by XRD indicates that B is distributed in Fe-rich phase. Areal fraction of these three phases are 40% (Ni-rich), 37% (Fe-rich) and 23% (Fe-Ni alloy). Thus, partitioning of the solute elements indicates that the Fe-rich grains correspond to the α-Fe and Fe3B phases as detected by the X-ray measurements (Fig. 1). The Ni-rich grains are fcc and the equi-atomic Fe50Ni50 regions are possibly made from L10 or fcc type of grains.
We obtained the nanobeam electron diffraction (NBD) patterns (probe size ~0.5 nm), which include, the superlattice reflections from an area within the equi-atomic FeNi alloy phase. Figure 2c,d show the [001]-zone NBD patterns obtained by scanning a grain marked by an encircled region in Fig. 2a,b. The existence of four-fold 110 superlattice reflections clearly indicates that the L10-type ordered phase is formed with the c-axis oriented normal to the specimen plane. This is consistent with the XRD measurements. Volume fraction of the L10 phase is roughly estimated to be ~8% based on the STEM-EDX elemental map together with NBD patterns by assuming a spatially random orientation of the c-axis. The long-range order (LRO) parameter (S) is approximately ~0.8 or above, which was estimated based on simulations of the NBD patterns as a function of LRO parameters. Surprisingly, this value is higher than that reported for natural meteorites (S = 0.608)16. It is possible that S is reduced due to heating of a natural meteorite surface upon entering the Earth’s atmosphere.
Figure 2e shows the simulated NBD pattern of the L10-FeNi structure with S = 0.8. Superlattice reflections are marked in red color. It should be mentioned that the polycrystalline nature may prevent frequent detection of the ordered structure; intensity of the superlattice reflection is sensitively degraded by misorientation from the exact zone axis. Additionally, the possible distribution of the degree of order cannot be detected; we found that the superlattice reflections are too weak and practically invisible in simulations when S is below 0.75. Regardless of the aforementioned effects, we have successfully detected the single crystal electron diffraction patterns as demonstrated in Fig. 2c,d. This is a strong experimental evidence for the L10 phase formation. Thus, the state-of-the-art electron imaging unveils the presence of the highly ordered L10 phase in annealed Fe42Ni41.3Si8B4P4Cu0.7 ribbons. Here, it is worth mentioning that such a high degree of chemical order and a clear presence of superlattice reflection for L10 FeNi have not been reported yet.
Figure 3a shows the temperature dependent magnetization curve for the Fe42Ni41.3Si8B4P4Cu0.7 alloy after annealing at 400 °C for 288 hours. There are two magnetic phases with Curie temperatures Tc1 ~ 500-550 °C and Tc2 ~ 700-750 °C. Based on our structural analysis and reported literature17,18, the Tc1 could be for L10 FeNi or Fe3B and Tc2 for α-Fe phases. Metalloid rich phases are believed to be non-magnetic at/above room temperature. Among all the magnetic phases present in the alloy, only L10 FeNi is hard magnetic. If it is so, the hysteresis curve can reveal the presence of soft and hard magnetic phases. Figure 3b shows the hysteresis curve measured by applying a maximum magnetic field of ~12,000 Oe perpendicular to the ribbon plane. The saturation magnetization (Ms) and coercivity are ~100 emu/g and 700 Oe, respectively. A rapid increase in the magnetization at a lower magnetic field and the linear variation at higher magnetic fields suggest two processes: (1) alignment of the out-of-plane magnetization at low fields by the domain wall motion and (2) rotation of the in-plane magnetization to the out-of-plane at higher fields. The second process can be easily understood based on the presence of soft magnetic phases (α Fe and Fe3B phases), which have magnetic easy axes in the ribbon plane.
Magnetic properties of Fe42Ni41.3Si8B4P4Cu0.7 alloy.
(a) Temperature dependent magnetization curve measured by applying a magnetic field of 5 kOe in out of plane, (b) Magnetic hysteresis (left: black) and dc demagnetization curves (right: red). Measurement conditions include applying a maximum magnetic field of ~12 kOe perpendicular to the ribbon plane for M Vs H curve and 10 kOe for Md(H) Vs H curve. Top inset shows the topographic AFM image, while the bottom inset is the corresponding magnetic force microscopy (MFM) image demonstrating the magnetic domains.
The magnetic easy axis of L10 FeNi is along the c-axis, which is perpendicular to the ribbon plane (due to texture). It seems the alignment of the out-of-plane magnetization at a lower field by the domain wall motion is due to the presence of hard magnetic L10 FeNi grains whose c-axis is along the field direction. Since the sample is polycrystalline, grains with mutually orthogonal c-axis ie. along [100] and [010] can contribute to linear increase in magnetization at higher fields (in addition to soft magnetic α-Fe and Fe3B phases). Such a linear increase in magnetization was also observed for the meteorites3,6. In the absence of a magnetic field, the magnetization of grains tends to remain along the easy axis of magnetization (i.e., out-of-plane for L10 FeNi and in-plane for the soft magnetic phases). Therefore, the remanent magnetization (Mr) in Fig. 3b is approximately due the L10 FeNi grains, but the Hc in the out-of-plane direction is strongly influenced by the rotation of the in-plane magnetization (higher the volume fraction of soft phase lower is the Hc)19. Low Mr (~10% of Ms) seems to be consistent with EDX elemental mapping, which suggest volume fraction of L10 phase is ~8%.
The magnetic reversal of L10 FeNi can be understood from the dc demagnetization remanent [Md(H)] curve (Fig. 3b). Basically, Md(H) is the remanent magnetization of the initially saturated L10 FeNi grains upon reversing the magnetic field. Figure 3b shows that a magnetic field of at least ~3.5 kOe is required to switch the magnetization of the L10 FeNi grains in the present alloy. It should be noted that the L10 FeNi grains oriented in other directions and strong demagnetizing effect resulting from high Ms of α-Fe grains can assist in magnetization switching at lower magnetic fields. We believe the magnetization switching field of the present L10 FeNi grains is higher than 3.5 kOe and it can increase further by increasing the volume fraction. Nevertheless, such a high switching field is consistent with the highly anisotropic nature of the L10 FeNi phase.
The magnetic domains were also imaged using magnetic force microscopy (MFM). A typical MFM image along with the surface topography is shown in the inset of Fig. 3b. To eliminate surface topography effects in the MFM image, the distance between the tip and the sample surface was varied from 25 nm to 100 nm. In all the cases, MFM images show the same features, suggesting that the image contrast mainly originates from the interaction of the magnetic tip with the out-of-plane magnetization of the sample. The magnetic domain patterns of the sample (shown in the inset of Fig. 3b) are similar to other hard magnetic nano-composites with soft and hard magnetic phases20,21. Both the structural and magnetic characterizations confirm that the highly ordered L10 FeNi phase is formed artificially in Fe42Ni41.3Si8B4P4Cu0.7 ribbon crystallized at 400 °C for 288 hours. Although, the annealing temperature (~400 °C) for formation of ordered phase is higher than the order-disorder transition temperature (320 °C), our measurements Fig. 3a show onset temperature for disordering is ~530 °C. The results obtained are very similar to NWA 6259 meteorite3,6.
Molecular dynamic (MD) simulations were performed to understand the phase stability (energy level). The Hamiltonians (H’s) for amorphous, bcc, fcc and L10 phases are –384.6, –393.3, –396.7 and –397.2 kJmol–1, respectively. According to H, the L10 phase is the most stable phase and the other phases are energetically destabilized in the sequence of bcc, fcc and amorphous. The G was also calculated for the amorphous (–20.9 kJmol–1), bcc (–24.6 kJmol–1) and fcc (–29.9 kJmol–1) phases based on the CALPHAD method. Although we were unable to evaluate G for the L10 phase, it is estimated to be –35 kJmol–1 by referring to more accurate calculations for the formation enthalpy of the L10 phase based on CALPHAD22 and ab initio methods23.
Figure 4 schematically diagrams the above thermodynamic results. The binary phase diagram of Fe–Ni Fig. 4a calculated using the widely accepted SSOL5 database demonstrates that Fe50Ni50 (at.%) is thermodynamically stable as a single fcc phase at T = 673 K (as drawn with both arrows). Analysis of G Fig. 4b also indicates a single fcc phase and Fe50Ni50 is the composition at the edge of the phase separation between bcc (Symbol E in Fig. 4b) and fcc (a composition close to Symbol C marked with open circle in Fig. 4b).
Calculated results and theoretical consideration for forming L10 from the amorphous and crystalline phases.
(a) FeNi phase diagram calculated with SSOL5 database. (b) Gibbs free energy curves at T = 673 K for liquid, bcc and fcc phases calculated with the SSOL5 database as functions of the Ni fraction together with G = –35 kJmol–1 for the L10 phase estimated from previous studies. (c) Characteristics of the phases of interest, including the driving force to precipitate L10 at T = 673 K. (d) Changes in Gibbs free energy (G) of fcc phase as a function of Si content in a hypothetical Fe50Ni50-Fe50−x/2Ni50−x/2Six system where G = –35 kJmol−1 was considered for L10 Fe50Ni50 phase. Based on lever rule (marked by red arrow), the volume fraction of the L10 phase is evaluated to be ~13% in Fe42Ni41.3Si8B4P4Cu0.7 alloy under an assumption that L10 FeNi phase precipitates from the fcc Fe45Ni45Si10, which is an equilibrium phase at T = 673 K in the alloy.
Thermodynamic analysis can be used to roughly estimate the volume fraction of L10 FeNi phase in Fe42Ni41.3Si8B4P4Cu0.7 alloy. Calculations were performed with Thermo-Calc by using TCFE7 database for Fe-based alloys and steels. As a result, the volume fraction of fcc Fe45Ni45Si10 phase, which is an equilibrium phase at T = 673 K in Fe42Ni41.3Si8B4P4Cu0.7 alloy is evaluated to be 77.6%. Probably L10 FeNi phase precipitates from fcc Fe45Ni45Si10. Therefore, by assuming G = –35 kJmol−1 for L10 Fe50Ni50 phase, we estimated the G for Fe50Ni50-Fe50−x/2Ni50−x/2Six system with different Si contents (Fig. 4d). Thermodynamically, it is possible to decompose Fe45Ni45Si10 into Fe50Ni50 and Fe88Ni88Si12. Based on lever rule (as indicated by red arrow in Fig. 4d), volume fraction of L10 FeNi phase was estimated as ~1/6th of 0.776 ie. ~13%. This is close to the experimental value of ~8 to 10%.
We believe that the formation of the ordered phase is due to simultaneously achieving three factors; 1. High diffusion rates of the constituent elements at lower temperatures when crystallizing from an amorphous phase, 2. A large driving force for precipitation of the L10 phase from the amorphous state and 3. Presence of compositional and structural fluctuations in the heterogeneous amorphous structure (similar to amorphous FeSiBPCu alloys14,15), which play a role of the nuclei (clusters) when forming the L10 phase.
Although, the volume fraction of L10 FeNi phase is low (8 ~ 13%), the hard magnetic L10 phase developed in the present study is both academically and industrially novel. First, the melt-spinning technique and low temperature annealing are able to produce the L10 FeNi phase at a much faster rate than the natural process (millions of years are required for meteorites). Second, the artificial L10 phase has a much higher chemical order than natural meteorites. Third, the non-equilibrium processing technique provides a new method to create a low temperature phase (such as L10 FeNi), which is difficult to obtain using conventional processing. Here, it is also important to mention that the quasicrystals were first formed through non-equilibrium processing technique only and later they were discovered even in meteorite24. Fourth, the present results shed light on hard magnetic materials, which have been stagnating since the discovery of rare-earth-based magnets almost 30 years ago. Fifth, thermodynamic analysis and non-equilibrium processing reported in this article should help in stimulating the research and development of new alloy systems with higher volume fractions of hard magnetic L10 FeNi grains. Sixth and most important, the realization of hard magnets free of rare-earth metals may help in resolving the global issues of resource exhaustion, which should become a critical in the near future. Hence, the successful synthesis of the chemically ordered L10 FeNi phase is one-step closer to the field of materials science for realizing a safe and sustainable society in the 21st century.
Methods
Experiments
Alloy ingots of Fe42Ni41.3SixB12–xP4Cu0.7 (x = 2 to 8 at.%) were made by high frequency melting. These alloy ingots were used to prepare ribbons via a single roller melt-spinning technique in air. Annealing was performed by sealing the ribbons in an Ar-gas filled silica tube, which was inserted in a furnace preheated to the required annealing temperature. A Rigaku (Smart Lab) X-ray diffractometer was used to identify the structure. Commercially available software (CrystalMaker) was used to fit the experimentally obtained X-ray diffraction curves. A vibrating sample magnetometer (VSM) was used to measure the saturation magnetization (Ms), coercivity (Hc) and dc demagnetization remanence [Md(H)] curves. To measure Md(H) in the out-of-plane direction, the ribbon sample was exposed to a positive magnetic field of 10,000 Oe, which was applied normal to the ribbon plane. The field was made to zero and a remanence magnetization was recorded. Then a small negative magnetic field was applied and then switch to zero and remanent magnetization was measured. Similar steps were repeated for the increasing negative magnetic field to obtain the Md(H) vs H curve. Some of the annealed ribbons were thinned by Ar ion milling for electron transparency. Microstructures of the specimens were characterized using a JEOL JEM-ARM200F scanning transmission electron microscope (STEM) operating at 200 kV with a CEOS aberration (Cs) corrector for the probe-forming lens and a cold field emission gun (cold-FEG). Nanobeam electron diffraction patterns were obtained by a scanning fine electron probe (probe size ~0.5 nm) with a beam convergence semi-angle of 3 mrad. Compositional analyses were carried out using an energy-dispersive X-ray spectrometer attached to the STEM. Specimen thickness was evaluated by electron energy-loss spectroscopy (EELS) in the STEM mode. The NBD patterns were simulated based on the Bloch wave calculation using the MacTempas software (Total Resolution LLC).
Simulations and calculations
Computational methodologies include molecular dynamics (MD) simulations and calculations of the phase diagrams and Gibbs free energy (G) based on equilibrium thermodynamics with targets of (a) amorphous, (b) bcc (body-centered cubic), (c) fcc (face-centered cubic) and (d) L10 phases using commercial software. The MD simulations were performed with Materials Explorer Version 5.0 (Fujitsu Production). For (a) amorphous, (c) fcc and (d) L10 phases, 4,000 atoms comprised of 2,000 Fe and 2,000 Ni atoms were dealt with in the MD simulations, which corresponds to 10 × 10 × 10 supercells in the conventional fcc lattice where four atoms are accommodated in the unit cell. On the other hand, 3,456 atoms in total were dealt with for (b) bcc phase, which corresponds to 12 × 12 × 12 supercells in the conventional bcc lattice with two atoms in the unit cell.
The following calculation conditions were applied to the MD simulations. The NTp ensemble was selected to keep the number of atoms (N), temperature (T) and pressure (p) constant, where p was set to atmospheric pressure (101.325 kPa). By an optimizing function in the software, the mass coefficient of a hypothetical heat bath in the Nosé scheme was initially determined to be 0.0643 for (a), (c) and (d) from the fcc supercell and 0.0529 for (b) from the bcc supercell. Un-distortable cubic lattices were used under GZ (GrujicicZhou)-type EAM (Embedded Atom Method) potentials with a cut-off distance of 1.02 nm (1.01 nm for (b)) and periodic boundary conditions. The aforementioned phases were created via the following procedure. (a) Amorphous phase was obtained by quenching at a cooling rate of 1015 K/s before and after holding the alloy for 2 ps at 1773 and 673 K, respectively. On the other hand, (b) bcc, (c) fcc and (d) L10 phases were created by holding the initial states at 673 K for 2 ps. During the common process at 673 K for 2 ps, we monitored the changes in parameters, such as T, p and lattice constants to avoid calculation errors (e.g., overshooting). Then each phase was further annealed at 673 K for 2 ps to evaluate the physical and thermodynamic values, such as density, lattice constants, as well as T, p and volume as the primary monitoring variables.
The thermodynamic calculations and investigations were performed based on approaches from CALPHAD (CALculation of PHAse Diagrams) and SGTE (Scientific Group Thermodata Europe)25. Specifically, we utilized commercial software, Thermo-Calc version 4.1 (Thermo-Calc Software AB), with the SSOL5 database for solid solutions as well as TCFE7 database for Fe-based alloys and steels equipped in the software under atmospheric pressure.
Additional Information
How to cite this article: Makino, A. et al. Artificially produced rare-earth free cosmic magnet. Sci. Rep. 5, 16627; doi: 10.1038/srep16627 (2015).
References
Goldstein, J. I. & Short, J. M. Cooling rates of 27 iron and stony-iron meteorites. Geochem. Cosmochim. Acta 31, 1001–1023 (1967).
Albertsen, J. F., Knudsen, J. M., Roy-Poulsen, N. O. & Vistisen, L. Meteorites and Thermodynamic Equilibrium in f.c.c. Iron-Nickel Alloys (25–50% Ni). Physica Scripta 22, 171–175 (1980).
Lewis, L. H. et al. De Magnete et Meteorite: Cosmically Motivated Materials. IEEE Magn. Lett. 5, 5500104 (2014).
Paulevé, J., Chamberod, A., Krebs, K. & Bourret, A. Magnetization Curves of Fe–Ni (50–50) Single Crystals Ordered by Neutron Irradiation with an Applied Magnetic Field. J. Appl. Phys. 39, 989–990 (1968).
Takayuki, K. et al. Addition of Co to L10 -ordered FeNi films: influences on magnetic properties and ordered structures. J. Phys. D: Appl. Phys. 47, 425001 (2014).
Lewis, L. H. et al. Inspired by nature: investigating tetrataenite for permanent magnet applications. J. Phys.: Condens. Matter 26, 064213 (2014).
Néel, L., Pauleve, J., Pauthenet, R., Laugier, J. & Dautreppe, D. Magnetic Properties of an Iron—Nickel Single Crystal Ordered by Neutron Bombardment. J. Appl. Phys. 35, 873–876 (1964).
Yang, C. W., Williams, D. B. & Goldstein, J. I. Low-temperature phase decomposition in metal from iron, stony-iron and stony meteorites. Geochem. Cosmochim. Acta 61, 2943–2956 (1997).
Geng, Y. et al. Defect generation and analysis in mechanically alloyed stoichiometric Fe–Ni alloys. J. Alloys Comp. 633, 250–255 (2015).
Shima, T., Okamura, M., Mitani, S. & Takanashi, K. Structure and magnetic properties for L10-ordered FeNi films prepared by alternate monatomic layer deposition. J. Magn. Magn. Mater. 310, 2213–2214 (2007).
Lee, S. et al. Formation of FeNi with L10-ordered structure using high-pressure torsion. Phil. Mag. Lett. 94, 639–646 (2014).
Suryanarayana, C. & Inoue, A. Iron-based bulk metallic glasses. Int. Mater. Rev. 58, 131–166 (2013).
Makino, A. Nanocrystalline Soft Magnetic Fe-Si-B-P-Cu Alloys With High B of 1.8–1.9 T Contributable to Energy Saving. IEEE Trans. Magn. 48, 1331–1335 (2012).
Makino, A., Men, H., Kubota, T., Yubuta, K. & Inoue, A. New Excellent Soft Magnetic FeSiBPCu Nanocrystallized Alloys With High Bs of 1.9 T From Nanohetero-Amorphous Phase. IEEE Trans. Magn. 45, 4302–4305 (2009).
Sharma, P., Zhang, X., Zhang, Y. & Makino, A. Competition driven nanocrystallization in high Bs and low coreloss Fe–Si–B–P–Cu soft magnetic alloys. Scripta Mater. 95, 3–6 (2015).
Kotsugi, M. et al. Structural, magnetic and electronic state characterization of L10-type ordered FeNi alloy extracted from a natural meteorite. J. Phys.: Condens. Matter 26, 064206 (2014).
Nakajima, T., Kita, E. & Ino, H. Crystallization process and magnetic properties of Fe100−xBx (10 ≦ × ≦ 35) amorphous alloys and supersaturated state of boron in α-Fe. J. Mater. Sci. 23, 1279–1288 (1988).
Passamani, E. C., Tagarro, J. R. B., Larica, C. & Fernandes, A. A. R. Thermal studies and magnetic properties of mechanical alloyed Fe2B. J. Phys.: Condens. Matter 14, 1975–1983 (2002).
Yaocen, W., Sharma, P. & Akihiro, M. Magnetization reversal in a preferred oriented (111) L10 FePt grown on a soft magnetic metallic glass for tilted magnetic recording. J. Phys.: Condens. Matter 24, 076004 (2012).
Yin, J.-h. et al. Magnetic properties and magnetic domain structure of Nd6Dy2Fe82Co4B6 nanocomposite magnets. J. Alloys Comp. 316, 296–298 (2001).
Sharma, P. et al. High coercivity characteristics of FePtB exchange-coupled nanocomposite thick film spring magnets produced by sputtering. Acta Mater. 55, 4203–4212 (2007).
Cacciamani, G., Dinsdale, A., Palumbo, M. & Pasturel, A. The Fe–Ni system: Thermodynamic modelling assisted by atomistic calculations. Intermetallics 18, 1148–1162 (2010).
Mishin, Y., Mehl, M. J. & Papaconstantopoulos, D. A. Phase stability in the Fe–Ni system: Investigation by first-principles calculations and atomistic simulations. Acta Mater. 53, 4029–4041 (2005).
Bindi, L., Steinhardt, P. J., Yao, N. & Lu, P. J. Natural Quasicrystals. Science 324, 1306–1309 (2009).
Dinsdale, A. T. Sgte Data for Pure Elements. Calphad 15, 317–425 (1991).
Acknowledgements
Part of the present study was supported by the “Tohoku Innovative Materials Technology Initiatives for Reconstruction (TIMT)” funded by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan and the Reconstruction Agency of Japan and a Grant-in-Aid for Challenging Exploratory Research (ID number of 30315642) from the Japan Society for the Promotion of Science (JSPS).
Author information
Authors and Affiliations
Contributions
A.M. oversaw the present study. Y.Z. fabricated the samples (master alloys and ribbons by melt-spinning) and carried out measurements (XRD, DSC, VSM) with K.T. under the direction of P.S. and A.M. P.S. was in charge of the analysis. K.S. carried out observations and structural analysis using TEM. A.T. performed the computational molecular dynamics simulations and thermodynamic calculations. All the authors (A.M., P.S., Y.Z., K.T., K.S. and A.T.) contributed to the discussion of the results. A.M., P.S., K.S. and A.T. wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Makino, A., Sharma, P., Sato, K. et al. Artificially produced rare-earth free cosmic magnet. Sci Rep 5, 16627 (2015). https://doi.org/10.1038/srep16627
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep16627
This article is cited by
-
Massive transformation in FeNi nanopowders with nanotwin-assisted nitridation
Scientific Reports (2022)
-
Allabogdanite, the high-pressure polymorph of (Fe,Ni)2P, a stishovite-grade indicator of impact processes in the Fe–Ni–P system
Scientific Reports (2019)
-
Synthesis of single-phase L10-FeNi magnet powder by nitrogen insertion and topotactic extraction
Scientific Reports (2017)
-
Self-anchored catalysts for substrate-free synthesis of metal-encapsulated carbon nano-onions and study of their magnetic properties
Nano Research (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.