Abstract
Relying on an exact time evolution scheme, we identify a novel transient energy transfer phenomenon in an exactly-solvable quantum microscopic model consisting of a three-level system coupled to two non-Markovian zero-temperature bosonic baths through two separable quantum channels. The dynamics of this model can be solved exactly using the quantum-state-diffusion equation formalism, demonstrating finite intervals of unidirectional energy flow across the system, typically, from the non-Markovian environment towards the more Markovian bath. Furthermore, when introducing a spatial asymmetry into the system, an analogue of the rectification effect is realized. In the long time limit, the dynamics arrives at a stationary state and the effects recede. Understanding temporal characteristics of directional energy flow will aid in designing microscopic energy transfer devices.
Similar content being viewed by others
Introduction
The analysis of simple-prototype quantum energy transfer problems1,2,3 assists in elucidating fundamental thermodynamic concepts in open quantum systems4. In the common construction, energy flow through a quantum system is generated by coupling it to two macroscopic objects, thermal reservoirs of different temperatures5,6. Alternatively, directional energy flow can be attained by supplying work into an asymmetric system7. Energy transfer problems are interesting for exploring the foundation of classical statistical mechanics, quantum dynamics and the crossover between the classical and quantum worlds8,9. For example, understanding the emergence of the Fourier’s law of heat conduction from the principles of open quantum systems is a long standing problem10,11,12,13,14. Moreover, achieving control over energy flow is of an enormous importance in many areas of science and technology, including energy management in functional nanoscale devices15,16,17,18, realization of information processing and computation in open quantum systems19,20, control over molecular reactivity and dynamics21 and refrigeration in metal-superconductor junctions22.
In microscopic devices, introducing a spatial asymmetry within an anharmonic structure can result in different magnitudes for the forward and backward currents, under the application of a reversed temperature bias23,24. This diode-like behavior had recently attracted considerable theoretical and experimental attention, including the demonstration of phononic25, electronic26,27,28,29 and photonic23,24,30,31,32,33,34,35 rectifications.
Given these developments, it is highly desirable to identify minimal conditions under which a diode-like behavior can be obtained, controlled and enhanced3,21. Studies of rectification and unidirectional energy flow in quantum devices2,3,16 were typically performed under certain-standard approximations (semiclassical operation, neglecting coherences in the subsystem, assuming a unique steady state), adopting quantum master equation approaches. Few works had considered design principles on exactly-solvable quantum models36. This problem is fundamentally important: Can we derive, from microscopic quantum theories, sufficient or necessary boundary conditions for realizing a certain nonlinear energy transport in atomic, molecular or a nanoscale system?
In this work, we aim at achieving unidirectional energy flow in an open quantum system. While our results correspond to a temporal behavior, they expose ingredients for asymmetric dissipation thus potentially, asymmetric nonlinear transport. We employ reservoirs with different (non-Markovian) spectral properties rather than with different temperatures. A structured-non-Markovian environment is characterized by the correlation timescale of its fluctuations37,38, while in a Markovian bath the memory time is shorter than any other characteristic timescale of the system of interest. The bath memory function dictates the manner in which information and energy flow from the system to the attached macroscopic bath and the back-action of the bath on the system. A finite memory time is crucial for achieving control over the state of an open quantum system (see, e.g.,39 and references therein). Essentially, there is nearly no revival of the system’s fidelity when it is attached to a memoryless Markovian bath (see, e.g.,40 and references therein). Therefore, if the system is coupled to two baths of different memory functions a unidirectional flow can emerge: energy is fed back from the non-Markovian bath to the system and simultaneously, the system is releasing its energy to the more Markovian bath.
We investigate the dynamics of our model by employing a nonperturbative master equation, derived from the quantum-state-diffusion (QSD) equation41,42,43,44 (see Method). We show that due to the assignment of distinct memory properties to the baths, a transient unidirectional energy flow develops in a prototype model for energy flow across a quantum open system. The model consists a three-level system45,46, one of the simplest realizations of quantum engines47 and two uncorrelated bosonic baths, bulk objects. Furthermore, we manifest that we can control the magnitude of the temporal energy flow by introducing a spatial asymmetry into the system, coupling it with different strengths to the contacts. This asymmetry grants an effect which can be categorized as a “transient diode effect”: the magnitude of the energy flow is different under forward and reversed operations, upon interchanging the channels connecting to the reservoirs.
Results
Unidirectional energy flow
To investigate the flow of energy in our system, purely induced by the distinct environmental memory functions, the two baths are assumed to be at zero temperature and the three-level system is assumed to be of a degenerate Λ-type, where the energy splitting between the high level  and the two lower levels,
and the two lower levels,  and
and  , is set as ω. The setup is shown in Fig. 1, where the energy current across the system is determined by the two energy flows between the system and the two baths. We use the following form for the correlation functions of the two baths,
, is set as ω. The setup is shown in Fig. 1, where the energy current across the system is determined by the two energy flows between the system and the two baths. We use the following form for the correlation functions of the two baths,  , with j = 1, 2, where Γj is the coupling strength of the system to the jth bath. This form corresponds to a Lorenz spectrum. When γj → 0, the jth bath is eminently non-Markovian with long memory time as desired. On average, the dissipation rate of the system to the jth bath is greatly suppressed with decreasing γj41,42. In contrast, when γj → ∞, the jth bath is memoryless. In this case, energy flow from the system to the bath is fully irreversible. Therefore, 1/γj could be used to measure the environmental memory time.
, with j = 1, 2, where Γj is the coupling strength of the system to the jth bath. This form corresponds to a Lorenz spectrum. When γj → 0, the jth bath is eminently non-Markovian with long memory time as desired. On average, the dissipation rate of the system to the jth bath is greatly suppressed with decreasing γj41,42. In contrast, when γj → ∞, the jth bath is memoryless. In this case, energy flow from the system to the bath is fully irreversible. Therefore, 1/γj could be used to measure the environmental memory time.
As our initial condition, we only excite state-3, ρ33(t = 0) = 1. We demonstrate now the transient energy transfer behavior in the system when α1(t, s) ≠ α2(t, s), before reaching the stationary long time solution ρ33 = 0. In Fig. 2 we use γ1 = 0.2ω and γ2 = 10ω and show that initially energy is released into both baths simultaneously. However, around ωt = 2.2 the system begins to absorb energy from bath-1. As presented in Method, energy flow then becomes unidirectional, directed from the left reservoir (bath-1) towards the right side (bath-2), i.e.,  and
and  . We end our simulation when ρ33 becomes extremely small and ρ11 and ρ22 reach the stationary states. The region of this unidirectional flow is embedded within a green-dashed frame.
. We end our simulation when ρ33 becomes extremely small and ρ11 and ρ22 reach the stationary states. The region of this unidirectional flow is embedded within a green-dashed frame.
The dynamics can be made more involved if both reservoirs are highly non-Markovian. In Fig. 3 we use γ1 = 0.2ω and γ2 = 1.0ω, resulting in multiple-alternating regions of bi-directional and unidirectional energy flow. Particularly, we observe three intervals (distinguished by the green-dashed frames) of unidirectional flow of energy, of nearly the same duration yet shrinking amplitude, before full relaxation of the excited state is reached. As expected, the directional flow takes place from the reservoir with longer memory time, to the side with shorter memory time, since at zero-temperature a completely Markovian bath can only absorb energy. The comparison of Figs 2 and 3 also reveals that, as expected, in the latter case the total evolution time towards the stationary solution is longer than in the first case.
A finite difference between the memory parameters,  , is a necessary yet insufficient condition for the emergence of unidirectional flow of energy. This is shown in Fig. 4, where we display the time duration of unidirectional flow in the first interval. Note that energy is flowing in opposite directions (R → L or L → R) in the regions below and above the diagonal in Fig. 4. Recall that in Fig. 3 we show that there may be more than one occurrence of unidirectional transfer in the overall dynamics. We find that to observe the effect, it is necessary to employ a reservoir with a long memory time, for example, γ1/ω < 0.5 and a second reservoir with a shorter memory time,
, is a necessary yet insufficient condition for the emergence of unidirectional flow of energy. This is shown in Fig. 4, where we display the time duration of unidirectional flow in the first interval. Note that energy is flowing in opposite directions (R → L or L → R) in the regions below and above the diagonal in Fig. 4. Recall that in Fig. 3 we show that there may be more than one occurrence of unidirectional transfer in the overall dynamics. We find that to observe the effect, it is necessary to employ a reservoir with a long memory time, for example, γ1/ω < 0.5 and a second reservoir with a shorter memory time,  .
.
Diode-like phenomenon
So far, we have demonstrated that within a certain time interval energy may flow in a unidirectional manner only due to differences in the memory capabilities of the two reservoirs. In Figs 2, 3 and 4, we used Γ1 = Γ2 and it is obvious that the direction and magnitude of the flow will be fully reversed upon the interchange of the quantum channels indicated by L1 and L2, which is equivalent to an interchange in the values γ1 and γ2. However, distinct memory times can not induce a diode-like phenomenon, an asymmetry in the magnitude of the unidirectional energy flow under opposite “polarities”, as we explain next.
We now show that the dynamics may be furthermore controlled by including an asymmetry in the coupling strengths of the three-level system to the baths, Γ1 ≠ Γ2. The resulting behavior corresponds to the thermal diode effect, see Figs 5 and 6. We consider the following two setups: (i) a “forward” configuration with γ1 > γ2 and Γ1 < Γ2; (ii) a reversed geometry, in which we exchange the values of the memory times but keep the interaction energy as in (i), thus γ1 < γ2 and Γj’s hold. We emphasize that the condition γ1 ≠ γ2 allows a unidirectional flow of energy and the spatial asymmetry  , provides the transient diode effect, yielding different magnitudes for energy flow in setups (i) and (ii).
, provides the transient diode effect, yielding different magnitudes for energy flow in setups (i) and (ii).
We first examine geometry (i) in Fig. 5. We use γ1/ω = 5 > γ2/ω = 0.2 and Γ1 = Γ2/2. Energy flows unidirectionally towards the more Markovian bath-1, as we found before, during the so called “diode-like behavior interval” 2.5 < ωt < 5. In geometry (ii) we employ γ2/ω = 5 > γ1/ω = 0.2 while keeping Γ1 = Γ2/2. Energy now flows (during almost the same interval) towards bath-2. In geometry (ii) the ratio of the energy flow towards the more Markovian bath of γ = 5ω is larger than in case (i), given the stronger coupling to this bath. It is interesting to note that when we modify Γ we largely affect the flow of energy into the more Markovian bath, as compared to changes in flow to the highly non-Markovian bath. We could explain this phenomenon by noting that Γ, the coupling strength of the system to the reservoirs, is the only parameter which determines the rate of energy flow to a Markovian bath. In contrast, the effectiveness of flow to a non-Markovian reservoir is predominated by the memory time of the bath, characterizing how effective it is in dissipating excess energy.
The duration of the diode-like behavior is plotted in Fig. 6 as a function of γ1 and γ1 − γ2. The calculation is performed on a configuration similar to geometry (i) with γ1 taken always larger than γ2, providing a unidirectional flow from bath-2 to bath-1. We find that the interval of the diode effect (considering the first interval) is highly sensitive to the memory time of the non-Markovian bath, while the difference γ2 − γ1 has a weaker overall effect. It is shown that a long diode-effect time is attainable when  ; the overall duration of the diode effect is fixed once
; the overall duration of the diode effect is fixed once  .
.
Discussion
We considered an exactly solvable model with two dissipation channels directed towards two reservoirs. We demonstrated that when adopting non-Markovian baths with different memory properties, the transient energy flow can become unidirectional, typically flowing from the highly non-Markovian to the more Markovian bath. This is the case as long as  is larger than a certain threshold. Our analysis departs from the regular thermodynamic setup in which energy flow is driven by a temperature gradient across the system, to consider zero-temperature situations with non-Markovian baths. Moreover, we showed that the magnitude of the energy flow can be controlled to achieve an effect reminiscent of the diode phenomenon, by coupling the system to two contacts with different strengths. In conclusion, a sufficiently large difference in
is larger than a certain threshold. Our analysis departs from the regular thermodynamic setup in which energy flow is driven by a temperature gradient across the system, to consider zero-temperature situations with non-Markovian baths. Moreover, we showed that the magnitude of the energy flow can be controlled to achieve an effect reminiscent of the diode phenomenon, by coupling the system to two contacts with different strengths. In conclusion, a sufficiently large difference in  yields the effect of transient unidirectional energy flow; a sufficiently large difference in
yields the effect of transient unidirectional energy flow; a sufficiently large difference in  , with the additional condition of an asymmetrical coupling strengths between system and baths, results in a diode-like phenomenon.
, with the additional condition of an asymmetrical coupling strengths between system and baths, results in a diode-like phenomenon.
Our 3-level system could be realized in the triplet ground electronic state of a nitrogen vacancy (NV) center48,49,50, when ω is regarded as the zero field splitting. Transitions from the lower degenerate levels to the upper state can be selectively addressed via optical fields51. Besides optical relaxation, one of the two channels could be realized through the vibrations of the diamond lattice and the atoms comprising the NV center point defect. In this case, the photonic field would serve as the strong non-Markovian bath while the phononic environment would act as the more Markovian one.
Transient unidirectional flow of energy can be achieved in open quantum systems prepared in a non-stationary state, when coupled to two different structured environments. This behavior, obtained in our work by a microscopic quantum model without further assumptions and approximations, can be exploited for estimating the relative memory capabilities and non-Markovianity of competing baths, for constructing nonlinear quantum devices for the transport of energy and for controlling unidirectional energy transfer and potentially reactivity, in molecules52. Finally, the principles governing the dynamics of the present system at zero-temperature could be employed for exploring the dynamics of a finite-temperature, driven three-level system, to study the combined role of anharmonicity, non-Markovianity, driving and asymmetry on energy transport phenomena53,54.
Method
The system takes a Λ-type configuration, with one excited state  and two degenerate lower levels,
and two degenerate lower levels,  and
and  . The excited state may decay to either of these lower levels and these dissipation processes (referred as “channels”) are directed by two different baths55. The baths are set at zero-temperature. The total Hamiltonian
. The excited state may decay to either of these lower levels and these dissipation processes (referred as “channels”) are directed by two different baths55. The baths are set at zero-temperature. The total Hamiltonian  is given by
is given by

Here, ω is the energy splitting between the upper level and the lower two states. The system-environment coupling operators are represented by  , where j = 1, 2. They open up energy transfer channels of the system into the jth bath.
, where j = 1, 2. They open up energy transfer channels of the system into the jth bath.  (ajk) is the creation (annihilation) operator for independent mode-k in the jth bath,
(ajk) is the creation (annihilation) operator for independent mode-k in the jth bath,  stands for the coupling constant between the system operator Lj and the kth mode in the reservoirs. In our design unidirectional-transient flow is achieved by utilizing reservoirs with different two-time correlation functions αj(t, s), defined below Eq. (2). Furthermore, when Γ1 ≠ Γ2, a process analogous to thermal rectification can be realized.
stands for the coupling constant between the system operator Lj and the kth mode in the reservoirs. In our design unidirectional-transient flow is achieved by utilizing reservoirs with different two-time correlation functions αj(t, s), defined below Eq. (2). Furthermore, when Γ1 ≠ Γ2, a process analogous to thermal rectification can be realized.
The wavefunction  denoted the solution to the Schrödinger equation with the total Hamiltonian (1) in the interaction picture with respect to
denoted the solution to the Schrödinger equation with the total Hamiltonian (1) in the interaction picture with respect to  . We define
. We define  where
where  stands for the tensor product of the Bargmann coherent states for the environment modes. The exact QSD equation41,42, for the stochastic wave-function
stands for the tensor product of the Bargmann coherent states for the environment modes. The exact QSD equation41,42, for the stochastic wave-function  , is given as
, is given as

Here  are correlated processes, describing the stochastic influence of the jth bath.
are correlated processes, describing the stochastic influence of the jth bath.  are individual Gaussian-distributed complex random variables, whose ensemble average is defined as
are individual Gaussian-distributed complex random variables, whose ensemble average is defined as  . (In our model, the two dissipation channels correspond to different bath operators thus cross correlations of the form
. (In our model, the two dissipation channels correspond to different bath operators thus cross correlations of the form  are missing. The case in which all dissipation channels couple to the same bath is considered in ref. 55.) The operator
are missing. The case in which all dissipation channels couple to the same bath is considered in ref. 55.) The operator  includes the effect of the jth bath on the system dynamics. The function
includes the effect of the jth bath on the system dynamics. The function  satisfies
satisfies

with fj(t) = 1 and j = 1, 2. The corresponding exact master equation for the reduced density matrix  can be constructed via the Novikov theorem56,
can be constructed via the Novikov theorem56,

Equation (4) immediately yields the solution of time-dependent populations of the three levels,

where  . Since the system is prepared in its excited state, ρ33(0) = 1 and
. Since the system is prepared in its excited state, ρ33(0) = 1 and  , the time-dependent energy current, defined positive when flowing from the system towards bath-1 and bath-2, is given by
, the time-dependent energy current, defined positive when flowing from the system towards bath-1 and bath-2, is given by  and
and  , respectively, where
, respectively, where  stands for real part. These expressions identify the current as the population relaxation rate times the energy difference for the transition. For example, state-3 decays to state-1 by giving up energy through channel-1 to bath-1. Population decays from level-3 to level-1 thus directly relates to the amount of energy flowing from the system to the attached bath. The transitory energy transfer can therefore be measured by the real part of dimensionless coefficients Fj(t), j = 1, 2, without invoking confusion, before ρ33 vanishes.
stands for real part. These expressions identify the current as the population relaxation rate times the energy difference for the transition. For example, state-3 decays to state-1 by giving up energy through channel-1 to bath-1. Population decays from level-3 to level-1 thus directly relates to the amount of energy flowing from the system to the attached bath. The transitory energy transfer can therefore be measured by the real part of dimensionless coefficients Fj(t), j = 1, 2, without invoking confusion, before ρ33 vanishes.
Placing bath-1 (2) at the left (right) side of the system, we now identify different transport situations: (A) when  and
and  , the three-level system is releasing energy to both sides; (B) the system is releasing energy to the left while absorbing energy from the right side when
, the three-level system is releasing energy to both sides; (B) the system is releasing energy to the left while absorbing energy from the right side when  and
and  ; (C) energy flows towards the right bath in the opposite scenario,
; (C) energy flows towards the right bath in the opposite scenario,  and
and  ; (D) the system is absorbing energy from both reservoirs at the same time if
; (D) the system is absorbing energy from both reservoirs at the same time if  and
and  . Manifesting the development of scenarios (B) and (C), with a (transient) unidirectional energy flow as indicated by
. Manifesting the development of scenarios (B) and (C), with a (transient) unidirectional energy flow as indicated by  , is the objective of our work. If the memory functions have the same spectral form,
, is the objective of our work. If the memory functions have the same spectral form,  , then
, then  from Eq. (3). As a result,
from Eq. (3). As a result,  and
and  acquire the same sign at all times, thus a unidirectional energy flow across the system cannot be realized, even when Γ1 ≠ Γ2. Evidently, to achieve our goal we should employ reservoirs with distinct memory properties.
acquire the same sign at all times, thus a unidirectional energy flow across the system cannot be realized, even when Γ1 ≠ Γ2. Evidently, to achieve our goal we should employ reservoirs with distinct memory properties.
Additional Information
How to cite this article: Jing, J. et al. Transient unidirectional energy flow and diode-like phenomenon induced by non-Markovian environments. Sci. Rep. 5, 15332; doi: 10.1038/srep15332 (2015).
References
Gemmer, J., Michel, M. & Mahler, G. Quantum Thermodynamics, Springer: Berlin Heidelberg, (2009).
Segal, D. & Nitzan, A. Heat rectification in molecular junctions, J. Chem. Phys 122, 194704 (2005).
Wu, L.-A. & Segal, D. Sufficient conditions for thermal rectification in hybrid quantum structures, Phys. Rev. Lett. 102, 095503 (2009).
Blencowe, M. Quantum electromechanical systems, Phys. Rep. 395, 159 (2004).
Rego, L. G. C. & Kirczenow, G. Quantized thermal conductance of dielectric quantum wires, Phys. Rev. Lett. 81, 232 (1998).
Schwab, K., Henriksen, E. A., Worlock, J. M. & Roukes, M. L. Measurement of the quantum of thermal conductance, Nature 404, 974 (2000).
Gong, J., Poletti, D. & Hänggi, P. Dissipationless directed transport in rocked single-band quantum dynamics, Phys. Rev. A 75, 033602 (2007).
Zurek, W. H. Decoherence and the transition from quantum to classical, Phys. Today 44(10), 36 (1991).
Briggs, J. S. & Eisfeld, A. Equivalence of quantum and classical coherence in electronic energy transfer, Phys. Rev. E 83, 051911 (2011).
Michel, M., Mahler, G. & Gemmer, J. Fourier’s law from Schrödinger dynamics, Phys. Rev. Lett. 95, 180602 (2005).
Steinigeweg, R., Breuer, H.-P. & Gemmer, J. Transition from diffusive to ballistic dynamics for a class of finite quantum models, Phys. Rev. Lett. 99, 150601 (2007).
Wu, L.-A. & Segal, D. Fourier’s law of heat conduction: Quantum mechanical master equation analysis, Phys. Rev. E 77, 060101(R) (2008).
Wu, L.-A. & Segal, D. Heat flux operator, current conservation and the formal Fourier’s law, J. Phys. A 42, 025302 (2009).
Martinez, E. A. & Paz, J. P. Dynamics and thermodynamics of linear quantum open systems, Phys. Rev. Lett. 110, 130406 (2013).
Segal, D. & Nitzan, A. Molecular heat pump, Phys. Rev. E 73, 026109 (2006).
Segal, D. Heat flow in nonlinear molecular junctions: Master equation analysis, Phys. Rev. B 73, 205415 (2006).
Chen, T., Wang, X.-B. & Ren, J. Dynamic control of quantum geometric heat flux in a nonequilibrium spin-boson model, Phys. Rev. B 87, 144303 (2013).
Cahill, D. G. et al. L. Nanoscale thermal transport II: 2003-2012, App. Phys. Rev. 1, 011305 (2014).
Wang, L. & Li, B. Thermal logic gates: Computation with phonons, Phys. Rev. Lett. 99, 177208 (2007).
Liu, Z. & Li, B. Heat conduction in simple networks: The effect of interchain coupling, Phys. Rev. E 76, 051118 (2007).
Uzer, T. & Miller, W. H. Theories of intramolecular vibrational energy transfer, Phys. Rep. 199, 73 (1991).
Boukobza, E. & Tannor, D. J. Thermodynamics of bipartite systems: Application to light-matter interactions, Phys. Rev. A 74, 063823 (2006).
Terraneo, M., Peyrard, M. & Casati, G. Controlling the energy flow in nonlinear lattices: A model for a thermal rectifier, Phys. Rev. Lett. 88, 094302 (2002).
Li, B., Wang, L. & Casati, G. Thermal diode: Rectification of heat flux, Phys. Rev. Lett. 93, 184301 (2004).
Chang, C. W., Okawa, D., Majumdar, A. & Zettl, A. Solid-state thermal rectifier, Science 314, 1121 (2006).
Scheibner, R. et al. Quantum dot as thermal rectifier, New J. Phys. 10, 083016 (2008).
Kobayashi, W., Teraoka, Y. & Terasaki, I. An oxide thermal rectifier, Appl. Phys. Lett. 95, 171905 (2009).
Giazotto, F. & Bergeret, F. S. Thermal rectification of electrons in hybrid normal metal-superconductor nanojunctions, Appl. Phys. Lett. 103, 242602 (2013).
Martinez-Pérez, M. J., Fornieri, A. & Giazotto, F. Rectification of electronic heat current by a hybrid thermal diode, Nat. Nanotechnol. 10, 303 (2015).
Ben-Abdallah, P. & Biehs, S.-A. Near-field thermal transistor, Phys. Rev. Lett. 112, 044301 (2014).
Hu, M., Keblinski, P. & Li, B. Thermal rectification at silicon-amorphous polyethylene interface, Appl. Phys. Lett. 92, 211908 (2008).
Yang, N., Zhang, G. & Li, B. Thermal rectification in asymmetric graphene ribbons, Appl. Phys. Lett. 95, 033107 (2009).
Hu, J., Ruan, X. & Chen, Y. P. Thermal conductivity and thermal rectification in graphene nanoribbons: A molecular dynamics study, Nano Lett. 9, 2730 (2009).
Wang, Y. et al. Phonon lateral confinement enables thermal rectification in asymmetric single-material nanostructures, Nano Lett. 14, 592 (2014).
Roberts, N. A. & Walker, D. G. A review of thermal rectification observations and models in solid materials, Int. J. Therm. Sci. 50, 648 (2011).
Davies, E. B. A model of heat conduction, J. Stat. Phys. 18, 161 (1978).
Chruściński, D., Kossakowski, A. & Rivas, Á. Measures of non-Markovianity: Divisibility versus backflow of information, Phys. Rev. A 83, 052128 (2011).
Clos, G. & Breuer, H.-P. Quantification of memory effects in the spin-boson model, Phys. Rev. A 86, 012115 (2012).
Jing, J., Bishop, C. A. & Wu, L.-A. Nonperturbative dynamical decoupling with random control, Sci. Rep. 4, 6229 (2014).
Jing, J. & Wu, L.-A. Overview of quantum memory protection and adiabaticity induction by fast signal control, Sci. Bull. 60, 328 (2015).
Diósi, L. & Strunz, W. T. The non-Markovian stochastic Schrödinger equation for open systems, Phys. Lett. A 235, 569 (1997).
Diósi, L., Gisin, N. & Strunz, W. T. Non-Markovian quantum state diffusion, Phys. Rev. A 58, 1699 (1998).
Strunz, W. T., Diósi, L. & Gisin, N. Open system dynamics with non-Markovian quantum trajectories, Phys. Rev. Lett. 82, 1801 (1999).
Jing, J. & Yu, T. Non-Markovian relaxation of a three-level system: Quantum trajectory approach, Phys. Rev. Lett. 105, 240403 (2010).
Rau, A. R. P. & Zhao, W. Time-dependent treatment of a general three-level system, Phys. Rev. A 71, 063822 (2005).
Uskov, D. & Rau, A. R. P. Geometric phases and Bloch-sphere constructions for SU(N) groups with a complete description of the SU(4) group, Phys. Rev. A 78, 022331 (2008).
de Galway, W. O. & Naudts, J. Energy transfer using unitary transformations, Entropy 15, 5121 (2013).
Hanson, R., Dobrovitski, V. V., Feiguin, A. E., Gywat, O. & Awschalom, D. D. Coherent dynamics of a single spin interacting with an adjustable spin bath, Science 320, 352 (2008).
Fuchs, G. D., Dobrovitski, V. V., Toyli, D. M., Heremans, F. J. & Awschalom, D. D. Gigahertz dynamics of a strongly driven single quantum spin, Science 326, 1520 (2009).
Rabl, P. et al. Strong magnetic coupling between an electronic spin qubit and a mechanical resonator, Phys. Rev. B 79, 041302(R) (2009).
Jelezko, F. et al. Single spin states in a defect center resolved by optical spectroscopy. Appl. Phys. Lett. 81, 2160 (2002).
Pein, B. C., Sun, Y. & Dlott, D. D. Unidirectional vibrational energy flow in nitrobenzene, J. Phys. Chem. A. 117, 6066 (2013).
Chen, P.-W., Jian, C.-C. & Goan, H.-S. Non-Markovian dynamics of a nanomechanical resonator measured by a quantum point contact, Phys. Rev. B 83, 115439 (2011).
Cresti, A., Ortmann, F., Louvet, T., Van Tuan, D. & Roche, S. Broken symmetries, zero-energy modes and quantum transport in disordered graphene: From supermetallic to insulating regimes, Phys. Rev. Lett. 110, 196601 (2013).
Broadbent, C. J., Jing, J., Yu, T. & Eberly, J. H. Solving non-Markovian open quantum systems with multi-channel reservoir coupling, Ann. Phys. 327, 1962 (2012).
Yu, T., Diósi, L., Gisin, N. & Strunz, W. T. Non-Markovian quantum-state diffusion: Perturbation approach, Phys. Rev. A 60, 91 (1999).
Acknowledgements
We acknowledge grant support from the Basque Country University UFI (Project No. 11/55-01-2013), the Basque Government (grant IT472-10), the Spanish MICINN (No. FIS2012-36673-C03-03), the NSFC No. 11175110 and Science and Technology Development Program of Jilin Province of China (20150519021JH). DS acknowledges support from an NSERC discovery grant and the Canada Research Chair Program. BWL acknowledges support from the Ministry of Education, Singapore, by Grant No. MOE2012-T2-1-114.
Author information
Authors and Affiliations
Contributions
J.J. performed numerical simulations, analyzed results and prepared figures. L.-A.W. contributed to the conception and development of the research problem. All authors (J.J., D.S., B.L. and L.A.W.) discussed the results and physical implications and wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Jing, J., Segal, D., Li, B. et al. Transient unidirectional energy flow and diode-like phenomenon induced by non-Markovian environments. Sci Rep 5, 15332 (2015). https://doi.org/10.1038/srep15332
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep15332
This article is cited by
-
A diatomic elastic metamaterial for tunable asymmetric wave transmission in multiple frequency bands
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

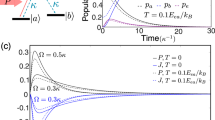


 with Γ1 = Γ2, γ1 = 0.2ω and γ2 = 10ω.
with Γ1 = Γ2, γ1 = 0.2ω and γ2 = 10ω.
 with Γ1 = Γ2, γ1 = 0.2ω and γ2 = ω.
with Γ1 = Γ2, γ1 = 0.2ω and γ2 = ω.

