Abstract
Bootstrap percolation is a general representation of some networked activation process, which has found applications in explaining many important social phenomena, such as the propagation of information. Inspired by some recent findings on spatial structure of online social networks, here we study bootstrap percolation on undirected spatial networks, with the probability density function of long-range links’ lengths being a power law with tunable exponent. Setting the size of the giant active component as the order parameter, we find a parameter-dependent critical value for the power-law exponent, above which there is a double phase transition, mixed of a second-order phase transition and a hybrid phase transition with two varying critical points, otherwise there is only a second-order phase transition. We further find a parameter-independent critical value around −1, about which the two critical points for the double phase transition are almost constant. To our surprise, this critical value −1 is just equal or very close to the values of many real online social networks, including LiveJournal, HP Labs email network, Belgian mobile phone network, etc. This work helps us in better understanding the self-organization of spatial structure of online social networks, in terms of the effective function for information spreading.
Similar content being viewed by others
Introduction
Bootstrap percolation was originally introduced by Chalupa, Leath and Reich1 in the context of magnetic disordered systems in 1979. Since then, it has been studied extensively by physicists and sociologists, mainly due to its connections with various physical models and a variety of applications such as neuronal activity2 and jamming transitions3. Bootstrap percolation can be essentially considered as an activation process on networks: (i) Nodes are either active or inactive; (ii) Once activated, a node remains active forever; (iii) Initially, each node is in an active state with a given probability p; (iv) Subsequently, inactive nodes become active if they have at least k active neighbors; (v) Nodes are activated in an iterative manner according to the condition in (iv), until no more nodes can be activated. This process has been investigated on different kinds of networks including lattices4,5, trees6,7, random networks8,9,10,11 and so on.
Bootstrap percolation has found applications in explaining many important social phenomena, such as the spreading of information12, the propagation of infection13,14, the adoption of new products and social behaviors15,16,17,18 including trends, fads, political opinions, belief, rumors, innovations and financial decisions. For instance, in emergence of cultural fads and adoption of new technology or objects, an individual can be positively influenced when there is a sufficient number of its close friends who have also done so19. In other words, one may decide to buy a product when recommended by at least k users and trust a message when told by at least k neighbors; cf. the well-known rule, “What I tell you three times is true”20. In this way, the process leads initially localized effects propagating throughout the whole network. Moreover, a broad range of generalized formulations of bootstrap percolation on social networks are investigated, such as Watts’ model of opinions21, in which k is replaced by a certain fraction of the neighbors and disease transmission models with different degrees of severity of infection22.
Real networks are often embedded in space23 and social networks are no exception. Previous empirical studies of online social networks24, email networks25 and mobile phone communication networks26 have confirmed a spatial scaling law, namely, the probability density function (PDF) of an individual to have a friend at distance r scales as  ,
,  27. In fact, prior to these empirical observations, Kleinberg28 has proposed a spatial network model by adding long-range links to a 2-dimensional lattice and he has proved that when
27. In fact, prior to these empirical observations, Kleinberg28 has proposed a spatial network model by adding long-range links to a 2-dimensional lattice and he has proved that when  , the structure is optimal for navigation. Recently, Hu et al.27 suggested the optimization of information collection as a possible explanation for the origin of this spatial scaling law.
, the structure is optimal for navigation. Recently, Hu et al.27 suggested the optimization of information collection as a possible explanation for the origin of this spatial scaling law.
Extensive studies have shown that the spatial organization can change the dimension29,30,31,32,33, which dominates many important physical properties of networks34,35,36,37,38,39,40,41. Moukarzel et al.42 studied k-core percolation on long-range spatial networks, which is built by taking a 2-dimensional lattice and adding to each node one or more long-range links. In the networks, the probability density function (PDF) of long-range links with length r scales as  . By numerical simulation, they found that the 3-core transition is of first-order for α > −1.75 (it is equivalent to the scaling of 2.75 found by Moukarzel et al.42) and of second-order for smaller α. In fact, k-core percolation has close relation to bootstrap percolation43,44, nevertheless the two processes have different features from each other, being strongly dependent on the network structure8,45. Although there is a deeper understanding of percolation processes and spatial networks now, how spatial organization influences the spreading process on social networks under the framework of bootstrap percolation remains further investigation.
. By numerical simulation, they found that the 3-core transition is of first-order for α > −1.75 (it is equivalent to the scaling of 2.75 found by Moukarzel et al.42) and of second-order for smaller α. In fact, k-core percolation has close relation to bootstrap percolation43,44, nevertheless the two processes have different features from each other, being strongly dependent on the network structure8,45. Although there is a deeper understanding of percolation processes and spatial networks now, how spatial organization influences the spreading process on social networks under the framework of bootstrap percolation remains further investigation.
In this paper, we numerically study bootstrap percolation on undirected Kleinberg’s spatial networks, which is a typical artificial social network. Setting the relative size of the giant active component to the network size as the order parameter, we find that the distribution of long-range links’ lengths can change the order of phase transition. In particular, our main findings are as follows: (i) We find a parameter-dependent critical value αc, above which a double phase transition46 is observed. Here, the so-called double phase transition means a mixture of two transitions at different critical points, consisting of a hybrid phase transition and a second-order one. In this paper, we use the hybrid phase transition to indicate a first-order phase transition in which the order parameter has a discontinuous jump between two non-zero values. (ii) Surprisingly, we find a parameter-independent critical value  , about which the two critical points for the double phase transition are almost constant. (iii) When
, about which the two critical points for the double phase transition are almost constant. (iii) When  , the first-order critical point decreases and the second-order critical point increases as α decreases. When α < αc, there is only a second-order phase transition with an increasing critical point as the decreasing of α. Furthermore, we test the universality of our findings by drawing the phase diagram and give a possible explanation of the rich phase transition phenomena by simulating on related networks. Our findings indicate that the spatial scaling
, the first-order critical point decreases and the second-order critical point increases as α decreases. When α < αc, there is only a second-order phase transition with an increasing critical point as the decreasing of α. Furthermore, we test the universality of our findings by drawing the phase diagram and give a possible explanation of the rich phase transition phenomena by simulating on related networks. Our findings indicate that the spatial scaling  , observed in real social networks, may be resulted from some deep-going principles in addition to the optimization of navigation and information collection, which is not yet fully understood now.
, observed in real social networks, may be resulted from some deep-going principles in addition to the optimization of navigation and information collection, which is not yet fully understood now.
Results
Kleinberg model28 is a typical spatial network model, which has been well justified by empirical data24,25,26. Here, the undirected Kleinberg’s spatial network is constrained on a 2-dimensional periodic square lattice consisting of N = L × L nodes. In addition to its initially connected four nearest neighbors, each node i has a random long-range link to a node j with probability  , where α is a tunable exponent and rij denotes the Manhattan distance, which quantifies the length of the shortest path between node i and node j, following strictly the horizontal and/or vertical links in lattices. Since the number of nodes at distance r to a given node is proportional to rd−1 in a d-dimensional lattice, the probability Q(rij) can be mapped to a probability density function (PDF),
, where α is a tunable exponent and rij denotes the Manhattan distance, which quantifies the length of the shortest path between node i and node j, following strictly the horizontal and/or vertical links in lattices. Since the number of nodes at distance r to a given node is proportional to rd−1 in a d-dimensional lattice, the probability Q(rij) can be mapped to a probability density function (PDF),  . In the present 2-dimensional case, where d = 2, the probability density function(PDF) scales as
. In the present 2-dimensional case, where d = 2, the probability density function(PDF) scales as  . An illustration of a 2-dimensional undirected Kleinberg’s spatial network can be found in Fig. 1.
. An illustration of a 2-dimensional undirected Kleinberg’s spatial network can be found in Fig. 1.
Illustration of the undirected Kleinberg’s spatial network constrained on a 2-dimensional periodic square lattice.
Each node has four short-range links (colored blue for node i) and one long-range link (colored black). The probability density function (PDF) of a node to have a long-range link at Manhattan distance r scales as  . For the target node i (colored red), when r = 2, there are eight candidate nodes (colored green), from which we can choose an uncoupled node j to make a connection. For another target node u, we can choose to connect it with node v when r = 3.
. For the target node i (colored red), when r = 2, there are eight candidate nodes (colored green), from which we can choose an uncoupled node j to make a connection. For another target node u, we can choose to connect it with node v when r = 3.
In the following, we focus on three indicators: (i) The relative size of the giant active component (Sgc) at the equilibrium, i.e., the probability that an randomly selected node belongs to the giant active component; (ii) The number of iterations (NOI) to reach the equilibrium, which is usually used to determine the critical point for the first-order phase transition47,48; (iii) The relative size of the second giant active component (Sgc2), which is usually used to determine the critical point for the second-order phase transition32,48.
Figure 2 shows rich phase transition phenomena when taking Sgc as the order parameter. When α ≥ −1, the curves of Sgc(p) are well overlapped and the system undergoes a double phase transition, mixed of a hybrid phase transition and a second-order one as shown in Fig. 2a. Notice that Sgc has a continuous increase at  (the second-order critical point), where the transition is of second-order. In contrast, Sgc has an abrupt jump directly from around 0.58 to almost 1 at
(the second-order critical point), where the transition is of second-order. In contrast, Sgc has an abrupt jump directly from around 0.58 to almost 1 at  (the first-order critical point), where there is a hybrid phase transition. Surprisingly, the two critical points seem to be constant when
(the first-order critical point), where there is a hybrid phase transition. Surprisingly, the two critical points seem to be constant when  , as indicated by the four overlapped Sgc(p) curves in Fig. 2a. When α < −1, there is only a second-order phase transition with an increasing pc2 as the decreasing of α (see Fig. 2b). Specifically,
, as indicated by the four overlapped Sgc(p) curves in Fig. 2a. When α < −1, there is only a second-order phase transition with an increasing pc2 as the decreasing of α (see Fig. 2b). Specifically,  when α = −2 and
when α = −2 and  when α = −5. Although Sgc goes up sharper after p exceeds pc2 as α getting smaller, simulations justify that the curve of Sgc(p) is still continuous, meaning that the transition is indeed of second-order when α < −1.
when α = −5. Although Sgc goes up sharper after p exceeds pc2 as α getting smaller, simulations justify that the curve of Sgc(p) is still continuous, meaning that the transition is indeed of second-order when α < −1.
Sgc, NOI and Sgc2 as a function of p for different α after k = 3 bootstrap percolation on undirected Kleinberg’s spatial networks.
Two different types of Sgc(p) curves are observed, including a double phase transition (a) and a second-order one (b). When α ≥ −1, Sgc(p) curves behave alike and a double phase transition is present. Sgc abruptly jumps to 1 at  , where NOI reaches its maximum (c). When α < −1, there is only a second-order phase transition with an increasing critical point as the decreasing of α, where Sgc2 reaches its maximum at different pc2 (d). Dash lines mark identification of critical points. Results are obtained by simulations on networks with fixed size L = 400 and averaged over 1000 realizations.
, where NOI reaches its maximum (c). When α < −1, there is only a second-order phase transition with an increasing critical point as the decreasing of α, where Sgc2 reaches its maximum at different pc2 (d). Dash lines mark identification of critical points. Results are obtained by simulations on networks with fixed size L = 400 and averaged over 1000 realizations.
Finding critical points via simulations is always a difficult task that requires high precision. When α ≥ −1, where a part of the double phase transition is a hybrid phase transition, we can determine the critical point pc1 by calculating the number of iterations (NOI) in the cascading process, since NOI sharply increases when p approaches pc1 for the first-order phase transitions47,48. Accordingly, pc1 is calculated by plotting NOI as a function of p. As shown in Fig. 2c, NOI reaches its maximum at the same p when α ≥ −1, which is the evidence that  is almost a constant value. Analogously, by plotting Sgc2 as a function of p, we can precisely identify pc232,48, at which Sgc2 reaches its maximum (see Fig. 2d). We can see that pc2 increases as α decreases, as
is almost a constant value. Analogously, by plotting Sgc2 as a function of p, we can precisely identify pc232,48, at which Sgc2 reaches its maximum (see Fig. 2d). We can see that pc2 increases as α decreases, as  (α ≥ −1), 0.176 (α = −2) and 0.256 (α = −5).
(α ≥ −1), 0.176 (α = −2) and 0.256 (α = −5).
Although to justify the hybrid phase transition and to determine the critical value αc by simulations in a finite discrete system are not easy, we solve this problem by a cross-validation on the critical point pc1 and the critical value αc. Firstly, we fix α = −1 to determine pc1. On the one hand, there is an intersection for curves of Sgc(p) at  under different network sizes as shown in Fig. 3a, which can be considered as the critical point according to the finite-size analysis48. On the other hand, the corresponding NOI reaches its maximum at
under different network sizes as shown in Fig. 3a, which can be considered as the critical point according to the finite-size analysis48. On the other hand, the corresponding NOI reaches its maximum at  when L = 800 as shown in Fig. 3b. Combining these two observations, a more appropriate critical point is identified as the average value
when L = 800 as shown in Fig. 3b. Combining these two observations, a more appropriate critical point is identified as the average value  . Conversely, we fix p = 0.263 to determine αc. From Fig. 3c, we can see that Sgc has two phases: about 0.58 or close to 1 when
. Conversely, we fix p = 0.263 to determine αc. From Fig. 3c, we can see that Sgc has two phases: about 0.58 or close to 1 when  , which is a strong evidence that Sgc undergoes a hybrid phase transition. If the increasing of Sgc is continuous, there is no such gap between the two phases. From Fig. 3d, we note that the corresponding averaging NOI reaches its maximum at
, which is a strong evidence that Sgc undergoes a hybrid phase transition. If the increasing of Sgc is continuous, there is no such gap between the two phases. From Fig. 3d, we note that the corresponding averaging NOI reaches its maximum at  . Combining these two evidences, we appropriately identify the critical value as the average value
. Combining these two evidences, we appropriately identify the critical value as the average value  .
.
Cross-validation of pc1 and αc.
(a,b) are for Sgc and NOI under different network size L when α = −1, respectively. There is an intersection of Sgc(p) at  , while NOI reaches its maximum at
, while NOI reaches its maximum at  when L = 800. Thus, pc1 is identified as the average value 0.263. (c,d) are for Sgc and NOI when p = 0.263 under different α, respectively. For
when L = 800. Thus, pc1 is identified as the average value 0.263. (c,d) are for Sgc and NOI when p = 0.263 under different α, respectively. For  , Sgc has two phases and NOI reaches its maximum at
, Sgc has two phases and NOI reaches its maximum at  . Thus, αc is identified as the average value −1. In (c,d), dark curves respectively represent the average values of Sgc and NOI, obtained from 1000 realizations and each data point stands for one realization.
. Thus, αc is identified as the average value −1. In (c,d), dark curves respectively represent the average values of Sgc and NOI, obtained from 1000 realizations and each data point stands for one realization.
In addition, pc1 for the hybrid phase transition should be almost constant when α ≥ αc, otherwise we cannot observe the separation of two phases in Fig. 3c for a fixed value p = 0.263. To verify that, we estimate errors of pc1 by varying α under fixed network size L. As shown in Fig. 4a, pc1 slightly decreases when α approaches the critical value  . Even though, when α is in the range [−1,4], the difference between maximum and minimum value of pc1 is only 0.0008 after over 1000 realizations, which is very small compared to the whole range of p (i.e. [0,1]), indicating that the value of pc1 is not sensitive to the parameter α when α ≥ −1. Based on these evidences, pc1 can be roughly considered as a constant and its value is about 0.2634, which is the mean value of pc1 when α in the range [−1,4]. Furthermore, taking α = −1 as an example, we consider the effects of finite-size of networks on these results. As shown in Fig. 4b, the mean value of pc1 gradually approaches an extreme value around 0.263 and the standard deviation of pc1 decreases as L goes to infinity. Similar results hold for the analysis of the critical point pc2 and its value is also almost constant as 0.134.
. Even though, when α is in the range [−1,4], the difference between maximum and minimum value of pc1 is only 0.0008 after over 1000 realizations, which is very small compared to the whole range of p (i.e. [0,1]), indicating that the value of pc1 is not sensitive to the parameter α when α ≥ −1. Based on these evidences, pc1 can be roughly considered as a constant and its value is about 0.2634, which is the mean value of pc1 when α in the range [−1,4]. Furthermore, taking α = −1 as an example, we consider the effects of finite-size of networks on these results. As shown in Fig. 4b, the mean value of pc1 gradually approaches an extreme value around 0.263 and the standard deviation of pc1 decreases as L goes to infinity. Similar results hold for the analysis of the critical point pc2 and its value is also almost constant as 0.134.
Error estimation and effects of finite-size.
(a) Error estimation of pc1 with fixed network size L = 800. As α approaches the critical value −1, pc1 slightly decreases, but being kept in a very narrow range. When α is in range [−1,4], the mean value of pc1 is 0.2634 and the difference between maximum and minimum value of pc1 is 0.0008. (b) Analysis on the effects of finite-size. The data point and the error bar are respectively mean value and standard deviation of the identified pc1 in the case of α = −1 under different network sizes L. As L goes to infinity (from the right side to the left side in (b)), the mean value of pc1 gradually approaches an extreme value around 0.263 and the standard deviation of the pc1 decreases. Results are obtained by averaging over 1000 realizations.
A representative phase diagram for Sgc in the p − α plane is shown in Fig. 5. We find that the varying of α, which dominates the distribution of long-range links’ lengths, can change the order of phase transition. Overall,  is confirmed to be a critical value, above which a double phase transition (region II) is present. When α ≥ −1, the curves of Sgc(p) are overlapped, suggesting that the properties of bootstrap percolation on these spatial networks are alike. When α < −1, the hybrid phase transition vanishes and Sgc only undergoes a second-order phase transition (region I) with an increasing critical point as the decreasing of α. The maximum of pc2 is about 0.259, which is obtained when
is confirmed to be a critical value, above which a double phase transition (region II) is present. When α ≥ −1, the curves of Sgc(p) are overlapped, suggesting that the properties of bootstrap percolation on these spatial networks are alike. When α < −1, the hybrid phase transition vanishes and Sgc only undergoes a second-order phase transition (region I) with an increasing critical point as the decreasing of α. The maximum of pc2 is about 0.259, which is obtained when  , i.e., all long-range links’ lengths are 2.
, i.e., all long-range links’ lengths are 2.
Phase diagram of k = 3 bootstrap percolation in the p − α plane.
The color marks the value of Sgc. Dashed lines with solid squares and circles represent pc1 and pc2, respectively. Separated by α = −1, a double phase transition is observed in the right region II with two almost constant critical points  and
and  . In the left region I, only a second-order phase transition is present with an increasing critical point as α decreases. The critical point is up to
. In the left region I, only a second-order phase transition is present with an increasing critical point as α decreases. The critical point is up to  , which is obtained in the case of all long-range links’ lengths are 2. Results are averaged over 1000 realizations with fixed network size L = 400.
, which is obtained in the case of all long-range links’ lengths are 2. Results are averaged over 1000 realizations with fixed network size L = 400.
To test the universality of the findings, we simulated on undirected Kleinberg’s spatial networks in parameter spaces (k, α, kl) and determined the critical points. Results are shown in Fig. 6. According to the relationship between the threshold k and half of the average degree of the network  , where
, where  , there are three regions in the phase diagram:
, there are three regions in the phase diagram:
-
When k is remarkably smaller than
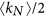 , e.g, k = 1 compared to
, e.g, k = 1 compared to  , there is only a trivial first-order phase transition at
, there is only a trivial first-order phase transition at  .
. -
When k is around
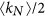 , e.g., k = 3 compared to
, e.g., k = 3 compared to  , there is a critical value αc, above which a double phase transition is observed. The value of αc depends on the choice of both k and kl. In particular,
, there is a critical value αc, above which a double phase transition is observed. The value of αc depends on the choice of both k and kl. In particular,  is found to be a parameter-independent critical value, about which the two critical points for the double phase transition are almost constant. Specifically, as shown in the phase diagram of Fig. 6, the color of data points for the same parameter k is nearly unchanged when α ≥ −1, which is a strong evidence that the values of pc1 and pc2 are almost constant. When
is found to be a parameter-independent critical value, about which the two critical points for the double phase transition are almost constant. Specifically, as shown in the phase diagram of Fig. 6, the color of data points for the same parameter k is nearly unchanged when α ≥ −1, which is a strong evidence that the values of pc1 and pc2 are almost constant. When 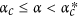 , pc1 decreases and pc2 increases as α decreases. Note that αc can be equal to
, pc1 decreases and pc2 increases as α decreases. Note that αc can be equal to 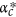 in some parameter spaces, such as
in some parameter spaces, such as 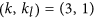 and
and 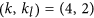 .
. -
When k is remarkably larger than
 , e.g, k = 5 compared to
, e.g, k = 5 compared to 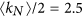 , the hybrid phase transition is absent and Sgc only undergoes a second-order phase transition with an increasing pc2 as the decreasing of α (see Supplementary Figs S1-S3 for the detailed shapes of Sgc(p) curves).
, the hybrid phase transition is absent and Sgc only undergoes a second-order phase transition with an increasing pc2 as the decreasing of α (see Supplementary Figs S1-S3 for the detailed shapes of Sgc(p) curves).
Phase diagram of bootstrap percolation on undirected Kleinberg’s spatial networks in parameter spaces (k, α, kl).
The color of data points in (a–c) marks the value of pc1, where there is a hybrid phase transition (or a first-order phase transition in the trivial cases where  and the color of data points in (d–f) marks the value of pc2, where the transition is of second-order. Blank areas stand for the absent of the corresponding phase transitions. Separated by the vertical dash line α = −1, on the right side, the color of data points is nearly unchanged for the same parameter k, meaning that the values of pc1 and pc2 are almost invariant.
and the color of data points in (d–f) marks the value of pc2, where the transition is of second-order. Blank areas stand for the absent of the corresponding phase transitions. Separated by the vertical dash line α = −1, on the right side, the color of data points is nearly unchanged for the same parameter k, meaning that the values of pc1 and pc2 are almost invariant.  is found to be a parameter-independent critical value, above which the critical points for the double phase transition are almost constant. When
is found to be a parameter-independent critical value, above which the critical points for the double phase transition are almost constant. When  , pc1 decreases and pc2 increases as α decreases. When α < αc, pc2 increases as α decreases. Results are averaged over 1000 realizations with fixed network size L = 400.
, pc1 decreases and pc2 increases as α decreases. When α < αc, pc2 increases as α decreases. Results are averaged over 1000 realizations with fixed network size L = 400.
Moreover, simulations confirm that our main results also hold for Kleinberg’s spatial networks with directed long-range links since  is still a critical value. However, there is only a first-order phase transition with pc1 being almost constant instead of the formal double transition when α ≥ −1 (see Supplementary Fig. S4). In addition, simulations on undirected Kleinberg’s spatial networks without periodic boundary conditions suggest that whether the square lattice has periodic boundary conditions does not essentially affect our main results (see Supplementary Fig. S5).
is still a critical value. However, there is only a first-order phase transition with pc1 being almost constant instead of the formal double transition when α ≥ −1 (see Supplementary Fig. S4). In addition, simulations on undirected Kleinberg’s spatial networks without periodic boundary conditions suggest that whether the square lattice has periodic boundary conditions does not essentially affect our main results (see Supplementary Fig. S5).
To provide the insights on the mechanism of the transition, we simulate on different networks and compare with other related transitions. These networks include a simple 2-dimensional lattice (Lattice), networks with all 5 links being long-range (LR) and networks without spatial structure, i.e. random 5-regular networks (RR). In the LR network, which is a special case of long-range percolation model in the 2-dimensional space49,50,51, each node is associated with only kl = 5 undirected long-range links instead of initially connected short-range links based on a 2-dimensional periodic lattice. As shown in Fig. 7, the curves of Sgc(p) on the spatial networks are between the ones on Lattice network and RR network. When α = −4, the Sgc(p) curve on the spatial network has similar trend with the one on Lattice network since the very long-range links are rare and the transition is of second-order. When α ≥ −1, there is a double phase transition and the curves of Sgc(p) are almost overlapped with the one on RR network. These observations indicate that, to turn the value of α, we can change the bootstrap percolation properties of spatial networks from Lattice network to RR network, or vice versa. More specifically, when α = −4, all long-range links are highly localized and the structure of spatial networks is similar to Lattice network, whereas when α ≥ −1, mainly due to the existence of very long-range links, the spatial networks behave like RR network.
Sgc as a function of P after k = 3 bootstrap percolation on different networks, including Lattice, LR, RR and the present spatial networks with different α.
When α = −4, the curve of Sgc(p) on the spatial network behaves like the one on Lattice network and the transition is of second-order. As α increases, the transition turns into a double phase transition when α ≥ −1, where the curves of Sgc(p) are almost overlapped with the ones on LR network and RR network. The parameter for LR network is set as α = −1. Results are averaged over 1000 realizations with fixed network size L = 400.
Together, it should be noted that the Sgc(p) curve on LR network when α = −1 acts like the ones on RR network and spatial networks when α ≥ −1. To better understand how does α affect the transition on LR network, taking kl = 5 as an example, we show the phase diagram after k = 3 bootstrap percolation in Fig. 8. The diagram is divided into three regions by critical values  and
and  . As α decreases, the transition is of second-order with an increasing pc2 when
. As α decreases, the transition is of second-order with an increasing pc2 when  (region I). There is a double phase transition when
(region I). There is a double phase transition when  (region II), where pc1 decreases and pc2 increases as α decreases. Once again, a double phase transition with two almost constant critical points,
(region II), where pc1 decreases and pc2 increases as α decreases. Once again, a double phase transition with two almost constant critical points,  and
and  , is observed when
, is observed when  (region III). Further simulations suggest that similar main results also hold under other combinations of k and kl (see Supplementary Fig. S6 for the phase diagram and Supplementary Figs S7–S11 for the shapes of Sgc(p) curves).
(region III). Further simulations suggest that similar main results also hold under other combinations of k and kl (see Supplementary Fig. S6 for the phase diagram and Supplementary Figs S7–S11 for the shapes of Sgc(p) curves).
Phase diagram of k = 3 bootstrap percolation in the p − α plane on LR networks with kl = 5.
The color marks the value of Sgc. When α decreases, the transition is of second-order with an increasing pc2 in the region I where α < −2. When α decreases, a double phase transition is observed in the region II where −2 ≤ α < −1, with a decreasing pc1 for the hybrid phase transition and an increasing pc2 for the second-order phase transition. In the region III where α ≥ −1, the double phase transition has two almost constant critical points, pc1 = 0.278 and pc2 = 0.111. Results are averaged over 1000 realizations with fixed network size L = 400.
In fact, for the original Kleinberg’s spatial networks with directed long-range links, Sen et al.52 found that the varying of α can change the network structure, namely, the network is regular-lattice-like when α < −2, small-world-like when −2 < α < −1 and random-like when α >−1. More recent studies30,31,32 also proposed three regimes: (i) When α > −1, the dimension of the spatial network is  and the percolation transition belongs to the university class of percolation in Erdös-Rényi networks. (ii) When
and the percolation transition belongs to the university class of percolation in Erdös-Rényi networks. (ii) When  , d decreases continuously from
, d decreases continuously from  to d = 2 and the percolation shows new intermediate behavior. (iii) When α < −3, the dimension is d = 2 and the percolation transition belongs to the university class of percolation in regular lattices. These previous findings suggest that the properties of spatial networks have qualitative changes when α is around −1, which is corresponding to the observation of these phase transition phenomena here.
to d = 2 and the percolation shows new intermediate behavior. (iii) When α < −3, the dimension is d = 2 and the percolation transition belongs to the university class of percolation in regular lattices. These previous findings suggest that the properties of spatial networks have qualitative changes when α is around −1, which is corresponding to the observation of these phase transition phenomena here.
Discussion
In summary, we have studied bootstrap percolation on spatial networks, where the distribution patterns of long-range links’ lengths can change the order of phase transition. In particular, we find a parameter-dependent critical value αc, above which a double phase transition, mixed of a hybrid phase transition at a higher p and a second-order phase transition at a lower p, is present. It is particularly interesting that we find a almost parameter-independent critical value  , about which the curves of Sgc(p) are well overlapped, indicating that the two critical points for the double phase transition are almost constant when α ≥ −1. As bootstrap percolation has not been studied yet on undirected Kleinberg’s spatial networks, our novel findings indicate that the topological properties of undirected Kleinberg’s spatial networks are alike when α ≥ −1 in the 2-dimensional space. In fact, the scaling law
, about which the curves of Sgc(p) are well overlapped, indicating that the two critical points for the double phase transition are almost constant when α ≥ −1. As bootstrap percolation has not been studied yet on undirected Kleinberg’s spatial networks, our novel findings indicate that the topological properties of undirected Kleinberg’s spatial networks are alike when α ≥ −1 in the 2-dimensional space. In fact, the scaling law  has been empirically observed in many real networks24,25,26, which may be resulted from complex self-organizing processes toward optimal structures for information collection27 and/or navigation28. Since the cascading processes on spatial networks are almost the same when α ≥ −1,
has been empirically observed in many real networks24,25,26, which may be resulted from complex self-organizing processes toward optimal structures for information collection27 and/or navigation28. Since the cascading processes on spatial networks are almost the same when α ≥ −1,  is indeed corresponding to the structure with the smallest average geographical length of links, which can exhibit as effective spreading of information as networks with even longer shortcut links. This is to some extent relevant to the principle of least effort in human behavior53.
is indeed corresponding to the structure with the smallest average geographical length of links, which can exhibit as effective spreading of information as networks with even longer shortcut links. This is to some extent relevant to the principle of least effort in human behavior53.
We find the varying of α can change the bootstrap percolation critical behavior from random regular networks to lattices, or vice versa. In particular, when  , the spatial networks behave like random regular networks and there is a double phase transition. When
, the spatial networks behave like random regular networks and there is a double phase transition. When  , there is a richer phase transition phenomena. More specifically, the double phase transition is still present when
, there is a richer phase transition phenomena. More specifically, the double phase transition is still present when  , however, instead of being constant, the first-order critical point decreases and the second-order critical point increases as α decreases. The observation of such results may be mainly due to the small-world-like network structure52,54, which leads the transition showing a intermediate behavior. When α < αc, the hybrid phase transition vanishes and there is only a second-order phase transition with an increasing critical point as the decreasing of α. When α goes to negative infinity, where all long-range links are highly localized, the spatial networks degenerates into regular lattices and the transition is of second-order. In this way, we give a possible explanation of the emergence of these phase transition phenomena.
, however, instead of being constant, the first-order critical point decreases and the second-order critical point increases as α decreases. The observation of such results may be mainly due to the small-world-like network structure52,54, which leads the transition showing a intermediate behavior. When α < αc, the hybrid phase transition vanishes and there is only a second-order phase transition with an increasing critical point as the decreasing of α. When α goes to negative infinity, where all long-range links are highly localized, the spatial networks degenerates into regular lattices and the transition is of second-order. In this way, we give a possible explanation of the emergence of these phase transition phenomena.
Moreover, our results are, to some extent, relevant to the control of information spreading. For example, when α ≥ αc, if we would like to make as many people as possible to know the information, the optimal choice of the fraction of initially informed people should be pc1, since larger initially informed population provides no more benefit but requires higher cost as shown in Fig. 2a. Therefore, the results help us in better understanding the self-organization of spatial structure of online social networks, in terms of the effective function for information spreading. Besides, our work can possibly find applications in studying the diffusion of virus spread in other spatial networks such as ad hoc, wireless sensor networks and epidemiological graphs. However, in the context of a numerical study, it is really hard to tell whether the critical value  is exactly −1 and whether the critical points are completely independent of α when
is exactly −1 and whether the critical points are completely independent of α when  . In addition, how does the transition depend on the spreading processes and what kind of transitions does it belong to for real social networks are still open questions. Hence, we expect to verify our findings in an analytical way and based on other generalized network models, including spatially constrained Erdös-Rényi networks55, network of networks (NON)56, multiplex networks57 and real social networks. Besides, to assign each node one long-range link is a high-cost strategy when generating artificial spatial social networks, we leave individualized number of long-range links associated with each node and partial spatial embedding as future works.
. In addition, how does the transition depend on the spreading processes and what kind of transitions does it belong to for real social networks are still open questions. Hence, we expect to verify our findings in an analytical way and based on other generalized network models, including spatially constrained Erdös-Rényi networks55, network of networks (NON)56, multiplex networks57 and real social networks. Besides, to assign each node one long-range link is a high-cost strategy when generating artificial spatial social networks, we leave individualized number of long-range links associated with each node and partial spatial embedding as future works.
Methods
To numerically implement the spatial scaling α when generating Kleinberg’s spatial networks, we add undirected long-range links to a 2-dimensional periodic square lattice in a smart way as follows. First, a random length r between 2 and L/2 is generated with probability  , which ensures the scaling in advance. Second, random segmentations of length r to Δx and Δy with the only constraint that
, which ensures the scaling in advance. Second, random segmentations of length r to Δx and Δy with the only constraint that  are done to determine candidate nodes, where Δx and Δy are both integers. Namely, for an uncoupled node i with coordinates (x, y), named target node, all candidate nodes are these with coordinates (x + Δx, y + Δy) such that
are done to determine candidate nodes, where Δx and Δy are both integers. Namely, for an uncoupled node i with coordinates (x, y), named target node, all candidate nodes are these with coordinates (x + Δx, y + Δy) such that  . The above procedure ensures all candidate nodes at distance r from the target node i are uniformly distributed. Hence, we can randomly choose an uncoupled candidate node (i.e., a node without any long-range link) to link with target node i. Be noted that, on a large system, a finite fraction of the nodes will have all candidate nodes already connected when α is very small. To deal with this problem, we additionally adopt an alternate procedure referring to the distance coarse graining procedure58, in which we randomly choose an uncoupled nearest neighbor node of these candidate nodes until the linking is accomplished. We repeat such procedure for the rest uncoupled nodes until each node of the network has one undirected long-range link such that the degree of each node is exactly 5.
. The above procedure ensures all candidate nodes at distance r from the target node i are uniformly distributed. Hence, we can randomly choose an uncoupled candidate node (i.e., a node without any long-range link) to link with target node i. Be noted that, on a large system, a finite fraction of the nodes will have all candidate nodes already connected when α is very small. To deal with this problem, we additionally adopt an alternate procedure referring to the distance coarse graining procedure58, in which we randomly choose an uncoupled nearest neighbor node of these candidate nodes until the linking is accomplished. We repeat such procedure for the rest uncoupled nodes until each node of the network has one undirected long-range link such that the degree of each node is exactly 5.
Additional Information
How to cite this article: Gao, J. et al. Bootstrap percolation on spatial networks. Sci. Rep. 5, 14662; doi: 10.1038/srep14662 (2015).
References
Chalupa, J., Leath, P. L. & Reich, G. R. Bootstrap percolation on a Bethe lattice. J. Phys. C: Solid State Phys. 12, L31 (1979).
Soriano, J., Martínez, M. R., Tlusty, T. & Moses, E. Development of input connections in neural cultures. Proc. Natl. Acad. Sci. USA 105, 13758–13763 (2008).
De Gregorio, P., Lawlor, A., Bradley, P. & Dawson, K. A. Exact solution of a jamming transition: Closed equations for a bootstrap percolation problem. Proc. Natl. Acad. Sci. USA 102, 5669–5673 (2005).
Kogut, P. M. & Leath, P. L. Bootstrap percolation transitions on real lattices. J. Phys. C: Solid State Phys. 14, 3187–3194 (1981).
Gravner, J., Holroyd, A. & Morris, R. A sharper threshold for bootstrap percolation in two dimensions. Probab. Theory Relat. Fields 153, 1–23 (2012).
Biskup, M. & Schonmann, R. Metastable behavior for bootstrap percolation on regular trees. J. Stat. Phys. 136, 667–676 (2009).
Bollobás, B., Gunderson, K., Holmgren, C., Janson, S. & Przykucki, M. Bootstrap percolation on Galton-Watson trees. Electron. J. Probab. 19, 1–27 (2014).
Baxter, G. J., Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Bootstrap percolation on complex networks. Phys. Rev. E 82, 011103 (2010).
Balogh, J. & Pittel, B. G. Bootstrap percolation on the random regular graph. Random Struct. Algorithms 30, 257–286 (2007).
Amini, H. & Fountoulakis, N. Bootstrap percolation in power-law random graphs. J. Stat. Phys. 155, 72–92 (2014).
Wu, C. et al. Multiple hybrid phase transition: Bootstrap percolation on complex networks with communities. Europhys. Lett. 107, 48001 (2014).
Shrestha, M. & Moore, C. Message-passing approach for threshold models of behavior in networks. Phys. Rev. E 89, 022805 (2014).
Bizhani, G., Paczuski, M. & Grassberger, P. Discontinuous percolation transitions in epidemic processes, surface depinning in random media and Hamiltonian random graphs. Phys. Rev. E 86, 011128 (2012).
Cui, P., Tang, M. & Wu, Z. X. Message spreading in networks with stickiness and persistence: Large clustering does not always facilitate large-scale diffusion. Sci. Rep. 4, 06303 (2014).
Ree, S. Effects of long-range links on metastable states in a dynamic interaction network. Phys. Rev. E 85, 045101(R) (2012).
Centola, D. The spread of behavior in an online social network experiment. Science 329, 1194–1197 (2010).
Lü, L., Chen, D. B. & Zhou, T. The small world yields the most effective information spreading. New J. Phys. 13, 123005 (2011).
Chen, Y. Z., Huang, Z. G. & Lai, Y. C. Controlling extreme events on complex networks. Sci. Rep. 4, 06121 (2014).
Bradonjić, M. & Saniee, I. Bootstrap percolation on random geometric graphs. in Proc. of the 10th Workshop on Analytic Algorithmics and Combinatorics (ANALCO) 18–24, New Orleans, Louisiana, USA (2013).
Carroll, L. The Hunting of the Snark (Macmillan, London, 1876).
Watts, D. J. A simple model of global cascades on random networks. Proc. Natl. Acad. Sci. USA 99, 5766–5771 (2002).
Ball, F. & Britton, T. An epidemic model with infector and exposure dependent severity. Math. Biosci. 218 105–120 (2009).
Barthélemy, M. Spatial networks. Phys. Rep. 499, 1–101 (2011).
Liben-Nowell, D., Novak, J., Kumar, R., Raghavan, P. & Tomkins, A. Geographic routing in social networks. Proc. Natl. Acad. Sci. USA 102 11623–11628 (2005).
Adamic, L. & Adar, E. How to search a social network. Soc. Networks 27, 187–203 (2005).
Lambiotte, R. et al. Geographical dispersal of mobile communication networks. Physica A 387, 5317–5325 (2008).
Hu, Y., Wang, Y., Li, D., Havlin, S. & Di, Z. Possible origin of efficient navigation in small worlds. Phys. Rev. Lett. 106, 108701 (2011).
Kleinberg, J. M. Navigation in a small world. Nature 406, 845 (2000).
Gao, J., Buldyrev, S. V., Stanley, H. E. & Havlin, S. Networks formed from interdependent networks. Nat. Phys. 8, 40–48 (2012).
Emmerich, T., Bunde, A., Havlin, S., Li, G. & Li, D. Complex networks embedded in space: Dimension and scaling relations between mass, topological distance and Euclidean distance. Phys. Rev. E 87, 032802 (2013).
Kosmidis, K., Havlin, S. & Bunde, A. Structural properties of spatially embedded networks. Europhys. Lett. 82, 48005 (2008).
Li, D. et al. Percolation of spatially constraint networks. Europhys. Lett. 93, 68004 (2011).
Li, D., Kosmidis, K., Bunde, A. & Havlin, S. Dimension of spatially embedded networks. Nat. Phys. 7, 481–484 (2011).
Moukarzel, C. F. Effective dimensions in networks with long-range connections. Physica A 356, 157–161 (2005).
Zhang, J., Li, X., Wang, X., Wang, W. X. & Wu, L. Scaling behaviours in the growth of networked systems and their geometric origins. Sci. Rep. 5, 09767 (2015).
Shekhtman, L. M., Berezin, Y., Danziger, M. M. & Havlin, S. Robustness of a network formed of spatially embedded networks. Phys. Rev. E 90, 012809 (2014).
Gao, J., Buldyrev, S. V., Havlin, S. & Stanley, H. E. Robustness of a network of networks. Phys. Rev. Lett. 107, 195701 (2011).
Huang, W., Chen, S. & Wang, W. Navigation in spatial networks: A survey. Physica A 393, 132–154 (2014).
Xie, Y. B. et al. Geographical networks evolving with an optimal policy. Phys. Rev. E 75, 036106 (2007).
Berezin, Y., Bashan, A., Danziger, M. M., Li, D. & Havlin, S. Localized attacks on spatially embedded networks with dependencies. Sci. Rep. 5, 08934 (2015).
Feng, L., Monterola, C. P. & Hu, Y. The simplified self-consistent probabilities method for percolation and its application to interdependent networks. New J. Phys. 17, 063025 (2015).
Moukarzel, C. F. & Sokolowski, T. Long-range k-core percolation. J. Phys.: Conf. Ser. 246, 012019 (2010).
Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. k-core organization of complex networks. Phys. Rev. Lett. 96, 040601 (2006).
Goltsev, A. V., Dorogovtsev, S. N. & Mendes, J. F. F. k-core (bootstrap) percolation on complex networks: Critical phenomena and nonlocal effects. Phys. Rev. E 73, 056101 (2006).
Baxter, G. J., Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Heterogeneous k-core versus bootstrap percolation on complex networks. Phys. Rev. E 83, 051134 (2011).
Colomer-de-Simón, P. & Boguñá, M. Double percolation phase transition in clustered complex networks. Phys. Rev. X 4, 041020 (2014).
Parshani, R., Buldyrev, S. V. & Havlin, S. Critical effect of dependency groups on the function of networks. Proc. Natl. Acad. Sci. USA 108, 1007–1010 (2011).
Liu, R. R., Wang, W. X., Lai, Y. C. & Wang, B. H. Cascading dynamics on random networks: Crossover in phase transition. Phys. Rev. E 85, 026110 (2012).
Schulman, L. S. Long range percolation in one dimension. J. Phys. A: Math. Gen. 16, L639 (1983).
Newman, C. M. & Schulman, L. S. One dimensional 1/|j − i|S percolation models: The existence of a transition for S ≤ 2. Commun. Math. Phys. 104, 547–571 (1986).
Benjamini, I. & Berger, N. The diameter of long-range percolation clusters on finite cycles. Random Struct. Algorithms 19, 102–111 (2001).
Sen, P., Banerjee, K. & Biswas, T. Phase transitions in a network with a range-dependent connection probability. Phys. Rev. E 66, 037102 (2002).
Zipf, G. K. Human behavior and the principle of least effort (Oxford Press, Oxford, 1949).
Watts, D. J. & Strogatz, S. H. Collective dynamics of “small-world” networks. Nature 393, 440–442 (1998).
Schmeltzer, C., Soriano, J., Sokolov, I. M. & Rüdiger, S. Percolation of spatially constrained Erdös-Rényi networks with degree correlations. Phys. Rev. E 89, 012116 (2014).
Gao, J., Buldyrev, S. V., Stanley, H. E., Xu, X. & Havlin, S. Percolation of a general network of networks. Phys. Rev. E 88, 062816 (2013).
Baxter, G. J., Dorogovtsev, S. N., Mendes, J. F. F. & Cellai, D. Weak percolation on multiplex networks. Phys. Rev. E 89, 042801 (2014).
Zeng, A., Zhou, D., Hu, Y., Fan, Y. & Di, Z. Dynamics on spatial networks and the effect of distance coarse graining. Physica A 390, 3962–3969 (2011).
Acknowledgements
The authors acknowledge Jun Wang and Panhua Huang for useful discussions. This work is partially supported by National Natural Science Foundation of China under Grants Nos. 61203156 and 11222543. J.G. acknowledges support from Tang Lixin Education Development Foundation by UESTC. T.Z. acknowledges the Program for New Century Excellent Talents in University under Grant No. NCET-11-0070 and Special Project of Sichuan Youth Science and Technology Innovation Research Team under Grant No. 2013TD0006.
Author information
Authors and Affiliations
Contributions
J.G. and Y.H. designed the research. J.G. executed the experiments and prepared the figures. J.G., T.Z. and Y.H. analyzed the results. J.G. and T.Z. wrote the manuscript. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gao, J., Zhou, T. & Hu, Y. Bootstrap percolation on spatial networks. Sci Rep 5, 14662 (2015). https://doi.org/10.1038/srep14662
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep14662
This article is cited by
-
Polluted bootstrap percolation with threshold two in all dimensions
Probability Theory and Related Fields (2019)
-
Social contagions on interdependent lattice networks
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.






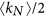 , e.g, k = 1 compared to
, e.g, k = 1 compared to  , there is only a trivial first-order phase transition at
, there is only a trivial first-order phase transition at  .
.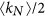 , e.g., k = 3 compared to
, e.g., k = 3 compared to  , there is a critical value αc, above which a double phase transition is observed. The value of αc depends on the choice of both k and kl. In particular,
, there is a critical value αc, above which a double phase transition is observed. The value of αc depends on the choice of both k and kl. In particular,  is found to be a parameter-independent critical value, about which the two critical points for the double phase transition are almost constant. Specifically, as shown in the phase diagram of
is found to be a parameter-independent critical value, about which the two critical points for the double phase transition are almost constant. Specifically, as shown in the phase diagram of 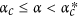 , pc1 decreases and pc2 increases as α decreases. Note that αc can be equal to
, pc1 decreases and pc2 increases as α decreases. Note that αc can be equal to 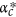 in some parameter spaces, such as
in some parameter spaces, such as 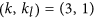 and
and 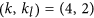 .
. , e.g, k = 5 compared to
, e.g, k = 5 compared to 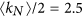 , the hybrid phase transition is absent and Sgc only undergoes a second-order phase transition with an increasing pc2 as the decreasing of α (see
, the hybrid phase transition is absent and Sgc only undergoes a second-order phase transition with an increasing pc2 as the decreasing of α (see 

