Abstract
We investigate the spatially optical solitons shedding from Airy beams and anomalous interactions of Airy beams in nonlocal nonlinear media by means of direct numerical simulations. Numerical results show that nonlocality has profound effects on the propagation dynamics of the solitons shedding from the Airy beam. It is also shown that the strong nonlocality can support periodic intensity distribution of Airy beams with opposite bending directions. Nonlocality also provides a long-range attractive force between Airy beams, leading to the formation of stable bound states of both in-phase and out-of-phase breathing Airy solitons which always repel in local media.
Similar content being viewed by others
Introduction
Self-accelerating Airy beams have drawn considerable attention1,2,3 after the experimental realization4 of nonspreading wave packets5. Airy beams have many unique properties in the propagation dynamics and the applications of all-optical devices6,7,8,9,10,11,12,13. Besides the linear regime of Airy beams6,7,8,9,10,11,12,13, the nonlinear control of Airy beams also contains many novel dynamics14,15,16,17,18,19,20,21,22,23,24,25,26,27. In particular, in nonlinear media, solitons can be formed with the Airy beams28,29,30. Furthermore, the interactions between Airy beams31,32 play an important soul in the generation of bound soliton pairs33,34.
However, all the works mentioned above were investigated in local nonlinear media. It has been shown that the boundary conditions of a strongly nonlocal media affect deeply the propagation dynamics of self-accelerating beams35. Recently, an analytical expression of an Airy beam propagating in a strongly nonlocal nonlinear media was derived to show the normalized intensity distribution of the Airy beam is always periodic36. In optical domain, generally, nonlocal nonlinearity means that the light-induced refractive index change of a material at a particular location is determined by the light intensity in a certain neighborhood of this location. Such a nonlocal optical nonlinearity exists in nematic liquid crystals37 and thermal media38. Many works have shown that nonlocality has profound effects on the solitons propagation39. Nonlocal nonlinearity also affects the interaction38 of out-of-phase bright solitons40,41,42 and dark solitons43,44,45.
In this paper, we investigate the solitons shedding from Airy beams and anomalous interactions of Airy beams in nonlocal nonlinear media numerically. We find that nonlocality has profound effects on the propagation dynamics of the solitons shedding from Airy beam. It is also shown that the strong nonlocality can support periodic intensity distribution of Airy beams with opposite bending directions. Nonlocality also provides a long-range attractive force between Airy beams, leading to the formation of stable bound states of both in-phase and out-of-phase breathing Airy solitons which always repel in local media.
Results
Dynamics of solitons shedding from airy beams in nonlocal nonlinear media
We consider an Airy beam propagating in a medium with a self-focusing nonlocal cubic nonlinearity. The envelope  of the Airy beam is described by the normalized nonlocal nonlinear Schrodinger equation,
of the Airy beam is described by the normalized nonlocal nonlinear Schrodinger equation,

where  corresponds to the normalized nonlocal response function. Without loss of generality, we consider the case of so-called Gaussian nonlocal response functions46:
corresponds to the normalized nonlocal response function. Without loss of generality, we consider the case of so-called Gaussian nonlocal response functions46:  , with the characteristic width
, with the characteristic width  to represent the degree of nonlocality. It describes a local and a strongly nonlocal media when
to represent the degree of nonlocality. It describes a local and a strongly nonlocal media when  and
and  39, respectively. In general, the realistic forms of the nonlocal response functions depend on the underlying physical process of the materials47. It has been shown that as long as the response function is monotonically decaying, the physical properties of solitons in nonlocal media do not depend strongly on the shape of the nonlocal response function48. Although the Gaussian nonlocal response function is phenomenological, it can describe the general properties of other actual nonlocal media47.
39, respectively. In general, the realistic forms of the nonlocal response functions depend on the underlying physical process of the materials47. It has been shown that as long as the response function is monotonically decaying, the physical properties of solitons in nonlocal media do not depend strongly on the shape of the nonlocal response function48. Although the Gaussian nonlocal response function is phenomenological, it can describe the general properties of other actual nonlocal media47.
Firstly, we study the propagation of a finite power Airy beam in nonlocal nonlinear media by considering the exponentially decaying version6

where  is the amplitude of the Airy beam and
is the amplitude of the Airy beam and  is the the decay factor to ensure containment of the infinite Airy tail and the finite power of the Airy beam6. For simplicity, we set
is the the decay factor to ensure containment of the infinite Airy tail and the finite power of the Airy beam6. For simplicity, we set  throughout this paper.
throughout this paper.
In Fig. (1), we show the propagation dynamics of Airy beams in nonlocal nonlinear media by direct numerical integration of Eq. (1) with split-step Fourier transform method. Firstly, we consider the case of local cubic media with  [Figs. 1(a–c)]. For small amplitude (low power), as shown in Fig. 1(a), the Airy beam performs the acceleration in space and subsequently it succumbs to diffraction. However, when
[Figs. 1(a–c)]. For small amplitude (low power), as shown in Fig. 1(a), the Airy beam performs the acceleration in space and subsequently it succumbs to diffraction. However, when  is sufficiently large28,30, a stationary soliton will be formed out of the centered energy about the Airy main lobe [Fig. 1(c)]. The intensity distribution of the Airy beam (
is sufficiently large28,30, a stationary soliton will be formed out of the centered energy about the Airy main lobe [Fig. 1(c)]. The intensity distribution of the Airy beam ( ) and the soliton (
) and the soliton ( ) are displayed in Figs. 2(a,b). It is obvious that the peak intensity of the soliton is larger than that of the main lobe of the Airy beam, which indicates that the tail power of the Airy beam is almost confined into the main lobe to shed a soliton. The soliton exhibits periodic oscillations in the soliton amplitude and width. Similar phenomena has been studied previously28, which is not our aim in this paper.
) are displayed in Figs. 2(a,b). It is obvious that the peak intensity of the soliton is larger than that of the main lobe of the Airy beam, which indicates that the tail power of the Airy beam is almost confined into the main lobe to shed a soliton. The soliton exhibits periodic oscillations in the soliton amplitude and width. Similar phenomena has been studied previously28, which is not our aim in this paper.
(a,b) The intensity distributions of Fig.1(c) at propagation distances  and
and 
(c,d) The intensity distributions of Fig. 3(c) at propagation distances  and
and  .
.
If we keep the amplitude of the soliton [Fig. 1(c)] invariant, the nonlocality (e.g.,  ) will weaken the stability of the soliton, as shown in Fig. 1(d). The period and intensity of oscillation in the soliton amplitude will become bigger and its width will become larger [Fig. 1(d)]. Although nonlocality can provide a long range attractive force to stabilize complex solitons states, it will always weaken the strength of the nonlinearity39. A stable soliton always require a larger amplitude with the increases of
) will weaken the stability of the soliton, as shown in Fig. 1(d). The period and intensity of oscillation in the soliton amplitude will become bigger and its width will become larger [Fig. 1(d)]. Although nonlocality can provide a long range attractive force to stabilize complex solitons states, it will always weaken the strength of the nonlinearity39. A stable soliton always require a larger amplitude with the increases of  46. As shown in Figs. 1(d–f) (
46. As shown in Figs. 1(d–f) ( ), the stability of the Airy soliton is better improved when the amplitude increase, exhibited as the decrease of the beam width as well as the period and intensity of oscillation in the soliton amplitude. The intensity of the soliton keeps almost uniform for sufficiently large amplitude with snake oscillations [Fig. 1(f)]. From Figs. 1(c,f), we can also see that when a soliton is formed, the soliton will always take the main part of the initial input power, while a small fraction of the power is transformed into a self-accelerating linear packet. This phenomena is similar with the solitons dynamics obtained by using the Zakharov-Shabat scattering problem in local media30.
), the stability of the Airy soliton is better improved when the amplitude increase, exhibited as the decrease of the beam width as well as the period and intensity of oscillation in the soliton amplitude. The intensity of the soliton keeps almost uniform for sufficiently large amplitude with snake oscillations [Fig. 1(f)]. From Figs. 1(c,f), we can also see that when a soliton is formed, the soliton will always take the main part of the initial input power, while a small fraction of the power is transformed into a self-accelerating linear packet. This phenomena is similar with the solitons dynamics obtained by using the Zakharov-Shabat scattering problem in local media30.
It is also interesting that the nonlinear media cannot support stationary solitons but the periodic intensity distribution of Airy beam with opposite bending directions in strongly nonlocal regime, as shown in Fig. (3). The intensity of these beam maintain good Airy-like profile with a main lobe and the decaying tails, as shown in Figs. 2(c,d). Our numerical results of periodic intensity distribution of Airy beam obtained here agree with the analytical works of Airy beam in strongly nonlocal media very well36. The period will become larger when the degree of nonlocality increases or the amplitude decrease. The reason is that in the regime of strong nonlocality, the nonlocal nonlinearity trends to linear39 which is hard to trap the Airy beam into a soliton. However, such a strong nonlocality have a strong impact on the beam trajectory35: it can cause the Airy beam bending in a opposite direction periodically36. Besides nonlocal nonlinear media35,36, the similar phenomenon of periodic intensity distribution of Airy beam with opposite bending directions also occurs to other different physical systems, such as in plasmons with a linear refractive index profile49,50 and in curved space51.
Anomalous interactions and bound states of airy solitons in nonlocal media
Next, we focus on the anomalous interactions and bound states of Airy solitons in nonlocal nonlinear media. We assume that the incident beam is composed of two shifted counter propagating Airy beams with a relative phase between them,

where  is the parameter controlling the phase shift and
is the parameter controlling the phase shift and  is the parameter controlling beam separations. In this report, we consider both in-phase and out-of-phase Airy beams with
is the parameter controlling beam separations. In this report, we consider both in-phase and out-of-phase Airy beams with  and
and  , respectively33,34.
, respectively33,34.
Bound states of in-phase airy solitons
In Fig. (4), we show the interactions between in-phase Airy beams ( ) with some different beam separations. For comparison, we also re-do some previous results in local media (
) with some different beam separations. For comparison, we also re-do some previous results in local media ( ) with
) with  33,34. For larger separations, the two Airy components form two parallel solitons33,34, whereas, for small separations, bound breathing solitons are formed with certain periods [Figs. 4(a–c)]. The smaller the separation, the stronger the attraction and the smaller the period of soliton breathing. The attraction is the biggest when
33,34. For larger separations, the two Airy components form two parallel solitons33,34, whereas, for small separations, bound breathing solitons are formed with certain periods [Figs. 4(a–c)]. The smaller the separation, the stronger the attraction and the smaller the period of soliton breathing. The attraction is the biggest when  with the smallest period of the formed soliton [Fig. 4(a)]34. With the same amplitude
with the smallest period of the formed soliton [Fig. 4(a)]34. With the same amplitude  , we show in Figs. 4(d–f) the interactions of the Airy beams in nonlocal nonlinear media with
, we show in Figs. 4(d–f) the interactions of the Airy beams in nonlocal nonlinear media with  . The dynamics of the interactions depend crucially on the separations of the Airy beams: for larger separations, the interactions of the Airy beams enhanced obviously [Fig. 4(f)], exhibited as the decrease of period and width, whereas, the interactions are weakened with the increase of the period and the width of the bound breathing solitons for smaller separations [Fig. 4(d)]. The nonlocality provides a long range attractive force which can enhance the interaction between solitons52. This is true for larger separated Airy beams [Fig. 4(f)]. For smaller separated in-phase Airy beams, the attractive force between them is big enough to form bound states with only local nonlinearity [Fig. 4(a)]. However, nonlocality will always weaken the interactions of smaller separated in-phase Airy beams [Fig. 4(d)] because of nonlocality can weaken the strength of the nonlinearity39.
. The dynamics of the interactions depend crucially on the separations of the Airy beams: for larger separations, the interactions of the Airy beams enhanced obviously [Fig. 4(f)], exhibited as the decrease of period and width, whereas, the interactions are weakened with the increase of the period and the width of the bound breathing solitons for smaller separations [Fig. 4(d)]. The nonlocality provides a long range attractive force which can enhance the interaction between solitons52. This is true for larger separated Airy beams [Fig. 4(f)]. For smaller separated in-phase Airy beams, the attractive force between them is big enough to form bound states with only local nonlinearity [Fig. 4(a)]. However, nonlocality will always weaken the interactions of smaller separated in-phase Airy beams [Fig. 4(d)] because of nonlocality can weaken the strength of the nonlinearity39.
Increasing the amplitude to  , in local media, compared with the Figs. 4(a–c), the interactions are weakened obviously [Figs. 5(a,b)] except for the larger separated beam [Fig. 5(c)]. In particular, the repulsion appears for the case
, in local media, compared with the Figs. 4(a–c), the interactions are weakened obviously [Figs. 5(a,b)] except for the larger separated beam [Fig. 5(c)]. In particular, the repulsion appears for the case  , as shown in Fig. 5(a)34. The repulsion can be balanced by the attractive force induced even by a small degree of nonlocality. We show such bound state of breathing solitons in Fig. 5(d) with a weak nonlocality
, as shown in Fig. 5(a)34. The repulsion can be balanced by the attractive force induced even by a small degree of nonlocality. We show such bound state of breathing solitons in Fig. 5(d) with a weak nonlocality  . The interactions of other separated beams are also enhanced [Figs. 5(e,f)].
. The interactions of other separated beams are also enhanced [Figs. 5(e,f)].
Bound states of out-of-phase airy solitons
For the out-of-phase Airy beams ( ), the interactions in local media and nonlocal media are shown in Figs. 6(a–c) and Figs. 6(d–f), respectively. From Figs. 6(a–c), we can see that the soliton pairs are formed from the incidence actually repel each other34. The smaller the interval, the stronger the repulsion. The strongest repulsion of the soliton pair happens to the case of
), the interactions in local media and nonlocal media are shown in Figs. 6(a–c) and Figs. 6(d–f), respectively. From Figs. 6(a–c), we can see that the soliton pairs are formed from the incidence actually repel each other34. The smaller the interval, the stronger the repulsion. The strongest repulsion of the soliton pair happens to the case of  [Fig. 6(a)]34. For a given amplitude
[Fig. 6(a)]34. For a given amplitude  , Figs. 6(d–f) clearly show the nonlocality (
, Figs. 6(d–f) clearly show the nonlocality ( ) will weaken the interactions in spite of the separation is large or small due to the fact that the nonlocality cannot balance the repulsion of the out-of-phase beams.
) will weaken the interactions in spite of the separation is large or small due to the fact that the nonlocality cannot balance the repulsion of the out-of-phase beams.
Stationary bound states of out-of-phase Airy solitons may be obtained with larger amplitude in local media when the strong self-focusing effect balances the out-of-phase repulsion, as shown in Figs. 7(a–c). We consider the strongly repulsive case with  . From Figs. 7(a–c), we can find that Airy beams with smaller separation always need larger amplitude to form a stable soliton pairs, e.g.,
. From Figs. 7(a–c), we can find that Airy beams with smaller separation always need larger amplitude to form a stable soliton pairs, e.g.,  for
for  [Fig. 7(a)]. Interestingly, we can even obtain two soliton pairs with different intensities at small separation
[Fig. 7(a)]. Interestingly, we can even obtain two soliton pairs with different intensities at small separation  [Fig. 7(a)]. The soliton pairs cannot obtained from in-phase Airy beams with larger amplitude due to that strong self-focusing and in-phase attractive force always break up the beam, leading to the collapse of the Airy beams.
[Fig. 7(a)]. The soliton pairs cannot obtained from in-phase Airy beams with larger amplitude due to that strong self-focusing and in-phase attractive force always break up the beam, leading to the collapse of the Airy beams.
Interaction of out-of-phase ( ) Airy beams in nonlocal nonlinear media.
) Airy beams in nonlocal nonlinear media.
The degrees of nonlocality are: (a–c)  (local media), (d)
(local media), (d)  , (e)
, (e)  and (f)
and (f)  . The amplitudes are
. The amplitudes are  for Figs. 7(a–c) and
for Figs. 7(a–c) and  for Figs. 7(d–f), respectively. The beam separations are: (a,d)
for Figs. 7(d–f), respectively. The beam separations are: (a,d)  , (b,e)
, (b,e)  and (c,f)
and (c,f)  .
.
The soliton pairs obtained in local media [Figs. 7(a–c)] with large amplitude may become unstable because of the strong self-focusing effect34. After some propagation distances, e.g.,  for
for  , the repulsion will overtake the attraction and soliton pairs will fly away in opposite directions34. Completely stable out-of-phase Airy solitons bound states can be obtained with the help of nonlocality, as shown in Figs. 7(d–f). The amplitudes should also be larger than that in local media [Figs. 7(a–c)]. For such stable soliton pairs, smaller separation (
, the repulsion will overtake the attraction and soliton pairs will fly away in opposite directions34. Completely stable out-of-phase Airy solitons bound states can be obtained with the help of nonlocality, as shown in Figs. 7(d–f). The amplitudes should also be larger than that in local media [Figs. 7(a–c)]. For such stable soliton pairs, smaller separation ( ) always require larger degree of nonlocality and amplitude [Fig. 7(d)]. In fact, the stable bound states of breathing soliton pairs is a result of balance between the effects of nonlocal, nonlineaity, diffraction and repulsion. Nonlocality provides a long range attractive force to balance the repulsion of out-of-phase Airy beams, leading to the formation of bound state which always repel in local media.
) always require larger degree of nonlocality and amplitude [Fig. 7(d)]. In fact, the stable bound states of breathing soliton pairs is a result of balance between the effects of nonlocal, nonlineaity, diffraction and repulsion. Nonlocality provides a long range attractive force to balance the repulsion of out-of-phase Airy beams, leading to the formation of bound state which always repel in local media.
Discussions
One of the most important and interesting dynamic of the solitons is their particle-like interactions53. In purely local nonlinear media, the bright solitons may attract, repel and even form bound states, depending on their relative phase54, whereas, the interaction of dark solitons is always repulsive55. Recently, the interactions of solitons have been investigated in media with spatially nonlocal nonlinearity. Nonlocal nonlinearity provides a long-range attractive force, leading to the formation of stable bound states of both out-of-phase bright solitons40,41,42 and dark solitons43,44,45. This long-range nonlocal nonlinearity also allow people to observe experimentally the multipole solitons-arrays of out-of-phase bright spots56.
Up to now, the interaction dynamics of Airy beam have only been investigated in local media31,32,33,34. For out-of-phase Airy beams, they are always repel in local media33,34. This repulsive force also exist in the in-phase Airy beams when their amplitudes (energy) are large enough34. Thus, a question arise naturally: can one obtain stable bound states (soliton pairs) of Airy beams in nonlinear media?
In this report, with the help of nonlocality, we have obtained such bound states (soliton pairs) of in-phase as well as out-of-phase Airy beams in nonlocal nonlinear media. We also numerically check the stability of the bound states. We perturb the initial Airy beams by 5% random noise perturbations and then simulate their evolutions numerically. As shown in Fig. (8), we only consider the case of out-of-phase Airy beams. We can see that the bound states of breathing Airy solitons are surely stable and propagate robustly against perturbations. In summary, nonlocality provides a long-range attractive force on Airy beams, leading to the formation of stable bound states of breathing Airy solitons which always repel in local media.
Evolution of out-of-phase ( ) Airy beams under 5% random noise perturbations in nonlocal nonlinear media.
) Airy beams under 5% random noise perturbations in nonlocal nonlinear media.
The degrees of nonlocality are: (a)  and (b)
and (b)  . The amplitudes are
. The amplitudes are  for Figs. 8(a,b), respectively. The beam separations are: (a)
for Figs. 8(a,b), respectively. The beam separations are: (a)  and (b)
and (b)  .
.
Methods
Split-step fourier transform method
In our numerical simulations of the propagation dynamics of Airy beams and interactions of them, the split-step Fourier tansform method is used to integrate the nonlinear Schrödinger equation [Eq. (1)]. This method relies on computing the solution in small steps and treating the linear and the nonlinear steps separately57. Firstly, we rewrite Eq. (1) as

with  and
and  are the linear and nonlinear operator,
are the linear and nonlinear operator,


respectively. For an optical beam  at propagation distance
at propagation distance  , in the next step
, in the next step  , the optical field distribution
, the optical field distribution  can be obtained with the Split-step method. In the first half of the step
can be obtained with the Split-step method. In the first half of the step  , we only consider the effect of the linear operator
, we only consider the effect of the linear operator

and then we consider the nonlinear operator in the whole step 

finally, in the second half of the step  , the linear operator is considered again and the optical field distribution
, the linear operator is considered again and the optical field distribution  can be obtained as
can be obtained as

Fourier transform of the nonlocal convolution term
In the numerical simulations with the split-step Fourier transform method, the Fourier transform of the convolution term of the nonlinear refractive index change  should be addressed here
should be addressed here

References
Baumgartl, J., Mazilu, M. & Dholakia, K. Optically mediated particle clearing using Airy wavepackets. Nat. Photon. 2, 675–678 (2008).
Polynkin, P., Kolesik, M., Moloney, J. V., Siviloglou, G. A. & Christodoulides, D. N. Curved plasma channel generation using ultraintense Airy beams. Science 324, 229–232 (2009).
Chong, A., Renninger, W. H., Christodoulides, D. N. & Wise, F. W. Airy-Bessel wave packets as versatile linear light bullets. Nat. Photon. 4, 103–106 (2010).
Siviloglou, G. A., Broky, J., Dogariu, A. & Christodoulides, D. N. Observation of accelerating Airy beams. Phys. Rev. Lett. 99, 213901 (2007).
Berry, M. V. & Balazs, N. L. Nonspreading wave packets. Am. J. Phys. 47, 264–267 (1979).
Siviloglou, G. A. & Christodoulides, D. N. Accelerating finite energy Airy beams. Opt. Lett. 32, 979–981 (2007).
Bandres, M. A. Accelerating beams. Opt. Lett. 34, 3791–3793 (2009).
Hu, Y. et al. Optimal control of the ballistic motion of Airy beams. Opt. Lett. 35, 2260–2262 (2010).
Greenfield, E., Segev, M., Wallasik, W. & Raz, O. Accelerating light beams along arbitrary convex trajectories. Phys. Rev. Lett. 106, 213903 (2011).
Kaminer, I., Bekenstein, R., Nemirovsky, J. & Segev, M. Nondiffracting accelerating wave packets of Maxwell's equations. Phys. Rev. Lett. 108, 163901 (2012).
Aleahmad, P. et al. Fully vectorial accelerating diffraction-free Helmholtz beams. Phys. Rev. Lett. 109, 203902 (2012).
Zhang, P. et al. Nonparaxial Mathieu and Weber Accelerating Beams. Phys. Rev. Lett. 109, 193901 (2012).
Minovich, A. et al. Generation and Near-Field Imaging of Airy Surface Plasmons. Phys. Rev. Lett. 107, 116802 (2011).
Ellenbogen, T., Voloch-Bloch, N., Ganany-Padowicz, A. & Arie, A. Nonlinear generation and manipulation of Airy beams. Nat. Photon. 3, 395–398 (2009).
Efremidis, N. K. & Christodoulides, D. N. Abruptly autofocusing waves. Opt. Lett. 35, 4045–4047 (2010).
Hu, Y. et al. Persistence and breakdown of Airy beams driven by an initial nonlinearity. Opt. Lett. 35, 3952–3954 (2010).
Chen, R., Yin, C., Chu, X. & Wang, H. Effect of Kerr nonlinearity on an Airy beam. Phys. Rev. A 82, 043832 (2010).
Abdollahpour, D., Suntsov, S., Papazoglou, D. G. & Tzortzakis, S. Spatiotemporal airy light bullets in the linear and nonlinear regimes. Phys. Rev. Lett. 105, 253901 (2010).
Jia, S., Lee, J., Fleischer, J. W., Siviloglou, G. A. & Christodoulides, D. N. Diffusion-Trapped Airy Beams in Photorefractive Media. Phys. Rev. Lett. 104, 253904 (2010).
Kaminer, I., Segev, M. & Christodoulides, D. N. Self-accelerating self-trapped optical beams. Phys. Rev. Lett. 106, 213903 (2011).
Ament, C., Polynkin, P. & Moloney, J. V. Supercontinuum generation with femtosecond self-healing airy pulses. Phys. Rev. Lett. 107, 243901 (2011).
Lotti, A. et al. Stationary nonlinear Airy beams. Phys. Rev. A 84, 021807(R) (2011).
Dolev, I., Kaminer, I., Shapira, A., Segev, M. & Arie, A. Experimental observation of self-accelerating beams in quadratic nonlinear media. Phys. Rev. Lett. 108, 113903 (2012).
Hu, Y. et al. Reshaping the trajectory and spectrum of nonlinear Airy beams. Opt. Lett. 37, 3201–3203 (2012).
Zhang, P. et al. Generation of linear and nonlinear nonparaxial accelerating beams. Opt. Lett. 37, 2820–2822 (2012).
Driben, R. & Meier, T. Nonlinear dynamics of Airy-Vortex 3D wave packets: Emission of vortex light waves. Opt. Lett. 39, 5539–5542 (2014).
Chen, R., Chew, K. -H. & He, S. Dynamic control of collapse in a vortex Airy beam. Sci. Rep. 3, 1406; 10.1038/srep01406 (2013).
Fattal, Y., Rudnick, A. & Marom, D. M. Soliton shedding from Airy pulses in Kerr media. Opt. Express 19, 17298–17307 (2011).
Driben, R., Konotop, V. V. & Meier, T. Coupled Airy breathers. Opt. Lett. 39, 5523–5526 (2014).
Allayarov, I. M. & Tsoy, E. N. Dynamics of Airy beams in nonlinear media. Phys. Rev. A 90, 023852 (2014).
Rudnick, A. & Marom, D. M. Airy-soliton interactions in Kerr media. Opt. Express 19, 25570–25582 (2011).
Wiersma, N., Marsal, N., Sciamanna, M. & Wolfersberger, D. All-optical interconnects using Airy beams. Opt. Lett. 39, 5997–6000 (2014).
Zhang, Y. et al. Soliton pair generation in the interactions of airy and nonlinear accelerating beams. Opt. Lett. 38, 4585–4588 (2013).
Zhang, Y. et al. Interactions of Airy beams, nonlinear accelerating beams and induced solitons in Kerr and saturable nonlinear media. Opt. Express 22, 7160–7171 (2014).
Bekenstein, R. & Segev, M. Self-accelerating optical beams in highly nonlocal nonlinear media. Opt. Express 19, 23706–23715 (2011).
Zhou, G., Chen, R. & Ru, G. Propagation of an Airy beam in a strongly nonlocal nonlinear media. Laser Phys. Lett. 11 105001 (2014).
Peccianti, M., Conti, C., Assanto, G., Luca, A. D. & Umeton, C. Routing of anisotropic spatial solitons and modulational instability in liquid crystals. Nature (London) 432, 733–737 (2004).
Rotschild, C., Alfassi, B., Cohen, O. & Segev, M. Long-range interactions between optical solitons. Nat. Phys. 2, 769–774 (2006).
Krolikowski, W. et al. Modulational instability, solitons and beam propagation in spatially nonlocal nonlinear media. J. Opt. B: Quantum Semiclass. Opt. 6, S288 (2004).
Rasmussen, P. D., Bang, O. & Krolikowski, W. Theory of nonlocal soliton interaction in nematic liquid crystals. Phys. Rev. E 72, 066611 (2005).
Peccianti, M., Brzdakiewicz, K. & Assanto, G. Nonlocal spatial soliton interactions in nematic liquid crystals. Opt. Lett. 27, 1460–1462 (2002).
Hu, W., Zhang, T., Guo, Q., Xuan, L. & Lan, S. Nonlocality-controlled interaction of spatial solitons in nematic liquid crystals. Appl. Phys. Lett. 89, 071111 (2006).
Nikolov, N. et al. Attraction of nonlocal dark optical solitons. Opt. Lett. 29, 286–288 (2004).
Kong, Q., Wang, Q., Bang, O. & Krolikowski, W. Analytical theory for the dark-soliton interaction in nonlocal nonlinear materials with an arbitrary degree of nonlocality. Phys. Rev. A 82, 013826 (2010).
Dreischuh, A., Neshev, D. N., Petersen, D. E., Bang, O. & Krolikowski, W. Observation of attraction between dark solitons. Phys. Rev. Lett. 96, 043901 (2006).
Buccoliero, D., Desyatnikov, A. S., Krolikowski, W. & Kivshar, Y. S. Laguerre and Hermite Soliton Clusters in Nonlocal Nonlinear Media. Phys. Rev. Lett. 98, 053901 (2007).
Wyller, J., Krolikowski, W., Bang, O. & Rasmussen, J. J. Generic features of modulational instability in nonlocal Kerr media. Phys. Rev. E 66, 066615 (2002).
Zhong, W. & Belic, M. Three-dimensional optical vortex and necklace solitons in highly nonlocal nonlinear media. Phys. Rev. A 79, 023804 (2009).
Zhang, P. et al. Plasmonic Airy beams with dynamically controlled trajectories. Opt. Lett. 36, 3191–3193 (2011).
Liu, W., Neshev, D. N., Shadrivov, I. V., Miroshnichenko, A. E. & Kivshar, Y. S. Plasmonic Airy beam manipulation in linear optical potentials. Opt. Lett. 36, 1164–1166 (2011).
Bekenstein, R., Nemirovsky, J., Kaminer, I. & Segev, M. Shape-Preserving Accelerating Electromagnetic Wave Packets in Curved Space. Phys. Rev. X 4, 011038 (2014).
Chen, W. et al. Interactions of nonlocal dark solitons under competing cubic-quintic nonlinearities. Opt. Lett. 39, 1764–1767 (2014).
Stegeman, G. I. & Segev, M. Optical Spatial Solitons and Their Interactions: Universality and Diversity. Science 286, 1518–1523 (1999).
Krolikowski, W., Saffman, M., Luther-Davies, B. & Denz, C. Anomalous Interaction of Spatial Solitons in Photorefractive Media. Phys. Rev. Lett. 80, 3240–3243 (1998).
Zhao, W. & Bourkoff, E. Interactions between dark solitons. Opt. Lett. 14, 1371–1373 (1989).
Rotschild, C. et al. Two-dimensional multi-pole solitons in nonlocal nonlinear media. Opt. Lett. 31, 3312–3314 (2006).
Agrawal, G. P. Nonlinear fiber optics (Academic Press, San Diego, 1995).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (nos. 11347180 and 61405135), the Natural Science Foundation of Jiangsu Province (no. BK20130265), the Innovation Program of Shanghai Municipal Education Commission and the Science and Technology Commission of Shanghai Municipal (no. 15ZR1415700).
Author information
Authors and Affiliations
Contributions
M.S. AND J.G. carried out the numerical simulations; L.G. analyzed theoretically the numerical results. Both authors wrote and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Shen, M., Gao, J. & Ge, L. Solitons shedding from Airy beams and bound states of breathing Airy solitons in nonlocal nonlinear media. Sci Rep 5, 9814 (2015). https://doi.org/10.1038/srep09814
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep09814
This article is cited by
-
Asymmetric impact of higher order diffraction on narrow beam dynamics in nonlocal nonlinear media
Applied Physics B (2023)
-
Counterpropagating interactions of self-focusing Airy beams
Scientific Reports (2019)
-
Spatiotemporal Airy Ince–Gaussian wave packets in strongly nonlocal nonlinear media
Scientific Reports (2018)
-
Dynamical behavior of self-accelerating beams in LiNbO3 crystal with background illumination
Applied Physics B (2018)
-
Propagation dynamics of Airy beams and nonlinear accelerating beams in biased photorefractive media with quadratic electro-optic effect
Applied Physics B (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


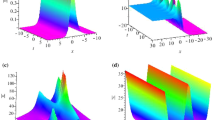

 (local) and (d–f)
(local) and (d–f)  . The amplitudes are: (a)
. The amplitudes are: (a)  , (b)
, (b)  , (c,d)
, (c,d)  , (e)
, (e)  and (f)
and (f)  .
.

 and (c,d)
and (c,d)  . The amplitudes are: (a)
. The amplitudes are: (a)  , (b,c)
, (b,c)  and (d)
and (d)  .
.
 ) Airy beams in nonlocal nonlinear media.
) Airy beams in nonlocal nonlinear media. (local media) and (d–f)
(local media) and (d–f)  . The amplitude is
. The amplitude is  for all the plots. The beam separations are: (a,d)
for all the plots. The beam separations are: (a,d)  , (b,e)
, (b,e)  and (c,f)
and (c,f)  .
.
 ) Airy beams in nonlocal nonlinear media.
) Airy beams in nonlocal nonlinear media. (local media) and (d–f)
(local media) and (d–f)  . The amplitude is
. The amplitude is  for all the plots. The beam separations are: (a,d)
for all the plots. The beam separations are: (a,d)  , (b,e)
, (b,e)  and (c,f)
and (c,f)  .
.
 ) Airy beams in nonlocal nonlinear media.
) Airy beams in nonlocal nonlinear media. (local media) and (d–f)
(local media) and (d–f)  . The amplitude is
. The amplitude is  for all the plots. The beam separations are: (a,d)
for all the plots. The beam separations are: (a,d)  , (b,e)
, (b,e)  and (c,f)
and (c,f)  .
.
