Introduction

Topological state is a fundamentally new quantum state which is topologically distinct from all conventional states of matter. The first example is the quantum Hall (QH) state which has a full gap in the bulk and gapless chiral modes at the edge1,2. In the QH system, an external magnetic field is applied, explicitly breaking time-reversal (TR) symmetry. Beside this, another topological class of materials have been demonstrated invariant under TR, in the presence of strong spin-orbit coupling, which is named as topological insulator or quantum spin Hall (QSH) effect3,4,5,6,7. The QSH state in two dimension (2D) can be roughly understood as two copies of the QH state, where states with opposite spin propagate in opposite directions at the edge7.

In 2008 Haldane and Raghu demonstrated the possibility of achieving photonic analogue of the QH edge states of electrons, based on the fact that the edge states are a property of a one-particle eigenstates problem, which can be mapped into the Maxwell normal-mode problem8. Such photonic edge states were soon realized in microwave experiments in photonic crystals made with magneto-optic media9,10. Since then, various configurations have been proposed to achieve photonic topological states, such as aperiodic coupled-resonator system11 and dynamically modulated photonic resonator lattice exhibiting an effective magnetic field12. These topologically protected edge states ensure the absence of backscattering of waves by disorder, which suggest potential applications ranging from on-chip isolation10 to delay line11. Meanwhile photonic simulations of topological insulator without the breaking of TR symmetry have been designed in photonic metacrystal made with bi-anisotropic media13 and a lattice of optical ring resonators14. More recently, photonic Floquet topological insulator has been experimentally realized in a honeycomb lattice composed of coupled helical waveguides15 and synthetic magnetic fields for photons have been achieved by using linear silicon photonics16.

Interestingly, there is another type of topological states in chiral topological superconductor (TSC) which has a pairing gap in the bulk and gapless bound state at the edge6,7. Besides the edge state, the existence of zero-energy mode at a vortex core has been theoretically predicted17,18, which attracts great attention in the recent decade19. The simplest model for the TR breaking TSC is proposed in px + ipy pairing states17, whose Hamiltonian is given as7

where is the momentum, U′ is the chemical potential and the off-diagonal elements are pairing potentials. In the weak pairing phase with U′ > 0, chiral edge states appear7. Although many attempts have been made to observe such edge states experimentally, there are still debates on them20,21,22,23.

In this work, we bridge the fields of TSC and photonics. A direct mapping is established between the px + ipy Hamiltonian of TSC and the effective Hamiltonian of a suitably designed electromagnetic medium. Photonic simulations of TSC edge state and zero-energy mode at a vortex are investigated. This study extends the essential physics of the px + ipy model to photonic systems, which may provide a clean and convenient platform to study topological states of TSC, due to the flexibility of material design and less difficulties in experimental observations. On the other hand, this idea may fertilize the study of photonic topological states and inspire researchers to explore more fruitful topological effects.

Results

Photonic analogue of the px + ipy Hamiltonian

The main challenges of achieving photonic analogue of the px + ipy Hamiltonian lie in two aspects: (i) one of the critical properties of TSC is particle-hole symmetry, of which the photonic counterpart may seem unimaginable at first sight; (ii) pairing potential of the px + ipy pairing state is required to be a linear function of momentum (see the off-diagonal elements of the Hamiltonian), whereas such kind of interaction is not common in electromagnetic media. Here we propose a two-step approach to give a solution.

In general, the propagating waves in 2D can be classified into transverse electric (TE) mode and transverse magnetic (TM) mode. Thanks to electromagnetic duality of Maxwell's equations, equations for TE mode can be converted into that for TM mode by making transformations of Ez → Hz, Hx → −Ex, Hy → −Ey, ε → μ and μ → ε. We suggest using band structures of TE and TM modes to mimic particle and hole states, respectively. However, electromagnetic duality is not enough for realizing photonic “particle-hole symmetry”, since particle-hole transformation also changes the sign of the kinetic energy. We design photonic band structures with positive- and negative-refractive-index bands by using metamaterials24,25,26,27,28,29, which are also known as right-handed and left-handed bands, to mimic the positive- and negative-energy bands of particle and hole, respectively. In this way, the particle-hole transformation in condensed matter physics is emulated by a combination of electromagnetic duality and handedness inversion in photonics, as schematically shown in figure 1a. For example, a right-handed TE band and a well-designed left-handed TM band can present photonic “particle-hole symmetry”.

Figure 1
figure 1

Photonic simulation of TSC band structures.

(a) A combination of electromagnetic duality and handedness inversion of photons mimics particle-hole transformation for electrons. For example, if a right-handed TE mode represent “particle”, a transformed left-handed TM mode can be considered as “hole”. (b,c) Band diagrams for particle-hole symmetric systems (b) without and (c) with px + ipy pairing potential. The px + ipy pairing potential leads to a gap with topological phase.

Full size image

Reference 29 demonstrated that one-dimensional (1D) Maxwell's equations can be transformed into a compact form that has the identical mathematical structure of the Dirac equation. By employing metamaterials having controllable dispersive permittivity and permeability, a simple two-band model was achieved, including an upper right-handed band and a lower left-handed band. Here, we extend this idea to 2D Maxwell's equations. Take for example the TE mode, the time-harmonic Maxwell's equations in k-space can be written as

where ω is the angular frequency, c is the speed of light in vacuum, ε0/μ0 are the permittivity/permeability of the vacuum, εz/μ⊥ are the relative permittivity/permeability of the medium, kx and ky are propagation constants in the x and y direction, respectively. Consider suitably designed metamaterial whose effective permittivity and permeability are described by the Drude model,

where ωpe/ωpm are the plasma/“magnetic plasma” frequency, γe/γm are losses and εz0/μ⊥0 are constants. For simplicity, we assume γe = γm = 0 and ωpe = ωpm ≡ ωp in theoretical investigations. Let and , where ω0 is a reference frequency that is chosen as the photonic analogue of zero energy of superconductor. As all interesting physics of TSC occur around zero energy, we focus on the vicinity of ω0 accordingly and do expansions,

By substituting equation (4) into equation (2), we get

where , , m is the effective mass, m = ω(δμ⊥ − δεz)/2c, U is the effective chemical potential, U = ω(δμ⊥ + δεz)/2c and Ω is the eigen-frequency, . The 3 × 3 matrix in the left-hand side of equation (5) can be considered as an effective Hamiltonian for TE mode, denoted by

By tuning m and U, one can obtain a two-band diagram, as shown in figure 1b (colored blue).

Taking advantage of electromagnetic duality of Maxwell's equations, we can readily obtain the corresponding equations for TM mode from equation (2), which plays the role of “hole” state. Then we introduce handedness inversion, which flips the sign of permittivity and permeability. The material parameters are required to meet the conditions of δμz = −δεz ≡ −δz and δε⊥ = −δμ⊥ ≡ −δ⊥. Consequently, the effective Hamiltonian of the TM mode is obtained, . The band diagram is plotted in figure 1b (colored pink). By tuning U to meet the condition U > m, the right-handed TE band and the left-handed TM band cross at a finite frequency, as shown in figure 1b. The crossing frequency is ω0, which can be considered as photonic counterpart of zero energy in superconductor.

Next step is to emulate px + ipy pairing potential, which is responsible for a gap opening at ω0. At first sight it might be very difficult to obtain photonic interaction that is a linear function of momentum. Here we introduce an alternative solution, which is named as odd-parity pairing30,31. In this picture, one can use constant interactions instead, if the interactions are applied between a wave function with odd parity and another with even parity. Note that for a single-orbital superconductor, odd-parity pairing is equivalent to p-wave pairing30.

To achieve the photonic “odd-parity pairing”, we introduce here the reflection operator M in 2D point groups32,33. Take for example the reflection Mx (x → −x, y → y) in the xy plane. Under this operation, kx changes its sign (kx → −kx). To keep Maxwell's equations invariant under Mx, we should have Hy → −Hy and Ey → −Ey. Similar arguments can be applied to My. In contrast, for any reflection M in the xy plane, Ez and Hz keep their signs. In this picture, Ex,y and Hx,y act as “odd-parity” wave functions, while Ez and Hz act as “even-parity” wave functions. Therefore, we introduce interactions between Ez and Ex,y and between Hz and Hx,y, respectively. We also notice that the required pairing potentials are expected for not only opening a gap but also breaking TR symmetry. As a result, the “odd-parity pairing” interactions are designed by employing complex off-diagonal elements in permittivity and permeability tensors,

Without loss of generality, we assume κ1 = κ2 = κ3 = κ4 = κ. In this case, the system has rotational symmetry in the kx,y plane.

After the above two steps, we obtain the effective Hamiltonian for the TSC-like photonic medium,

where Δ = ωκ/c. This Hamiltonian presents “particle-hole symmetry”,

The pairing potential results in a TSC-like gap centered at ω0, as shown in figure 1c. To verify the topological feature of the TSC-like medium, we analytically calculate the winding number. It is known that topological nature of a system changes only when the gap closes. This property enables us to investigate topological feature in the extreme case that the gap has nearly zero width. Here we use a general method of approximation for this problem. First, consider the case of absent pairing potential, as shown in figure 1b. The eigen-functions can be obtained by diagonalizing the 6 × 6 Hamiltonian described by equation (7). As all interesting physics are determined by the bands crossing zero energy, one may extract the 6 × 2 eigen-functions for the corresponding two bands and project out the others. Next, we open an extremely small gap by introducing a very weak pairing potential. An appropriate approximation is used here: for sufficiently small variation of k, treat this term as a perturbation, so as to get an expression for the Hamiltonian in terms of the gapless solutions. Consequently, we use the 6 × 2 eigen-functions of the gapless solutions to extract the 2 × 2 sub-matrix of the pairing case approximately,

where σx,y,z are the Pauli matrices. It can be directly mapped into the px + ipy TSC Hamiltonian described by equation (1). From equation (9), one can calculate the winding number analytically,

In the present model, it gives Nw = θ(|U| − |m|) = 1, providing a direct evidence for the topological phase.

Simulation of TSC edge state

The non-zero winding number promises a chiral edge state localized at the interface between the TSC-like medium and another opaque medium. Let the interface be at x = 0 and the opaque medium be located in the region x < 0. The dispersion relation of the edge state is illustrated by the red line in figure 2a, where the shaded areas indicate the projected band diagram of infinite TSC-like medium. The material parameters of the TSC-like medium are taken as ε⊥0 = 0.8, εz0 = 1.1, μ⊥0 = 1.2, μz0 = 0.9, (which lead to δε⊥ = −δμ⊥ = −0.2, δεz = −δμz = 0.1), ωp = 89 and κ = 0.04 (with the unit of GHz). These parameters ensure the particle-hole-like symmetry of the effective Hamiltonian. From figure 2a, one can see a single branch of edge state with positive group velocity, which suggests broken TR symmetry and is expected to support one-way propagation. Note that another branch with negative group velocity can be realized by changing the permittivity and permeability tensors described by equation (6) into their conjugations, which makes the winding number flip its sign. To demonstrate the edge state intuitively, we also perform numerical calculations in real space by employing finite-difference frequency-domain (FDFD) method. As shown in figure 2b, the edge state distributes almost uniformly along the interface between two media and can pass through sharp bends at the corner without scattering.

Figure 2
figure 2

Manifestation of chiral edge state in both reciprocal and real space.

(a,b) Perfect analogy of TSC Hamiltonian and edge state with ideal material parameters. (a) Projected band diagram of infinite TSC-like photonic structure (shaded areas) and edge state at the interface between a semi-finite TSC-like medium in the region x > 0 and a semi-finite opaque medium in the region x < 0 (red line). (b) Magnetic field (Hz) distributions of edge state for a finite TSC-like medium. (c,d) Non-perfect TSC-like edge state with reduced material parameters. The results in (a) and (c) are analytically calculated by solving Maxwell's equations and those in (b) and (d) are numerically simulated by employing FDFD method.

Full size image

One may question that the material parameters described by equation (6) with certain symmetries might be very difficult to be realized. Fortunately, it is known that topological nature of a system would not change if the gap doesn't close and thus the edge state is topologically protected and insensitive to small perturbations. Taking advantage of this property, the strict requirements for material parameters with four pairs of off-diagonal elements could be reduced. Here, we remove two of them by letting κ2 = κ3 = 0 in equation (6) and perturb the symmetric Drude parameters of permittivity and permeability, for example, ε⊥ = 2 − 1402/ω2, εz = 2 − 1212/ω2, μ⊥ = 1 − 772/ω2, μz = 1 − 942/ω2, κ1 = 0.08 and κ2 = 0.04 (with the unit of GHz). In this case, the perfect form of the TSC-like Hamiltonian described by equation (7) no longer remains and the band structure adiabatically deforms from the symmetric one without gap closing. Compared with figures 2a and 2c, the bulk gap in figure 2c is narrower and the edge state in figure 2d shows broken rotational symmetry in the kx,y plane (the wavelength along the y direction is shorter than that along the x direction). Nevertheless, the edge state still exists. It provides an evidence for the topologically protected edge state against material-parameter perturbations, which may facilitate experimental realizations.

Simulation of zero-energy mode at a vortex

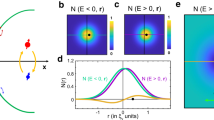
Another prominent feature of px + ipy superconductor is zero-energy mode at a vortex17,34,35,36,37. It is a solution of the Bogoliubov-de Gennes (BdG) equation in polar coordinates with Δ(r,θ) = Δ0(r)exp(±iθ), characterized by a bound state at zero energy at a vortex core which can be roughly considered as a small circular edge with vanishing density at the center17. Zero-energy mode is another important topological excitation, but earlier works in photonics only concentrated on edge states. Here we introduce azimuth-dependent off-diagonal elements in permittivity and permeability tensors with cylindrical symmetry, for example, κ1 = κ2 = κ exp(−iθ) and κ3 = κ4 = κ exp(+iθ). This design mimics a counter-clockwise vortex with a singularity at the center. FDFD method is employed to numerically calculate the field distributions in a finite medium at zero energy (ω0). The results are shown in figure 3. Two types of bound states are clearly seen: one appears at the edge and the other locates at the center “vortex core”. We have also confirmed that the bound state at the vortex only exists at ω0, which is indeed a “zero-energy” mode. It is known that the zero-energy modes at the vortex and at the edge can be described as the Jackiw-Rebbi solution in the 1D Dirac equation at the domain wall38,39. Here we reproduce them in photonic structures. Further calculations illustrate that the mode around the center rotates counter-clockwise around the vortex core, while the other rotates clockwise along the edge. The electric and magnetic fields also show different patterns between these two modes: in one mode Ez and Hz oscillate in phase, while in the other Ez and Hz oscillate out of phase.

Figure 3
figure 3

Manifestation of photonic zero-energy modes at a vortex and at edges.

The mode at the vortex propagates counter-clockwise around the center vortex core, while the mode at the edge propagates clockwise. Azimuth-dependent off-diagonal elements in permittivity and permeability tensors are introduced to mimic a vortex with a singularity at the center.

Full size image

Discussion

It should be pointed out that the effective TSC Hamiltonian proposed in this work is based on the presence of complex off-diagonal elements in permittivity and permeability tensors, which can be brought by gyrotropic responses of materials. We note that in the past decade, the study of metamaterials has made remarkable progress in tailoring ε and μ of an effective medium, offering flexible ways for manipulating electromagnetic wave propagation, such as cloaking40,41, optical analogue of quantum interference42 and Fano resonance43 and also mimicking black hole44. Most recently, the increased interests in achieving topological phases and edge states in photonic systems suggest that the presence of gyrotropic and chiral responses in materials may lead to fruitful results8,9,10,11,12,13 and some of them have already been realized in experiments10,15,45. For more complicated cases, such as the vortex model in this work, position-dependent gyrotropic parameters are taken into account. It may inspire researchers to tailor gyrotropic responses of materials as well as ε and μ in the future.

In summary, we have established a direct mapping between the px + ipy model of topological superconductor and suitably designed electromagnetic medium. Two essential points of this mapping, particle-hole symmetry and px + ipy pairing, have been investigated in detail. A combination of electromagnetic duality and handedness inversion of photons was proposed to mimic particle-hole transformation for electrons. The analogous px + ipy pairing potentials are achieved by introducing complex off-diagonal elements in permittivity and permeability tensors. Finally, we obtained a 2 × 2 effective Hamiltonian that has the identical mathematical structure of the TSC Hamiltonian and mimicked TSC edge state and zero-energy mode at a vortex. This study bridges the fields of superconductor and photonics, providing a good platform for simulating wave behaviors in superconductor physics at room temperature. The px + ipy model for TSC is the first example and other interesting effects such as Andreev reflection will be further investigated.

Methods

Band dispersions of both bulk media and edge states were obtained by analytically solving Maxwell's equations with effective permittivity and permeability. The effective Hamiltonian of the proposed photonic structures and its mapping into the px + ipy model of topological superconductor were carried out by theoretical deduction under appropriate approximations. Winding number was calculated analytically from the effective Hamiltonian. Numerical simulations were performed by using FDFD method.