Abstract
Thanks to its high electrical conductivity, a graphene plane presents a good shielding efficiency against GHz electromagnetic radiations. Several graphene planes separated by thin polymer spacers add their conductivities arithmetically, because each of them conserves the intrinsic properties of isolated graphene. Maximum absorption of radiations for frequency around 30 GHz is achieved with six separated graphene planes, which is the optimum number. This remarkable result is demonstrated experimentally from electromagnetic measurements performed in the Ka band on a series of multilayers obtained by piling 1, 2, 3 … graphene/PMMA units on a silica substrate. Theoretical calculations convincingly explain the observed absorption and transmission data in the GHz domain. It is concluded that graphene/PMMA multilayers can be used as an efficient optically transparent and flexible shielding media.
Similar content being viewed by others
Introduction
Microwave is the ultimate range for open space communication. The rapid growth of satellite data transmission in last decades, reinforced by the Internet traffic, makes inevitable the overcrowding of the spectral bands allocated to the different communication channels. Along with the increasing density of emitters in the environment, this has made the Electromagnetic Compatibility (EMC) an important issue1. EMC rules require that each new equipment have adequate immunity in order to function consistently and reliably, be resilient to major electromagnetic (EM) disturbances and coexist with other equipments. In order to meet these requirements, there is a real need for new materials to be used as coating layers, shields and filters in future nanoelectronic devices. These materials must have high electrical conductivity to achieve a good EM shielding effectiveness, defined as the reciprocal of the transmission factor. It is worth noting, however, that EM radiations reflected from the protective coatings do contribute to the microwave pollution. Consequantly, absorption rather than reflection losses should dominate the EM attenuation in the new materials. In addition, protection of the future nanodevices require submicron thick shields, making useless conventional conductive coatings capable to produce an EM attenuation of up to 3 dB/μm.
The challenging problem of the electromagnetic interference (EMI) protection at the nanoscale may be resolved if one exploits the unusual electronic properties of graphene. Very recently we have proposed microwave shielding based on nanometrically thin pyrolytic carbon (PyC) films2 composed of intertwined graphene ribbons. Specifically, 30–35 nm thick PyC films secure about 60% attenuation at 28 GHz mainly due to absorption of the EM radiations. The absorption efficiency of the EM protective coating can be increased even further by replacing PyC with few-layer graphite (FLG), which is capable to absorb 40% of microwave radiation at a thickness of only 5 nm3. Interlayer interactions affect the band structure of FLGs near the Fermi level in a qualitative way: compared to graphene, the dispersion of the π bands is no longer linear around the Dirac points4. This modification has direct consequences on properties such as the electrical conductivity that crucially depend on the topology of the Fermi surface5. When the distance between the graphene layers exceeds that realized in graphite by a fraction of a nanometer and more, the interlayer interaction plays no role anymore. In these conditions, the measured sheet conductivity increases in proportion to the number of graphene layers6. Therefore, one may expect that by separating graphene layers from one another in a controlled way by dielectric spacers, one can create a nano-metamaterial with enhanced shielding efficiency. This approach has been recently theoretically discussed in terms of an ultra-broadband THz absorber7, in which high-order surface plasmon resonances can be introduced by patterning graphene layers with micrometer periodicity.
In this paper we demonstrate both experimentally and theoretically that a stack of PMMA thin films sandwiching graphene sheets between them has remarkable microwave EMI shielding effectiveness. Specifically, in the Ka band (frequency range between 26.5 and 40 GHz), strong absorption of the EM radiation can be achieved without pre-patterning of the graphene whose overall thickness of two nanometers is enough to absorb 50% of the incident EM power.
Results
Experiment
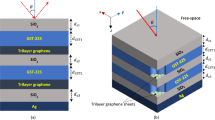
Fig. 1 shows schematically the graphene/PMMA multilayers produced for EM shielding analysis. The thickness of the PMMA spacers is in the range 600–800 nm. These sandwich structures were produced as follows. The first graphene layer was synthesized by chemical vapor deposition (CVD) at 1000°C in methane atmosphere on a copper foil. It was next covered by a PMMA layer obtained by spin coating, after what Cu was wet etched in ferric chloride. The obtained PMMA film with its graphene layer was washed in distilled water, placed on a quartz (fused silica) substrate and dried. The very same procedure was repeated several times, each newly-produced graphene/PMMA unit being deposited on top of the stack obtained at the previous step. This procedure allowed us to fabricate sandwich multilayers containing several graphene sheets.
Schematic representation of graphene sandwich fabrication, consisting of a number of repeating steps and final graphene/PMMA multilayer structure containing here four graphene sheets (the thickness of the different layers were not drawn in scale).
The lateral dimensions of the samples are 7.2 mm × 3.4 mm.
The SEM image reproduced in Fig. 2(a) demonstrates that the PMMA-based transfer technique8 allowed us to produce a continuous graphene sheet with a tiny number of holes. In addition, the optical transmittance of a graphene layer without the carrier PMMA film, taking out the response of the bare substrate (see Fig. 2(b)), was 97.8% at 800 nm, which is only 0.3% below that expected for a single graphene layer9. This measurement indicates that areas covered by bi- and multi-layer graphene are small. The Raman spectrum shown in Fig. 2(c) presents sharp G and 2D lines. More specifically, a sharp G peak (GFWHM < 20 cm−1) and the absence of D peak point to a high crystallinity of the graphene layer10. Furthermore, the 2D line peaks at 2688 cm−1 is typical for graphene monolayer10. However, the 2D peak is slightly broader (~40 cm−1) than expected for a graphene monolayer (30 cm−1), indicating some presence of bilayer graphene.
Microwave measurements were made with a scalar network analyzer R2-408R (ELMIKA, Vilnius, Lithuania). The setup includes a sweep generator, a waveguide reflectometer and an indicator unit. The IEC 62431:2008(E) standard for reflectivity measurements of EM materials was used. The frequency stability of the oscillator was controlled at the 10−6 level by a frequency meter. The power used was 7.0 mW ± 10 μW. The error on the measured EM attenuation was 7% in the range 0 to −40 dB. The ratios of transmitted/input (S21) and reflected/input (S11) signals were measured at 30 GHz before and after insertion of the specimen into the waveguide. The lateral dimensions of the samples fitted precisely the waveguide 7.2 × 3.4 mm2 cross section.
The transmission (T) and reflection (R) coefficients of graphene/PMMA sandwich structure consisting of one to four graphene layers were deduced from the measured S parameters. The measurements were performed for the two possible normal orientations of the samples: in the first orientation, the guided EM wave enters the sample through the silica substrate and leaves it from the graphene/PMMA side (upward), the second orientation (downward) being just the reverse. Fig. 3(a) displays the variation of the absorption coefficient A = 1 − T − Rversus the number N of graphene/PMMA units for the upward geometry: the absorbance varies between 25% (one graphene layer) to 48% (four graphene layers). The silica substrate and PMMA being non-absorbing in the Ka band, all the incident EM power is absorbed by the graphene layers. The absorption coefficient is approximately a factor of 1.2 smaller for the downward geometry (Fig. 3(b)) compared to the upward geometry: A varies between 21% (one graphene layer) to 40% (four graphene layers). The transmission coefficient (Fig. 3(c)) is the same for both orientations of the sample. It decreases monotonously between 58% and 25%, the silica substrate itself reflects 21% of the incident radiation.
Absorption (a,b) and transmission (c) coefficients at 30 GHz of graphene/PMMA multilayers on silica containing  graphene/PMMA units. In panel (a), the incident EM waves come from the side of the silica substrate (upward orientation of the graphene/PMMA sandwiches), in (b) they come from the other side of the samples (downward). The upward or downward orientation of the samples has no influence on the transmission. Both measured and calculated (eq. 5) values are represented.
graphene/PMMA units. In panel (a), the incident EM waves come from the side of the silica substrate (upward orientation of the graphene/PMMA sandwiches), in (b) they come from the other side of the samples (downward). The upward or downward orientation of the samples has no influence on the transmission. Both measured and calculated (eq. 5) values are represented.
Theory
Before proceeding to a quantitative analysis of these measurements, it is worth understanding why graphene is so good in absorbing EM radiations in the Ka band. Indeed, a single graphene layer was shown to absorb 21 to 25% of the incident radiation3, which is a lot for a one-atom thick material. For a qualitative explanation, it is sufficient to refer to the Fresnel formulas for the transmission and reflection of a plane wave at the interface between two dielectric media when the interface sustains an infinitely thin –at the scale of the incident wavelength– conducting layer. In normal incidence, the electric and magnetic fields are parallel to the interface. Their amplitudes must satisfy the boundary conditions

where the subscripts i, r and t refer to the incident, reflected and transmitted waves, respectively. The last term in the second relation is the surface current density induced by the electric field in the interfacial layer with sheet conductance σ. Starting from the boundary conditions (eq. 1), the reflectance R, transmittance T and absorbance A of the interfacial layer between media with refractive indices n1 and n2 are readily derived11,12. In particular,

where  is the vacuum permittivity and c the speed of light in vacuum. Both T and A are functions of the real and imaginary parts of the interfacial layer conductance. The maximum of absorbance is reached when Im σ = 0 and
is the vacuum permittivity and c the speed of light in vacuum. Both T and A are functions of the real and imaginary parts of the interfacial layer conductance. The maximum of absorbance is reached when Im σ = 0 and  . The maximum value of A is n1/(n1 + n2). When EM radiations propagating in air (n1 = 1) enter a dielectric medium coated by a thin conductive layer (analogue of the downward sample orientation, Fig. 3(b)), the bigger the refractive index n2 of the dielectric, the lower the absorbance. However if EM radiations propagate in the opposite direction, i.e. from the dielectric medium to air (n2 = 1) (analogue of the upward sample orientation, Fig. 3(a)), the bigger the refractive index n1 of the dielectric, the higher the absorbance. In particular the absorbance can exceed 50% when n1 > n211. Reaching maximum absorption requires
. The maximum value of A is n1/(n1 + n2). When EM radiations propagating in air (n1 = 1) enter a dielectric medium coated by a thin conductive layer (analogue of the downward sample orientation, Fig. 3(b)), the bigger the refractive index n2 of the dielectric, the lower the absorbance. However if EM radiations propagate in the opposite direction, i.e. from the dielectric medium to air (n2 = 1) (analogue of the upward sample orientation, Fig. 3(a)), the bigger the refractive index n1 of the dielectric, the higher the absorbance. In particular the absorbance can exceed 50% when n1 > n211. Reaching maximum absorption requires  , typically.
, typically.
As shown below,  for a single graphene layer already reaches 0.32 in the Ka band. Such a large value of the sheet conductance comes from intraband transitions almost exclusively and is determined by Drude type conductivity. Indeed, even a very small doping of graphene blocks the interband transitions for frequencies in the GHz domain and below13,14. This is not the case in the optical range, where the intraband transitions are much less efficient than the interband transitions, the latter yielding the well-known result13,15
for a single graphene layer already reaches 0.32 in the Ka band. Such a large value of the sheet conductance comes from intraband transitions almost exclusively and is determined by Drude type conductivity. Indeed, even a very small doping of graphene blocks the interband transitions for frequencies in the GHz domain and below13,14. This is not the case in the optical range, where the intraband transitions are much less efficient than the interband transitions, the latter yielding the well-known result13,15 .
.
For a quantitative interpretation of the experimental data plotted in Fig. 3, plane waves must be replaced by guided waves2. The electromagnetic field propagating in a plane-stratified medium put inside a waveguide can be expressed in terms of the longitudinal electric and magnetic components

where the ± signs label the incident and reflected modes counter-propagating along the waveguide axis (z direction) and subscript j = 1, 2 and 3 label air, PMMA and silica, respectively. In eqs.(3),  ,
,  and Kj are the relative dielectric permittivity, wavevector and the mode propagation constant in the jth medium, respectively. For the transverse electric TE01 mode of a rectangular waveguide, Ez = 0 while the longitudinal magnetic component Hz can be presented in the following form:
and Kj are the relative dielectric permittivity, wavevector and the mode propagation constant in the jth medium, respectively. For the transverse electric TE01 mode of a rectangular waveguide, Ez = 0 while the longitudinal magnetic component Hz can be presented in the following form:

where a is the waveguide dimension in x direction,  . In Eq. 4,
. In Eq. 4,  are the mode amplitudes in the jth medium that are related to each other through the boundary conditions (eq. 1) at the successive interfaces.
are the mode amplitudes in the jth medium that are related to each other through the boundary conditions (eq. 1) at the successive interfaces.
The PMMA layers, being transparent and having a very small optical thickness in the GHz domain, can be ignored. Thus a multilayer containing N graphene/PMMA units on its silica substrate behaves like a bilayer composed of the silica substrate slab and N non-interacting graphene sheets squeezed at one of its two interfaces with air. This simplified approach allows us to arrive at the following equations for the reflectance and transmittance of the graphene/PMMA sandwich placed in the waveguide for the upward (silica + graphene, R1 and T1) and downward (graphene + silica, R2 and T2) geometries, respectively:

Here α = Ksubstrate/Kair,  with σ1 the sheet conductance of a single graphene layer and e± = exp(±iKsubstrated) with d the substrate thickness.
with σ1 the sheet conductance of a single graphene layer and e± = exp(±iKsubstrated) with d the substrate thickness.
Discussion
The above formalism yields values of the absorption and transmission coefficients plotted in Fig. 3. The agreement with the experimental measurements is excellent. The dielectric constant of the silica substrate (d = 0.5 mm) used in the calculations was 3.716. The only adjustable parameter that remained in the theory was  , which was taken at 0.32. By comparison, the sheet conductance of graphene grown by CVD on Ni, measured between 1 GHz and 1 THz17, at the frequency of the experiment, ν = 30 GHz is very close (0.37) to our adjusted value. For six layer of graphene, the dimensionless sheet conductance is
, which was taken at 0.32. By comparison, the sheet conductance of graphene grown by CVD on Ni, measured between 1 GHz and 1 THz17, at the frequency of the experiment, ν = 30 GHz is very close (0.37) to our adjusted value. For six layer of graphene, the dimensionless sheet conductance is  . It is worth mentioning that a graphite slab having a thickness equivalent to 6 graphene layers (2 nm) would give
. It is worth mentioning that a graphite slab having a thickness equivalent to 6 graphene layers (2 nm) would give  , 20 time smaller than here if we take a typical value 125000 S/m for the in-plane conductance of graphite. This simple argument demonstrates the tremendous superiority of separated graphene planes over graphite in the present context.
, 20 time smaller than here if we take a typical value 125000 S/m for the in-plane conductance of graphite. This simple argument demonstrates the tremendous superiority of separated graphene planes over graphite in the present context.
The calculated dependence of the absorbance on the number N of graphene layers for both upward and downward geometries is plotted in Fig. 4. There is a point with maximum absorption equal to 54% for the upward geometry and 41% for the downward geometry. In each case, the maximum corresponds to six graphene layers. The transmission computed for N = 6 is 21% for both sample orientations.
Such an interesting electromagnetic response of the sandwich structure can be captured by eq. 2. Forgetting the PMMA spacers, which are very thin compared to wavelength, the interfacial conducting layer stands for the number N of graphene layers contained in the graphene/polymer multilayer, with total conductivity σ = Nσ1. The two dielectric media are the air and the silica substrate. It follows from eq. 2 that the transmission coefficient decreases monotonously with N. The absorption A increases, reaches a maximum value at some Nopt as mentioned above and then decreases asymptotically like 1/N. The asymmetry of the absorption for both sample orientations can be qualitatively understood from the presence of the prefactor n1 in the expression (Eq. 2) of A. For a self-supported film (n1 = n2 = 1), the maximum absorption would be 50%.
The overall thickness of a graphene/PMMA sandwich sample containing 6 graphene layers is about 4.2 μm, not including the silica substrate. The overall thickness could be reduced to 2 μm by using twice as thin PMMA films. A metallic film of 2-μm thickness would give better shielding efficiency than graphene/PMMA multilayers of equivalent thickness. However, the low transmittance of a metallic film is the result of high reflectivity more than than high absorption. For applications where reflecting microwaves back is not desirable, absorption must be favoured over reflection, which requires decreasing the film thickness drastically. For ultrathin aluminium films on glass, for instance, the maximum of absorption at 37.5 GHz is realized for a film thickness of 2.5 nm18 and reaches 50% in the upward geometry. Graphene makes it possible to obtain similar and even slightly better characteristics, not mentioning the big advantages of graphene over any artificial metallic layer that are its high flexibility and mechanical strength.
Conclusions
To summarize, we have demonstrated both experimentally and theoretically a remarkable shielding efficiency in the Ka band of graphene layers separated by thin PMMA films. The transmission coefficient of the multilayers decreases monotonously with the number of graphene/PMMA units. At 30 GHz and around, the absorption coefficient reaches a maximum for 6 graphene layers, which is the optimum number. The largest contribution to the shielding then comes from radiation absorption by the separated graphene layers. Increasing the number of layers above the optimum value lowers the absorption coefficient and increases the reflection contribution to the shielding. A strong radiation absorption by extremely small thickness of graphene sandwiches is very appealing for nanodevice shielding applications and for the detection of low-power electromagnetic signals. It is worth mentioning that the idea of using graphene/dielectric multilayers for EM wave absorption is not new. An ultra-broadband absorbing multilayer operating in the THz has been theoretically proposed7. In this device, the graphene layers are patterned at the micrometer scale in order to generate high-order surface plasmon resonances. Nothing similar is required with our devices, which are much simplest, but work at smaller frequencies. Still, experiments performed by time domain spectroscopy on one samples containing three graphene/PMMA units was shown to shield (by absorption and reflection) 75% of the incident power at 1 THz, which remains appreciable.
References
Ott, H. Electromagnetic compatibility engineering (John Wiley and Sons, New York 2009).
Batrakov, K. et al. Enhanced microwave shielding effectiveness of ultrathin pyrolytic carbon films. Appl. Phys. Lett. 103, 073117-1-3 (2013).
Kuzhir, P. et al. Multilayered graphene in Ka-band: Nanoscale coating for aerospace applications. J. Nanosci. Nanotechn. 13, 5864–5867 (2013).
Latil, S. & Henrard, L. Charge carriers in few-layer graphene films. Phys. Rev. Lett. 97, 036803-1-4 (2006).
Charlier, J. C., Gonze, X. & Michenaud, J. P. First-principles study of the electronic properties of graphite. Phys. Rev. B 43, 4579–4589 (1991).
Bae, S. et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes. Nature Nanotechn. 5, 574–578 (2010).
Amin, M., Farhat, M. & Bağcι, H. An ultra-broadband multilayered graphene absorber. Optic Express 21, 29938.1–10 (2013).
Li, X. et al. Transfer of Large-Area Graphene Films for High-Performance Transparent Conductive Electrodes. Nano Lett. 9, 4359–4363 (2009).
Gaskell, P. E., Skulason, H. S., Rodenchuk, C. & Szkopek, T. Counting graphene layers on glass via optical reflection microscopy. Appl. Phys. Lett. 94, 143101-1-3 (2009).
Malard, L. M., Pimenta, M., Dresselhaus, G. & Dresselhaus, M. Raman spectroscopy in graphene. Phys. Rep. 473, 51–87 (2009).
Apell, S. P., Hanson, G. W. & Hägglund, C. High optical absorption in graphene. eprint arXiv 1201.3071 (2012).
Bludov, Yu. V., Peres, N. M. R. & Vasilevskiy, M. I. Unusual reflection of electromagnetic radiation from a stack of graphene layers at oblique incidence. J. Optics 15, 114004-1-13 (2013).
Falkovsky, L. A. Optical properties of graphene. J. Phys.: Conf. Series 129, 012004-1-7 (2008).
Gusynin, V. P., Sharapov, S. G. & Carbotte, J. P. Unusual microwave response of Dirac quasi-particles in graphene. Phys. Rev. Lett. 96, 256802-1-4 (2006).
Mak, K. F. et al. Measurement of the optical conductivity of graphene. Phys. Rev. Lett. 101, 196405-1-4 (2008).
Lamb, J. W. Miscellaneous data on materials for millimetre and submillimetre optics. Intern. J. Infrared Milimeter Waves 17, 1997–2030 (1996).
Rouhi, N. et al. Broadband conductivity of graphene from DC to THz. 11th IEEE International conference on Nanotechnolgy. Portland, USA, p. 1205–1207 (2011).
Andreev, V. G., Vdovin, V. A. & Voronov, P. S. An experimental study of millimeter wave absorption in thin metal films. Techn Phys. Lett. 29, 953–955 (2003).
Acknowledgements
The work was partially supported by the EU FP7 IRSES projects FP7-247007 CACOMEL and FP7-318617 FAEMCAR and by the NP-Nano FiDiPro-project of the Finnish Funding agency for Technology and Innovation (TEKES). It has been performed within the context of the EU 7th Framework Programme under grant NO 604391 Graphene flagship.
Author information
Authors and Affiliations
Contributions
K.B. developed the theory for wave-guide geometry and prepared the figures; A.P. and S.V. performed the electromagnetic and optical measurements; T.K. made the samples together with A.P. and conducted the Raman experiments; P.K. and Y.S. analyzed the data and reviewed the manuscript together with S.M.; Ph.L. prepared the main manuscript text.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Batrakov, K., Kuzhir, P., Maksimenko, S. et al. Flexible transparent graphene/polymer multilayers for efficient electromagnetic field absorption. Sci Rep 4, 7191 (2014). https://doi.org/10.1038/srep07191
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07191
This article is cited by
-
A review on graphene and graphene composites for application in electromagnetic shielding
Graphene and 2D Materials (2023)
-
Effective EMI shielding behaviour of thin graphene/PMMA nanolaminates in the THz range
Nature Communications (2021)
-
Electromagnetic Properties of 3D Carbon-Based Porous Structures in High Frequency Range
Russian Physics Journal (2021)
-
Lightweight carbon-red mud hybrid foam toward fire-resistant and efficient shield against electromagnetic interference
Scientific Reports (2020)
-
An Analytical Study of Magneto-Plasmons in Anisotropic Multi-layer Structures Containing Magnetically Biased Graphene Sheets
Plasmonics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.