Abstract
Despite their wide spread applications, the mechanical behavior of helically coiled structures has evaded an accurate understanding at any length scale (nano to macro) mainly due to their geometrical complexity. The advent of helically coiled micro/nanoscale structures in nano-robotics, nano-inductors and impact protection coatings has necessitated the development of new methodologies for determining their shear and tensile properties. Accordingly, we developed a synergistic protocol which (i) integrates analytical, numerical (i.e., finite element using COMSOL®) and experimental (harmonic detection of resonance; HDR) methods to obtain an empirically validated closed form expression for the shear modulus and resonance frequency of a singly clamped helically coiled carbon nanowire (HCNW) and (ii) circumvents the need for solving 12th order differential equations. From the experimental standpoint, a visual detection of resonances (using in situ scanning electron microscopy) combined with HDR revealed intriguing non-planar resonance modes at much lower driving forces relative to those needed for linear carbon nanotube cantilevers. Interestingly, despite the presence of mechanical and geometrical nonlinearities in the HCNW resonance behavior the ratio of the first two transverse modes f2/f1 was found to be similar to the ratio predicted by the Euler-Bernoulli theorem for linear cantilevers.
Similar content being viewed by others
Introduction
Nature has inspired scientists through its multitude of nonlinear complex structures that exhibit tailored properties and diverse functionalities on multiple length scales. For example, biomolecules including DNA, bacterial flagella and various proteins adapt nonlinear geometries, particularly spring-like or helically coiled morphologies (e.g., double-helix, α-coils or helices) which facilitate specific functionalities in living organisms. Indeed, this ubiquitous nanoscale helically coiled morphology has been proposed for enabling elastic memory devices1, flexible electronics2, impact protection3, nanoinductors and efficient electromagnetic shielding4. Albeit their enormous potential, helically coiled topologies suffer from poor characterization, especially mechanical properties and thus remain severely under-utilized in the realization of robust electronic, mechanical and optical devices. While a few studies have focused on investigating the elastic properties using axial elongation5/compression6 and atomic force microscopy (or force modulation microscopy)7,8,9, an in-depth study of the dynamic mechanical response of helically coiled structures is incomplete due to the difficulties involved in exciting purely longitudinal/transverse resonances. This difficulty stems from the distinct helical geometry which exhibits convoluted shear and tensile motions when the singly-clamped coil is transversely driven. Theoretically, the resulting motion is a set of coupled 12th order differential equations10,11 that are nearly impossible to analytically solve for the Eigen modes and their associated frequencies. In view of this mathematical complexity, helical coils are often treated as straight pillars8,12 without completely accounting for the shear/tensile component, which prevents the acquisition of accurate Eigen modes and frequencies.
Here, we employed the Harmonic Detection of Resonance (HDR) method13,14 to experimentally resonate isolated helically coiled nanowires (HCNWs) and deduced their shear modulus by concurrently validating experiments with analytical and numerical models. In particular, we developed an analytical model that elucidates the contribution of shear stress when a helical coil is subjected to a transverse moment. By collating the individual components of shear and bending stresses, we derived a closed form expression for the fundamental transverse resonance of HCNWs as a function of both the Young's (E) and the shear modulus (G). The values of G obtained in our analytical model provided only a coarse estimate due to several limitations imposed by our assumptions. Accordingly, we employed the numerical finite element COMSOL technique to find accurate G values from the coarse analytical estimates (Fig. 1). Furthermore, we observed intriguing resonance modes (e.g., circularly polarized mode) in HCNWs with a characteristic signature in the HDR signal, thus facilitating the electrical detection of nonlinear resonance modes. In general, we demonstrated that the HDR technique in tandem with our analytical model and COMSOL simulations can serve as a standard protocol for probing the shear properties of coiled geometries circumventing the need for solving 12th order differential equations.
The protocol followed during the study.
Three methods viz. experimental (using Harmonic Detection of Resonance), analytical and computational (COMSOL) are used in conjunction to create a model that predicts the resonance frequency (f) of the helically coiled nanowire (HCNW) and calculates the shear modulus (G) of its material.
Methods
A forest of randomly oriented HCNWs was synthesized using a previously reported two–stage, liquid precursor based thermal chemical vapor deposition (CVD) method15. The as-prepared HCNWs were characterized using scanning (SEM; Hitachi SU-6600) and transmission (TEM; Hitachi 9500) electron microscopy (Fig. 2). For further discussion, we introduced the following labels for the physical parameters of a HCNW (Fig. 3) r- radius of the wire; D- diameter of HCNW; p- pitch of HCNW; n- number of turns; l- length of HCNW (note that l = n.p); M- Moment experienced by a turn of HCNW upon bending with a radius of curvature ζ; and α-pitch angle of HCNW.
(a) Scanning electron microscope image of as-prepared HCNWs. The coiled structures are solid wires as evident in the transmission electron microscope (TEM) image shown in (b). The dotted region of (b) shows layered stacking at the surface of the coil in the high-resolution TEM image shown in (c). The selected area diffraction pattern (d) reconfirms the polycrystalline nature of HCNWs.
(a) Geometrical parameters of an HCNW (b) One turn of the coil modeled as a planar ring connected with a rigid rod, compensating for the pitch. (c) Left panel- one turn of the coil with no moment. Right Panel- Bending of the coil under Moment M. An imaginary cylinder (dashed lines) is a guide to understand the bending mechanism. (d) Vector diagram of the displacements upon bending as seen in (c).
For HDR experiments, an isolated HCNW mounted on an electrochemically etched tungsten tip (W-tip) was used as the cantilever (see supplementary information Fig. S1). The W-tip was brought into contact with a double-sided conducting carbon adhesive tape (PELCO TabsTM; Ted Pella) and then used to isolate a single HCNW from a forest. The HDR setup consists of another bare W-tip which serves as the counter electrode (CE) and a three-directional nano-positioning stage (PI Block Nano Positioning System) that facilitates a fine control of the relative orientation and gap distance between the cantilevered HCNW and the CE. The HDR setup was used with either an SEM chamber (Hitachi SU-6600 or S-3400) to provide a stable vacuum (<1 Pa) which mitigated damping losses, or a dark-field optical microscope (Nikon epiphot; 50× and 100× objective). Importantly, the mechanical resonances observed under the SEM were simultaneously detected “electrically” using the HDR method. The HCNW was actuated via an AC peak signal-Vac (to induce periodic motion) with a DC offset Vdc (to overcome work potentials). To avoid a zero crossing in the net excitation voltage (Vnet = Vac + Vdc), Vdc was maintained at values higher than Vac. For all experiments discussed below, Vdc was held constant at 9 V while Vac was varied within ±9 V. A detailed discussion of the HDR method can be found elsewhere16,17,18. Briefly, in the HDR method, a cantilever is actuated by either static or dynamic charge induction depending on several factors such as the presence of static charges, functional groups and intrinsic electrical conductivity of the cantilevered structure. In the absence of Vdc, the dynamic (static) charge induction mechanism often resulted in a vibration at twice (same) the driving frequency for well-grounded electrically conducting cantilevers19. Accordingly, we observed the motion of a cantilevered HCNW ~1 Hz under the dark-field optical microscope to confirm the presence of dynamic charge induction mechanism and ensure that HCNW was properly grounded. However, we observed that HCNWs were always positively charged when exposed to an electron beam, possibly due to the ejection of electrons. Nonetheless, the HCNWs were found to be neutral when the electron beam was turned off, as observed from our dark-field experiments.
In previous studies, we found a strong correlation between the presence of structural defects and the mechanical properties of nano-cantilevers20. In view of this correlation and to eliminate the effects of sample heterogeneity in this study, we consistently selected all HCNWs from the same synthesis batch (all HCNWs are identical in terms of chemical composition and defect density albeit differences in structural parameters; HCNW1- HCNW4 shown in Table 1). It is worth noting that the harmonics and resonance modes overlap in the traditional doubly clamped geometry, e.g., strings in a guitar; therefore, we used the singly clamped geometry to distinguish the resonance modes of HCNWs from their harmonics.
Results and discussion
Modeling
The transverse resonance frequency (f) of a singly clamped cantilever can be calculated by the well-known relationship, f = 1/2π (k/meff)1/2 where k is the spring constant and meff is the effective mass of the cantilever21. In contrast to a straight cantilever, k for the transverse bending mode of a HCNW is a function of both E and G of the material, which makes it difficult to compute the resonance frequencies. This motivated us to adapt the following protocol (see Fig. 1) to obtain an experimentally validated closed form expression for resonance frequency (fANA). We employed the HDR method to obtain the frequencies of first two modes (f1 and f2) of HCNWs and deduced their shear modulus by simultaneously validating experiments with analytical and numerical models.
Initially, we consider one turn under a moment (M) in the plane of the HCNW axis. To simplify the model, we approximated one HCNW turn as a planar ring connected with a rigid rod as shown by Wahl22 (Fig. 3b). The bending of the HCNW due to the application of electrical driving force in our experiments naturally creates an internal shear stress. The resulting deflection angle ϕ (Fig. 3c) of a turn (under M) of the HCNW is a sum of bending (ϕb) and twisting (ϕt) angles:

where I = πr4/4 and J = πr4/2 are the area and polar moments of inertia of the HCNW (See supporting information and Fig. S2). Note that an extra factor of cos2α was included in equation 1 to compensate for larger pitch angles (see supporting information). For a complete turn of a HCNW, k is defined as F/z where z is the resulting displacement due to the force F acting on a single turn. As shown Fig. 3d, z may be expressed as a function of ϕ and p under the small angle approximation (see supporting information) as: 
Since F = M/p = kz in a HCNW,

Hence for one complete turn, equations (1) and (2) yield

Equation 3 is obtained by combining the components due to bending  and twisting
and twisting  of the HCNW.
of the HCNW.
For a HCNW of n turns, we can obtain the spring constant from equations (2) and (3) by incorporating an n3 term, analogous to a straight cantilever (Fig. S3),

Hence, we can then obtain fANA as

which was validated by comparing to iteratively calculated resonance frequencies (cf. Fig. 1).
Next, using a finite element based COMSOL technique, we simulated the resonance frequency fCOM for various HCNWs with different geometric parameters (n, r, D, p). Based on our COMSOL results, fANA matched within 12% of fCOM, which was scaled by a dimensionless factor s = 0.88 to account for the simplification of a HCNW to a planar ring attached to a rigid rod

The closed-form expression (equation 6) is a solution for HCNW resonance frequency, which includes the effects of both E and G. As described in Fig. 1, experimentally obtained resonance parameters of HCNWs can be used in conjunction with equation 6 to obtain G. It is noteworthy that equation 6 is not limited to HCNWs and may be used to obtain the G (or f) of any helically coiled geometry whose E and f (or G) are known.
Measuring resonance parameters
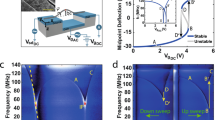
The flexural spring constant of HCNWs is expected to be lower than its axial spring constant due to their moderately high aspect ratio (ratio of length to diameter of the HCNW ~ 102). Hence, the probability of actuating transverse resonance modes (perpendicular to HCNW axis) is much higher relative to axial modes (parallel to HCNW axis). Figs. 4a–4c and 4d–4e show the transverse modes for two different HCNWs (parameters listed in Table 1), HCNW1 (r- 63.5 nm; D-290 nm; p- 876 nm; l- 42.4 μm) and HCNW2 (r- 112 nm; D-750 nm; p- 1116.3 nm; l- 26.8 μm). A direct visual examination under the SEM revealed that the HCNW1 (HCNW2) resonated at frequency f1 ~ 30 kHz (82.35 kHz) at its first mode (Fig. 4b) and at f2 ~ 190 kHz (547 kHz) at its second mode (Fig. 4c). The corresponding HDR amplitude signal for the first mode of HCNW2 (excited with 5 Vac at ~1 Pa; Fig. 4f) showed a single transverse resonance peak with a quality factor (defined as the resonance frequency/full width at half maximum of the power spectrum) of ~150.
SEM images of a singly clamped HCNWs.
(a) HCNW1 (radius 63.5 nm; coil diameter 290 nm; pitch 876 nm) off resonance, (b) first and (c) second transverse modes of HCNW1 at driving frequency f1 ~ 30 kHz and f2 ~ 190 kHz.The dotted lines serve as a guide to the eye. (d) HCNW2 (radius 112 nm; coil diameter 750 nm; pitch 1116.3 nm) off resonance (e) first transverse mode of HCNW2 (f1 ~ 82.5 kHz). (f) Harmonic Detection of Resonance (HDR) signal (amplitude in blue trace and phase in black trace) for transverse mode for HCNW2 with driving voltages Vac = 5 V, Vdc = 9 V.
To examine the coupling between bending and shearing moduli of ‘geometrically’ nonlinear HCNW cantilevers, we actuated HCNWs at a higher driving force by either increasing the AC driving voltage (~8 Vac) or reducing the gap distance between HCNW and the CE. A higher driving force was observed to result in ‘mechanical’ nonlinearities such as the characteristic Duffing-like jumps in cantilever motion (see Fig. 5). Interestingly, as shown in Fig. 5, we found that: i) the HCNWs resonated in a non-planar circular mode when the driving voltage was increased >8 Vac (or the gap distance is reduced <5 μm) and ii) simultaneous with the observation of the circular mode, the HDR amplitude signal exhibited a bifurcation of an otherwise single transverse resonance peak (Fig. 5b). Through visual comparison, we confirmed that the lower (higher) frequency peak corresponded only to the planar transverse (non-planar circular) resonance. As we varied the driving frequencies (from 85 to 95 kHz), we observed the onset of the non-planar modes between 90–94 kHz and a clear rotation of the plane of resonance (circular mode as seen in Fig. 5a). As shown in Fig. S4, the onset of non-planar motion was also evident for an independent HCNW3 (r- 103 nm; D-330 nm; p- 1014 nm; l- 40.6 μm, see Table 1). During the reverse frequency sweep, we observed a typical hysteresis (as indicated by the hatched area in Fig. 5b) associated with mechanical nonlinearities (i.e., non-planar circular mode). The hysteresis was more prominent for the higher frequency peak or circular mode (gray) relative to the lower frequency peak or transverse mode (green). It is worth noting that the bifurcation of the resonance signal disappeared upon restoring the initial actuation conditions (i.e., Vac ~ 5 V) indicating that the difference between the driving forces necessary for actuating planar vs. non-planar mechanical modes is significantly low for HCNWs relative to straight cantilevers (e.g., multi–wall carbon nanotube or MWCNTs). Indeed, the high actuation threshold for non-planar modes in straight cantilevers has been a major bottleneck in understanding mechanical nonlinearities (e.g., Duffing-like circular modes). Although non-planar modes were reported previously in some straight nanocantilevers23 (SiC nanowires, MWCNTs and Si nanocantilevers24), the necessary driving force was sufficiently large to destroy the samples impeding detailed studies of their nonlinear mechanical behavior. The helically coiled geometry plays a pivotal role in enabling the actuation of otherwise inaccessible non-planar modes at significantly lower AC voltages (~8 V) due to two reasons: i) a low transverse k of HCNWs allows them to bend easily relative to their straight counterparts (e.g., MWCNT); and ii) the inherent asymmetry of HCNWs separates the otherwise degenerate x-, y-polarizations in mechanical resonance. As described below, our numerical analysis using COMSOL also confirmed that the helically coiled geometry leads to non-degenerate x-, y-planar modes that can be actuated simultaneously to produce the observed non-planar modes (see Fig. S5). Although the nature of the electrical force in HDR experiments is such that it favors the excitation of only one of the two (x or y) modes, the coupling between bending and shear moduli in a HCNW provides a channel for the exchange of energy between x- and y-modes resulting in non-planar resonance. Therefore, the resonance analysis of other materials (e.g., Si and ZnO) in their helically coiled geometry will allow for elucidating the nonlinear mechanical properties without breaking or destroying the cantilever. We also attempted to actuate a purely axial mode parallel to the axis of HCNW by placing a blunt W–tip in tip–to–tip geometry (3 Vac, 9–10 Vdc) with HCNW. However, the parametric nature of the driving force always resulted in an asymmetric combination mode (distinct from the circular mode) consisting of transverse resonance and axial stretching (Fig. 6).
Returning to Fig. 1, the analysis of transverse resonance modes in COMSOL revealed that the ratio of the second and first modes (f2/f1) is 6.27- a ratio predicted by Euler-Bernoulli (EB) theory exclusively for straight cantilevers. Our HDR experiments showed that f2/f1 ~ 6.75 ± 0.38 for 3 different HCNWs, deviating only slightly from the straight cantilever case, in agreement with COMSOL. The experimental and COMSOL results prove that although EB theory is insufficient to predict the motion of HCNWs accurately, the ratio f2/f1 is a true transcendental constant independent of the geometry of the resonating cantilever. Such an observation allows us to predict the second mode of transverse resonance by the following relation

The protocol described in Fig. 1 was applied to HCNWs to obtain their shear modulus (G). The HCNWs isolated for HDR studies were carefully characterized to accurately obtain r, R, p and n. We calculated the HCNW resonance frequency (fCOM) using Eigen-frequency study under the fixed-free boundary condition and a fine mesh construction for a numerically stable solution in COMSOL. We used equation 6, experimental HDR results and an estimated E = 120 GPa (similar to MWCNTs) to obtain an initial estimate for GANA for HCNWs. Subsequently, we implemented a series of COMSOL simulations on HCNWs 1–4 (see Table 1) by varying E ~ 80–200 GPa (in steps of ~20 GPa) and G ~ 5–10 GPa (in steps of ~1 GPa) to obtain a fCOM that matched f1. Since there could be more than one set of E & G values that could result in a fcom ~ f1, we used the experimental and COMSOL data from HCNWs 1–4 to identify correct E and G values. As shown in Table 1, HCNW 1–4 resulted in a GCOM value ranging from 5.8 to 10.3 GPa with an average value of ~8 ± 2 GPa.
The Poisson ratio(υ = E/2G-1) of HCNWs was found to be as high as 2.88–16.24 based on the values of GCOM shown in Table 1 suggesting that the HCNWs may be anisotropic i.e., the elastic properties are different in the direction parallel and perpendicular to the axis, or that HCNWs are inhomogeneous.
Conclusion
In summary, we mechanically resonated HCNWs and studied their resonance modes using the HDR technique. Clearly the HDR electrical signals were found to inherently carry the signature of the excited resonance mode (circular vs planar) as seen under an SEM. We developed a model (based on experimental, analytical and numerical methods) capable of predicting the first and the second transverse resonance modes applicable to any helically coiled cantilevers irrespective of their dimensions. Our experiments showed that HCNWs had a shear modulus ~8 ± 2 GPa. The corresponding Poisson ratios suggested a possible anisotropy in the HCNWs.
References
Joo-han, C., Kang, D.-h., Young-kwan, C. & Wan-jun, P. Patent No. US 7,816,175 B2. (2010).
Xu, F., Lu, W. & Zhu, Y. Controlled 3D Buckling of Silicon Nanowires for Stretchable Electronics. Acs Nano 5, 672–678 (2010).
Daraio, C., Nesterenko, V. F., Jin, S., Wang, W. & Rao, A. M. Impact response by a foamlike forest of coiled carbon nanotubes. J Appl Phys 100 (2006).
Faraby, H. M., Rao, A. M. & Bandaru, P. R. Modeling High Energy Density Electrical Inductors Operating at THz Frequencies Based on Coiled Carbon Nanotubes. Ieee Electr Device L 34, 807–809 (2013).
Chen, X. et al. Mechanics of a Carbon Nanocoil. Nano Lett 3, 1299–1304 (2003).
Poggi, M. A. et al. Measuring the Compression of a Carbon Nanospring. Nano Lett 4, 1009–1016 (2004).
Volodin, A. et al. Imaging the elastic properties of coiled carbon nanotubes with atomic force microscopy. Phys Rev Lett 84, 3342–3345 (2000).
Volodin, A. et al. AFM detection of the mechanical resonances of coiled carbon nanotubes. Appl Phys A 72, S75–S78 (2001).
Volodin, A. et al. Coiled Carbon Nanotubes as Self-Sensing Mechanical Resonators. Nano Lett 4, 1775–1779 (2004).
Love, A. E. M. The propagation of waves of elastic displacement along a helical wire (n.p. 1899).
Lee, J. & Thompson, D. J. DYNAMIC STIFFNESS FORMULATION, FREE VIBRATION AND WAVE MOTION OF HELICAL SPRINGS. J Sound Vib 239, 297–320 (2001).
Sato, S., Pan, L. J., Nakayama, Y. & Akita, S. Resonant vibration of cantilevered carbon nanocoil. Microprocesses and Nanotechnology 2007, Digest of Papers, 468–469 (2007).
Saini, D., Behlow, H. W., Serkiz, S. M., Skove, M. J. & Rao, A. M. Harmonic Detection of Resonance: A Review. Recent Patents on Materials Science 7, 173–194 (2014).
Taylor, J. D. et al. [Harmonic detection of resonance mehods for micro- and nanocantilevers: Theory and selected application]. The Oxford Handbook of Nanoscience and Technology, Volume II: Materials [Narlikar A. V. and Fu Y. Y. (ed.)] [249–284] (Oxford University Press, New York, 2010).
Wang, W., Yang, K. Q., Gaillard, J., Bandaru, P. R. & Rao, A. M. Rational synthesis of helically coiled carbon nanowires and nanotubes through the use of tin and indium catalysts. Adv Mater 20, 179–182 (2008).
Gaillard, J., Skove, M. J., Ciocan, R. & Rao, A. M. Electrical detection of oscillations in microcantilevers and nanocantilevers. Rev Sci Instrum 77 (2006).
Ciocan, R., Gaillard, J., Skove, M. J. & Rao, A. M. Determination of the bending modulus of an individual multiwall carbon nanotube using an electric harmonic detection of resonance technique. Nano Lett 5, 2389–2393 (2005).
Dickel, D., Skove, M. J. & Rao, A. M. An analytic characterization of the harmonic detection of resonance method. J Appl Phys 106, 044515 (2009).
Saini, D. et al. Fundamental mechanism for electrically actuated mechanical resonances in ZnO nanowhiskers. Phys Rev B 86, 205312 (2012).
Gaillard, J., Skove, M. & Rao, A. M. Mechanical properties of chemical vapor deposition-grown multiwalled carbon nanotubes. Appl Phys Lett 86, 233109 (2005).
Younis, M. I. MEMS Linear and Nonlinear Statics and Dynamics [107–108] (Springer, New York, 2011).
Wahl, A. M. Mechanical Springs (McGraw-Hill Book Company, New York, 1963).
Perisanu, S. et al. Beyond the linear and Duffing regimes in nanomechanics: Circularly polarized mechanical resonances of nanocantilevers. Phys Rev B 81, 165440 (2010).
Villanueva, L. G. et al. Nonlinearity in nanomechanical cantilevers. Phys Rev B 87 (2013).
Acknowledgements
The authors are grateful to Lamar Durham and Jonathan Simpson, Physics Research Laboratory, for their assistance in fabrication of experimental set up; The authors are thankful to Dr. Keqin Yang for his assistance in CVD growth of HCNWs, Prof. Terry Tritt (Clemson University) for the use of the SEM S3400; Dr. JoAn Hudson (Electron microscopy facility, Clemson University) for allowing the use of SEM 6600 and Haijun Qian (Clemson University) for his assistance in TEM.
Author information
Authors and Affiliations
Contributions
D.S., B.P. and D.D. have done the experiments. D.S., H.B. and M.J.S. developed the analytical model. D.S. validated experimental results using numerical methods. D.S., H.B., S.M.S., M.J.S., R.P. and A.M.R. analyzed the data. D.S., R.P. and A.M.R. drafted the results.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Mechanical Resonances of Helically Coiled Carbon Nanowires
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Saini, D., Behlow, H., Podila, R. et al. Mechanical Resonances of Helically Coiled Carbon Nanowires. Sci Rep 4, 5542 (2014). https://doi.org/10.1038/srep05542
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05542
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.