Abstract
Soccer balls are typically constructed from 32 pentagonal and hexagonal panels. Recently, however, newer balls named Cafusa, Teamgeist 2 and Jabulani were respectively produced from 32, 14 and 8 panels with shapes and designs dramatically different from those of conventional balls. The newest type of ball, named Brazuca, was produced from six panels and will be used in the 2014 FIFA World Cup in Brazil. There have, however, been few studies on the aerodynamic properties of balls constructed from different numbers and shapes of panels. Hence, we used wind tunnel tests and a kick-robot to examine the relationship between the panel shape and orientation of modern soccer balls and their aerodynamic and flight characteristics. We observed a correlation between the wind tunnel test results and the actual ball trajectories and also clarified how the panel characteristics affected the flight of the ball, which enabled prediction of the trajectory.
Similar content being viewed by others
Introduction
The uniqueness of the shape and design of a ball to a particular sport has meant that there were very little changes over time. However, in more recent years, there have been dramatic changes in the shape and design of soccer balls. Particularly, there have been substantial changes in the shape and design of the panels used to construct the official balls of FIFA World Cup tournaments. The Teamgeist 2, which was the official ball of the 2008 EURO Cup in Austria and Swiss, comprised 14 panels and was significantly different from a conventional soccer ball, which is typically constructed from 32 pentagonal and hexagonal panels. The revolutionary shape of the 14-panel Teamgeist 2 has attracted much attention. At the 2010 FIFA World Cup in South Africa, an eight-panel ball produced by Adidas, named Jabulani, was introduced, which incorporated further modification of the shapes of the panels. The 2013 FIFA Confederations Cup in Brazil adopted another 32-panel ball produced by Adidas as the official ball. The latter ball, named Cafusa, is presently used by many professional soccer leagues and for international matches. Similar to a conventional ball, a Cafusa ball comprises 32 panels. However, whereas the panels of a conventional ball are pentagonal and hexagonal and are arranged in a simple manner, those of a Cafusa ball significantly differ in shape and orientation, although they can be roughly classified into two orientations with eight panels. At the upcoming 2014 FIFA World Cup, which will be held in Brazil, the Brazuca, a six-panel ball also produced by Adidas, will be the official ball.
Previous aerodynamics studies on soccer balls can be broadly divided into those that examined the basic aerodynamic properties by wind tunnel tests1,2, those that analytically determined the flight characteristics using various techniques including simulations3,4,5 and those that measured the actual flight paths6,7. There have also been studies in recent years to examine the flight characteristics of soccer balls using both the wind tunnel and actual flight paths8,9,10. Furthermore, there was a recent report on the effect of the surface geometry on the flight trajectory, which was determined by trajectory analysis and high-speed cameras11. In a more recent study, trajectory analysis and wind tunnel experiments were used to glean information for comparing the non-spin aerodynamics of Jabulani and Brazuca12.
However, there has been no study on the correlation between the results of wind tunnel tests and the actual flight paths of soccer balls with respect to the shape, number and orientation of their panels. Thus, in the present study, we examined this correlation using modern soccer balls, including the Brazuca and also investigated the extent to which wind tunnel test results could explain the actual flight path of a soccer ball. Based on the observed correlation between the wind tunnel results and the actual ball trajectories, we clarified how the panel characteristics affect the flight of a soccer ball, which enables prediction of the trajectory.
Results
Drag force in the wind tunnel
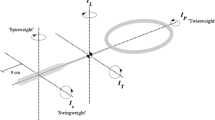
The wind tunnel tests were conducted using different new soccer balls, namely, Brazuca (Adidas, six-panel), Cafusa (Adidas, 32-panel), Jabulani (Adidas, eight-panel), Teamgeist 2 (Adidas, 14-panel) and conventional (Vantaggio, Molten, 32-panel). The balls were mounted as shown in Figure 1. Two panel orientations of the soccer balls identified as orientations A and B (see Figure 2) were used for the study and the corresponding aerodynamic properties were measured.
Soccer balls used for the test and their panel orientations.
(a, b) Adidas Brazuca: small dimple and six panels, (c, d) Adidas Cafusa: small grip texture and 32 modified panels, (e, f) Adidas Jabulani: small ridges or protrusions and eight panels, (g, h) Adidas Teamgeist 2: small protuberances and 14 panels; (i, j) Molten Vantaggio (conventional soccer ball): smooth surface and 32 pentagonal and hexagonal panels. (Photo by S.H.).
It was observed that the drag varied substantially with the ball type (Figure 3). The variation of the drag coefficient with the panel orientation was also significant for Cafusa and Jabulani, whereas it was relatively small for Brazuca, Teamgeist 2 and the conventional ball. The drag crisis regime, which indicates a sudden change in the drag coefficient Cd, was lowest for Brazuca, followed by the conventional ball, Cafusa, Teamgeist 2 and Jabulani, in increasing order. In the case of Cafusa, Cd decreased from ~0.5 to ~0.2 or less at a Reynolds number Re of 1.7 × 105 for panel orientation A and at Re of 1.5 × 105 for panel orientation B (Figure 3b). The critical Reynolds numbers for Cafusa were ~2.9 × 105 (Cd ≈ 0.14) and ~2.4 × 105 (Cd ≈ 0.16) for panel orientations A and B, respectively. The critical Reynolds number for Jabulani for panel orientation B was ~3.6 × 105 (Cd ≈ 0.12), which was less than the value of ~3.3 × 105 (Cd ≈ 0.16) for panel orientation A. These values were less than those for the other balls (Figure 3c). The variation of the drag coefficient with the panel orientation was observed to be small for Brazuca, Teamgeist 2 and the conventional ball (Figures 3a, 3d and 3e). The critical Reynolds numbers for Brazuca were determined to be ~2.5 × 105 (Cd ≈ 0.15) and ~2.2 × 105 (Cd ≈ 0.16) for panel orientations A and B, respectively. The corresponding values for Teamgeist 2 were ~3.0 × 105 (Cd ≈ 0.17) and ~2.8 × 105 (Cd ≈ 0.15) and those for the conventional ball were ~2.5 × 105 (Cd ≈ 0.16) and ~2.8 × 105 (Cd ≈ 0.17), respectively. It was further observed that the variation of the drag on Jabulani with the panel orientation was relatively substantial for Reynolds numbers in the range of 3.0 × 105–5.0 × 105.
Side and lift forces in the wind tunnel
Figure 4 shows the scatter diagrams of the lift and side forces that acted on the soccer balls. The diagrams indicate that the irregular fluctuations increased as the flow velocity was increased from 20 to 30 m·s−1. The same trend was observed when the panel orientations were changed. The change in the irregular fluctuation with increasing speed was least for Teamgeist 2 (Figures 4g-1 and 4h-1) and greatest for panel orientation A of Jabulani (Figure 4f-1). The irregular fluctuation was more prominent for the conventional ball when the flow velocity increased. The SD of the side and lift forces also increased with increasing flow velocity (Figures 4k and 4l). This trend was also observed when the panel orientation was changed. The SD of the forces was highest for Jabulani for a flow velocity of 20 m·s−1 and the irregular fluctuations were observed at the intermediate velocity. The SD of the side forces for panel orientation A of Jabulani did not increase with increasing flow velocity. Furthermore, the SD of the side and lift forces for panel orientation B of Jabulani decreased with increasing flow velocity, which was different from the cases of the other balls.
Scatter plots of the side and lift forces of the balls and SDs of the respective forces for each flow velocity (after 9 s).
As the flow velocity increased from 20 m·s−1 (a–j) to 30 m·s−1 (a-1– j-1), the irregular fluctuations of the side and lift forces increased. The SD of the side (k) and lift (l) forces increased with increasing flow velocity.
The correlation between the growth rates of the SD of the side and lift forces when the flow velocity was increased from 20 to 30 m·s−1 and the extended total distances of the panel bonds are shown in Figure 5. Here, the growth rate is defined as the average of the SD of the side and lift forces. The extended total distance of the panel bonds and the number of panels were as follows: 3.32 m and six panels for Brazuca, 4.47 m and 32 panels for Cafusa, 1.98 m and eight panels for Jabulani, 3.47 m and 14 panels for Teamgeist 2 and 3.84 m and 32 panels for the conventional ball. A strong correlation was observed between these parameters and the flow velocity increment (r = 0.64).
Figure 6 shows the unsteady aerodynamic forces (side force and lift force) of each soccer ball as amplitudes in the low-frequency range (10 Hz and lower) as per Fast Fourier Transform (FFT). This tended to increase the amplitudes by approximately 2.5 Hz in most cases. In particular, panel orientation B of the Jabulani ball (Figures 6f and 6f-1) and panel orientation B of the conventional ball (Figures 6j and 6j-1) indicated greater amplitudes compared to the other soccer balls in this lower frequency region (2.5 Hz).
Deviations of the coordinates of the impact points
The balls were actually launched by an impact-type kick robot toward a goal net 25 m away and the points at which they hit the goal net were plotted as shown in Figure 7. The initial velocity of the launch was 30 m·s−1 and the number of ball rotations was less than 1 (no rotation). The launch was repeated 20 times for each panel orientation of each type of ball. The points of impact of Brazuca and the conventional ball were observed to be relatively stable, whereas those of the other three balls (Cafusa, Jabulani and Teamgeist 2) varied substantially with the panel orientation. The impact of Jabulani was unstable and its trajectory varied considerably with the panel orientation (Figure 7c). The trajectories of Cafusa and Teamgeist 2 also varied significantly with the panel orientation (Figures 7b and 7d). The changes in the flight characteristics (points of impact) of Cafusa and Teamgeist 2 with the panel orientation were particularly drastic, which indicated that their panel orientation significantly affected their flight characteristics. Brazuca and the conventional ball exhibited relatively stable and regular flight trajectories compared to Cafusa, Teamgeist 2 and Jabulani, whose panel shapes varied significantly with the orientation and were characterized by relatively irregular flight trajectories. Despite Cafusa having the same number of panels (32) as the conventional ball, it exhibited a large variation in its flight trajectory with the panel orientation.
Furthermore, the standard deviations (SDs) of the impact point of Cafusa for orientations A and B were respectively 0.17 and 0.16 m in the vertical direction and 0.36 and 0.68 m in the horizontal direction. The corresponding values for Jabulani were 0.14 and 0.51 m and 0.49 and 0.43 m, those for Teamgeist 2 were 0.13 and 0.16 m and 0.22 and 0.32 m, those for the conventional ball were 0.36 and 0.19 m and 0.51 and 0.48 m and those for Brazuca were 0.45 and 0.22 m and 0.22 and 0.20 m. Thus, the SDs of the impact point of Cafusa for panel orientation B was the highest in the horizontal direction, whereas that of Jabulani for panel orientation B was the highest in the vertical direction.
In the scatter plots of the SDs in Figure 8, the horizontal axis represents the SDs of the side and lift forces, respectively and the vertical axis represents the horizontal and vertical SDs of the impact point of the ball on the goal, respectively. A strong correlation was observed between the SDs of the horizontal impact point and the side force (r = 0.62) (Figure 8a) and between the SDs of the vertical impact point and the lift force (r = 0.53) (Figure b).
Discussion
The results of the wind tunnel tests indicated that the drag on the Cafusa and Jabulani balls varied with their panel orientation. The drag crisis regime, in which a significant change in the drag occurs, was lowest for Brazuca, followed by the conventional, Cafusa, Teamgeist 2 and Jabulani, in increasing order. The results suggested that the aerodynamic force acting on the balls varied when their panel orientation was changed. These results are in accordance with a recent report on the drag characteristics of Brazuca and Jabulani12 and agree with the results from comparisons of Jabulani and Tango12 (official game balls for Euro 2012 with panel shapes identical to those of Cafusa)13. Our results also showed the same tendencies as those found in a prior study conducted on the four types of modern soccer balls (Jabulani, Teamgeist2, Tango12 and Roteiro)1. Preceding studies on drag characteristics of soccer balls reported that different types of soccer balls have different levels of aerodynamic forces9,14,15. Based on these findings, we verified the validity of our measurement system. Therefore, we argue that the drag acting on soccer balls varies depending on the type of ball and change in the panel orientation.
Regarding the relationship between the lift and side forces acting on the ball and the panel orientation, the variation of the irregular fluctuation was observed to increase as the flow velocity increased from 20 to 30 m·s−1 (Figure 4). The same trend was observed when the panel orientation was changed. However, the SDs for Jabulani were much higher than those for the other balls for the intermediate velocity of 20 m·s−1 and above. It was further observed that the SDs for Jabulani did not increase with increasing flow velocity (Figures 4k and 4i). These observations suggested that Jabulani may fluctuate irregularly compared to the other balls at the intermediate velocity and above.
The growth rate of the average of the lift and side force when the flow velocity was increased from 20 to 30 m·s−1 was 380% for Cafusa, 322% for the conventional ball, 318% for Brazuca, 143% for Teamgeist 2 and 103% for Jabulani. The total distance of the ball bonds was 4.47 m for Cafusa, 3.84 m for the conventional ball, 3.32 m for Brazuca, 3.47 m for Teamgeist 2 and 1.98 m for Jabulani. It was observed that the total distance of the ball bonds was correlated with the growth rate of the average force. Therefore, when the ball velocity increased from the intermediate velocity (20 m·s−1) to a high velocity (30 m·s−1), the total distance of the ball bonds affected the variation of the lift and side forces.
The amplitude of the unsteady aerodynamic forces acting on the soccer balls tended to greatly vary depending on the type of soccer ball (Figure 6). In addition, we found that this amplitude is highly variable depending on the panel orientation, even when the soccer balls are identical. These results led us to conclude that the amplitude of the unsteady aerodynamic forces acting on soccer balls changes according to the number of panels as well as the directions they are facing.
The observed flight characteristics with respect to the point of impact of the balls when launched by an impact-type kick robot indicated that the trajectories of the balls were substantially affected by the orientation of the panel, implying that the panel orientation significantly affected the flight. It was also observed that balls with the same number of panels (Cafusa and the conventional ball) had different trajectories due to the differing panel shapes and orientations. It is thus our consideration that the panel shape and orientation have greater effects on the trajectory of a ball than the number of panels.
The effect of the panel orientation on the SDs of the lift and side forces in the wind tunnel was investigated. The growth rate of the horizontal SD when the velocity was increased from 20 to 30 m·s−1 was highest for Cafusa for panel orientation B (710%) and that of the vertical SD was highest for Jabulani for panel orientation B (870%). This substantiates the observation that the growth rate of the SD of the measured goal impact point was closely related to that of the wind tunnel test. This suggests that Cafusa is likely to wobble horizontally during flight and that Jabulani is likely to wobble vertically. The results of the kick robot tests indicated that the goal impact point of Cafusa varied significantly for panel orientation B compared to panel orientation A. This can be explained by the side and lift forces of the wind tunnel tests. The SDs of the side and lift forces for panel orientation B were 2.2 and 2.1 N, respectively. This is relatively high compared to those for panel orientation A (1.0 and 1.8 N, respectively) and panel orientation B (1.6 and 2.1 N, respectively). Regarding Jabulani, the SD of the goal impact points for panel orientation B was higher than that for panel orientation A. This was also supported by the wind tunnel test results, wherein the SDs of the goal impact points for panel orientation B (2.0 and 3.1 N, respectively) were higher than those for panel orientation A (1.1 and 1.4 N, respectively), which suggested that the irregular changes in the side and lift forces (Figure 4f-1) significantly affected the trajectory. This was also the trend for Brazuca and the conventional ball (Figures 4a-1, 4b-1, 4i-1 and 4j-1). Regarding Teamgeist 2, the SDs of the side and lift forces for panel orientation A were 0.6 and 0.9 N, respectively and those for panel orientation B were 0.7 and 0.9 N, respectively, which are lower than those for the other balls (Figures 4g-1 and 4h-1), implying that its goal impact points were more stable. The lift force transition for a flow velocity of 30 m·s−1 after 9 s for panel orientation B (−1.8 N) was greater than that for panel orientation A (0.5 N) and the difference affected the goal impact point. This suggested that the transition of the lift and side forces significantly affected the trajectory.
The observed strong correlation between the SD of the forces measured in the wind tunnel and the impact point determined from the kick robot tests suggests the possibility of predicting the trajectory of a ball. Furthermore, the observed effect of the panel orientation on the flight characteristics is beneficial for practical soccer coaching and the design of new soccer balls. The scientific clarification of the effects of different surface shapes (numbers and orientations of the panels) of soccer balls would facilitate the learning of more efficient shooting techniques, contribute to enhanced player performance and improve physical education teaching methods in schools. However, the factors that affect the aerodynamic forces acting on a soccer ball are not limited to the surface shape but also include the surface roughness and material, the bonding method and the symmetry of the panels. The effects of these other features would be clarified in a future study.
Methods
Wind tunnel tests
The tests were conducted in a closed-circuit wind tunnel (San Technologies Co., Ltd., Tochigi, Japan) at the University of Tsukuba. The maximum flow velocity of the tunnel was 55 m·s−1, the size of the blower outlet was 1.5 m × 1.5 m, the flow velocity distribution was within ±0.5% and the turbulence was 0.1% or less. The aerodynamic forces were measured for values of the flow velocity U ranging from 7 to 35 m·s−1 and different panel orientations, which were achieved by rotation. The panel orientations of the different balls are shown in Figure 6. The forces acting on the balls were measured using a sting-type six-component force detector (LMC-61256, Nissho Electric Works). Each measured aerodynamic force was converted into the drag coefficient Cd, lift coefficient Cl and side coefficient Cs using the following equations:



where ρ is the air density (1.2 kg·m−3), U is the flow rate and A is the projected area of the ball given by A = π × 0.112 m = 0.038 m2.
Kick robot tests
The flight characteristics of the soccer balls were investigated based on their point of impact on a goal net when launched by an impact-type kick robot. A real standard-sized soccer goal was positioned 25 m from the kick robot, which was used to kick the ball without spin from a point along the centre line of the goal. A semi-high-speed video camera (EX-F1, Casio Computer Co., Ltd., Tokyo, Japan; 300 fps; 720 × 480 pixels) was positioned 0.5 m to the left of the kick robot to record each kick.
The kick robot was used to launch the ball at an initial velocity of 30 m·s−1 without spin (less than 1 rotation). The point at which the ball hit the goal net was recorded by another camera of the same type as the first positioned 25 m in front of the goal. Each type of ball was launched 20 times for each panel orientation and the recorded points of impact were analysed.
References
Asai, T. & Seo, K. Aerodynamic drag of modern soccer balls. SpringerPlus 2, 171 (2013).
Passmore, M. et al. The aerodynamic performance of a range of FIFA-approved footballs. Proceedings of the Institution of Mechanical Engineers, Part P: J. Sports Eng. Technol. 226, 61–70 (2012).
Bray, K. & Kerwin, D. G. Modelling the flight of a soccer ball in a direct free kick. J. Sports Sci. 21, 75–85 (2003).
Cook, B. G. & Goff, J. E. Parameter space for successful soccer kicks. Eur. J. Phys. 27, 865–874 (2006).
Myers, T. G. & Mitchell, S. L. A mathematical analysis of the motion of an in-flight soccer ball. Sports Eng. 16, 29–41 (2013).
Asai, T. & Kamemoto, K. Flow structure of knuckling effect in footballs. J. Fluids Struct. 27, 727–733 (2011).
Hong, S. et al. Unsteady aerodynamic force on a knuckleball in soccer. Procedia Eng. 2, 2455–2460 (2010).
Goff, J. E. & Carré, M. J. Investigations into soccer aerodynamics via trajectory analysis and dust experiments. Procedia Eng. 34, 158–163 (2012).
Mizota, T. et al. The strange flight behaviour of slowly spinning soccer balls. Sci. Rep. 3, 1871; 10.1038/srep01871 (2013).
Rogers, D. et al. An experimental validation method of wind tunnel measurements on FIFA approved footballs using kicking tests in wind-free conditions. Procedia Eng. 2, 2481–2486 (2010).
Barber, S. & Carré, M. J. The effect of surface geometry on soccer ball trajectories. Sports Eng. 13, 47–55 (2010).
Goff, J. E., Asai, T. & Hong, S. A comparison of Jabulani and Brazuca non-spin aerodynamics. Proc JMechE Part P: J. Sports Eng. Technol. (in press)
Asai, T. et al. Characteristics of modern soccer balls. Procedia Eng. 34, 122–127 (2012).
Alam, F. et al. A Comparative Study of Football Aerodynamics. Procedia Eng. 34, 146–151 (2012).
Oggiano, L. & Sætran, L. Aerodynamics of modern soccer balls. Procedia Eng. 2, 2473–2479 (2010).
Acknowledgements
This work was supported by JSPS KAKENHI Grant Number 25750283 of the Ministry of Education, Culture, Sports, Science and Technology of the Japanese government.
Author information
Authors and Affiliations
Contributions
S.H. and T.A. designed the study and experiments. S.H. conducted the experiments and analysed the collected data. Both authors participated in the discussion of the experimental results and made contributions throughout the project and the writing of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Hong, S., Asai, T. Effect of panel shape of soccer ball on its flight characteristics. Sci Rep 4, 5068 (2014). https://doi.org/10.1038/srep05068
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep05068
This article is cited by
-
Aerodynamics of the newly approved football for the English Premier League 2020–21 season
Scientific Reports (2021)
-
Visualization of air flow around soccer ball using a particle image velocimetry
Scientific Reports (2015)
-
Secret publishing deals exposed
Nature (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.