Abstract
X-ray ptychography is a scanning variant of coherent diffractive imaging with the ability to image large fields of view at high resolution. It further allows imaging of non-isolated specimens and can produce quantitative mapping of the electron density distribution in 3D when combined with computed tomography. The method does not require imaging lenses, which makes it dose efficient and suitable to multi-keV X-rays, where efficient photon counting, pixelated detectors are available. Here we present the first highly resolved quantitative X-ray ptychographic tomography of an extended object yielding 16 nm isotropic 3D resolution recorded at 2 Å wavelength. This first-of-its-kind demonstration paves the way for ptychographic X-ray tomography to become a promising method for X-ray imaging of representative sample volumes at unmatched resolution, opening tremendous potential for characterizing samples in materials science and biology by filling the resolution gap between electron microscopy and other X-ray imaging techniques.
Similar content being viewed by others
Introduction
Computed tomography provides valuable information to materials science, biology and physics in a non-destructive way that is amenable to complementary tests during or after the measurement. Multi-keV X-rays provide a penetration depth allowing tomography of large and thus representative sample volumes. In the past few years, coherent diffractive imaging (CDI) has been established as one way to overcome limiting factors in resolution, such as X-ray imaging optics, which are replaced by phase retrieval algorithms1,2,3,4. A particularly robust modality of CDI is ptychography, where a sample is scanned in two dimensions perpendicular to a spatially confined coherent X-ray beam and at each position a coherent diffraction pattern of the transmitted radiation is recorded5. Redundant information from overlapping illuminated areas significantly adds robustness and improves convergence of the iterative image reconstruction algorithms. This technique allows imaging of arbitrarily extended objects in 2D and by recording several 2D projections of a sample at different orientations with respect to the X-ray beam, quantitative 3D images of the electron density of large objects can be obtained6,7. The instrumentation related to high-resolution X-ray tomography is demanding and many developments are pursued and implemented worldwide8,9,10,11. The achievable resolution in ptychography is determined by the scanning positioning accuracy, the stability of the whole measurement system and by the angular extent of the X-ray scattering of the sample that can be measured with a sufficient signal-to-noise ratio, which in turn is determined by sample composition, exposure time and the detection system. Given this, there is a strong potential for X-ray ptychographic tomography to reach unmatched resolution while imaging representative sample volumes. Here we present the first experimental demonstration reaching an isotropic 3D resolution of 16 nm.
Results
Prior to an evaluation of the 3D capabilities of ptychography it is useful to assess resolution in 2D, where ptychography has demonstrated to reach the 10 nm resolution range12,13,14. Resolution tests of 2D samples at different tomographic orientations help to identify and diagnose problems or limitations of the tomography system. Our measurements were carried out at the cSAXS beamline at the Paul Scherrer Institut, Switzerland, using an instrument based on that described in Ref. 15 and schematically shown in Fig. 1. Significant modifications to this setup were instrumental for the improved performance and are described in the Methods Section and Supplementary Method 2. The position and positioning stability of the sample is measured interferometrically with respect to the beam defining optics, yielding a precision (average standard deviation) of 12.1 nm during detector exposures. Ptychographic measurements of a 2D Siemens star test pattern were performed at 6.2 keV photon energy using a beam diameter of 700 nm. Far-field diffraction patterns were recorded with a Pilatus 2M detector16,17 at a distance of 2.363 meters and the reconstructions were performed to a real-space pixel size of 6.9 nm. Details on the 2D sample, its measurement and the reconstructions can be found in the Supplementary Method 1.
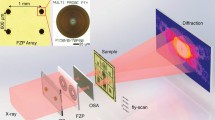
Tomography setup, composed of X-ray optics and sample stage units.
The optics stage contains a central stop (CS), a Fresnel zone plate (FZP) and an order-sorting aperture (OSA) for conditioning the X-ray beam. The sample stage performs the 2D scans and allows a rotation θy around the y-axis for tomography. The relative position of sample and optics Δx and Δy, as well as the wobble angle of the sample stage θz is measured via optical interferometry.
As an initial evaluation of the instrument performance, three independent measurements of the same 2 × 2 μm2 area of the sample were recorded at different tomographic orientations θy, i.e. at different rotation angles around the y-axis as defined in Fig. 1. Specifically, two images at θy = 0° and one at θy = 180° were acquired. For the comparison of the results, the image at 180° was mirrored about its vertical axis. In Fig. 2(a) we show the phase of the ptychographic reconstruction of the sample at θy = 0°, revealing the projected density of the object along the X-ray propagation direction. After subpixel image registration18, the resolution and repeatability of the measurement was evaluated from a pair of independent measurements using Fourier shell correlation (FSC). For this a correlation curve in Fourier domain is obtained between the two images and the resolution is estimated by its intersection with a threshold curve19. Figure 2(b) shows the FSC curve for the two independent images recorded at a sample rotation angle θy = 0° with an estimated half-period resolution of 10.2 nm and for those obtained at θy = 0° and θy = 180° for which we obtain a resolution estimate of 11.1 nm. Such evaluation of repeatability and resolution at different sample rotation angles gives an indication of the adequate performance of the instrument for tomographic imaging.
Results of the measurements on the 2D test sample.
(a) Phase image from the ptychographic reconstruction of a 2D test pattern. (b) Resolution estimation of the image in (a) by Fourier shell correlation with an independently measured image recorded at θy = 0° and at θy = 180°, respectively. Because we estimate here the resolution of the individual images rather than their average, we use the 1-bit threshold criterion.
While two dimensional test objects are useful for characterizing the resolution that can be achieved in an individual 2D projection of a tomography method, such measures do not necessarily correspond to achievable 3D resolution. This is because such 2D resolution tests or even tomography data of a 2D sample measured over a limited angular range do not include characterization of effects such as a wobble motion of the axis of rotation, angular error motions of scan stages, thermal drifts, misalignments or depth of focus in a thick object. A true measure of 3D resolution requires a 3D test object that provides small and sharp features, yet having curved interfaces to avoid X-ray reflections and tomographic reconstruction artifacts from extended flat surfaces. A 3D test sample should provide a well-characterized complex-structure, strong X-ray interaction and be resistant to radiation damage. Here we developed a sample based on a porous SiO2 structure of 139 nm mean pore size that was later coated by a Ta2O5 layer of 37 nm thickness. The sample was further milled in a quasi cylindrical shape to a size of about 6 μm diameter, for further details see “3D sample preparation” in the Methods. The field of view of the 2D projections acquired for this sample was 9 × 3 μm2. In total, four sub-tomograms of 180 projections each were recorded sequentially at interleaved angles, resulting in a total of 720 projections taken with equal angular spacing and spanning a range from θy = 0° to θy = 180°. The reconstructions of the projections, one of them shown in Fig. 3, were performed to a real-space pixel size of 10 nm and a tomogram was then computed from the phase reconstructions, providing a 3D map of the density of the object. For details see “Data acquisition and tomographic reconstruction” in the Methods. A cross section of this tomogram is depicted in Fig. 4(a) and a zoom in Fig. 4(b) where we can clearly observe the base porous structure and the thin Ta2O5 layer surrounding the pore structure. Figure 4(a) is complemented by supplementary movie 1, giving an overview of the sample.
Results of the tomographic reconstuction.
(a) Section of the tomogram parallel to the rotation axis. Three distinct gray levels are visible for air (black), glass (gray) and a thin layer of Ta2O5 (white) conformal to the pores. (b) Zoom in of a region indicated by the yellow rectangle in (a). (c) Line profile indicated by a red line in (a) and (b) showing 16.4 nm edge response using the 10%–90% criteria. (d) Resolution estimation by Fourier shell correlation (FSC) computed using all 720 projections.
To estimate the tomogram resolution, the full data set of 720 projections was divided in half and two independent tomograms with double angular spacing and consequently half the number of projections were reconstructed. Figure 4(d) shows the FSC curve between these independent 3D reconstructions and gives a half-period resolution estimate of 15.9 nm where the ½ bit threshold curve intersects the FSC. The determined 3D resolution is supported by line cuts, as shown in Fig. 4(c). Table 1 shows a comparison between the resolution we obtained by the FSC half-bit criterion and the resolution limit defined by Nyquist angular sampling, given by (π/2) × sample thickness/#projections, when taking a different number of projections into account. As expected, the resolution continuously improves when adding projections to the tomogram and our measured resolution is close to the expected resolution. The reconstructed pixel size of 10 nm was not limiting our tomographic resolution, as confirmed by a reconstruction performed to a pixel size of 6.9 nm. The FSC intersects the threshold value of 0.5, which is often used in electron microscopy, at 18.4 nm. Since there are many ways of defining resolution, we provide an extracted sub-volume of the tomogram as tiff-stack as supplementary dataset 1. This volume is also represented in supplementary movie 2 with an identical color scale as used in Fig. 4(a).
In the tomographic slice in Fig. 4(a) three distinct gray levels are visible for air (black), glass (gray) and a thin layer of Ta2O5 (white). The porous glass structures are conformally coated by Ta2O5 atomic layer deposition (ALD) and a gradient of the Ta2O5 layer thickness can be observed due to the limited diffusion of the precursor into the porous structure20,21. The sample cylinder is surrounded by material with different density values, as observed at either side of the sample in Fig. 4(a), arising from material redeposition during sample preparation using focused ion beam milling. Electron density can be converted to mass density when the chemical composition of the sample is known and the measurement is taken away from absorption edges of the sample materials7. As an example, we measured a glass density of 2.1 g/cm3 with a standard deviation of 0.5 g/cm3, obtained from the peak in the histogram taken from a volume within the tomogram of about (2 μm)3. This value agrees with the documented average density of the material22 of 2.20 g/cm3.
Discussion
Our measurements on the 2D test object show a similar FSC at identical and 180 degree complementary projection angles θy. This proves the correct alignment of detector pixels with respect to the tomography axis and that image deformations and distortions caused by the instrumentation, for instance by sample mispositioning, occur on a smaller length scale. The FSC is a measure of signal-to-noise ratio and in Fig. 2(b) it shows a very high repeatability at low spatial frequencies and a sharp transition to the low-SNR regime near the cutoff. When specifying the resolution of a tomography instrument, such correlation information of both identical and complementary 180 degrees projection angles provides important information on the instrument performance that cannot be adequately assessed by the quality obtained at a single projection angle which may be subject to systematic errors and not be representative of the 3D imaging capabilities. It is also a fast verification method of the instrument performance and therefore is a good routine check prior tomographic data acquisition.
The interferometrically measured stability of our setup of 12.1 nm during exposures is in agreement with our estimated resolution on the 2D sample. Although it may be difficult to quantify we found no evidence of image degradation caused by this intra-exposure jitter and we found this to be the limiting factor for the obtained 2D resolution, meaning that increasing the exposure time did not lead to a resolution better than 10 nm. The averaged relative positions between sample and X-ray optics of each detector exposure are directly used in the ptychography reconstructions, which compensates low-frequency instabilities such as thermal drift and makes algorithm refinement of scanning positions23,24,25 unnecessary. This is an important property of our instrument as position refinement is ultimately limited by sample contrast and may have unsatisfactory performance on weakly scattering specimens such as biological material.
The tomogram resolution continuously improves when adding projections to the tomogram. For the FSC, the tomograms to compare are obtained from half the number of projections. Because these measurements are limited by angular sampling, their correlation at high spatial frequencies is diminished which makes the FSC estimate conservative. On the other hand, the Nyquist angular sampling can be too stringent for realistic samples. While, potentially, the full tomogram of 720 projections could have higher resolution, the determined 3D resolution is supported by line cuts, as shown in Fig. 4(c) and is in good agreement with the 2D projection resolution of 15.5 nm, determined using the FSC 1 bit criterion19 between two projections at the same rotation angle before and after the tomographic measurement.
The tomographic resolution is still worse than that obtained on the flat 2D sample, which is partially attributed to radiation damage induced in the 3D sample during the measurement. Radiation damage was assessed by FSC of individual projections taken at the same angle θy = 0° before, in the middle and after recording the tomogram. For two projections prior to the tomographic measurement we obtain a 2D resolution estimate of 13.4 nm using the 1 bit criterion. When comparing a projection from the beginning with one recorded in the middle of the tomogram we determine a slight decrease to 14.1 nm and a comparison of a projection from the beginning with a projection from after the tomogram results in a further decrease to 15.5 nm. This motivates our conclusion that radiation damage limited our resolution to around 16 nm. Another possible limiting factor for resolution is the sample thickness which affects both CDI and ptychography3,26. We have investigated this issue through numerical simulations characterizing the effect of sample thickness on the width of the point spread function (PSF), which ultimately can be used to estimate resolution. From these simulations we conclude that, although the shape and sidelobe intensity of the PSF changes, its width is preserved to 16 nm for a sample up to 7 microns in thickness. Further discussion can be found in the Supplementary Method 3.
The estimated total dose deposited in the material during the measurement of 720 projections was 1.2 × 1010 Gray. As an attempt to test the instrumentation limits, the dose was not minimized in the measurement. On a 2D projection we found that a fourfold reduction of exposure time produces results with identical resolution, which gives us confidence that a dose of 3 × 109 Gray would have sufficed for the entire tomogram at the achieved 3D resolution of 16 nm. Cleary such dose is relatively high but when compared with previous measurements6 it is also expected as the required dose for imaging scales with resolution to the forth power27.
We demonstrated that ptychographic tomography is a promising technique that combines imaging of representative sample volumes with high resolution by combining coherent diffractive imaging and a scanning approach, thereby closing the resolution gap between electron microscopy and X-ray imaging techniques. Although our demonstration was performed on an artificial test sample with enhanced contrast via heavy atom deposition, its complexity is comparable to realistic materials such that this demonstration paves the way to accurate analysis of representative sample volumes in materials science or even life science samples. However, it also shows that even on radiation tolerant samples like our nanoporous glass, damage already plays a role and limits resolution. To reach a 3D resolution towards 10 nm, cryogenic sample preservation will become mandatory for most sample materials and efforts are underway to achieve this.
Methods
Instrumentation
The tomography setup, depicted in Fig. 1, is based on the instrument described in Ref. 15, where significant modifications were implemented to drastically improve the 3D resolution. The instrument consists of two mechanical units. Firstly, a sample stage allows precise movements for scanning the sample through the beam and is equipped with a rotation axis for tomography. Secondly, an optics stage for the optical elements is used to define the beam illuminating the sample. In our measurements we use a diffractive X-ray lens, a Fresnel zone plate, with 100 μm diameter and an outermost zone width of 100 nm to define the illumination incident on the sample. Differential laser interferometry is used to measure the relative positions (Δx, Δy) between the X-ray optics and sample and to close the mechanical loop ensuring accurate and stable sample positioning. A further interferometer measures the angular error motion θz of the scanning mechanism. Using the positions (Δx, Δy) and angular measurement θz a corrected sample position was calculated and directly used in the ptychographic reconstructions. Further details can be found in the Supplementary Method 2.
3D sample preparation
The tomography sample is based on nanoporous glass with a mean pore size of 139 nm, which is intended for use in the calibration of high pressure mercury porosimeters. As a reference material it has the advantage of being already well characterized by several methods22. A Ta2O5 film was fabricated on the surface of this glass material by atomic layer deposition from Ta(OC2H5)5 and H2O at 250°C using a SUNALE reactor (Picosun Oy, Finland)28. The final film thickness was 37 nm in the outermost region of the glass beads. Using a focused ion beam, a cylinder of 6 microns diameter of this material was milled and mounted on a sample holder. This sample allows tomographic data to be taken at any projection angle without missing wedge, providing isotropic 3D resolution. It is ideal for evaluating the performance of high-resolution X-ray tomography instrumentation as it is radiation tolerant and it provides features of 37 nm and 139 nm that are well distributed in their three-dimensional position and orientation at two distinct high-contrast levels.
Data acquisition and tomographic reconstruction
A tomogram of the 3D sample was recorded using ptychographic tomography. As mentioned previously, 720 projections were recorded with equal angular spacing and spanning a range of θy = 0° to θy = 180°, divided in four sequentially recorded sub-tomograms, each consisting of 180 projections. Each projection was acquired using a ptychographic scan of 343 exposures arranged in concentric circles with 250 nm radial step size, covering an area of 9 × 3 μm2 with an exposure time of 0.6 s per point and a beam diameter of 600 nm. Ptychographic measurements were performed at 6.2 keV photon energy and the diffraction patterns were recorded with a Pilatus 2M detector with a pixel size of 172 μm16,17 at a distance of 2.363 m. Including sample positioning and detector readout, the measurement of each projection took about 280 s. Of the diffraction patterns a region of 270 × 270 pixels was used in the reconstructions, resulting in a pixel size of 10 nm.
Reconstructions were performed by sharing information between consecutive scans taken at different projection angles. To measure information lost in the gaps between Pilatus modules, the detector is moved transversely to the direction of X-ray propagation. In previous work, akin to the measurements on the 2D sample, the measurement of each projection was repeated at each detector position and reconstructions were performed from the pair of measurements with suitable valid masks13. However, repeating the scan for each projection caused a significant overhead. For this work a scan on each tomography angle is performed only once while the detector position is alternated and for two successive scans the illumination is enforced to be the same during the iterative reconstruction. By sharing information on the illumination in such a way we sufficiently constrain the intensities within the detector gaps and avoid repeating measurements which double the overhead caused by the positioning time of the sample scanner and detector movements. Such approach of sharing information on the illumination, object or both has other important applications such as allowing for long scans without suffering from long timescale changes on the illumination29, imaging with large field of view or stitching images from different scans automatically. Such a pair of scans was reconstructed using 200 iterations of the difference map algorithm30 followed by 100 iterations of maximum likelihood refinement23,31. The refinement step provides a significant improvement of the projection resolution estimate from 20 nm to 14.1 nm using the 1-bit FSC threshold. For tomography the phase information of the reconstructed projections was processed and aligned following the procedure described by Guizar-Sicairos et al.32 and is quantitatively related to electron density.
References
Fienup, J. R. Phase retrieval algorithms - a comparison. Appl. Opt. 21, 2758–2769 (1982).
Miao, J. W., Charalambous, P., Kirz, J. & Sayre, D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 400, 342–344; 10.1038/22498 (1999).
Chapman, H. N. et al. High-resolution ab initio three-dimensional x-ray diffraction microscopy. JOSA A 23, 1179–1200; 10.1364/josaa.23.001179 (2006).
Williams, G. J. et al. Fresnel coherent diffractive imaging. Phys. Rev. Lett. 97, 025506; 10.1103/PhysRevLett.97.025506 (2006).
Rodenburg, J. M. & Faulkner, H. M. L. A phase retrieval algorithm for shifting illumination. Appl. Phys. Lett. 85, 4795–4797; 10.1063/1.1823034 (2004).
Dierolf, M. et al. Ptychographic X-ray computed tomography at the nanoscale. Nature 467, 436–439; 10.1038/nature09419 (2010).
Diaz, A. et al. Quantitative x-ray phase nanotomography. Phys. Rev. B 85, 020104; 10.1103/PhysRevB.85.020104 (2012).
Peterson, I. et al. Nanoscale Fresnel coherent diffraction imaging tomography using ptychography. Opt. Express 20, 24678–24685 (2012).
Vine, D. J. et al. An in-vacuum x-ray diffraction microscope for use in the 0.7–2.9 keV range. Rev. Sci. Instrum. 83; 10.1063/1.3688655 (2012).
Kim, J., Lauer, K., Yan, H., Chu, Y. S. & Nazaretski, E. Compact prototype apparatus for reducing the circle of confusion down to 40 nm for x-ray nanotomography. Rev. Sci. Instrum. 84, 035006; 10.1063/1.4798546 (2013).
Shapiro, D. et al. Development of coherent scattering and diffractive imaging and the COSMIC facility at the Advanced Light Source. J. Phys. Conf. Ser. 425, 192011; 10.1088/1742-6596/425/19/192011 (2013).
Takahashi, Y. et al. Towards high-resolution ptychographic x-ray diffraction microscopy. Phys. Rev. B 83, 214109; 10.1103/PhysRevB.83.214109 (2011).
Vila-Comamala, J. et al. Characterization of high-resolution diffractive X-ray optics by ptychographic coherent diffractive imaging. Opt. Express 19, 21333–21344 (2011).
Schropp, A. et al. Hard x-ray scanning microscopy with coherent radiation: Beyond the resolution of conventional x-ray microscopes. Appl. Phys. Lett. 100, 253112; 10.1063/1.4729942 (2012).
Holler, M. et al. An instrument for 3D x-ray nano-imaging. Rev. Sci. Instrum. 83, 073703; 10.1063/1.4737624 (2012).
Henrich, B. et al. PILATUS: A single photon counting pixel detector for X-ray applications. Nucl. Instrum. Methods Phys. Res. Sect. A-Accel. Spectrom. Dect. Assoc. Equip. 607, 247–249; 10.1016/j.nima.2009.03.200 (2009).
Kraft, P. et al. Characterization and Calibration of PILATUS Detectors. Ieee trans. nucl. sci. 56, 758–764; 10.1109/tns.2008.2009448 (2009).
Guizar-Sicairos, M., Thurman, S. T. & Fienup, J. R. Efficient subpixel image registration algorithms. Opt. Lett. 33, 156–158; 10.1364/ol.33.000156 (2008).
van Heel, M. & Schatz, M. Fourier shell correlation threshold criteria. J. Struct. Biol. 151, 250–262; 10.1016/j.jsb.2005.05.009 (2005).
Elam, J. W., Routkevitch, D., Mardilovich, P. P. & George, S. M. Conformal coating on ultrahigh-aspect-ratio nanopores of anodic alumina by atomic layer deposition. Chem. Mater. 15, 3507–3517; 10.1021/cm0303080 (2003).
Gordon, R. G., Hausmann, D., Kim, E. & Shepard, J. A kinetic model for step coverage by atomic layer deposition in narrow holes or trenches. Chem. Vap. Dep. 9, 73–78; 10.1002/cvde.200390005 (2003).
European reference material ERM FD122, BAM Federal Institute for Materials Research and Testing, Section: 1.3 Strukturanalytik, Germany, http://www.bam.de/de/rm-certificates_media/rm_cert_porous_materials/erm_fd120_121_122rep.pdf (Date of access 2013/12).
Guizar-Sicairos, M. & Fienup, J. R. Phase retrieval with transverse translation diversity: a nonlinear optimization approach. Opt. Express 16, 7264–7278; 10.1364/oe.16.007264 (2008).
Zhang, F. et al. Translation position determination in ptychographic coherent diffraction imaging. Opt. Express 21, 13592–13606; 10.1364/oe.21.013592; (2013).
Schropp, A. et al. Full spatial characterization of a nanofocused x-ray free-electron laser beam by ptychographic imaging. Sci. Rep. 3; 10.1038/srep01633 (2013).
Rodenburg, J. M. & Bates, R. H. T. The theory of superresolution electron-microscopy via wigner-distribution deconvolution. Phil. Trans. Roy. Soc. A 339, 521–553; 10.1098/rsta.1992.0050 (1992).
Howells, M. R. et al. An assessment of the resolution limitation due to radiation-damage in X-ray diffraction microscopy. J. Electron Spectrosc. Relat. Phenom. 170, 4–12; 10.1016/j.elspec.2008.10.008 (2009).
Kukli, K., Ritala, M. & Leskela, M. Atomic layer epitaxy growth of tantalum oxide thin-films from TA(OC2H5)(5) and H2O. J. Electrochem. Soc. 142, 1670–1675; 10.1149/1.2048637 (1995).
Zanette, I. Ptychographic reconstructions using shared data sets. Paper presented at Coherence: International workshop on Phase Retrieval and Coherent Scattering, Japan. Place of publication: Hilton Fukuoka Sea Hawks, Fukuoka, Japan; Manuscript in preparation by M. Dierolf. (2012, 06).
Thibault, P. et al. High-resolution scanning x-ray diffraction microscopy. Science 321, 379–382 (2008).
Thibault, P. & Guizar-Sicairos, M. Maximum-likelihood refinement for coherent diffractive imaging. N. Jour. Phys. 14; 10.1088/1367-2630/14/6/063004 (2012).
Guizar-Sicairos, M. et al. Phase tomography from x-ray coherent diffractive imaging projections. Opt. Express 19, 21345–21357 (2011).
Acknowledgements
We thank B. Sarafimov and X. Donath for technical assistance and R. Wepf and J. Da Silva for fruitful discussions. This work was supported by the Swiss National Science Foundation SNF (Funding scheme R'QUIP, Project number 145056, “OMNY”), the Competence Centre for Materials Science and Technology (CCMX) of the ETH-Board, Switzerland and the Academy of Finland (Finnish Centre of Excellence in Atomic Layer Deposition and project 250968).
Author information
Authors and Affiliations
Contributions
The experiment was set up and carried out by M.H., A.D., M.G., J.R., A.M. and O.B. The data was analyzed by M.G., A.D. and M.H. The tomography instrument was conceived and built by M.H., J.R. and A.D. The 2D sample was created by P.K. and the atomic layer deposition coating was done by E.F., E.H. and M.R. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Methods
Supplementary Information
Overview of the tomogram
Supplementary Information
Zoom of a tomogram sub-volume
Supplementary Information
Dataset 1
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Holler, M., Diaz, A., Guizar-Sicairos, M. et al. X-ray ptychographic computed tomography at 16 nm isotropic 3D resolution. Sci Rep 4, 3857 (2014). https://doi.org/10.1038/srep03857
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03857
This article is cited by
-
Nanoscale imaging of Fe-rich inclusions in single-crystal zircon using X-ray ptycho-tomography
Scientific Reports (2024)
-
Understanding the microstructure of a core–shell anode catalyst layer for polymer electrolyte water electrolysis
Scientific Reports (2023)
-
4D nanoimaging of early age cement hydration
Nature Communications (2023)
-
Decoding the nanoscale porosity in serpentinites from multidimensional electron microscopy and discrete element modelling
Contributions to Mineralogy and Petrology (2023)
-
Scale-Independent Rock Heterogeneity Classification Algorithm Applied to Microtomography Images
Transport in Porous Media (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.