Abstract
Optical tweezers is an example how to use light to generate a physical force. They have been used to levitate viruses, bacteria, cells and sub cellular organisms. Nonetheless it would be beneficial to use such force to develop a new kind of applications. However the radiation pressure usually is small to think in moving larger objects. Currently, there is some research investigating novel photonic working principles to generate a higher force. Here, we studied theoretically and experimentally the induction of electromagnetic forces in one-dimensional photonic crystals when light impinges on the off-axis direction. The photonic structure consists of a micro-cavity like structure formed of two one-dimensional photonic crystals made of free-standing porous silicon, separated by a variable air gap and the working wavelength is 633 nm. We show experimental evidence of this force when the photonic structure is capable of making auto-oscillations and forced-oscillations. We measured peak displacements and velocities ranging from 2 up to 35 microns and 0.4 up to 2.1 mm/s with a power of 13 mW. Recent evidence showed that giant resonant light forces could induce average velocity values of 0.45 mm/s in microspheres embedded in water with 43 mW light power.
Similar content being viewed by others
Introduction
The concept of radiation pressure has been used in the past for manipulating micro-objects1 and biological organisms2. The fast development of electromagnetic wave driven micro motors has motivated several research groups to investigate novel working principles for such micro motors3, but there is a main obstacle, normally the radiation pressure is too small for this kind of applications4. Nonetheless some resonance principles can be used to increase the force significantly. For instance, a waveguide made of lossless dielectric blocks, where the direction of the force exerted on the dielectric is parallel to the waveguide axis5,6. A second approach is a Bragg waveguide, based on a Fabry-Perot cavity in which the peak of the force only appears at the structures' resonant frequencies and the force is normal to the waveguide wall7. However in this design the force tends to separate the two mirrors that form the Fabry-Perot cavity, having as a consequence a dramatic reduction of the force4. A third approach can use a one-dimensional photonic crystal with structural defects, where a localized mode results in strong electromagnetic fields around the position of the defect. Thus, the strong fields enhance the tangential and normal force on a lossy dielectric layer4. Recently8 a resonant light pressure effect has been used to prove the existence of strong peaks of the optical forces by studying the optical propulsion of dielectric microspheres along tapered fibers. They observed giant optical propelling velocities for submerged polystyrene microspheres. Such velocities exceed previous observations by more than one order of magnitude.
This work is organized as follows: in the first section we present the experimental details to fabricate the photonic structure and how to measure the auto and forced oscillations. Secondly, we describe briefly the theory to induce an electromagnetic force in the photonic structure. We present a dynamical model that can be used to describe either auto or forced oscillations of the photonic structure and we compare the experimental results with the model. Finally, we wrap-up the work by giving some conclusions.
Results and discussion
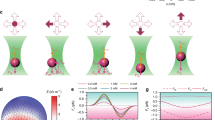
Details of the experimental setup for the oscillation measurements can be seen in figure 1 and its full description can be found in methods. Sample fabrication information is also found in methods and references 9, 10. Figure 2a shows a cartoon of both foils overlapped over the glass substrate to create the photonic oscillator and figure 2b shows the scheme of the bifoil structure used for theoretical calculations. Now, consider the structure depicted on figure 2b. Let us assume that light impinges on the off-axis direction at angle θ0 with the electric field polarized in the y-direction (TE polarization) and magnitude:

where

where all Ai's and Bi's are the complex amplitudes of the electric field in each region of the structure plus the air (0 label) and the substrate (s label) and the ki's are the wavevectors at the different regions on the structure in the x-direction and β is the wavevector in the z-direction given by ωn0Sin(θ0)/c, where n0 and θ0 are the refractive index and angle of incidence of the air region, c is the speed of light and ω is the light angular frequency. The ki's are given by ωniCos(θi)/c, where ni and θi are the refractive index and angle of incidence of region i, the latter given by θi = sin−1(n0sinθ0/ni). By using a similar formalism as presented in4,11 it is possible to show that for lossless dielectrics the surface force density only exists in the x-direction and is given by:

where ε0 is the vacuum permittivity and N is the total number of layers. The complex amplitudes Ai's and Bi's and their phases φi can be calculated by using the well known transfer matrix method12. Figure 2c shows the harmonic variation of the force density with the defect length at a light power of 13 mW (632 nm wavelength), angle of incidence of 35 degrees and TE polarization. We can observe that this force density oscillates between values of 3.5 and 2 mN/m2 for defect lengths ranging from 10 nm up to more than 1 mm.
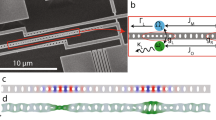
Experimental setup for the oscillation measurements.
(a), Auto-oscillation experimental configuration: 1) bifoil photodyne, 2) rotary and linear XY stages, 3) Neutral filter wheel, 4) Infrared band-pass filter, 5) He-Ne laser, 6) Mechanical chopper, 7) Vibrometer laser, 8) Photocell, 9) Computer, 10) Oscilloscope, 11) Vibrometer interface, 12) Linear polarizer. The circuit shown represents a Schmitt Trigger. (b), Forced oscillations experimental configuration: 1) bifoil photodyne, 2) rotary and linear XY stages, 3) Neutral filter wheel, 4) Infrared band-pass filter, 5) He-Ne laser, 6) Mechanical chopper, 7) Vibrometer laser, 8) Photocell, 9) Computer, 10) Oscilloscope, 11) Function generator, 12) Linear polarizer. The insert image displays the main components of the real set up.
The bifoil photodyne and its working principle.
(a), Scheme on how the two porous silicon foils are set up to create the photonic oscillator. (b), Scheme of the bifoil structure used for theoretical calculations. (c), Theoretical surface force density at different L gap lengths. The surface density force oscillates between 2 and 3.5 mN/m2 with gap lengths of more than 1 mm.
The simplest auto-oscillating system consists of a constant source of energy, a regulatory mechanism that supplies energy to the oscillating system and the oscillating system itself. There are two necessary features of auto-oscillations. The first is its feedback nature: on the one hand, the regulatory mechanism controls the motion of the oscillating system but, on the other, it is the motion of the oscillating system that influences the operation of the regulatory mechanism. The second feature consists in the fact that the loss of energy must be compensated by a constant source of energy. An example of a very simple oscillating system that can produce either auto or forced oscillations is a pendulum in a viscous frictional medium, acted upon by a force of constant magnitude. The differential equation of this dynamical system is

where,  , mpsi and A are the mass and the active surface area of the PSi bifoil, h is a damping coefficient, ω0 is the natural frequency of the system, nlight defines the duty cycle (fraction of the period where the light is on) which should take a value of 0.5 for the auto-oscillation case and j + 1 is the number of cycles that the light is on and off. The period T is related to the oscillator's frequency ω as usual by T = 2π/ω and it is related to the natural frequency and damping coefficient as
, mpsi and A are the mass and the active surface area of the PSi bifoil, h is a damping coefficient, ω0 is the natural frequency of the system, nlight defines the duty cycle (fraction of the period where the light is on) which should take a value of 0.5 for the auto-oscillation case and j + 1 is the number of cycles that the light is on and off. The period T is related to the oscillator's frequency ω as usual by T = 2π/ω and it is related to the natural frequency and damping coefficient as  . The self-oscillations arise in principle in the following manner. Consider the circuit of figure 1a, there the energy is provided by a polarized laser light (5,12) and a chopper (6). Initially, when the light is on, the electromagnetic force push downs the bifoil (descending part). Now suppose that the energy dissipated throughout this part of the period is compensated by energy from the laser-chopper, since it is only then that the laser is in effective operation. If the compensation is exact in this part of the period, i.e. if there is neither gain nor loss of energy, a prolonged oscillation will be reached. That is to say, the system will go into a steady oscillatory state with period T. In the second part of the period the bifoil naturally goes into a damped oscillation until it stops and returns back to the original position (ascending part). Mathematically we can calculate this condition as
. The self-oscillations arise in principle in the following manner. Consider the circuit of figure 1a, there the energy is provided by a polarized laser light (5,12) and a chopper (6). Initially, when the light is on, the electromagnetic force push downs the bifoil (descending part). Now suppose that the energy dissipated throughout this part of the period is compensated by energy from the laser-chopper, since it is only then that the laser is in effective operation. If the compensation is exact in this part of the period, i.e. if there is neither gain nor loss of energy, a prolonged oscillation will be reached. That is to say, the system will go into a steady oscillatory state with period T. In the second part of the period the bifoil naturally goes into a damped oscillation until it stops and returns back to the original position (ascending part). Mathematically we can calculate this condition as  for t ∈ [0, T/2], we can approximate this condition, without knowing the exact solution of equation (4), by using the maximum values for the displacement xp and velocity Vp. Therefore the auto-oscillation condition reads
for t ∈ [0, T/2], we can approximate this condition, without knowing the exact solution of equation (4), by using the maximum values for the displacement xp and velocity Vp. Therefore the auto-oscillation condition reads

In figure 3a we observe the experimental bifoil velocity time series, where we can see an asymmetry between the descending (positive voltage) and the ascending (negative voltage) parts, implying that the damping coefficient of the descending part is higher than the coefficient of the ascending part. Figure 3b shows the power spectral density (PSD) of the velocity time series and only one peak appears at 16.1 Hz. We found experimental values for xp = 4.12028 microns and Vp = 0.42 mm/s. We can estimate the parameter  as follows: The surface area of this photonic device was 3 mm2 and the total thickness is 20 × (761 × 10−9) m2 this gives a volume of 4.566 × 10−11 m3. The volumetric density of each layer is the product of (1 − P) × 2330 kg/m3, where P means porosity. The value of 2330 kg/m3 corresponds to the volumetric density of c-Si. Since each foil is a multilayer structure that contains two different porosities therefore there are two different volumetric densities. In order to obtain an effective volumetric density, we can take a weight average of both densities where the weights correspond to each thickness. The final result is 586 kg/m3. Multiplying the volume times the effective volumetric density give us the mass estimation, which has a value of 2.67568 × 10−8 Kg. We used an in house made optical microscope capable to resolve 5 microns to scan the gap distance between foils and we observed distances ranging from 5 microns up to 1 mm approximately. For that reason, we take the average value between the maximum and minimum values (see figure 2c) for
as follows: The surface area of this photonic device was 3 mm2 and the total thickness is 20 × (761 × 10−9) m2 this gives a volume of 4.566 × 10−11 m3. The volumetric density of each layer is the product of (1 − P) × 2330 kg/m3, where P means porosity. The value of 2330 kg/m3 corresponds to the volumetric density of c-Si. Since each foil is a multilayer structure that contains two different porosities therefore there are two different volumetric densities. In order to obtain an effective volumetric density, we can take a weight average of both densities where the weights correspond to each thickness. The final result is 586 kg/m3. Multiplying the volume times the effective volumetric density give us the mass estimation, which has a value of 2.67568 × 10−8 Kg. We used an in house made optical microscope capable to resolve 5 microns to scan the gap distance between foils and we observed distances ranging from 5 microns up to 1 mm approximately. For that reason, we take the average value between the maximum and minimum values (see figure 2c) for  that equals 2.75 × 10−3 N/m2 and since A = 3 × 10−6 m2 the value for
that equals 2.75 × 10−3 N/m2 and since A = 3 × 10−6 m2 the value for  is 0.3083333 m/s2. According with the values obtained for xp, Vp, T and
is 0.3083333 m/s2. According with the values obtained for xp, Vp, T and  we found that the auto-oscillation condition (equation 5) gives a value for h of 115.95.
we found that the auto-oscillation condition (equation 5) gives a value for h of 115.95.
We simulated equation (4) by using Matlab and the best fit we found uses the aforementioned parameters and only the parameter h needed to be multiplied by 16.4 instead of 2 in the descending part and we use the experimental value nlight = 0.52. Figures 3c–d shows the simulated velocity time series and its PSD, which fits nicely with the experimental measurements. In order to take into account uncontrollable vibration effects, 60 Hz noise, etc. we added a zero-mean random noise to the simulated velocity time series. The amplitude of this noise signal was 25% of the peak velocity amplitude. Figure 3e shows the simulated displacement time series with a maximum value of 4.119 microns.
For the forced oscillation simulation, we kept the same parameter values for h, ω0,  and we only changed T and nlight. As an example figures 4a and 4b show the experimental results for a driven frequency of 9 Hz. It is notorious that the bifoil vibrates mainly at 8.6 Hz but the appearance of high harmonics is evident. The maximum displacement was 8.17597 microns. We used nlight = 0.75. The theoretical results are observed in figures 4c, 4d and 4e. Again, the fit is very good and we were able to reproduce the first three harmonics and a maximum displacement of 8.540 microns.
and we only changed T and nlight. As an example figures 4a and 4b show the experimental results for a driven frequency of 9 Hz. It is notorious that the bifoil vibrates mainly at 8.6 Hz but the appearance of high harmonics is evident. The maximum displacement was 8.17597 microns. We used nlight = 0.75. The theoretical results are observed in figures 4c, 4d and 4e. Again, the fit is very good and we were able to reproduce the first three harmonics and a maximum displacement of 8.540 microns.
Conclusions
In conclusion we were able to use light to induce electromagnetic forces in a photonic crystal structure. Note that the electromagnetic force could be increased by adding more layers in a tandem-like array or by working at a resonance state. In the latter case the force could be increased 25 times for a similar structure13. The structure showed to be stable for several hours when the light pumping was controlled by the function generator, in the case of auto-oscillator the stability shown was as short as few minutes. This is so because the conditions (active bifoil area, elastic recovery forces, irregular PSi pieces surface, etc.) are more critical for the close loop operation (auto-oscillator) implementing the loop via a Schmitt Trigger. In the open loop operation type we find several movement modes which amplitudes reduces at higher frequencies according to a non-linear attenuation along the frequency interval limited to 100 Hz. While in the close loop (auto-oscillator) operation type the displacement mode presents a narrow spectrum centered at the main oscillation frequency.
Finally, there are at least two photonic applications where this kind of principle would be beneficial. The first is a mechanically tuneable photonic crystal that uses the concept of applying a mechanical force through a MEMS device to achieve dynamic tuneability of the photonic band structure14. The second application is a mechanically tuneable detector interface that uses a PSi layer integrated with a MEMS structure15. When a voltage is applied, the MEMS structure bends the PSi layer at different angles. If a laser beam hits the PSi surface the reflected beam can be spatially tuned and select different detectors. If we use the principle of force generation we have presented here the MEMS device in both applications could be replaced to create devices activated only with light.
Methods
Porous silicon (PSi) photonic crystals were prepared by electrochemical anodization of crystalline silicon (c-Si)9. PSi was fabricated by wet electrochemical etching of highly boron-doped c-Si substrates with orientation (100) and electrical resistivity of 0.001–0.005 Ohm-cm (room temperature = 25°C, humidity = 30%). On one side of the c-Si wafer, an aluminum film was deposited and then heated at 550°C during 15 minutes in nitrogen atmosphere to produce a good electrical contact. In order to have flat interfaces, an aqueous electrolyte composed of HF/ethanol/glycerol was used to anodize the silicon substrate. It is well known that the PSi refractive index increases by decreasing the electrical current applied during the electrochemical etching. However, reducing the porosity too much might stop the electrolyte flow through the porous and limit the subsequent high porosity layer that makes the contrast. One way to allow the electrolyte to flow is by increasing the ethanol fraction in the solution. For this reason, an electrolyte composition of 3:7:1 was used. In addition, the HF concentration was maintained constant during the etching process using a peristaltic pump to circulate the electrolyte within the Teflon™ cell. Anodization begins when a constant current is applied between the c-Si wafer and the electrolyte by means of an electronic circuit controlling the anodization process. To produce the multilayers, current density applied during the electrochemical dissolution was alternated from 3 mA/cm2 (layer a) to 40 mA/cm2 (layer b) and 10 periods (20 layers) were made. The current density conditions give layers with porosities of 65% and 88% respectively. In order to obtain a free standing PSi photonic crystals, at the end of the formation process an anodic electropolishing current pulse (500 mA/cm2 for 2 s) was applied to lift off the structure. PSi samples were partially oxidized at 350°C for 10 minutes. The best refractive index values we found that fit the experimental photonic bandgap structure (not shown) are n1 = 1.1 and n2 = 2. We have experimentally measured the refractive indexes of single PSi layers made with the same electrochemical conditions as for the multilayers9 and we found that n1 = 1.4 and n2 = 2.2. Nevertheless, it is known that the refractive index and etching rate for a single layer are modified in the presence of a multilayer structure up to approximately 14%, a phenomenon that has been systematically observed10. This result might have the consequence of compromising the mechanical stability of the structure. Indeed, in certain regions of the samples the high porosity layers appear to be collapsed. Scanning electron microscopy (SEM) was used to measure the films thicknesses, which were d1 = 326 ± 11 nm and d2 = 435 ± 11 nm.
The oscillator configuration consisted of two fixed porous silicon (PSi) foils stuck together forming a microcavity structure. One problem we encountered is that the PSi foil is not a flat membrane. After being fabricated the multilayer porous structure and separated from the c-Si. The resulting membrane accumulates mechanical stress that deforms slightly the original flat structure. For building the vibrating device, two pieces of these samples have to be placed in a mirror like symmetry with a gap space between them. One of the advantages of this configuration is that both foils became more flat because the equilibrium forces for both pieces of foil make them react one against each other. The experimental results confirmed that this configuration worked effectively and it was stable. As the PSi foil is an elastic and very fragile material, it is difficult to manipulate, because it is susceptible to present static electric charges. These characteristics, added to the poor mechanical resistance of the multilayer structure, impose the concept of building a device as simple as possible. Once we gain some experience in manipulating the foil, as much as in mounting the device, we produced a dozen prototypes with small differences in the pieces shape, and/or in the overlapped portion of PSi foils. The device showed a great robustness for all the prototypes tested.
For the auto-oscillations, figure 1a shows the experimental setup were we introduced the bifoil device (1), which is mounted on a rotary and XY linear stages (2), into a positive loop formed by the movement measuring interferometer signal, that is the real time velocity signal provided by a very sensitive vibration meter (metro laser, model 500 v) (7,9,11) processed through an Schmitt Trigger circuit, which output controls the pumping laser and chopper (5,6). This means that when the bifoil device starts moving, immediately the circuit blocks the laser light by mean of the chopper. And when the device returns to the initial position it triggers the pumping laser again and so on. Once the loop was closed the device oscillated for a few seconds at different frequencies between 2 Hz and 50 Hz. After that period the device showed a clear trend to stabilize the auto-oscillation at 16.1 Hz with a duty cycle of 52%. At this frequency the movement presented a more pure spectrum with a narrow frequency spread and the device was stable for as long as 5 minutes. We chose a Schmitt Trigger circuit based on an operational amplifier. By doing so, we have a wide range of parameters to adjust the circuit performance and a high-speed loop reaction in reference to the mechanical deformation of the bifoil. The Schmitt Trigger compares the velocity signal voltage of the vibration meter with a reference voltage. The resulting electric pulsed signal controlled the chopper. By means of the oscilloscope and a photocell (figure 2a components 8,10), we verified the signal and we could recognize the desired pulses of +/−5 VDV and the presence of a 60 Hz signal component (some millivolts induced from the power line) We did not filter this “noise” of 60 Hz because it is useful to excite the loop because it helps to break the inertia. That is, it helps in starting the device movement by adding a small vibration to the chopper blade that originates pumping light spikes. Otherwise, we excited the circuit by interrupting the pumping beam pass (manually) at a frequency of 2 to 3 Hz. This manoeuvre started the oscillation at that low frequency which is soon increased until reaching its stable oscillation mode, as said, around 16.1 Hz.
For the forced oscillations we used a similar setup but (Figure 1b) the Schmitt Trigger circuit was removed and it was replaced by a function generator (11) with an offset signal to control the duty cycle, which was chosen to be 75%. The rest of the experimental setup remained the same, including the laser light power and we forced the bifoil to move at specific frequencies between 4 Hz and 40 Hz and we found a very stable performance that lasted sometimes more than 20 hours (until the samples presented physical damage). In order to prevent undesirable reflection signals enter to the vibration meter we used an infrared band-pass filter (780 nm) and the option of playing with different power light intensities was considered as well by adding a neutral wheel filter (figure 1a, component 3).
References
Kishan, D., Spalding, G. & MacDonald, M. Optical tweezers: the next generation. Physics World. 31–35 (2012).
Ashkin, A. & Dziedzic, J. M. Optical trapping and manipulation of viruses and bacteria. Science. 235, 1517–1520 (1987).
Higurashi, E., Ohguchi, O., Tamamura, T., Ukita, H. & Sawada, R. Optically induced rotation of dissymmetrically shaped fluorinated polyimide micro-objects in optical traps. J. Appl. Phys. 82, 2773–2779 (1997).
Li, J. M., Dong, T. L. & Shan, G. J. Enhancement of electromagnetic force by localized fields in one-dimensional photonic crystals. PIER M. 10, 59–70 (2009).
Gomez-Medina, R. et al. Resonant radiation pressure on neutral particles in a waveguide. Phys. Rev. Lett. 86, 4275–4277 (2001).
Mizrahi, A. Torque and longitudinal force exerted by eigenmodes on circular waveguides. Phys. Rev. A. 78, 023802 (2008).
Povinelli, M. L., Ibanescu, M., Johnson, S. G. & Joannopoulos, J. D. Slow-light enhancement of radiation pressure in an omnidirectional-reflector waveguide. Appl. Phys. Lett. 85, 1466 (2004).
Yangcheng, L. et al. Giant resonant light forces in microspherical photonics. LSA. 2, 10.1038/lsa.2013.20 (2013).
Nava, R., de la Mora, M. B., Taguena-Martinez, J. & del Rıo, J. A. Refractive index contrast in porous silicon multilayers. Phys Status Solidi C. 6, 1721 (2009).
Pavesi, L. Porous silicon dielectric multilayers and microcavities. La Rivista del Nuovo Cimento. 20, 1 (1997).
Mizrahi, A. & Schachter, L. Electromagnetic forces on the dielectric layers of the planar optical Bragg acceleration structure. Phys. Rev. E. 74, 036504 (2006).
Pochi, Y. Optical waves in layered media (John Wiley & Sons, 1988).
Lugo, J. E. et al. Proc SPIE. 8915, 10.1117/12.2037993 (2013).
Lee, W. P. & Lee, J. B. Mechanically Tunable Photonic Crystals. Optics and Photonics News 20, 41–45 (2009).
Song, D., Tokranova, N., Gracias, A. & Castracane, J. New approaches for chip-to-chip interconnects: integrating porous silicon with MOEMS. J. Micro/Nanolith. MEMS MOEMS. 7, 021013, 10.1117/1.2909279 (2008).
Acknowledgements
This work was supported by the NSERC-Essilor Research Chair and an NSERC operating grant.
Author information
Authors and Affiliations
Contributions
R.D. and J.E.L. performed all the experiments. J.E.L. and R.D. performed all the data analysis. J.F., M.B., de la Mora., N.S. and J.A. del Rio contributed with reagents, materials and analysis tools. J.E.L., R.D., J.F. and J.A. del Rio wrote the manuscript. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Lugo, J., Doti, R., Sanchez, N. et al. The bifoil photodyne: a photonic crystal oscillator. Sci Rep 4, 3705 (2014). https://doi.org/10.1038/srep03705
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03705
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.