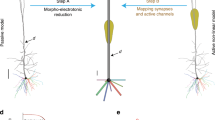
Abstract
The cellular mechanisms underlying higher brain functions/dysfunctions are extremely difficult to investigate experimentally and detailed neuron models have proven to be a very useful tool to help these kind of investigations. However, realistic neuronal networks of sizes appropriate to study brain functions present the major problem of requiring a prohibitively high computational resources. Here, building on our previous work, we present a general reduction method based on Strahler's analysis of neuron morphologies. We show that, without any fitting or tuning procedures, it is possible to map any morphologically and biophysically accurate neuron model into an equivalent reduced version. Using this method for Purkinje cells, we demonstrate how run times can be reduced up to 200–fold, while accurately taking into account the effects of arbitrarily located and activated synaptic inputs.
Similar content being viewed by others
Introduction
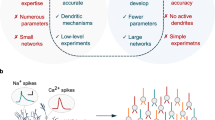
It is widely acknowledged that many cellular mechanisms underlying brain functions and dysfunctions can be conveniently investigated by realistic modeling of neurons and networks, since the complex interplay between neurons to form higher brain functions is unknown and almost impossible to investigate experimentally. However, these types of models are mathematically intractable and their networks require a processing power that outreach the capabilities of current supercomputers. Using highly artificial networks based on point-neuron models1,2,3,4 has the major problems of losing both a direct link with several critical experimental observables and the ability to take into account arbitrary synaptic inputs location and activation, in contrast with biophysically realistic multicompartmental models5,6,7. A widely used alternative approach has thus been to reduce the simulation time by mapping a realistic model into an equivalent reduced version, with only one or a few compartments with or without Hodgkin-Huxley-like ionic conductances8,9. Although the resulting models are often sufficient to reproduce the somatodendritic interactions that govern spiking10 or bursting11, they still present one or more drawbacks: a) overall poor results in terms of run times reduction that can be achieved in order to maintain a relatively good somatic trace accuracy12,13, b) the need, in many cases, of intensive fitting and tuning procedures to be carried out independently on each neuron that must be reduced13,14,15,16,17 and c) a limited field of application, restricted in most cases to passive dendritic trees and/or without taking into account synaptic inputs12,15,18.
We have recently shown19 how all these problems can be solved by using a fast and accurate reduction method that, when adapted to hippocampal CA1 pyramidal neurons, was able to reduce the run times of a realistic model for these cells by up to 40 times, while maintaining the same average I/O properties. Here, by including Strahler's analysis of the neuron morphologies20,21,22,23,24, we generalize our method in such a way it can be applied to any neuron type implemented with any kind of conductance-based model, with arbitrary dendritic distribution of ion channels and synaptic inputs. The results for Purkinje cells demonstrate that complex realistic neuron models can be reduced, without any fitting or tuning procedures, by up to ≈200 times while maintaining a somatic membrane dynamics statistically indistinguishable from the corresponding morphologically realistic model.
Results
We tested our general method using Purkinje cells, highly branched neurons controlling motor coordination functions through a poorly understood integration process involving an impressive number of synaptic inputs25. The experimental analysis of their network is almost impossible and there are currently no methods to reduce the complexity of realistic Purkinje cell models with active currents and synaptic inputs. We first carried out a series of simulations with 10 different morphologies ( Supplementary Fig. 1 ) from mice, rats and guinea pigs, downloaded from the neuromorpho.org public archive26, using a published set of ion channels for Purkinje cells27 and targeting different dendritic areas with different kinds of stimulations ( Supplementary Fig. 2a ). We found that the synaptic activation frequency, rather than the number of active synapses, was the best parameter to obtain the full range of firing frequencies observed experimentally ( Supplementary Fig. 2b ). The somatic ISIs generated during any simulation were characterized by the CV2 coefficient29 and by their distribution, as shown in Supplementary Fig. 2c for typical cases. Under all kinds of stimulation the results were consistent with the experimental findings28, validating the model and forming a broad and significant reference set of data that we used to test our method. Taken together, they demonstrated that Purkinje cells are quite robust in their I/O properties as long as the entire dendritic tree is stimulated by synaptic inputs.
The reduction method, illustrated in Fig. 1a–b for the quite elaborated Purkinje cell dendritic tree in cell e4cb3a1, is an automatic process mapping a realistic morphology into an equivalent reduced neuron in less than 3 sec on a desktop PC (see Methods). It starts by assigning a Strahler's number20 to each dendrite. For Purkinje cells, this ends up with spiny dendrites having Strahler's numbers 1–3 and the soma having the highest number. Dendrites are then clustered according to Strahler's method, their properties modified by merging and scaling rules and, finally, synapses are repositioned19 (see Methods). We were interested in reproducing the full range of physiological firing rates. Purkinje cells are under a constant barrage of synaptic inputs activated up to 1 KHz and, in vivo, they fire action potentials at ≈30–150 Hz with an average of 48 Hz28,29. The method was tested using three different stimulation protocols, illustrated in Fig. 2a (see Methods): Full, random inputs on the entire tree; Partial, random inputs on the spiny dendrites of a restricted dendritic area; Segregated: four different dendritic areas with random inputs activated synchronously within each area and asynchronously between areas. In preliminary simulations we also confirmed that the method was able to reproduce ( Fig. 2b–c ) the results of the full model for more specific Purkinje cells properties, such as the amplification of parallel fibers inputs by Calcium currents and activation of asynchronous excitatory and inhibitory inputs45. Typical simulation findings for all stimulation protocols are presented in Fig. 2d and demonstrate that the reduced model is able reproduce very closely the somatic trace of the realistic model with an extremely high accuracy (99.2, 93.3 and 94.3%, for full, partial and segregated stimulation, respectively) and ISIs statistically indistinguishable from those obtained with the realistic model (Wilcoxon Signed Rank Sum test p = 0.75212, 0.910214 and 0.548826). A quantitative agreement was obtained under all stimulation conditions ( Fig. 2e (Wilcoxon Signed Rank Sum test p = 0.760427, 0.663029, 0.386875 for the AP frequency and p = 0.742666, 0.930987, 0.623176 for ISIs)) and different perturbations of peak ionic conductances of the original model ( Supplementary Fig. 3 ). These results show that, without any tuning or fitting procedure, but just applying merging rules and scaling factors, it is possible to accurately reduce a realistic model taking into account synaptic inputs. It should be stressed that Strahler's analysis and thus the method's applicability, is not limited to Purkinje cells but it can be used to reduce any neuron cell morphology.
The method maps a realistic model and its synaptic inputs into an indistinguishable reduced version;
(a) the Strahler's analysis for a typical dendritic subtree (left) and for cell e4cb3a1 (middle); (right) color legend of Strahler's numbers; (b) the reduction method in a typical case: the 859 segments of cell e4cb3a1 (left) are mapped into a reduced model of about 40–segments (right).
The method is able to reproduce specific properties of Purkinje cells, as exhibited by the full model;
(a) representation of the stimulation conditions; colored dendrites represent typical partial and segregated areas; (b) amplification of PF inputs by Calcium currents: somatic membrane potential following a single synchronous activation of a cluster of parallel fibers in the full (left) or the reduced (right) model with (thick traces) or without (thin traces) Ca++ currents included in the model; synapse locations are represented by red dots in the full (left) and reduced (right) model; (c) somatic spiking response for the full (red traces) and the reduced (black traces) model to asynchronous excitatory inputs (on the spiny dendrites) and inhibitory inputs (one on each smooth dendrite) inputs during simulations in which the excitatory inputs where activated at the indicated frequency and the inhibitory inputs at 20 Hz. As in ref. 42,43, rise and decay time constants for the inhibitory inputs were 0.9 and 26.5 ms, respectively, with a reversal potential of −80 mV. Cell e4cb3a1 was used in all cases. (d) (left) somatic potential of the realistic (black) and the reduced (red) model; below each trace is the accuracy (light green: True Positive; dark green: True Negative; light pink: False Positive; dark pink: False Negative); (right) normalized ISI distribution of the full (black) and reduced (red) model for the simulations on the left; (e) average (n = 5, ±sd) AP frequency and ISI. All simulations were carried out with 1000 synapses.
The average run time for the full model cells reduced using s = 5 (see Methods) was 20.9 ± 8.3 times lower than its realistic version ( Fig. 3a , left, red symbols), going from over three minutes to less than 10 seconds. There were little differences among the various stimulation types and synaptic activation frequency, although for partial stimulations we observed a reduction factor up to 30–fold ( Fig. 3a , triangles). It is important to stress that all simulations were compared pairwise (full and reduced models) and that the reduced model was able to reproduce the difference, as observed at the soma, between a couple of localized strong synaptic inputs eliciting a somatic spike and the same two inputs on two different dendrites generating a subthreshold response Supplementary Fig. 4 . Simple point neurons cannot reproduce this result unless they are arranged to do so ad hoc. On average, as shown in Fig. 3a (middle), we obtained > 90% trace accuracy (see Methods) and, in most cells, more than 70% of the spike times were statistically indistinguishable ( Fig. 3a , right). More specific results are shown in Supplementary Fig. 5 . These results were quite robust also when using different morphologies, in spite that they were reconstructed from different animal species ( Supplementary Fig. 1 ) and exhibited a wide range of total membrane area and number of compartments (see Supplementary Table ). A closer inspection at the right plot in Fig. 3a suggests that the reduction of larger cells (in terms of total membrane area and thus with a low input resistance) tended to be less precise in reproducing the spike times of the corresponding full model. To test the limitations of our method, using Strahler'a analysis the dendrites were clustered to just 3–compartments (soma, spiny and smooth dendrites) and the results tested with a full stimulation. This is an important point, since it is widely assumed that such an extreme reduction (or even a single compartment) might be a good model of Purkinje cells. In this case, a 3–compartment reduction gave impressive results: for three cells (alxP, e1cb4a1 and p19) the reduced model ran more than two orders of magnitude (130–204 times) faster than the full model ( Fig. 3b , left), with 100% trace accuracy and 100% of the spike times without significant differences ( Fig. 3b , middle and right). In 7 cells, however, higher synaptic activation frequencies resulted in some spike times discrepancy, although the overall trace accuracy remained quite high (above 90%). Typical traces for cells purk2 and p20 are shown in Supplementary Fig. 6 . The failure of the 3–compartment reduction for most of the cells did not seem to be correlated with intrinsic properties of the full morphologies (such as input resistance, number of compartments, distribution of Strahler's number, or total membrane area) or with the input resistance and compartments' area of their reduced version (see Supplementary Table ). Given the variety and the relatively small set of cells included in this study we did not investigate further this point, to avoid possible interpretation errors caused by specific reconstructions. When used “as is” for CA1 pyramidal neurons the new method gave good results ( Supplementary Fig. 7 ) and, most importantly, it allowed to avoid the calculation of the additional parameter (called max Stim in19) needed to reproduce in the reduced model a specific intrinsic property exhibited by these cells (the depolarization block8). Taken together these results demonstrate that it is possible to accurately map realistic model neurons into a much faster version while maintaining the effects of dendritic inputs, opening new opportunities for multiscale simulations of large realistic networks.
The method reduces by up to 200–fold the run time of a realistic Purkinje cell model;
(a) (left) average run time for 1 sec simulations and run time reduction factor; error bars represent 95% confidence interval; average accuracy (middle) and percent of spikes times statistically indistinguishable from the realistic model, with the input resistance of each cell (Rin) coded by bar's color (right); average values calculated from 3450 simulations; (b) (left) average run time and reduction factor for three cells under full stimulations, mapping dendrites into three compartments; accuracy (middle) and percent of spikes times statistically indistinguishable (right).
Discussion
The reduction of a morphological neuron model into a much simpler and computationally equivalent, version is quickly becoming a major problem of computational neuroscience, since it would allow to run large networks without losing a direct connection with fundamental experimental observables. However, it requires a delicate balance between the simplification rules and the need to maintain sufficient details to account for the complex single-cell dynamics. Analytical approaches to implement simplified models with electric behavior equivalent to more detailed representations started with the classic works by Rall30,31, demonstrating how to collapse an idealized branching dendritic tree into a single constant-diameter cylinder with the same total membrane area and electrotonic distance from soma. The method prescribed precise mathematical constraints, i.e., all dendrites must end at the same electrotonic distance from soma AND the specific membrane resistance, membrane capacitance and axial resistivity must be uniform throughout the structure, AND branch points diameter must follow the “3/2 power rule30,31”. Unfortunately these requirements are not fullfilled by real neurons and, most importantly, the method cannot be applied to cells with nonuniform active channels. To the best of our knowledge, only in Ohme and Schierwagen (1998)32 was it attempted to extend the 3/2 power rule to branching neuronal trees with active ion channels. However, their main mathematical result (Equivalent Cable Theorem) applies only to toy models, i.e., ideal neuronal trees with very specific geometrical and electrical requirements. When the method was applied to realistic neuron morphologies it required an additional adaptation for specific cell parameters leading to a procedure that was computationally more expensive than a heuristic method32. Several additional ways to implement a suitable theoretical or algorithmic reduction of conductance-based realistic neurons model have been published33,34,35,36,14,15,16,17,12. We have previously discussed in details19 their main drawbacks, the most important of which is that they all require optimal parameters that must be independently obtained for each cell, by multiple objectives optimization and fine tuning techniques, with computationally quite long and intensive procedures13. It should also be clear that there is no way to obtain the same results using point-neurons, without a preceding extensive (and probably unsuccessful) ad hoc fitting procedure applied to every individual neuron AND every combination of synaptic inputs.
In contrast, here we have devised a method that is able to map any kind of morphology, equipped with any kind of ligand- or voltage-gated conductance arbitrarily distributed over the entire dendritic tree. This was obtained by using a merging rule based on Strahler's analysis, which does not depend on the type of neuron to be reduced20,21,22,23,24. This resulted in a procedure that is morphology-independent and, thus, it can be directly applied to any reconstruction of a given model neuron without any fitting or tuning. It allowed significant conceptual advances with respect to what we have previously published19, especially in two aspects: 1) it allowed a one-to-one comparison of the traces obtained using the full or the reduced morphology, rather than their average behavior as in the previous method, 2) it avoids the extra calculation of parameters needed to model specific neurons behavior, such as the depolarization block for CA1 pyramidal neurons. It should also be noted that using this method there would be no need to apply a regularization theory37, which might bias the reduction using assumptions that, though plausible, would be arbitrary. The major limitation of the method, so far, is that it takes accurately into account the effects of the dendritic dynamics at the soma rather than the local membrane dynamics at individual compartments (i.e., the time course of the dendritic membrane potential in the full model is not explicitly mapped into specific compartments of the reduced model). The performances, robustness, generality and applicability of our method make it ideally suited to be integrated into large multi-scale simulations of the brain which are widely considered to be one of most promising future emerging technologies (e.g. the Human Brain Project, http://www.humanbrainproject.eu/).
Methods
Computational details
We performed our simulations using v7.3 of the NEURON simulation environment38. The model and simulation files will be available for public download under the ModelDB section of the Senselab database (http://senselab.med.yale.edu/ModelDB, accession number 149000). To ensure a representative range of morphological properties, we used 10 3D reconstructions of Purkinje cells39,40,41 downloaded from public archive neuromorpho.org26. The same passive properties, voltage-dependent ionic channels, kinetic and distribution were used for all morphologies. The relative model files and parameters were those used in the original model27, downloaded from the ModelDB public depository (acc.n. 17664). This model is based on ref. 42 and incorporates 12 types of voltage-gated ion channels, six of which (the fast and persistent sodium channel, T–type calcium channel, anomalous rectifier channel, A–type potassium channel and persistent potassium channel) were identical to those used in42. In the work by Miyasho et al.27, P–type calcium channel, delayed rectifier, high-threshold calcium-activated potassium channel and low-threshold calcium-activated potassium channel were slightly modified and, finally, D–type K+ channel and class–E Ca2+ channel were added. To the best of our knowledge, this is currently the only published realistic NEURON model implementation of Purkinje cells. It should be noted that the focus here is not on implementing or testing the performances of a given realistic model but, rather, on the ability of our method to reproduce the full model's behavior, whatever they are, under different stimulating conditions without any tuning (see Fig. 2b–e ).
To simulate a generic background excitatory synaptic activity, synapses were modeled as a double exponential conductance change with 0.5 and 1.2 ms for rise and decay time, respectively (corresponding to granule cells inputs42) and randomly distributed in the spiny dendrites, with peak conductance drawn from a Gaussian distribution of 5 ± 0.5 nS. They were synchronously or asynchronous activated at a random (Poisson) frequency in the range 10–280 Hz. This is consistent with in vivo experiments showing that granule cells can discharge over an extraordinarily wide range of frequencies (from tonic firing at a few hertz to phasic bursts up to 1 kHz44. In all cases, results for any given stimulation condition for each morphology were averaged from 5 simulations, randomly redistributing synaptic locations and activation times. In view of the activity of Purkinje cells observed in vivo28,29 (mean firing rate 48 Hz, maximum firing rate 130 Hz), three different kinds of stimulation were tested for all morphologies (see Fig. 2a ):
-
Full: synapses randomly distributed over the entire (spiny) dendritic area, synchronously activated at a random (Poisson) frequency with average value in the range 50–200 Hz;
-
Partial: synapses randomly distributed on the spiny dendrites of a restricted dendritic area, synchronously activated at a random (Poisson) frequency with average value in the range 50–280 Hz; for each morphology four different areas (1–4) were defined by a geometrical subdivision of the dendritic tree in four quadrants;
-
Segregated: synapses randomly distributed in the four different dendritic areas activated synchronously within each area and asynchronously among areas at a random (Poisson) frequency with an average value in the range 10–100 Hz;
Unless explicitly noted otherwise, 1000 synapses were used in all cases. All simulations were carried out for 2 sec, with the last 1000 ms of somatic membrane potential used to analyze the results.
Merging rules, mapping synaptic inputs location and scaling of ionic and synaptic conductances
We first quantitatively analyzed the morphological complexity of a Purkinje cell by performing a Strahler's analysis of the dendritic tree20,21,22,23,24, in which every unbranched membrane section is ordered as follows. Terminal sections are given order number 1. When two order n branches join, an n + 1 order is created, whereas an order n + 1 branch remains of the same order when joining an order n branch. This method always assigns the highest order to the soma and the major branches connected to it (order 6 for the cell in Fig. 3a and 6–8 for the morphologies used in this work). All dendrites of each morphology were clustered according to their Strahler's order.
The dendritic tree topology and the electrophysiological and synaptic properties of Purkinje cells, suggest that these cells have three different functional regions that can be characterized by their different Strahler's order20,27:
-
soma and initial major branches, with the maximum Strahler's order of the cell: m;
-
smooth dendrites, branches of order i: 3 < i < m;
-
spiny dendrites, branches of order ≤ 3.
To implement a reduced model from a complex morphology we first choose a Strahler's number s. Then, each dendrite of order ≥ s is identically mapped in a compartment, otherwise dendrites of order < s are grouped in two ensembles, for smooth and spiny sections, each of them mapped into one compartment. With preliminary simulations, we tested several different values of s and found that s = 5 gave the best compromise between a higher reduction factor (which reduces computing time) and a better overall accuracy under all stimulation conditions.
Depending on the complexity of the dendritic tree, this process results in the morphological model being partitioned in a finite set of clusters, each of them mapped into one of the compartments composing the reduced model.
Next, the method closely follows a procedure that we have recently suggested to reduce hippocampal CA1 pyramidal neurons19. The length of the compartment equivalent to a given cluster, Leq, was thus defined as

where

and Li and Si are the lengths and the areas of the i–th dendrite (belonging to sequential (seq) or branched (br) dendrites in the cluster), respectively.
The diameter of the equivalent compartment is next chosen by taking into account the axial resistance of the ensemble of dendritic segments it represents19

where

and Ra is the specific axial resistance of each dendrite in the cluster and ra,i is the axial resistance of the i–th dendrite. Moreover, as in19, we set

where H is the total number of the dendrites in the cluster and  in the specific axial resistance in the equivalent compartment.
in the specific axial resistance in the equivalent compartment.
The effect of dendritic inputs is implemented by repositioning the synapses in the equivalent model, according to the same procedure used for CA1 neurons19. Let's consider synapse i on cluster C of the realistic model, we define the axial path resistance, ri,PATH, as

where ra,h is the axial resistance of the h–th segment of the path consisting of the unique sequence of j membrane segments leading from the soma to the dendrite on which the synapse is positioned.
Let rmax and rmin be the maximum and the minimum axial path resistance of cluster C, i.e.,

where rPATH indicates the axial path resistance of a given dendrite belonging to cluster C. Each cluster C of the morphological model is mapped in a single compartment C′ in the reduced model. To define the number of membrane segments, n′, composing each one of these C′ compartments we used45

where

and  is defined in Eq. (5).
is defined in Eq. (5).
To find the most appropriate segment of C′ to place the i–th synapse, we define

where k represents the number of segments from the soma to compartment C′ and  the axial resistance of the h–th segment of C′. Then, the segment si of C′ where the i–th synapse will be placed is defined by its axial path resistance
the axial resistance of the h–th segment of C′. Then, the segment si of C′ where the i–th synapse will be placed is defined by its axial path resistance  in such a way that19
in such a way that19

To preserve the electrotonic properties of the equivalent neuron, a scaling factor,  , is next defined as a function of the spatial distribution of the synapses and applied to the specific membrane capacitance Cm, the specific membrane resistance Rm and the ion channels peak conductance gionic:
, is next defined as a function of the spatial distribution of the synapses and applied to the specific membrane capacitance Cm, the specific membrane resistance Rm and the ion channels peak conductance gionic:


where Seq, is the surface area of the equivalent compartment and wi = 1 if in the i–th dendrite there is at least one synapse and 0 otherwise. A final scaling factor is then applied to the peak synaptic conductance as

where  is the original peak conductance of the i–th synapse of the realistic neuron.
is the original peak conductance of the i–th synapse of the realistic neuron.
The various steps described above, do not require any fitting or tuning procedures and are independent from any specific cell morphological or electrophysiological parameter. As long as the distribution of the ion channels does not change, any given morphology of a specific neuronal population can be reduced in the same way. For Purkinje cells, which have a quite elaborate dendritic tree, the entire reduction process takes, on average, less than 3 sec of CPU time on a Windows PC with an Intel Xeon processor at 2.93 GHz. Specifically, cell e4cb3a1 ( Fig. 3 ) required 0.36 sec for the initial setup, 1 sec to arrange clusters and reduce the morphology, 0.27 sec to initialize synapses's location and activation time, 0.62 sec to scale the passive and active properties and 0.67 sec to reposition the synapses.
Spike times analysis
A train of simple spikes (SSs) elicited in Purkinje cells have been previously analyzed in terms of regular firing periods interrupted by longer and irregular interspike intervals (ISIs) termed pauses28. A widely measure used to classify the ISIs in an SS train as belonging to different regular firing periods is the CV2 coefficient, which compares consecutive ISIs:

In this way, a regular pattern is defined as consecutive ISIs where all CV2 values are less or equal to a threshold. In this work, as threshold we choose the value 0.2, as in29. The beginning of a regular pattern is thus marked by a spike with a preceding CV2 > 0.2 and following by an ISI with a CV2 < 0.2. All ISIs not belonging to a regular patterns were classified as singles. We used the CV2 coefficient as one way to validate the results obtained with the realistic model (see Supplementary Fig. 2c ) respect to in vivo results28.
Accuracy calculation and statistical analysis
For each morphology we carried out an extensive number of simulations (11, 10, 4 × 12 sets of simulations at increasing stimulation frequencies for full, partial and segregated stimulation, respectively, each repeated 5 times with random redistribution of synaptic location and peak conductance). This resulted in a total of 3450 simulations. The quality of the reduction method was evaluated, for each simulation of any given morphology under any fixed stimulation, by comparing the traces obtained using the realistic and the reduced model and calculating the accuracy factor as

where TP (True Positives), is the number of spikes from the morphological neuron that are also found in the reduced model; TN (True Negatives) is the number of intervals in which the neuron does not fire a spike in both the morphological and the reduced model; FP (False Positives) is the number of mismatched spikes in the reduced model; FN (False Negatives) is the number of spikes from the morphological neuron that are not matched in the reduced model. Calculated in this way, the accuracy takes into account how accurately the reduced model reproduces both spiking periods and pauses of the realistic model. A value of 100% indicates a perfect match between the simulations. More details about its calculation can be found in19, where we have also shown that it is a robust measure.
The ISIs from each pair of simulations (full and reduced model) were tested for their statistical difference using the Wilcoxon Signed Rank-sum test (zero, null hypothesis with a significance level of 0.05).
References
Vogels, T. P., Rajan, K. & Abbott, L. F. Neural Network Dynamics. Annu. Rev. Neurosci. 28, 357–376 (2005).
Izhikevich, E. M. Simple model of spiking neurons. IEEE Trans Neural Netw. 14, 1569–72 (2003).
Tuckwell, H. C., Rodriguez, R. & Wan, Y. M. Determination of ring times for the stochastic FitzHugh-Nagumo neuronal model. Neural Comput. 15, 143–159 (2003).
Morris, C. & Lecar, H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J. 35, 193–213 (1981).
Traub, R. D. et al. Single column thalamocortical network model exhibiting gamma oscillations, sleep spindles and epileptogenic bursts. J. Neurophysiol. 93, 2194–2232 (2005).
Bazhenov, M., Timofeev, I., Steriade, M. & Sejnowski, T. J. Model of thalamocortical slow-wave sleep oscillations and transitions to activated States. J. Neurosci. 22, 8691–8704 (2002).
Migliore, M., Hines, M. L., McTavish, T. S. & Shepherd, G. M. Functional roles of distributed synaptic clusters in the mitral-granule cell network of the olfactory bulb. Front. Integr. Neurosci. 4, 122 (2010).
Bianchi, D. et al. On the mechanisms underlying the depolarization block in the spiking dynamics of CA1 pyramidal neurons. J. Comput. Neurosci. 33, 207–225 (2012).
Herz, A. V., Gollisch, T., Machens, C. K. & Jaeger, D. Modeling single-neuron dynamics and computations: a balance of detail and abstraction. Science 314, 80–85 (2006).
Kuznetsov, A. S., Kopell, N. J. & Wilson, C. J. Transient high-frequency firing in a coupled-oscillator model of the mesencephalic dopaminergic neuron. J. Neurophysiol. 95, 932–947 (2006).
Kepecs, A., Wang, X. J. & Lisman, J. Bursting neurons signal input slope. J. Neurosci. 15, 9053–9062 (2002).
Brown, S. A., Moraru, I. I., Schaff, J. C. & Loew, L. M. Virtual NEURON: a strategy for merged biochemical and electrophysiological modeling. J. Comput. Neurosci. 31, 385–400 (2011).
Bahl, A., Stemmler, M. B., Herz, A. V. M. & Roth, A. Automated optimization of a reduced layer 5 pyramidal cell model based on experimental data. J. Neurosci. Methods 210, 22–34 (2012).
Bush, P. C. & Sejnowski, T. J. Reduced compartmental models of neocortical pyramidal cells. J. Neurosci. Methods 46, 159–166 (1993).
Destexhe, A., Neubig, M., Ulrich, D. & Huguenard, J. Dendritic low-threshold calcium currents in thalamic relay cells. J. Neurosci. 18, 3574–3588 (1998).
Destexhe, A. Simplified models of neocortical pyramidal cells preserving somatodendritic voltage attenuation. Neurocomputing 38, 167–173 (2001).
Tobin, A. E., Van Hooser, S. D. & Calabrese, R. L. Creation and reduction of a morphologically detailed model of a leech heart interneuron. J. Neurophysiol. 96, 2107–2120 (2006).
Davison, A. P., Feng, J. & Brown, D. A reduced compartmental model of the mitral cell for use in network models of the olfactory bulb. Brain Res. Bull. 51, 393–399 (2000).
Marasco, A., Limongiello, A. & Migliore, M. Fast and accurate low-dimensional reduction of biophysically detailed neuron models. Sci. Rep. 2, 928 (2012).
Shelton, D. P. Membrane resistivity estimated for the Purkinje neuron by means of a passive computer model. Neurosci. 14, 111–131 (1985)
Kim, M. D., Jan, L. Y. & Jan, Y. N. The bHLH-PAS protein Spineless is necessary for the diversification of dendrite morphology of Drosophila dendritic arborization neurons. Genes Dev. 20, 2806–819 (2006).
Rothnie, P. et al. Functionally relevant measures of spatial complexity in neuronal dendritic arbors. J. Theor. Biol. 238, 505–526 (2006).
Jinushi-Nakao, S. et al. Knot/collier and cut control different aspects of dendrite cytoskeleton and synergize to define final arbor shape. Neuron 56, 963–978 (2007).
Liu, Q. A. & Shio, H. Mitochondrial Morphogenesis, Dendrite Development and Synapse Formation in Cerebellum Require both Bcl-w and the Glutamate Receptor δ2. PLoS Genet. 4, e1000097 (2008).
Llinas, R. R. & Walton, K. D. The Cerebellum., The Synaptic Organization of the Brain Shepherd G. M. (ed.) 255–288 (Oxford University Press, New York, 1998).
Ascoli, G. A. Mobilizing the base of neuroscience data: the case of neuronal morphologies. Nat. Rev. Neurosci. 7, 318–24 (2006).
Miyasho, T. et al. Low-threshold potassium channels and a low-threshold calcium channel regulate Ca2+ spike firing in the dendrites of cerebellar Purkinje neurons: a modeling study. Brain Res. 891, 106–115 (2001).
Shin, S.-L. et al. Regular patterns in cerebellar Purkinje cell simple spike trains. PLoS ONE 2, e485 (2007).
De Schutter, E. & Steuber, V. Patterns and pauses in Purkinje cell simple spike trains: experiments, modeling and theory. Neurosci. 162, 816–826 (2009).
Rall, W. Branching dendritic trees and motoneuron membrane resistivity. Exp. Neurol. 1, 491–527 (1959).
Rall, W., Segev, I., Rinzel, J. & Shepherd, G. M. (eds.) The Theoretical Foundation of Dendritic Function (MIT Press, Cambridge, 1995).
Ohme, M. & Schierwagen, A. An equivalent cable model for neuronal trees with active membrane. Biol. Cybern. 78, 227–243 (1998).
Stratford, K., Mason, A., Larkman, A., Major, G. & Jack, J. The modeling of pyramidal neurones in the visual cortex., The Computing Neuron Durbin R., Miall C., & Mitchison G. (eds.) 296–331 (Addison-Wesley, Workingham, UK, 1989).
Hendrickson, E. B., Edgerton, J. R. & Jaeger, D. The use of automated parameter searches to improve ion channel kinetics for neural modeling. J. Comput. Neurosci. 30, 301–321 (2011).
Kellems, A., Roos, D., Xiao, N. & Cox, S. Low-dimensional, morphologically accurate models of subthreshold membrane potential. J. Comput. Neurosci. 27, 161–176 (2009).
Kellems, A., Chaturantabut, S., Sorensen, D. & Cox, S. Morphologically accurate reduced order modeling of spiking neurons. J. Comput. Neurosci. 28, 477–494 (2010).
Gerstner, W., Sprekeler, H. & Deco, G. Theory and simulation in Neuroscience. Science 338, 60–65 (2012).
Hines, M. L. & Carnevale, N. T. The NEURON simulation environment. Neural Comp. 9, 1179–1209 (1997).
Martone, M. E. et al. The cell-centered database: a database for multiscale structural and protein localization data from light and electron microscopy. Neuroinformatics 1, 379–395 (2003).
Vetter, P., Roth, A. & Hausser, M. Propagation of action potentials in dendrites depends on dendritic morphology. J. Neurophysiol. 85, 926–937 (2001).
Rapp, M., Segev, I. & Yarom, Y. Physiology, morphology and detailed passive models of cerebellar Purkinje cells. J. Physiol. (London) 474, 101–118 (1994).
De Schutter, E. & Bower, J. M. An active membrane model of the cerebellar Purkinje cell. II. Simulation of synaptic responses. J. Neurophysiol. 71, 401–419 (1994).
De Schutter, E. & Bower, J. M. Simulated responses of cerebellar Purkinje cells are independent of the dendritic location of granule cell synaptic inputs. Proc Natl Acad Sci U S A. 91, 4736–4740 (1994).
Valera, A. M. et al. Adaptation of granule cell to Purkinje cell synapses to high-frequency transmission. J. Neurosci. 32, 3267–3280 (2012).
Hines, M. L. & Carnevale, N. T. NEURON: A tool for neuroscientists. Neuroscientist 7, 123–135 (2001).
Acknowledgements
This work has been partially supported by the Scientific Project F.A.R.O. 2013/02 “Mathematical methods for modeling natural phenomena”.
Author information
Authors and Affiliations
Contributions
A.M. and M.M. wrote the manuscript text and A.L. carried out the simulations. All authors prepared the figures and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
supplementary figures
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Marasco, A., Limongiello, A. & Migliore, M. Using Strahler's analysis to reduce up to 200-fold the run time of realistic neuron models. Sci Rep 3, 2934 (2013). https://doi.org/10.1038/srep02934
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02934
This article is cited by
-
An efficient analytical reduction of detailed nonlinear neuron models
Nature Communications (2020)
-
Simulation of alcohol action upon a detailed Purkinje neuron model and a simpler surrogate model that runs >400 times faster
BMC Neuroscience (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.