Abstract
The recent crisis has brought to the fore a crucial question that remains still open: what would be the optimal architecture of financial systems? We investigate the stability of several benchmark topologies in a simple default cascading dynamics in bank networks. We analyze the interplay of several crucial drivers, i.e., network topology, banks' capital ratios, market illiquidity and random vs targeted shocks. We find that, in general, topology matters only – but substantially – when the market is illiquid. No single topology is always superior to others. In particular, scale-free networks can be both more robust and more fragile than homogeneous architectures. This finding has important policy implications. We also apply our methodology to a comprehensive dataset of an interbank market from 1999 to 2011.
Similar content being viewed by others
Introduction
The impact of network topology on systemic risk is a central topic of the science of complex networks1,2, not only because of its theoretical interest, but also because of its many empirical applications, for instance on infrastructure networks3 and financial systems4.
In a cascading dynamics, some network nodes are assumed to fail at the beginning of the process. Their failures increase the load (or the level of distress) of the neighboring nodes. When this load at a node exceeds its threshold (i.e. its individual robustness) the node fails, possibly triggering a cascade. This type of propagation dynamics has been applied to a variety of social and economic contexts5,6. Several analytical investigations have been carried out regarding the cascade size (i.e. the number of nodes eventually failing in this process)7, including the effect of heterogeneity in the thresholds8 and the cases of degree-correlated networks9, clustered networks10, multiplex networks11. A large body of works has investigated numerous model variants, including: a) the propagation of fractures in a system of fibers12; b) the case in which the load at every node is the total number of shortest paths passing through the node13,14; c) the case in which links (rather than nodes) topple15; d) cascades of rewiring of links leading to self-organized scale-free networks16; e) the sandpile model17, as well as its variant on several interdependent networks18; f) the percolation process in interdependent networks3. Most of the attention in these works has focused on the conditions under which the distribution of the cascade size follows a power-law. Interestingly, many of these variants can be mapped into few classes8.
Epidemic spreading and contagion models can also be seen as a widely studied instance of systemic risk. In the Susceptible-Infected-Susceptible (SIS) model, scale-free networks behave markedly differently from random graphs since the epidemic threshold of the infection rate tends to zero for large network size19.
While in most load redistribution models, adding links in the network tends to dilute the effect of a failure on the neighbors, in contagion models more links rather tend to propagate failures more effectively. In many situations, including in particular the financial system, both effects are present. On the one hand, links allow agents to diversify risk. On the other hand, agents with many links tend also to import distress from others20 and are exposed to amplification effects such as bank runs or trend reinforcement21. Load redistribution and contagion have been studied so far mostly in separate settings. In contrast, they need to be taken into account simultaneously in order to understand the role of network topology.
Our paper aims to contribute to the question – brought to the fore by the recent crisis and still remaining open – regarding what would be the optimal architecture of financial systems. More precisely, we want to analyze the stability of several benchmark topologies under various scenarios. While empirical studies show that financial networks display heterogenous degree distributions22,23,24, it is not clear if and how they could be made more robust. The cascading dynamics we use for our investigation25 is simple enough to allow us to run very extensive simulations on a variety of scenarios. At the same time, the model is derived from basic facts of banks balance sheets and overall the approach is very similar in spirit to the state-of-the-art stress-tests carried out at central banks26,27. It is also in line with a few works that have studied systemic risk using cascading dynamics28,29, based on the idea that financial institutions are connected in a network of liabilities and claims30.
Unlike previous works, we deliver a comprehensive study of the interplay of the main drivers of systemic cascades: (1) network topology, (2) individual nodes robustness (i.e. banks' capital ratios), (3) relative strength of contagion (which is related to market illiquidity) and (4) random vs targeted initial shocks.
We find that, in general, topology does not matter when the load redistribution component of the model is the only one at work. In contrast, it substantially matters when the contagion component is present, that is when the market is illiquid. Remarkably, we also find that it is false that certain topologies are always superior to others. In particular, scale-free networks can be both more robust and more fragile than homogeneous architectures. This finding has profound policy implications. It means that the optimal architecture depends on the level of market liquidity and suggests that regulators should be aware of the topology they are confronted with, before making decisions regarding liquidity injections.
As an empirical exercise, we also carry out simulations on a comprehensive dataset of an interbank market from 1999 to 2011, which shows, with some caveats, what would have been the effect of defaults and liquidity interventions in a range of scenarios regarding capital ratios and market illiquidity.
Results
We investigate a model that was introduced25 to describe the propagation of defaults among banks connected in a network of liabilities. Previous work on such model focused on the analytical computation of the expected cascade size in regular networks. Here instead, we carry out extensive numerical studies by varying all the parameters of the model, including different degree distributions and different levels of illiquidity.
The model can be summarized as follows. The nodes in the network represent financial institutions (hereafter “banks” or “agents”) and links represent lending relationships (i.e. a bank lends money to another one), with the convention that the direction of the link is taken from the lender to the borrower. For the sake of mathematical tractability, we define the individual financial robustness ηi of each bank as the ratio between the bank equity (i.e., its net capital) and the amount of its assets invested in the interbank market. When bank i faces losses due to some defaulting borrowers, its equity and thus its robustness decreases in proportion to its relative exposure to those borrowers. We assume that there is no asset recovery in the short run and that a bank defaults when its robustness drops below zero. This is a standard approach following from balance-sheet identities28,29.
Notice that in the basic case of a “liquid market” (i.e. when it is easy for a bank to find buyers for the assets the bank needs to liquidate) and homogenous link weights, the dynamics of our model can be mapped into the classic threshold dynamics investigated by5 and subsequently by6. One difference is that in our model the variance of the robustness (equivalent to the threshold in5,6,7) depends itself on the connectivity (see Methods).
In contrast, when markets are not liquid, then depending on how many defaults it faces and on how large is its initial robustness, bank i may have to face an additional decrease of robustness, as described by Eq.1. In brief, bank i may face an additional loss due to its short term lenders deciding not to renew their loans (i.e. there is a so-called “credit run” on bank i), forcing bank i to sell some assets below their market price (a so-called “fire-selling”). This effect, which increases with the illiquidity of the market for assets, is captured by the parameter b and emerges in the model from the assumptions on the behavior of the short term lenders of the bank25 - see more detail in Methods and in Supplementary Material (SM). From the point of view of dynamical processes on networks, the credit run constitutes an amplification mechanism of losses which introduces a contagion component in the model. The parameters of the model include the network structure, which remains fixed during the dynamics and the level b of the market illiquidity. The dynamics depends also on the initial conditions, i.e. the distribution of initial robustness ηi(0) across the nodes and the nodes that initially fail (i.e. the shocks). One of the problems in investigating cascading dynamics in networks lies in the many different ways of allocating the initial robustness and the shocks. Therefore, we consider the following choices.
-
We vary the type of shock (random or targeted)
-
We vary the type of correlation between robustness and degree (no correlation; the higher the degree node the higher the robustness and vice versa).
-
We vary the degree distribution (among scale-free, random graph or regular), in one case imposing a correlation between in-degree and out-degree. In another case, we impose only the out-degree and leave the in-degree random and uncorrelated with the out-degree. In the last case we take the opposite situation (i.e., we impose the in-degree and leave the out-degree random and uncorrelated with the in-degree).
-
We vary the market illiquidity (the parameter b = 0 or b > 0)
A combination of the above choices is indicated in the following as a “scenario”. In each scenario then, we study the cascade size as a function of the average out-degree k in the network and the average value m of initial individual robustness. The initial robustness ηi(0) is allocated across banks according to a Gaussian probability distribution with mean μ and variance σ (the latter being a function of k). Negative values of ηi(0) imply that the corresponding banks are in default at the beginning. We refer to these as endogenous shocks. In addition, a fraction y0 of banks is additionally set to default. These are referred to as exogenous shocks.
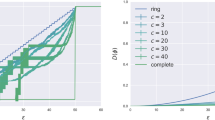
The results for the cascade size are illustrated in the form of phase diagrams (see for instance Figure 1a) where each curve in the diagram represents, for a given network topology, the frontier between large and very small cascades in the space of average out-degree k and average initial robustness m (see Methods). As one may expect, for a given value of k, by increasing m we can always move away from the region of large cascades. Thus, the higher the frontier is the more “fragile” the network is as a whole in the given scenario. This implies that higher levels of initial robustness (or initial core capital) are needed in order to prevent the triggering of large cascades. The figure then allows to see whether a network topology becomes more or less fragile by increasing the density of links and to compare it with the behaviour obtained through the use of different topologies.
Similarly, in each scenario, we also study the cascade size as a function of the market illiquidity b and the average value m of initial individual robustness. In this case, the average out-degree k is fixed. The results are also shown in a phase diagram (see for instance Fig. 3a). The figure allows to see how different network topology are affected by illiquidity and what level of average core capital (robustness) would be needed to move into the safe region. Additionally to the curves, we associate a color with each topology. For all figures, colored regions represent large cascades outcomes and white regions represent small or no cascades outcomes.
Frontier of large cascades evolution in an asset illiquid market, b = 0.4.
For convenience, we use γs = γ10−3. (a) Random exogenous defaults and random individual robustness σ = 0.3, y0 = 0.03, γs = 0.1. (b) Random exogenous defaults and positive correlation between degree and individual robustness σ = 0.3, y0 = 0.04, γs = 0.13. (c) Random exogenous defaults and negative correlation between degree and individual robustness σ = 0.3, y0 = 0.04, γs = 0.13. (d) Targeted exogenous defaults and positive correlation between degree individual robustness σ = 0.3, y0 = 0.04, γs = 0.13.
Frontier of large cascades evolution with fixed average degree,  .
.
For convenience, we use γs = γ10−3. (a) Random exogenous defaults and random individual robustness, σ = 0.3, y0 = 0.03, γs = 0.1. (b) Random exogenous defaults and positive correlation between degree and individual robustness, σ = 0.3, y0 = 0.04, γs = 0.13. (c) Random exogenous defaults and negative correlation between degree and individual robustness, σ = 0.3, y0 = 0.04, γs = 0.13. (d) Targeted exogenous defaults and positive correlation between degree individual robustness, σ = 0.3, y0 = 0.04, γs = 0.13.
Random exogenous defaults and random individual robustness
We start from the most general case, where individual financial robustness is uncorrelated with the degree and the banks initially defaulting are randomly chosen. When the market is liquid, i.e. b = 0, (Fig. 1a) the three network topologies present very similar frontiers in the phase diagram. The frontier decreases with k implying less fragility at the system level. Indeed, at a fixed large k it takes a smaller level of average individual initial robustness m to move into the safe region of no cascades, i.e. below the frontier. These results (obtained with simulations of the cascading process on 1000 realizations of networks consisting of 1000 nodes) confirm previous findings based on simulations on larger networks7. They confirm also the results based on the analytical expression of the expected cascade size that were obtained as fixed point of the recursive expression for the number of defaulting nodes7,25. Nevertheless, here we explicitly compare the phase diagram for scale free networks and random graphs and we emphasize that they are very similar even for networks of medium size (i.e. N = 1000). Therefore, the topology seems not to play a role as long as the basic case of the model is considered. Notice also that a difference between the phase diagram of scale free networks and random graphs was reported instead in6, where the calculation of the cascade size is analytical and based on the generating function formalism.
In contrast, when the market is illiquid, i.e. b > 0 (Fig. 2a) the frontier of large cascades depends non monotonically on k. This is because when k is large, defaults trigger more runs of short-term lenders and thus more fire-sales and cost for the banks (see Methods). The result for regular and random topologies is also in line with previous analytical findings25. Notice that for the scale-free topology, the frontier of large cascades is systematically higher than for the other cases, making scale-free networks more fragile. Fig. 3a shows the phase diagram in the space b, m. As it appears, scale-free networks are more sensitive to the increase of illiquidity. While the frontier for regular and random topologies saturate for values around b = 0.2, the frontier for scale-free continues to increase, implying a higher fragility when illiquidity b is high.
Random exogenous defaults and correlation between degree and individual robustness
The following experiments focus on settings where the individual financial robustness is correlated to the degree. Two types of scenario are at stake: The positive one where the agents with higher degree are endowed with higher financial individual robustness - The negative one where the agents with higher degree are endowed with lower financial individual robustness. As results for liquid asset market do not differ from the general case (Fig. 1a), they are reported in the SM.
However, when the asset market becomes illiquid, different outcomes occur. Fig. 2b shows the results for the positive scenario. Even though all classes provide similar shapes when k increases, the regular topology becomes the most fragile as its area of large cascades is higher than the other types of networks. Remarkably, the scale-free topology has the lowest frontier and, hence, is the least fragile of the three topologies. This is opposite to the general case in Fig. 2a. As the results from random networks fall between the two previous classes, it appears that, under the current positive scenario, the more heterogenous the structure is, the less fragile the system becomes. In the negative scenario, this statement is reversed and more heterogeneity leads to more fragility of the system as Fig. 2c shows. In fact, the ranking in terms of fragility profile is in line with the general case in Fig. 2a, even though the gap between the three frontiers is higher for low values of k and diminishes as k increases.
Fig. 3 displays the results of both positive and negative scenarios for increasing levels of the illiquidity b. In Fig. 3b, the scale-free class shows to be less sensitive and, thus, less fragile than the two others once b > 0.1. Nevertheless, when b is higher then 0.3, the frontier for the regular and random graphs does not increase anymore while the scale-free continues to increase with b albeit at a slower rate. In Fig. 3c, the three topologies share the same frontier until a point around b = 0.2, beyond which the frontier for regular and random graphs subsequently stop increasing while the sensitivity of the frontier for the scale-free graph continues to grow.
Targeted exogenous defaults and positive correlation between degree individual robustness
In the previous scenarios, agents enduring exogenous shocks were selected randomly. Fig. 1b, Fig. 2d and Fig. 3d retrieve results of simulations where the exogenous shocks affect the agents with the largest degree as described in the Methods. Those figures imply a scenario of positive correlation between degree and financial individual robustness. Results from random and negative correlations are reported in the SM. Hence, here, the shocks are targeted towards the highly connected agents. The three figures exhibit a sharp difference between scale-free networks and the more homogenous ones. In fact, the frontiers of large cascades for the former structure are systematically higher than the latter. For any state of market liquidity, the fragility of scale-free networks is exacerbated when hubs are targeted (confirming a classical observation of complex networks behaviors). This result holds even in the case of completely liquid assets, which was blind to the underlying topology under random shocks and remains valid for any type of correlation between distributions of individual financial robustness and degree (see SM).
Empirical case: the e-MID
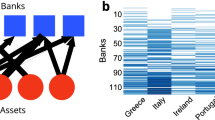
Finally, we apply our approach to the empirical data of a specific interbank market. Notice that this is not a validation of the model, which would require to have detailed information over time on the financial state of the banks in order to follow chains of default or distress events across the network. Our dataset consists of a collection of monthly snapshots of the network of the so-called e-MID interbank money market (see Methods). Links represent lending flows among banks aggregated at the time scale of a month. The data span the period between January 1999 and December 2011. We analyze the evolution of frontiers of large cascades for the months of January of each year between 1999 and 2011 in the space of average robustness m and market illiquidity b, as it was previously done in Fig. 3 in the case of synthetic networks.
In order to better interpret our findings, a network analysis of the structural changes occurring in the e-MID market over the years is provided in the SM. In essence, it appears that since 1999, essentially due to a wave of merging and acquisitions in the banking sector, the interbank market has gradually shrunk in terms of size (i.e., number of active banks) and density (i.e., number of active edges). It is also important to notice that the total volume (the aggregate level of money lent) was generally growing (more then doubled between 2000 and 2007) until the global financial crisis where it has been markedly reduced: the total volume in January 2009 is almost a sixth of the total volume in 2007. These networks have been found to display heterogenous degree distribution and core periphery24,31.
As shown in Fig. 4, the frontiers corresponding to the period between 1999 and 2008 can be separated from those in the period between 2009 and 2011. The former curves exhibit a smooth and linear dependence on illiquidity b. The latter curves are located at lower values of individual robustness m and tend to be less sensitive to illiquidity. The years of 2007 and 2008 correspond to the highest frontier (i.e., to the highest potential fragility) although the trend in the preceding years is not monotonic. Notice that the year of 2009 corresponds to the lowest frontier, which would imply that large cascades are more difficult to be triggered.
Frontier of large cascades evolution of the e-MID market in the period between January 1999 and January 2011 under random exogenous defaults and random individual robustness distirbution.
Impact of illiquidity on the structure of January of each year, σ = 0.3, y0 = 0.04, γs = 0.13. For convenience, we use γs = γ10−3.
The period between January 2008 and January 2009 corresponds to the post-Lehman Brothers era, marked by (i) an important rise of interbank rates for all major currencies and (ii) a takeover of central banks to provide liquidity and guarantees to banks. As banks became more reluctant to engage in credit exposures with other banks and started trading with the central bank (that is not present in our dataset), default cascades across the interbank market became obviously much less likely to be triggered. This explains the sudden drop of the 2009 frontier with respect to the previous years and its smaller sensitivity to illiquidity (i.e. smaller slope). After 2009, banks slowly started to engage again in the interbank market making it more sensitive to illiquidity as it is shown by the 2010 and 2011 curves in Figure 4.
These results illustrate how a model like ours can be exploited to explore the systemic impact of a shock on an interbanking network for various levels of capital ratios and illiquidity. This can help central bankers in designing ex-ante capital structure requirements and liquidity provisioning schemes ex-post. Despite the lack of data available for parameters like the average financial individual robustness, we are nevertheless able to identify some features that can be paramount in the analysis of action to be taken by regulators.
In particular, the case of 2009 provides insights on the impact of big provision policy guaranteed by the European Central Bank (ECB) at that time. Starting from the Fall of 2008, this action along with the important rise of interbank rates made banks less active in the interbank market. This, in turn, decreased the sensitivity of the market to illiquidity: in the presence of a smaller system in terms of both size and density, the amplification phenomenon depicted by our model loses its impact. In simpler terms, banks lend less to each other, thus reducing the impact of a credit run on any bank. Finally, we can imagine that this apparent benefit is not without drawbacks since the ECB is not recorded in our data: part of the previously captured risk has been transferred from the e-MID to the ECB. In light of the results from the synthetic simulations, introducing the ECB would indeed increase the heterogeneity of the underlying network. The case would become extreme: the ECB would appear as the node of last resort to avoid a system collapse.
Discussion
In this paper, we have presented an analysis of the impact that network topology can have on systemic risk. In the context of the recent financial crisis, this work contributes to the ongoing debate spurring around the architecture of financial markets and their fragility. In addition, our results take into consideration the role of capital requirements on individual institutions. In this respect, we have carried out a systematic study of the interplay among several drivers of systemic default cascades: (1) network topology (in terms of different degree distributions), (2) capital ratios across banks, (3) intensity of contagion (which in our model is related to the level of market illiquidity) and (4) the type of shock, i.e. random vs targeted.
With respect to the benchmark classes of regular and random graphs, scale-free networks are characterized by a higher level of heterogeneity in the number of financial linkages (e.g., in the ability to lend to and borrow from other agents). This translates into a stronger market concentration which makes some players becoming the hubs for others. On the one hand, this architecture could be thought of as being more efficient (e.g., because hubs play a broker role) and more robust against shocks (e.g., because hubs are able to diversify shocks). On the other hand, from classical works on epidemic spreading, scale-free networks are also known to be proner to contagion processes. In the banking context, the existence of big universal banks serving only as pass-through for many others might render the system more fragile if these institutions are not individually robust enough.
Our work shows, for the first time in a systematic fashion, that the network topology alone does not determine the stability of the system. The optimal architecture depends first of all on the level of market liquidity. We have found that, in liquid markets and under random shocks, the topology does not matter in contrast with what one could think ex ante. This result is in line with lessons learned from previous crises (e.g., the Swedish case32). In contrast, in the case of illiquid markets, where agents can suffer from additional losses due to forced fire-sales, topology does play a role. In particular, scale-free networks show stability profiles markedly different from those of the two other network classes, in line with many previous results from the complex networks literature.
However – and importantly – it is far from true that certain topologies are always superior to others. We have shown that scale-free networks can be both more robust and more fragile than more homogeneous architectures, depending on two additional determinants, namely: (1) the allocation of core capital across the balance sheets of the institutions (i.e., initial endowments) and (2) the correlation between the number of lenders and borrowers (i.e., correlation between in and out degree). The second determinant can be thought of as a proxy for the liquidity capacity of the system as it represents the flow balance between the capacity to lend and the capacity to refinance.
On the one hand, scale-free topology is more robust when the most active agents (i.e., highest degree level) have the highest individual robustness and shocks are not targeted. This is consistent with the logic of having a better explicit buffer when the institution is more active in its lending and borrowing activity. On the other hand, scale-free topology is more fragile when the most active agents turn out to be the most vulnerable ones and, also, when shocks become targeted. However, it is worth noticing that even in the general case (i.e., no correlations and random shocks), scale-free networks are more fragile than regular and random graphs. This is due to the fact that the presence of hubs increases the chances of contagion between various parts of the network. It is also due to the fact that, when markets are illiquid, having a very larger number of borrowers exposes – ceteris paribus – the hubs to a larger number of defaults that in our model is the trigger of possible creditors's runs.
To conclude, in our model the optimal topology depends on the balance between the dilution effect of load redistribution and the amplification effect of contagion. Both effects are present in the cascade dynamics in many contexts, ranging from power grids to biological contagion, especially when the human factor plays a role. Therefore, these findings could be relevant for the design of robust complex networks in several domains.
Methods
Distress channels
We consider two channels of distress propagation in the model. The first channel consists of the losses due to the defaults of borrowers of a given bank. The second channel works as follows. If, after suffering from losses due to the default of some borrowers, the short-term creditors of the bank decide to run on their loans, the bank has to sell part of its assets in order to honor the loans. In an illiquid market, i.e. when selling those assets in a short time is not easy, the bank is forced to sell below the market price (“fire-selling”) incurring in additional losses. The second propagation channel is thus an amplification mechanism for the first channel.
Agents
The agents in the model (also referred to as “banks”) represent financial institutions and they are kept at a minimal level of sophistication. They are described by their balance-sheet, the list of their counterparties (i.e. borrowers and lenders) and an update rule of their financial robustness. An individual financial robustness indicator is devised according to the ratio of an agent's net worth over its assets invested in the current market:  , where Ai and Li are the total assets and liabilities of agent i and
, where Ai and Li are the total assets and liabilities of agent i and  is its total lending to other agents. This measure is used as a proxy to describe the financial status of agent i. The default of an agent occurs once her own equity becomes negative, an effect which is translated into the condition ηi(t) < 0.
is its total lending to other agents. This measure is used as a proxy to describe the financial status of agent i. The default of an agent occurs once her own equity becomes negative, an effect which is translated into the condition ηi(t) < 0.
The initial value of robustness ηi(0) is assigned to each agent according to a Gaussian probability distribution with mean μ and variance  where μ and σ are exogenous parameters for the experiments. The relationship between σρ and the average number of connection of the system k reflects the assumption that a larger number of credit counterparties leads to a smaller variance in the return of the credit portfolio of each agent and, thus, in the individual robustness. As a gaussian distribution of robustness can produce negative values, agents starting with ηi(0) < 0 are considered to be endogenously set in default. In addition, exogenous shocks are introduced by putting some agents with ηi(0) > 0 into default according to an external parameter y0.
where μ and σ are exogenous parameters for the experiments. The relationship between σρ and the average number of connection of the system k reflects the assumption that a larger number of credit counterparties leads to a smaller variance in the return of the credit portfolio of each agent and, thus, in the individual robustness. As a gaussian distribution of robustness can produce negative values, agents starting with ηi(0) < 0 are considered to be endogenously set in default. In addition, exogenous shocks are introduced by putting some agents with ηi(0) > 0 into default according to an external parameter y0.
Under the assumption that each agent manages an equally weighted portfolio (i.e., the relative exposure to each borrower is equal and amounts to 1/ki, where ki is agent i's number of borrowers), Equation 1 describes the law of motion of agents' financial robustness:

In the equation above, N is the total number of agents in the system, while kfi(t) is the number of agent i's borrowing counterparties that have defaulted so far according to:

where χj(t) is a binary value that indicates whether agent j has defaulted at time t or at any time before t and Vi is the set of agent i's borrowers. The parameter b measures the cost of the credit run and γ is a scale factor for the threshold above which the credit run occurs. The two latter parameters are homogenous across agents. The equation above can be derived from balance sheet identities as in25 (see SM for more details).
Financial networks
The market structure is meant as the underlying network of the financial system where nodes are agents and links are lender-borrower relationships. Formally, our network is defined as directed and weighted. The direction of a link goes from the lender to the borrower and the weight of a link corresponds to the amount in stake from the lender's perspective.
We consider three different classes of network based on the degree distribution:
-
1
regular where directed edges between nodes are assigned randomly under the constraint that all nodes have the same degree k.
-
2
random where the degree distribution follows a Possion distribution:

-
3
scale-free where the degree distribution follows a power-law distribution: P(k) ~ k−α.
Since networks are directed, two different distributions should be distinguished. The out-degree distribution characterizes the lending behavior, while the in-degree distribution describes the borrowing behavior. As a consequence, three different cases are to be investigated: (1) the impact of different out-degree distributions, (2) the impact of different in-degree distributions and (3) the impact of differently correlated in and out degree distributions. Here we will focus on the last case while the two other cases are analyzed in the SM.
In order to generate the aforementioned networks, for each class of topology, we produce two equal degree sequences with respect to the type of degree distribution. We then use the Configuration Model for directed networks33 to generate a multigraph in which we finally remove all self-loops and multiple edges. Keeping the average degree very small with respect to the total size (i.e. 0 < k < 40 for networks of 1000 nodes) allows for the resulting degree distributions to be acceptable with respect to the class of topology they refer to (see SM).
Robustness-degree correlation
In order to also inspect the effect of the potential correlation between the degree of an agent and its financial robustness, we impose degree constraints for the individual financial robustness allocation. Two opposite scenarios are implemented, namely, the positive correlation scenario and the negative correlation scenario. In the former case, we sort the values of degree and robustness and we assign them in such a way that the most financially robust agents get the highest number of counterparties with respect to the overall distribution while the least robusts agents have the least amounts of counterparties. The latter case considers the opposite allocation of financial robustness.
Targeted defaults versus random exogenous defaults
Introducing different structural roles also allows us to inspect how the system reacts to targeted shocks under the different distributions. Random exogenous defaults refer to fact that as a result of the allocation of initial robustness according to a gaussian distribution, a fraction of agents has negative robustness and thus is in default from the beginning of the simulation. In addition, we also consider a targeted attack scenario in which we are interested in the effect of targeting the hubs, i.e. the agents with the largest number of counterparties. This type of test is in line with standard approaches in complex networks when assessing the resilience of a network. Thus, a fraction y0 of agents with ηi(0) > 0 is chosen to be put into default at the beginning of the simulation, by selecting the top y0n agents, ordered by decreasing values of their degree.
Simulations
All synthetic simulations start with a population of 1.000 agents, each endowed with an individual financial robustness attribute. This attribute value is obtained from a Gaussian distribution, with mean m and variance σ and is either assigned randomly or with respect to the agent's degree, depending on the scenario implemented. An exogenous shock is then applied to the system by setting agents into default with respect to the scenario implemented. The amount of agents to be shocked is set up by the relative parameter y0. Each default can, in turn, provoke the default of others and the simulation stops when no more default events are observed. At the end, the size of the cascade, i.e., the total amount of defaulted agents, is recorded. The motivation for the values of parameters relates to the study implemented in previous analytical work25 along with some fine tuning in order to improve the salience and the clarity of the results being displayed. For convenience, we devise the variable γs = γ10−3 and use it as parameter of reference when retrieving the value of parameters for the simulations.
One simulation generates a network and runs the cascading process on it. Given a type of topology, we run 1.000 simulations for each pair of values of (b, m) and (k, m). The mean m of the individual robustness distribution ranges between 0 and 1 with incremental steps of 0.01; the credit run cost b ranges between 0 and 0.5 with incremental steps of 0.01; k, the average out-degree of the nodes ranges between 5 and 40 with incremental steps of 1. Hence, to obtain each of the reported figures for the synthetic networks, we run between 10 × 106 and 15 × 106 simulations. In the empirical case, we run more then 66 × 106 simulations. For each pair of values of (b, m) and (k, m), we record the average cascade size. In order to provide deviation estimations, typical standard errors from the results are reported in the SM. Additionally, we also report, in the SM, results when varying the size of the system.
We then determine the average transition curve, that is, the curve representing the frontier in the parameter space between the region where large cascades occur and the region where small cascades occur. In order to do so, we define a set of thresholds Θ. Let us take the case where the x-axis is the average degree k. For a given threshold θi ∈ Θ, we compute  for each k value, as follows:
for each k value, as follows:

where s(m, k) retrieves the value of the cascade size for the couple (m, k) relative to the size of the system. As an example: if θ1 = 0.9, then  for a given k will represent the minimum mean robustness required for the system to avoid cascades that will wipe out more the 90% of the banks. We then compute the average minimum mean,
for a given k will represent the minimum mean robustness required for the system to avoid cascades that will wipe out more the 90% of the banks. We then compute the average minimum mean,  defined as:
defined as:

where nΘ is the number of thresholds. The average transition curve is the set of  given a range of k and a set of thresholds Θ. The same process applies when the x-axis is the credit run cost b by replacing k with b in Eq. 3 and Eq. 4. For the synthetic results, we used Θ = {0.5, 0.6, 0.7, 0.8, 0.9}. For the empirical data, for few pairs (b, m) it can happen that there is no cascades size higher then 0.8 or 0.9, due to the fact the network gets disconnected for certain years (e.g., 2009, see SM). Therefore, in this case we used the set Θ = {0.5, 0.6, 0.7}.
given a range of k and a set of thresholds Θ. The same process applies when the x-axis is the credit run cost b by replacing k with b in Eq. 3 and Eq. 4. For the synthetic results, we used Θ = {0.5, 0.6, 0.7, 0.8, 0.9}. For the empirical data, for few pairs (b, m) it can happen that there is no cascades size higher then 0.8 or 0.9, due to the fact the network gets disconnected for certain years (e.g., 2009, see SM). Therefore, in this case we used the set Θ = {0.5, 0.6, 0.7}.
Technically it is questionable to call a network of 1000 nodes a scale-free graph. However, real world interbank networks in most countries consist of no more than a few hundred nodes. The theoretical question that we address in the paper is whether it would be a good idea to have an interbank market arranged like a scale-free graph in the sense of having a power-law or at least a fat-tailed degree distribution. In this perspective, we choose to generate networks with a mechanism that, while in the limit of large N would produce a true scale-free graph, for a size of 1000 or less is affected by size effects on the degree distribution. One should also bear in mind that for each choice of the parameter values we consider 1000 realizations of the network, thus accounting for variations across realizations that might result from the finite size. Finally, the size of 1000 nodes was the largest size for which it is feasible to conduct a systematic study of the phase diagram of the cascade size. We were using a computer cluster of 1084 CPU nodes running between 2.1 and 2.4 Ghz and arranged in 4 racks with memory ranging between 4 and 64 GB Ram. Each simulation (figure) would take between 20 and 30 minutes to run. Considering that we explore dozens of scenarios and that there is queuing system to use such a cluster, every experimental session requires several days.
Empirical dataset of the e-MID interbank market
For the simulations on empirical data, we use a collection of daily snapshots of the Italian interbank money market originally provided by the Italian electronic Market for Inter-bank Deposits from January 1999 to December 2011. The data is maintained by e-MID S.p.A, Società Interbancaria per l'Automazione, Milan, Italy and we refer to it as e-MID in the text. After aggregating the lending relations on a monthly basis, we extract the structures of interaction between banks. Hence, we use a collection of empirical networks describing the chronological evolution of the successive topologies that the Italian interbank money market went through from the beginning of 1999 up to the end of 2011.
References
Barrat, A., Barthlemy, M. & Vespignani, A. Dynamical processes on complex networks (Cambridge University Press, 2008).
Barabási, A. The network takeover. Nature Physics 8, 14 (2011).
Buldyrev, S., Parshani, R., Paul, G., Stanley, H. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028 (2010).
Battiston, S., Puliga, M., Kaushik, R., Tasca, P. & Caldarelli, G. Debtrank: Too central to fail? financial networks, the fed and systemic risk. Sci. Rep. 2 (2012).
Granovetter, M. Threshold models of collective behavior. Am. J. of Sociology 83, 1420–1443 (1978).
Watts, D. J. A simple model of global cascades on random networks. PNAS 99, 5766–5771 (2002).
Gleeson, J. P. & Cahalane, D. J. Seed size strongly affects cascades on random networks. Phys. Rev. E 75, 056103 (2007).
Lorenz, J., Battiston, S. & Schweitzer, F. Systemic risk in a unifying framework for cascading processes on networks. Eur. Phys. J. B 71, 441–460 (2009).
Payne, J. L., Dodds, P. S. & Eppstein, M. J. Information cascades on degree-correlated random networks. Phys. Rev. E 80, 026125 (2009).
Hackett, A., Melnik, S. & Gleeson, J. Cascades on a class of clustered random networks. Phys. Rev. E 83, 056107 (2011).
Brummitt, C. D., Lee, K.-M. & Goh, K.-I. Multiplexity-facilitated cascades in networks. Phys. Rev. E 85, 045102 (2012).
Kim, D., Kim, B. & Jeong, H. Universality class of the fiber bundle model on complex networks. Phys. Rev. Lett. 94, 25501 (2005).
Motter, A. & Lai, Y. Cascade-based attacks on complex networks. Phys. Rev. E 66, 065102 (2002).
Crucitti, P., Latora, V. & Marchiori, M. Model for cascading failures in complex networks. Phys. Rev. E 69, 045104 (2004).
Moreno, Y., Pastor-Satorras, R., Vázquez, A. & Vespignani, A. Critical load and congestion instabilities in scale-free networks. Europhys. Lett. 62, 292 (2007).
Bianconi, G. & Marsili, M. Clogging and self-organized criticality in complex networks. Phys. Rev. E 70, 035105 (2004).
Goh, K., Lee, D., Kahng, B. & Kim, D. Sandpile on scale-free networks. Phys. Rev. Lett. 91, 148701 (2003).
Brummitt, C., DSouza, R. & Leicht, E. Suppressing cascades of load in interdependent networks. PNAS 109, E680–E689 (2012).
Pastor-Satorras, R. & Vespignani, A. Epidemic dynamics in finite size scale-free networks. Phys. Rev. E 65, 035108 (2002).
Stiglitz, J. E. Risk and global economic architecture: Why full financial integration may be undesirable. Am. Econ. Rev. 100, 388–92 (2008).
Battiston, S., Delli Gatti, D., Gallegati, M., Greenwald, B. & Stiglitz, J. E. Liaisons dangereuses: Increasing connectivity, risk sharing and systemic risk. J. of Econ. Dyn. and Control 36, 1121–1141 (2012).
Boss, M., Elsinger, H., Summer, M. & Thurner, S. An empirical analysis of the network structure of the austrian interbank market. Oesterreichesche Nationalbanks Financial Stability Report 7, 77–87 (2004).
Soramäki, K., Bech, M., Arnold, J., Glass, R. & Beyeler, W. The topology of interbank payment flows. Physica A 379, 317–333 (2007).
Iori, G., De Masi, G., Precup, O. V., Gabbi, G. & Caldarelli, G. A network analysis of the italian overnight money market. J. of Econ. Dyn. and Control 32, 259–278 (2008).
Battiston, S., Delli Gatti, D., Gallegati, M., Greenwald, B. & Stiglitz, J. E. Default cascades: When does risk diversification increase stability? J. of Fin. Stability 8, 138–149 (2012).
Mistrulli, P. Assessing financial contagion in the interbank market: Maximum entropy versus observed interbank lending patterns. J. of Banking & Fin. 35, 1114–1127 (2011).
Elsinger, H., Lehar, A. & Summer, M. Risk Assessment for Banking Systems. Manag. Science 52, 1301–1314 (2006).
Gai, P. & Kapadia, S. Contagion in financial networks. Proc. Royal Soc. A 466, 2120, 2401–2423 (2010).
Cont, R., Moussa, A. & Santos, E. B. Network Structure and Systemic Risk in Banking Systems. Social Science Research Network Working Paper Series (2011). URL http://dx.doi.org/10.2139/ssrn.1733528.
Eisenberg, L. & Noe, T. Systemic Risk in Financial Systems. Manag. Science 47, 236–249 (2001).
Fricke, D. & Lux, T. Core-periphery structure in the overnight money market: Evidence from the e-mid trading platform. Tech. Rep., Kiel Working Papers (2012).
Jonung, L. The swedish model for resolving the banking crisis of 1991–93. seven reasons why it was successful. Tech. Rep., Directorate General Economic and Monetary Affairs, European Commission (2009).
Newman, M., Strogatz, S. & Watts, D. Random graphs with arbitrary degree distributions and their applications. Phys. Rev. E 64, 026118 (2001).
Acknowledgements
The authors acknowledge the financial support he Swiss National Science Foundation (Grant CR12I1-127000) and the European Commission FET Open Project “FOC” 255987. Tarik Roukny acknowledges the financial support from the F.R.S.-FNRS of Belgium's French Community and the National Bank of Belgium.
Author information
Authors and Affiliations
Contributions
Computer simulations were carried out by T.R. Numerical experiments were supervised by S.B. All authors, T.R., H.B., H.P., G.C. and S.B. have contributed to the determination of the research questions, to the discussion of the results and to the editing of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Roukny, T., Bersini, H., Pirotte, H. et al. Default Cascades in Complex Networks: Topology and Systemic Risk. Sci Rep 3, 2759 (2013). https://doi.org/10.1038/srep02759
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep02759
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.