Abstract
We demonstrate that in mesoscopic type II superconductors with the lateral size commensurate with London penetration depth, the ground state of vortices pinned by homogeneously distributed columnar defects can form a hierarchical nested domain structure. Each domain is characterized by an average number of vortices trapped at a single pinning site within a given domain. Our study marks a radical departure from the current understanding of the ground state in disordered macroscopic systems and provides an insight into the interplay between disorder, vortex-vortex interaction and confinement within finite system size. The observed vortex phase segregation implies the existence of the soliton solution for the vortex density in the finite superconductors and establishes a new class of nonlinear systems that exhibit the soliton phenomenon.
Similar content being viewed by others
Introduction
Vortex matter in the presence of structural defects forms a wide variety of phases with specific properties depending on the relation between the vortex-vortex and vortex-defect interactions1,2. The findings of Refs. 3,4, which revealed significant enhancement of vortex pinning in high-temperature superconductors by ion irradiation, broke ground for a new direction in vortex physics. Heavy ions leave the tracks of the damaged amorphous material where superconductivity is suppressed. Thus the vortices penetrating the sample occupy columnar defects where the vortex energy is appreciably less than in the undamaged material. A theory of the resulting vortex Bose glass phase was developed in Refs. 5,6, where the physics of flux lines in superconductors pinned by columnar defects was mapped onto boson localization in two dimensions. The distribution of vortices in the Bose glass state that forms in the infinite (i.e. thermodynamically large) samples, containing columnar defects, is a uniform one. A question about what happens to the Bose glass in the finite samples is most natural in view of explosively developing studies of small superconductors, i.e. superconductors with the lateral sizes Rs comparable to the London screening length λ or even with the coherence length ξ. Indeed even the samples without columnar defects reveal that the properties of the homogeneous vortex state change dramatically as  . The boundaries start to affect the distribution of vortices and makes it nonuniform. Experimental study of mesoscopic superconducting discs with the total vorticity L < 40 revealed formation of the concentric shells of vortices7 in accord with the results of numerical simulations8. The analysis of shell filling with increasing L allowed the authors of Ref. 7 to identify magic numbers corresponding to the appearance of consecutive new shells. At the same time, vortex distribution over the sample remains “quasi-homogeneous” with the vortex density gradually changing with the distance from the sample center. For example, the experimental and numerical studies of the samples containing a macroscopic number of vortices showed that, almost everywhere, vortices arrange themselves into a nearly perfect Abrikosov lattice, containing the few disclinations necessary to match the cylindrical symmetry of the sample. Only within a few, 2–3, shells adjacent to the surface, vortex distribution differs noticeably from that in the bulk.
. The boundaries start to affect the distribution of vortices and makes it nonuniform. Experimental study of mesoscopic superconducting discs with the total vorticity L < 40 revealed formation of the concentric shells of vortices7 in accord with the results of numerical simulations8. The analysis of shell filling with increasing L allowed the authors of Ref. 7 to identify magic numbers corresponding to the appearance of consecutive new shells. At the same time, vortex distribution over the sample remains “quasi-homogeneous” with the vortex density gradually changing with the distance from the sample center. For example, the experimental and numerical studies of the samples containing a macroscopic number of vortices showed that, almost everywhere, vortices arrange themselves into a nearly perfect Abrikosov lattice, containing the few disclinations necessary to match the cylindrical symmetry of the sample. Only within a few, 2–3, shells adjacent to the surface, vortex distribution differs noticeably from that in the bulk.
At the same time, theoretical consideration of the critical state in a superconducting slab containing a lattice of strong pins9 predicted that instead of the expected in the critical state constant gradient in the vortex density a terraced piecewise vortex structure structure can form. This terraced vortex distribution, unexpected from the viewpoint of an orthodox concept of the critical state, is, formally, nothing but a standard soliton solution for the one-dimensional commensurate structures, which appeared first as a 1D model for dislocations10,11. The physical reason for emerging such a structure is the competition between the effect of the critical current flowing uniformly through the slab and thus implying the constant gradient of the vortex density across the sample and the action of the lattice of strong pinning sites that tend to trap vortices enforcing them into a regular array with the commensurate period. As a result, a metastable structure forms, comprising vortex domains of a piecewise constant vortex density. The originally uniform current is compressed into the current filaments concentrated along the boundaries between the domains i.e. in the narrow regions of the maximal gradient of the vortex density. The terraced metastable critical state, which was indeed found experimentally12, establishes a fruitful connection between the breaking down of a vortex configuration into the domains, characterized by the different vortex density and a general concept of formation of the regular patterns in non-linear media, which often allows for a description in a general framework of the soliton physics.
Here we consider an equilibrium vortex system and report that the ground state of vortices pinned by homogeneously distributed large columnar defects can form a hierarchical nested domain structure, where each domain is characterized by its own filling factor, the average number of vortices trapped at a single pinning site. In view of the above connection between vortex phase segregation and soliton description of the commensurate structures, our finding also breaks ground to novel approach to soliton physics. Contrasting past models where soliton structures were established by the explicit writing-down of an analytical solution to a particular nonlinear 1D equation, our work rigorously proves the principal and fundamental existence of a soliton terraced solution for equilibrium vortex density. Significantly, by considering a cylindrical sample with an arbitrary base, our approach goes beyond the 1D physics. We develop our approach in the context of vortex pinning by large columnar defects in a small superconductor with  in the low field range H < Hc1, where Hc1 is the lower critical field. Since the energy of trapped vortices is less than those in the bulk, vortices penetrate the superconductor even in this field range. The thermodynamics of the Bose glass at H < Hc1 was investigated in Ref. 13, where the equation of states and the Bose-glass transition line were found, but the effects of the finite size were not addressed. Here we show that the interplay of vortex interaction and pinning in a mesoscopic superconductor can result in a hierarchical domain structure of the ground vortex state. Importantly, after the coarse graining procedure described below, our model becomes quasicontinuous and the discreteness (or periodicity) of pinning arrays does not come explicitly into play.
in the low field range H < Hc1, where Hc1 is the lower critical field. Since the energy of trapped vortices is less than those in the bulk, vortices penetrate the superconductor even in this field range. The thermodynamics of the Bose glass at H < Hc1 was investigated in Ref. 13, where the equation of states and the Bose-glass transition line were found, but the effects of the finite size were not addressed. Here we show that the interplay of vortex interaction and pinning in a mesoscopic superconductor can result in a hierarchical domain structure of the ground vortex state. Importantly, after the coarse graining procedure described below, our model becomes quasicontinuous and the discreteness (or periodicity) of pinning arrays does not come explicitly into play.
Results
We consider a large but finite superconducting sample in the form of a generalized cylinder, with a base of arbitrary shape, see Fig. 1, with the characteristic linear size of the base  , where
, where  is the London penetration length, containing a square array (with spacing a such that
is the London penetration length, containing a square array (with spacing a such that  ) of cylindrical (columnar) vortex traps with radii R much exceeding the vortex core size ξ. This is an exemplary model system for superconductors that contain arrays of either columnar defects or artificially engineered arrays of holes. Such systems are extensively used in studies of the so-called vortex matching effect, one of the central avenues of contemporary vortex physics (see, for example Ref. 14 and references therein). Since the energy of a vortex trapped by a cylindrical defect is less then its energy in the bulk of an undamaged material, vortices start to occupy the sample containing CDs at fields H below than the thermodynamic lower critical field Hc1, at which the thermodynamically stable vortices start to exist in a superconductor without CDs13. It is this range of fields H < Hc1 we investigate in our work.
) of cylindrical (columnar) vortex traps with radii R much exceeding the vortex core size ξ. This is an exemplary model system for superconductors that contain arrays of either columnar defects or artificially engineered arrays of holes. Such systems are extensively used in studies of the so-called vortex matching effect, one of the central avenues of contemporary vortex physics (see, for example Ref. 14 and references therein). Since the energy of a vortex trapped by a cylindrical defect is less then its energy in the bulk of an undamaged material, vortices start to occupy the sample containing CDs at fields H below than the thermodynamic lower critical field Hc1, at which the thermodynamically stable vortices start to exist in a superconductor without CDs13. It is this range of fields H < Hc1 we investigate in our work.
To quantify the spatial distribution of trapped vortices we introduce the coarse-grained filling factor density D(r) = Nva2/Ar, where r is the coordinate perpendicular to the cylinder axis z, Ar is some area surrounding the point r and containing many CDs and Nv is the number of vortex quanta trapped by CDs within this area. So if, for example, each CD in this domain contains exactly one single-quantum vortex, D(r) = 1; if CDs outnumber the trapped vortex quanta, then D(r) < 1. We show that the vortex system confined within such a sample can break up into a sequence of the distinct nested domains (listing from the sample border inward):  , with the filling factors
, with the filling factors  , see Fig. 2, respectively. Our analysis shows that D can be any positive integer or a fraction, depending on the relation between the radius of CDs, the superconducting coherence length ξ and the strength of the magnetic field. Accordingly, there exists a sequence of characteristic fields H1 < H2… < Hn < Hc1 such that at Ha < H1 < Hc1 the superconductor retains its vortex-free Meissner state, at H1 < Ha < H2 < Hc1, appears the finite compact domain Ω1 with the filling factor D1 ≤ 1 and so on. The possible maximal number of the distinctly filled domains, nmax and the corresponding maximal filling factor,
, see Fig. 2, respectively. Our analysis shows that D can be any positive integer or a fraction, depending on the relation between the radius of CDs, the superconducting coherence length ξ and the strength of the magnetic field. Accordingly, there exists a sequence of characteristic fields H1 < H2… < Hn < Hc1 such that at Ha < H1 < Hc1 the superconductor retains its vortex-free Meissner state, at H1 < Ha < H2 < Hc1, appears the finite compact domain Ω1 with the filling factor D1 ≤ 1 and so on. The possible maximal number of the distinctly filled domains, nmax and the corresponding maximal filling factor,  , are determined by the maximal number of vortices which CD can trap as given by the expression15 nmax = [R/2ξ] (nmax is derived from the condition that the circular current around the CD due to trapped flux cannot exceed the superconducting pair-breaking current). Using a square array of CDs does not result in a loss of generality and ensures that the observed vortex phase separation is an inherent property of vortex systems that stems from the subtle balance between the confinement and vortex-vortex and vortex-defect interactions rather then a trivial consequence of fluctuations in the defect density.
, are determined by the maximal number of vortices which CD can trap as given by the expression15 nmax = [R/2ξ] (nmax is derived from the condition that the circular current around the CD due to trapped flux cannot exceed the superconducting pair-breaking current). Using a square array of CDs does not result in a loss of generality and ensures that the observed vortex phase separation is an inherent property of vortex systems that stems from the subtle balance between the confinement and vortex-vortex and vortex-defect interactions rather then a trivial consequence of fluctuations in the defect density.
Phase separation in distribution of vortices captured by the columnar defects.
Instead of homogeneous distribution all over the sample the vortices form a nested sequence of the domains characterized by the filling factor of the defects which grows from the borders towards the center of the sample. Namely, the vortex system breaks up into a sequence  , with the filling factors
, with the filling factors  , correspondingly, where D is the average number of vortices per columnar defect in the respective domain.
, correspondingly, where D is the average number of vortices per columnar defect in the respective domain.
We will be describing superconductivity of our system and the resulting vortex state within the Ginzburg-Landau (GL) formalism. The ground state is determined by the standard GL functional:

where the cylindrical sample and the applied magnetic field Ha are aligned with the z-axis, Ψ(r) is the superconducting order parameter, r is the coordinate vector in the plain perpendicular to the z-axis, m and –e are electron mass and charge, respectively, A(r) is the vector potential related to the magnetic induction by B = curl A and the integration is taken over the sample volume Ω. The coherence length and London penetration length are expressed through the coefficients of the GL functional as ξ2 = ℏ2/(4m|α|) and λ2 = (mc2β)/(8πe2|α|), respectively. The properties of a superconducting material are characterized by the Ginzburg-Landau parameter κ = λ/ξ. We consider an extreme type II superconductor such that  . As usual in the GL analysis, it is convenient to introduce the dimensionless order parameter u = Ψ/Ψ0, where
. As usual in the GL analysis, it is convenient to introduce the dimensionless order parameter u = Ψ/Ψ0, where  and measure lengths in the units of λ and the magnetic fields in the units of 2Hc1/ln κ = Φ0/(2πλξ). The dimensionless columnar defect radius is
and measure lengths in the units of λ and the magnetic fields in the units of 2Hc1/ln κ = Φ0/(2πλξ). The dimensionless columnar defect radius is  .
.
To determine the conditions for the emergence of the vortex domain structure, we require that the CD spacing is not extremely small such that  . Further we let the CD radius be very small and parametrize it as ρ = exp(−γ/ε 2), where γ is a constant of the order of unity. This means that the characteristic lengths separation is exponentially stronger as compared to the condition
. Further we let the CD radius be very small and parametrize it as ρ = exp(−γ/ε 2), where γ is a constant of the order of unity. This means that the characteristic lengths separation is exponentially stronger as compared to the condition  . And, finally, we parametrize the dimensionless magnetic field as h = σ/ε2, where
. And, finally, we parametrize the dimensionless magnetic field as h = σ/ε2, where  . The key point of our approach is the observation that under the chosen relations between the characteristic parameters of our system, for the purpose of the determination of the vorticity the amplitude of the order parameter can be taken |u| = 1 everywhere in the bulk of the sample except in CDs. This implies that the (dimensionless) GL free energy (depending solely on the distribution of the magnetic field h = curl A) can be reduced to the following form [see Supplementary Information (SI) section]:
. The key point of our approach is the observation that under the chosen relations between the characteristic parameters of our system, for the purpose of the determination of the vorticity the amplitude of the order parameter can be taken |u| = 1 everywhere in the bulk of the sample except in CDs. This implies that the (dimensionless) GL free energy (depending solely on the distribution of the magnetic field h = curl A) can be reduced to the following form [see Supplementary Information (SI) section]:

which we call the harmonic map functional. In other words, the distribution of vortices, derived by the minimization of  coincides with that obtained by the minimization of
coincides with that obtained by the minimization of  . Varying Eq. (2) with respect to h and taking into account the boundary conditions at the boundaries of CDs, one finds the equation for the magnetic field:
. Varying Eq. (2) with respect to h and taking into account the boundary conditions at the boundaries of CDs, one finds the equation for the magnetic field:

where  , rj is the coordinate of the j-th CD and dj is its corresponding vorticity which can also be zero if there are no flux trapped at the particular CD. The remaining task is finding the configuration of the field, i.e. the unknown numbers dj which minimize the free energy
, rj is the coordinate of the j-th CD and dj is its corresponding vorticity which can also be zero if there are no flux trapped at the particular CD. The remaining task is finding the configuration of the field, i.e. the unknown numbers dj which minimize the free energy  . To implement this we coarse grain Eq. (3) over the distances exceeding the CD spacing. As a results the r.h.s. of the equation for the coarse grained field
. To implement this we coarse grain Eq. (3) over the distances exceeding the CD spacing. As a results the r.h.s. of the equation for the coarse grained field  will assume the form 2πD(r), where the average vorticity introduced above can now be rigorously defined as D(r) = limε→0μ(r). The boundary conditions for the field now become simply
will assume the form 2πD(r), where the average vorticity introduced above can now be rigorously defined as D(r) = limε→0μ(r). The boundary conditions for the field now become simply  at the sample's boundary. The phase separation picture emerges from exploring the dependence of D(r) on the parameter σ, characterizing the magnitude of the magnetic field. Our main finding can be formulated as follows (see Methods for more detail). Let the radii of the holes (in dimensionless units) be ρ = exp(−γ/ε2) and the applied magnetic field be ha = σ/ε2. There exists a strictly increasing sequence of the critical values σcrj, j = 1, 2… such that if σcrj < σ < σcr(j+1), then the average vorticity assumes the constant values in domains Ωk, where Ωk ≡ Ωk(σ), k = 0, 1, 2, …, j are strictly nested sets characterized by distinct vorticities. Namely, the vorticity D(r) = 0 in Ω0 and D(r) = k in Ωk, k ≤ j − 1. We further show that when
at the sample's boundary. The phase separation picture emerges from exploring the dependence of D(r) on the parameter σ, characterizing the magnitude of the magnetic field. Our main finding can be formulated as follows (see Methods for more detail). Let the radii of the holes (in dimensionless units) be ρ = exp(−γ/ε2) and the applied magnetic field be ha = σ/ε2. There exists a strictly increasing sequence of the critical values σcrj, j = 1, 2… such that if σcrj < σ < σcr(j+1), then the average vorticity assumes the constant values in domains Ωk, where Ωk ≡ Ωk(σ), k = 0, 1, 2, …, j are strictly nested sets characterized by distinct vorticities. Namely, the vorticity D(r) = 0 in Ω0 and D(r) = k in Ωk, k ≤ j − 1. We further show that when  one of the two possibilities can realize: (i) if σ < 2πj + (j − 1/2)γ, then j − 1 < D(r) < j, otherwise (ii) D(r) = j.
one of the two possibilities can realize: (i) if σ < 2πj + (j − 1/2)γ, then j − 1 < D(r) < j, otherwise (ii) D(r) = j.
To illustrate this we consider the evolution of the distribution of the trapped vortices upon increasing magnetic field. Let σk = 2πk + γ/2, k = 0, 1, 2…. One can show now, that if 0 < σ < σcr1 ≡ γ/(2 max |f1|), where f1 is the solution to the equation Δf1 − f1 = 1,  and f1 = 0 if
and f1 = 0 if  , where ∂Ω means the boundary of the sample, D(r) = 0 and there are no trapped vortices at all (see, Fig. 3a). If γ is such that σcr1 < σ1, then for σcr1 < σ < σ1 the superconductor breaks up into two phases, see Fig. 3b: the vortex-free phase in Ω0 and the phase of trapped vortices with 0 < D(r) < 1 in the domain Ω1. If now γ is such that max{σcr1, σ1} < σ < σcr2 (the procedure for deriving σcrk is described in the Methods section), then in the filled phase D(r) = 1 (i.e. each columnar defect traps exactly one vortex), see Fig. 3c. Continuing this process we find that if γ is such that σcr2 < σ2 then for σcr2 < σ < σ2 the superconductor comprises three nesting hierarchical phases: Ω0, with no vortices in it, D(r) = 0, Ω1, where D(r) = 1 and Ω2, where 1 < D(r) < 2. The latter means that some of the CDs in the “interior” trapped double-quanta vortices, but some CDs have only a single vortex captured, so the average filling factor in Ω2 is less then 2, see Fig. 3d. And if γ is such that max{σcr2, σ2} < σ < σcr3, then the three nesting phases have the vorticity D(r) = 0, 1 and 2 respectively. That is all the CDs of the internal phase are filled with double-quanta vortices. This process can be continued till the maximal possible multi-quanta vortices appear. The maximal multiplicity is determined by the condition nmax = [R/2ξ].
, where ∂Ω means the boundary of the sample, D(r) = 0 and there are no trapped vortices at all (see, Fig. 3a). If γ is such that σcr1 < σ1, then for σcr1 < σ < σ1 the superconductor breaks up into two phases, see Fig. 3b: the vortex-free phase in Ω0 and the phase of trapped vortices with 0 < D(r) < 1 in the domain Ω1. If now γ is such that max{σcr1, σ1} < σ < σcr2 (the procedure for deriving σcrk is described in the Methods section), then in the filled phase D(r) = 1 (i.e. each columnar defect traps exactly one vortex), see Fig. 3c. Continuing this process we find that if γ is such that σcr2 < σ2 then for σcr2 < σ < σ2 the superconductor comprises three nesting hierarchical phases: Ω0, with no vortices in it, D(r) = 0, Ω1, where D(r) = 1 and Ω2, where 1 < D(r) < 2. The latter means that some of the CDs in the “interior” trapped double-quanta vortices, but some CDs have only a single vortex captured, so the average filling factor in Ω2 is less then 2, see Fig. 3d. And if γ is such that max{σcr2, σ2} < σ < σcr3, then the three nesting phases have the vorticity D(r) = 0, 1 and 2 respectively. That is all the CDs of the internal phase are filled with double-quanta vortices. This process can be continued till the maximal possible multi-quanta vortices appear. The maximal multiplicity is determined by the condition nmax = [R/2ξ].
Sequential vortex domain formation upon increasing magnetic field.
At smallest fields vortices are not trapped at all, upon increasing field the central domain where D < 1, i.e. where part of the defects captured one vortex forms. With further increasing field, all the traps in the central domain get filled by one vortex each; then, finally, the sequence of domains with D = 0, D = 1 and 1 < D < 2, forms.
Finally, to complete our consideration we have to check the stability of the established domain structure. To this end we first estimate the typical sizes RD of our domains. Considering for brevity the circular domain Ω = B(0, 1) and determining the dimensionless radius  of a subdomain Ω1 in the case when there are just two phases D(r) = 0 and 0 < D(r) ≤ 1 (in the radially symmetrical case Ω1 is also a ball), one finds, coming back to dimensional units (see SI)
of a subdomain Ω1 in the case when there are just two phases D(r) = 0 and 0 < D(r) ≤ 1 (in the radially symmetrical case Ω1 is also a ball), one finds, coming back to dimensional units (see SI)

Now we have to check that density of the current Js, circulating within the interface between the domains does not exceed the pairbreaking current density  . Evaluating the current, we take into account that the width of the interface between the adjacent domains is of the order of the defect spacing a. Now, let us take a single central domain of the linear size L, containing the traps that capture exactly one vortex and make use the expression vs = nℏ/2mr for the Cooper pair velocity around the vortex at distances
. Evaluating the current, we take into account that the width of the interface between the adjacent domains is of the order of the defect spacing a. Now, let us take a single central domain of the linear size L, containing the traps that capture exactly one vortex and make use the expression vs = nℏ/2mr for the Cooper pair velocity around the vortex at distances  . Then employing the definition of the supercurrent Js = nsevs, one easily arrives at the estimate Js ~ J0RDξ/a2. This implies that for the domain to be stable the inequality
. Then employing the definition of the supercurrent Js = nsevs, one easily arrives at the estimate Js ~ J0RDξ/a2. This implies that for the domain to be stable the inequality

must hold. Now let us write down the chain of inequalities which constitute the base of our consideration:

i.e.  . Therefore
. Therefore

so the condition (5) of the stability of the domains automatically follows from the assumed hierarchy of the lengths involved. Therefore, the domains are stable. This analysis can be straightforwardly generalized to an arbitrary number of domains.
Discussion
We have demonstrated that the equilibrium ground state of a cylindrical superconductor with a base of arbitrary shape, containing uniformly distributed columnar pins, can develop an hierarchical structure of nesting domains, where each distinct vortex domain is characterized by a sequence of different filling factors. This result takes us beyond the frontiers of conventional soliton physics, where soliton structures resulted from explicit solutions of a particular 1D nonlinear equation. For example, the terraced vortex distribution found in a nonequilibrium (metastable) distribution of vortices in a critical state carries a direct analogy with the soliton structure derived for a 1D system of atoms adsorbed on a periodic substrate16. Also, the obtained domain structure differs fundamentally from the nonuniform vortex distribution found in17, which is generated by the nonuniform arrangement of pinning sites.
The essential feature of our model that ensures a sequence of nested domains is the large radii,  , of columnar defects which enable them to capture a large number of flux quanta. The formation of the multiply quantized vortices in the forest of large CDs was already discussed in18, although the possibility of the formation of distinct domains with different multi-vorticity was not explored. The phase separation discussed above arises as a result of the subtle balance between the different logarithmic contributions to energy of the vortex system: repulsive interaction between the vortices favouring homogenization of their spatial distribution, Meissner currents pushing vortices towards the center of the sample and interactions of vortices with their images that appear both outside the sample and within the columnar cavities. This suggests that although our results were proved in a mathematically rigorous way, only for specific parameters, one should expect that the main conclusion about vortex phase separation retamains valid well beyond the restrictions of the particular model. Note, in this connection, an interesting experimental work19 where the formation of the vortex clusters and multiquanta vortices was observed. Note that as we have already mentioned, the effect of vortex phase separation can realize in the vortex matching systems with regular arrays of large,
, of columnar defects which enable them to capture a large number of flux quanta. The formation of the multiply quantized vortices in the forest of large CDs was already discussed in18, although the possibility of the formation of distinct domains with different multi-vorticity was not explored. The phase separation discussed above arises as a result of the subtle balance between the different logarithmic contributions to energy of the vortex system: repulsive interaction between the vortices favouring homogenization of their spatial distribution, Meissner currents pushing vortices towards the center of the sample and interactions of vortices with their images that appear both outside the sample and within the columnar cavities. This suggests that although our results were proved in a mathematically rigorous way, only for specific parameters, one should expect that the main conclusion about vortex phase separation retamains valid well beyond the restrictions of the particular model. Note, in this connection, an interesting experimental work19 where the formation of the vortex clusters and multiquanta vortices was observed. Note that as we have already mentioned, the effect of vortex phase separation can realize in the vortex matching systems with regular arrays of large,  , holes and with CD spacing still much exceeding R. In this respect, direct scanning tunneling microscopy and spectroscopy (STM/STS) experiments, that have revealed strong confinement effects on the vortex arrangements in extreme type II superconductors and enabled to discriminate between the multi-vortex and multi-quanta vortex formations20, seem to be a very adequate approach for the search of the vortex phase separation. Furthermore, in the case where vortices are pinned by weak point defects in the collective pinning regime, one can view a pinned vortex line as confined within the slightly curved tube-like potential well of radius ξ, which arises self-consistently from the interplay between the pinning and elastic energies1. One thus can anticipate that pinned vortices may cluster together to form an array of compact domains of pinned vortices separated by distances well exceeding the size of a domain. The remarkable possibility of searching for segregation of localized phases can be realized in the7Li atomic gas21,22 where the interaction strength can be tuned by a Feshbach resonance, thus achieving the required balance between the competing repulsive, pinning and confining forces.
, holes and with CD spacing still much exceeding R. In this respect, direct scanning tunneling microscopy and spectroscopy (STM/STS) experiments, that have revealed strong confinement effects on the vortex arrangements in extreme type II superconductors and enabled to discriminate between the multi-vortex and multi-quanta vortex formations20, seem to be a very adequate approach for the search of the vortex phase separation. Furthermore, in the case where vortices are pinned by weak point defects in the collective pinning regime, one can view a pinned vortex line as confined within the slightly curved tube-like potential well of radius ξ, which arises self-consistently from the interplay between the pinning and elastic energies1. One thus can anticipate that pinned vortices may cluster together to form an array of compact domains of pinned vortices separated by distances well exceeding the size of a domain. The remarkable possibility of searching for segregation of localized phases can be realized in the7Li atomic gas21,22 where the interaction strength can be tuned by a Feshbach resonance, thus achieving the required balance between the competing repulsive, pinning and confining forces.
Methods
The central point of our consideration is minimizing the free energy functional (2) with respect to vorticity numbers dj, given the constraint (3). The first step in this process is the coarse graining procedure introducing the coarse-grained vorticity D(r) and magnetic field  . Then the problem reduces to minimization of the coarse-grained energy functional
. Then the problem reduces to minimization of the coarse-grained energy functional

where

is a piecewise parabolic function, see Fig. 3, under the constraint  ,
,  and
and  on ∂Ω. Making use of the Legendre transform of the function πγΦ(D/2π) such that Φ*(f) = 2π supD[Df − (γ/2)Φ(D)], one arrives at the effective energy functional
on ∂Ω. Making use of the Legendre transform of the function πγΦ(D/2π) such that Φ*(f) = 2π supD[Df − (γ/2)Φ(D)], one arrives at the effective energy functional

which is to be minimized with respect to the auxiliary field f dual to  so that for minimizing the configuration
so that for minimizing the configuration  . Function Φ* is a piecewise linear function of f enveloped by a parabola, see Fig. 4.
. Function Φ* is a piecewise linear function of f enveloped by a parabola, see Fig. 4.
Sequential phase segregation as a function of the auxiliary field f.
The stages of the domain formations are the same as in the Fig. 3.
Now one can follow the evolution of the solution upon increasing σ. It follows from (10) that f = 0 for σ = 0 and therefore  where Φ* = 0 for sufficiently small σ. The variation with respect to f in (6) leads to Δf − f = σ with f = 0 for
where Φ* = 0 for sufficiently small σ. The variation with respect to f in (6) leads to Δf − f = σ with f = 0 for  . Since 2πD(r) = −Δf + f + σ, we have D(r) = 0. Function Φ* remains zero until min f reaches value −γ/2, which defines σcr1 = γ/(2 max |f1|). Upon further increase in σ beyond σcr1, Φ* acquires the first oblique linear piece and (10) leads to the energy
. Since 2πD(r) = −Δf + f + σ, we have D(r) = 0. Function Φ* remains zero until min f reaches value −γ/2, which defines σcr1 = γ/(2 max |f1|). Upon further increase in σ beyond σcr1, Φ* acquires the first oblique linear piece and (10) leads to the energy

Disregarding for the moment the gradient term in (11) (which only penalizes variations of f) we see a competition of the positive term f2 + 4π(|f| − γ/2)+ and the negative one 2σf (note that always f ≤ 0). Now if σcr1 < 2π + γ/2, then the competition eliminates f < −γ/2 for σcr1 < σ < 2π + γ/2. Then we get f = −γ/2 for  , where we obtain 0 < D(r) < 1. If σcr1 ≥ 2π + γ/2, then the negative term wins for f < −γ/2 that corresponds
, where we obtain 0 < D(r) < 1. If σcr1 ≥ 2π + γ/2, then the negative term wins for f < −γ/2 that corresponds  , where we have Δf − f = σ − 2π and we get D(r) ≡ 1. The continuation of this procedure further generates a sequence of critical values of σ and defines the corresponding sequence of nested domains with the increasing (towards to the inner part of the sample) vorticity as described in the main text. The evolution of the CD filling and formation of the spatially inhomogeneous vortex state with the increase of the reduced field σ is illustrated in Fig. 4.
, where we have Δf − f = σ − 2π and we get D(r) ≡ 1. The continuation of this procedure further generates a sequence of critical values of σ and defines the corresponding sequence of nested domains with the increasing (towards to the inner part of the sample) vorticity as described in the main text. The evolution of the CD filling and formation of the spatially inhomogeneous vortex state with the increase of the reduced field σ is illustrated in Fig. 4.
References
Blatter, J., Feigelman, M. V., Geshkenbein, V. B., Larkin, A. I. & Vinokur, V. M. Vortices in high temperature superconductors. Rev. Mod. Phys. 66, 1125 (1994).
Nattermann, T. & Scheidl, S. Vortex-glass phases in type-II superconductors. Advances in Physics 49, 607–704 (2000).
Konczykowski, M. et al. Effect of 5.3-GeV Pb-ion irradiation on irreversible magnetization in Y-Ba-Cu-O crystals. Phys. Rev. B 44, 7167–7170 (1991).
Civale, L. et al. Vortex confinement by columnar defects in YBa2Cu3O7 crystals: Enhanced pinning at high fields and temperatures. Phys. Rev. Lett. 67, 648–651 (1991).
Nelson, D. R. & Vinokur, V. M. Boson localization and pinning by correlated disorder in high-temperature superconductors. Phys. Rev. Lett. 68, 2398–2401 (1992).
Nelson, D. R. & Vinokur, V. M. Boson localization and correlated pinning of superconducting vortex arrays. Phys. Rev. B 48, 13060–13097 (1993).
Grigorieva, I. V. et al. Direct observation of vortex shells and magic numbers in mesoscopic superconducting disks. Phys. Rev. Lett. 96, 077–005 (2006).
Bedanov, V. M. & Peeters, F. M. Ordering and phase transitions of charged particles in a classical finite two-dimensional system. Phys. Rev. B 49, 2667 (1994).
Cooley, L. D. & Grishin, A. M. Pinch Effect in Commensurate Vortex-Pin Lattices. Phys. Rev. Lett. 74, 2788–2791 (1995).
Frenkel, Y. I. & Kontorova, T. On the theory of plastic deformation and twinning. Zh. Eksp. Teor. Fiz. 8, 1340–1348 (1938).
Frank, F. C. & Van der Merwe, J. H. One–Dimensional Dislocations. I. Static Theory. Proc. R. Soc. Lond. A. Mathematical and physical scoences 198, 205–216 (1949).
Silhanek, A. V., Gutierrez, J., Kramer, R. B. G., Ataklti, G. W., Van de Vondel, J. & Moshchalkov, V. V. Microscopic picture of the critical state in a superconductor with a periodic array of antidots. Phys. Rev. B 83, 024509 (2011)
Larkin, A. I. & Vinokur, V. M. Bose and Vortex Glasses in High Temperature Superconductors. Phys. Rev. Lett. 75, 4666 (1995).
Thakur, A. D. et al. Vortex matching effect in engineered thin films of NbN. Appl. Phys. Lett. 94, 262501 (2009).
Mkrtchyan, G. S. & Shmidt, V. V. Interaction Between a Cavity and a Vortex in a Superconductor of the Second Kind. Sov. Phys. JETP 34, 195–196 (1972).
Burkov, S. E. & Talapov, A. L. One-dimensional incommensurate structures at finite temperatures. J. Physique - LETT. 41, L-387–L-390 (1980).
Mis'ko, V. R. & Nori, F. Magnetic flux pinning in superconductors with hyperbolic-tessellation arrays of pinning sites. Phys. Rev. B 85, 184506 (2012)
Buzdin, A. I. Multiple-quanta vortices at columnar defects. Phys. Rev. B 47, 11416 (1993).
Grigor'eva, I. V. et al. Pinning-Induced Formation of Vortex Clusters and Giant Vortices in Mesoscopic Superconducting Disks. Phys. Rev. Lett. 99, 147003 (2007).
Cren, T., Serrier-Garcia, L., Debontridder, F. & Roditchev, D. Vortex Fusion and Giant Vortex States in Confined Superconducting Condensates. Phys. Rev. Lett. 107, 097202 (2011).
Pollack, S. E. et al. Extreme tunability of interactions in a 7Li Bose-Einstein condensate. Phys. Rev. Lett. 102, 090402 (2009).
Haler, E. et al. Realization of an excited strongly correlated quantum gas phase. Science 325, 1224–1227 (2009).
Acknowledgements
The work of V.V. was supported by the U.S. Department of Energy Office of Science under the Contract No. DEAC02- 06CH11357. The work of LB, VR and OI was supported by NSF grant DMS-1106666.
Author information
Authors and Affiliations
Contributions
V.V. and L.B. conceived and defined the problem, O.I., L.B. and V.R. carried out the calculations, V.V. prepared the manuscript and all the authors commented on the manuscript, L.B. supervised the project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Vortex phase separation in mesoscopic superconductors: Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Iaroshenko, O., Rybalko, V., Vinokur, V. et al. Vortex phase separation in mesoscopic superconductors. Sci Rep 3, 1758 (2013). https://doi.org/10.1038/srep01758
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01758
This article is cited by
-
Rayleigh approximation to ground state of the Bose and Coulomb glasses
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

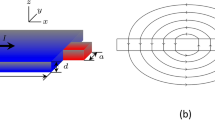

 . The period a of the square array of holes of the radii
. The period a of the square array of holes of the radii  satisfies the condition
satisfies the condition  .
.

