Quantifying disparities in intimate partner violence: a machine learning method to correct for underreporting

Abstract

The first step towards reducing the pervasive disparities in women’s health is to quantify them. Accurate estimates of the relative prevalence across groups—capturing, for example, that a condition affects Black women more frequently than white women—facilitate effective and equitable health policy that prioritizes groups who are disproportionately affected by a condition. However, it is difficult to estimate relative prevalence when a health condition is underreported, as many women’s health conditions are. In this work, we present PURPLE, a method for accurately estimating the relative prevalence of underreported health conditions which builds upon the literature in positive unlabeled learning. We show that under a commonly made assumption—that the probability of having a health condition given a set of symptoms remains constant across groups—we can recover the relative prevalence, even without restrictive assumptions commonly made in positive unlabeled learning and even if it is impossible to recover the absolute prevalence. We conduct experiments on synthetic and real health data which demonstrate PURPLE’s ability to recover the relative prevalence more accurately than do previous methods. We then use PURPLE to quantify the relative prevalence of intimate partner violence (IPV) in two large emergency department datasets. We find higher prevalences of IPV among patients who are on Medicaid, not legally married, and non-white, and among patients who live in lower-income zip codes or in metropolitan counties. We show that correcting for underreporting is important to accurately quantify these disparities and that failing to do so yields less plausible estimates. Our method is broadly applicable to underreported conditions in women’s health, as well as to gender biases beyond healthcare.

Introduction

There are enormous disparities in women’s health across race, age, socioeconomic status, and other dimensions. Mitigating these disparities requires accurate estimates of the extent to which a medical condition disproportionately affects different groups. The relative prevalence does so by capturing how much more frequently a condition occurs in one group compared to another—$\frac{\,{{\mbox{prevalence in group A}}}}{{{\mbox{prevalence in group B}}}\,}$—with high relative prevalence estimates suggesting concrete areas to increase funding, research, and resources. Public health decisions often rely on such estimates to develop, allocate, and advocate for interventions. For example, research revealing startling disparities in maternal mortality between Black and white women¹ led to Congressional policy that has invested billions in funding towards evidence-based interventions to improve Black maternal health².

However, it remains challenging to produce accurate relative prevalence estimates for many conditions in women’s health and healthcare more generally due to widespread underreporting (Fig. 1A). With underreported health conditions, only a small percentage of true positives may be labeled as positive; worse, the probability of correctly diagnosing a positive case can vary by group³. This is especially relevant to intimate partner violence, a notoriously underreported condition: true cases are only correctly diagnosed an estimated ~25% of the time, and this probability varies across racial groups⁴. Underreporting in one group and not another can skew estimates of health disparities, making it appear that a condition is equally prevalent in two populations when it is not or more prevalent in one population than in another when it is not. These errors obscure where resources are most needed and consequently inhibit the development of effective health policy.

Fig. 1: Underreporting can skew observed relative prevalences and conceal health disparities.

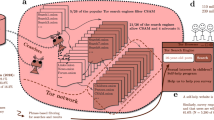
PURPLE is designed to estimate the relative prevalence while correcting for underreporting. A Underreporting leads to inaccurate observed relative prevalences. Understanding the relative prevalence of a health condition between groups g—for example, men and women—is important to effective medical care. However, these estimates are often based on diagnoses s (i.e., positive diagnosis vs. no diagnosis) instead of the true patient state y (sick vs. not sick). Underreporting, which is known to vary by demographic groups, leads to inaccurate relative prevalence estimates that can hide the groups most affected by a condition. B PURPLE uses data on patient diagnoses s, symptoms x, and group membership g to accurately estimate the relative prevalence of a condition. PURPLE first estimates the group-specific diagnosis probability, p(s = 1∣y = 1, g), and disease likelihood, p(y = 1∣x), up to constant multiplicative factors and then combines these estimates to compute the relative prevalence. We show this is possible under three widely-made assumptions: no false positives, random diagnosis within groups, and constant p(y = 1∣x) between groups.

Efforts in both epidemiology and machine learning have addressed these challenges but often rely on either data that is unavailable or assumptions that are unrealistic in women’s health contexts (refer to the Supplement for a detailed discussion of related work). Epidemiological work aims to quantify true prevalences in the context of imperfect diagnostic tests and commonly assumes the presence of information that is not always available (for example, ground truth annotations^5,6,7,8,9, multiple tests^10,11,12, or informative priors¹³). For conditions in women’s health, we often have no access to ground truth, only a single diagnosis per patient, and little notion of how accurate that diagnosis truly is¹⁴. The machine learning literature has modeled underreporting using the positive-unlabeled (PU) learning framework, which assumes that only some positive cases are correctly labeled as positive, and the unlabeled examples consist of both true negatives and unlabeled true positives. In order to recover prevalence in the presence of underdiagnosis, many PU learning methods assume that there is a region of the feature space where cases are certain to be true positives. However, this is a restrictive assumption which, while potentially suitable in other PU settings, is unlikely to hold in health data¹⁵ because it is rare that a set of symptoms corresponds to a health condition with 100% certainty. This is especially true in the context of intimate partner violence, where symptoms are frequently not specific to a particular condition (for example, pregnancy complications, which are well-known to occur at higher rates among IPV patients¹⁶, could suggest a number of underlying conditions).

Here, we present PURPLE (Positive Unlabeled Relative PrevaLence Estimator), a method that is complementary to the prior epidemiology and PU learning literature. In contrast to epidemiological approaches, it requires no external information (for example, the sensitivity and specificity of a test) to recover the relative prevalence of an underreported disease. In contrast to the prior PU learning literature, PURPLE relies on no assumptions about the overlap in symptom distribution of positive and negative cases. PURPLE is designed to address underreporting in intimate partner violence and women’s health more broadly by estimating the relative prevalence of the condition given three assumptions: (1) no false-positive diagnoses; (2) random diagnosis within the group; and (3) constant p(y = 1∣x) between groups, i.e., that the probability of having a disease conditional on symptoms remains constant across groups. The first two assumptions are standard in PU learning; the third, which is specific to our method, replaces PU assumptions about the separability of the positive and negative classes. We show that if these assumptions are satisfied, it is possible to recover the relative prevalence even if it is not possible to recover the absolute prevalence: that is, $\frac{\,{{\mbox{prevalence in group A}}}}{{{\mbox{prevalence in group B}}}\,}$ can be estimated even if neither the numerator nor denominator can. PURPLE does this by jointly estimating the conditional probability that a case is a true positive given a set of symptoms and the diagnosis probability (i.e., the probability a positive case is diagnosed as such; Fig. 1B). We demonstrate via experiments on synthetic and real health data that PURPLE recovers the relative prevalence more accurately than do existing methods. We provide procedures for checking whether PURPLE’s underlying assumptions hold and show that even under a plausible violation of the assumptions, PURPLE still provides a useful lower bound on the magnitude of disparities.

Having validated PURPLE, we use it to estimate the relative prevalence of the condition that motivates this work—intimate partner violence (IPV)—in two widely-used datasets of electronic health records, which together describe millions of emergency department visits: MIMIC-IV¹⁷ and NEDS¹⁸. Across both datasets, we find higher prevalences of IPV among patients who are on Medicaid than among those who are not. Relative prevalences are higher among non-white patients (though these disparities are noisily estimated in the MIMIC dataset). We also quantify the relative prevalence of IPV across income quartiles, marital statuses, and the rural–urban spectrum, finding that IPV is more prevalent among patients who are lower-income, not legally married, and in metropolitan counties. Finally, we show that PURPLE’s corrections for underreporting are important: they yield more plausible estimates of how relative prevalence varies with income than estimation methods that do not correct for underreporting. Specifically, PURPLE estimates that the relative prevalence of IPV decreases with income, consistent with prior work^19,20,21. In contrast, failing to correct for underdiagnosis (i.e., computing relative prevalence estimates using observed diagnoses) yields estimates that do not show any consistent trend with respect to income and which are harder to explain. Overall, this analysis contributes to the literature on IPV disparities in several ways: it uses some of the largest and most recent samples; evaluates robustness across multiple datasets; and corrects for underreporting.

Together, our analyses illustrate how PURPLE is a general method for estimating relative prevalences in the presence of underreporting, allowing practitioners to discover and quantify group-specific disparities in a wide range of settings in which underreporting is common, including outcomes in women’s health and beyond.

Results

Here, we introduce PURPLE, a method to quantify disparities in the prevalence of a health condition between groups given only positive and unlabeled data. A key idea underpinning our method is that knowing the exact prevalence in a group is not necessary to calculate the relative prevalence across groups: one can estimate the fraction $\frac{\,{{\mbox{prevalence in group A}}}}{{{\mbox{prevalence in group B}}}\,}$ without knowing its numerator or denominator. We adopt terminology standard in the PU learning literature and assume that we have access to three pieces of data for the ith example: a feature vector x_i; a group variable g_i; and a binary observed label s_i. We let y_i denote the true (unobserved) label. In healthcare, example i may correspond to a specific patient and their presenting symptoms (x_i), race (g_i), and observed diagnosis (s_i). Here, y_i corresponds to whether the patient truly has the medical condition. We first introduce PURPLE and then validate our approach on synthetic and semi-synthetic data.

Overview of PURPLE: Positive-Unlabeled Relative PrevaLence Estimation

We provide a conceptual overview of PURPLE here and describe the full details in the “Deriving the Relative Prevalence–Implementation” Section. PURPLE is designed to address how, for underreported women’s health conditions, the ratio of diagnosis rates between demographic groups may not equal the ratio of true prevalences due to differential underreporting across groups. To address this, PURPLE first uses the observed data to learn a model of which symptoms correlate with having the condition; so long as this relationship between symptoms and the condition remains constant across groups, we will be able to estimate the relative prevalence. Mathematically, PURPLE first estimates p(y = 1∣x) up to a constant multiplicative factor; second, it uses this estimate to compute the relative prevalence between groups. We use p to denote the true probabilities in the underlying data distribution and $\hat{p}$ to denote PURPLE’s estimates of these probabilities.

• 1. Estimate p(y = 1∣x) up to a constant factor. PURPLE fits the following model:

$${\underbrace{{{\hat{p}}( s = 1\vert{g},{x})}}_{{\rm{probability}}\, {\rm{patient}} \atop{\rm{is}}\, {\rm{diagnosed}}}} ={\underbrace{{{\hat{p}}(y = 1\vert{x})}}_{{\rm{probability}}\, {\rm{patient}} \atop{\rm{truly}}\, {\rm{has}}\,{\rm{condition}}}}\,\cdot\,{\underbrace{{{\hat{p}}(s = 1\vert{y}=1,{g})}}_{{\rm{probability}}\, {\rm{true}}\, {\rm{positives}} \atop{\rm{are}}\,{\rm{correctly}}\,{\rm{diagnosed}}}}$$

(1)

In other words, PURPLE models the probability a patient is diagnosed with a condition as the product of two terms: the probability the patient truly has the condition and the probability that true positives are correctly diagnosed. The first term is constant across groups g, while the second can vary, accounting for underdiagnosis. This decomposition is valid under three assumptions which we discuss below. To estimate the two terms on the right-hand side of Eq. (1), we parameterize the first term as a logistic regression and the second as a constant c_g ∈ [0, 1] for each group g. We optimize these parameters by minimizing the cross-entropy loss between the predicted $\hat{p}(s=1| g,x)$ and the empirical p(s = 1∣g, x), which is possible because s, g, and x are all observed (“Implementation” Section). Note that we can only estimate both terms on the right-hand side up to a constant multiplicative factor because multiplying the first term by a non-negative β and dividing the second term by β leaves $\hat{p}(s=1| g,x)$ unchanged.

• 2. Estimate the relative prevalence using $\hat{p}(y=1| x)$. Fortunately, even though $\hat{p}(y=1| x)$ is only correct up to a constant multiplicative factor, this suffices to estimate the relative prevalence $\frac{p(y=1| g=a)}{p(y=1| g=b)}$, as we derive in the “Deriving the relative prevalence” Section. Specifically, our estimator of the relative prevalence is

$$\frac{{\sum }_{x}\hat{p}(y=1| x)\hat{p}(x| g=a)}{{\sum }_{x}\hat{p}(y=1| x)\hat{p}(x| g=b)}$$

(2)

In practice, this is simply the mean value of $\hat{p}(y=1| x)$ for samples from group a divided by the mean value of $\hat{p}(y=1| x)$ for samples from group b.

It is impossible to estimate outcome prevalence in PU settings without assumptions²². Our estimation procedure relies on three assumptions: (1) observed positives are true positives (the positive-unlabeled assumption common to all PU methods), (2) within each group, diagnosis s depends only on y (the random diagnosis within group assumption, commonly made in PU settings) and (3) the probability of having a disease conditional on symptoms remains constant across groups (the constant p(y∣x) assumption, common to work in both domain adaptation^23,24 and healthcare²⁵). Details about the required assumptions can be found in the “Assumptions” Section. We also provide checks to assess whether the assumptions hold (“Assumption checks” Section) and show that even under a plausible violation of these assumptions, PURPLE is guaranteed to produce a lower bound on the true magnitude of disparities (“Robustness to violations of the Constant p(y|x) assumption” Section). An illustration of PURPLE’s behavior under violations of the PU assumption and the random-diagnosis-within-group assumption is available in the “Effect of positive-unlabeled assumption violations” and “Effect of random-diagnosis-within-groups assumption violations” Sections, respectively. We provide the full derivation of our estimation procedure in the “PURPLE: positive unlabeled prevalence estimator” Section.

PURPLE recovers the true relative prevalence in synthetic data

Prior to applying PURPLE to estimate the relative prevalence of IPV, we confirm that the method can correctly recover the true prevalence on synthetic data where the true relative prevalence is known, a standard machine learning check. We compare PURPLE to four previous machine learning methods (“Baselines” Section) drawn from the literature on PU learning, where estimating prevalence is a critical step²⁶. We generate the synthetic data by simulating group-specific features (p(x∣g)) and labels using a decision rule (p(y∣x)). The two groups, a and b, correspond to 5D Gaussian distributions with different means (see “Gauss-Synth” Section for full data generation details).

Figure 2B compares PURPLE’s performance to the performance of the other methods on purely synthetic data. We evaluate each approach in both separable (in which the datapoints with y = 1 and the datapoints with y = 0 can be perfectly separated in the feature space x) and non-separable settings. We perform this comparison because existing methods rely on separability assumptions which often do not hold in realistic health settings¹⁵. PURPLE is the only method that accurately recovers the relative prevalence in both the separable and non-separable settings. We also show that PURPLE maintains consistent performance regardless of the extent to which p(x), or the distribution of symptoms, differs between groups (Fig. S1B).

Fig. 2: Validation of PURPLE on synthetic and semi-synthetic data.

A Methods in positive-unlabeled learning commonly make assumptions about the separability of the positive and negative distributions. Settings in which underreporting occurs map directly to work in positive-unlabeled learning, in which learning algorithms have access to a set of positive labeled examples and an unlabeled mixture of positive and negative examples. Most works in positive-unlabeled learning assume A (left panel), or a positive subdomain. PURPLE makes no assumptions about the separability of the positive and negative distributions and instead assumes that p(y = 1∣x) remains constant across patient subgroups. B PURPLE accurately recovers the relative prevalence on both separable and nonseparable synthetic data. The vertical axis plots the ratio of estimated relative prevalence to true relative prevalence, with 1 (dotted line) indicating perfect performance. We report variation across 5 randomized train, validation, and test splits. Negative, KM2, BBE, and DEDPUL baselines do not always accurately estimate the relative prevalence, especially on nonseparable data. Oracle is impossible to implement in practice because it relies on ground truth labels y which are not available; it is provided as a metric for ideal performance. C PURPLE recovers the relative prevalence accurately in simulations based on real health data. We generate semi-synthetic data by using patient visits from MIMIC-IV²⁷ and simulating a disease label given a set of symptoms. This allows us to test PURPLE on a real, high-dimensional distribution of symptoms while retaining access to ground truth labels. Each dataset simulates disease likelihood on the basis of a different symptom set: (1) symptoms that appear most frequently, (2) symptoms that occur frequently in one group but not the other, (3) symptoms that co-occur frequently with endometriosis, and (4) symptoms known to indicate risk of intimate partner violence based on past literature. We define group A to be Black patients and group B to be white patients. Across symptom sets and a range of group-specific diagnosis frequencies, PURPLE produces more consistently accurate relative prevalence estimates than existing work. Two semisynthetic experiments involving real conditions in women’s health—endometriosis and intimate partner violence—demonstrate the potential to apply PURPLE to conditions in women’s health and produce accurate, actionable relative prevalence estimates.

PURPLE recovers the true relative prevalence in realistic semi-synthetic health data

Having established that PURPLE outperforms previous work on synthetic data, we investigate its performance on more realistic data: specifically, MIMIC-IV²⁷, a dataset of electronic health records that describes ~450,000 patient hospital visits between 2008 and 2018. We generate realistic semi-synthetic data based on these records to examine PURPLE’s performance on the high-dimensional, sparse data common in clinical settings. Specifically, we use the patient symptoms x—encoded as a binary one-hot vector of ICD codes—to simulate whether the patient truly has the medical condition, y. Using data in which we know y allows us to assess how accurately PURPLE recovers the relative prevalence; in contrast, if we did not simulate y, we would not have access to ground truth and could not assess relative prevalence estimates. We simulate y for four settings: (1) a condition with common symptoms, (2) a condition that is less common among Black patients, (3) endometriosis, and (4) intimate partner violence (see Section “MIMIC-semi-synth” for full details).

Across the semi-synthetic settings we consider, the estimation error of previous methods is large, with some methods producing relative prevalence estimates more than 4x the true value (Fig. 2C). Further, each previous method produces both overestimates and underestimates of the true relative prevalence depending on how underreported the medical condition is. In contrast, PURPLE remains accurate across the different settings.

Quantifying the relative prevalence of intimate partner violence

We have validated PURPLE’s accuracy in recovering the relative prevalence by using synthetic and semi-synthetic datasets where the true relative prevalence is known. We now use PURPLE to estimate relative prevalence on two real datasets where the true relative prevalence is unknown. Specifically, we apply PURPLE to quantify the relative prevalence of the underdiagnosed condition motivating this work—intimate partner violence (IPV)—across different demographic groups.

Datasets

We conduct our study using two widely-used datasets of emergency department visits: MIMIC-IV ED¹⁷ and the 2019 Nationwide Emergency Department Sample (NEDS)¹⁸. MIMIC-IV ED describes 293,297 emergency department visits to a single, Boston-area hospital; NEDS is a nationwide sample that is approximately one hundred times as large (it contains 33.1 million emergency department visits, which, when reweighted, represent the universe of 143 million US emergency department visits in 2019). We assess results across multiple datasets to verify the robustness of the disparities we observe. Because our sample consists of emergency department visits, we estimate the relative prevalence of IPV conditional on going to the emergency department—in particular, our data does not allow us to quantify disparities among populations who do not interact with the healthcare system at all²⁸. Relative prevalence estimates among patients who visit emergency departments, however, remain of interest to IPV researchers due to the unique role emergency departments play as a point of care and intervention for patients who experience IPV²⁹.

For both datasets, we filter for female patients because the symptoms associated with IPV in male patients are less well understood, and the constant p(y = 1∣x) assumption may not hold³⁰; we also filter out patients younger than 18 years old because symptoms that indicate intimate partner violence could be instances of child abuse in this patient subgroup^31,32. We describe all preprocessing steps in the “Datasets” Section. All point estimates and uncertainties reported below represent the mean and standard deviation, respectively, across five randomized train/test splits of each dataset.

Analysis

Results are plotted in Fig. 3 (we verify that PURPLE passes the assumption checks detailed in the “Assumption checks” Section in SI Figs. 4–6). We find, in both datasets, that intimate partner violence is more common among patients on Medicaid (NEDS relative prevalence 2.44 ± 0.07 in Medicaid patients vs non-Medicaid patients; MIMIC-IV relative prevalence 2.65 ± 0.31) and less common among patients on Medicare (NEDS relative prevalence of 0.37 ± 0.01; MIMIC-IV relative prevalence of 0.38 ± 0.04). Of course, Medicaid is likely not the causal factor underlying IPV risk; rather, it acts as a proxy that identifies populations who are disproportionately affected by IPV.

Fig. 3: Estimates of the relative prevalence of intimate partner violence across demographic subgroups.

We apply PURPLE to two large emergency department datasets: NEDS¹⁸ and MIMIC-IV ED¹⁷. We compute each relative prevalence with respect to each group’s complement (i.e., estimating the prevalence of IPV among married patients vs. non-married patients). Relative prevalences are higher among non-white patients overall (A) though these disparities are noisily estimated in the MIMIC-IV ED dataset, and the ordering across race groups is not completely consistent. We also find higher prevalences among patients who are on Medicaid (B), not legally married (C), in lower-income zip codes (D), and in metropolitan counties (E). Counties with more than 1 million residents are further differentiated by how urban they are (as “central” or “fringe"). Error bars report the standard deviations for each estimate across 5 randomized train/test splits of each dataset. Panels C–E are reported on only a single dataset due to different demographic feature availability in the two datasets; note the slightly larger y-axis range on Panel B due to the greater range of the estimates.

Examining racial differences reveals disparities that are smaller and less consistent than disparities by insurance status. In both datasets, white patients have the lowest relative prevalence of the four race groups, and in the NEDS dataset, white patients have significantly lower prevalence than non-white patients overall (relative prevalence for white patients vs. non-white patients equal to 0.82 ± 0.02). However, in MIMIC-IV, racial disparities are more noisily estimated due to the smaller size of the dataset, yielding an ordering of race groups that is similar but not completely consistent across the two datasets. This attests to the importance of using large samples and assessing results across multiple datasets.

The MIMIC-IV dataset provides information on patient marital status, allowing us to estimate that IPV is more common among patients who are “Legally Unmarried”, or not officially married but may still be in relationships (relative prevalence equal to 1.48 ± 0.21). The NEDS dataset provides information on the population density and estimated median household income of areas where patients live. We estimate higher rates of IPV among patients living in central metropolitan counties with a population > 1 million (relative prevalence equal to 1.18 ± 0.02). We also find that IPV prevalence decreases with income (relative prevalence equal to 1.16 ± 0.02 in the bottom income quartile versus 0.87 ± 0.03 in the top income quartile).

In Fig. S3, we report the prevalence of observed IPV diagnoses—i.e., p(s = 1∣g)—without correcting for underdiagnosis. While often the trends are qualitatively similar, in some cases correcting for underdiagnosis is important to yield plausible trends. For example, failing to correct for underdiagnosis produces an inconsistent relationship between IPV prevalence and income which is difficult to reconcile with past work, which consistently documents that IPV prevalence decreases with income^19,20,21. This suggests the importance of using methods like PURPLE, which attempts to correct for underdiagnosis. Our income results also suggest that IPV is less likely to be correctly diagnosed in lower-income women, a finding that reflects the broader phenomenon of underdiagnosis among lower-income patients, as has been shown in the context of dementia^33,34, asthma^35,36, and depression^37,38,39.

Discussion

In this work, we provide a method for estimating relative prevalence even in the presence of underreporting, a difficult but essential task in healthcare and public health. We show that we can estimate the relative prevalence even in settings where absolute prevalence estimation is impossible, by exchanging the restrictive separability assumptions typical in the PU learning literature for the constant p(y = 1∣x) assumption, which is arguably more appropriate in clinical settings. Although this assumption may not hold for all settings—for example, the conditional probability of intimate partner violence is known to be dependent on a patient’s age group⁴⁰—it is realistic in many settings, and we provide methods for checking its validity and a lower-bound guarantee even when it fails to hold. Based on these assumptions, we present a method for relative prevalence estimation, PURPLE, a complementary approach to those in the epidemiology and PU learning literature: it works when one does not have the external information that epidemiological methods generally require and cannot make the separability assumptions PU learning methods rely on. We show PURPLE outperforms previous methods in terms of its ability to recover the relative prevalence on both synthetic and real health data.

We apply PURPLE to estimate the relative prevalence of intimate partner violence in two widely-used, large-scale datasets of emergency department visits. We find that IPV is more prevalent among patients who are on Medicaid, non-white, not legally married, in lower-income zip codes, and in metropolitan counties. We also show that correcting for underdiagnosis produces estimates of IPV prevalence across income groups which are more plausible in light of prior work^19,20,21, highlighting the importance of modeling underdiagnosis. In general, past work on IPV disparities corroborates the plausibility of our findings. Our finding that intimate partner violence is more common among patients on Medicaid compared to patients who are not is consistent with earlier results that show that IPV is ^40,41,42 more common among patients who live below the poverty line^20,43,44. Past work documenting higher IPV prevalences among unmarried women^45,46,47 and in metropolitan areas^19,48,49 also corroborates the plausibility of our findings. Our finding that IPV is more common among non-white patients is corroborated by some past work^4,19,50. However, the fact that we find that racial disparities are smaller and not completely consistent across datasets is also concordant with past work documenting inconsistent racial differences across samples^44,51,52,53. This suggests the importance of using large samples and multiple datasets to assess how consistently and robustly racial disparities emerge. Overall, our analysis contributes to the literature on IPV disparities by using large samples; evaluating robustness across multiple datasets; and correcting for underreporting.

Our work is motivated by the widespread underreporting of women’s health, and we foresee numerous opportunities for future work. PURPLE could be applied to obtain relative prevalence estimates for many other health conditions that are known to be underreported, including polycystic ovarian syndrome⁵⁴, endometriosis⁵⁵, and traumatic brain injuries⁵⁶. Additionally, quantifying relative prevalence in the presence of underreporting is a problem of interest in many domains beyond healthcare and public health: for example, quantifying the relative prevalence of underreported police misconduct across precincts or quantifying the relative prevalence of underreported hate speech across demographic groups. We believe that PURPLE can also yield useful insight into disparities in these non-healthcare settings.

Methods

PURPLE: Positive Unlabeled Relative PrevaLence Estimator

PURPLE estimates p(y = 1∣x) up to a constant multiplicative factor in order to estimate the relative prevalence of a condition y. Underlying this procedure are two insights: first, that estimating p(y = 1∣x) up to a constant factor suffices to estimate the relative prevalence, and second, that it is possible to produce this estimate using the observed labels s, symptoms x, and group statuses g. We first describe the three assumptions underlying PURPLE and show how these statements follow from them in the “Deriving the relative prevalence” Section and M1.3. We describe implementation details in the “Implementation” Section. We provide checks to determine whether PURPLE’s assumptions hold true (“Assumption checks” Section) and show that even under a plausible violation of our assumptions, PURPLE produces a lower bound on the true magnitude of disparities (“Robustness to violations of the Constant p(y|x) assumption” Section).

Assumptions

Neither the exact prevalence nor the relative prevalence can be recovered without making assumptions about the data-generating process: intuitively, without further assumptions, it is impossible to distinguish between whether a medical condition is truly rare or merely rarely diagnosed. We adopt terminology standard in the PU learning literature and assume that we have access to three pieces of data for the ith example: a feature vector x_i; a group variable g_i; and a binary observed label s_i. We let y_i denote the true (unobserved) label. In healthcare, example i may correspond to a specific patient and their presenting symptoms (x_i), race (g_i), and observed diagnosis (s_i). Here, y_i corresponds to whether the patient truly has the medical condition. This is an unobserved binary variable, and because the medical condition is underreported, not all patients who truly have the condition are diagnosed with it, so p(s_i = 1∣y_i = 1) < 1. Because we are interested in health disparities, we focus on groups g defined by sensitive attributes (e.g., gender, race, or socioeconomic status) but our method is applicable to any set of groups for which our assumptions hold. We make three assumptions:

• 1. No false positives: We assume that examples labeled as positive (s = 1) are truly positive (y = 1): i.e., p(y = 0∣s = 1) = 0 (and thus, by Bayes’ rule, p(s = 1∣y = 0) = 0). This is the positive unlabeled assumption and is the foundational assumption of PU learning methods⁵⁷.

• 2. Random diagnosis within groups: We assume that positive examples within a specific group are equally likely to be labeled as positive: p(s = 1∣y = 1, g = a) = c_a, where c_a represents the diagnosis frequency of group a (i.e., the probability that a positive case is diagnosed as such). Random diagnosis within groups amounts to the commonly made Selected-Completely-at-Random assumption⁵⁸ within each group. We allow c_a to vary across groups to allow for group-specific underdiagnosis rates.

• 3. Constant p(y = 1∣x) between Groups: We assume that p(y = 1∣x) remains constant across groups: examples in different groups with the same features are equally likely to be true positives. In the medical setting, this means that patients in different groups with the same symptoms have the same probability of truly having a condition. This is equivalent to assuming only a covariate shift between groups, a commonly made assumption in the literature on domain adaptation^23,24 and healthcare²⁵.

Notably, we make no assumptions about the separability of the positive and negative distributions. Past work in PU learning has shown that the true prevalence p(y = 1) can be recovered under a restrictive set of assumptions about the structure of the positive and negative distributions⁵⁹, which we refer to as “separability assumptions”. Many PU learning methods assume that the positive distribution is not completely contained within the negative distribution: in healthcare, this means there is a region of the feature space where all examples are true positives^57,60,61,62 (Fig. 2A). This assumption is unrealistic in medical settings because it is unlikely that a set of symptoms maps to a diagnosis with 100% probability⁶³, and as a result, PURPLE makes no such assumption.

While it is necessary to make assumptions to infer the relative prevalence, no assumptions will hold on all datasets, a point we consider in the Discussion. To ensure PURPLE is applied to appropriate datasets, we provide two checks for violations of PURPLE’s assumptions (“Assumption checks” Section). We also show that even under a plausible violation of the Constant p(y = 1∣x) assumption, PURPLE provides a useful lower bound on the magnitude of health disparities (“Robustness to violations of the Constant p(y|x) assumption” Section).

Deriving the relative prevalence

Here, we show that an estimate of p(y = 1∣x) up to a constant multiplicative factor recovers the relative prevalence between groups a and b (ρ_a,b) exactly. The derivation is as follows:

$${\rho }_{a,b}:=\frac{p(y=1| g=a)}{p(y=1| g=b)}$$

(3)

$$=\frac{{\sum }_{x}p(y=1| x,g=a)p(x| g=a)}{{\sum }_{x}p(y=1| x,g=b)p(x| g=b)}$$

(4)

$$=\frac{{\sum }_{x}p(y=1| x)p(x| g=a)}{{\sum }_{x}p(y=1| x)p(x| g=b)}$$

(5)

$$\begin{array}{rcl}&=&\frac{{\sum }_{x}\hat{p}(y=1| x)p(x| g=a)}{{\sum }_{x}\hat{p}(y=1| x)p(x| g=b)}\\ &&\,{{\mbox{for all}}}\,\hat{p}(y=1| x)\propto p(y=1| x)\end{array}$$

(6)

where Eq. (5) follows from the constant p(y = 1∣x) assumption and Eq. (6) follows because estimates of p(y = 1∣x) up to a constant multiplicative factor will yield a constant term in the numerator and denominator which cancels. Thus, estimates of p(y = 1∣x) up to a constant multiplicative factor suffice to compute the relative prevalence. p(x∣g) is directly observable from the data, so we can estimate the numerator as the mean of $\hat{p}(y=1| x)$ over all x in group a and similarly estimate the denominator as the mean of $\hat{p}(y=1| x)$ over all x in group b.

Estimating p(y = 1∣x) up to a constant multiplicative factor

We have shown that if we can estimate p(y = 1∣x) up to a constant multiplicative factor, we can use this estimate to compute the relative prevalence ρ_a,b. Now we show how to estimate p(y = 1∣x) up to a constant multiplicative factor. We do so by applying our three assumptions to derive a decomposition for p(s = 1∣x, g):

$$\begin{array}{l}p(s=1| x,g)=p(y=1| x,g)p(s=1| y=1,x,g)\\ \qquad\qquad\qquad\,+\,p(y=0| x,g)p(s=1| y=0,x,g)\end{array}$$

(7)

$$=\quad p(y=1| x,g)p(s=1| y=1,x,g)$$

(8)

$$=\quad p(y=1| x,g)p(s=1| y=1,g)$$

(9)

$$=\quad p(y=1| x)p(s=1| y=1,g)$$

(10)

Applying the No False Positives assumption allows us to remove the second term in Eq. (7), producing Eq. (8). The Random Diagnosis within Groups assumption removes the dependence of the diagnosis probability on x, leading to Eq. (9). The Constant p(y = 1∣x) assumption leads to Eq. (10).

Thus, p(s = 1∣x, g) can be decomposed as the product of two terms: the probability the patient truly has the condition given their symptoms, p(y = 1∣x), and the probability that true positives are correctly diagnosed, p(s = 1∣y = 1, g). The fact that the second term varies across groups accounts for group-specific underdiagnosis. This decomposition can be fit via maximum likelihood estimation with respect to the empirical p(s = 1∣x, g), since s, x, and g are observed. Note that this only allows estimation of the two terms on the right side of Eqn. (10) up to constant multiplicative factors, since we can multiply p(y = 1∣x) by a non-negative β and divide p(s = 1∣y = 1, g) by β while leaving our estimate of p(s = 1∣x, g) unchanged. However, constant-factor estimation of p(y = 1∣x) suffices to estimate the relative prevalence. Concretely, we estimate p(y = 1∣x) and p(s = 1∣y = 1, g) up to constant multiplicative factors by fitting to p(s = 1∣x, g); we then use our constant-factor estimate of p(y = 1∣x) to estimate the relative prevalence as described in Section “Deriving the relative prevalence”.

We note that the probabilistic model described by Eqn. (10) has been previously applied to estimate absolute prevalence in PU settings²⁶. Our novel contribution is to derive a precise set of assumptions in which this probabilistic model can be used to estimate relative prevalence and provide an estimation method to do so.

Implementation

Thus far, we have shown that it is possible to estimate the relative prevalence of an underreported condition by estimating p(y = 1∣x) up to a constant factor and provided a way to conduct this estimation given only the observed data. One can apply PURPLE to a new dataset in two steps:

• 1. Estimate p(y = 1∣x) up to a constant multiplicative factor using the observed diagnoses and the following probabilistic model:

$$\hat{p}(s=1| g,x)=\hat{p}(y=1| x)\hat{p}(s=1| y=1,g)$$

(11)

• 2. Plug our constant multiplicative factor estimate, $\hat{p}(y=1| x)$, into Eq. (6) to produce the relative prevalence estimate. Specifically, we estimate the relative prevalence ρ_a,b as:

$$\frac{{\sum }_{x}\hat{p}(y=1| x)\hat{p}(x| g=a)}{{\sum }_{x}\hat{p}(y=1| x)\hat{p}(x| g=b)}$$

(12)

In practice, we can compute this fraction simply by taking the mean value of $\hat{p}(y=1| x)$ in each group to compute the numerator and denominator.

We implement the model in PyTorch⁶⁴ using a single-layer neural network to represent $\hat{p}(y=1| x)$ and group-specific parameters ${c}_{g}=\hat{p}(s=1| y=1,g)$ for each group g. Note that a single layer neural network, followed by a logistic activation, is functionally equivalent to a logistic regression, as they both learn a linear transformation of the input features followed by a logistic transformation to produce a predicted probability of the positive class. We train the model using the Adam optimizer with default parameters (i.e., a learning rate of 0.001, epsilon of 10⁻⁸, and weight decay of 0) and implement early stopping based on the cross-entropy loss on the held-out validation set. For the semi-synthetic and real data, we use L1 regularization because these experiments are conducted on high-dimensional vectors describing thousands of symptoms, most of which we expect to be unrelated to the medical condition, and select the regularization parameter λ ∈ [10⁻², 10⁻³, 10⁻⁴, 10⁻⁵, 10⁻⁶, 0] using the held-out validation set by maximizing the AUC with respect to the diagnosis labels s. While we use a single-layer neural network because our symptoms x are one-hot encoded and we do not anticipate interactions between symptoms, our approach is general and could be applied with deeper neural network architectures to accommodate interactions and nonlinearities.

Assumption checks

Like all PU learning methods, PURPLE must rely on assumptions. To prevent users from applying PURPLE to datasets where these assumptions do not hold, we provide two empirical tests whose failure implies at least one of the underlying assumptions fails:

• Compare the model fit of PURPLE to the fit of an unconstrained model. If PURPLE’s assumptions hold, the diagnosis likelihood p(s = 1∣x, g) decomposes as the product of two terms: p(s = 1∣x, g) = p(y = 1∣x)p(s = 1∣y = 1, g). This is a constrained model of p(s = 1∣x, g): for example, it does not allow for interaction terms between group g and symptoms x. We can compare the performance of PURPLE to a fully unconstrained model for p(s = 1∣x, g) which allows these interaction terms. If the unconstrained model better fits the data, metrics, including the AUC and AUPRC, will be higher on a held-out set of patients. If the constrained and constrained models exhibit similar performance, it is still possible for one of the assumptions to not be true; however, if the models exhibit different performance, it is a sign that PURPLE’s assumptions are not appropriate.

• Compare calibration across groups. PURPLE estimates a probabilistic model of diagnosis, p(s = 1∣x, g), which means we can check how well the outputted probabilities reflect the real data by examining model calibration, a standard check⁶⁵. Concretely, we expect that a proportion z of examples that our model gives a probability z of receiving a positive diagnosis truly receive a positive diagnosis, and we expect this to be true for each group. Violations of PURPLE’s assumptions will often cause group-specific calibration to not hold. For example, if p(y = 1∣x) differs between groups beyond a scalar constant factor, PURPLE’s estimate of p(s = 1∣x, g) cannot be correct for both groups (since PURPLE assumes p(y = 1∣x) remains constant).

We note that these assumption checks cannot rule out all forms of model misspecification—and, indeed, no assumption checks can. Since only x, g, and s are observed, it is impossible to prove anything about the distribution of y. However, the assumption checks will rule out some forms of model misspecification and guide users away from datasets where applying PURPLE is clearly inappropriate.

Robustness to violations of the constant p(y∣x) assumption

In this section, we show that under a plausible violation of the central new assumption of our work (constant p(y = 1∣x) between groups), PURPLE produces a lower bound on the magnitude of disparities. This lower bound is useful because we can be confident that if PURPLE infers that a group suffers disproportionately from a condition, that is, in fact, the case, and we can be confident in targeting policy to that group.

Specifically, we relax the assumption of constant p(y = 1∣x) across groups by assuming that if group A has a higher overall prevalence of a condition than group B—i.e., p(y = 1∣g = A) > p(y = 1∣g = B)—group A also has a higher prevalence by a constant factor given the same set of symptoms—i.e., p(y = 1∣x, g = A) = α ⋅ p(y = 1∣x, g = B), α > 1. This assumption is a reasonable one: when a condition is more prevalent in one group than another, the same symptoms plausibly correspond to higher posterior probabilities p(y = 1∣x) in the disproportionately affected group. For example, female patients are more likely than male patients to be victims of intimate partner violence overall³⁰, and if a woman and a man arrive in a hospital with the same injuries, doctors are plausibly more likely to suspect intimate partner violence as the cause of the woman’s injuries.

Proof 1

Without loss of generality, assume that group A is the group with higher overall disease prevalence: p(y = 1∣g = A) > p(y = 1∣g = B). We make the following assumptions:

• 1. Disease prevalence in group A conditional on symptoms is higher by a constant multiplicative factor: p(y = 1∣x, g = A) = α ⋅ p(y = 1∣x, g = B), α > 1.

• 2. The other PURPLE assumptions hold: that is, p(y = 1∣s = 1) = 1 (PU assumption) and p(s = 1∣y = 1, g, x) = p(s = 1∣y = 1, g) (random diagnosis within groups).

Under these assumptions, we show that PURPLE’s estimate provides a lower bound on the true relative prevalence. As before, we use p to denote the true probabilities in the underlying data distribution and $\hat{p}$ to denote PURPLE’s estimates of these probabilities. We have

$$\begin{array}{l}p(s=1| x,g=A)=p(s=1| y=1,g=A)\cdot p(y=1| x,g=B)\cdot \alpha \\ p(s=1| x,g=B)=p(s=1| y=1,g=B)\cdot p(y=1| x,g=B)\end{array}$$

PURPLE estimates $\hat{p}(s=1| x,g)=\hat{p}(s=1| y=1,g)\cdot \hat{p}(y=1| x)$. It can minimize the cross-entropy loss by achieving an estimate $\hat{p}(s=1| x,g)$ which matches the true p(s = 1∣x, g) by setting:

$$\begin{array}{rcl}\hat{p}(y=1| x)&=&\beta \cdot p(y=1| x,g=B)\\ \hat{p}(s=1| y=1,g=A)&=&\frac{1}{\beta }\cdot \alpha \cdot p(s=1| y=1,g=A)\\ \hat{p}(s=1| y=1,g=B)&=&\frac{1}{\beta }\cdot p(s=1| y=1,g=B)\end{array}$$

where β is a positive constant (this captures the fact that, as discussed previously, PURPLE only ever estimates p(y = 1∣x) up to a constant multiplicative factor). In other words, PURPLE can perfectly match the true probabilities p(s = 1∣g, x) by pushing the variation across groups in p(y = 1∣x) into $\hat{p}(s=1| y=1,g)$ (since PURPLE assumes $\hat{p}(y=1| x)$ remains constant across groups.) Given its estimate $\hat{p}(y=1| x)$, PURPLE’s estimate ${\hat{\rho }}_{A,B}$ of the relative prevalence is

$$\begin{array}{rcl}{\hat{\rho }}_{A,B}&=&\frac{{\sum }_{x\in {{{\mathcal{A}}}}}\hat{p}(y=1| x)}{{\sum }_{x\in {{{\mathcal{B}}}}}\hat{p}(y=1| x)}\\ &=&\frac{{\sum }_{x\in {{{\mathcal{A}}}}}\beta \cdot p(y=1| x,g=B)}{{\sum }_{x\in {{{\mathcal{B}}}}}\beta \cdot p(y=1| x,g=B)}\\ & < &\frac{{\sum }_{x\in {{{\mathcal{A}}}}}p(y=1| x,g=A)}{{\sum }_{x\in {{{\mathcal{B}}}}}p(y=1| x,g=B)}\\ &=&{\rho }_{A,B}\end{array}$$

so PURPLE’s estimate ${\hat{\rho }}_{A,B}$ provides a lower bound on the true relative prevalence ρ_A,B.

Empirical validation

We verify this behavior empirically under synthetic violations of the constant p(y∣x) assumption, again using the synthetic data described in Section “Gauss-Synth”. Concretely, we vary the difference in the probability of a positive case between group a and group b (p(y = 1∣x, g = a) − p(y = 1∣x, g = b)), where p(y = 1∣g = a)≥p(y = 1∣g = b).

Figure 1B in the Supplement demonstrates how PURPLE consistently underestimates the true relative prevalence behavior empirically by plotting PURPLE’s behavior over a range of values for α, where α ∈ [0, 1] and αp(y = 1∣x, g = a) = p(y = 1∣x, g = b). In each case, PURPLE provides a lower bound on the true relative prevalence. We replicate this analysis for varying separations of the group-specific Gaussian distributions, where darker shades of purple correspond to group-specific distributions that are further from one another.

Effect of positive-unlabeled assumption violations

Here we demonstrate how PURPLE’s performance varies when the positive-unlabeled assumption is violated, meaning that the sample of observed positives contains some number of negatives. This can arise if the diagnostic test used to create the set of observed positives exhibits a non-zero false positive rate. In SI Fig. 2A, we plot the behavior of PURPLE as we increase the extent to which the setting violates the PU assumption; specifically, we vary the percentage of the observed positives that truly are negative—p(y = 0∣s = 1)—from 0% to 20%. When p(y = 0∣s = 1) = 0, this is equivalent to the positive-unlabeled assumption, and PURPLE recovers the relative prevalence exactly, as expected. At greater violations of the PU assumption, PURPLE’s performance degrades somewhat, as expected.

Effect of random-diagnosis-within-groups assumption violations

We illustrate PURPLE’s behavior under violations of the random-diagnosis-within-groups assumption in Fig. S2B. The assumption states that the probability that a true positive is diagnosed as such does not depend on x or that p(s = 1∣y = 1, g, x) = p(s = 1∣y = 1, g). We simulate violations of the assumption by generating s according to p(s = 1∣y = 1, g, x) = c_g ⋅ σ(β ⋅ x₀). In other words, the diagnosis frequency for group g is scaled by the sigmoid function of parameter β multiplied by the first component of x. For β = 0, the setting adheres to the random-diagnosis-within-groups assumption. Higher values of β translate to a higher correlation between the diagnosis probability and x₀. As Fig. S2B demonstrates, PURPLE recovers the relative prevalence under no violation of the assumption (β = 0) and incurs small errors in the estimated relative prevalence as β increases.

Datasets

We make use of five datasets. We begin with two synthetic datasets: Gauss-Synth, a completely synthetic dataset, and MIMIC-Semi-Synth, a semi-synthetic dataset based on real health data. We then apply PURPLE to three non-synthetic datasets: MIMIC-IV ED, a dataset of electronic health records collected from a single hospital in the Boston area, and NEDS, a dataset of emergency department visits occurring in the US in 2019.

We begin with synthetic and semi-synthetic data so that the ground truth labels y are known, as is standard in the PU learning literature²², enabling us to assess how well methods recover the relative prevalence. To assess the performance of all methods in our synthetic and semi-synthetic experiments, we report the mean ratio of the estimated relative prevalence to the true relative prevalence over 5 random train/test splits of the dataset; values closer to 1 correspond to better performance. Code to reproduce all experiments can be found at https://github.com/epierson9/invisible-conditions.

Gauss-Synth

We generate completely synthetic data by simulating group-specific features (p(x∣g)), and labels using a decision rule (p(y∣x)). Formally, we simulate groups a and b using two 5D Gaussian distributions with different means:

$${x}_{i} \sim \left\{\begin{array}{l}{{{{\mathcal{N}}}}}_{5}(-{{{\bf{1}}}},16\cdot {{{\bf{1}}}})\,{{\mbox{if}}}\,{g}_{i}=a\quad \\ {{{{\mathcal{N}}}}}_{5}({{{\bf{1}}}},16\cdot {{{\bf{1}}}})\,{{\mbox{if}}}\,{g}_{i}=b\quad \end{array}\right.$$

(13)

The likelihood function (p(y = 1∣x)) is a logistic function of the signed distance to a hyperplane through the origin. Observed labels s are drawn such that positive labels in group i are observed with a probability of ${c}_{{g}_{i}}$. The generative model for y and s is:

$${y}_{i} \sim \,{{\mbox{Bernoulli}}}\,(\sigma (({{{{\bf{1}}}}}^{T}{x}_{i})/\parallel {{{\bf{1}}}}\parallel ))$$

(14)

$${s}_{i} \sim \,{{\mbox{Bernoulli}}}\,({c}_{{g}_{i}}{y}_{i})$$

(15)

where σ represents a logistic function ($\sigma (x)=\frac{1}{1+{e}^{-x}}$) and ${c}_{{g}_{i}}$ is the group-specific diagnosis frequency for g_i. We draw 10,000 observations for group a and 20,000 for group b. We create the separable data by modifying the generative model described above, which does not generate separable data. Specifically, we replace each p(y = 1∣x) > 0.5 with p(y = 1∣x) = 1 and each p(y = 1∣x) < 0.5 with p(y = 1∣x) = 0, and remove the 40% of the data closest to the original decision boundary to ensure the classes are cleanly separable, as illustrated in Fig. 2A.

MIMIC-semi-synth

We generate semi-synthetic data using MIMIC-IV, a public dataset of real patient visits to a Boston-area hospital over the course of 2008–2018²⁷. We filter out ICD codes that appear 10 or fewer times, leaving 5544 unique ICD codes. Each feature vector x_i is a one-hot vector corresponding to the ICD codes assigned in a particular patient visit to the hospital. We generate true labels y based on a set of suspicious symptoms. Formally, this replaces Eq. (15) in our generative model with:

$${y}_{i} \sim \,{{\mbox{Bernoulli}}}\,(\sigma ({v}_{sym}^{T}{{{{\bf{x}}}}}_{{{{\bf{i}}}}})/\parallel {v}_{sym}\parallel )$$

(16)

where v_sym is a one-hot encoding of the suspicious symptoms and ${v}_{sym}^{T}{x}_{i}$ corresponds to the number of suspicious symptoms present during a hospital visit. Thus, the probability a patient has a medical condition is a logistic function of the number of suspicious symptoms. As before, we have ${s}_{i} \sim \,{{\mbox{Bernoulli}}}\,({c}_{{g}_{i}}{y}_{i})$.

In all experiments, we compute the relative prevalence for Black (group a) versus white (group b) patients since these are the largest race groups in MIMIC data. We filter the dataset for patients belonging to each group. However, our method can be applied to more than 2 groups, as described above. To assess how our method performs under diverse conditions, we experiment with selecting the suspicious symptoms v_sym in four different ways:

Common symptoms

We identify the 50 most common ICD codes in MIMIC-IV and randomly select 25 to be suspicious symptoms (described fully in the Supplement). Group a consists of 73,090 visits from Black patients (p(y = 1∣g = a) = 0.157), and group b consists of 305, 002 visits from White patients (p(y = 1∣g = b) = 0.185).

High relative prevalence symptoms

We filter out ICD codes that appear fewer than 50 times in each group and patients less than 18 years old. After ranking the ICD codes by relative prevalence—prevalence among visits by white patients, divided by prevalence among visits by Black patients—we select the top 10 ICD codes as our suspicious symptom set (described fully in the Supplement). Group a contains 14,618 visits from Black patients p(y = 1∣g = a) = 0.061), and group b contains 61,000 visits from white patients (p(y = 1∣g = b) = 0.098).

Correlated symptoms

We consider endometriosis, a widely under-diagnosed condition⁶⁶. We define our suspicious symptoms as the symptoms most highly associated with known endometriosis codes. We first identify a set of patients who receive any one of 10 gold-standard ICD endometriosis diagnosis codes (described fully in the Supplement). We then identify the ICD codes which are most highly associated with a gold-standard diagnosis of endometriosis: for each ICD code, we compute the ratio $\frac{\,{{\mbox{prevalence of ICD code among endometriosis patients}}}}{{{\mbox{prevalence of ICD code among all patients}}}\,}$. We define our suspicious symptoms as the 25 ICD codes with the highest value of this ratio, which includes known endometriosis symptoms such as “Excessive and frequent menstruation with regular cycle” and “Pelvic and perineal pain” (all codes are included in the Supplement). We do not include the 10 ICD codes used to determine the 25 suspicious symptoms in x. We filter for female patients because endometriosis is extremely rare among male patients⁶⁷, leaving 47,138 unique hospital visits from Black patients (p(y = 1∣g = a) = 0.0534) and 165,653 unique hospital visits from white patients (p(y = 1∣g = a) = 0.0495).

Recognized symptoms for IPV

Prior work has found that suspicious symptoms for IPV include head, neck, and facial injuries⁶⁸. The symptoms in this experiment consist of the 100 ICD codes corresponding to these injuries (described fully in the Supplement). We filter for female patients because the symptoms associated with IPV in male patients are not well understood³⁰. We also filter out patients less than 18 years old because it is difficult to distinguish between intimate partner violence and child abuse in minors. This results in a dataset with p(y = 1∣g = a) = 0.0541 (25,546 unique patient visits) and p(y = 1∣g = b) = 0.0568 (80,227 unique patient visits).

In Sections “MIMIC-IV ED” and “NEDS”, we describe the construction of the two non-synthetic datasets, MIMIC-IV and NEDS. In all these datasets, y is unknown, so we need only define the features x and known positive examples in which s = 1.

MIMIC-IV ED

Data filtering

MIMIC-IV contains two related databases: one representing diagnoses made in the hospital (which we will refer to as the hospital database) and one representing diagnoses made in the emergency department. There are slight inconsistencies between the two, as is to be expected; for example, one emergency department stay can be associated with multiple unique hospital admissions. We exclude 600 hospital admissions linked to multiple emergency department stays and exclude 59 emergency department stays associated with invalid hospital admissions. For emergency department stays that result in hospital admission, we include all diagnoses assigned in the emergency department or hospital. We also include patient visits that appear only in the hospital database but indicate admission through the emergency department via the “admission_location” field. We provide code to replicate these preprocessing steps.

We further filter for patients who are female and above 18. We do so because we are interested in the relative prevalence of intimate partner violence between subgroups of adult female patients. This leaves 293,297 individual hospital visits over 133,470 unique patients. For each demographic attribute we wish to analyze disparities over (ethnicity, insurance status, and marital status), we also filter out patients who are missing data for this attribute. This translates to 192,768 stays across marital statuses, 208,512 stays across ethnicities, and 108,948 stays across insurance statuses. We have significantly fewer stays in the insurance subgroups because we only have patients for whom the insurance status is known (i.e., Medicare and Medicaid recipients). We produce 5 randomized dataset splits, where we reserve 60% of the data for training, 20% for validation, and 20% for testing. Each patient appears in only one of these sets.

Defining features x

We represent each patient visit as a one-hot encoding of the ICD codes assigned. Concretely, 15,699 features represent each patient visit, where each feature corresponds to the presence or absence of one ICD code (across the ICD-9 and ICD-10 standards). Note that this is different from the semi-synthetic setup and we do not filter out codes that appeared fewer than 10 times. We do this because IPV itself is rare, and we do not want to exclude symptoms that are predictive of IPV and do not occur frequently.

Defining s = 1

To define examples where s = 1 (known positive examples), we use criteria for reported instances of intimate partner violence from prior work. The most specific code is E967.3, or ”Battering by an intimate partner”, drawn from the ICD-9 standard. Other codes include V6111, or ”Counseling for a victim of spousal or partner abuse”. The full code set can be found in Table S6. If a patient receives any one of the codes in the positive code set, the visit is deemed to be positively labeled for intimate partner violence.

Defining g

We define the groups over which we quantify disparities via demographic variables associated with each electronic health record. These include race/ethnicity (Black, white, Asian, Hispanic/Latino), insurance status (Medicare or Medicaid), and marital status (Legally Unmarried, Married, Divorced).

NEDS

The National Emergency Department Sample (NEDS) is the largest publicly available, all-payer database describing visits to hospital-owned emergency departments in the United States and is commonly used in studies of disease prevalence. In this work, we make use of NEDS 2019. The survey from this year produced a dataset containing 33.1 million visits, which represents the 143 million total visits occurring in hospital-owned EDs across the United States in 2019. To create nationally representative estimates, NEDS releases “discharge weights”, which allow the analyst to reweight estimates to represent the universe of emergency department visits. We follow this procedure to reweight our relative prevalence estimates.

Data filtering

As with MIMIC-IV, we include visits from patients who are female and above the age of 18. The resulting dataset contains 15,357,528 visits.

Defining features x

As before, we treat the ICD codes logged during a visit as the input features, as a proxy for the symptoms a patient presents with. The feature set consists of 19,710 ICD-10 codes (excluding those used to identify positive cases, as described in the next section), which we one-hot encode to create features for each ED visit.

Defining s = 1

We use the same criteria to identify positive cases as with MIMIC-IV: we consider a case to be labeled positive if it is associated with if it has any of the codes described in the Supplement.

Defining g

We define groups according to race/ethnicity groups, insurance status, income quartile, and urban/rural designation. The income quartile is calculated using the estimated median household income in the patient’s zipcode. In 2019, the first quartile corresponds to an estimated median household income between $0 and $48k, the second to $48k to $61k, the third to $61k–$82k, and the fourth to the remaining zip codes. The urban/rural designations are based on the population of the patient’s home county. From most to least rural, the four categories are 50k residents to 250k residents, 250k residents to 1 million residents, 1 million residents in a fringe metropolitan county, and 1 million residents in a central metropolitan county.

Baselines

Each of the baseline methods described below is designed to estimate the absolute prevalence. To obtain the relative prevalence, we apply each baseline to groups a and b individually to obtain estimates of the absolute prevalence in each group; we then divide the resulting quantities to produce an estimate of the relative prevalence. To provide consistent comparisons, we constrain each baseline to use the same function class as PURPLE. We do not compare to baselines in the epidemiology literature because they assume access to external information (e.g., diagnostic accuracy) that is often not available; we also do not consider work that places parametric assumptions on p(y = 1∣x)^69,70,71,72 because these assumptions will not hold in general.

• Negative: Assign all unlabeled examples a negative label. This approach replaces p(y = 1∣x) with p(s = 1∣x) and assumes no underreporting occurs. Past work refers to this model as a nontraditional classifier⁵⁷ (NTC). We use sklearn’s logistic regression implementation with no regularization and default settings for all other hyperparameters, trained with target s.

• KM2: Models the distribution of unlabeled examples as a mixture of the positive and negative distribution and estimates the proportion of positives using a kernel mean embedding approach⁶². This method is known to perform poorly on large datasets with many features⁷³. KM2 assumes that there exists a function that only selects positive examples.

• DEDPUL: Uses a non-traditional classifier to map each example to a predicted probability of diagnosis and performs mixture proportion estimation using the classifier’s outputs on the unlabeled examples⁷³. Specifically, the method applies heuristics to the estimated densities of the positive and unlabeled distribution.

• BBE: Identifies a small subset of positive examples using the outputs of an non-traditional classifier on the positive and unlabeled sample⁷⁴. The method uses this subset to infer the proportion of positive examples in the unlabeled sample.

• Oracle: Uses the true label y to estimate p(y = 1∣x). Importantly, this method cannot actually be applied in real data since y is unobserved, but it represents an upper bound on performance.