Introduction

Interatomic potentials (or force fields) are essential quantities for describing the mechanical properties of materials with sub-nanometer scale resolution. Many numerical methods such as Monte-Carlo or molecular dynamics (MD) simulations, widely used in statistical physics, materials science and soft-matter studies, rely on interatomic potentials1,2. In particular, MD simulations of large atomic structures are crucial for many different research fields3,4. In order to calculate the atomic energies and forces during the simulation, first-principle (or ab-initio) methods like density functional theory (DFT) can be applied5. DFT describes the necessary underlying quantum mechanical effects very accurately, but simulations based on DFT are limited to at most 1000 atoms and to picosecond timescales6,7,8. On larger spatial and temporal scales, however, the atomic interactions need to be treated classically by using an interatomic potential, which is either constructed in a data-driven way or is derived from physical assumptions and approximations.

In the last years, interatomic potentials based on machine-learning (ML) methods like neural networks have become more and more popular. They allow to perform highly efficient atomistic simulations with first-principles accuracy and therefore have gained huge interest among researchers9,10,11. In general, ML potentials are used to perform large-scale simulations of materials that are assumed to be in the electronic ground state, which is a reasonable approximation for many thermodynamical processes at low temperatures (i.e., much lower than the Fermi temperature). However, this assumption fails in the case of laser-excited materials.

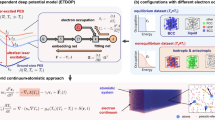
Ultrashort laser pulses with a pulse duration in the order of a few femtoseconds (1 fs = 10−15 s) are essential for many fields such as biological imaging12, surgery13, or material processing14. Among others, they are used for surface texturing with applications in the microelectronics and photovoltaic industry15. A femtosecond laser pulse primarily interacts with the electrons and leaves the ions almost unaffected, leading to an extreme non-equilibrium state of hot electrons at an increased temperature Te and “cold” ions (see Fig. 1a). The potential energy surface (PES) generated by the hot electrons differs significantly from the one resulting when electrons are at the ground state or very low temperatures. After the laser excitation, the electronic temperature decreases and equilibrates with the ionic temperature on a picosecond timescale due to the electron–phonon coupling. Therefore, interatomic potentials for simulations of laser-excited solids have to depend explicitly on the electronic temperature to account for both, changes in interatomic bonding and the electronic temperature decrease. Since standard ML potentials from the literature do not fulfill this requirement, they are not suitable for this specific task even if they are trained on a dataset generated at high Te. In the past, interatomic potentials with an explicit Te-dependency were only constructed empirically based on physical approximations16,17,18. Therefore, they lack the advantages of modern ML potentials like increased flexibility and, in particular, ab-initio accuracy.

Fig. 1: Modeling laser-excited materials with a Te-dependent neural network interatomic potential.
figure 1

a A femtosecond laser pulse excites the electrons of an atomic structure to high temperatures Te ≫ 300 K. For a few picoseconds, the ions remain cold until the energy starts to transfer from the electrons to the lattice due to electron–phonon coupling. b The Cartesian coordinates of the atoms are described by symmetry functions gi, which are passed to the neural network potential together with the electronic temperature Te. The network is evaluated individually for every atom in the structure and the results are summed to obtain the total cohesive energy Φcoh. c The atomic neural network in the case of two hidden layers. The input values are the Nsf symmetry function values for atom i and the electronic temperature Te. The network function fnn is also evaluated for gi = 0 and subtracted from the output value to obtain the atomic cohesive energy Φi.

Full size image

Highly accurate Te-dependent ML potentials could strongly increase our theoretical understanding of laser-excited materials. For example, they could be used to simulate ultrafast non-thermal phenomena like structural phase transitions19,20,21,22 and transient phonon effects23,24,25,26, which result from bond softening, bond hardening, or lattice instabilities27,28,29 caused by laser-induced changes to the PES. These effects occur within the first picoseconds after the laser excitation, when the electrons can still be treated as if their temperature was suddenly increased to a high constant value. On longer timescales, however, the Te-dependency of the interatomic potential becomes even more important because the electronic temperature cannot be assumed to be constant anymore due to the electron–phonon coupling. Only with Te-dependent interatomic potentials it can be possible to perform large- and ultralarge-scale MD simulations treating laser-induced bond changes and incoherent lattice heating via electron–phonon coupling on the same accuracy level30. Further utilizing the benefits of ML potentials could provide insights on interesting long-term effects like the spontaneous formation of laser-induced periodic surface structures31,32,33, which is still not fully understood.

In their first versions, early ML potentials based on neural networks could only be applied to small molecules due to the fast growth of the network size for larger systems and the challenging task of finding appropriate symmetric coordinates34,35,36,37. However, the introduction of atom-centered symmetry functions and the high-dimensional neural network architecture opened the possibility to handle arbitrarily large structures, in principal38,39. These kinds of ML potentials were shown to reach ab-initio accuracy for many different systems40,41,42 and in contrast to classical interatomic potentials, they do not require human experts to derive complex system-specific interaction terms.

Since the introduction of high-dimensional neural network potentials, several modifications to the model were suggested, e.g., extensions to multicomponent systems43,44, magnetic systems45, or the inclusion of non-local long-range interactions46,47,48. Furthermore, interatomic potentials based on other ML algorithms than neural networks were proposed, e.g., Gaussian approximation potentials49,50, spectral neighbor analysis potentials51,52, or moment tensor potentials53,54. Convolutional and graph neural networks have also been used to construct interatomic potentials55,56,57,58.

Despite these many modifications and extensions, ML potentials were still not able to describe laser-excited systems so far. In this work, we propose the first ML potential that includes a dependency on the electronic temperature Te and is therefore applicable to large-scale simulations of materials excited by femtosecond laser-pulses. Our model, which is based on the high-dimensional neural network potential, is exemplarily applied to silicon (Si) but the method is general and could easily be transferred to other materials. We show that our derived interatomic potential can describe many important physical properties of laser-excited and unexcited Si with ab-initio accuracy and furthermore, the successful application of the model in MD simulations involving more than 160,000 Si atoms is demonstrated in this work.

Results

Neural network potential for laser-excited silicon

We propose an interatomic potential that can be applied in MD simulations of laser-excited materials. Thereby, we describe the PES as a function Φ(r1, …, rN, Te) of the atomic positions ri and the electronic temperature Te. Furthermore, we consider a configuration with N identical atoms. The total potential energy Φ of this configuration can be split up into the total cohesive energy Φcoh and the Helmholtz free energy of the isolated atoms Φ0:

$$\Phi ({{{{{{{{\bf{r}}}}}}}}}_{1},\ldots ,{{{{{{{{\bf{r}}}}}}}}}_{N},{T}_{{{{{{{{\rm{e}}}}}}}}})={\Phi }_{{{{{{{{\rm{coh}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{1},\ldots ,{{{{{{{{\bf{r}}}}}}}}}_{N},{T}_{{{{{{{{\rm{e}}}}}}}}})+N\cdot {\Phi }_{0}({T}_{{{{{{{{\rm{e}}}}}}}}}).$$
(1)

We designed a ML model that predicts Φcoh from r1, …, rN, and Te and is able to learn this relationship from an ab-initio training dataset. As a useful example, we explicitly construct the model for laser-excited Si. In order to obtain the total potential energy Φ, we calculate Φ0(Te) using an existing polynomial model for Si from the literature (see “Methods”).

Our model for Φcoh is a Te-dependent neural network interatomic potential (Te-NNP). It is based on the high-dimensional neural network architecture introduced by Behler and Parrinello in 200738, in which the potential energy is treated as a sum of local atomic contributions. A feed-forward neural network is trained to predict the atomic energy from special symmetric coordinates describing the atomic environment. We extend this concept to the description of laser-excited systems by implementing a Te-dependency in the form of an additional input node to the neural network, which is depicted schematically in Fig. 1b (high-dimensional neural network architecture) and Fig. 1c (atomic neural network).

Our aim is to train the model to predict the cohesive energy and the atomic forces for structures occurring in large-scale MD simulations of laser-excited Si with ab-initio accuracy. Therefore, we train the Te-NNP on a specially designed dataset that consists of atomic configurations obtained from several ab-initio calculations of a small supercell containing a Si thin film. By choosing this geometry, we are not only taking into account bulk but also surface effects. Using Te-dependent DFT, we perform MD simulations of the thin film at different constant electronic temperatures from a wide range of values. Furthermore, the training dataset contains artificial compressions and expansions of the structure to also include atomic configurations with extreme local pressures and densities. For all calculations, the Si atoms are initialized in the diamond-like crystal structure.

In order to determine the models generalization capability and to prevent overfitting, we also monitor its accuracy on a distinct validation dataset. It contains similar ab-initio calculations carried out at intermediate Te’s between the Te-steps of the training set (see “Methods” for details on the training and validation set). Figure 2a shows the evolution of the training and validation set error Γ (see Eq. (10)) during the training process. Despite some small fluctuations, the validation set error does not increase during the training process, which would be an indicator for overfitting.

Fig. 2: Training curve and prediction errors.
figure 2

a The loss function Γ evaluated on the training and validation set during the training process. b The relative prediction errors γE and γF for the total cohesive energy and the atomic forces as a function of the electronic temperature Te averaged over all configurations occurring in the MD simulations from the training and validation set.

Full size image

Performance validation

As a first approach to validate the accuracy of the trained neural network interatomic potential, we analyze the relative prediction errors of the total cohesive energy and the atomic forces occurring during the MD simulations from the training and validation set as a function of the electronic temperature, as depicted in Fig. 2b. Thereby, we use the relative root-mean-square errors γE and γF, as defined in Eq. (10). The energy error is below 2% for Te < 25,000 K and only increases significantly for extremely high electronic temperatures far above the non-thermal melting threshold at Te = 17,052 K59. The relative prediction error for the atomic forces is between 8 and 12% at most temperatures and only increases at very low electronic temperatures as well as in the range slightly above the non-thermal melting threshold.

Although measuring the performance of the model in terms of the energy and forces errors is a reasonable approach, low prediction errors do not guarantee a physically meaningful description of the PES. Therefore, we also evaluate the models performance by calculating different atomic and electronic properties and comparing the results to ab-initio data in a qualitative way. First, we calculate the cohesive energy per atom as a function of the lattice parameter for different ideal crystal structures. We perform these calculations at various Te’s and on configurations similar to those in the training dataset (diamond-like structure) as well as on configurations not contained in the training dataset (sc, fcc, and bcc). The results are shown exemplarily for Te = 12,631 K in Fig. 3a (see Supplementary Fig. 1 for results at other electronic temperatures). For all considered electronic temperatures and ideal crystal structures, the cohesive energy curves are almost perfectly reproduced by the Te-NNP. Furthermore, the cohesive energies are correctly predicted to approach to zero for large interatomic distances. Note that these kind of structures are not included in the training dataset and that the correct modeling of the underlying physics is achieved by a special neural network architecture (see “Methods”).

Fig. 3: Physical properties reproduced by the Te-dependent neural network interatomic potential.
figure 3

a The Helmholtz free cohesive energy per atom at Te = 12,631 K as a function of the lattice parameter for different crystal structures. b The phonon band structure of bulk diamond Si at Te = 12,631 K. c The internal energy Ue of the electrons as a function of Te for bulk diamond Si. d The specific heat Ce of the electrons as a function of Te for bulk diamond Si. e The root-mean-square displacement (RMSD) of the Si atoms as a function of time after the laser excitation at Te = 12,631 K. f The root-mean-square displacement (RMSD) of the Si atoms as a function of time after the laser excitation at Te = 22,104 K. The width of the curves in (e) and (f) corresponds to twice the standard error of the mean over multiple simulation runs. For all figures, ab-initio results are shown in black, while results obtained with the Te-NNP are colored.

Full size image

Besides the cohesive energies, we also calculate the phonon band structure of bulk Si in the diamond-like crystal structure at various Te’s. Again, the ab-initio-results are reproduced with high accuracy, as can be seen in Fig. 3b for Te = 12,631 K (see Supplementary Fig. 2 for results at other electronic temperatures). Both the optical and acoustic phonon modes are well described. Furthermore, our model correctly predicts a bond softening for increasing electronic temperatures indicated by decreasing phonon frequencies. Note that the overall accuracy in the description of this property is significantly higher than that of most classical Te-dependent interatomic potentials for Si from the literature16,\17. Only the interatomic potential by Bauerhenne et al.18 achieves a comparable accuracy (see ref. 30 for an extensive comparison of literature models).

In order to test if the Te-NNP is also able to reproduce electronic properties, we further determine the internal energy Ue and the specific heat Ce of the electrons for bulk diamond Si using the thermodynamic relations

$${U}_{{{{{{{{\rm{e}}}}}}}}}=\Phi -{T}_{{{{{{{{\rm{e}}}}}}}}}\frac{\partial \Phi }{\partial {T}_{{{{{{{{\rm{e}}}}}}}}}},\quad {C}_{{{{{{{{\rm{e}}}}}}}}}=-{T}_{{{{{{{{\rm{e}}}}}}}}}\frac{{\partial }^{2}\Phi }{\partial {T}_{{{{{{{{\rm{e}}}}}}}}}^{2}}.$$
(2)

In Fig. 3c, d, these two properties are plotted against the electronic temperature. While the internal energy is almost perfectly reproduced, the deviations from the DFT results are slightly higher for the specific heat. Nevertheless, the overall description of this property is qualitatively correct and the Te-NNP is indeed capable of reproducing electronic properties, which is remarkable since the electronic temperature Te is the only information on the electrons that is passed to the model.

Next, we use the trained Te-NNP to perform MD simulations on laser-excited bulk Si at various electronic temperatures. Thereby, the Si atoms are initiated in the ideal diamond-like crystal structure and periodic boundary conditions are applied in all spatial directions. The root-mean-square displacement RMSD(t) of the Si atoms is shown as a function of time during the first picosecond after the laser excitation at Te = 12,631 K (Fig. 3) and Te = 22,104 K (Fig. 3f). The corresponding results at Te = 15,789 K and Te = 18,947 K are provided in Supplementary Fig. 3. The simulations are repeated several times and the width of the curves corresponds to twice the standard error of the mean over all simulation runs. For temperatures below the non-thermal melting threshold, the RMSD(t) oscillates and indicates phonon antisqueezing, while for higher temperatures, it increases monotonously and a non-thermal melting of the crystal structure can be observed. Both of these effects are reproduced correctly by the neural network interatomic potential.

Finally, we calculate the melting temperature of Si by simulating the coexistence of liquid and crystal using a simulation setup described in ref. 30. We determine the melting temperature

$${T}_{{{{{{{{\rm{m}}}}}}}}}(p)=(1263\pm 2)\,{{{{{{{\rm{K}}}}}}}}-(25\pm 2)\,{{{{{{{\rm{K}}}}}}}}\,{{{{{{{{\rm{GPa}}}}}}}}}^{-1}\times p$$
(3)

near zero pressure p. This value agrees with Tm(p) = (1300 ± 50) K − 58 K GPa−1 × p from DFT using the local density approximation (LDA)60. Thus, the Te-dependent neural network interatomic potential correctly reproduces the melting temperature given by the reference method used to generate its training data. Note that this value differs significantly from the experimental value Tm(p) = (1687 ± 5) K − 58 K GPa−1 × p61,62. However, this only affects the timescale for the recrystallization of the material at t > 100 ps after the laser-excitation. Nevertheless, we propose a possible approach to correct the melting temperature in the Discussion.

Application to large-scale molecular dynamics simulation

We perform large-scale MD simulations using our derived Te-dependent interatomic potential to demonstrate its practical applicability for systems that cannot be treated with DFT anymore. We consider a simulation cell containing a Si thin film with more than 160,000 atoms, which is more than 500 times the number of atoms contained in the supercell used for the training dataset. Furthermore, we insert two different kinds of spherically shaped surface impurities centered on the top layer of the thin film: A hill and a sink, each with a diameter of 2 nm. We simulate the effect of the laser excitation on these structures separately and compare the results for various pulse energies.

In addition to performing MD simulations on larger length scales, we also increase the simulation time to 10 ps. On this timescale, the energy is transferred from the electronic to the ionic system and thereby, Te decreases while the ionic temperature Ti increases. We explicitly consider the electron–phonon coupling in our simulations using an extended two-temperature model MD (TTM-MD) setup (see “Methods”). The method strictly requires a Te-dependent interatomic potential that provides a physically meaningful specific heat of the electrons with Ce ≥ 0. The Te-NNP is fulfilling this requirement as can be seen in Fig. 3d.

We find that the laser-excited thin film undergoes a period of expansion and shrinking, which is more pronounced for higher pulse energies. During the expansion, the thickness of the thin film increases by a rate between 1.9% for a pulse energy of 0.1 eV and 11.1% for 0.5 eV. It reaches its maximum value between 4 to 5 ps after the laser excitation. The time evolution of the thickness of the thin film is shown in Supplementary Fig. 4. After 10 ps, the surface of the thin film gets slightly coarser and for pulse energies greater than 0.3 eV, both kinds of surface impurities vanish. Figure 4 shows the surface of both structures at t = 0 ps, t = 5 ps, and t = 10 ps after a laser excitation with a pulse energy of 0.35 eV. The corresponding results at t = 10 ps after laser excitations with other pulse energies (0.1, 0.3, and 0.5 eV) are shown in Supplementary Fig. 5.

Fig. 4: Large-scale MD simulation using the Te-dependent neural network interatomic potential.
figure 4

The top layer of two different Si thin films (a–c Sink-like surface defect, d–f Hill-like surface defect) is shown at three times (0 ps, 5 ps, 10 ps) after a laser excitation with a pulse energy of 0.35 eV. Both surface defects vanish within 10 ps after the laser excitation. The MD simulations were performed using the Te-NNP on a supercell containing more than 160,000 atoms.

Full size image

Discussion

The Te-dependent neural network interatomic potential can be evaluated very efficiently compared to DFT and since it scales linearly with the number of atoms, it can be applied to arbitrary system sizes. At the same time, we demonstrated that it is able to achieve ab-initio accuracy both in MD simulations as well as in reproducing important physical properties like the phonon band structure or the specific heat of the electrons.

We also showed that the Te-dependent neural network interatomic potential is correctly reproducing the melting temperature of Si given by the underlying reference DFT method used to generate the training data. However, this value differs from the experimental result by more than 300 K. A possible approach to force the neural network interatomic potential to reproduce the experimental melting temperature would be to replace the training data for atomic configurations at an ionic temperature Ti near the melting temperature with data generated by a different method that is known to give a more accurate melting temperature, e.g., the random phase approximation63. Both methods could be combined in a weighted sum with Ti-dependent weights to ensure a smooth transition between them. An alternative approach would be to combine the different reference methods in a hierarchical fashion using a multi-fidelity approach64.

A transfer of our model to other laser-excited materials could be accomplished with only a few changes. First, the symmetry function parameters would have to be readjusted for the new dataset (see “Methods”). Second, an expression for the energy Φ0(Te) of the isolated atoms is required, but this could for example be done with a simple polynomial model fitted to easily generateable ab-initio data. Finally, our model could be directly adopted for the training on a sufficiently large and diverse ab-initio dataset of other laser-excited materials including varying electronic temperatures.

In conclusion, we want to emphasize that our model is easier to derive compared to existing empirically determined Te-dependent interatomic potentials due to its data-driven approach and furthermore, it is more flexible in terms of possible extensions. For example, in early stages of the laser excitation (10–100 fs) the electrons have not thermalized to a Fermi distribution yet. In order to better describe this situation, the Te-input-node could be replaced by multiple input nodes representing a suitable discretization of a non-equilibrium electron distribution. We seek to investigate this possibility in a future work.

Methods

T e-dependent high-dimensional neural network potential

Our model is a Te-dependent neural network interatomic potential (Te-NNP) based on the high-dimensional architecture introduced by Behler and Parrinello in 200738 and is depicted in Fig. 1b. It treats the cohesive energy Φcoh as a sum of atomic contributions Φi,

$${\Phi }_{{{{{{{{\rm{coh}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{1},\ldots ,{{{{{{{{\bf{r}}}}}}}}}_{N},{T}_{{{{{{{{\rm{e}}}}}}}}})=\mathop{\sum }\limits_{i=1}^{N}{\Phi }_{i}({{{{{{{{\bf{g}}}}}}}}}_{i}({{{{{{{{\bf{r}}}}}}}}}_{1},\ldots ,{{{{{{{{\bf{r}}}}}}}}}_{N}),{T}_{{{{{{{{\rm{e}}}}}}}}}).$$
(4)

Thereby, gi is a set of atom-centered symmetry functions describing the environment of atom i in terms of the atomic coordinates r1, …, rN.

A feed-forward neural network is trained to predict Φi for a single atom from the symmetry functions gi and the electronic temperature Te (see Fig. 1c). The same network, which from now on will be referred to as the atomic neural network, is evaluated individually for every atom in the structure and the results are summed up to obtain the total cohesive energy. Training the model can be carried out by comparing the network output with reference DFT data and applying gradient-based optimization. Once the network is trained, it can be applied to large-scale atomistic simulations at low computational costs compared to DFT.

To implement the dependency of Φcoh on the electronic temperature Te, we introduce an additional input node to the atomic neural network that represents Te. With this modification, it is possible to train the model on the physical relevant atomic configurations appearing in MD simulations at different Te’s. Thus, the network output Φi is a function of the symmetry functions gi describing the environment of atom i (they are, in turn, functions of the atomic positions ri) and the electronic temperature Te. For numerical stability, we scale these input values to the range [0, 1].

We use the standard mathematical expression of a feed-forward neural network, i.e., a sequence of matrix multiplications combined with a non-linear activation function fact. In most neural network applications, a trainable bias vector is also added to each hidden layer. Since the influence of the bias on the prediction accuracy is rather small, we increase the physical meaning of the model and its capability to describe physical properties like the cohesive energy per atom for different crystal structures by introducing a special bias architecture. It is based on the observation that all symmetry functions will be zero if every interatomic distance is greater than the cutoff radius. In this case of very large interatomic distances the cohesive energy per atom approaches to zero. However, biases generally lead to a non-zero network output in the case of only zeros as inputs. Therefore, we omit the biases of the hidden layers completely and only introduce a fixed non-trainable bias to the output layer to compensate for the non-zero Te-input-node. This bias corresponds to the network output evaluated for gi = 0 and is subtracted from the original output value. In the case of two hidden layers the atomic potential energy can thus be written as

$${\Phi }_{i}({{{{{{{{\bf{g}}}}}}}}}_{i},{T}_{{{{{{{{\rm{e}}}}}}}}})={f}_{{{{{{{{\rm{nn}}}}}}}}}({{{{{{{{\bf{g}}}}}}}}}_{i},{T}_{{{{{{{{\rm{e}}}}}}}}})-{f}_{{{{{{{{\rm{nn}}}}}}}}}({{{{{{{\bf{0}}}}}}}},{T}_{{{{{{{{\rm{e}}}}}}}}})$$
(5)

with

$${f}_{{{{{{{{\rm{nn}}}}}}}}}({{{{{{{{\bf{g}}}}}}}}}_{i},{T}_{{{{{{{{\rm{e}}}}}}}}}) = \, \mathop{\sum }\limits_{l=1}^{{N}_{{{{{{{{\rm{hid}}}}}}}}}^{(2)}}{w}_{l1}^{(23)}\cdot {f}_{{{{{{{{\rm{act}}}}}}}}}^{(2)}\left(\mathop{\sum }\limits_{k=1}^{{N}_{{{{{{{{\rm{hid}}}}}}}}}^{(1)}}{w}_{kl}^{(12)} \cdot {f}_{{{{{{{{\rm{act}}}}}}}}}^{(1)} \left(\mathop{\sum }\limits_{j=1}^{{N}_{{{{{{{{\rm{sf}}}}}}}}}}{w}_{jk}^{(01)}\cdot {g}_{i,j}+{w}_{{N}_{{{{{{{{\rm{sf}}}}}}}}}+1,k}^{(01)}\cdot {T}_{{{{{{{{\rm{e}}}}}}}}}\right)\right).$$
(6)

Here, \({N}_{{{{{{{{\rm{hid}}}}}}}}}^{(p)}\) is the number of nodes in the p-th layer, \({f}_{{{{{{{{\rm{act}}}}}}}}}^{(p)}\) is the non-linear activation function applied in the p-th layer, W(pq) is the weight matrix connecting layer p with layer q and Nsf is the number of symmetry functions.

In order to calculate the total potential energy of a system using Eq. (1) and to correctly reproduce the derivative of Φ with respect to Te, one also has to calculate the energy Φ0(Te) of the isolated atoms. In this work, we use an existing model for Si from the literature, which is based on polynomials18.

Atom-centered symmetry functions

We use the concept of atom-centered symmetry functions39 in order to describe the atomic environments in the form of input values for the atomic neural network. However, we propose a different functional form that can be calculated very efficiently because it does not involve the repeated expensive computation of the exponential function like commonly used functions10. The functions are inspired by the functional form of the Te-dependent interatomic potential for Si proposed by Bauerhenne et al.18. Our radial symmetry functions are constructed as sums of two-body terms to describe the radial environment of atom i and are defined by

$${g}_{i}^{{{{{{{{\rm{rad}}}}}}}}}=\mathop{\sum }\limits_{j=1}^{N}{f}_{{{{{{{{\rm{c}}}}}}}}}\left({R}_{ij},{\eta }^{{{{{{{{\rm{rad}}}}}}}}}{R}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{rad}}}}}}}}}\right),$$
(7)

where Rij is the distance from atom i to its j-th neighboring atom and fc(Rij, Rc) is the cutoff function controlling the atomic interaction range,

$${f}_{{{{{{{{\rm{c}}}}}}}}}({R}_{ij},{R}_{{{{{{{{\rm{c}}}}}}}}})=\left\{\begin{array}{ll}{\left(1-\frac{{R}_{ij}}{{R}_{{{{{{{{\rm{c}}}}}}}}}}\right)}^{2},\quad &{R}_{ij}\le {R}_{{{{{{{{\rm{c}}}}}}}}}\\ 0,\quad &{R}_{ij} \, > \, {R}_{{{{{{{{\rm{c}}}}}}}}}\end{array}\right..$$
(8)

Here, different values of ηrad with \({\eta }^{{{{{{{{\rm{rad}}}}}}}}}\in {\mathbb{R}},0 \, < \, {\eta }^{{{{{{{{\rm{rad}}}}}}}}}\le 1\) are used, which means that the function is evaluated for different cutoff radii \({R}_{{{{{{{{\rm{c}}}}}}}}}={\eta }^{{{{{{{{\rm{rad}}}}}}}}}{R}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{rad}}}}}}}}}\) up to a fixed maximum cutoff radius \({R}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{rad}}}}}}}}}\). Furthermore, we also take three-body interactions into account by using angular symmetry functions defined as

$${g}_{i}^{{{{{{{{\rm{ang}}}}}}}}} = {2}^{1-\zeta }\mathop{\sum }\limits_{{j,k\ne i}\atop {j < k}}^{{{{{{{{\rm{all}}}}}}}}}{\left(1+\lambda \cos {\theta }_{ijk}\right)}^{\zeta } \cdot {f}_{{{{{{{{\rm{c}}}}}}}}}({R}_{ij},{\eta }^{{{{{{{{\rm{ang}}}}}}}}}{R}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{ang}}}}}}}}})\cdot {f}_{{{{{{{{\rm{c}}}}}}}}}({R}_{ik},{\eta }^{{{{{{{{\rm{ang}}}}}}}}}{R}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{ang}}}}}}}}}),$$
(9)

where \(\zeta \in {\mathbb{N}}\) and λ = ±1. Moreover, \({\theta }_{ijk}={{{{{{{\rm{acos}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{ij}\cdot {{{{{{{{\bf{r}}}}}}}}}_{ik}/{R}_{ij}\cdot {R}_{ik})\) is the angle centered at atom i with respect to two neighboring atoms j and k. The function \({G}_{i}^{{{{{{{{\rm{ang}}}}}}}}}\) essentially corresponds to the functional form proposed in ref. 38, except that the radial parts are replaced by the cutoff function fc. In general, the cutoff radii \({\eta }^{{{{{{{{\rm{ang}}}}}}}}}{R}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{ang}}}}}}}}}\) used for the angular symmetry functions are chosen differently from those used for the radial symmetry functions because different interatomic distances may play a role for two- and three-body interactions.

The parameters ηrad, ηang, ζ, and λ in Eqs. (7) and (9) are varied to cover the whole atomic environment up to the maximum cutoff radii \({R}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{rad}}}}}}}}}\) and \({R}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{ang}}}}}}}}}\). The number Nsf of used symmetry functions differing in these parameters determines the resolution of the atomic environment description. The exact parameters we use in this work are summarized in Tables 1 and 2.

Table 1 Parameters of the radial symmetry functions.
Full size table
Table 2 Parameters of the angular symmetry functions.
Full size table

Note that the parameters of the symmetry functions have to be treated as hyperparameters which are specific to the material that is investigated and are not learned by the model during training. Therefore, they have to be adjusted when transferring the model to other materials. However, the space of possible solutions can be reduced by restricting the parameters ηrad and ηang to be equidistant. In this way, only the spacing between these parameters as well as the maximum cutoff radii \({R}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{rad}}}}}}}}}\) and \({R}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{ang}}}}}}}}}\) have to be optimized using standard hyperparameter optimization techniques. An alternative method to find the symmmetry function parameters is to minimize the linear correlation between a fixed number of symmetry functions evaluated on the training dataset. This technique is used in this study to find the ζ parameters for the angular symmetry functions.

Training and optimization

In this work, we use an atomic neural network with two hidden layers and \({N}_{{{{{{{{\rm{hid}}}}}}}}}^{(1)}={N}_{{{{{{{{\rm{hid}}}}}}}}}^{(2)}=50\). Furthermore, we use the tanh activation function after the first hidden layer and the Gaussian error linear unit (GELU)65 after the second hidden layer. Especially the choice of the activation functions strongly influences the quality of the reproduction of physical properties. For example, we find that using the exponential linear unit (ELU)66 results in anomalies in the cohesive energy curves at small lattice parameters.

The cost function for the gradient-based training process is based on the error function used in ref. 18 and is defined by

$$\Gamma = \frac{1}{2}\left({\gamma }_{{{{{{{{\rm{E}}}}}}}}}^{2}+{\gamma }_{{{{{{{{\rm{F}}}}}}}}}^{2}\right)\\ = \frac{1}{2}\cdot \left(\frac{{\sum }_{t}{\left({\Phi }_{{{{{{{{\rm{coh}}}}}}}}}^{(t)}-{E}^{(t)}\right)}^{2}}{{\sum }_{t}{\left({E}^{(t)}\right)}^{2}}+\frac{{\sum }_{t}{\sum }_{i}{\left\vert -{\nabla }_{{{{{{{{{\bf{r}}}}}}}}}_{i}^{(t)}}{\Phi }_{{{{{{{{\rm{coh}}}}}}}}}^{(t)}-{{{{{{{{\bf{F}}}}}}}}}_{i}^{(t)}\right\vert }^{2}}{{\sum }_{t}{\sum }_{i}{\left\vert {{{{{{{{\bf{F}}}}}}}}}_{i}^{(t)}\right\vert }^{2}}\right).$$
(10)

Here, E is the reference ab-initio total Helmholtz free cohesive energy and Fi is the ab-initio force acting on atom i. The particular form of this relative error function is selected to guarantee that the network learns to predict the energies and forces in both situations, near equilibrium as well as at high electronic temperatures, with similar relative accuracy despite strongly varying magnitudes of the predicted quantities. For one weight update, the cost function is evaluated as the mean over multiple training examples indexed by t within a batch of size Nbatch (which we set to 20). During one training epoch, the batches are selected randomly from the training set without repetition until the model has processed every example of the training set (minibatch learning). For this stochastic gradient-based optimization of the cost function we further use the Adam algorithm67 with the learning rate α = 0.001 and the exponential decay rates β1 = 0.9 and β2 = 0.999 for the first and second moment estimates. The neural network is trained for 50 epochs with an integrated early stopping mechanism which is activated when the validation set error does not decrease for ten epochs in a row. However, this condition was not fulfilled during our experiments.

Details on DFT calculations and MD simulations

All ab-initio calculations in this work, including those contained in the training dataset, are carried out using our in-house Te-dependent DFT program CHIVES (Code for Highly excIted Valence Electron Systems)7,68,69. CHIVES yields a very good agreement with experiment70 as well as established DFT codes, including Wien2k and ABINIT, and is more than 200 times faster than ABINIT at the same degree of accuracy71.

The dataset used to train the Te-NNP was originally generated in ref. 18 for the construction of a classical Te-dependent interatomic potential for laser-excited Si. It contains ab-initio calculations of a Si thin film at 316 K as well as at ten higher electronic temperatures ranging from 3158 to 31,578 K in steps of 3158 K ≈ 10 mHa. Further ab-initio calculations of the thin film at intermediate electronic temperatures from 1579 to 29,999 K in equally sized steps are used as the validation dataset.

At each electronic temperature in the training and validation dataset, three different types of ab-initio calculations are performed:

  1. 1.

    MD simulation: The laser-induced dynamics are simulated by suddenly increasing Te from room temperature to a constant value. The duration of the MD simulations is set to 1 ps with a step size of 2 fs resulting in 501 different thin film configurations with corresponding energies and forces for each electronic temperature.

  2. 2.

    Artificial compression: The Si thin film is compressed stepwise and the corresponding energies and forces are calculated to also include atomic configurations with high local atomic densities in the training dataset, which are likely to occur after a laser-excitation. In this way, 25 additional data points are generated for each electronic temperature.

  3. 3.

    Artificial expansion: Since laser-excitations can also lead to high local negative pressures with decreased local atomic densities, mechanical expansions of the thin film are simulated and the corresponding energies and forces are calculated. In this way, 501 data points are added to the dataset for all Te < 25,000 K. For higher temperatures, the thin film is already naturally expanding during the MD simulation.

All in all, both the training and the validation dataset contain more than 9000 different atomic configurations of the thin film with corresponding labels for the cohesive energy as well as the three force components for each atom. We decided to use a comparatively small percentage of the total available data for training to emphasize the data efficiency of our model.

The thin film used in this study has a thickness of 5.3 nm and consists of 320 atoms. The simulation supercell is constructed by arranging 2 × 2 × 10 conventional unit cells. Since CHIVES uses periodic boundary conditions in all spatial directions, a vacuum is inserted on top of the thin film by doubling the supercell size in z-direction in order to simulate surface effects. The Si atoms are prepared in the ideal diamond-like crystal structure and initialized to room temperature using an Andersen thermostat72.

Among others, the model performance is evaluated by comparing the atomic root-mean-square displacement during MD simulations of bulk Si with results from ab-initio calculations (see Fig. 3e, f). Note that these configurations are not contained in the training or validation dataset. For the bulk MD simulations at Te = 12,631 K and Te = 15,789 K, we use a simulation cell containing 640 atoms in total and consisting of 4 × 4 × 5 conventional unit cells. We repeat the simulation 10 times. For Te = 18,947 K and Te = 22,104 K, the simulation cell contains 288 atoms (3 × 3 × 4 conventional unit cells) and we repeat the simulation 40 times. The simulation duration and step size is chosen similarly to the ab-initio calculations of the thin film. The bulk MD simulations are first performed using CHIVES and then repeated with the Te-NNP using the same initializations.

Details on large-scale MD simulations

The large-scale MD simulations are carried out on a simulation cell containing a Si thin film with a thickness of 29.7 nm. It is constructed by arranging 19 × 19 × 56 conventional unit cells. Again, in order to simulate surface effects despite of periodic boundary conditions, we further insert a vacuum of 50 nm on top of and below the thin film. The surface impurities are spherically shaped and both have a diameter of 2 nm. The exact number of atoms contained in the simulation cells are 161,836 (hill) and 161,633 (sink). We perform MD simulations of the laser excitation at various pulse energies in the range from 0.1 to 0.5 eV with a step size of 0.05 eV. The simulation duration is set to 10 ps with a step size of 1 fs.

As described previously, the electron–phonon coupling has to be taken into account if the simulation time exceeds a few picoseconds. In this case, the electronic temperature cannot be treated as constant anymore. Therefore, we perform the MD simulations in the frame of the two-temperature model (TTM-MD)73 as formulated by Ivanov and Zhigilei74. In this combined atomistic-continuum approach, the electrons with their individual temperature Te are treated in a continuum, while the ions are modeled by a classical ground state interatomic potential. Furthermore, the electron–phonon coupling is included by performing a velocity scaling. However, since we are using a Te-dependent interatomic potential to also take non-thermal effects into account, we deploy the extended MD simulation setup introduced by Bauerhenne30, which includes the electron–phonon coupling as well as the usage of a Te-dependent interatomic potential. Thereby, we use the electron–phonon coupling constant for Si from ref. 75.

The TTM-MD scheme has been shown to yield an accurate description of laser-induced mechanical relaxation processes in materials leading to spallation, ablation, formation of nanoparticles, and nanostructuring of surfaces and thin films76,77,78,79.