Introduction

The transformation from a rapid prototyping tool to a technique for the large-scale production of functional parts has always been a goal of the metal additive manufacturing (AM) industry. Achieving its promised higher productivity is critical for AM technologies, especially laser powder bed fusion (L-PBF), to compete with the conventional manufacturing methods in many industrial sectors1,2. With the release of the multi-laser powder bed fusion systems3,4, the application of the economic kW class fiber lasers5,6,7, and the active development of the beam shaping technologies8,9,10,11 and scan path optimization algorithms12,13, the AM industry is making significant progress towards increased productivity. The standard linear scan strategy with a Gaussian beam profile has been extensively studied in L-PBF for the last decade14,15,16,17. It does offer a reasonably extensive process window while handling the nominal levels of laser power and scan speed, i.e., usually below 500 W and below 1500 mm s−1, 18,19; however, it has already shown its limitations under certain conditions. For example, it often fails to control porosity formation or bead-up due to the high peak fluence at the center of a gaussian beam profile at power and speed levels exceeding the nominal range. High-speed beam oscillation offers an attractive method to implement a hierarchical delivery of laser energy both spatially and temporally to unlock both increased productivity, and through melt-pool shaping, deliver additional controls over the as-built microstructure to benefit the AM part quality.

Laser beam oscillation itself can be a stand-alone technique to mitigate defect content while complementing the aforementioned techniques for build rate improvement. It has found utility in laser welding, particularly for joining dissimilar metals. As far back as the 1990s, Rubben et al.20 showed the benefits of using an oscillating laser in the production of tailored blanks. Kuryntsev & Gilmutdinov21 and Yuce22 both demonstrated that laser oscillation can heal defects formed at the first welding pass and bridge larger gaps, which are essential to applications with imperfect faying interfaces. Hao et al.23,24 tested a wide range of oscillation frequencies from 20 to 1000 Hz on dissimilar steel systems to reveal the melt pool shape and melt track topology. Shah et al.25 showed that a circular oscillation pattern at 1 kHz produced a wider heat dissipation area and improved penetration depth into Mg-Ni-Al joints mitigating the formation of an Al-rich brittle fusion zone. Wang et al.26 compared a few beam oscillation patterns at 20–30 Hz and concluded that the circular pattern promoted the formation of finer and more equiaxed grains through a diminished thermal gradient and interrupted fluid flow. The finer equiaxed grains resulted in better ductility of the joints. Jiang et al.27 made similar observations about grain refinement in an Invar alloy at a laser oscillation frequency of up to 80 Hz.

Despite the aforementioned advantages of beam oscillation, these prior studies have focused on laser welding, which necessitated frequencies (up to 2 kHz) due to the limited linear scan speed. By contrast, the applicable frequencies in L-PBF must be significantly higher because of the faster linear scan speeds. The high-speed manipulation of laser beams posed challenges associated with overcoming the inertia of scan mirrors. However, with the development of piezoelectric actuated mirrors, the multi-kHz manipulation of lasers can now be applied in L-PBF to realize the benefits already enjoyed in laser welding. To the best of our knowledge, our study is the very first attempt in the field to reveal the spatiotemporal evolutions of keyholes under a kHz laser oscillation mode in an emulated L-PBF setup by utilizing a synchrotron-based in-situ X-ray imaging technique. The observations are compared against a multiphysics model to validate our understanding of the keyhole dynamics and offer insights into the potential for melt pool shape control.

Results and discussion

Dynamics of the oscillating keyhole

In contrast to the steady-state linear scan strategy, the oscillating laser strategy is a dynamic process which operates at continuously and periodically varying thermal conditions. Each of the four key positions on an oscillation unit, as shown in Fig. 1, represents a different thermal condition and, thus, a different melting response of the material. To date the dynamics of oscillating keyholes are difficult to capture, while most of the available understanding in the field derives from metallographic characterization or top-down observation25,27,28. Here, dynamic X-ray radiography (DXR) offers a unique capability for visualizing the spatiotemporal evolution of an oscillating keyhole.

Fig. 1: Laser oscillation schematic.
figure 1

A schematic of a circular oscillation superimposed on a linear laser scan path highlighting the key dimensions and positions during the periodic laser movement.

Full size image

Figure 2a shows the net result of the linear and circular oscillation at 400 mm s−1 linear scan speed and 0.12 mm circular oscillation diameter. The oscillation units were slightly distorted by the linear scan vector to form an oval shape. As the scan speed increases, both the remelting and the number of oscillation units within a constant path should decrease. Instead of a constant speed, the transient speed of the laser oscillation can be described by a continuous and periodic wave function, as shown in Fig. 2b. Given that the oscillating frequency is constant, the amplitude (blue arrows) and the mean (red arrow) of the transient speed function correlate linearly with the linear scan speed and the oscillation unit diameter, respectively, as shown in Fig. 2d.

Fig. 2: Laser oscillation path and quantification.
figure 2

a Laser scan path, b calculated transient speed, and c calculated transient speed and experimental keyhole depth profile of an oscillation cycle between 3.28 and 3.44 ms of an experiment with process parameters of 400 W, 400 mm s−1 linear scan speed, and 0.12 mm circular oscillation diameter. Note that the corresponding DXR video frames can be found in Fig. 3a. The blue and red arrows in b highlight the response of the transient speed profile to the increasing linear scan speed and the increasing oscillation diameter, which is also summarized in d.

Full size image

Figure 2c overlays a segment of the transient speed profile over the corresponding keyhole depth profile to show that the occurrences of the deepest and the shallowest keyholes are not synchronous with the minimum and maximum transient speeds. The depth of an oscillating keyhole is controlled by several other factors together with the transient speed, which is often the sole factor in a linear scan given a constant power. This implies that introducing laser oscillation is not equivalent to reducing energy density by increasing linear laser speed. The fluid flow, the laser absorption, and the pre-heat condition at the different positions of an oscillation unit (Fig. 1) should have critical impacts on the keyhole morphology.

Figure 3a shows a series of exemplar radiographs for process parameters of 400 mm s−1 linear scan speed and 0.12 mm circular oscillation diameter. Figure 3c shows a comparative fluctuating keyhole during processing without circular oscillation resulting in the formation of a keyhole pore. Given the same laser power and speed, it is rather easy to distinguish the differing responses to laser oscillation from those to the conventional strategy. As evident in the depth profiles in Fig. 3e, with no oscillation, the keyhole depth exhibited a smaller short-range variation, while the oscillating keyhole resulted in up to 125 µm difference between the deepest and the shallowest conditions within the same oscillation unit. Owing to the higher transient laser speed, the average keyhole depth in the oscillation experiment (99 ± 39 µm) is significantly shallower than its straight counterpart (267 ± 28 µm). The depth profiles of the simulated keyholes show reasonable agreement with the experimental data, especially in the absence of oscillation where the average keyhole depth is 284 ± 7 µm. In the experiment, a few instances of keyhole pore formation, which resulted in outliers in the depth profile, contributed to the larger depth variation. No keyhole pore formed in the simulation, although the FaSTLaB code can simulate such events. Some protrusions were found within the keyhole, as shown in Fig. 3d. They are often considered as precursors for the formation of keyhole pores29.

Fig. 3: Comparison of an oscillating keyhole and a non-oscillating keyhole.
figure 3

DXR video frames reveal the keyhole geometries in the experiments and the corresponding simulations at 400 W laser power and 400 mm s−1 laser scan speed with a, b 0.12 mm circular oscillation diameter and c, d no oscillation. Note that the timestamp at each frame is the accumulated time since the laser was triggered. The sequences in a, b are also labeled with the respective positions, A, B, C, D, of an oscillation unit. The green color (no temperature dependence) on the sample indicates the melted/solidified part of the track and the green color in the keyhole cavity represents the traced rays. The corresponding keyhole depth profiles are shown in e and the corresponding laser absorption profiles for both the simulated oscillation and linear cases calculated from the traced rays are shown in f. (See Supplementary Movies 01–04.).

Full size image

In an oscillating melt pool, the local pre-heat conditions at the point of laser-matter interaction vary continuously throughout the oscillation unit, as highlighted in Fig. 1. The keyhole fluctuation can be visualized in Fig. 3a where the sequence started at position A (3.28 ms) then passed through positions B, C, and D at 3.32, 3.36, and 3.40 ms. At position C, the laser traverses through the hotter underlying material, which may still be molten from the previous pass. Conversely, the underlying material at position A is cooler because of being further away from the active melt pool. The transient laser speeds are identical at the two positions where the scan vector of the oscillation unit is normal to the linear scan direction. As shown in Fig. 3e, the depth evolution curve corresponding to the case in Fig. 3a suggests that the keyhole penetrated >100 µm deep at position C (3.36 ms) thanks to the higher pre-heat. The simulation captured the keyhole fluctuation showing an average keyhole depth of 146 ± 22 µm. Better agreement occurred at position C (3.36 ms), where the keyhole was at its deepest; but at position A (3.28 ms), the simulated keyhole is deeper by around 50 µm. Since the experiments were performed on thin plates, we speculate that the edge effect might cause this discrepancy by limiting the fluid flow and thermal diffusion along the X-ray direction.

At positions B and D, the melt pool depths are similar, although the difference in transient speeds is maximum as the oscillation vectors are opposite to each other and also parallel to the linear scan vector. This implies that the pre-heat condition affects the keyhole depth more than the transient speed. However, the keyhole shape was different at these two positions, which was confirmed in both the experiment and the simulation. A protrusion formed on the opposite side walls of the keyhole due to the opposite oscillation vectors (see 3.89 vs. 3.93 ms in Fig. 3b).

As shown in Fig. 3f, the oscillation and the linear case display distinct laser absorption patterns. The linear case has higher absorptions at around 70% with a shorter fluctuation range which is consistent with the deeper keyhole observed; by contrast, the laser absorptivity varies with the oscillation at a longer range and is correlated with the transient laser speed with a phase shift. Interestingly, the absorption profile is delayed with respect to the transient speed profile by ~50 µs (~0.3 of an oscillation unit, 0.56\({{{{{\rm{\pi }}}}}}\)), i.e., the minimum absorption is delayed with respect to the maximum transient speed. This agrees with the mismatch between the experimental keyhole depth profile and the measured laser transient speeds shown in Fig. 2c and suggests that the laser absorptivity is mostly driven by the keyhole morphology. We also found that the phase shift is process parameters and material properties dependent. Further investigations on the phase shift will be carried out in the future, including experimental validations of the model.

Chevron pattern formation

Many studies have reported the observations of the chevron pattern on solidified melt tracks. The pattern contains information about the cooling length and the geometry of the melt pool, which are dictated in turn by the laser processing parameters30. In a linear scan, the appearance of the chevron pattern is often dense, with a lack of periodicity, as shown in Fig. 4d; however, with an oscillating laser, as shown in Fig. 4b, c, the chevron units showed long-range patterns, which were also observed in the DXR experiments and confirmed by the simulations. This link is further evidenced by the fact that the number of chevron units matches the number of oscillation cycles. The two events were synchronized by the surface swelling caused by the keyhole movement, which was observed experimentally, Fig. 3a. Figure 4a shows a complete sequence of the formation of a surface swelling wave highlighted in orange. The sequence started at 7.56 ms when was right before the laser reached position C of the oscillation unit. The hotter liquid gained backward momentum here as the laser had traveled only from position B to position C. At 7.58 ms, the surface swelling wave quickly built up since the hotter fluid met the cooler recoil fluid from the tail wall of the melt pool induced by the previous oscillation. Meanwhile, a valley (the depletion of the molten metal as a manifestation of the forward-moving recoil fluid) formed near the tail of the melt pool and caused local cool down, which accelerated solidification. Figure 4b, e quantified this phenomenon by tracking the distances between the reference line and the melt pool features. As the peak of the swelling wave traveled backward, the tail of the melt pool moved further away from the reference line suggesting the formation of a chevron unit. As shown in Fig. 4e, the formation of the new chevron unit was completed at 7.64 ms and for the second half of the oscillation unit, i.e., from position A to position C, the solidification front only advanced a much shorter distance.

Fig. 4: The formation of a chevron pattern.
figure 4

The centerline cross-sectional views of a simulated oscillating melt track (400 W laser power and 400 mm s−1 laser scan speed with 0.12 mm circular oscillation diameter) in a show the formation of the surface swelling, which is highlighted in orange and the corresponding top-down views in b show the formation a chevron unit. A comparison in d shows a no-oscillation case with the same laser parameters. The optical image in c provides an example of the chevron pattern on a DXR melt track. The plot in e summarizes the relative positions of the peak of the surface swelling and the melt pool tail with respect to the dashed reference line. (See Supplementary Movie 04).

Full size image

One of the potential benefits of an oscillating laser is to control the shape of the melt pool. Comparing Fig. 4b–d, the oscillating beam reduced the length-to-width ratio of the melt pool at the same laser power and speed. Moreover, the unique chevron pattern also implies that the laser oscillation could introduce periodicity into the solidification process. This unique property of the laser oscillation may have potential applications in controlling microstructural/surface texture and enabling different scan strategies.

Keyhole depth analysis

The welding experiments surveyed three laser powers 300, 400, and 500 W. At each power level, we tested five circular oscillation diameters (0, 0.09, 0.12, 0.18, and 0.24 mm) and six linear scan speeds (0.2, 0.4, 0.6, 0.8, 1, and 1.2 m s−1) resulting in a total of 90 parameter sets as shown in Table 1. Figure 5 summarizes the average keyhole depth and the standard deviation at each parameter set which were extracted from the DXR videos. The average keyhole depth is strongly correlated with the circular oscillation diameter and the laser scan speed, which have linear relationships with the mean and the amplitude of the transient speed profile, as shown in Fig. 2d. The keyhole dimensions follow the same trend across all three laser powers, i.e., depth decreased with a larger oscillation diameter and a faster scan speed. This is reasonable given that the average keyhole depth is mainly controlled by the energy density16. Faster laser scan speed leads to lower energy density, thus, smaller average keyhole depth. As shown in Fig. 5, the correlation between the keyhole depth and the variation of the transient speed is non-linear. At the same power and oscillation diameter, the keyhole shrank drastically as the laser scan speed increased from 0.2 m s−1 but plateaued after 0.6 m s−1. The transition from the keyhole to the conduction melting mode resulted in different depth responses to the change in the laser condition. By contrast, the effects of the oscillation could be more subtle. Increasing the oscillation diameter distributes the same amount of laser energy over a wider area, which in turn reduces the laser energy density received by the top sample surface and results in a shallower keyhole. The oscillation strategy achieves similar impacts as beam defocusing or annular beam shaping but in a dynamic manner and without the need for complex diffractive optical elements. The standard deviations of the keyhole depths shown in Fig. 5d–f are indicators of keyhole stability. When excluding the linear scan cases, an increased oscillation diameter generally decreased the fluctuation of the keyholes. Note that the longer-range periodic fluctuation, primarily due to the different depths between position A and position C, is the major contributor to the larger deviations. Interestingly, as the oscillation diameter continues to increase, we start to observe that the standard deviations drop below the nominal levels of the corresponding linear scans, i.e., the stochastic fluctuations. That said, laser oscillation has the potential to compete with the conventional linear strategy to further reduce keyhole instability in an appropriate parameter space.

Table 1 Laser oscillation parameters used in the DXR experiments.
Full size table
Fig. 5: Summary of keyhole dimension and fluctuation.
figure 5

The plots of keyhole depth versus circular oscillation diameter at laser powers of 300, 400, and 500 W where a–c show the average values of keyhole depth and d–f show the corresponding standard deviations. Note that the arrows indicate the corresponding keyhole depth profiles, which were converted to frequency spectrums using the fast Fourier transform shown in g.

Full size image

Figure 5g provides examples of the frequency spectrums in the Fourier space of the keyhole depth profiles for four different oscillation conditions (oscillation diameter = 0, 0.09, 0.12, and 0.18 mm) under the same laser power (400 W) and speed (0.2 m s−1). Note that all three oscillation cases present a characteristic peak at around 5.5 kHz, which corresponds to the periodic keyhole fluctuation induced by the laser oscillation. The intensity of the peak for 0.18 mm oscillation diameter is weaker than those of the other two oscillation cases mainly due to the reduction of the energy density as the scan path was spread out. Oscillating at 0.18 mm resulted in a melt pool that was constantly switching between the keyhole and the conduction melting mode. Therefore, the difference between the maximum and the minimum keyhole depths is smaller and this translates to the weaker peak intensity at 5.5 kHz in the Fourier space. Furthermore, as suggested by the corresponding average keyhole depth and variation indicated by the arrows at 0.18 mm oscillation diameter shown in Fig. 5b, e, the keyhole depth could approach zero at the minimum of an oscillation unit. A single oscillation unit could be registered as two in the frequency analysis; thus, a peak appears at around 11 kHz, which is double the characteristic frequency. By contrast, the linear scan case resulted in no characteristic pattern but higher intensities across the whole frequency spectrum (except at 5.5 kHz) compared with the oscillation cases. The laser oscillation frequency directly reflects itself in the keyhole depth fluctuation while suppressing other frequencies which are stronger in the linear scan case. This observation suggests that laser oscillation may potentially be used to regulate keyhole fluctuation once the mechanisms are fully understood.

To elaborate further, Fig. 6 shows two groups of DXR series, which were collected at 400 W laser power and 0.2 m s−1 laser scan speed. The top series captures the evolution of the keyhole shape for the linear scan and the bottom one shows the keyhole evolution for the circular oscillation with a diameter of 0.12 mm. As shown in Fig. 5e, at 400 W and 0.2 m s−1, a reduction in the standard deviation of keyhole depth was achieved by adding the laser oscillation. The top DXR series highlights the more severe keyhole fluctuation seen in the linear scan compared with their oscillation counterparts. The oscillation series sampled keyholes at many positions with respect to a single oscillation unit; yet, the fluctuation of the keyhole depths appears to be less even when the longer-range fluctuation was present. Additionally, the linear scan resulted in many keyhole pores which interact dynamically with the keyhole and contribute to the depth deviation. We believe that this reduction in the formation of keyhole pores might be facilitated by the reduction in the keyhole instability introduced by laser oscillation.

Fig. 6: Keyhole porosity mitigation due to laser oscillation.
figure 6

DXR images capture the keyhole depth evolution. The top series a shows the keyhole evolution in the case of linear scan and the bottom series b shows the corresponding case with a circular oscillation diameter of 0.12 mm. Both scans used 400 W laser power and 0.2 m s−1 scan speed. Note the timestamp shows the elapsed time since the laser was triggered. (See Supplementary Movies 05, 06.).

Full size image

Five processing conditions were modeled in our simulation, for which the parameters are shown in Table 1. These include two linear scan cases and three oscillating cases. As a quick validation of the simulations, Fig. 7 compares the maximum keyhole depths from the experiments with those from the simulations. There is good agreement between the simulations and the experiments based on the datapoints being close to the diagonal reference line. This highlights the ability of the model to capture the complex physics in an oscillating melt pool and suggests that more in-depth studies of the laser oscillation-induced fluid flow will be feasible in the future.

Fig. 7: Keyhole morphology comparison between the simulations and the experiments.
figure 7

Comparison of the experiments and the simulations for the maximum keyhole depth along with the corresponding keyhole images with 150 µm scale bars. Note that \(P\) is the laser power, \(V\) is the linear scan speed, and \(D\) is the circular oscillation diameter. (See Supplementary Movies 01–04, 07–12.).

Full size image

Porosity reduction

The DXR videos also provide valuable insights into porosity formation, as the two examples in Fig. 8 show. The main finding is that laser oscillation can greatly increase the threshold for the onset of keyhole porosity. Figure 8a shows the post-solidification fusion zones of four different welds processed by the same laser power and speed, but different oscillation settings. The linear scan in Fig. 8a resulted in a large cluster of keyhole pores. As the oscillation diameter increased, even the smallest diameter (\(D\) = 0.09 mm) eliminated all the pores. One possible reason is that laser oscillation simply decreased the laser fluence impinging on the sample top surface and thus contributed to the occurrence of a less violent melt pool during solidification, which in turn reduced the formation of keyhole porosity. The linear scan case has the highest energy density (12.5 J mm−2) among the four. Laser oscillation reduced the energy density down to 8 J mm−2 at 0.09 mm diameter, 7.14 J mm−2 at 0.12 mm diameter, and 5.88 J mm−2 at 0.18 mm diameter. Note that the energy density was derived from \(\frac{P}{{vd}}\) where \(P\) is the laser power, \(v\) is the laser linear scan speed, and \(d\) is the prescribed scan path width, i.e., laser spot size plus oscillation diameter.

Fig. 8: X-ray images of solidified melt tracks.
figure 8

The DXR images of the post-solidified melt track show the porosity reduction induced by a increasing the laser oscillation from 0 to 0.18 mm at laser power of 400 W and speed of 0.2 m s−1 and b introducing laser oscillation to maintain similar energy densities. The red arrows highlight the pores caused by the unstable keyhole.

Full size image

To further investigate, one DXR result for the linear scan case at 400 W and 0.4 m s−1 was chosen as the baseline to compare with two other oscillating cases of the higher energy densities shown in Fig. 8b. Porosity only occurred in the no-oscillating case despite the higher energy densities used in the other two oscillating cases. That said, the laser energy density is only one of many critical factors that control the formation of keyhole porosity. Here, the results emphasize the importance of the keyhole/melt pool shape. We speculate that the formation of keyhole porosity is influenced by (1) keyhole shape, as the keyholes with higher aspect ratios tend to incur keyhole collapse and pore separation; (2) keyhole depth, which dictates the initial position and the mean escape path length of the keyhole pores; (3) melt pool length, which affects the average available escape time31,32. In terms of suppressing keyhole porosity, the oscillating keyhole is more stable than its linear counterpart because it has a more equiaxed morphology and resides in a larger molten volume. Additionally, the formation of keyhole porosity depends on several other factors, such as fluid flow and thermal distribution, which determine the force equilibrium and the mobility of a pore. Involving laser oscillation in welding inevitably changes all the factors mentioned above.

Conclusions

In this work, we revealed the keyhole dynamics of the oscillating scan strategy using a synchrotron-based X-ray operando technique and a Lattice Boltzmann multiphysics model. The oscillating keyhole displayed unique continuous and periodic fluctuations when compared with the conventional linear scan. These intrinsic fluctuations are mainly controlled by the underlying temperature of the point of laser-matter interaction and the laser transient speed. Laser oscillation reduced the keyhole depth by distributing laser energy over a wider area. Meanwhile, the oscillating strategy can also control the keyhole instability as the larger oscillation unit promotes the formation of a steady-state keyhole which maintains similar depths at the minimum and maximum. Both the experiments and the simulations linked the solidification sequence of the chevron pattern on the bead surface to the laser oscillation movements; the oscillating cycle was also found to be responsible for the formation of this distinctive periodic pattern on the melt track surface.

Similarly, laser oscillation can increase the threshold for the onset of keyhole porosity. It suppressed the keyhole porosity at energy densities which could cause pore formation when added to a linear scan. A complete explanation for the reduction in keyhole porosity remains to be determined since this phenomenon could be affected by many factors. Adding laser oscillation inevitably changes the fluid dynamics, the thermal distribution, and the keyhole instability, which are investigated by our ongoing studies. However, the shallower and more persistent oscillating melt pool can certainly reduce the probability of pore entrapment. The oscillating strategy shows great promise in increasing productivity and melt pool shape control, which can be a good future direction to pursue.

Methods

Dynamic X-ray radiography

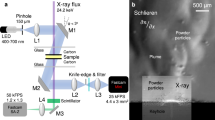
Multi-kHz DXR is a characterization technique underpinned by large X-ray flux afforded by synchrotron radiation sources. The L-PBF process replicator used in this work was developed at the 32-ID-B beamline of advanced photon source (APS) at Argonne National Laboratory33,34. APS provides high-energy X-rays that can penetrate thick metallic samples and therefore enables imaging dynamic processes in optically opaque metal samples with high temporal and spatial fidelity. It is an effective tool for operando analysis of the melting and solidification processes in laser oscillation experiments.

The specimen was placed in an argon atmosphere (1 atm) and kept at room temperature. During the experiment, a ytterbium fiber laser (IPG YLR-500-AC, IPG Photonics, Oxford, USA, wavelength of 1070 nm, maximum output power of 540 W) is coupled to a GE proprietary fast scanning mirror (FSM) module35,36 at the upstream of a galvo laser scanner (IntelliSCANde 30, SCANLAB GmbH, Puchheim, Germany) with a 340 mm f-Theta objective lens focused at the sample top surface. The optical output of the FSM, which operated at 5.5 kHz, and the conventional scan optics enabled a circular oscillation to be superimposed on a linear scan with a focused spot size of 160 µm. Meanwhile, the X-ray beam penetrated the sample orthogonal to the laser and was then imaged at a frame rate of 50 kHz by a high-speed camera downstream (SA-Z, Photron Inc., Japan) via a LuAG:Ce scintillator (100 μm thickness). The intensity of the transmitted X-rays varies inversely with the average local density of the sample according to the Beer–Lambert law. Temperature change and phase transformation locally change the density of the sample and therefore reflect the dynamics in terms of the contrast in the image. This allowed the obtain of the spatiotemporal evolution of the melt pool/keyhole in the laser melting process. In our current work, DXR was used to examine the keyhole dynamics during the melting of a set of Ti-6Al-4V samples in the form of plates (with no powder added). To optimize the X-ray absorption contrast, all samples were prepared with dimensions of about 50 mm long, 3 mm tall, and 0.5 mm thick. The keyhole depth in this study was measured from the top of the substrate to the bottom of the keyhole.

Multiphysics modeling

The melt-pool modeling was performed with the FaSTLaB (FaST Lattice Boltzmann) metal powder bed fusion additive manufacturing code37 that has been previously validated by several physical tests as well as a direct comparison of simulated track morphologies with experimental data for alloys of Ni and Ti. The model includes full ray tracing with multiple reflections, phase transitions, and detailed liquid dynamics of the molten metal, influenced by the metal evaporation and the recoil pressure. Lattice Boltzmann Method is an efficiently parallelizable method that works best for low flow speeds (low Mach number) and quasi-incompressible processes. Metal vapor and cover gas dynamics, potentially important contributors to the melt pool physics in the keyhole regime, are not included in the current version of the simulations.

The geometry and dynamics of the melt-pool surface play key roles in metal PBF AM because they directly affect the laser energy deposition38. The ability to model, understand, and predict the effects of the beam oscillation at the melt-pool scale are expected to help with achieving combined high power and scan speed and provide guidance to practical applications of the enhanced process control capability. To test the model’s ability to adequately represent and predict the laser oscillation process, we have performed several simulations and comparisons of the model predictions with experimental results. All simulations were performed on a 3200 µm \(\times\) 960 µm \(\times\) 1920 µm (xyz) domain with a relatively coarse 10 µm space resolution and 100 ns time step.